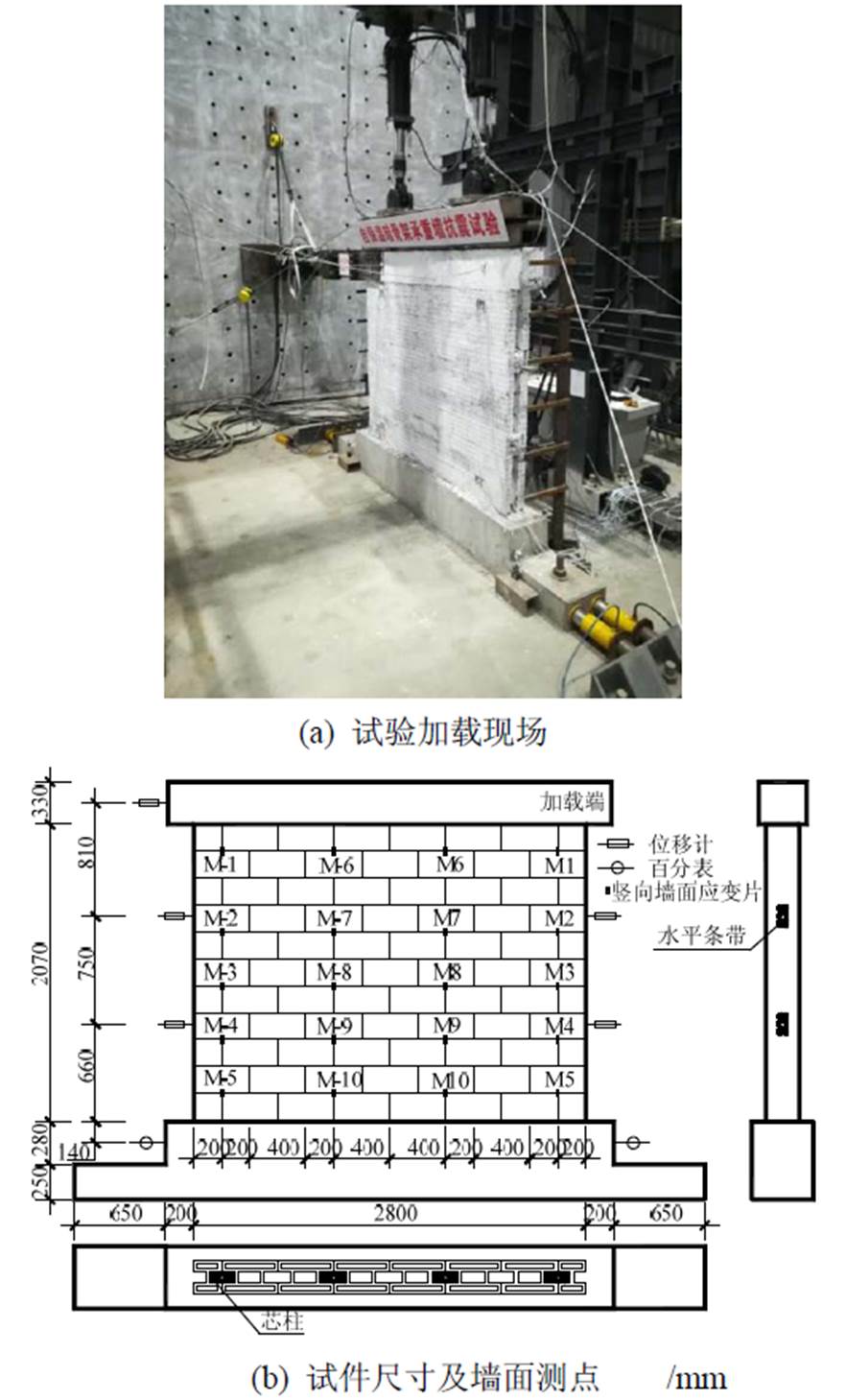
图1 试件尺寸及加载现场图
Fig.1 Specimen size and the overlooking of loading site
摘 要:从抗震节能一体化出发,研发了自保温暗骨架承重墙及其结构体系。通过水平低周反复荷载试验研究了自保温暗骨架承重墙的抗震性能,揭示了该新型抗震墙体受力机制的转化过程,即抗震失效全过程可分为共同工作、转化过渡和弱框架工作三个阶段。结合试验成果开展理论分析,针对自保温暗骨架承重墙剪切破坏模式,分别建立了基于等效弹性板模型的墙体开裂荷载计算方法和基于修正软化拉压杆模型的墙体抗剪极限承载力计算方法,与实测值相比误差分别是3.2%、3.3%,故构建的理论计算方法精度高、物理力学概念清晰。结果表明:自保温暗骨架承重墙具有多道抗震防线,抗震性能好,加之施工方便快捷、造价低廉,特别适宜在村镇住宅等多层建筑中推广应用。
关键词:自保温暗骨架承重墙;暗骨架约束系数;等效弹性板模型;修正软化拉压杆模型;抗震试验
针对村镇建筑广泛应用的混凝土空心砌块砌体结构在地震过程中暴露出的承载能力差、抗震防线薄弱等缺点[1―2],从抗震节能一体化出发,课题组研发了自保温暗骨架承重墙结构体系[3]。该结构体系使用三排孔混凝土小型空心砌块,通过在外侧双排填置秸秆压缩块提高结构保温隔热性能,实现自保温;通过在混凝土空心砌块及水平条带砌块的孔腔内浇筑混凝土分别形成芯柱、水平条带,整体浇筑的芯柱和水平条带组成暗骨架,至此形成自保温暗骨架承重墙;辅以梁、板等水平构件形成自保温暗骨架承重墙结构体系。课题组前期已对墙体的热工性能、静力性能进行了系统研究[4―5],然而针对其抗震性能仅进行了有限元模拟研究[6]。低周反复荷载因其具有评价指标明确以及试验过程可控性强等优点,被广泛应用于墙体抗震性能试验研究[7―8],在前期研究基础上,通过低周反复荷载试验揭示自保温暗骨架承重墙的失效机制,建立其抗震承载力计算方法尤为必要。
国内相关规范并未涉及配筋砌块砌体结构开裂荷载的计算方法,极限荷载则是采用建立在大量试验基础上选取偏下限值的经验方法,缺乏明晰的物理概念,且计算精度不高。由此,明晰构件间的相互作用机理,建立受力机制更加明确的承载力计算模型,成为近年来的研究热点[9―14]。而在配筋砌块砌体中引入承载力计算模型,多是在大量试验基础上,采用数据拟合的方法得到适用于不同砌体结构的参数值。此方法并未从模型建立内在逻辑上考虑不同砌体构件的相互作用机理,对于自保温暗骨架承重墙的承载力计算分析更未直接涉及。
基于上述研究,本文进行了足尺自保温暗骨架承重墙的低周反复荷载试验,旨在揭示自保温暗骨架承重墙受力机制的转化过程,定量评价内置暗骨架对墙体抗震性能的影响;在试验研究基础上,根据墙体不同组块间相互作用机理,提出自保温暗骨架承重墙理论计算模型,建立了墙体开裂荷载、极限承载力的理论求解方法。
以自保温暗骨架承重墙结构体系在村镇建筑中的应用为基础,选取某四层村镇住宅建筑底层墙体为试验研究对象。设计并砌筑的足尺试验模型如图1所示,试件总高2.97 m、宽2.8 m,其中底梁高0.53 m,墙体和顶梁分别高2.07 m、0.33 m。共布置4根芯柱,其中墙体两端各布置1根、墙中每隔0.8 m布置1根;水平条带沿墙体高度均匀布置两道,芯柱、水平条带内分别配置1根直径14 mm的HRB335级钢筋。
图2为试验所用全角、半角及U型砌块平面尺寸图,三种砌块的高度、厚度分别是190 mm、240 mm。暗骨架使用C30混凝土(根据预留混凝土试块测得的其抗压强度平均值为32.6 MPa,弹性模量为30 GPa)浇筑而成,混凝土小型空心砌块的强度等级为MU10(弹性模量为9 GPa)。试件底梁通过地脚螺栓及水平向千斤顶固定,能够确保试验加载时下部不发生移动、转动;试验水平向和竖向分别通过反力墙、竖向反力架提供反力,采用MTS电液伺服控制系统加载。

图1 试件尺寸及加载现场图
Fig.1 Specimen size and the overlooking of loading site
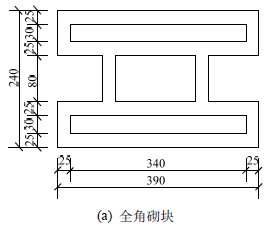
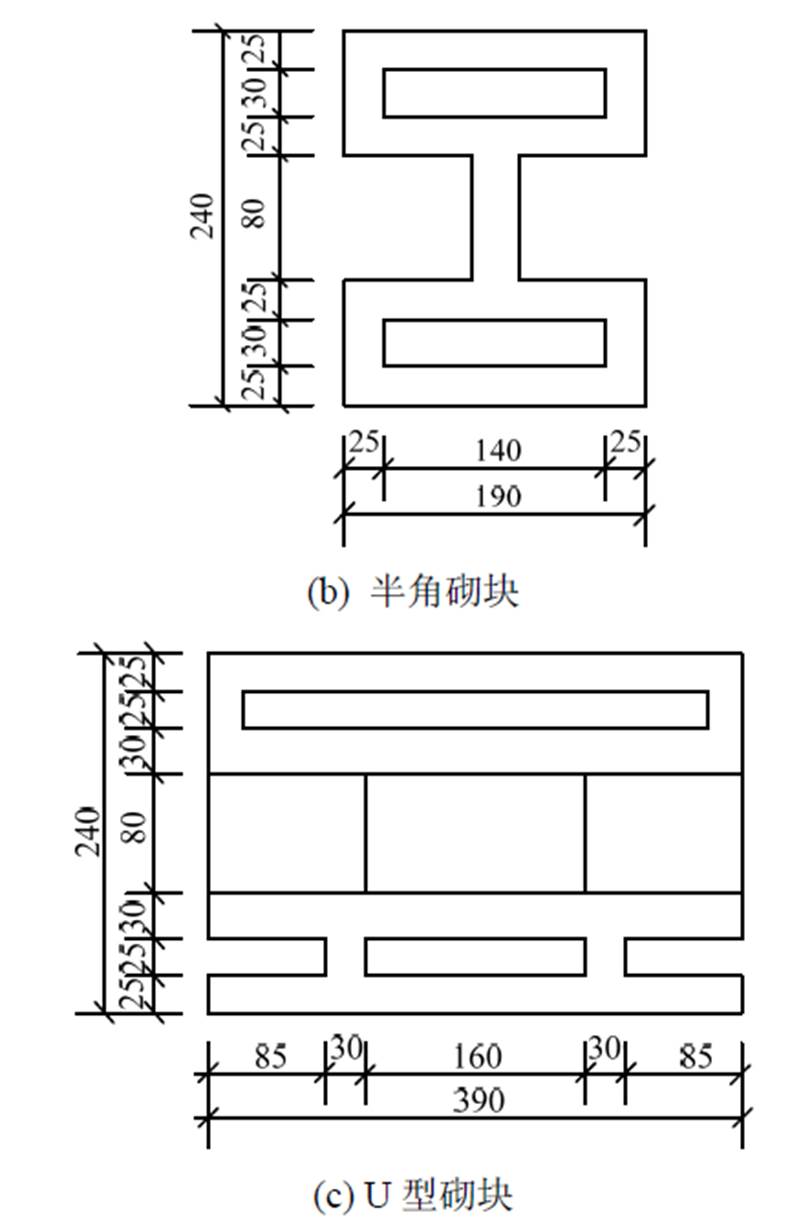
图2 砌块尺寸标注图 /mm
Fig.2 Block’s dimension drawings
试件在加载过程中采集的主要信息包括:水平作动器出力与位移、墙体表面与内置钢筋的应变、裂缝开展与发育过程、墙体侧向变形等。其中,加载端作动器出力与位移数据由MTS系统自动采集;墙体不同高度处的侧向变形采用位移计进行采集;裂缝采用“ZBL-F103裂缝宽度观测仪”进行观测。为了便于观察裂缝开展,尽量减轻试验过程中对应变片连接导线的扰动,试验中将墙面东侧作为应变片主要粘贴侧,相应的应变测点布置方式如图1(b)所示。为了便于观测裂缝开展对芯柱受力性能的影响,芯柱钢筋上的应变片设置在水平灰缝分布位置;水平条带钢筋的应变片则分布在暗骨架结点以及芯柱中点对应位置,如图3所示。为了判断墙体在不同破坏阶段暗骨架与砌块间的协同受力性能,特将墙面与对应芯柱钢筋的应变测点布置在同一高度位置。
本次试验使用MTS内置的MPE软件编写加载程序,考虑典型四层村镇住宅底层墙体承担的竖向压力并扣除墙体顶梁和刚性压梁的自重作用,首先使用力控方式将每个竖向作动器施加至55 kN并保持恒压至试验结束,对应墙顶竖向平均压应力为0.35 MPa,即底层墙体承受的上部荷载作用;然后施加水平低周反复荷载至墙体失效。水平荷载的施加采用力与位移双控制的混合加载方式,其中,力加载阶段以20 kN为级差每级循环加载1次,由于墙体屈服荷载难以精准把控,为了顺利完成力控到位移控制的加载过渡,当墙体出现第1道裂缝时(对应侧向位移为3.51 mm)即由力控制改为位移控制加载;位移加载阶段以4 mm的倍数为级差,当加载位移为12 mm时,承载力已下降至极限承载力的85%,试验可以结束,但为了得到墙体更为明显的失效破坏模式,进行了14 mm侧向位移加载。位移加载阶段每级均循环3次。
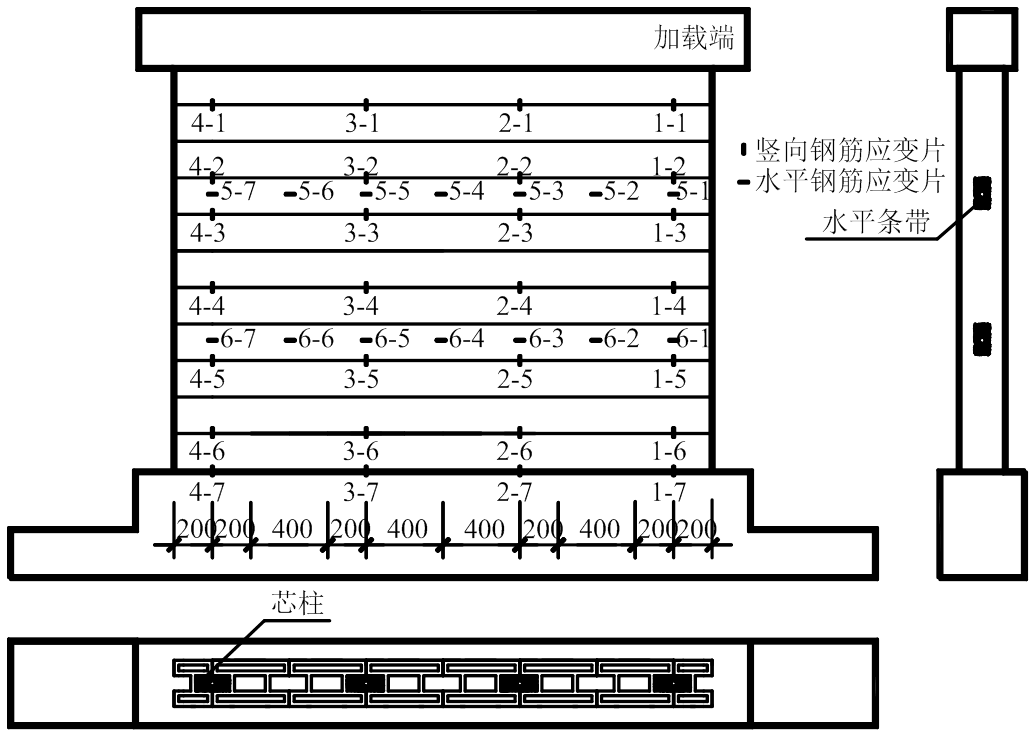
图3 钢筋应变片布置 /mm
Fig.3 Layout of the bar’s gauge
为准确描述试验现象,将水平作动器伸长时对应的水平力规定为正向,表示墙体受水平推力作用;反之为负向,表示墙体受水平拉力作用。
当水平力加载至负向170 kN时,在墙体右下角第2、第3皮(墙体皮数编号如图4所示标注)砌块上方各出现1道长度为0.6 m的水平灰缝裂缝。此时加载端水平位移为-3.51 mm,墙体开裂,加载方式由力控转为位移控制加载。
进入位移加载阶段墙体裂缝迅速开展,在±4 mm的位移加载步中,墙体上部的水平条带以下相互交叉的阶梯状裂缝基本形成,砌体第3、第6皮砌块上部水平灰缝迅速开裂发展,其中第6皮砌块上部水平裂缝基本贯通。
当位移加载至±8 mm时,墙体裂缝急剧开展,每加载到一个循环峰值时墙体均产生连续的嘶嘶声响。当荷载为第1级正向8 mm时,伴随着一声闷响墙体达到极限承载力255.9 kN(墙体在极限承载力破坏情况如图4所示);此加载阶段上部水平条带至墙体左、右下角的阶梯状裂缝完全形成,墙体在上部水平条带上方出现一小段随着荷载减小趋于闭合的阶梯状裂缝,第6皮、第3皮砌块上方(即水平条带下方)先后形成完全贯通的水平通缝,对应水平裂缝的最大宽度分别为1.15 mm (0 kN时裂缝宽度减小为0.4 mm)。

水平条带位置
图4 极限承载力时墙体的破坏
Fig.4 Failure of ultimate capacity
当位移加载至±12 mm时,裂缝宽度变化明显,承载力下降到极限承载力的85%,墙体进入破坏阶段,墙体两侧面于下部水平条带下方均出现贯通到底梁的竖向裂缝,最大裂缝宽度为9 mm。当位移加载至±14 mm时,第2皮砌块上方水平裂缝贯通,随着墙体左、右下角出现剪切破坏,砌块剥离、脱落现象明显,如图5所示;此时,墙体承载力迅速下降至155.6 kN,墙体失效,停止加载。
通过低周反复荷载试验,得到了该墙体的滞回曲线(图6),将墙体滞回曲线各级加载的承载力峰值点连接,即可得到图7所示骨架曲线,可见开裂荷载之前骨架曲线近似呈线性趋势;开裂荷载到极限荷载过程中墙体屈服,但承载力仍在增大;之后,承载力迅速下降,墙体逐渐失去承载力而破坏。

图5 墙体最终剪切破坏模式
Fig.5 Shear failure model of the wall

图6 滞回曲线
Fig.6 Hysteresis curve
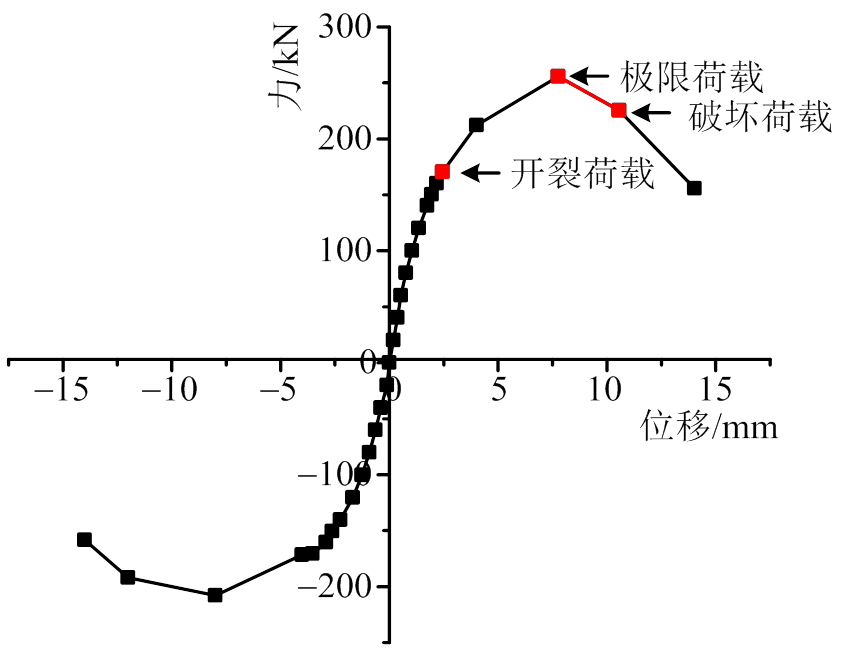
图7 骨架曲线
Fig.7 Skeleton curve
图8反映了墙体同一高度位置(三个位置:M8、M-4、M-10)在墙面及内置钢筋的应力(使用墙体砌块表面及钢筋实测应变值,分别乘以砌块、钢筋的弹性模量9 GPa、200 GPa得出)对比,墙体开裂前,两者应力增长速度基本相同;开裂到墙体达到极限承载力阶段,两者应力均迅速增加,但钢筋应力增长速度明显高于墙面砌块;达到极限荷载后,开裂区墙面应变片(M8、M-4位置)被拉坏,墙体表面的砌块开裂严重,砌块已逐渐退出承载,而钢筋应变减小幅度不明显;未开裂区墙面应变片(M-10位置)应变变化规律与对应位置钢筋基本一致,但钢筋承担的应力远高于墙面砌块,说明该阶段暗骨架作为第二道抗震防线已发挥主要作用。
依据上述分析,把开裂荷载、极限荷载作为分界点,将墙体破坏过程分为共同工作、转化过渡、弱框架工作三个阶段。
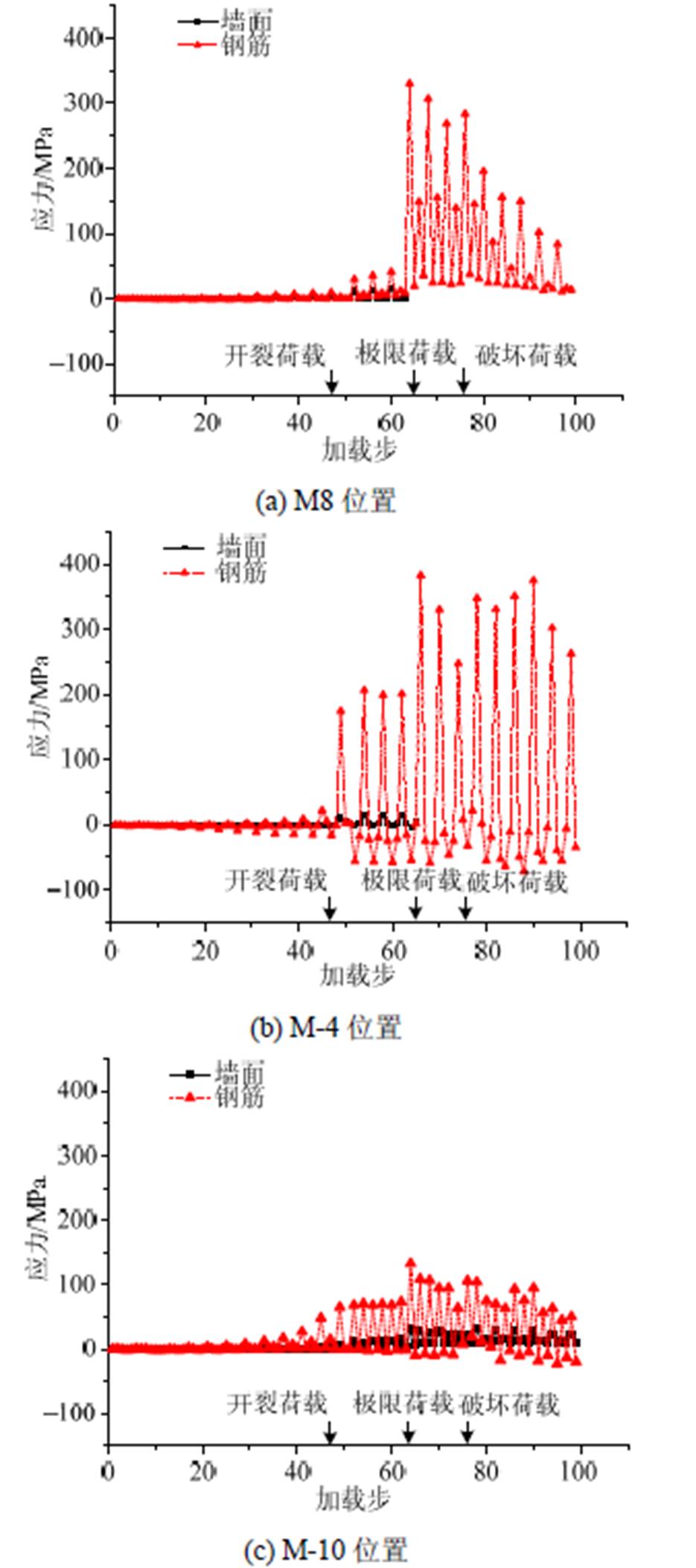
图8 墙面及相同高度位置钢筋的应力对比
Fig.8 The stress comparison between block and corresponding bar
1) 共同工作阶段
在水平荷载加至墙体开裂之前,墙体基本处于弹性受力状态,砌块与暗骨架之间具有较强的相互约束作用,共同承担墙体剪力,二者共同工作;该阶段墙体具有等效弹性板模型的受力特征。
通过每级正反向荷载绝对值之和与对应正反向墙顶位移绝对值之和的比值计算各时期墙体刚度[15],得到图9所示刚度退化曲线。分析可知,以开裂荷载为分界点,刚度退化速度在墙体开裂后明显快于开裂前,进一步验证墙体开裂前砌块与暗骨架之间的协同受力、共同工作特性。
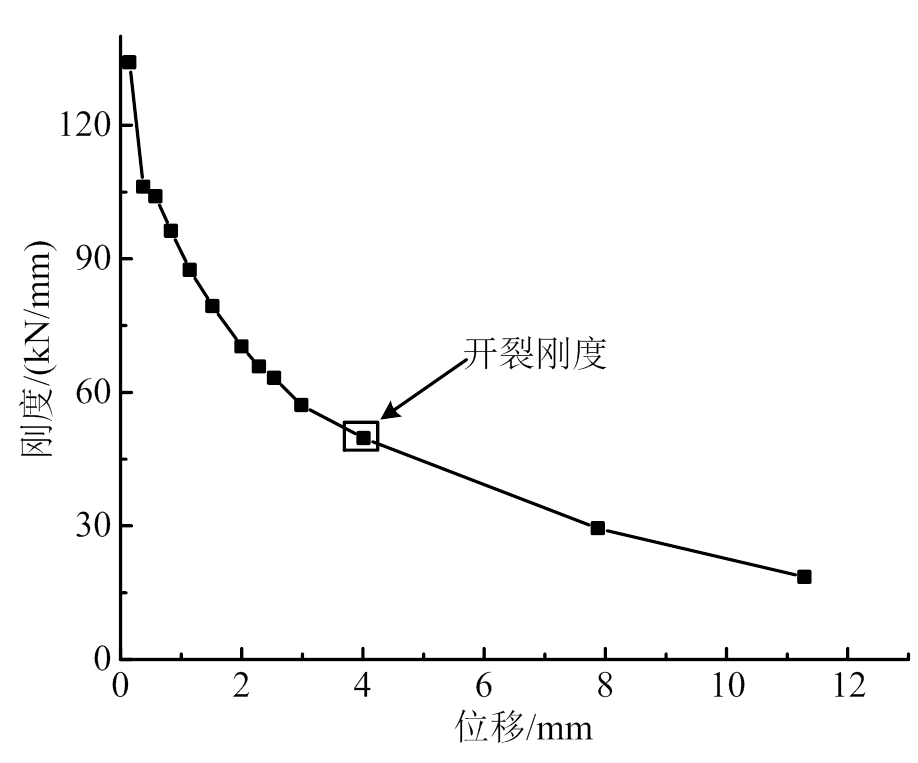
图9 刚度退化曲线
Fig.9 Stiffness degradation curve
2) 转化过渡阶段
墙体开裂至达到极限承载力这个过程定义为转化过渡阶段。随着墙面裂缝不断发展,墙体受力机制由砌块与暗骨架共同工作向暗骨架单独承担墙体荷载的弱框架体系转化,此阶段随着砌块承载作用的逐渐降低,暗骨架的存在使得墙体极限承载力大幅度提高。
该阶段墙体同一高度位置对应的墙面及钢筋应力迅速增长,然而钢筋应力增长的幅度明显高于墙面,说明二者承载均明显增加,但暗骨架已经明显开始取代砌块成为主要受力构件。图10反映不同加载阶段墙体侧向变形特征,以极限荷载为界,墙体的变形曲线由弯曲型转变为剪切型,开始表现出框架结构的变形特点,说明随着砌块逐渐退出工作,暗骨架单独承载的弱框架结构体系已逐渐形成。
3) 弱框架工作阶段
从墙体达到极限承载力到荷载降至极限荷载的85%(破坏荷载)这个过程称为弱框架工作阶段。此加载阶段,砌块作为承力构件的作用进一步减弱,暗骨架几乎承担了全部水平侧向荷载作用,实现了“坏而不倒”的抗震设防目标。
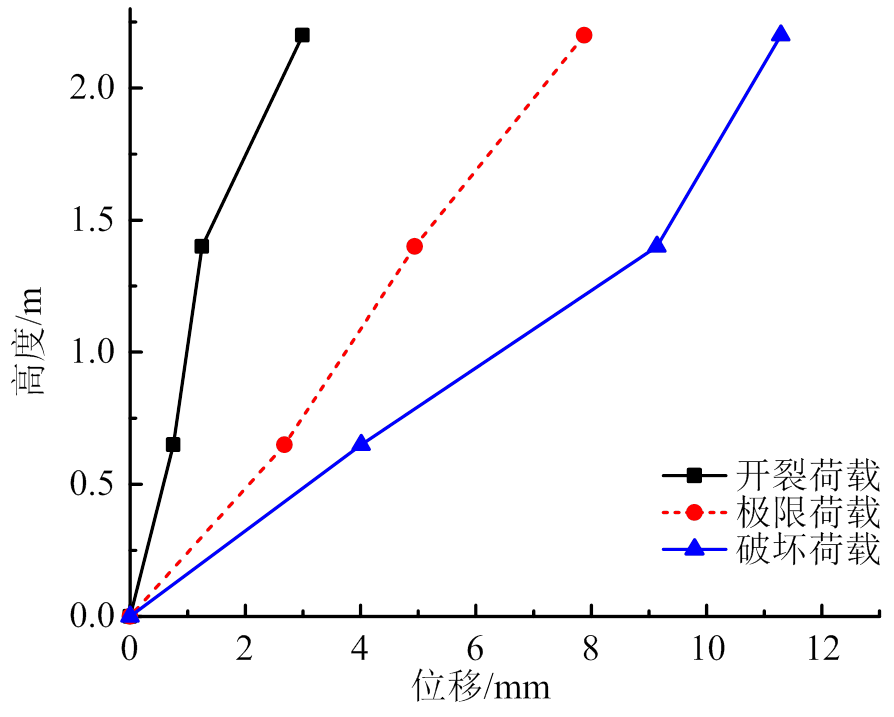
图10 墙体侧向变形曲线
Fig.10 Lateral deformation of the wall’s
综上分析可知,暗骨架与砌块之间良好的协同工作性能使墙体具备了建立软化拉压杆模型的理论分析基础。一方面,暗骨架的存在约束了砌块的剪切变形,提高了砌块承受反复拉压荷载的能力;另一方面,砌块填充在暗骨架之间,两者能够形成完整的传力压杆。暗骨架中的钢筋则承担了模型中拉杆的作用。此外,图5反映了墙体的最终破坏位于底部边脚处砌块压坏,该破坏模式与模型中压杆交汇处节点最终破坏的失效模式相吻合。
据钢筋进场试验报告,其屈服应变为1850 me。图11和图12分别反映了端部芯柱与中部芯柱钢筋应变随加载步的变化,测点位置如图3所示。其中1-5#和2-5#应变值均明显超过钢筋屈服应变,与该位置出现贯通且不断变宽的水平裂缝试验现象相吻合;其它位置的应变在墙体达到极限承载力时亦在钢筋屈服应变上下波动,但随着墙体承载力的下降钢筋应变又恢复到弹性范围以内。
图13反映的是下部水平条带内置钢筋应变测点实测应变随加载步的变化规律,不同于芯柱钢筋的应变特征,在墙体达到极限承载力之前该部分钢筋应变均很小,墙体进入破坏阶段之后钢筋应变突然增加,但其应变极限值仍小于钢筋屈服应变;上部水平条带钢筋应变规律与下部基本相同,但对应极限应变值更小。由此可知,水平条带自身承载能力利用程度较低。
通过试验现象可直观看出,上部水平条带限制了其上方墙面裂缝的发展,上方墙体塑性变形较小,在试验各阶段该部分墙体均具有较好的位移一致性,即共同工作性能。导致以上方水平条带(墙体1.4 m高度位置)为界,该界限以上墙体侧向变形曲线斜率基本不变,如图10所示。该区域裂缝并未充分开展影响了墙体耗能能力的进一步提高,故从耗能角度考虑,水平条带间距可适当增大。
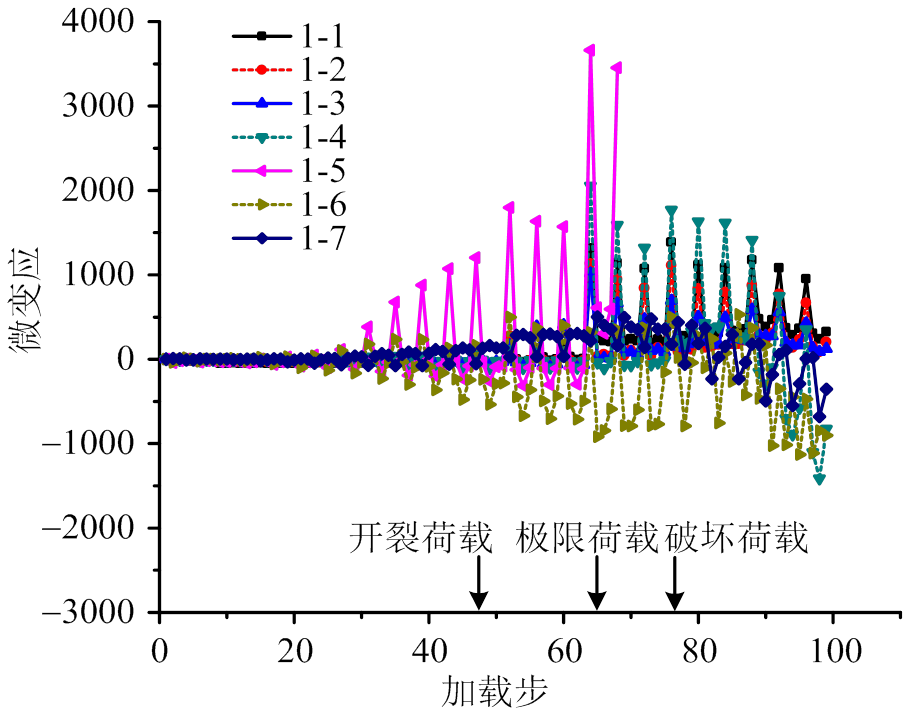
图11 1-1#至1-7#应变
Fig.11 Strain: 1-1# - 1-7#
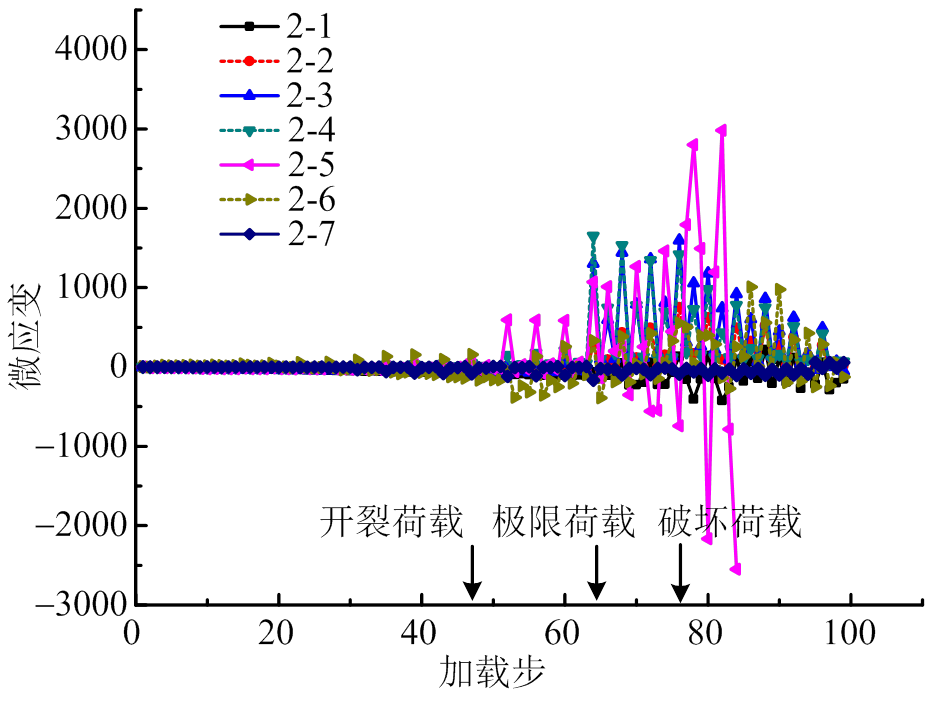
图12 2-1#至2-7#应变
Fig.12 Strain: 2-1# - 2-7#
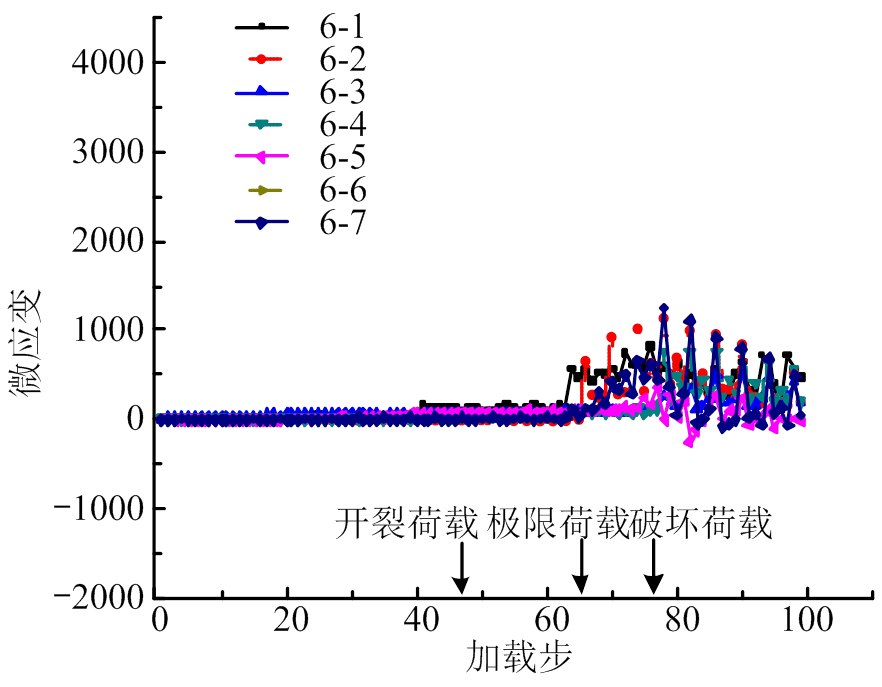
图13 6-1#至6-7#应变
Fig.13 Strain: 6-1# - 6-7#
综上分析可知,水平条带主要在共同工作、弱框架工作阶段发挥作用。一方面,在共同工作阶段,其与芯柱整浇形成的暗骨架与砌块相互约束、协同工作;另一方面,在弱框架工作阶段水平条带承载能力迅速增大,减缓了墙体阶梯型裂缝的开展及承载力的下降速度。但由于水平条带自身承载力的利用程度较低,并考虑其对墙体耗能性能的影响,建议布置间距可在每隔3皮砌块基础上有所增大。
上述关于试验结果的分析表明,墙体开裂前砌块与暗骨架处于共同工作状态,墙体表现为图14所示的等效弹性板模型受力特征。等效弹性板模型按平面应力问题考虑,将墙体开裂前视为弹性受力阶段,可按照线性叠加原理计算开裂荷载。根据双剪统一强度理论提出的开裂荷载计算公式[16],结合自保温暗骨架承重墙的受力特点,考虑暗骨架布置方式对墙体的约束影响面积,引入暗骨架约束系数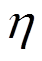 ,
,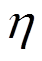 =m/n,m为暗骨架约束墙体面积;n为墙体总面积。根据暗骨架与不同砌块粘结作用的不同,m依据如下假定得到:1) 若芯柱从单一砌块的内置孔腔通过则影响整个砌块面积,若从两个砌块对接形成的孔腔通过则仅影响所通过区域的砌块面积;2) 水平条带影响其所在的U型砌块所占的面积。由于暗骨架内置在混凝土空心砌块的孔腔内,与砌块在开裂前表现出良好的共同工作性能,能显著提高墙体开裂荷载,故采用暗骨架混凝土的弹性模量Ec与砌块弹性模量Eb的比值反映开裂前暗骨架对其影响范围内墙体刚度的提高作用。综上,可得开裂荷载计算式(1):
=m/n,m为暗骨架约束墙体面积;n为墙体总面积。根据暗骨架与不同砌块粘结作用的不同,m依据如下假定得到:1) 若芯柱从单一砌块的内置孔腔通过则影响整个砌块面积,若从两个砌块对接形成的孔腔通过则仅影响所通过区域的砌块面积;2) 水平条带影响其所在的U型砌块所占的面积。由于暗骨架内置在混凝土空心砌块的孔腔内,与砌块在开裂前表现出良好的共同工作性能,能显著提高墙体开裂荷载,故采用暗骨架混凝土的弹性模量Ec与砌块弹性模量Eb的比值反映开裂前暗骨架对其影响范围内墙体刚度的提高作用。综上,可得开裂荷载计算式(1):
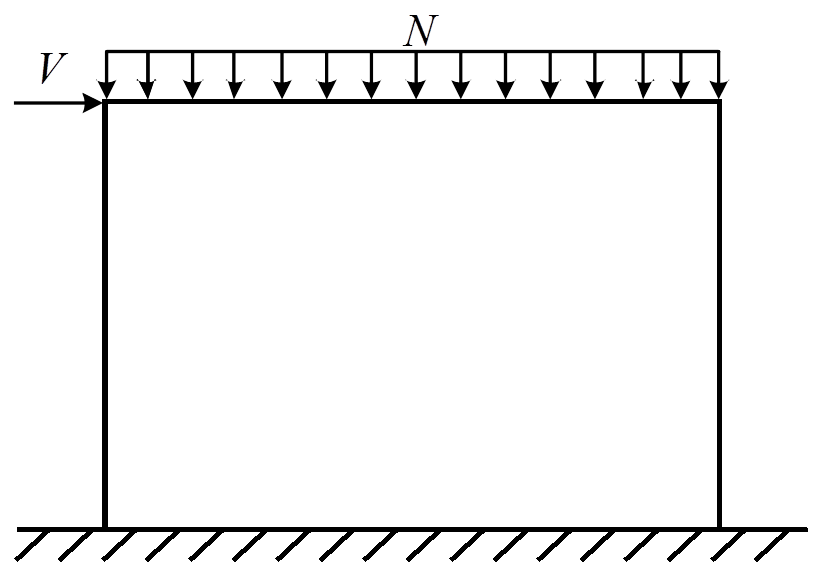
图14 等效弹性板模型
Fig.14 Equivalent elastic plate model
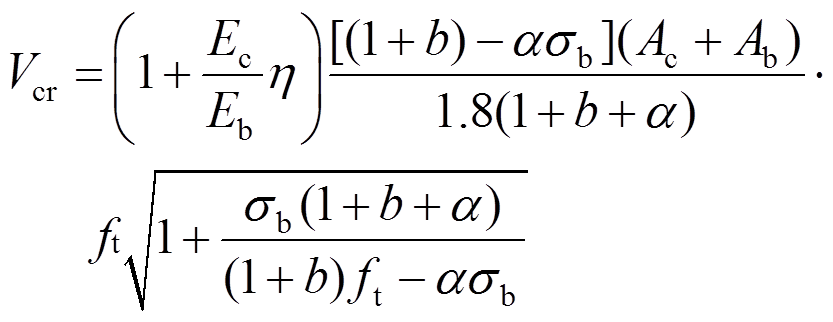 (1)
(1)式中: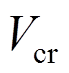 为墙体开裂荷载;
为墙体开裂荷载;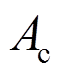 为暗骨架中芯柱混凝土截面积;
为暗骨架中芯柱混凝土截面积;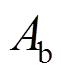 为砌块扣除孔洞的净截面面积;
为砌块扣除孔洞的净截面面积;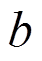 反映中间切应力及相应面上正应力对材料破坏强度的影响,取值0.5;
反映中间切应力及相应面上正应力对材料破坏强度的影响,取值0.5;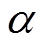 为砌块拉压强度比,取值0.1;
为砌块拉压强度比,取值0.1;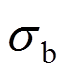 为砌块分担的竖向压应力;
为砌块分担的竖向压应力;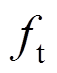 为砌块间灰缝的抗拉强度设计值。
为砌块间灰缝的抗拉强度设计值。
由开裂前共同工作阶段暗骨架混凝土与砌块在竖向应变的一致性,可得:
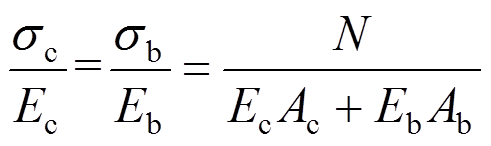 (2)
(2)由式(2)可得:
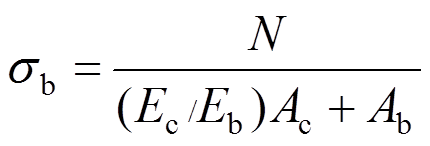 (3)
(3)
式中: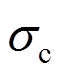 为暗骨架分担的竖向压应力;N为墙体承担的上部竖向压力;Ec和Eb取值见本文1.1节。
为暗骨架分担的竖向压应力;N为墙体承担的上部竖向压力;Ec和Eb取值见本文1.1节。
根据试验现象,墙体于右下角第2、3皮砌块上方各出现一道水平裂缝,分析其出现的原因为砌块间剪应力超过极限承载力,取ft=fv,fv为砌块实测抗剪强度平均值。故可根据文献[17]提出的抗剪承载力计算公式得到:
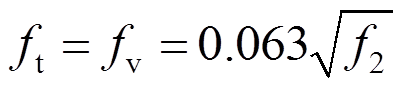 (4)
(4)式中:f2为砂浆抗压强度平均值,根据预留砂浆抗压强度试验,f2=15 MPa。
据上述方法,将模型各参数代入式(1),计算得到的开裂荷载为175.5 kN,与试验实测开裂荷载170.0 kN相比大3.2%。究其原因主要是理论计算中未考虑墙体开裂前往复循环加载引起构件内部损伤积累的降低作用,墙体施工制作等不确定性也是潜在的影响因素。
软化拉压杆模型[18]建立在经典桁架模型基础上,考虑应变协调关系及反复荷载作用下开裂混凝土的软化效应,适用于深梁、剪力墙(高宽比小于2)等不符合平截面假定的混凝土应力紊乱区受剪设计。结合前述试验结果的分析和图15所示的软化拉压杆模型分析可知,自保温暗骨架承重墙内置暗骨架中的水平、竖向钢筋构成拉杆,竖向芯柱和水平条带组成的暗骨架约束砌块承担了模型中压杆的作用。该模型能同时满足平衡方程、变形协调及材料本构关系,具有明确的物理概念,力学计算结果唯一,可应用于自保温暗骨架承重墙抗剪承载力的计算。但运用该模型求解受剪承载力需编写程序,反复迭代计算,求解过程的复杂性阻碍了其在实际工程中的推广应用[19]。为此,Hwang等[20]将软化拉压杆模型进一步简化,得到了混凝土应力紊乱区受剪极限承载力Vj的计算公式:
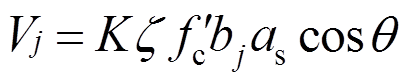 (5)
(5)式中:K为拉压杆系数; 为软化强度系数;
为软化强度系数;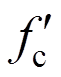 为砌块设计强度对应的圆柱体抗压强度;
为砌块设计强度对应的圆柱体抗压强度; 为斜压杆有效宽度;
为斜压杆有效宽度;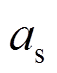 为斜压杆有效高度;
为斜压杆有效高度;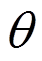 为墙体对角线与水平方向的夹角。
为墙体对角线与水平方向的夹角。
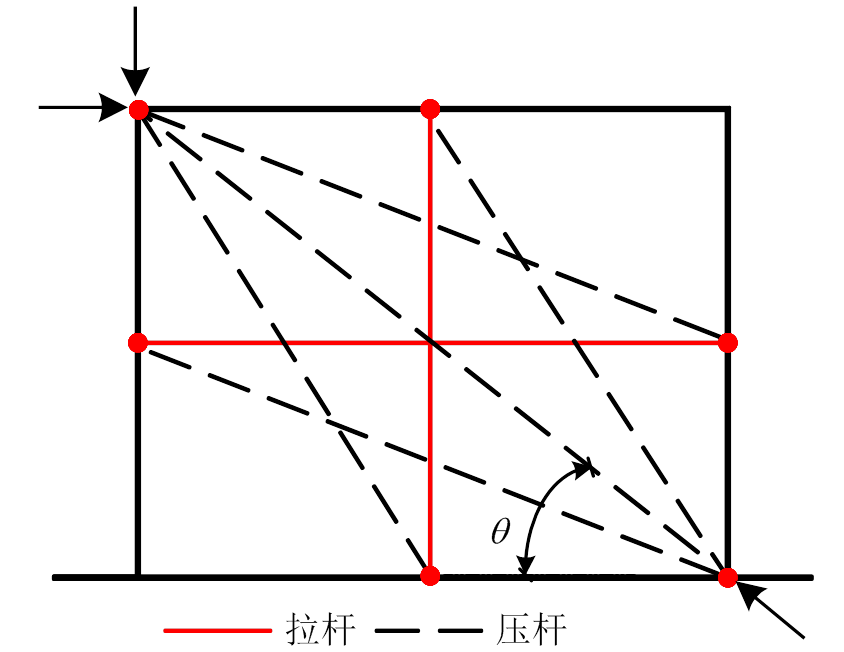
图15 软化拉压杆模型
Fig.15 Softened strut-and-tie model
前文已述,该模型最终破坏模式为墙体底部两侧边脚砌块在墙体表面被剪坏,对应位置暗骨架混凝土并未出现明显破坏。由此,结合暗骨架构造特点,自保温暗骨架承重墙可视为以砌块为基体,暗骨架作为约束连接体的连续砌体组合结构。同时,考虑到内置暗骨架对墙体产生的约束效应,引入暗骨架约束系数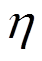 ,建立自保温暗骨架承重墙的修正软化拉压杆计算公式:
,建立自保温暗骨架承重墙的修正软化拉压杆计算公式:
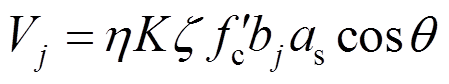 (6)
(6)需要指出的是,式(6)的适用条件是:自保温暗骨架承重墙发生剪切破坏模式。
试验测试结果表明,加载全过程暗骨架内置钢筋均未出现明显屈服,可认为模型中拉杆钢筋始终保持在弹性工作状态,故有:
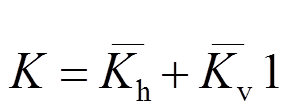 (7)
(7)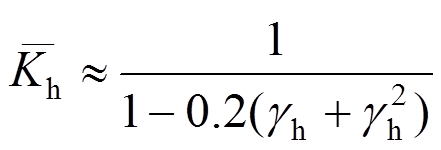 (8)
(8)
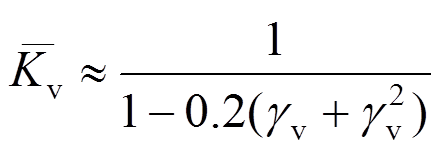 (9)
(9)
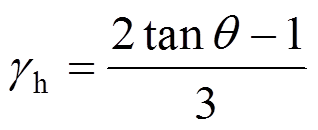 (10)
(10)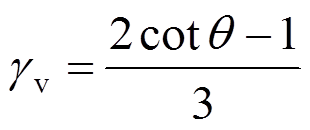 (11)
(11)
式中: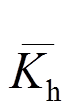 、
、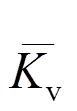 分别为弹性水平、弹性竖向拉杆指标;
分别为弹性水平、弹性竖向拉杆指标;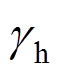 表示没有竖向拉杆时,水平拉杆承担的水平剪力系数;
表示没有竖向拉杆时,水平拉杆承担的水平剪力系数;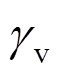 表示没有水平拉杆时,竖向拉杆承担的竖向剪力系数。
表示没有水平拉杆时,竖向拉杆承担的竖向剪力系数。
软化强度系数 的计算公式为:
的计算公式为:
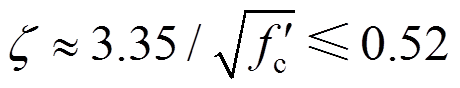 (12)
(12)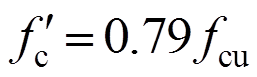 (13)
(13)
式中,fcu/MPa为砌块对应的抗压强度设计值。
取斜压杆有效高度as等于aw,aw为墙体受压区高度:
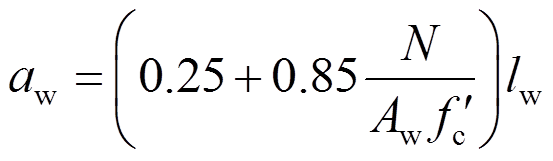 (14)
(14)式中,Aw、lw分别为墙体截面受压面积和高度。
图16所示为试验使用的三排孔砌块截面构造简图。由于砌块存在较大的孔洞率,斜压杆有效宽度 不能取整个砌块厚度,考虑暗骨架混凝土对砌块的粘结效应,
不能取整个砌块厚度,考虑暗骨架混凝土对砌块的粘结效应, 计算公式如下:
计算公式如下:
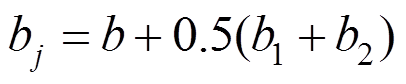 (15)
(15)
图16 砌块构造图 /mm
Fig.16 Block’s structure
根据本文建立的修正软化拉压杆模型,将模型参数代入式(6),计算所得抗剪极限承载力为247.4 kN,与试验抗剪极限承载力实测值255.9 kN相比,小3.3%。显然,计算精度高,满足工程实践抗震承载计算需求。
(1) 通过自保温暗骨架承重墙水平低周反复荷载试验,揭示了该新型抗震墙体受力机制的转化过程,即抗震失效全过程可分为共同工作、转化过渡和弱框架工作三个阶段;深入分析了暗骨架在各阶段参与墙体整体受力的工作机理,为承载力理论模型构建奠定了基础。
(2) 考虑暗骨架对墙体刚度的影响,借助双剪统一强度理论修正建立了墙体开裂荷载计算公式;根据墙体的构造特点及受力破坏特征,引入暗骨架约束系数,建立了适用于墙体的软化拉压杆模型,提出了其极限承载力计算公式并给出了该公式的适用条件。开裂荷载、极限荷载的理论计算结果与实测结果相比,误差分别是3.2%、3.3%,公式求解精度高、物理概念清晰。
(3) 暗骨架作为第二道抗震防线保证了墙体能够满足“坏而不倒”的抗震设防目标,水平条带布置间距可在现有基础上有所增大。试验与理论分析表明,自保温暗骨架承重墙具有良好的抗震性能,加快其推广应用对于增加村镇建筑结构安全性具有重要意义。
参考文献:
[1] 姚新强, 孙柏涛, 王明振, 等. 我国农村典型砖砌体墙片拟静力试验研究[J]. 工程力学, 2017, 34(6): 198―209.
Yao Xinqiang, Sun Botao, Wang Mingzhen, et al. Study on the pseudo-static tests of typical brick masonry walls in rural China [J]. Engineering Mechanics, 2017, 34(6): 198―209. (in Chinese)
[2] 谭平, 徐凯, 刘晗, 等. 村镇建筑新型简易隔震技术研究[J]. 工程力学, 2017, 34(增刊1): 233―238.
Tan Ping, Xu Kai, Liu Han, et al. Study of new seismic isolation technology for rural buildings [J]. Engineering Mechanics, 2017, 34(Suppl 1): 233―238. (in Chinese)
[3] 刘福胜, 崔兆彦, 武义馨, 等. 一种自保温暗骨架承重墙结构[P]. 中国, ZL201520227613. 9, 2015. Liu Fusheng, Cui Zhaoyan, Wu Yixin, et al. A kind of self-insulating structural wall with inner skeleton [P]. China, ZL201520227613.9, 2015.(in Chinese)
[4] Hou Shaodan, Liu Fusheng, Wang Shaojie, et al. Coupled heat and moisture transfer in hollow concrete block wall filled with compressed straw bricks [J]. Energy and Buildings, 2017, 135: 74―84.
[5] 周涛, 王少杰, 刘福胜, 等. 混凝土夹心秸秆块砌块砌体偏心受压承载力试验研究[J]. 建筑科学, 2017, 33(9): 65―70.
Zhou Tao, Wang Shaojie, Liu Fusheng, et al. Experimental study on the eccentric compressed bearing capacity of hollow concrete block filling with compressed straw bricks [J]. Building Science, 2017, 33(9): 65―70. (in Chinese)
[6] 孙雷, 刘福胜, 王少杰, 等. 短周期村镇砌体建筑振动特性实测与抗震性能分析[J]. 土木工程学报, 2013, 46(增刊2): 57―62.
Sun Lei, Liu Fusheng, Wang Shaojie, et al. Dynamic characteristic test and seismic performance analysis of short-period masonry [J]. China Civil Engineering Journal, 2013, 46(Suppl 2): 57―62. (in Chinese)
[7] Wilding B V, Dolatshahi K M, Beyer K. Influence of load history on the force-displacement response of in-plane loaded unreinforced masonry walls [J]. Engineering Structures, 2017, 152: 671―682.
[8] Messali F, Metelli G, Plizzari G. Experimental results on the retrofitting of hollow brick masonry walls with reinforced high performance mortar coatings [J]. Construction and Building Materials, 2017, 141: 619―630.
[9] 蔡勇. 砌体在剪-压复合作用下抗震抗剪强度分析[J]. 建筑结构, 2011, 41(2): 74―77.
Cai Yong. Analysis on aseismic shear strength of masonry under shear-compression composite action [J]. Building Structure, 2011, 41(2): 74―77. (in Chinese)
[10] Morfidis K, Kostinakis K. The role of masonry infills on the damage response of R/C buildings subjected to seismic sequences [J]. Engineering Structures, 2017, 131: 459―476.
[11] Edri I E, Yankelevsky D Z. An analytical model for the out-of-plane response of URM walls to different lateral static loads [J]. Engineering Structures, 2017, 136: 194―209.
[12] 郭猛, 袁泉, 常鹏, 等. 基于水平薄弱层破坏准则的密肋复合墙受剪承载力计算[J]. 建筑结构学报, 2012, 33(9): 148―153.
Guo Meng, Yuan Quan, Chang Peng, et al. Calculation method for shear bearing capacity of multi-grid composite wall based on horizontal weak-layer failure criteria [J]. Journal of Building Structures, 2012, 33(9): 148―153. (in Chinese)
[13] Ghaisas K V, Basu D, Brzev S, et al. Strut-and-Tie model for seismic design of confined masonry buildings [J]. Construction and Building Materials, 2017, 147: 677―700.
[14] Furtado A, Rodrigues H, Arêde A. Modelling of masonry infill walls participation in the seismic behaviour of RC buildings using OpenSees [J]. International Journal of Advanced Structural Engineering, 2015, 7(2): 117―127.
[15] 刘文锋, 王来其, 高彦强, 等. 高强钢筋混凝土框架抗震性能试验研究[J]. 土木工程学报, 2014, 47(11): 64―74.
Liu Wenfeng, Wang Laiqi, Gao Yanqiang, et al. Experimental study on seismic behavior of high-strength reinforced concrete frame [J]. China Civil Engineering Journal, 2014, 47(11): 64―74. (in Chinese)
[16] 黄炜, 陈国新, 姚谦峰, 等. 基于统一强度理论的密肋复合墙体开裂荷载计算[J]. 工程力学, 2008, 25(7): 94―99.
Huang Wei, Chen Guoxin, Yao Qianfeng, et al. Calculation on cracking load of multi-ribbed composite wall based on twin shear unified strength theory [J]. Engineering Mechanics, 2008, 25(7): 94―99. (in Chinese)
[17] 武义馨, 刘福胜, 赵井辉, 等. 新型节能承重砌块砌体抗剪强度试验研究[J]. 混凝土与水泥制品, 2016(3): 67―70.
Wu Yixin, Liu Fusheng, Zhao Jinghui, et al. Experimental study on shear strength of new energy-saving and load-bearing block masonry [J]. China Concrete and Cement Products, 2016 (3): 67―70. (in Chinese)
[18] Hwang S J, Fang W H, Lee H J, et al. Analytical model for predicting shear strength of squat walls [J]. Journal of Structural Engineering, 2001, 127(1): 43―50.
[19] 邢国华, 刘伯权, 牛荻涛. 钢筋混凝土框架中节点受剪承载力计算的修正软化拉压杆模型[J]. 工程力学, 2013, 30(8): 60―66.
Xing Guohua, Liu Boquan, Niu Ditao. Shear strength of reinforced concrete frame joints using modified softened strut-and-tie model [J]. Engineering Mechanics, 2013, 30(8): 60―66. (in Chinese)
[20] Hwang S J, Lee H J. Strength prediction for discontinuity regions by softened strut-and-tie model [J]. Journal of Structural Engineering, 2002, 128(12): 1519―1526.
SEISMIC EXPERIMENT AND THEORETICAL ANALYSIS ON SELF-INSULATING STRUCTURAL WALLS WITH INNER SKELETON
Abstract: A self-insulating structural wall with inner skeleton and its structural system were designed for realizing the integration of anti-seismic and energy-saving performance. A horizontal low-cyclic load test was conducted to investigate the wall’s seismic performance, and it revealed the transformation process of the wall’s failure mechanisms. Accordingly, the failure process was divided into three stages, including common working stage, transition stage and weak frame working stage. This study proposed cracking load and ultimate capacity formulas based on the wall’s final failure mode and theoretical analysis of the test results. The two formulas were respectively established on the basis of the elastic equivalent model and the modified softened strut-and-tie model. The relative errors between theoretical analysis and test results were 3.2% and 3.3%, respectively, indicating the theoretical formulas have a clear physical significance and an adequate level of accuracy. Additionally, the experiment results verified the wall’s superiorities, including seismic behavior, construction convenience and economic performance. The wall is well-suitable for application in multi-story residential buildings such as villages and towns.
Key words: self-insulating structural wall with inner skeleton; inner skeleton constraint coefficient; elastic equivalent model; modified softened strut-and-tie model; seismic experiment
文章编号:1000-4750(2019)04-0158-09
中图分类号:TU365
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.02.0093
收稿日期:2018-02-02;
修改日期:2018-06-21
基金项目:山东省自然科学基金项目(ZR2017BEE022);国家自然科学基金项目(51708115);中国博士后科学基金面上项目(2017M622239)
刘福胜(1964―),男,山东潍坊人,教授,工学博士,博导,从事结构工程、工程力学等研究(E-mail: liufsh@sdau.edu.cn);
岳艺博(1992―),女,河北张家口人,硕士生,从事新型砌体结构抗震研究(E-mail: mysyyb@163.com);
刘 康(1992―),男,山东济宁人,硕士生,从事结构抗震研究(E-mail: 765189209@qq.com);
黄兴淮(1986―),男,江苏淮安人,讲师,工学博士,从事结构抗震与振动控制研究(E-mail: huangxh@seu.edu.cn).