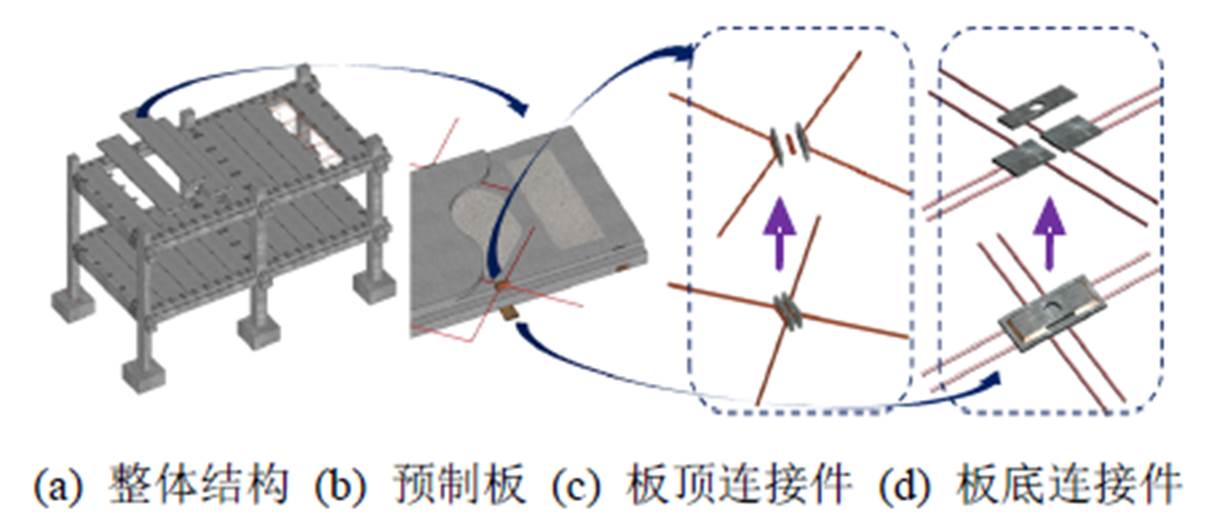
图1 DCNPD体系示意图
Fig.1 Schematic diagram of DCNPD
摘 要:在分布式连接新型全装配RC楼盖中,板与板之间通过连接件连接实现横板向传力。为研究新型楼盖竖向承载力计算方法,进行了新型楼盖在竖向荷载作用下的内力与变形分析。结果表明:基于正交各向异性弹性薄板小挠度理论和单三角级数法得到四边简支新型楼盖在竖向均布荷载作用下的弯矩与挠度表达式,提出了新型楼盖横板向刚度计算方法,并通过与试验和有限元结果对比,验证了所提方法的准确性;新型楼盖的挠度在两个方向呈空间抛物面分布,表明新型楼盖具有良好横板向传力性能;板缝连接可有效传递板内弯矩,但正交的两个方向弯矩传递效果存在差异,表现为顺板向弯矩的传递效果优于横板向。研究成果可为分布式连接全装配RC楼盖的研究和应用提供参考。
关键词:分布式连接;全装配式RC楼盖;板缝连接;横板向刚度;竖向承载力
楼(屋)盖是建筑结构的重要组成部分,在采用装配式RC楼盖的建筑结构抗震设计方面,较为统一的观点是基于弹性楼盖的抗震设计方法[1]。当前,我国主要采用叠合式楼盖,研究表明[2]:叠合式楼盖拼缝处混凝土在温度和体积收缩作用下常产生裂缝;对于同时采用机械连接件和后浇层的楼盖,混凝土开裂后板缝平面内承载力和刚度迅速降低到仅有机械连接件时的水平。Baran[3]研究发现,叠合层可提高楼盖竖向初始刚度和开裂荷载,但在达到极限荷载前叠合作用已丧失。Hawkins和Ghosh[4]指出:如果存在一种合理的方案替代现浇层里的钢筋来传递预制板之间内力,那么采用干式连接的弹性楼盖与叠合式弹性楼盖的在传递水平地震作用上是没有本质区别的。美国和日本等国家已将诸如“SP”板(SpanCrete)的干式楼盖应用于多高层建筑,并经受了1994北岭地震和1995年阪神大地震的考验[4]。
国外应用较多的干式楼盖为双T板楼盖,板-板之间、梁(墙)-板之间采用分布式机械连接件连接[5]。这种装配式双T板楼盖已经在我国长春一汽停车楼等工程中得到应用[6]。但一汽停车楼在双T板上方增加了80 mm后浇层,以满足我国规范要求(叠合厚度≥60 mm)[7]。
双T板楼盖可满足重载、大跨等现代楼盖的设计要求,但板底不平整、结构高度大,适用范围有限。因此,需拓展干式楼盖的应用形式,开发新型楼盖体系。根据国内外规范对装配式楼盖受力和抗震性能的要求,庞瑞等[8]研发了基于分布式连接的新型全干式RC楼盖体系(Discrete Connected New-type Precast Diaphragms (DCNPD)),并通过楼盖平面内受力性能和竖向承载能力等试验验证了楼盖具有良好的平面内刚度和竖向承载能力[9―10]。DCNPD是以预制企口平板和挑耳梁(墙)为基本构件,梁(墙)-板之间和板-板之间采用上下匹配的分布式机械连接件连接的全干式楼盖体系,如图1所示。

图1 DCNPD体系示意图
Fig.1 Schematic diagram of DCNPD
DCNPD研发的理念是:在水平荷载作用下,板缝连接节点可传递楼盖平面内剪力和弯矩,提高楼盖的平面内刚度(隔板作用)和整体性;在竖向荷载作用下,板底和板顶连接件形成力偶可传递横板向的弯矩(双向传力)、企口传递竖向剪力;梁(墙)-板连接可传递一定的负弯矩,提高楼盖的承载力和刚度。
板缝连接节点采用上企口为发卡式连接件(抗剪性能好),下企口为盖板式连接件(兼顾平面内抗剪和平面外抗弯,通过开口尺寸与焊缝设计实现与发卡式连接件强(刚)度匹配,发挥最大效用)的发卡-盖板混合式板缝节点。板缝连接节点详图如图2所示。
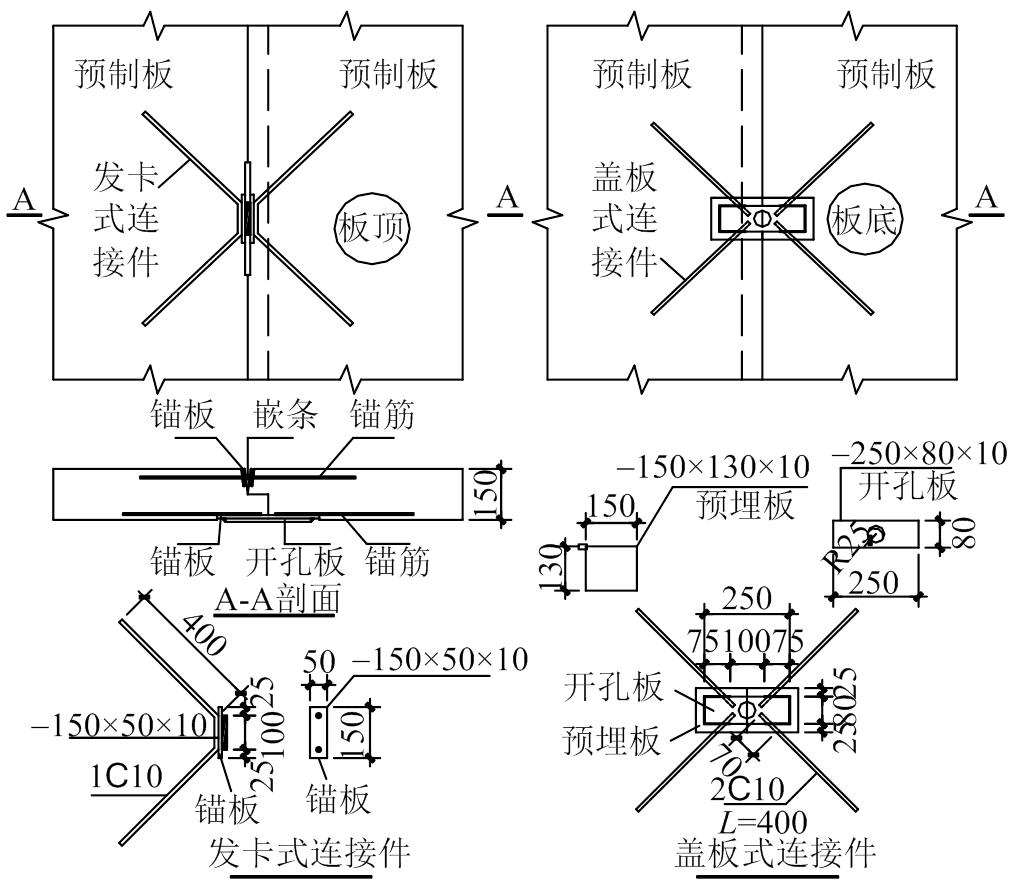
图2 板缝连接节点大样图 /mm
Fig.2 Details of slab joint connection
在叠合式楼盖结构中,对于底板为预制混凝土薄板的楼盖,当板内横向钢筋进行搭接连接的,可按普通双向板设计[11―13];而对于预制底板为预制空心板的楼盖,大多将加强其整体性和抗渗性的现浇层作为面载,而未考虑现浇混凝土和空心板的共同作用[14―15]。对于叠合式双T板楼盖,叠合层亦作为自重的一部分考虑[5];对于全干式双T板楼盖,其板缝连接形式与DCNPD相似,但在双T板楼盖中,仅考虑板缝的平面内传力作用,未考虑应力在横板缝方向的传递。
试验表明[10],板缝处上下匹配布置的连接件可传递横板向弯矩和竖向剪力,使得DCNPD具有双向受力性能,提高了楼盖的竖向承载力和刚度。但横板向抗弯刚度小于顺板向刚度,属于正交异性板范畴,其承载力计算方法尚不明确。鉴于此,本文以DCNPD竖向承载力机理为研究对象,研究基于分布式连接件连接的全装配RC楼盖竖向承载力与变形计算方法,为该类楼盖的研究与应用提供参考和依据。
钢筋混凝土板的线弹性分析是基于板开裂之前的状态,混凝土处于弹性,钢筋应力很小。可通过弹性力学理论,建立板的平衡微分方程,得到正常使用状态下的弯矩与挠度分布的规律。由于弹性理论弯矩是混凝土板极限承载力的下限值,目前我国《混凝土结构设计规范》(GB 50010―2010)[16]和美国ACI规范[17]中均包含以板的弹性弯矩作为截面配筋依据的方法。对板弹塑性阶段的承载力和刚度的分析,主要是以弹性分析结果为基础,再进行一定的修正。
竖向荷载作用下,在纵横两个方向弯曲且都不能忽略的板称为双向板。双向板楼盖具有承载力高和刚度大的优点,是较为普遍采用的楼盖结构形式。在四边支承板中,截出任意两个相互垂直单位宽度板带进行分析,如图3所示。
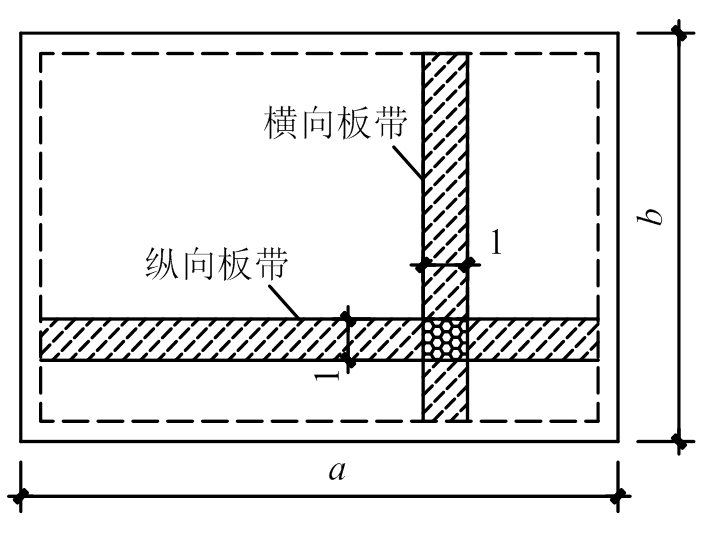
图3 双向板计算示意图
Fig.3 Analysis schematic of two-way slab
在竖向荷载作用下,受到相邻板带约束,使得实际位移和弯矩比按独立板带计算值减小。两个相邻板带的竖向位移是不相等的,在相邻板带之间存在着竖向剪切力。这种竖向剪切力构成了扭矩,而扭矩的存在减小了按独立板带计算的弯矩值。通常,可将双向板的弯矩计算简化为按独立板带计算的弯矩乘以小于1的修正系数来考虑扭矩的影响。
当板厚远小于板短边边长的1/30,且挠度远小于板厚时,钢筋混凝土双向板可基于弹性薄板小挠度理论[18],根据不同边界条件,计算挠度与弯矩弹性系数进行双向板设计。DCNPD板缝连接使其在横板向和顺板向受力性能存在较大差异,不能直接采用《建筑结构静力计算手册》[19]进行计算,本文尝试基于弹性薄板小挠度理论并考虑两个方向受力性能的差异进行楼盖竖向承载力分析。
1.1.1 基本假定
求解满足所有弹性理论的薄板微分方程比较困难,可采用变形几何假定,将薄板的弯曲变形分析简化为二维问题。具体如下[20-22]:
1) 弯曲后中面保持无应变,不计垂直于中面方向线应变εz,即横向位移w只是x和y的函数,不随z而变;2) 垂直中面的初始平截面,在中面弯曲后保持为平面并与中面垂直;3) 垂直于中面的应力分量τxz、τyz、σz远小于其余三个应力分量,它们引起的形变可忽略,即中面的法线在薄板弯曲时保持不伸缩,并成为弹性曲面的法线;4) 薄板中面内的各点都没有平行于中面的位移,即(u)z=0=0,(v)z=0=0。
1.1.2 微分方程的建立
由于位移很小,位移对力作用点的影响可忽略,可将微小隔离体上的内力向中面简化,来考虑其平衡条件。假设正交各向异性板边缘分别平行于弹性方向,其坐标系如图4所示。
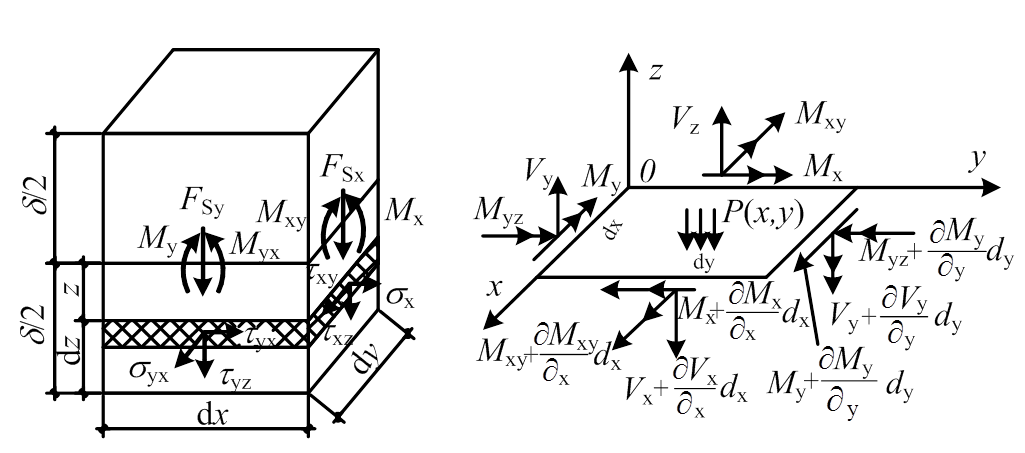
图4 薄板微元体力素示分布示意图
Fig.4 Force distribution in thin plate micro unit
由在z方向的主矢平衡条件,得:
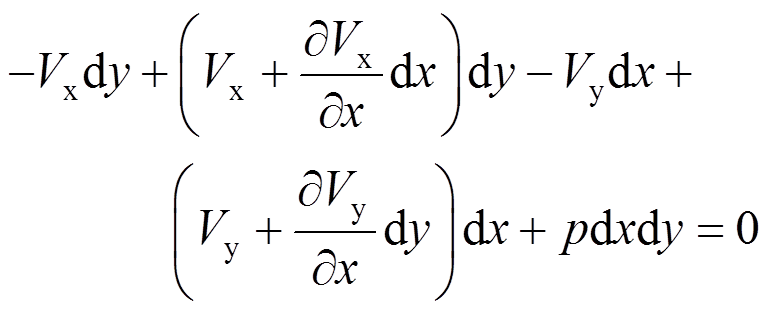
整理得:
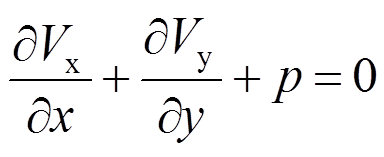 (1)
(1)
由绕y轴的主矩平衡条件 My=0,略去高阶微量整理得:
My=0,略去高阶微量整理得:
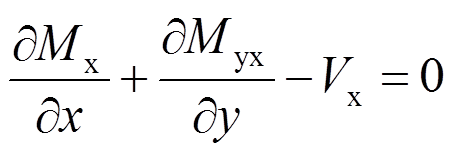 (2)
(2)同理,由绕x轴的主矩平衡条件 Mx=0,得:
Mx=0,得:
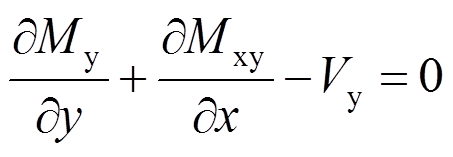 (3)
(3)
由式(2)得:
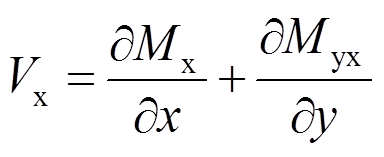 (4)
(4)由式(3)得:
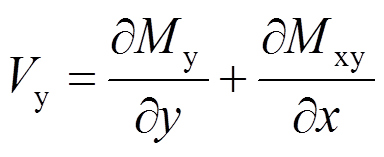 (5)
(5)
将式(4)、式(5)代入式(1)得:
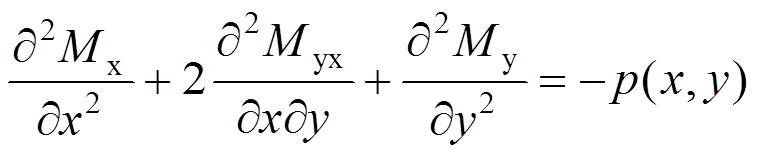 (6)
(6)板挠曲后产生x、y、z三个方向的变形为u、v、ω。板截面上某点的纵向伸长为u或v到中性面的距离为z。u、v与挠度ω的几何关系为:
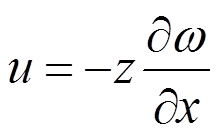 ,
,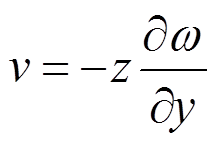
应变分量与ω的关系为:
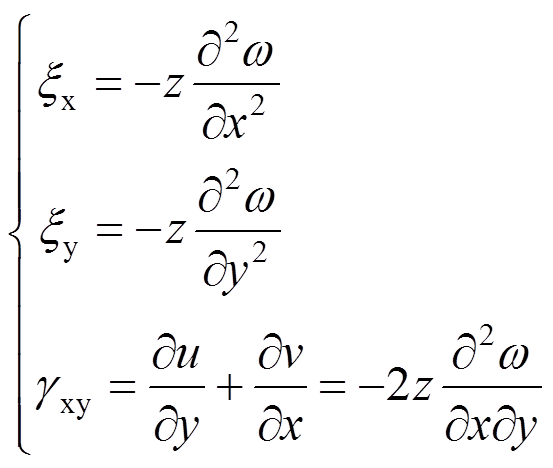 (7)
(7)对于线弹性各向同性体,由二维广义虎克定律:
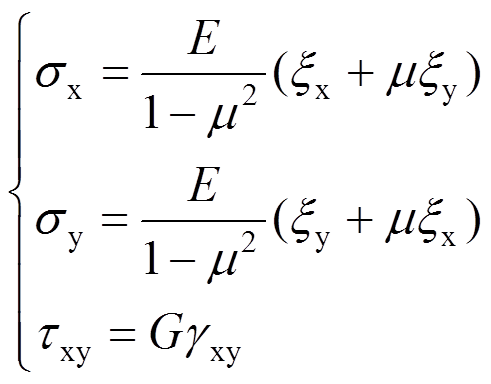 (8)
(8)
式中:G、E为剪切和弹性模量;μ为泊松比。
将式(7)代入式(8)可得用挠度ω的表示的应力关系式:
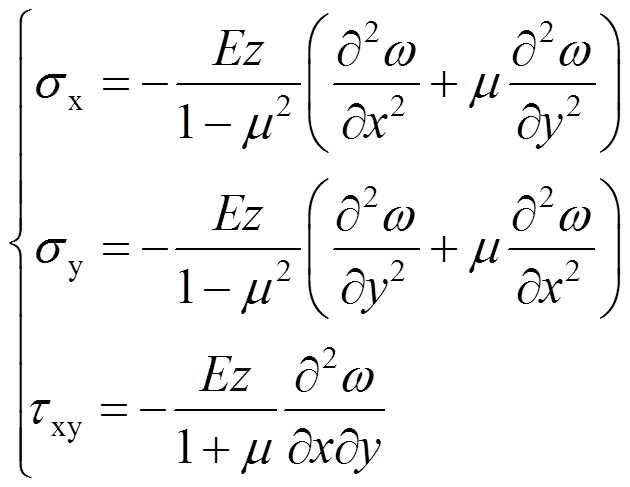 (9)
(9)板壳理论中规定,所有内力均指单位中面长度的力值,因此,单位中面长度的弯矩Mx为:
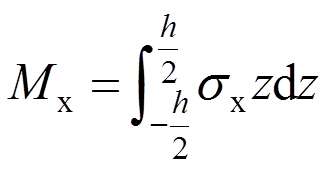
同理: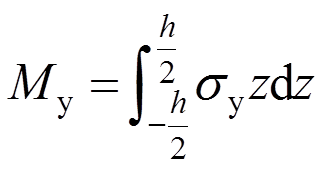 ,
,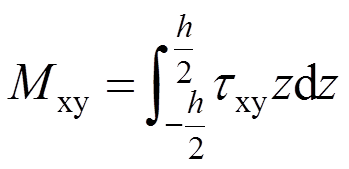
将式(9)代入整理可得:
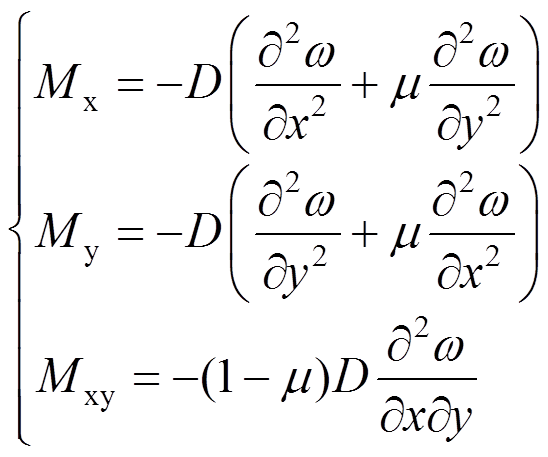 (10)
(10)式中:D为板的抗弯刚度,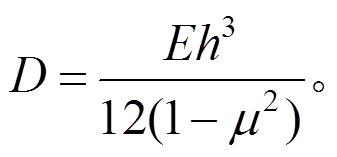
对于线弹性各向异性体,可得:
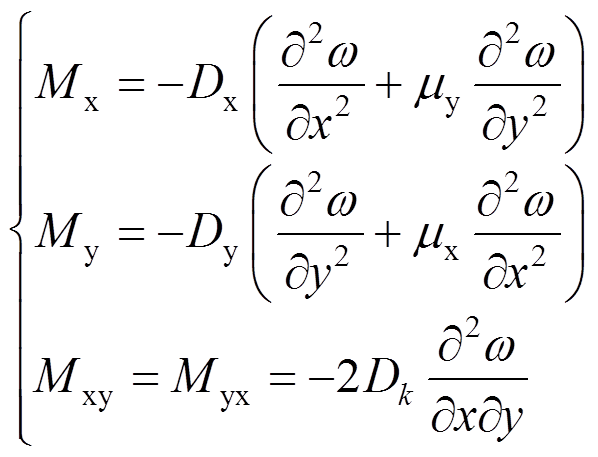 (11)
(11)式中:Dx为x向弯曲刚度;Dy为y向弯曲刚度;Dk为扭转刚度;μy为y方向的泊松比;μx为x方向的泊松比。
将式(11)代入式(6)可得到用挠度ω表示的薄板小挠度弯曲基本平衡方程为:
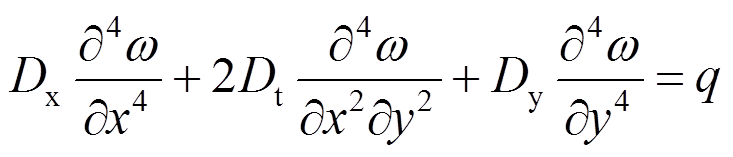 (12)
(12)式中,Dt为等厚度双向板的有效抗扭刚度。
根据主矢和主矩平衡条件可得:
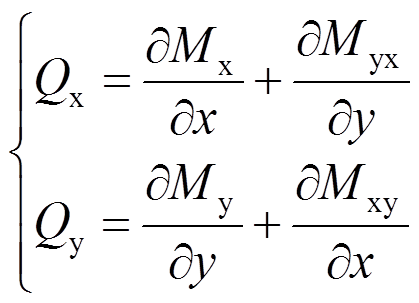 (13)
(13)板的边缘剪力包括横向剪力和板边缘扭矩效应产生的剪力两部分,考虑到板的边缘在x和y方向上均有法线,因此垂直边缘剪力可写为:
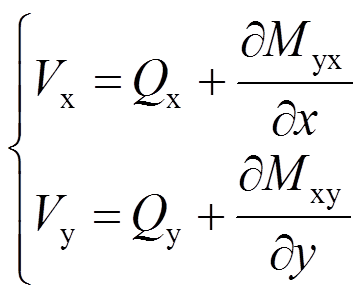 (14)
(14)
将式(11)、式(13)代入式(14),可得板边缘剪力的表达式为:
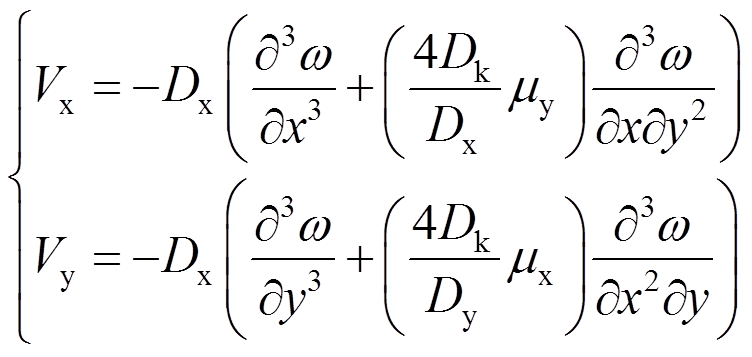 (15)
(15)对于已知的荷载和边界条件,可按式(12)求出挠度的解析式或数值解,从而按式(9)、式(11)和式(15)求出板的应力和内力。
对于单跨双向板和多跨连续双向板的边区格板一般按简支考虑。四边简支矩形板及其所在坐标系如图5所示。
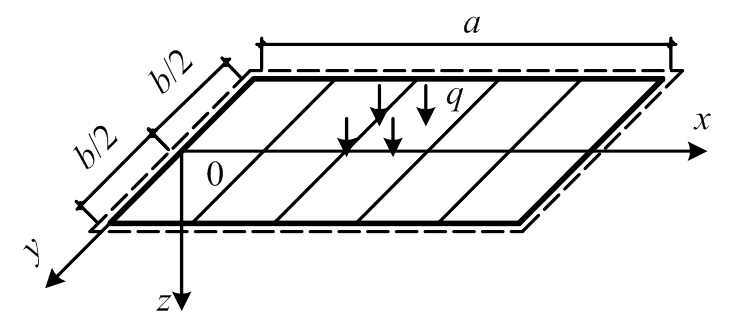
图5 四边简支双向板示意图
Fig.5 Sketch of simply supported two-way slab
求解调和偏微分方程时,采用单重正弦三角级数比双重三角级数有更好的收敛性,可将挠度函数ω分离变量时展开为如下形式:
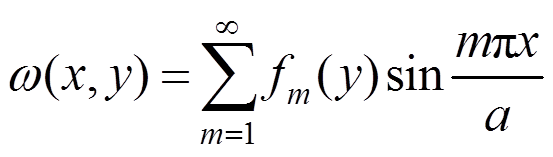 (16)
(16)在x=0,a和y=±b/2时,边界条件如下:
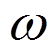 =0,
=0,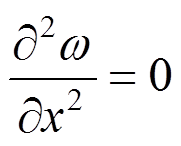 ,
,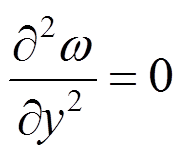 (17)
(17)
荷载p(x,y)亦展开为单三角级数:
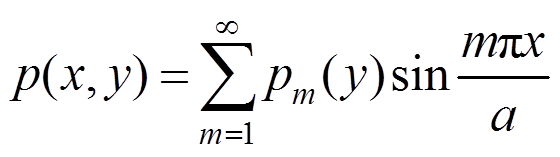 (18)
(18)式中:pm(y)只是y的函数,以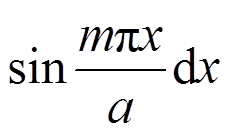 乘以等号两边,从0到a积分便可求得:
乘以等号两边,从0到a积分便可求得:
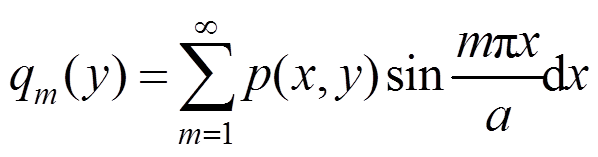 (19)
(19)
在均布荷载下,p(x,y)=q=常量,由式(19)得:
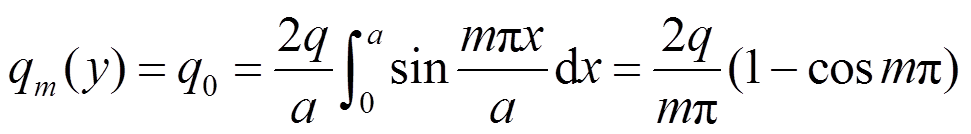 (20)
(20)将式(17)代入控制微分方程式(12),比较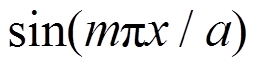 的系数,得:
的系数,得:
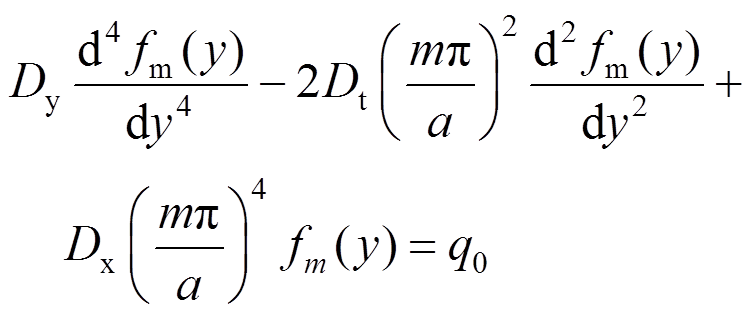 (21)
(21)
该方程特解为:
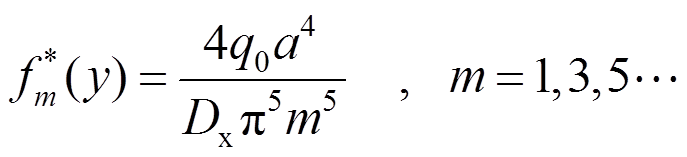 (22)
(22)当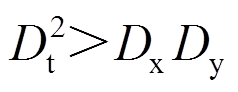 时,式(21)的齐次解有四个不等实根±r1,±r2,(r1>0,r2>0),其通解为:
时,式(21)的齐次解有四个不等实根±r1,±r2,(r1>0,r2>0),其通解为:
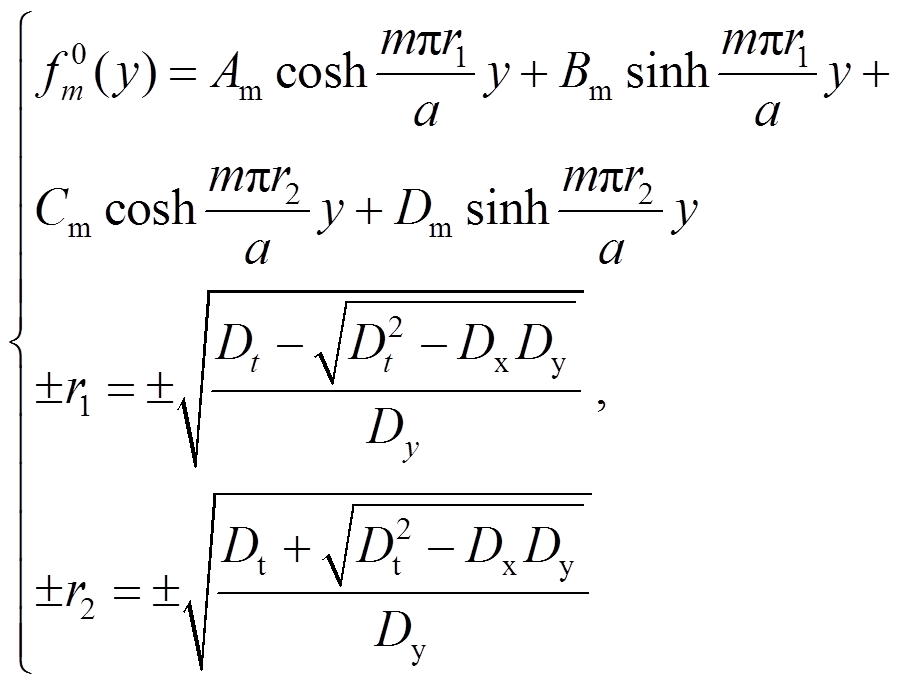 (23)
(23)
DCNPD在顺板缝方向的弯曲刚度为:
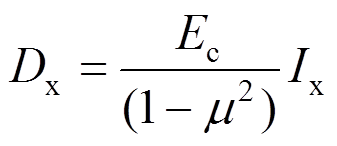 (24)
(24)式中:Ec为混凝土弹性模量;μc为混凝土的泊松比;Ix为平行板缝方向板的横截面惯性矩。
对于正交各向异性双向板,Dy和Dt为:
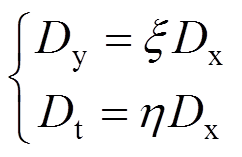 (25)
(25)式中,ξ、η为抗弯刚度和抗扭刚度系数,则有:
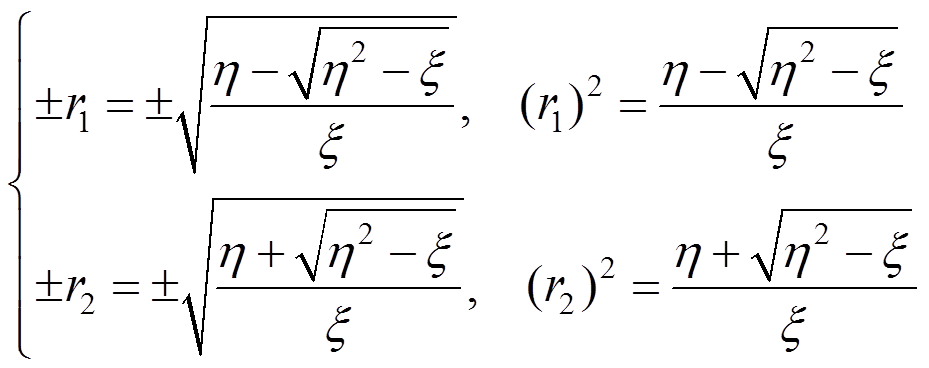 (26)
(26)
将式(22)、式(23)代入式(16),并考虑到薄板的挠度为y的偶函数,因而必有Bm=0,Dm=0。则挠度函数的解答为:
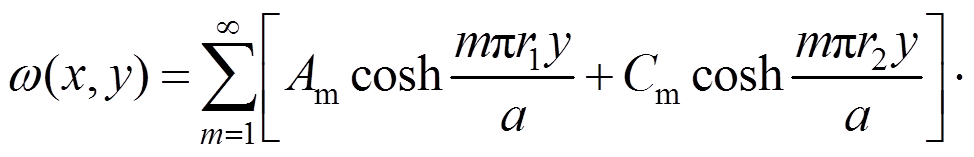
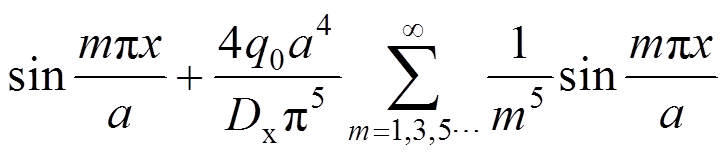 (27)
(27)
考虑,在y=±b/2边界上,有:
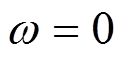 ,
, (28)
(28)将边界条件式(28)代入式(27),则得:
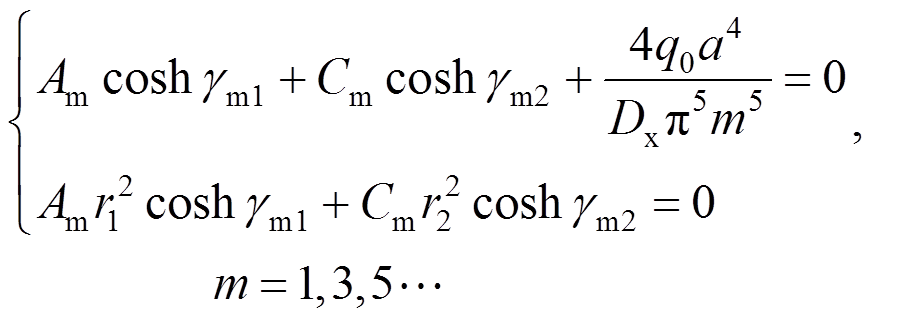 (29)
(29)
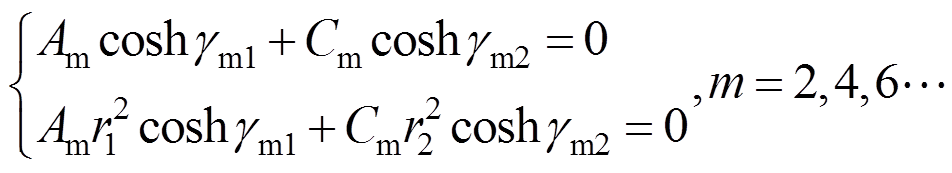 (30)
(30)式中,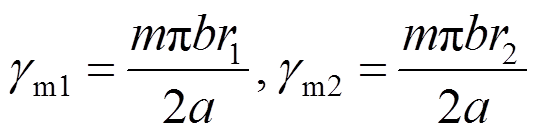 ,解Am,Cm,得:
,解Am,Cm,得:
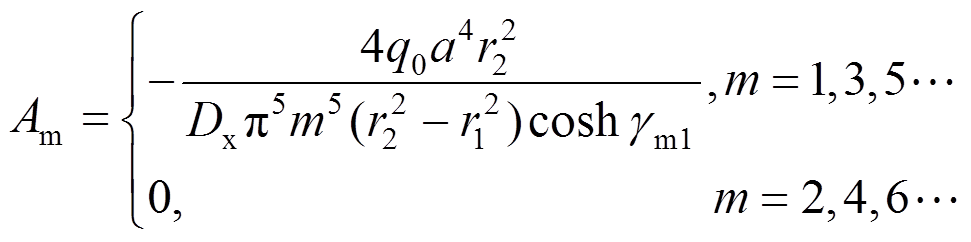 (31)
(31)
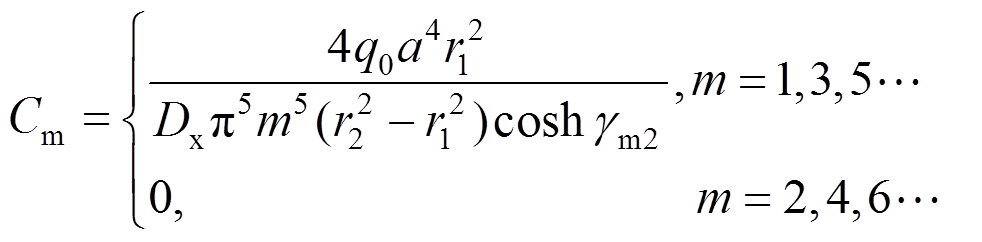 (32)
(32)将式(31)、式(32)代入式(27)可得:
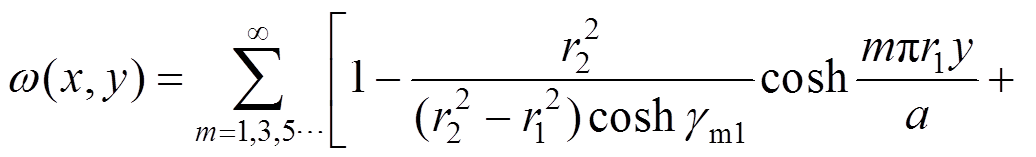
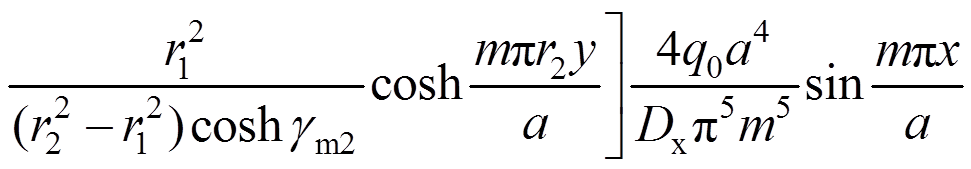 (33)
(33)将式(33)代入式(11),可得两个方向弯矩Mx、My的表达式:
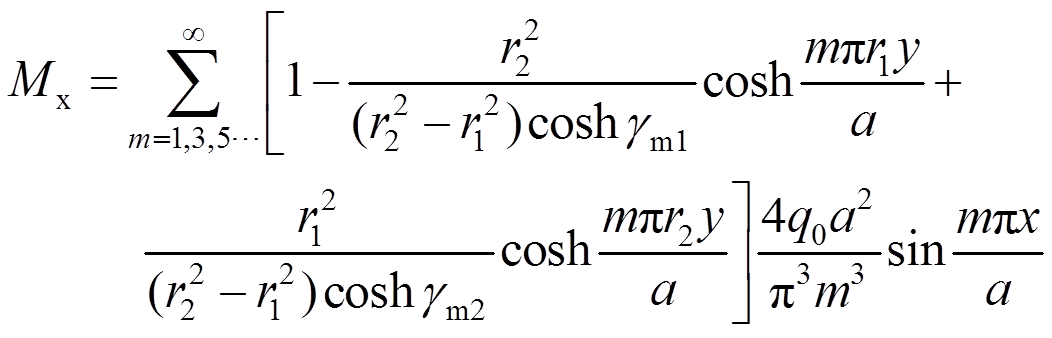 (34)
(34)
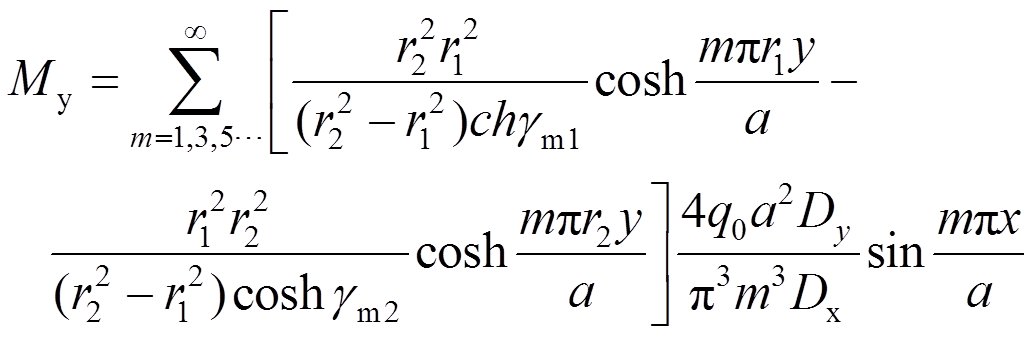 (35)
(35)最大挠度产生于板中心处,将x=a/2,y=0代入式(33)、式(34)和式(35),得:
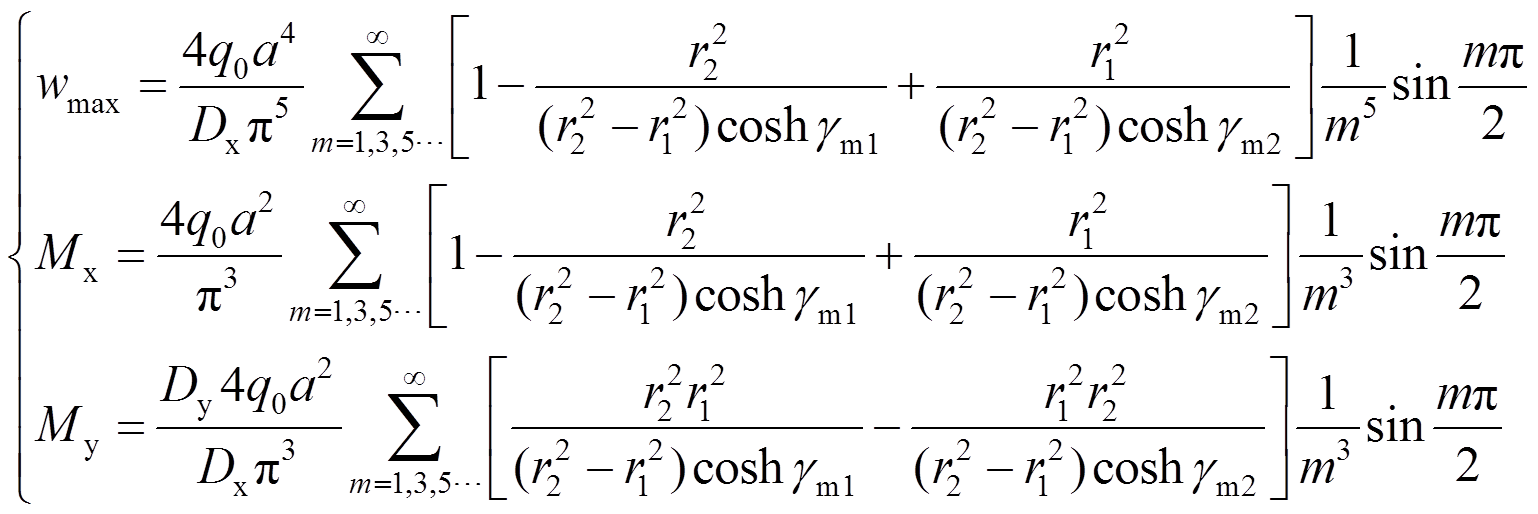 (36)
(36)
在双向板内力计算中要考虑泊松比μ的影响,则板内弯矩可按下式计算:
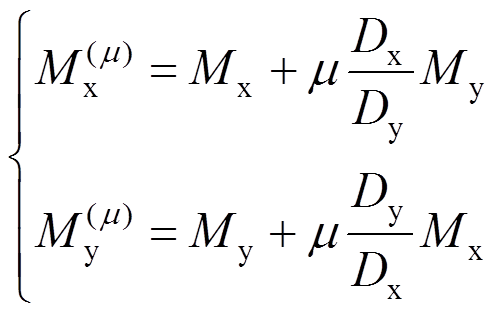 (37)
(37)通过式(36)和式(37)即可求得不同刚度比下的四边简支新型楼盖的挠度和弯矩值。
DCNPD本身材料的弹性性质是各向同性的,但板缝的存在使其在两个方向上的力学性能存在差异,属于构造正交异性板。由各向异性薄板的弯曲理论可得正交异性板的弯曲刚度[23−24],即
绕x轴的抗弯刚度:
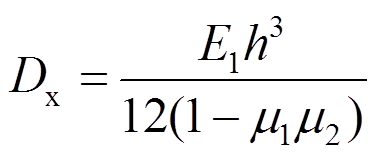 (38)
(38)绕y轴的抗弯刚度:
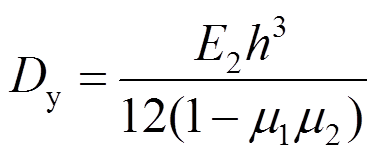 (39)
(39)
绕z轴的抗扭刚度:
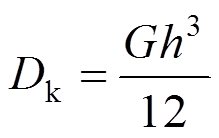 (40)
(40)式中:E1、E2为x向和y向材料弹性模量;μ1、μ2为x向和y向材料泊松比;G、h材料的剪切模量和板的厚度。
在正交各向异性弯曲控制方程式(12)中,还有一个参数Dt,该参数被称为有效扭转刚度或折算刚度[23]。
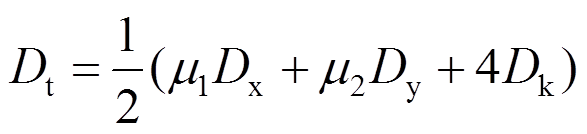 (41)
(41)在DCNPD的解答中,最为关键的是楼盖在x方向和y方向的抗弯刚度和有效扭转刚度。在研究各向异性弹性体时,特别是研究板中的应力和变形时,按照一般通用的模型,把弹性体视为连续体或连续介质。DCNPD中板缝的存在使得楼板不连续,而连接件又使得楼盖在横板缝方向具有一定的连续性,因此不能直接由通用弹性模型进行计算,需要进行一些简化和处理,进而借鉴连续弹性体理论进行新型楼盖的计算。
按照圣维南原理并结合相关文献,取连接件两侧各1倍的连接件锚板长度作为单个连接件影响范围内的横板向抗弯刚度计算宽度,见图7和图8中的计算宽度b。在横板向存在两个控制截面,即图6中1-1和2-2截面,但1-1截面的惯性矩更小,为关键受力截面。可求出截面1-1的惯性矩,代入式(10)便可求出DCNPD在连接件区域的抗弯刚度 :
:
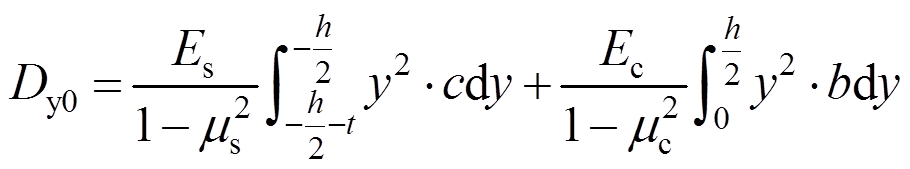 (42)
(42)
式中:b/mm为计算宽度;t/mm为开孔板厚度;c/mm为开孔板在截面宽度;Es/MPa、Ec/MPa为开孔板和混凝土的弹性模量;μs和μc为开孔板和混凝土的泊松比。
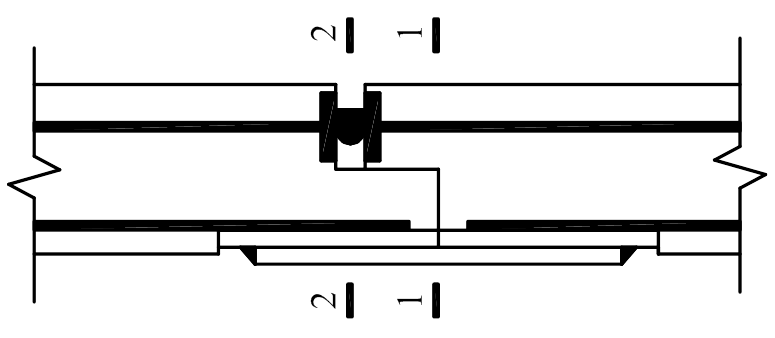
图6 横板向截面位置示意图
Fig.6 Sketch of sections in transversal direction of slab
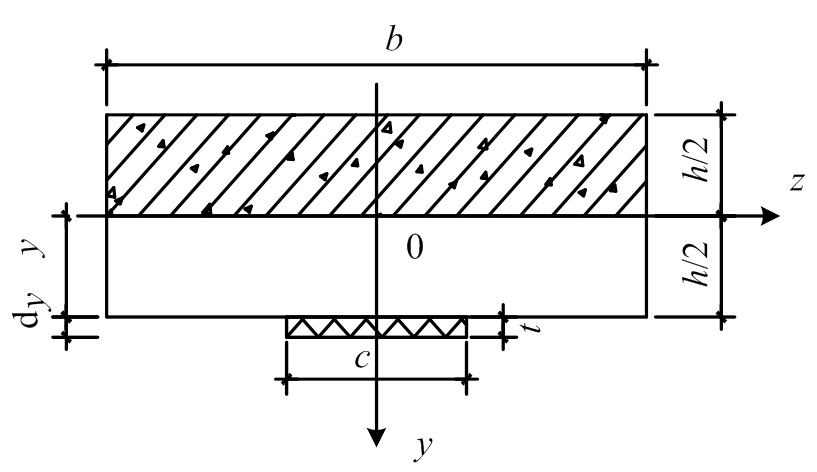
图7 板缝1-1截面示意图
Fig.7 Sketch of 1-1 section
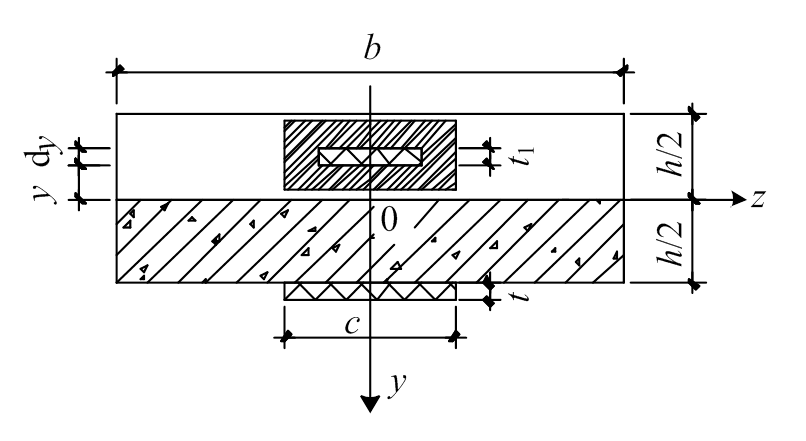
图8 板缝2-2截面示意图
Fig.8 Sketch of 2-2 section
可得1-1截面的抗弯刚度值Dy:
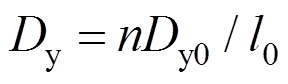 (43)
(43)式中:n为拼缝上预埋机械连接件个数;l0为楼盖顺板缝方向计算跨度(m)。
将Dx、Dy和Dk代入式(41)可得Dt,进而求出新型楼盖在竖向均布荷载下的挠度和弯矩。
试验为新型楼盖的一个1/2缩尺模型,由5块预制板和预制框架拼装而成。模型柱网尺寸为3500 mm×3500 mm,楼盖模型平面布置如图8所示。新型楼盖的梁-板连接与文献[9]中的连接方法相同,板-板连接采用发卡-盖板混合式连接节点(HP-CPC)。限于篇幅,预制框架尺寸、配筋和梁柱节点连接,预制板、预埋件、板缝连接方式与详细尺寸等信息可参考文献[10]。
新型楼盖的竖向受力性能试验采用尺寸为260 mm×140 mm×85 mm的配重块(重20 kg)进行堆积加载,模拟楼盖在竖向均布荷载作用下的受力性能。试验采用《混凝土结构试验方法标准》(GB 50152—2012)推荐方法加载,楼盖模型平面布置图与测点位置详见图9,加载装置详见图10。
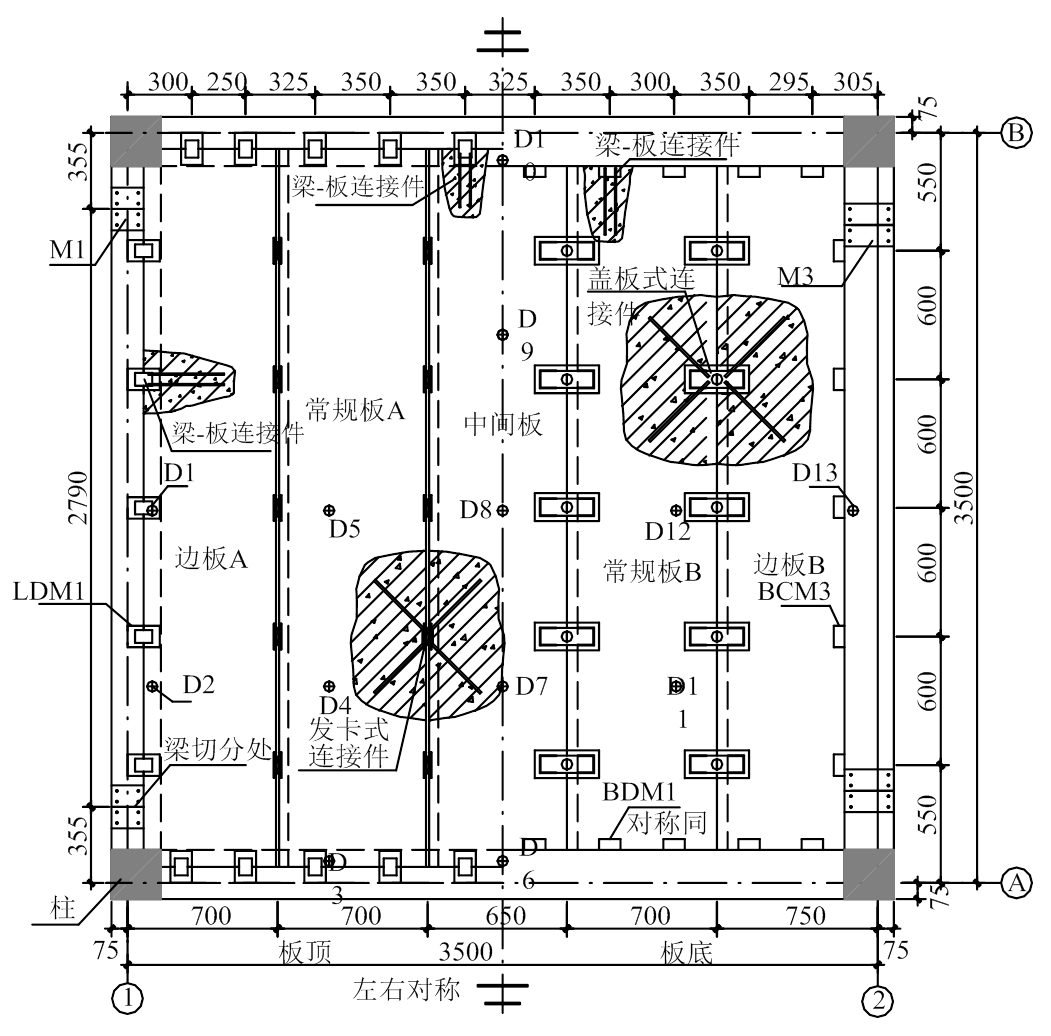
图9 楼盖模型试件平面布置图 /mm
Fig.9 Plan of test specimen

图10 试验加载装置实景图
Fig.10 Photo of test setup
试件主要测点在各级荷载下的挠度变化规律如图11所示,由图可知:跨中位置处挠度最大,1/4跨度处挠度次之,支座处挠度最小;对称位置处的挠度值和挠度增长趋势都非常接近,楼盖在纵横向的变形基本对称,说明楼盖具有较好的横板向传力性能与双向受力性能。
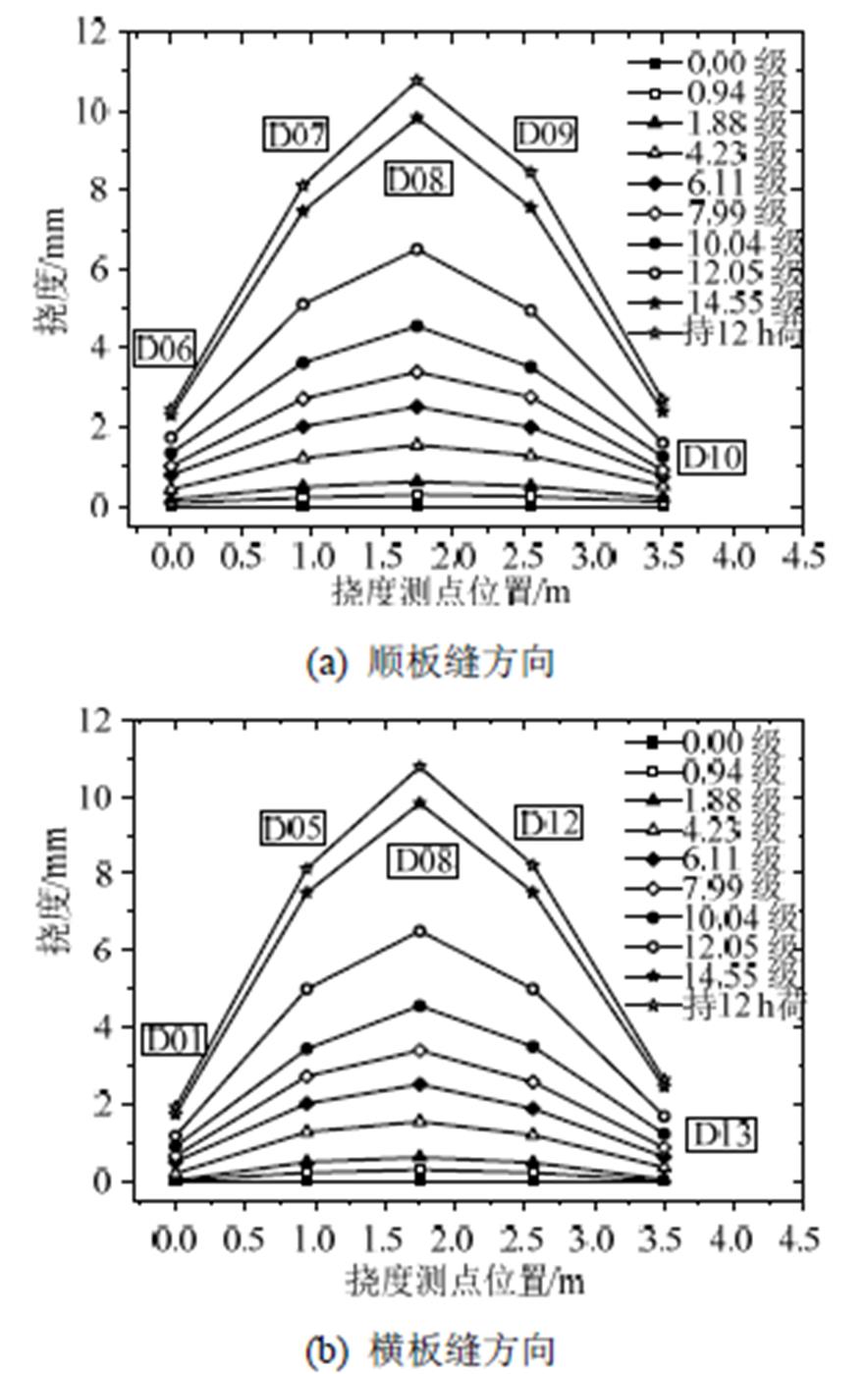
图11 各级荷载下楼盖挠度变化曲线
Fig.11 Deflections of test specimens
为验证理论计算方法的正确性,将新型楼盖刚度理论计算值与试验值和有限元计算值进行对比分析。将新型楼盖在竖向荷载作用下的试验实测值代入式(36)和式(37),应用MATLAB进行数值迭代运算,可得新型楼盖的顺板缝方向刚度、横板缝方向刚度和有效扭转刚度,进而得到新型楼盖各向异性板的抗弯刚度系数和抗扭刚度系数。在无穷级数展开式中保留了前50项,以获取合理的精度。采用ABAQUS程序建立了新型楼盖模型试验试件的有限元模型[25],将计算结果通过迭代算法得出新型楼盖模型的抗弯刚度系数和抗扭刚度系数。新型楼盖刚度系数理论值、试验值和有限元计算值对比结果如表1所示。
由对比可知,新型楼盖抗弯刚度系数ξ和抗扭刚度刚度系数η的理论方法计算值与试验值和有限元分析值吻合较好。
表1 试验结果和有限元结果与理论值的比较
Tabal 1 Comparison between test result, FEA and theoretical result

试验值理论值有限元值理论值/试验值理论值/有限元值 ξ0.2340.2500.1981.0681.389 η0.7740.6250.6410.8070.975
注:ξ为抗弯刚度系数,η抗扭刚度系数
将抗弯刚度系数和抗扭刚度系数代入式(33)~式(35),应用MATLAB程序可得与试验试件同条件下新型楼盖的挠度和弯矩的三维分布图。新型楼盖挠度分布图如图12和图13所示。
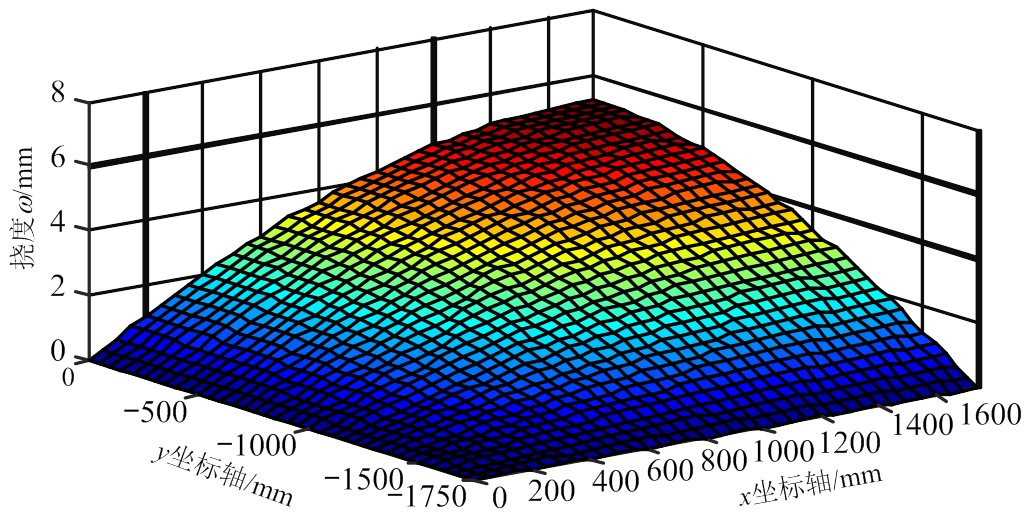
图12 1/4楼盖挠度三维分布图(试验)
Fig.12 Deflection of 1/4 floor (experimental)
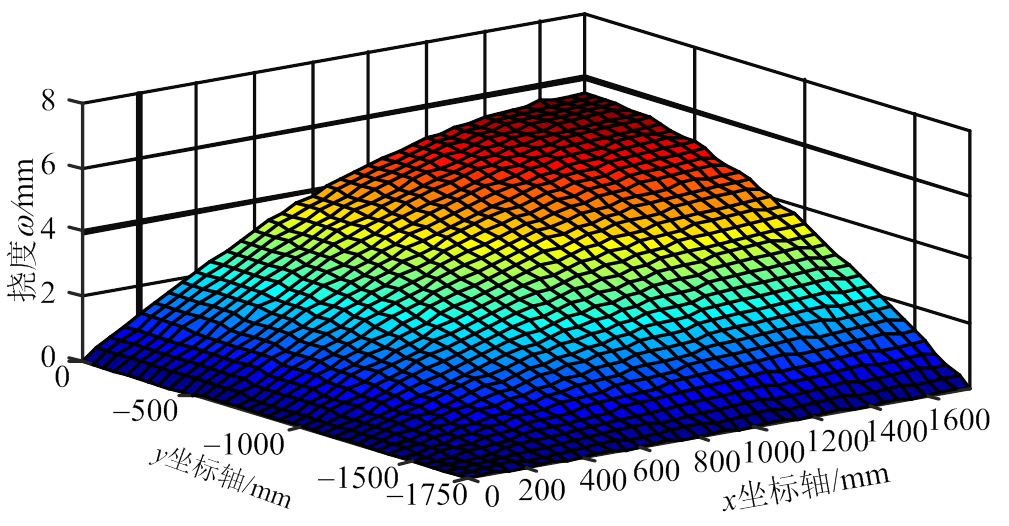
图13 1/4楼盖挠度三维分布图(理论)
Fig.13 Deflection of 1/4 floor (theoretical)
将图12和图13中沿x方向和y方向的跨中截面的挠度数值绘制于图14。图例中,TH为按理论刚度计算方法(简称理论方法)得到的楼盖跨中挠度曲线;EX为用试验数据通过正交异性板理论迭代得到的楼盖刚度值(简称试验方法)代入式(33)得到的跨中挠度曲线。由图可知:在x、y两个方向上(其中,垂直板缝方向为x向,平行板缝方向为y向),理论方法计算值与试验值吻合良好,且理论计算值偏于安全;沿y方向的挠度值与沿x方向的挠度值非常接近,且挠度在两个方向均呈较理想空间抛物面分布。
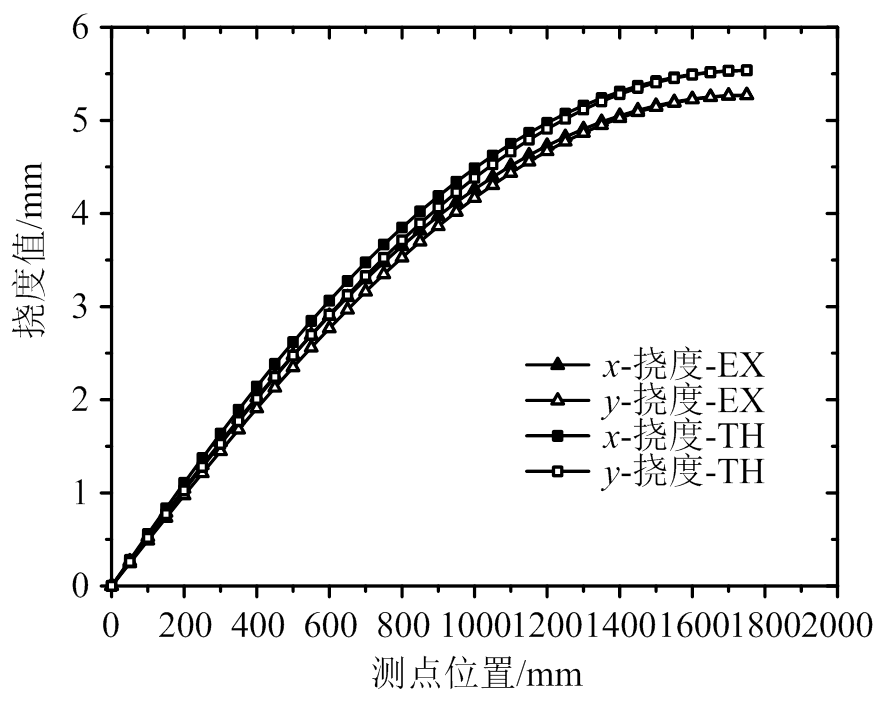
图14 试验最大荷载下楼盖跨中挠度
Fig.14 Middle span deflection under ultimate load
图15和图16为按试验方法和理论方法计算的楼盖弯矩Mx的三维分布图。
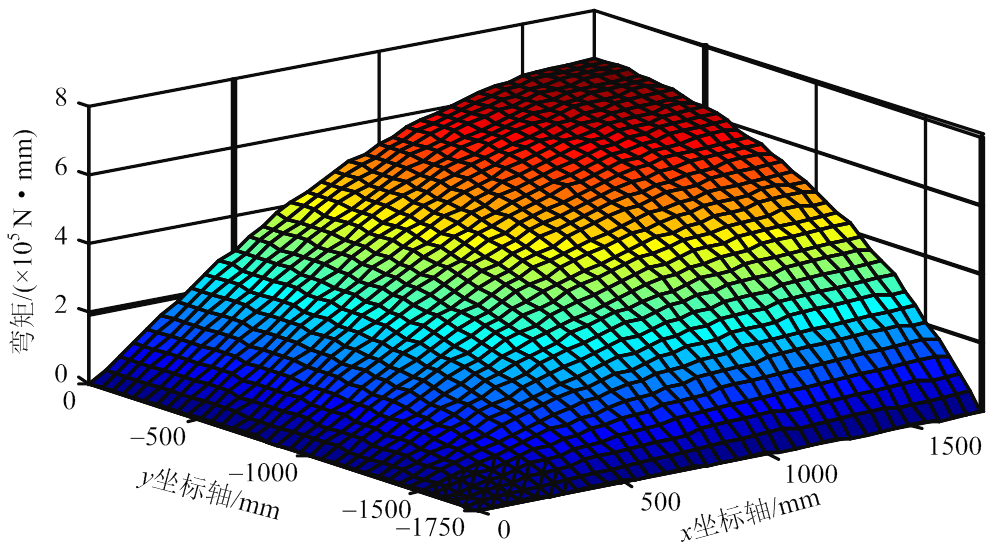
图15 1/4楼盖弯矩Mx(试验)
Fig.15 Mx distribution of 1/4 floor (experimental)
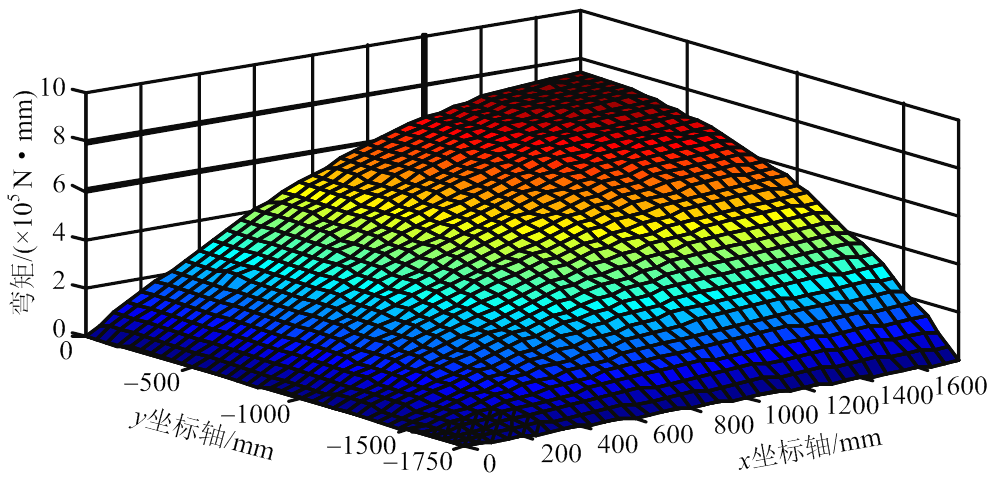
图16 1/4楼盖弯矩Mx(理论)
Fig.16 Mx distribution of 1/4 floor (theoretical)
将图15和图16中的沿x方向和y方向的跨中截面的x向弯矩的数值绘制于图17。由图可知:在x、y两个方向上,理论方法计算跨中截面x向弯矩略大于试验方法得到的x向弯矩;沿x方向的x向弯矩值略大于沿y方向的x向弯矩值;Mx在两个方向均呈空间抛物面分布。
图18和图19为按试验方法和理论方法计算的楼盖弯矩My的三维分布图。
由图可知:理论方法计算的y向弯矩略小于试验方法得到的y向弯矩;由于横板向刚度小于顺板向刚度,使得沿x方向的y向弯矩值小于沿y方向的y向弯矩值;My在两个方向的抛物面形状呈现出一定的不对称性,在y坐标轴方向基本呈抛物线形,而在x坐标轴方向跨中附近出现了较长的平直段,这是因为垂直于板缝方向的抗弯刚度较小,在竖向荷载作用下y向弯矩在离支座不远处便已接近峰值;但在数值上,y向弯矩比x向弯矩小很多(见图15和图18),仅为x向弯矩的25%左右,这与抗弯刚度系数ξ值较为接近,说明采用正交异性薄板理论分析新型楼盖是可行的。
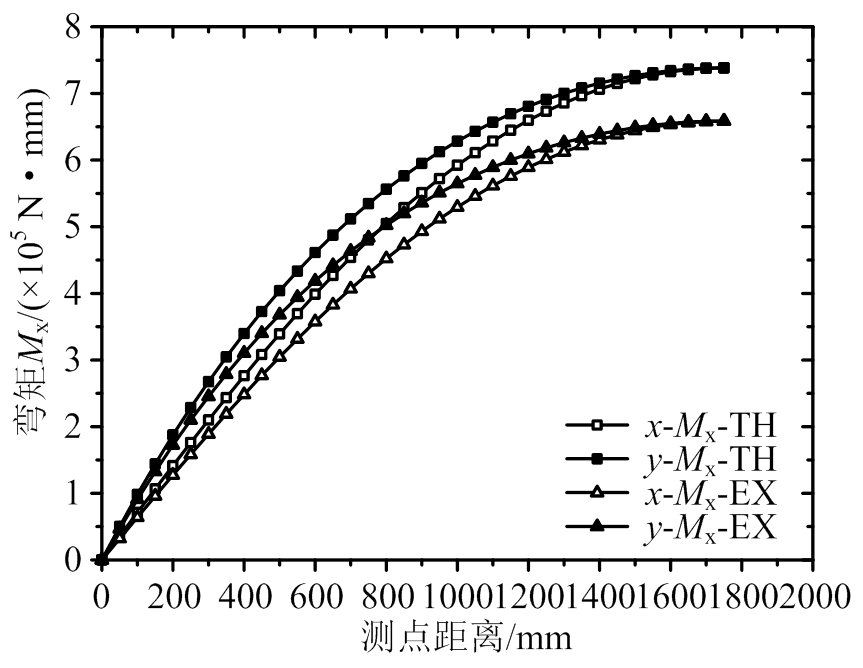
图17 单位荷载下弯矩Mx
Fig.17 Moment in x direction, Mx, under unit load
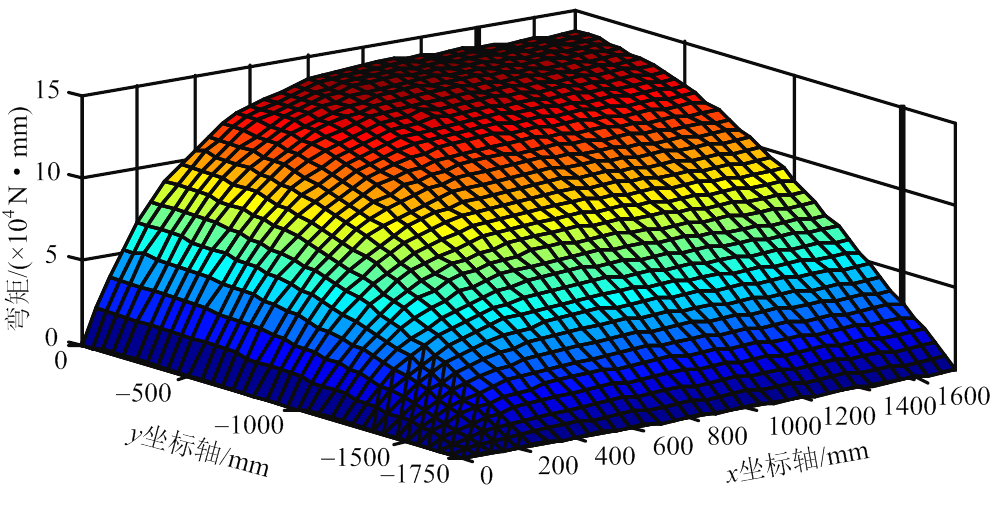
图18 1/4楼盖弯矩My(试验)
Fig.18 My distribution of 1/4 floor (experimental)
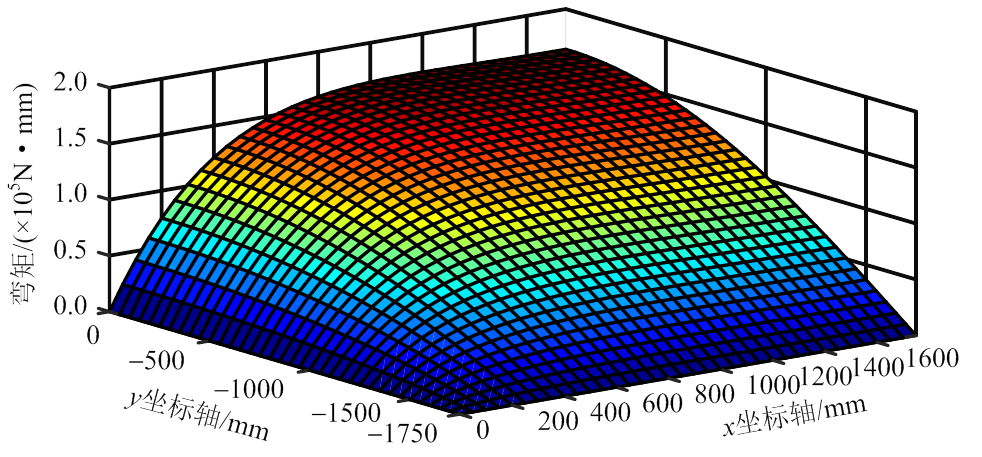
图19 1/4楼盖弯矩My(理论)
Fig.19 My distribution of 1/4 floor (theoretical)
将图18和图19中沿x方向和y方向的跨中截面y向弯矩绘制于图20。由图可知:在x、y两个方向上,理论方法计算跨中截面y向弯矩略大于试验方法得到的y向弯矩,偏于安全,两种计算方法得到的截面弯矩曲线形状非常相似;由于Dy小于Dx,沿y方向预制板承担的y向弯矩Y-My值大于沿x方向的y向弯矩值X-My,说明板缝传递y向弯矩的效果没有传递x向(顺板)弯矩好。
新型楼盖在竖向荷载下跨中挠度ωmax、x向弯矩Mx和y向弯矩My的试验值、理论值和有限元值列于表2。由表可知:由于楼盖板底在加载的后将期板底混凝土开裂使得楼盖的跨中挠度的理论计算值比试验值小11.58%,而理论计算值与有限元计算值相差不大;单位荷载下楼盖的x向和y向弯矩理论计算值与试验值和有限元计算值较为吻合,且理论计算值偏于安全,可采用本文推荐的方法进行新型楼盖的分析与计算。
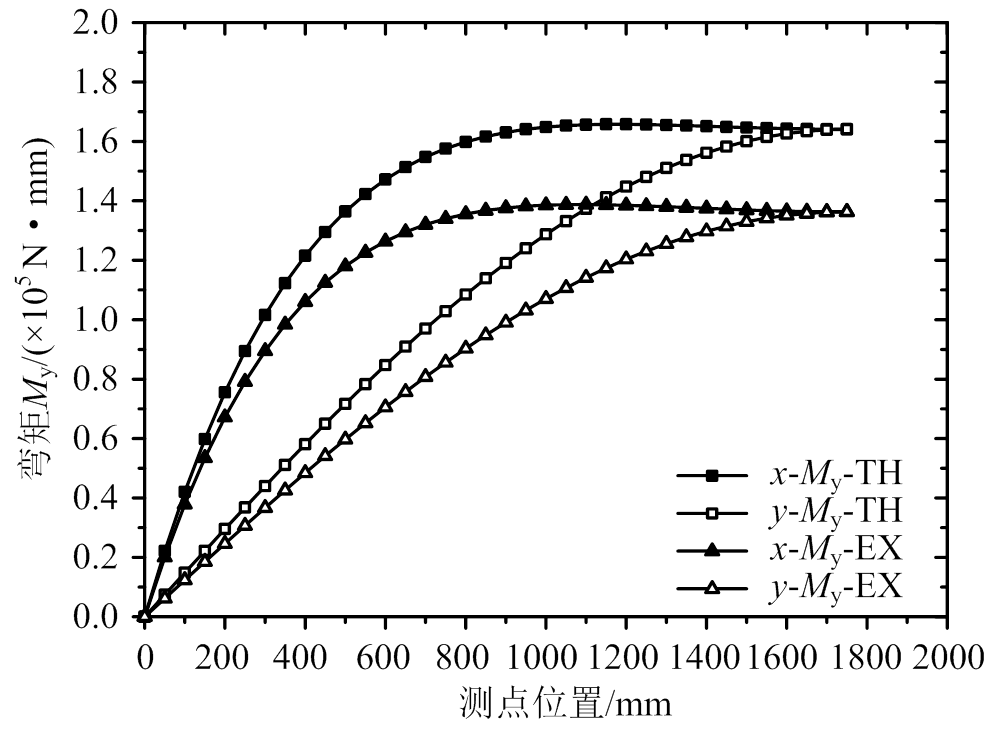
图20 单位荷载下弯矩My
Fig.20 Moment in y direction, My, under unit load
表2 试验结果和有限元结果与理论值的比较
Tabal 2 Comparison between test result, FEA and theoretical result
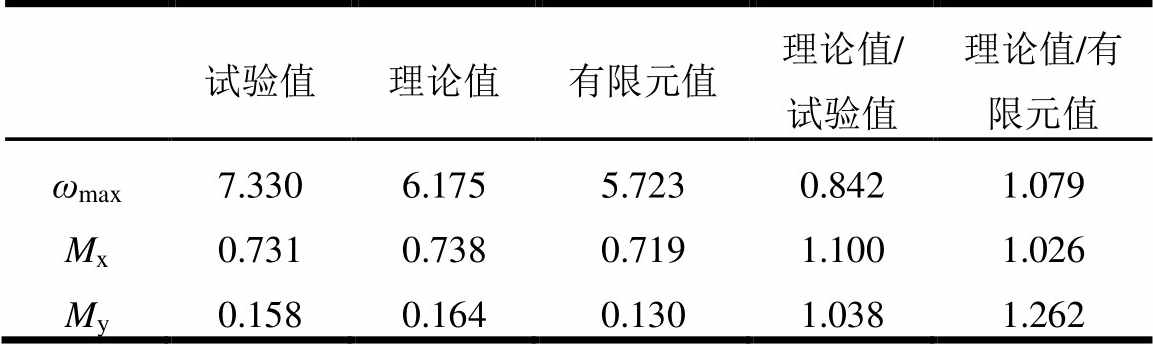
试验值理论值有限元值理论值/试验值理论值/有限元值 ωmax7.3306.1755.7230.8421.079 Mx0.7310.7380.7191.1001.026 My0.1580.1640.1301.0381.262
注:ωmax/mm为跨中挠度;Mx/(N·mm)、My/(N·mm)为单位荷载下弯矩。
通过上述方法可以求出新型楼盖在特定板厚和连接件型号及其铺设方式下的抗弯刚度和有效抗扭刚度系数,进而进行楼盖的分析与设计。
可参考国家标准《预应力砼空心板》(GB/T 104040)和PCI Design Handbook(7th edition)等选择并计算各规格预制板组成的新型楼盖在不同板厚、连接件型号、连接件个数和楼盖跨度等条件下的抗弯刚度系数ξ和抗扭刚度系数η,并绘制成表,以便工程设计时选用。
本文介绍了分布式连接新型全装配RC楼盖及其组成,在试验的基础进行了新型楼盖的竖向承载力与变形的理论分析。主要结论如下:
(1) 基于正交各向异性弹性薄板小挠度理论推导了新型楼盖弯曲微分方程,并给出了四边简支新型楼盖在竖向均布荷载作用下的解析解。
(2) 提出了新型楼盖横板向刚度理论计算方法,引入了抗弯刚度系数ξ和有效抗扭刚度系数η,通过与试验值和数值分析结果的对比分析,验证了所提刚度计算方法的正确性。
(3)新型楼盖挠度和弯矩的理论计算值与试验实测值吻合良好,且偏于安全,验证了采用正交各向异性弹性薄板小挠度理论分析新型楼盖竖向承载能力的可行性。
(4) 新型楼盖挠度的在两个方向均呈较为理想的空间抛物面分布,较好地实现了分布式连接件的横板向传力;板缝连接可有效传递板内弯矩,但在正交的两个方向传递效果存在差异,具体表现为顺板缝方向弯矩传递效果优于横板缝方向;新型楼盖变形与弯矩分布规律表明新型楼盖具有较好的双向受力性能。
(5) 在理论分析的基础上,提出了新型楼盖面向工程应用的竖向承载力分析方法和建议。
参考文献:
[1] Cleland N M, Ghosh S K. Untopped precast concrete diaphragms in high-seismic application [J]. PCI Journal, 2002, 47(6): 94―99.
[2] Davies G, Elliott K S, Omar W. Horizontal diaphragm action in precast concrete floors [J]. The Structural Engineer, 1990, 68(2): 25―32.
[3] Baran E. Effects of cast-in-place concrete topping on flexural response of precast concrete hollow-core slabs [J]. Engineering Structures, 2015, 98(9): 109―117.
[4] Hawkins N M, Ghosh S K. Proposed revisions to 1997 NEHRP recommended provisions for seismic regulations for precast concrete structures: part 3–diaphragms [J]. PCI Journal, 2000, 45(6): 49―58.
[5] PCI design handbook: Precast and prestressed concrete (8th edition) [S]. Chicago, PCI: PCI Industry Handbook Committee, 2017.
[6] 祁成财, 蒋勤俭. 一汽停车楼装配式结构深化设计关键技术研究[R]. 第五届中国(国际)预制混凝土技术论坛, 厦门, 2015: 1―26.
Qi Chengcai, Jiang Qinjian. Key techniques on the YIQI parking building detailed design [R]. The Fifth China (International) Forum on Precast Concrete Technique, Xiamen, 2015: 1―26. (in Chinese)
[7] JGJ1―2014, 装配式混凝土结构技术标准[S]. 北京: 中国建筑工业出版社, 2014.
JGJ1―2014, Technical code for precast concrete building [S]. Beijing: China Building Industry Press, 2014. (in Chinese)
[8] 庞瑞, 陈桂香, 倪红梅, 等. 全干式连接预制混凝土板、楼盖及其抗震性能提升方法[P]. 中国ZL 2015 1 0247926. 5 [P]. 2017. 07. 14.
Pang Rui, Chen Guixiang, Ni Hongmei, et al. Untopped precast slab and floor diaphragm [P]. China Patent: ZL 2015 1 0247926. 5, 2017. 07. 14. (in Chinese)
[9] 庞瑞, 许清风, 梁书亭, 等. 全装配RC楼盖平面内受力性能试验研究[J]. 建筑结构学报, 2012, 33(10): 67―74.
Pang Rui, Xu Qingfeng, Liang Shuting, et al. In-plane mechanism of untopped precast RC floor diaphramgs [J]. Building Structures, 2012, 33(10): 67―74. (in Chinese)
[10] 朱筱俊, 庞瑞, 梁书亭. 全装配式钢筋混凝土楼盖竖向受力性能试验研究[J]. 建筑结构学报, 2013, 34(1): 123―130.
Zhu Xiaojun, Pang Rui, Liang Shuting, et al. Vertical bearing capacity of untopped precast RC floor diaphramgs [J]. Building Structures, 2013, 34(1): 123―130. (in Chinese)
[11] 王晓锋. 单向预应力双向叠合板楼盖试验研究[D]. 北京: 中国建筑科学研究院, 2003: 3.
Wang Xiaofeng. Experimental study of a prestressed two-way composite slab floor [D]. Beijing: China Academy of Building Research, 2003: 3. (in Chinese)
[12] 周绪红, 张微伟, 吴方伯, 等. 预应力混凝土四边简支双向叠合板的设计方法[J] . 建筑科学与工程学报, 2006, 23(4): 54―57.
Zhou Xuhong , Zhang Weiwei , Wu Fangbo, et al. Design method of prestressed concrete simply supported on four sides of two-way composite slab [J]. Journal of Architecture and Civil Engineering, 2006, 23(4): 54―57. (in Chinese)
[13] 吴方伯, 黄海林, 陈伟, 等. 肋上开孔对预制预应力混凝土带肋薄板施工阶段挠度计算方法的影响研究[J]. 工程力学, 2011, 18(11): 64―71.
Wu Fangbo, Huang Hailin, Chen Wei, et al. Influence of preformed holes on flexural deflection calculation methods of precast prestressed concrete ribbed panels for composite slabs [J]. Engineering Mechanics, 2011, 28(11): 64―71. (in Chinese).
[14] 周旺华. 现代混凝土叠合结构[M]. 北京: 中国建筑工业出版社, 1998: 154―196
Zhou Wanghua. Modern concret e composite structures [M]. Beijing: China Architecture & Building Press, 1998: 154―196 . (In Chinese)
[15] 吴方伯, 刘彪, 罗继丰. 预应力混凝土叠合空心楼板的受剪性能试验研究[J]. 工程力学, 2016, 33(3): 196―203.
Wu Fangbo, Liu Biao, Luo Jifeng. Experimental study on shear resisting properties prestressed concrete composite hollow core slabs [J]. Engineering Mechanics, 2016, 33(3): 196―203. (in Chinese)
[16] GB 50010—2010, 混凝土结构设计规范(2015version)[S]. 北京: 中国建筑工业出版社, 2016.
GB 50010—2010, Code for design of concrete structures (2015version) [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[17] ACI 318—14, Building code requirements for structural concrete [J]. Farmington Hills, MI: American Concrete Institute, 2014.
[18] 田春雨, 聂建国. 组合楼盖竖向承重体系中楼板变形及内力分析[J]. 工程力学, 2006, 23(5): 62―66
Tian Chunyu, Nie Jianguo. Analysis of deflection and internal force in composite slab-on-girder floor system [J]. Engineering Mechanics, 2006, 23(5): 62―66. (in Chinese)
[19] 建筑结构静力计算手册[M]. 北京: 中国建筑工业出版社, 2001: 194―239.
Static calculation mual of building structures [M]. Beijing: China Architectural & Building Press, 2001: 194―239. (in Chinese)
[20] Timoshenko S, Woinowsky-Krieger S. Theory of plates and shells [M]. 2nd ed. New York: McGraw-Hill, 1959: 105―225.
[21] 张大山, 董毓利, 房圆圆. 考虑受拉薄膜效应的板块平衡法修正及在混凝土双向板中的应用[J]. 工程力学, 2017, 34(3): 204―210, 240.
Zhang Dashan, Dong Yuli, Fang Yuanyuan. Modification of Segment of equilibrium method through considering tensile member an effects and its application in two-way concrete slabs [J]. Engineering Mechanics, 2017, 34(3): 204―210, 240. (in Chinese)
[22] 肖闪闪, 陈普会. 集中载荷下四边固支正交各向异性矩形板的线性弯曲问题[J]. 工程力学, 2015, 32(6): 26―32.
Xiao Shanshan, Chen Puhui. Analytical solutions for bending of clamped orthotropic rectangular plates under a concentrated force [J]. Engineering Mechanics, 2006, 32(6): 26―32. (in Chinese)
[23] Reddy J N. Theory and analysis of elastic plates and shells 2nd ed [M]. Boca Raton: CRC Press, 2007: 215―259.
[24] 程远兵, 程文瀼, 党纪. 均布荷载下简支蜂窝式空心板的解析解[J]. 工程力学, 2009, 26(8): 34―39.
Cheng Yuanbing, Cheng Wenrang, Dang Ji. Analytical solution of cellular hollow plates simply supported subjected to uniformly distributed loads [J]. Engineering Mechanics, 2009, 26(8): 34―39. (in Chinese)
[25] 吴见丰. 新型全预制装配式楼盖的竖向受力性能研究[D]. 南京: 东南大学, 2011
Wu Jianfeng. Experimental research and theoretical analysis on the vertical mechanical behavior of a new all prefabricated floor [D]. Nanjing: Southeast University, 2011. (in Chinese)
ANALYSIS OF THE VERTICAL STRENGTH AND DEFLECTION OF DISCRETELY CONNECTED PRECAST RC FLOOR SYSTEMS
Abstract: In discretely connected precast RC floor/diaphragms (DCNPD), slab joints are connected by connectors to transfer internal force. An analysis program of internal force and deflection under vertical load was conducted to accureately determine the vertical strength of DCNPDs. The moment and deflection eqations of a DCNPD simply supported on four sides under uniformly distributed load are derived according to the small deflection theory of elastic thin perpendicular heterogeneous plates and are solved with trigonometric series. A model for estimating the bending stiffness of a DCNPD in the transverse direction is proposed and validated by comparing with finite element solutions and experimental results. The moment and deflection distributions of a DCNPD are ideally spatial parabolical, indicating that the DCNPD has excellent bidirectional mechanical behavior. The moment can be effectively transferred by the slab joints, especially in the slab laying direction rather than the orthogonal direction.
Key words: discrete connection; untopped precast RC floor diaphragm; slab joint connection; bending stiffness in transverse direction; vertical strength
文章编号:1000-4750(2019)04-0147-11
中图分类号:TU375.2
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.02. 0092
收稿日期:2018-02-08;
修改日期:2018-09-28
基金项目:国家自然科学基金项目(51778214);河南省科技攻关项目(152102210066);河南省高等学校青年骨干教师资助计划项目 (2015GGJS-037);河南工业大学青年骨干教师培育计划项目(21420004);河南省高等学校重点科研项目(17A560003)
梁书亭(1964―),男,河南许昌人,教授,工学博士,主要从事结构工程研究(E-mail: stliang@seu.edu.cn );
朱筱俊(1972―),男,江苏宜兴人,教授级高工,工学博士,主要从事结构工程研究(E-mail: zhu_share@tom.com);
吴见丰(1985―),男,福建宁德人,一级注册结构工程师,工学硕士,主要从事工程结构设计与研究(E-mail: 6528647@qq.com).