
图1 FGM梁模型
Fig.1 FGM beam model
摘 要:功能梯度梁热后屈曲特性研究对于推进功能梯度材料在航天器热防护设计中的应用有着重要意义。基于经典梁的几何非线性理论和物理中面的概念,建立了热载荷作用下功能梯度梁的运动微分方程,通过化简得到一个仅关于挠度的四阶微分-积分方程,并与固支边界条件构成特征值问题,分析研究了功能梯度梁的热后屈曲及在此基础上的振动问题。首先证明了通过哈密顿原理推导的运动方程是轴线可伸长理论的近似形式。接着考虑热对材料物性参数的影响,并对梁的长细比、功能梯度指数和温度比作了详细分析,研究了这些参数对热后屈曲路径和后屈曲振动的影响规律。结果表明:只有在长细比较大时才可以不考虑温度对材料物性参数的影响,否则误差较大;长细比、功能梯度指数和温度比的增大会增大无量纲热屈曲载荷,同时使屈曲路径和频率-载荷曲线向热载荷增大的方向移动。
关键词:功能梯度梁;热后屈曲;振动;解析解;基频
功能梯度材料(functionally graded material,FGM)是一类结构和性能在长度或厚度方向上连续变化的新型复合材料[1]。由于FGM材料属性连续变化,所以结构内部不存在明显的分界面,从而减小了层间应力,与传统层合复合材料相比具有比强度更高,耐热性、韧性更好等优点。近些年来,航天器飞行速度的提高对热防护材料的设计提出了更高的要求,也使FGM在航天领域得到了更加广泛的应用,而气动加热下的稳定性和动力学问题也给学者们带来了新的挑战。关于FGM稳定性分析,文献[2―5]可供参考。Majumdar和Das[6]考虑了热对材料参数的影响,并利用能量变分原理推导了欧拉-伯努利梁的控制方程,通过迭代求解特征值问题得到了临界热屈曲载荷。热环境下的动力学问题主要通过两个方面来进行研究:一是温度较低时的线性振动,此类研究相对较为丰富[7-10];二是当温度超过临界屈曲温度后的非线性热后屈曲振动,这方面的研究相对较为复杂。
目前关于梁热后屈曲振动的研究大多集中于近似数值解法,如有限元法[11-13]、里兹法[14-15]、扰动法[16-17]、轴线可伸长理论-打靶法[18-21]等。轴线可伸长理论是一种精确的建模方法,它考虑了梁屈曲时轴线的伸长,并利用几何非线性理论建立了横向载荷作用下梁的动力学方程,最后利用打靶法数值求解所得的高阶非线性动力学方程。解析法只有少数几篇文献可供参考,Nayfeh和Emam[22]基于经典梁理论建立了轴向载荷作用下梁后屈曲变形的封闭解析解。马连生和顾春龙[23]将其进行了推广,考虑了一阶剪切变形并对梁热后屈曲的解析解进行了研究,结果表明长细比越大,剪切变形所造成的影响越小。Ma和Lee[24]考虑了一阶剪切变形效应,并研究了均匀温度场下FGM梁的动力学特性。Levyakov[25]对两端不可移动简支FGM梁的热弯曲进行了研究,基于物理中面消除了本构方程中的拉弯耦合,建立了勒让德椭圆积分形式的弯曲变形解析解。崔德福[26]对存在轴向粘滞-滑移-约束边界的简支金属梁热屈曲、热前-后屈曲自由振动进行了研究,并得到了每种情况下梁屈曲温度及固有频率的解析表达式。毛丽娟和马连生[27]对非均匀热载荷作用下FGM梁的非线性静态响应进行了研究,并证明了固支和简支梁有着很大差别的静力学行为特征。She等[17]又深入地研究了其它高阶剪切模型的热屈曲问题。Ebrahimi和Jafari[28-29]还考虑了孔隙分布对简支FGM梁热振动的影响。文献[30―33]研究了弹性支撑下的梁、板及壳结构的临界热屈曲载荷及热屈曲变形。赵伟东等[34]研究了FGM扁球壳在均匀温度场下的热屈曲行为。
现有文献对FGM梁热屈曲振动的研究大多集中在均匀温度场下,且只有少数几篇文章考虑了温度对材料组分的影响,而且鲜有文献针对既考虑热对材料参数的影响又考虑非均匀温度场的FGM梁热后屈曲振动解析解法进行详细研究,更没有文献指出过基于物理中面的解析法与轴线可伸长理论的联系。本文首先根据梁的几何非线性理论和物理中面的概念,采用哈密顿原理建立FGM梁的运动微分方程组,接着又从轴线可伸长理论出发,在满足一定近似条件下得到了相同的运动方程。消去方程中的轴向自由度,将两个微分方程化为一个仅关于挠度的四阶非线性积分-微分方程,与边界条件一起构成了特征值问题。本文用解析法研究了FGM梁的热后屈曲行为,并分析了梁长细比、功能梯度指数和梁顶面、底面温度比(以下简称温度比)等参数对后屈曲静、动态特性的影响。以期为热防护材料在航天器设计中的进一步发展与应用提供理论指导与技术支持。
考虑初始长度为l,初始截面宽为b,高为h的矩形横截面FGM梁,如图1所示。x轴沿梁轴线方向,y轴和z轴分别沿梁的宽度和厚度方向,xoy平面位于梁未变形时的中面位置。

图1 FGM梁模型
Fig.1 FGM beam model
假设FGM梁的顶面材料和底面材料分别是陶瓷和金属,中间为陶瓷到金属的过渡变化材料,沿厚度任意位置处金属的体积含量可以表示为Vm(z)=[(h-2z)/2h]n,陶瓷的体积含量可以表示为Vc(z)=1-Vm(z),其中幂指数n表示FGM梁梯度指数。若n=0,则梁为金属梁。采用Voigt等应变线性混合率模型[35-36],可以将FGM的材料属性表示金属和陶瓷材料属性的加权平均形式,权函数分别为Vm(z)和Vc(z),表达式如下:
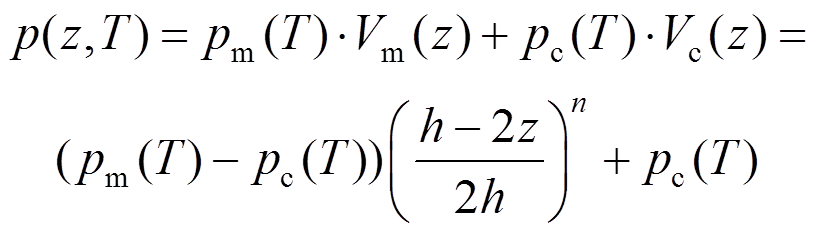 (1)
(1)式中:m表示金属;c表示陶瓷;材料属性p可以表示弹性模量E、质量密度ρ、热膨胀系数α;T表示开尔文温度。
考虑FGM材料属性对温度的敏感性。根据文献[37-38],可用三次函数来拟合单一组分(陶瓷和金属)的材料属性随温度的变化规律,如下式:
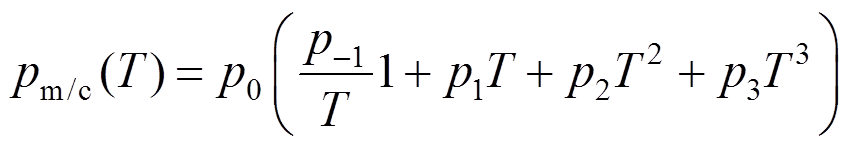 (2)
(2)式中:p为材料属性;pi表示组分材料的温度敏感系数。
对于温度仅沿梁厚度方向变化的稳态温度场,按照热传导定率。
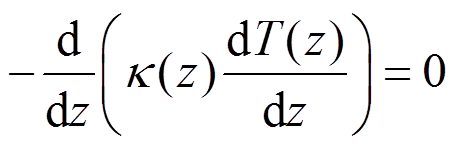 (3)
(3)式中,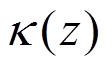 为热传导系数。
为热传导系数。
当温度边界条件为T(h/2)=Tc和T(-h/2)=Tm时(温度比为Tr=Tc/Tm),可以求得任意厚度位置处的温度为:
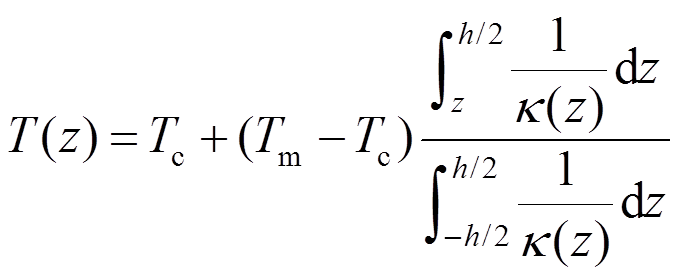 (4)
(4)式(4)的解很难用初等函数表示,所以采用幂级数解法来进行近似求解。
设:
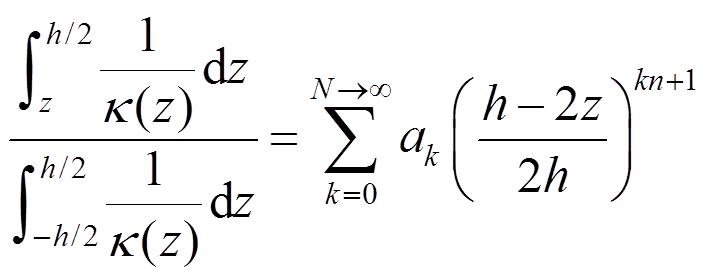 (5)
(5)当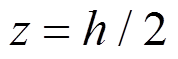 时,可以得到
时,可以得到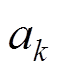 满足的表达式:
满足的表达式:
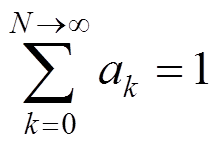 (6)
(6)
将式(4)代入式(3)后,整理可得:
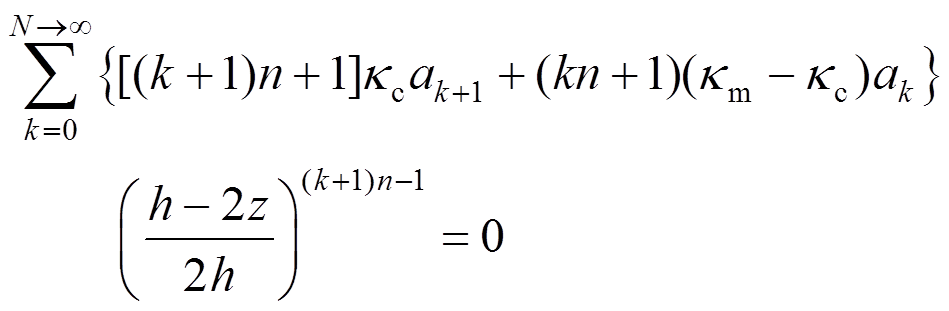 (7)
(7)比较两端,即得递推关系:
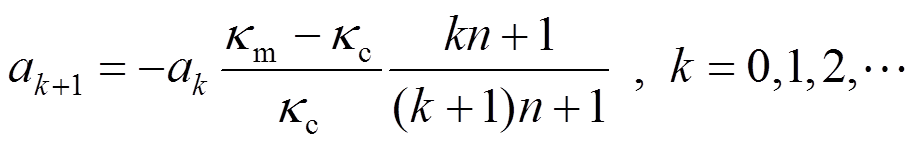 (8)
(8)
取五阶级数,这时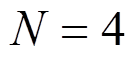 。联立式(6)与式(8)可以求得系数
。联立式(6)与式(8)可以求得系数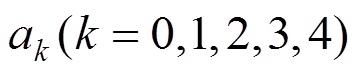 ,从而得到:
,从而得到:
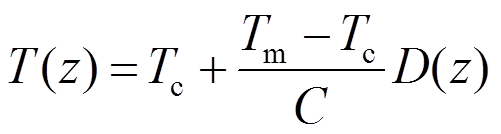 (9)
(9)其中的系数为:
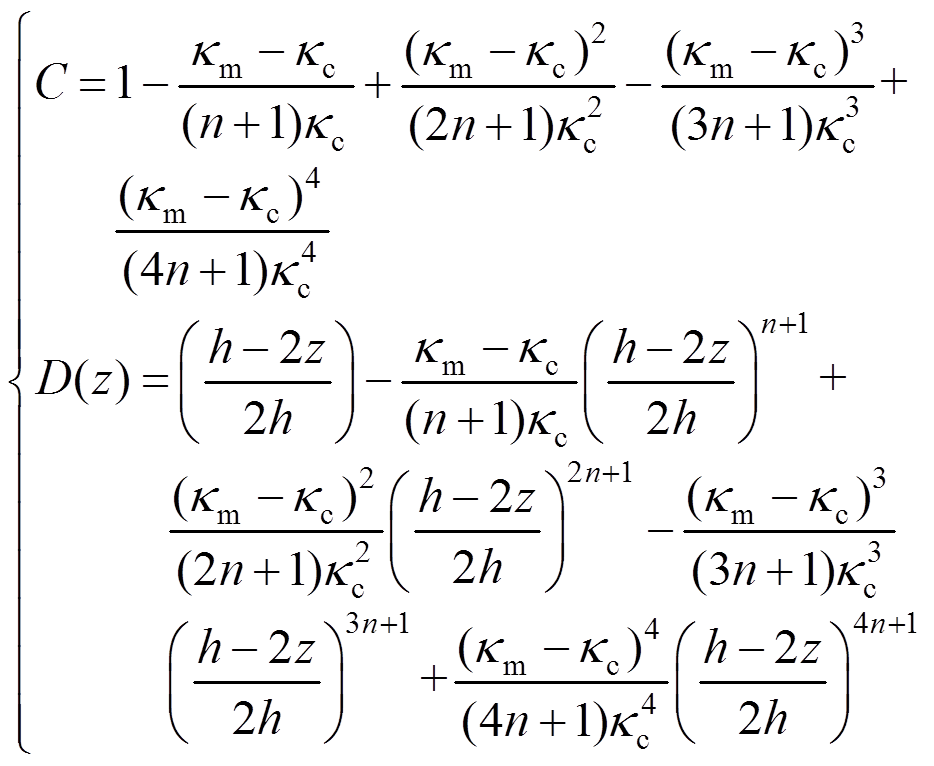 (10)
(10)
1) 方法1:哈密顿原理
由文献[39],为了使梁的本构方程中不存在拉弯耦合,取梁的物理中面为z=z0。
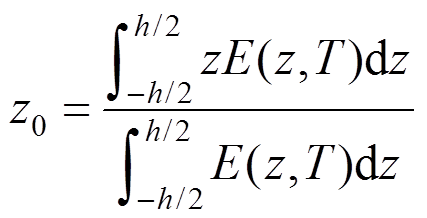 (11)
(11)假设梁物理中面处沿x和z方向的位移分别为u0(x,t)和w0(x,t)。这样,按照经典梁理论,梁上任意位置两个方向的位移可以表示为:
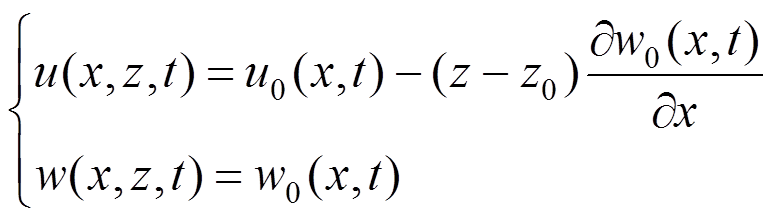 (12)
(12)
由von-Karmon几何大变形理论,梁的非线性几何方程可以写为:
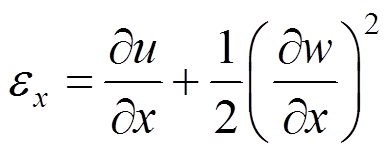 (13)
(13)将式(12)代入式(13)中,得到:
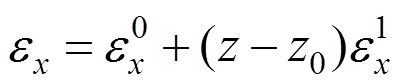 (14)
(14)
其中物理中面的轴向应变和曲率分别为:
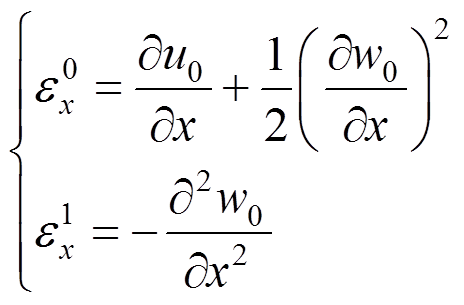 (15)
(15)热环境下的物理方程可以写为:
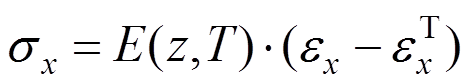 (16)
(16)
式中:温度应变为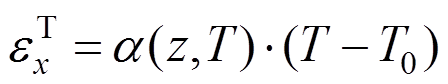 。
。
将σx在面内积分得到内力表达式为:
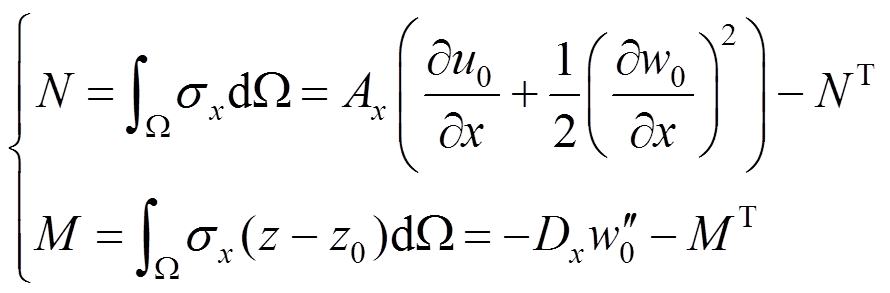 (17)
(17)式中:
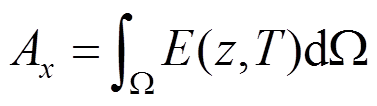 ,
,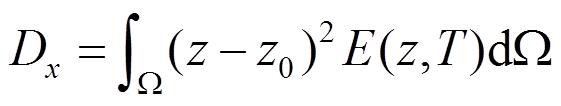 ,
,
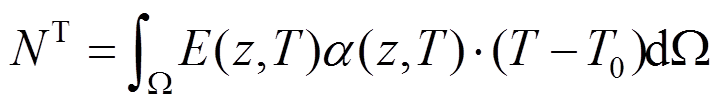 ,
,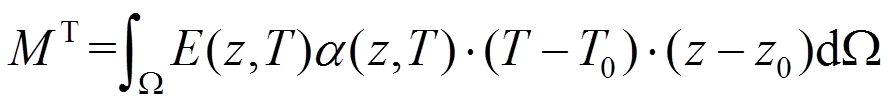 ,
,
Ω表示梁的横截面。
根据式(18)所示的哈密顿方程建立FGM梁的运动微分方程:
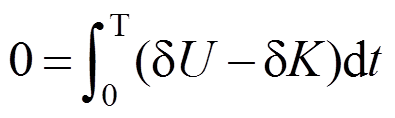 (18)
(18)式中的虚应变能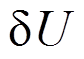 和虚动能
和虚动能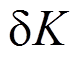 可以表示为(忽略梁轴向运动的动能和转动动能)。
可以表示为(忽略梁轴向运动的动能和转动动能)。
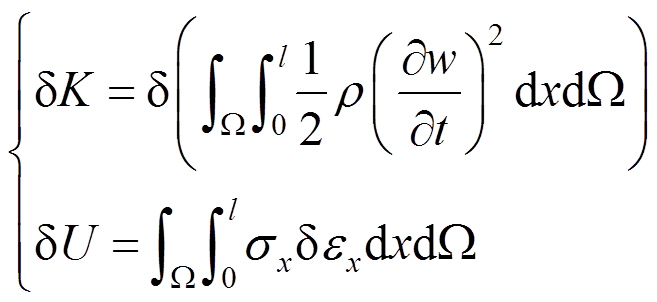 (19)
(19)
将w和εx表达式代入式(19),将得到的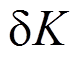 和
和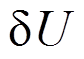 代入式(18),令
代入式(18),令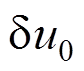 和
和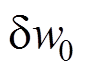 前的系数为0可以得到以内力表示的运动方程为:
前的系数为0可以得到以内力表示的运动方程为:
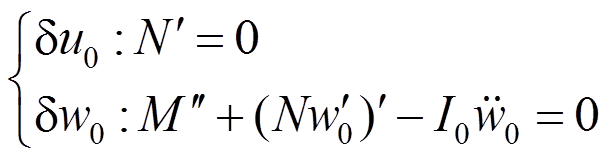 (20)
(20)式中:长度密度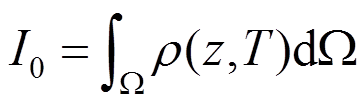 。
。
将内力的具体表达形式代入式(20),可以得到以物理中面轴向位移和挠度表示的运动微分方程为:
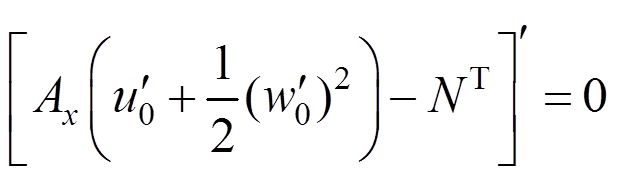 (21)
(21)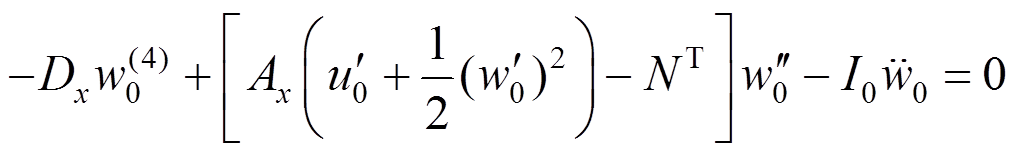 (22)
(22)
2) 方法2:轴线可伸长原理:
根据文献[18-19, 21],按照轴线可伸长理论建立的几何方程和平衡方程可以写为:
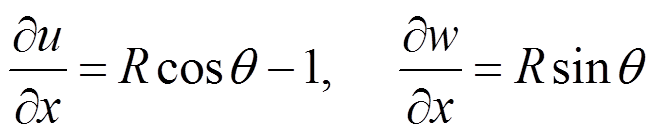 (23)
(23)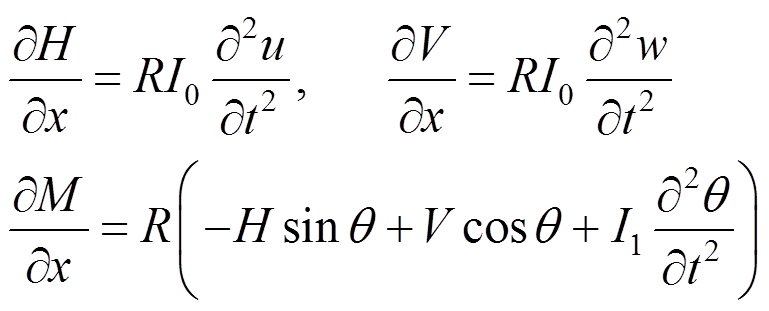 (24)
(24)
式中: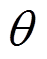 为变形后轴线切线与轴的夹角;H和V分别为内力合力在x和y的分量。轴线伸长率
为变形后轴线切线与轴的夹角;H和V分别为内力合力在x和y的分量。轴线伸长率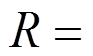
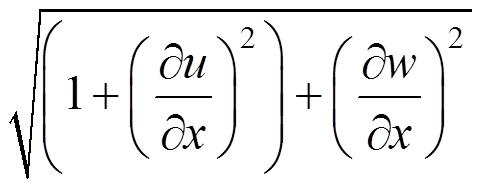 ,梁变形后单位长度转动惯量
,梁变形后单位长度转动惯量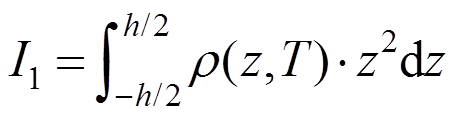 。
。
与上述文献中不同的是本文几何方程和平衡方程中的u、w为物理中面z=z0处的轴向位移和挠度。所以,梁任意位置的应变可以表示为:
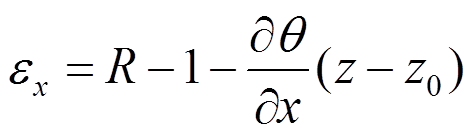 (25)
(25)由式(16)可以得出内力:
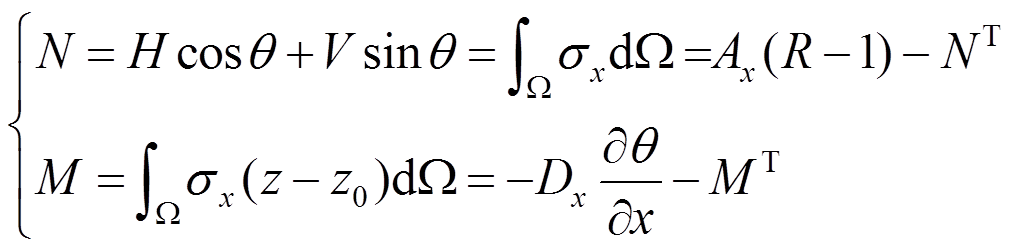 (26)
(26)
其中与方法1中名称相同的变量,含义与表达式均相同。
在进行线性分析时,可令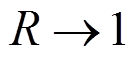 ,
,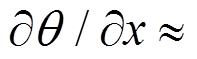
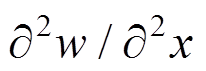 ,
,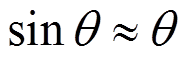 ,
,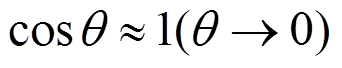 [18],同时忽略转动惯量。这时:
[18],同时忽略转动惯量。这时:
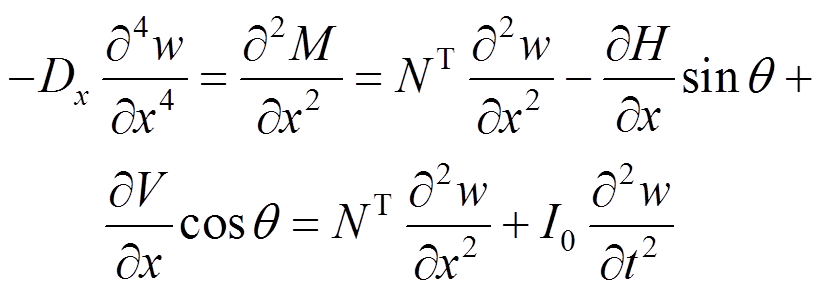 (27)
(27)从而:
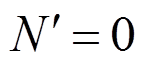 (28)
(28)
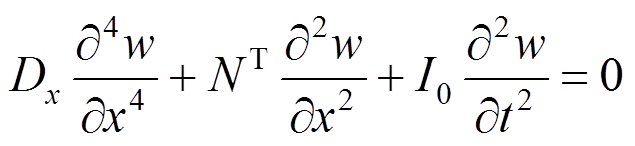 (29)
(29)式(28)、式(29)是线性热屈曲控制方程,利用他们可以计算屈曲前的振动频率,以及通过求解特征值问题计算屈曲温度。在推导线性方程式(28)~式(29)时只考虑了由温度产生的内力,而忽略了由于梁弯曲变形,轴向长度变化产生的内力。在推导非线性热屈曲控制方程时,需要补充由梁弯曲变形引起的内力。式(26)的第一式指出了总内力N与温度内力NT的关系,只需将式(29)中的NT替换为-N就可以得到考虑非线性的热屈曲控制方程,如下:
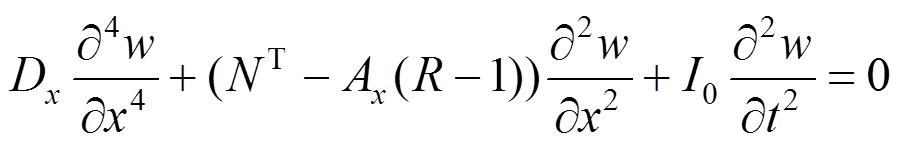 (30)
(30)
忽略高阶小量后可以得到:
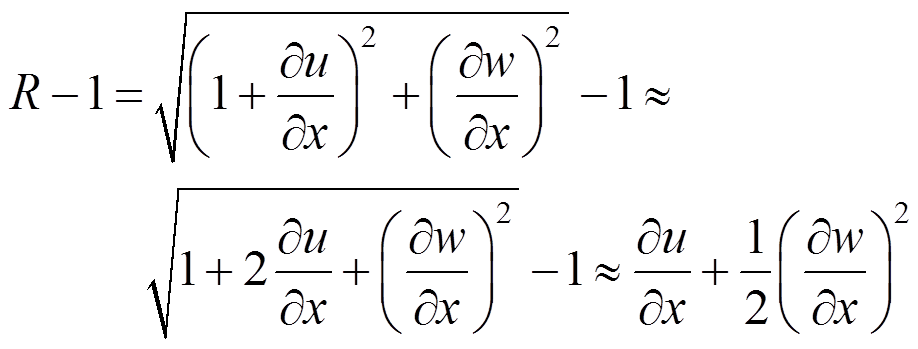 (31)
(31)将式(31)代入式(30)中便得到了与式(22)相同的表达形式。所以,由式(28)~式(29)可得出式(21)~ 式(22)。从而证明了,由哈密顿原理推导出的运动微分方程是轴线可伸长理论在忽略高阶小量情况下的近似形式。
首先积分式(21),可以得到:
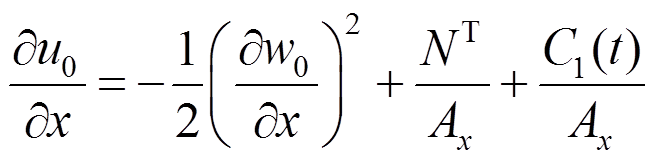 (32)
(32)对式(32)积分,可以得到:
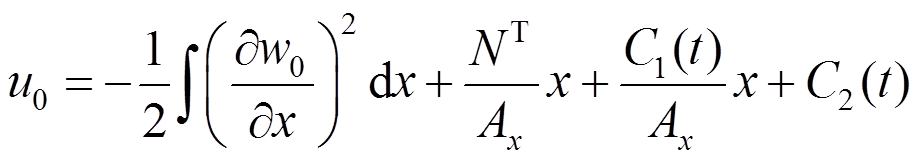 (33)
(33)
固支FGM梁的边界条件可以写为:
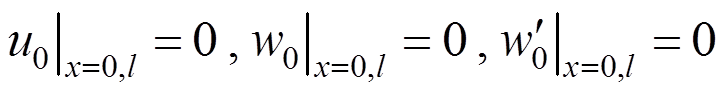 (34)
(34)由关于轴向位移的边界条件可以得到两个待定系数为:
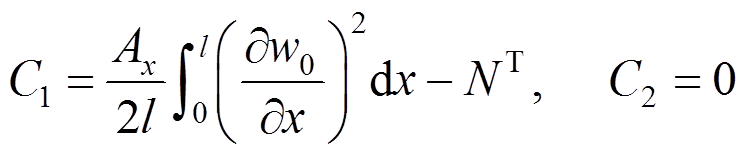 (35)
(35)
从而得到轴向位移u0的表达式,将其代入式(22)中,可以得到由挠度w0表示的运动微分方程为:
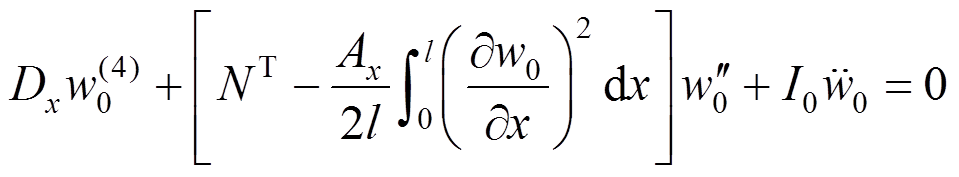 (36)
(36)热后屈曲梁的振动形式为谐振动叠加于屈曲静变形之上,所以挠度可以设为:
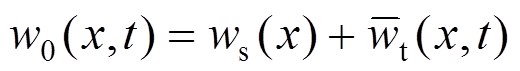 (37)
(37)
式中:ws(x)为位移的静态部分(屈曲静变形);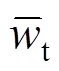 (x,t)为位移的动态部分(谐振动)。
(x,t)为位移的动态部分(谐振动)。
假设谐振动为:
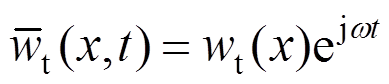 (38)
(38)其中,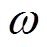 为梁的固有频率。
为梁的固有频率。
1) 热后屈曲解析求解
忽略式(36)中的质量项,并令ws代替w0可得到屈曲静变形满足下式:
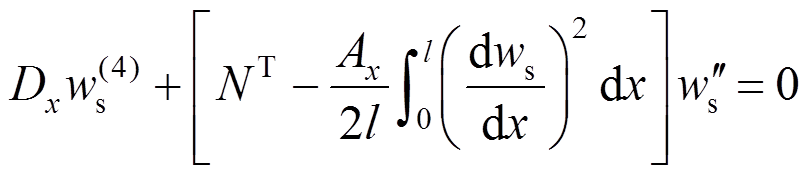 (39)
(39)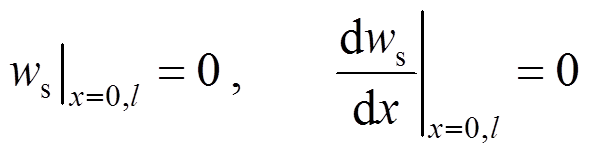 (40)
(40)
不失一般性,设无量纲参数:
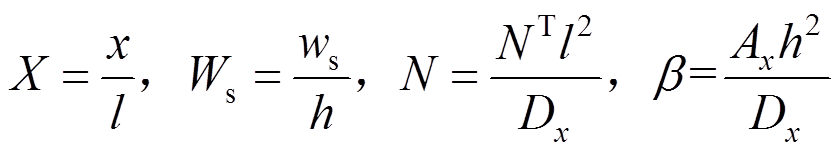 (41)
(41)可以得到热屈曲静态控制方程式(39)~式(40)的无量纲形式为:
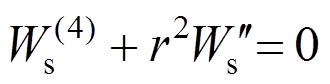 (42)
(42)
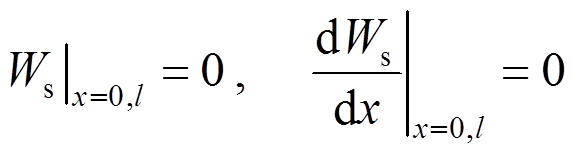 (43)
(43)式中: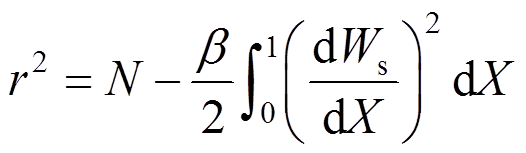 ;A为横截面的面积。
;A为横截面的面积。
式(42)~式(43)是一个特征值问题,易得屈曲静变形为:
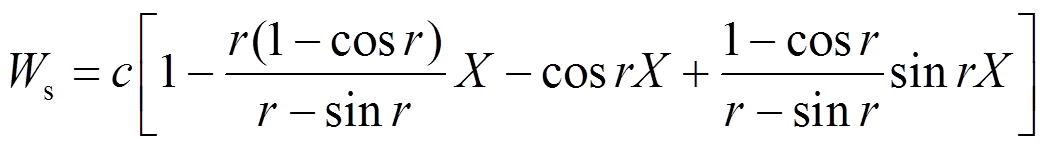 (44)
(44)式中: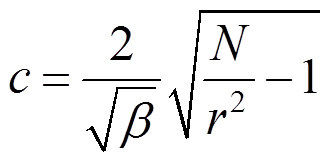 。易知,梁中点处的无量纲热屈曲变形为
。易知,梁中点处的无量纲热屈曲变形为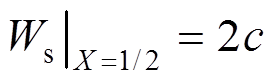 。
。
各阶特征值r如表1所示。
表1 固支梁各阶特征值
Table 1 Characteristic values of clamped beam

模型12345 r2π2.8606π4π4.9181π6π
2) 热后屈曲振动解析求解
将式(37)代入式(36)中,利用式(39)并略去非线性项,可以得到:
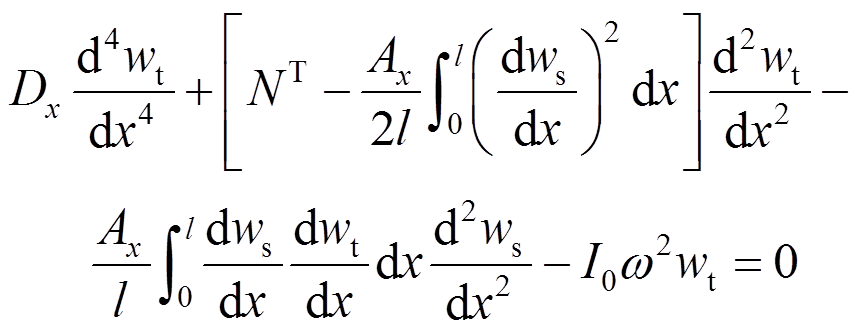 (45)
(45)除式(41)的无量纲参数之外,另设无量纲参数:
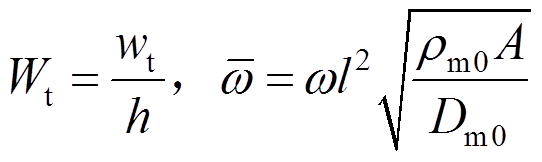 (46)
(46)
所以,式(45)变为:
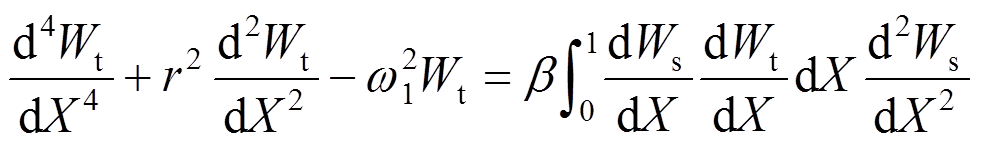 (47)
(47)其中: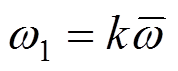 ,
,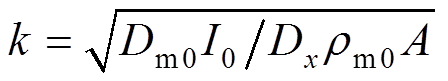 ,
,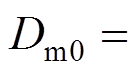
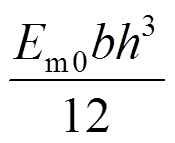 (角标带0表示初始温度下的材料属性)。
(角标带0表示初始温度下的材料属性)。
边界条件为:
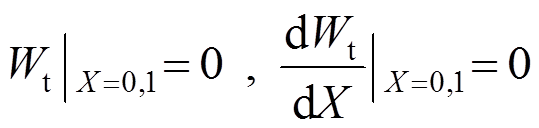 (48)
(48)式(47)为四阶非齐次常微分方程,所以可设其解为通解和特解和的形式:
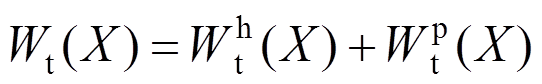 (49)
(49)
通解和特解分别满足下面两式:
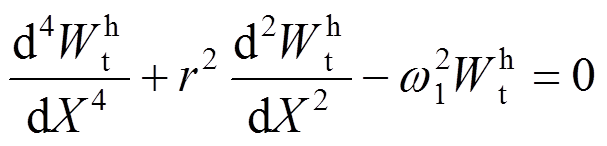 (50)
(50)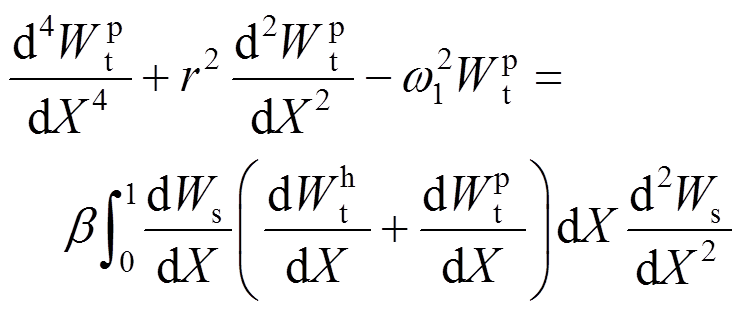 (51)
(51)
由式(50)可以解得通解为:
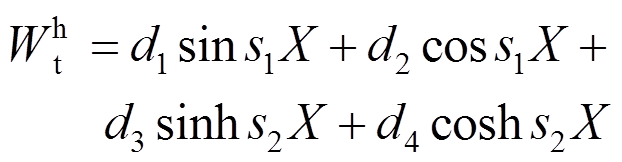 (52)
(52)式中: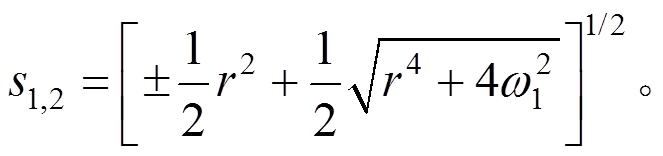
理论上特解可以取为任意形式,但当其取为如下形式时将大大简化公式的推导过程[22]:
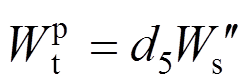 (53)
(53)将其代入式(51),可以得到:
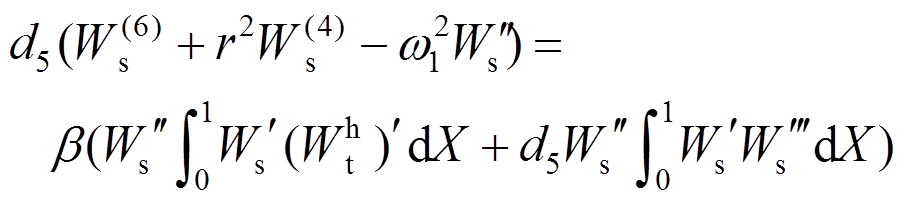 (54)
(54)
由式(42),式(54)化简为:
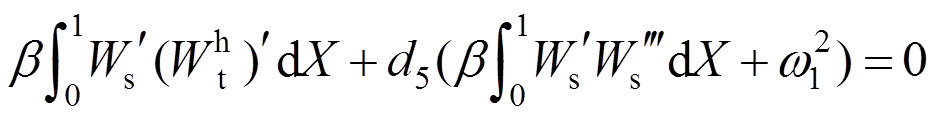 (55)
(55)综上,式(47)~式(48)解的形式可以写为:
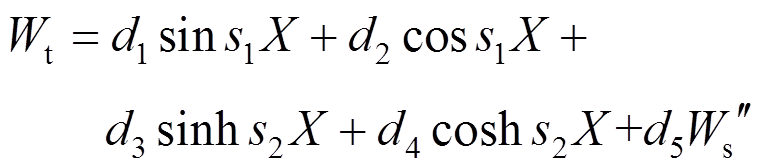 (56)
(56)
代入边界条件式(48)中,可以得到:
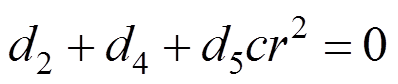 (57)
(57)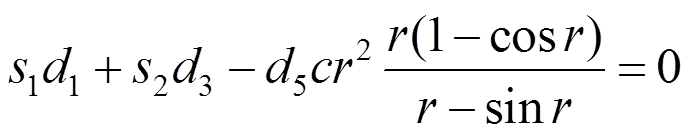 (58)
(58)
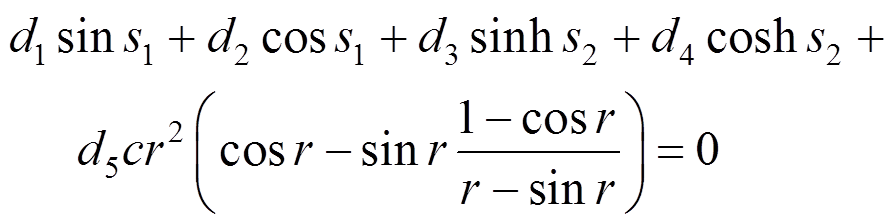 (59)
(59)
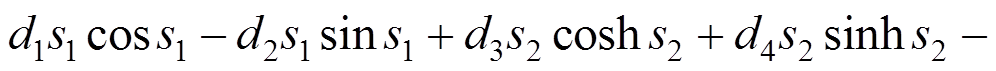
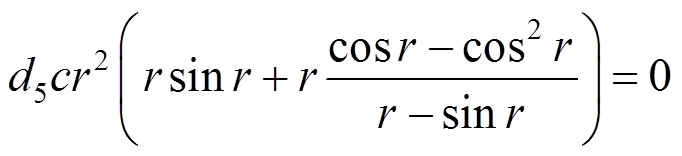 (60)
(60)
通过求解式(55)、式(57)~式(62)构成的特征值问题,可以得到FGM梁的各阶固有频率。
本节考虑Si3N4/SUS304功能梯度梁,材料属性见表2(p-1和p3均为0,所以没有列在表中。另设,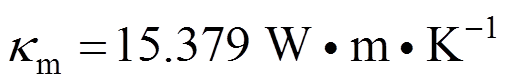 ,
,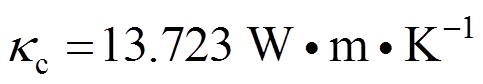 )。本文中FGM梁的几何参数为:h=0.1 m,宽对无量纲结果没有影响,所以无需列出。无量纲热载荷定义为:
)。本文中FGM梁的几何参数为:h=0.1 m,宽对无量纲结果没有影响,所以无需列出。无量纲热载荷定义为:
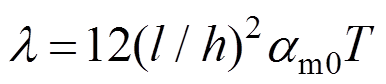 (61)
(61)在下面的讨论中:Td (Temperature Dependent)表示考虑材料的热敏性;Tid (Temperature Independent)表示不考虑材料的热敏性,取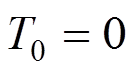 。可以证明,在不考虑温度对材料属性的影响时,梁后屈曲路径及无量纲振动频率不随长细比的变化而变化,见附录A。
。可以证明,在不考虑温度对材料属性的影响时,梁后屈曲路径及无量纲振动频率不随长细比的变化而变化,见附录A。
表2 功能梯度材料组分温敏系数[40]
Table 2 Thermal sensitivity of functionally graded material[40]

材料P0P1P2 E/GPaSUS304201.043.079×10-4-6.534×10-7 Si3N4348.43-3.07×10-42.16×10-7 ρ/(kg/m3)SUS304816600 Si3N4237000 α/(1/K)SUS30412.330×10-68.086×10-40 Si3N45.8723×10-69.095×10-40
本小节对FGM梁的热后屈曲路径进行了研究。图2~图4所示的屈曲变形随着热载荷的增大均先保持为零,后迅速增大。这表明,梁在热载荷低于临界屈曲温度时不发生屈曲变形,但当热载荷高于临界屈曲温度时发生屈曲并且变形幅值迅速增大。图2对考虑和不考虑材料属性随温度变化这两种情况在不同长细比下的热屈曲变形进行了研究。结果显示,当不考虑材料热敏性时,长细比为15和100的梁热后屈曲路径完全重合,这说明无量纲热屈曲变形不随梁长细比的变化而变化,与附录A中的理论推导结果一致;但在考虑温度对材料属性的影响时,长细比的增大会增大无量纲热屈曲载荷而且使热屈曲路径向高温方向移动并逐渐接近不考虑材料热敏性时的热屈曲路径,从而说明了只有在长细比较大时才可以忽略温度对材料的影响。图3研究了在考虑材料的热敏性时热屈曲路径与梯度指数的关系。结果表明,梯度指数的变化并不影响屈曲路径的变化趋势,只是梯度指数越大,无量纲热屈曲载荷越大;当材料性质介于陶瓷和金属之间时,后屈曲挠度也介于二者之间。图4研究了在考虑材料的热敏性时热屈曲路径与温度比的关系。结果表明,温度比越大,无量纲热屈曲载荷越大,同一热载荷下的挠度越小。
本小节对FGM梁在热环境下的振动进行了研究。图5~图7所示的梁频率-热载荷关系曲线均呈V字形。这表明,随着无量纲热载荷的增大,在屈曲前第一阶频率逐渐降低,在后屈曲阶段频率逐渐升高,这是因为屈曲前后阶段温度对梁刚度的影响相反[41],而当频率恰好为零时表明梁处于临界热屈曲状态。图5中对考虑和不考虑材料热敏性这两种情况在不同长细比下频率随热载荷的变化趋势进行了研究。结果显示,在不考虑材料的热敏性时,长细比为15和100时的无量纲频率-热载荷曲线完全重合,这说明无量纲频率不随梁长细比的变化而变化,这同样与附录A的结论相同;但在考虑温度对材料属性的影响时,长细比的增大会使频率下降更加缓慢且频率变化曲线向高温方向移动并逐渐接近不考虑材料热敏性时的频率变化曲线,从而说明了只有在长细比较大时才可以忽略温度对材料属性的影响,这与2.1节的结论相同。图6研究了在考虑材料热敏性时不同梯度指数下频率随热载荷的变化趋势。结果表明,梯度指数并不影响频率随热载荷的变化趋势,但梯度指数的增大会使频率变化曲线向高温方向移动。图7研究了在考虑温度对材料属性的影响时不同温度比下频率随热载荷的变化趋势。结果表明,温度比的增大会使频率变化曲线向高温方向移动。从三个图中,各曲线与y轴交点可以看出,在没有热载荷作用时,无量纲频率只与梯度指数有关,与长细比和温度比均无关。
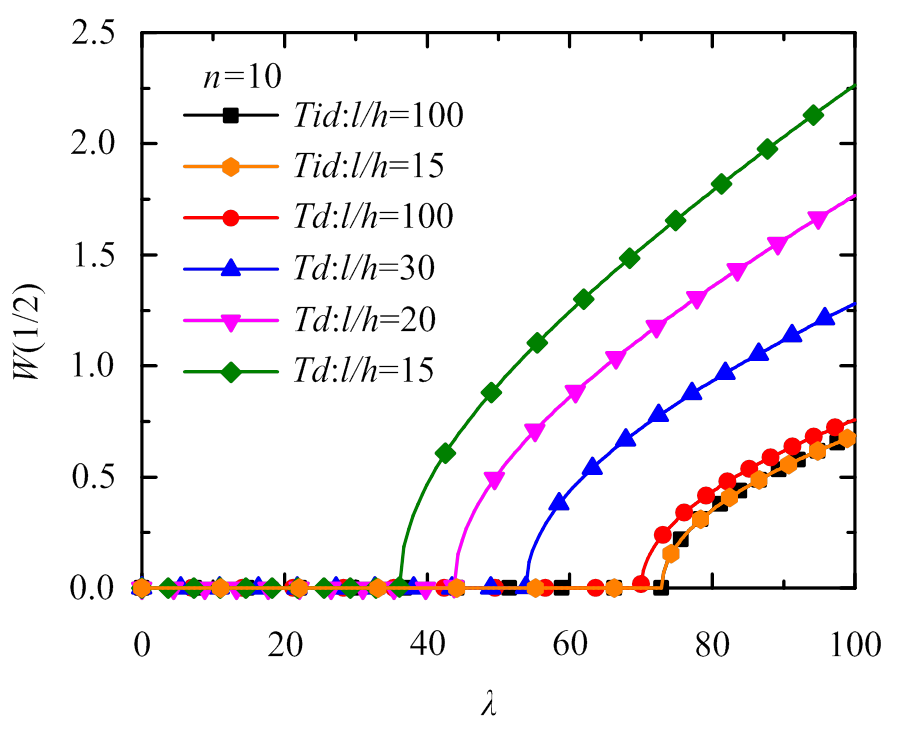
图2 不同长细比下固支FGM梁热屈曲路径
Fig.2 Thermal buckling paths of clamped FGM beam with different slenderness ratios
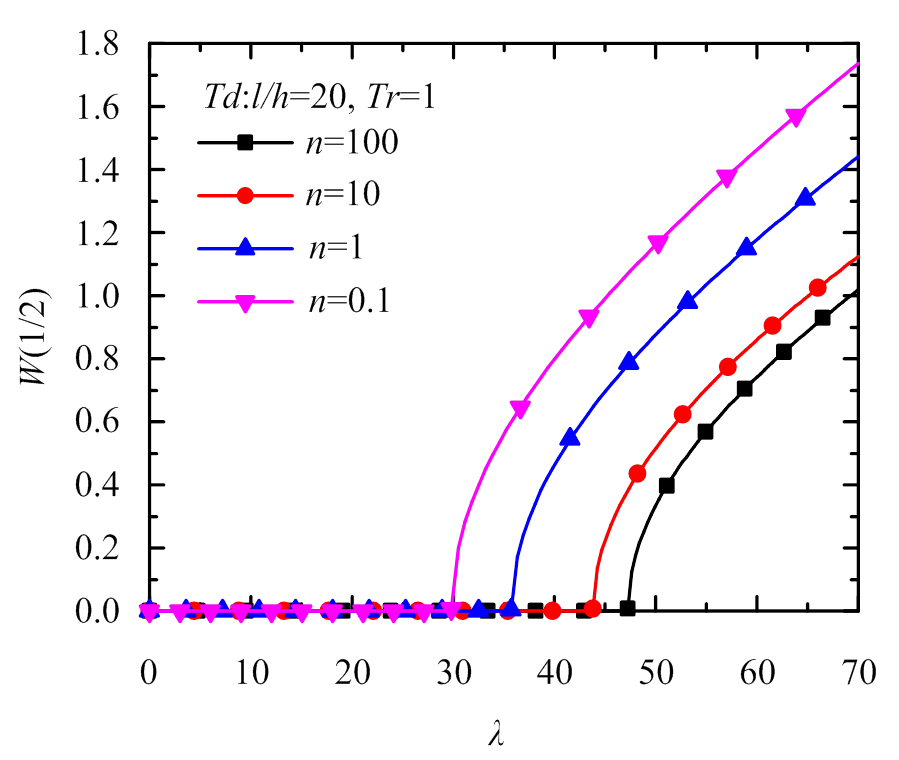
图3 不同梯度指数下固支FGM梁热屈曲路径
Fig.3 Thermal buckling paths of clamped FGM beam under different gradient indexes
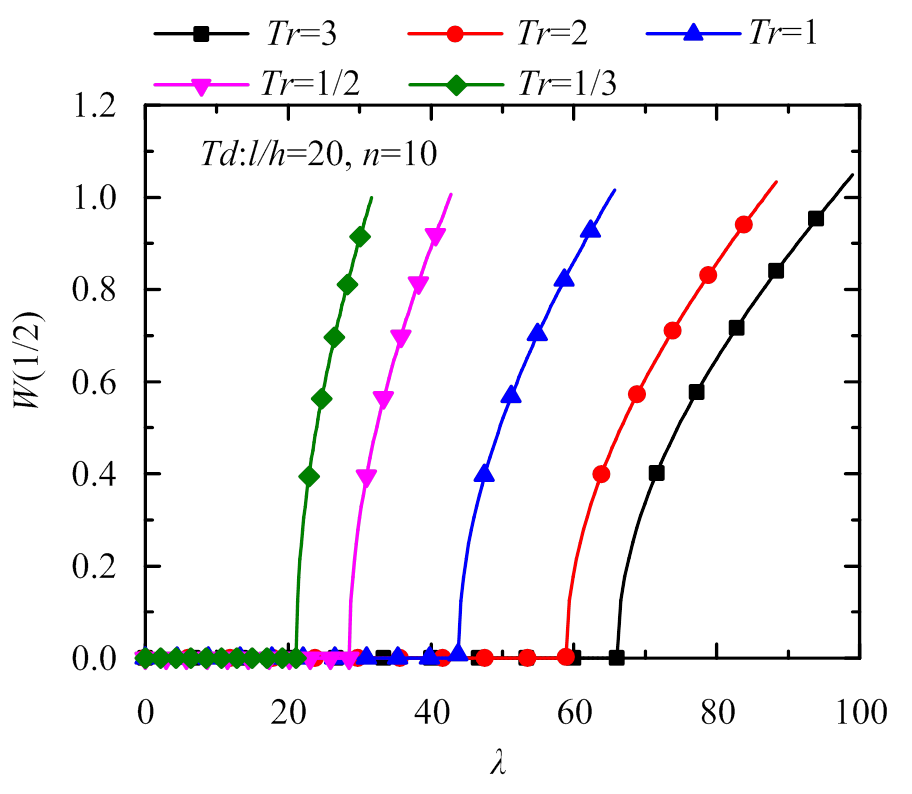
图4 不同温度比下固支FGM梁热屈曲路径
Fig.4 Thermal buckling paths of clamped FGM beam under different temperature ratios
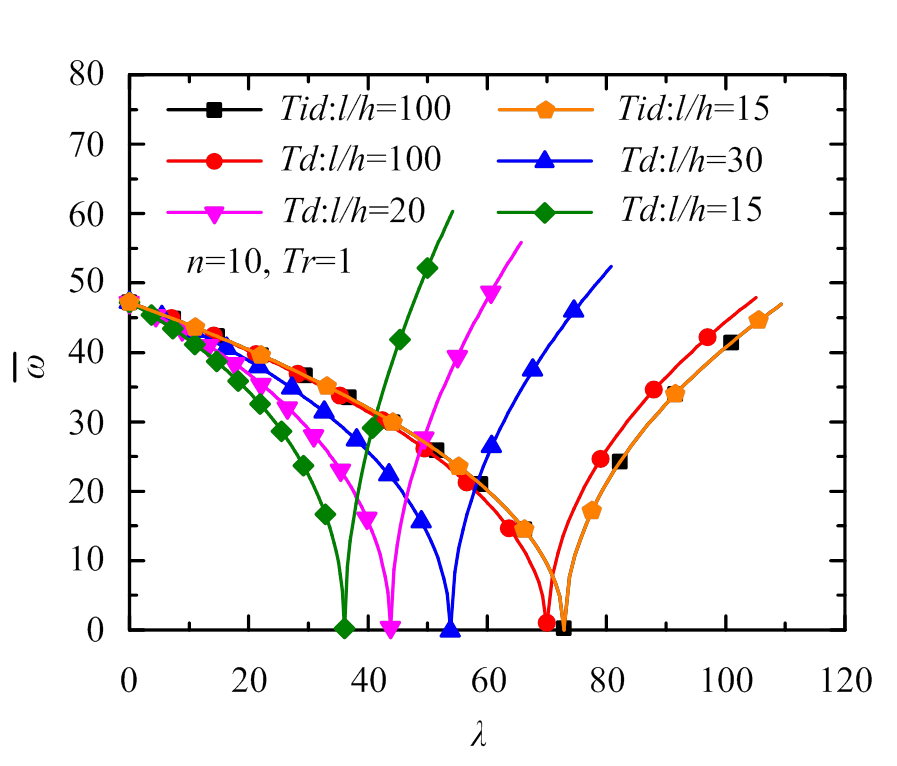
图5 不同长细比下固支FGM梁频率-热载荷关系曲线
Fig.5 Relationship between frequency and thermal load of clamped FGM beam with different slenderness ratios
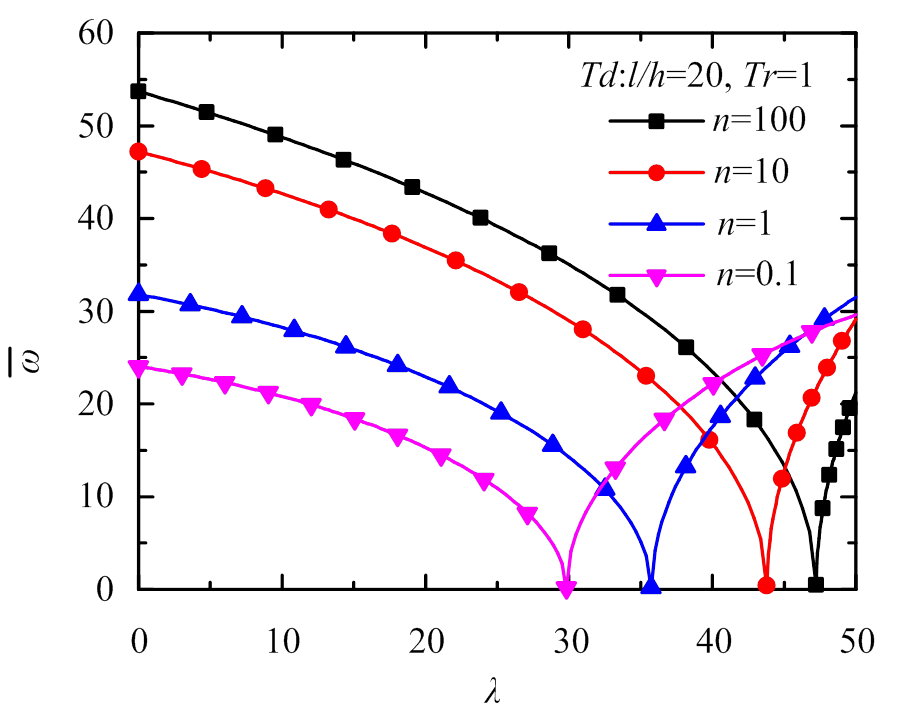
图6 不同梯度指数下固支FGM梁频率-热载荷关系曲线
Fig.6 Relationship between frequency and thermal load of clamped beam under different gradient indexes
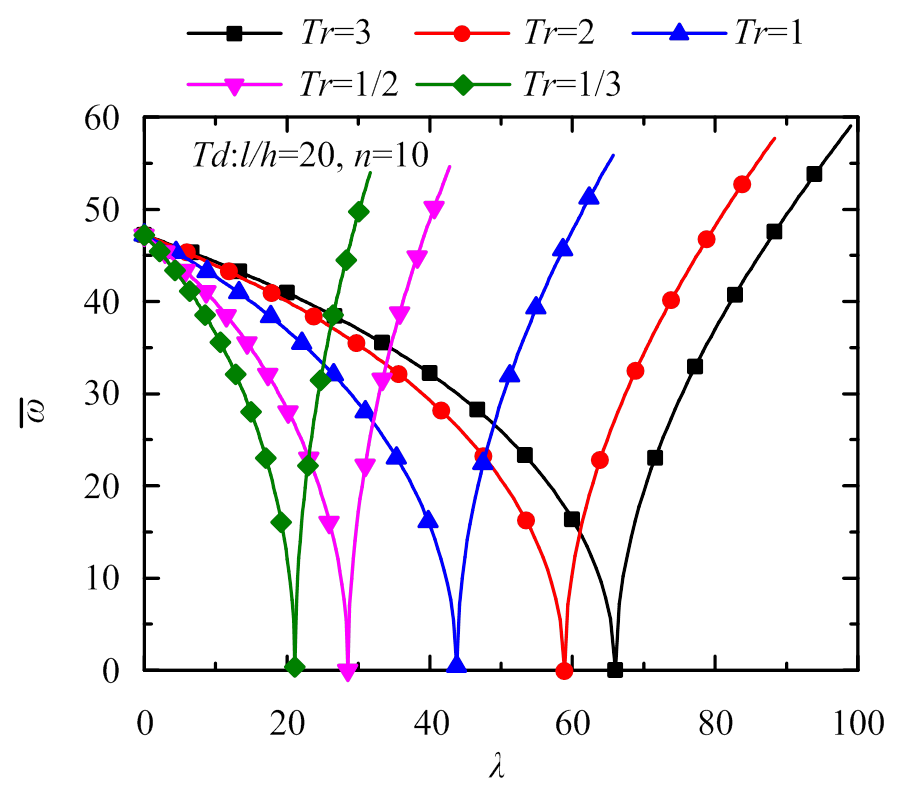
图7 不同温度比下固支FGM梁频率-热载荷关系曲线
Fig.7 Relationship between frequency and thermal load of clamped beam under different temperature ratios
本文通过两种不同的方法得到了热环境中功能梯度梁的运动微分方程,并且证明了通过轴线可伸长理论得到的结果在忽略高阶小量时与哈密顿原理得到的结果相同。将两个关于轴向位移和挠度的非线性运动方程化简为一个仅关于挠度的控制方程。假设振动形式为屈曲静变形叠加简谐微振动。代入控制方程后与边界条件联立,通过求解特征值问题便可以得到振动频率。证明了在不考虑材料的热敏性时,无量纲热屈曲路径和无量纲频率-热载荷变化曲线均不随梁长细比的变化而变化。通过对梁静、动力学行为的相关计算,可以得到:只有在长细比较大时才可以忽略温度对材料属性的影响,在长细比较小时误差较大;在考虑温度对材料属性的影响时,无量纲热屈曲路径和频率-热载荷曲线的变化趋势不会随着梁梯度指数或温度比的变化而变化。但梯度指数或温度比越大,无量纲临界热屈曲载荷越高,且热屈曲路径和频率-热载荷曲线均向无量纲热载荷增大的方向移动。
参考文献:
[1] 赵磊, 胡超. 功能梯度材料应用及动力学分析[J]. 飞航导弹, 2011(8): 93―96.
Zhao Lei, Hu Chao. Application and kinetic analysis of functionally graded materials [J]. Winged Missiles Journal, 2011(8): 93―96. (in Chinese)
[2] Duc N D, et al. Nonlinear stability of eccentrically stiffened S-FGM elliptical cylindrical shells in thermal environment [J]. Thin-Walled Structures, 2016, 108: 280―290.
[3] Huang H W, Zhang Y Q, Han Q. Stability of hydrostatic-pressured FGM thick rings with material nonlinearity [J]. Applied Mathematical Modelling, 2017, 45: 55―64.
[4] 李清禄, 栾玮荻, 李世荣. 功能梯度材料圆板在随从力作用下的稳定性[J]. 玻璃钢/复合材料, 2016(10): 5―10.
Li Qinglu, Luan Weidi, Li Shirong. The stability of FGM circular plates subjected to follower force [J]. Fiber Reinforced Plastics/Composites, 2016(10): 5―10. (in Chinese)
[5] Bouderba B, Houari M S A, Tounsi A, et al. Thermal stability of functionally graded sandwich plates using a simple shear deformation theory [J]. Structural Engineering & Mechanics, 2016, 58(3): 397―422.
[6] Majumadar A, Das D. A study on thermal buckling load of clamped functionally graded beams under linear and nonlinear thermal gradient across thickness [J]. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2018, 232(9): 769―784.
[7] Eroglu U. In-plane free vibrations of circular beams made of functionally graded material in thermal environment: Beam theory approach [J]. Composite Structures, 2015, 122: 217―228.
[8] Ebrahimi F, Barati M R. Vibration analysis of nonlocal beams made of functionally graded material in thermal environment [J]. European Physical Journal Plus, 2016, 131(279): 1―22.
[9] 蒋坤. 功能梯度材料薄板热模态分析[D]. 河北: 河北工程大学, 2017.
Jiang Kun. Thermal modal analysis of functionally graded plate [D]. Hebei: Hebei University of Engineering, 2017. (in Chinese)
[10] 刘文光, 舒斌, 郭隆清, 等. 热环境对FGM壳模态频率的影响[J]. 振动与冲击, 2017, 36(4): 127―131.
Liu Wenguang, Shu Bin, Guo Longqing, et al. Impacts of thermal environment on modal frequency of FGM shells [J]. Journal of Vibration and Shock, 2017, 36(4): 127―131. (in Chinese)
[11] Bhangale R K, Ganesan N. Thermoelastic buckling and vibration behavior of a functionally graded sandwich beam with constrained viscoelastic core [J]. Journal of Sound & Vibration, 2006, 295(1/2): 294―316.
[12] Kapuria S, Bhattacharyya M, Kumar A N. Bending and free vibration response of layered functionally graded beams: A theoretical model and its experimental validation [J]. Composite Structures, 2008, 82(3): 390―402.
[13] Kocaturk T, Akbas S D. Post-buckling analysis of Timoshenko beams made of functionally graded material under thermal loading [J]. Structural Engineering & Mechanics, 2012, 41(6): 775―789.
[14] Lee Y Y, Zhao X, Reddy J N. Postbuckling analysis of functionally graded plates subject to compressive and thermal loads [J]. Computer Methods in Applied Mechanics & Engineering, 2010, 199(25/26/27/28): 1645―1653.
[15] Wattanasakulpong N, Prusty B G, Kelly D W. Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams [J]. International Journal of Mechanical Sciences, 2011, 53(9): 734―743.
[16] Shen H S. Postbuckling of shear deformable FGM cylindrical shells surrounded by an elastic medium [J]. International Journal of Mechanical Sciences, 2009, 51(5): 372―383.
[17] She G L, Yuan F G, Ren Y R. Thermal buckling and post-buckling analysis of functionally graded beams based on a general higher-order shear deformation theory [J]. Applied Mathematical Modelling, 2017, 47: 340―357.
[18] Li S R, Batra R C. Thermal buckling and postbuckling of euler-bernoulli beams supported on nonlinear elastic foundations [J]. Aiaa Journal, 2007, 3(45): 712―720.
[19] 李清禄, 李世荣. 功能梯度材料梁在后屈曲构形附近的自由振动[J]. 振动与冲击, 2011, 30(9): 76―78.
Li Qinglu, Li Shirong. Free vibration of FGM Euler beam with post-buckling configuration subjected to axial force [J]. Journal of Vibration and Shock, 2011, 30(9): 76―78. (in Chinese)
[20] 钮鹏, 李旭, 李世荣, 等. 弹性地基上复合材料夹层梁的热过屈曲[J]. 工程力学, 2017, 34(增刊1): 26―30.
Niu Peng, Li Xu, Li Shirong, et al. The thermal buckling of composite sandwich beams on elastic foundations [J]. Engineering Mechanics, 2017, 34(suppl 1): 26―30. (in Chinese)
[21] Sun Y, Li S R, Batra R C. Thermal buckling and post-buckling of FGM Timoshenko beams on nonlinear elastic foundation [J]. Journal of Thermal Stresses, 2016, 39(1): 11―26.
[22] Nayfeh A H, Emam S A. Exact solution and stability of postbuckling configurations of beams [J]. Nonlinear Dynamics, 2008, 54(4): 395―408.
[23] 马连生, 顾春龙. 剪切可变形梁热过屈曲解析解[J]. 工程力学, 2012, 29(2): 172―176.
Ma Liansheng, Gu Chunlong. Exact solutions for thermal post-buckling of shear deformable beams [J]. Engineering Mechanics, 2012, 29(2): 172―176. (in Chinese)
[24] Ma L S, Lee D W. A further discussion of nonlinear mechanical behavior for FGM beams under in-plane thermal loading [J]. Composite Structures, 2011, 93(2): 831―842.
[25] Levyakov S V. Elastica solution for thermal bending of a functionally graded beam [J]. Acta Mechanica, 2013, 224(8): 1731―1740.
[26] 崔德福. 含粘滞-滑移-约束边界的梁和板的热屈曲及热振动研究[D]. 南京: 南京航空航天大学, 2015.
Cui Defu. Thermal buckling and thermal vibration of beams and plates with stick-slip-stop boundaries [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. (in Chinese)
[27] 毛丽娟, 马连生. 非均匀热载荷作用下功能梯度梁的非线性静态响应[J]. 工程力学, 2017, 34(6): 1―8.
Mao Lijuan, Ma Liansheng. Nonlinear static responses of FGM beams under non-uniform thermal loading [J]. Engineering Mechanics, 2017, 34(6): 1―8. (in Chinese)
[28] Ebrahimi F, Jafari A. A higher-order thermomechanical vibration analysis of temperature-dependent fgm beams with porosities [J]. Journal of Engineering, 2016, 2016(2): 1―20.
[29] Ebrahimi F, Jafari A. A four-variable refined shear-deformation beam theory for thermo-mechanical vibration analysis of temperature-dependent FGM beams with porosities [J]. Mechanics of Advanced Materials & Structures, 2018, 25(3): 212―224.
[30] 钮鹏, 李旭, 李世荣, 等. 弹性约束下Timoshenko夹层梁的热屈曲行为研究[J]. 工程力学, 2018, 35(增刊1): 13―16, 39.
Niu Peng, Li Xu, Li Shirong, et al. The thermal buckling behavior of Timoshenko sandwich beam under elastic constraint [J]. Engineering Mechanics, 2018, 35(Suppl 1): 13―16, 39. (in Chinese)
[31] Taati E. On buckling and post-buckling behavior of functionally graded micro-beams in thermal environment [J]. International Journal of Engineering Science, 2018, 128: 63―78.
[32] Bagheri H, Kiani Y, Eslami M R. Asymmetric thermal buckling of temperature dependent annular FGM plates on a partial elastic foundation [J]. Computers and Mathematics with Applications, 2018, 75(5): 1566―1581.
[33] Do Q C, Dao V D, Le K H. Thermal buckling analysis of stiffened FGM truncated conical shells resting on elastic foundations using FSDT [J]. Acta Mechanica, 2018, 229(5): 2221―2249.
[34] 赵伟东, 高士武, 马宏伟. 功能梯度扁球壳在热-机械荷载作用下的屈曲分析[J]. 工程力学, 2018, 35(12): 220―228.
Zhao Weidong, Gao Shiwu, Ma Hongwei. Thermomechanical buckling analysis of functionally graded shallow spherical shells [J]. Engineering Mechanics, 2018, 35(12): 220―228. (in Chinese)
[35] Shen H S. Functionally graded materials nonlinear analysis of plates and shells [M]. USA: CRC Press, 2009: 3―7.
[36] Kim Y W. Temperature dependent vibration analysis of functionally graded rectangular plates [J]. Journal of Sound & Vibration, 2005, 284(3): 531―549.
[37] Reddy J N, Chin C D. Thermomechanical analysis of funuctionally graded cylinders and plates [J]. Journal of Thermal Stresses, 1998, 21(6): 593―626.
[38] Yang J, Shen H S. Vibration characteristics and transient response of shear-deformable functionally graded plates in thermal environments [J]. Journal of Sound & Vibration, 2002, 255(3): 579―602.
[39] 马连生, 张璐. 面内热载荷作用下功能梯度梁热过屈曲精确解[J]. 兰州理工大学学报, 2015, 41(1): 164―167.
Ma Liansheng, Zhang Lu. Exact solutions for thermo-post-buckling of functionally graded material beams under in-plane thermal loading [J]. Journal of Lanzhou University of Technology, 2015, 41(1): 164―167. (in Chinese)
[40] Shahrjerdi A, Bayat M, Majid D L A. Free vibration analysis of solar functionally graded plates with temperature-dependent material properties using second order shear deformation theory [J]. Journal of Mechanical Science & Technology, 2011, 25(9): 2195―2209.
[41] 牛牧华, 马连生. 基于物理中面FGM梁的非线性力学行为[J]. 工程力学, 2011, 28(6): 219―225.
Niu Muhua, Ma Liansheng. Nonlinear mechanical behaviors of FGM beams based on the physical neutral surface [J]. Engineering Mechanics, 2011, 28(6): 219―225. (in Chinese)
当不考虑材料热敏性时,可以得到:
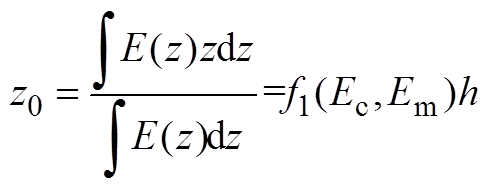 (A1)
(A1)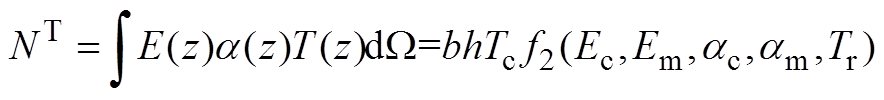 (A2)
(A2)
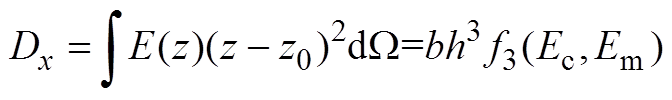 (A3)
(A3)
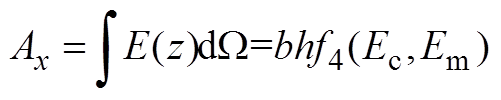 (A4)
(A4)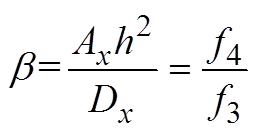 (A5)
(A5)
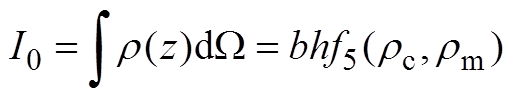 (A6)
(A6)
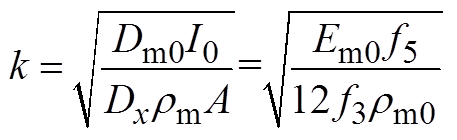 (A7)
(A7)1) 不考虑材料热敏性时无量纲热屈曲载荷与长细比无关
当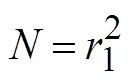 时发生热屈曲。此时:
时发生热屈曲。此时:
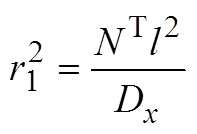 (A8)
(A8)根据式(A8)可以求得临界热屈曲温度为:
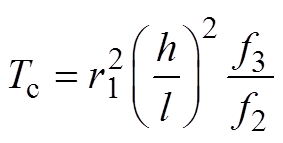 (A9)
(A9)
从而无量纲热屈曲载荷为:
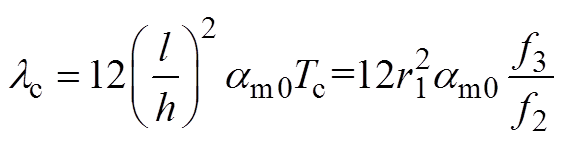 (A10)
(A10)所以,无量纲热屈曲载荷与梁的长细比无关,且临界屈曲温度与长细比的平方成正比。
2) 不考虑材料热敏性时同一无量纲热载荷下无量纲热屈曲变形与长细比无关
式 (61)、式(A2)和式(A3)联立可得:
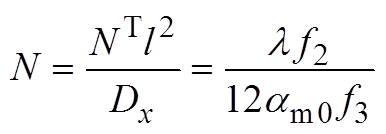 (A11)
(A11)从而:
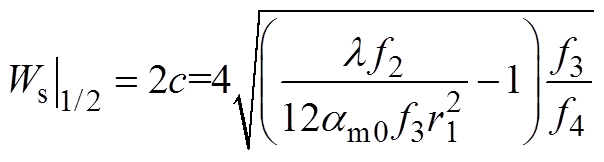 (A12)
(A12)
所以,对于一个给定的无量纲热载荷,无量纲热屈曲变形与长细比无关。
3) 不考虑材料热敏性时同一无量纲热载荷下无量纲频率与长细比无关
式 (55)、式(57)~ 式(60)中的c和β均不随长细比变化而变化,所以根据特征值问题求得的ω1也不随长细比变化,从而无量纲频率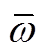 不随长细比变化。
不随长细比变化。
THERMAL POST-BUCKLING ANALYSIS OF FGM BEAMS CONSIDERING THE HEAT EFFECT ON MATERIALS
Abstract: Thermal post-buckling analysis of functionally graded beams is of great significance for the practical implementation of functionally graded materials for the thermal insulation of spacecrafts. The governing equations of the functionally graded beam in thermal environment are obtained based on the geometrical nonlinear theory and the introduction of the physical neutral surface. By simplification, a fourth-order integral-differential equation with respect to transverse deformation is obtained, and the eigenvalue problem is solved with the clamped boundary condition. The thermal post-buckling and the vibration on the basis of the buckled configuration are investigated. Firstly, the governing equations obtained by the Hamilton's principle are proved to be approximate equations obtained by the axial extension theory. Then, considering the heat effect on the properties of the material, the influence of the slenderness ratio, functionally gradient index and temperature ratio on post-buckling vibration is analyzed in detail. The heat effect on the properties of the material can be neglected when the slenderness is large enough. Increasing the slenderness ratio, functionally gradient index or temperature ratio will increase the non-dimensional thermal buckling load.
Key words: functionally graded beam; thermal post-buckling; vibration; analytical solution; first order frequency
文章编号:1000-4750(2019)04-0052-10
中图分类号:O343
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.03.0142
收稿日期:2018-03-13;
修改日期:2018-12-20
基金项目:国家自然科学基金项目(11372084)