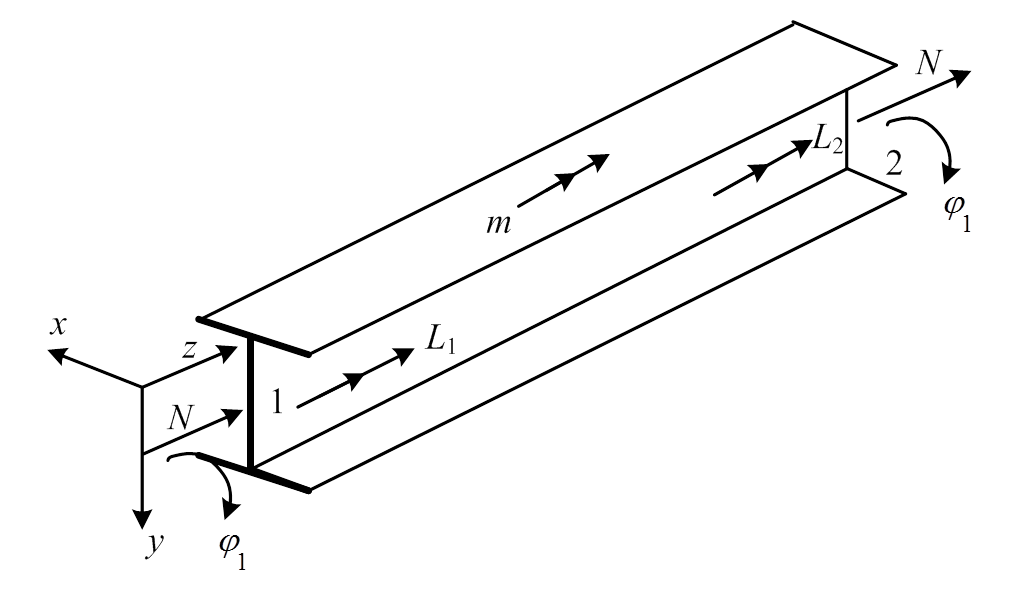
图1 压扭杆单元
Fig.1 Bar element under compression and torsion
摘 要:为提高压扭杆件内力和变形分析的精度和效率,以Vlasov扭转理论为基础,根据压扭杆件位移控制方程,考虑大位移和截面翘曲影响,构建了压扭杆的单元位移形函数,采用势能原理建立了压扭杆势能泛函。利用势能驻值变分原理得出了解析型压扭杆单元列式,并推导了用于杆件内力分析的单元刚度矩阵。将其与理论解、插值多项式单元进行对比,结果表明:该文构造的单元计算压扭杆转角及翘曲率和临界荷载的精度高于插值多项式单元,且不需划分单元,即可保证计算结果与理论解一致,满足了高精度、高效率的要求,可应用于解决实际工程问题。
关键词:压扭;解析形函数;变分原理;有限元;单元刚度矩阵
压扭杆,指承受以轴力为主,同时可能有扭曲变形的杆件,由于开口薄壁杆的抗扭刚度较小,因此压杆扭转变形更多发生在此类截面的杆件之中。由于开口薄壁杆件加工成型工艺简单、截面具有较大的抗弯刚度,因此实际工程中,开口薄壁杆件应用较广,如轧制型钢、冷弯薄壁连杆或桁架杆等轴心受压杆;也可以指承受轴力和扭矩共同作用的杆件,如送变电杆塔、海上采油平台腿柱[1]等。
抗弯刚度很大但抗扭刚度较小的轴心受压杆,当所受轴力达到某一临界值时压杆的稳定平衡状态被打破,发生微扭转变形;随着轴力增大,扭转变形迅速增大而使构件丧失承载力,发生扭转屈曲或扭转失稳[2],此类杆件的扭转屈曲临界荷载的计算是杆件设计的基础;在轴力和扭矩作用下,杆件易发生扭转变形,受轴力影响,构件扭转变形进一步增大产生二阶扭矩,这属于构件几何非线性问题。若分析压扭杆受力性能时不考虑二阶扭矩影响,将导致杆件内力计算结果偏低,影响结构安全性。因此,对轴心受压杆的扭转屈曲问题及压扭杆的非线性问题进行分析并提高分析方法的精度和效率非常必要。同时,研究压扭杆受力性能是研究其他复杂受力状态下杆件力学性能的基础[3]。
根据压扭杆受力特征,许多学者采用静力法和能量法等解析法对此类杆件进行了研究[4-8]。静力法是利用压扭分析理论,建立杆件的扭转刚度方程,通过直接求解刚度方程或初参数法求得杆件变形及内力。能量法是利用能量原理,通过假定含待定参数的几何可能位移场建立结构的能量泛函,利用能量驻值条件计算杆件或杆件结构的内力及变形。这些理论方法可精确解决少数简单工况下压扭杆受力性能的计算问题,对于承受复杂工况、或沿杆长存在均布轴力或扭矩的杆件分析,静力法和能量法均无法得到满意解。
为研究复杂工况情况下压扭杆受力,不同学者[9-12]通过试验和理论计算法对压扭杆受力性能进行了研究。Rasmussen和Hancock[13]、聂诗东 等[14]、李国强等[15]考虑构件受力状态得出了轴心受压构件稳定极限承载力并提出了合理的设计建议;Hsu和Liang[16]、Hsu和Hsieh[17]、黄宏等[3]基于试验和理论研究对轴力和扭矩荷载作用下构件受力性能进行了研究。但这些方法都是基于线性分析或试验计算杆件在扭转屈曲或压扭复合受力下的承载力,难以反映所有构件的实际受力情况。
数值计算方法,如有限元法[18-24]以其理论基础严密、构造方法简单、分析步骤标准,被很多学者认为是最有效的分析压扭杆受力性能的方法。实际分析中,常采用插值形函数法构造的压扭杆单元对压扭杆受力进行分析,但该方法在建立位移形函数时采用的函数为多项式插值函数,该多项式插值函数为位移的近似方程,计算结果存在截断误差,计算精度较低。为取得较好计算精度,须采取多划单元,加密节点的技术,必然造成计算效率的降低。Cao等[25]、Tang等[26]、李潇等[27]、李静等[28]提出了构建杆件单元解析形函数法的一般理论,并构造出一系列解析型单元,该方法构造的单元只需将复杂杆件划分为一个单元,即可求得杆件真实位移,既保证了计算精度又提高了计算效率。
本文以压扭杆为研究对象,基于Vlasov扭转理论和有限元法,考虑截面翘曲和大位移影响,建立了压扭杆解析形函数,进而构造了解析型压扭杆单元。将本单元与解析解、插值多项式函数单元计算的压扭杆转角及翘曲率、临界荷载结果进行对比,验证了本解析型单元的高精度、高效性,该解析型单元可用于截面为双轴对称的压扭杆受力分析中。
压扭杆单元的坐标系如图1所示。z轴与所研究的杆件轴线方向重合,取向右的方向为正方向,坐标的零点位置位于压扭杆左端,y轴定义为向下为正方向,整体直角坐标系与右手螺旋法则规定方向保持一致。图中的所有荷载,均统一规定与坐标轴的方向一致时为正方向;轴力拉为正,压为负;位移(挠度及转角)正方向与坐标轴方向一致时为正。

图1 压扭杆单元
Fig.1 Bar element under compression and torsion
图1中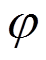 为扭转角,m(z)为沿杆长方向分布的外扭矩集度,L为截面扭矩。对于压扭杆单元,任意截面的扭转位移,可以由两个杆端部位的四个端点位移、即单元的四个自由度表示。其形式可表达为:
为扭转角,m(z)为沿杆长方向分布的外扭矩集度,L为截面扭矩。对于压扭杆单元,任意截面的扭转位移,可以由两个杆端部位的四个端点位移、即单元的四个自由度表示。其形式可表达为: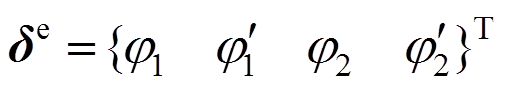 ,其中,
,其中,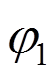 、
、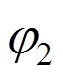 分别表示节点1和2处的扭转角,
分别表示节点1和2处的扭转角,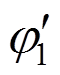 、
、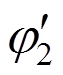 分别表示节点1和2处的翘曲率。
分别表示节点1和2处的翘曲率。
压扭杆的位移控制方程为[4]:
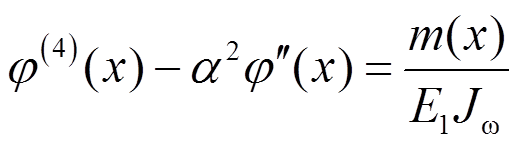
该压扭杆位移控制方程的齐次方程为:
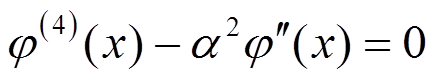 (1)
(1)
式中: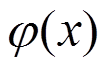 为扭转角;m(x)为沿杆长分布的外扭矩集度;
为扭转角;m(x)为沿杆长分布的外扭矩集度;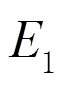 为折算弹性模量;
为折算弹性模量;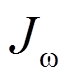 为截面的主扇形惯性矩;
为截面的主扇形惯性矩;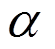 为系数,
为系数,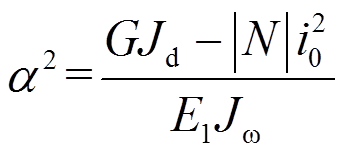 ,
,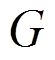 为剪切模量,Jd为截面的自由扭转惯性矩,GJd为自由扭转刚度,N为压力,根据图1和坐标系定义,N值为负,故式中取绝对值,i0为绕剪切中心的极回转半径,
为剪切模量,Jd为截面的自由扭转惯性矩,GJd为自由扭转刚度,N为压力,根据图1和坐标系定义,N值为负,故式中取绝对值,i0为绕剪切中心的极回转半径,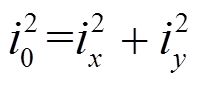 ,ix、iy分别为截面回转半径,
,ix、iy分别为截面回转半径,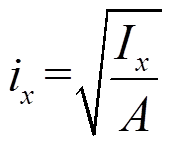 ,
,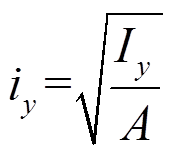 ,Ix、Iy、A分别为压杆截面x轴和y轴方向惯性矩、截面面积。
,Ix、Iy、A分别为压杆截面x轴和y轴方向惯性矩、截面面积。
式(1)通解为:
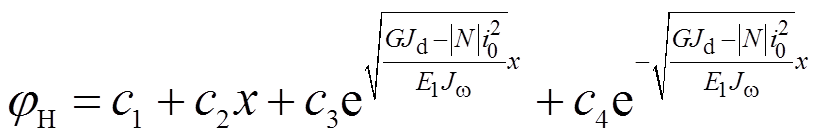
当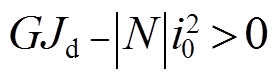 时,式(1)通解为:
时,式(1)通解为:
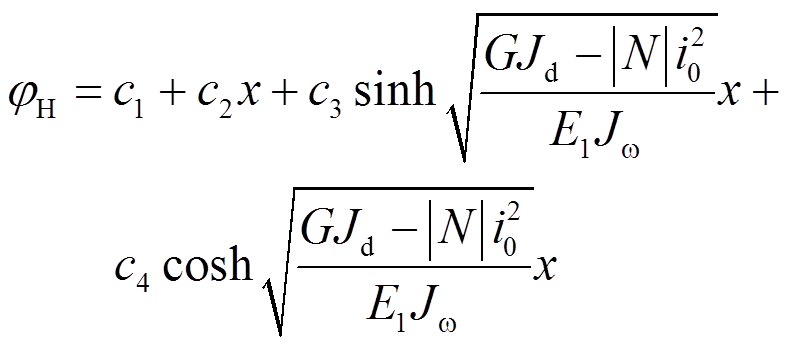
当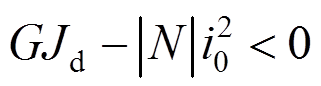 时,式(1)通解为:
时,式(1)通解为:
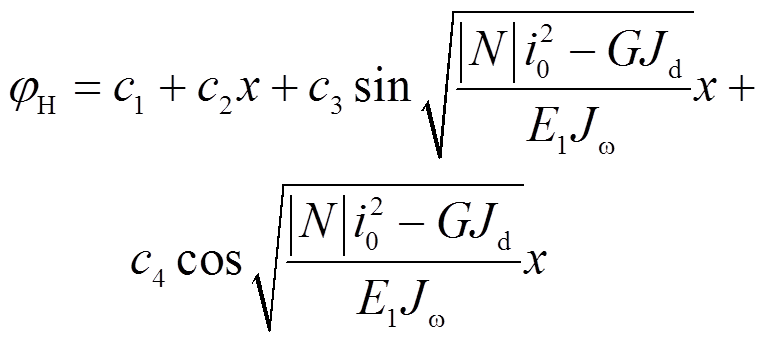
当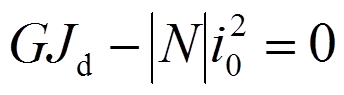 时,式(1)通解为:
时,式(1)通解为:
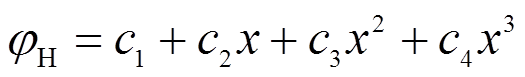
经计算,对于考虑压扭耦合的压扭杆,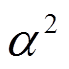 不会等于零;当杆件处于线弹性阶段时,若
不会等于零;当杆件处于线弹性阶段时,若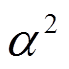 小于零,则杆件已经失稳,故
小于零,则杆件已经失稳,故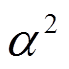 小于零的情形不存在;所以一般情况,式(1)只考虑
小于零的情形不存在;所以一般情况,式(1)只考虑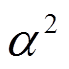 大于零的情况。
大于零的情况。
1.2.1 压扭杆位移
式(1)的通解矩阵形式可表示为:
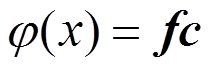 (2)
(2)式中: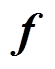 为位移基函数向量,是4阶列向量;
为位移基函数向量,是4阶列向量;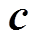 为待定系数向量,是4阶行向量:
为待定系数向量,是4阶行向量:
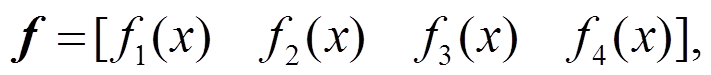
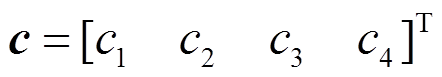 (3)
(3)式中: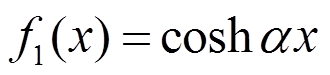 、
、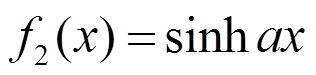 、
、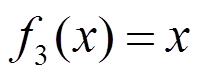 、
、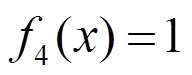 ;c1~c4为待定位移系数。
;c1~c4为待定位移系数。
对式(3)求导,可得:
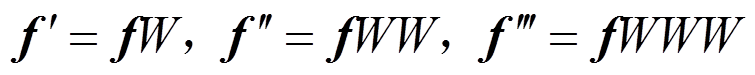 (4)
(4)式中,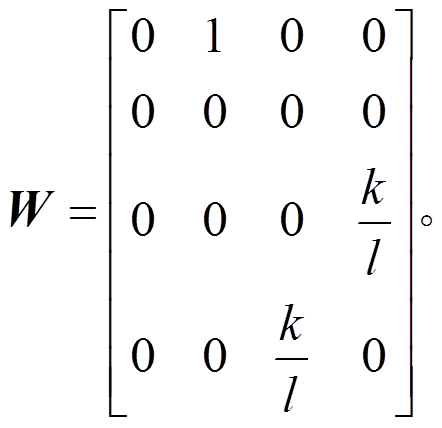
翘曲率可表示为:
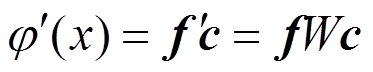 (5)
(5)1.2.2 压扭杆内力
压扭杆截面上扭矩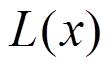 由自由扭转扭矩
由自由扭转扭矩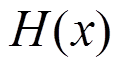 和约束扭转弯扭力矩
和约束扭转弯扭力矩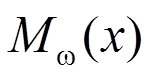 组成。
组成。
总扭矩可表示为[8]:
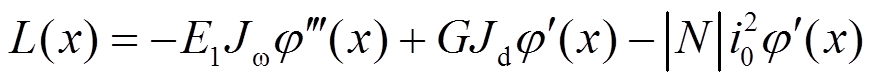
截面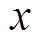 处的广义双力矩
处的广义双力矩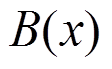 表示为:
表示为:
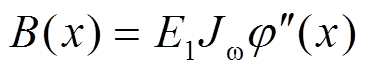
1) 边界条件及方程
杆左端,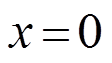 时:
时:
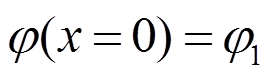 ,
,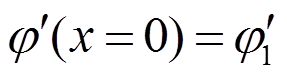 (6)
(6)杆右端,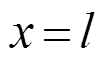 时:
时:
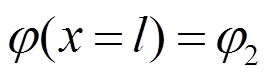 ,
,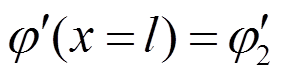 (7)
(7)
根据各截面位移计算公式及定解条件,可以得到位移系数定解方程为:
 (8)
(8)方程化简为:
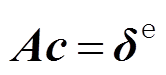 (9)
(9)
2) 位移系数
由定解方程式(8)可得位移系数表达式为:
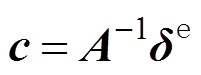 (10)
(10)3) 位移形函数
将式(10)代入式(2)中,得:
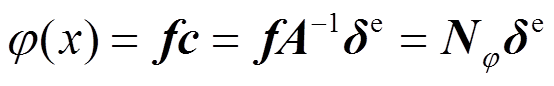 (11)
(11)则位移形函数可表示为:
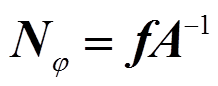 (12)
(12)
对式(12)求导,可得:
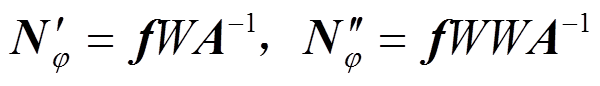 (13)
(13)式中,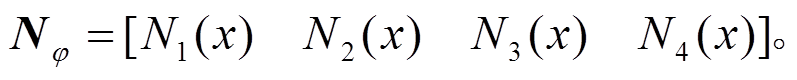
则压扭解析形函数具体形式如下:
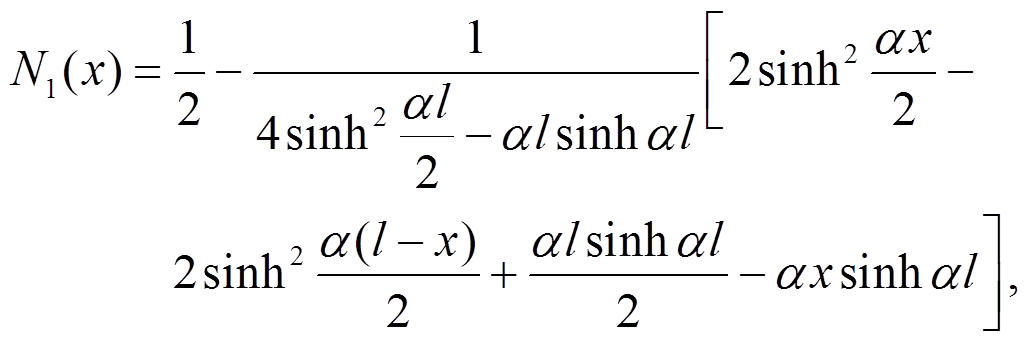
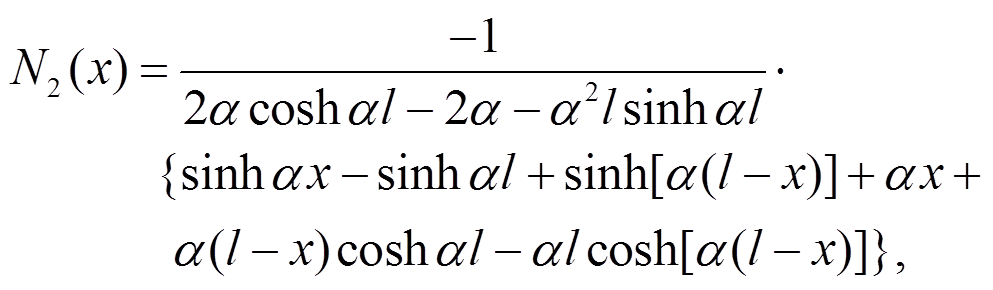
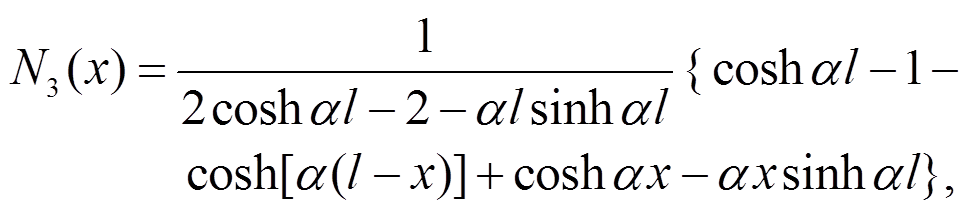
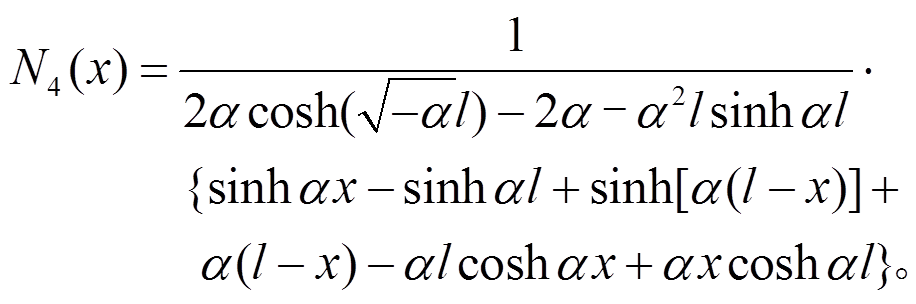
压扭耦合杆件的应变能可表示为:
![]() (14)
(14)
将式(9)代入,得:
式中,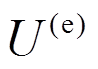 为压扭杆应变能。
为压扭杆应变能。
假设杆件上的外力荷载有:沿杆件轴向均布的扭矩m,作用于坐标xp处的集中扭矩Lp,并且杆件的端部还作用有扭矩大小为L和B的外力。 由外力荷载势能的原始定义可知是由荷载与相应的位移乘积值,取其负值形式。可求出杆件的外力势能为:
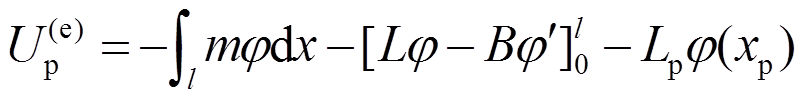 (16)
(16)将式(9)代入,得:
![]() (17)
(17)
式中:
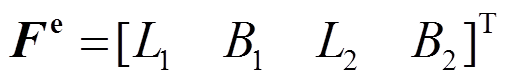 (18)
(18)杆件的总体势能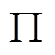 可分别由两部分组成:应变能
可分别由两部分组成:应变能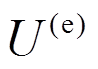 和外力势能
和外力势能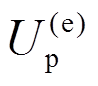 ,其形式可以表达为:
,其形式可以表达为:
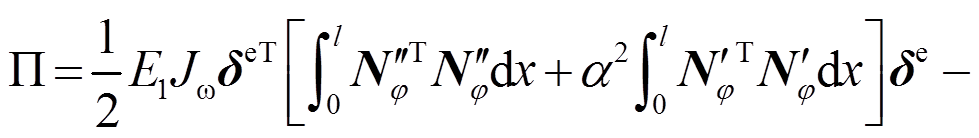
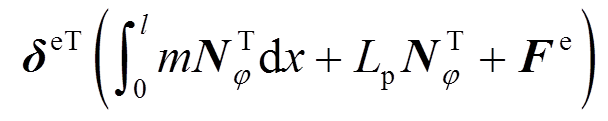 (19)
(19)
根据势能变分原理,相应于结构的真实位移,有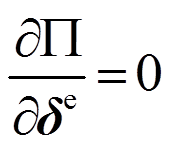 ,则:
,则:
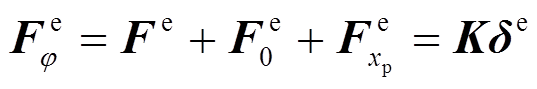 (20)
(20)式中: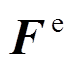 为杆端力;
为杆端力;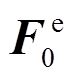 为等效节点力;
为等效节点力;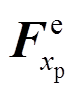 为集中扭矩等效节点力;
为集中扭矩等效节点力;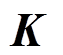 为单元刚度矩阵,其中:
为单元刚度矩阵,其中:
![]() (21)
(21)
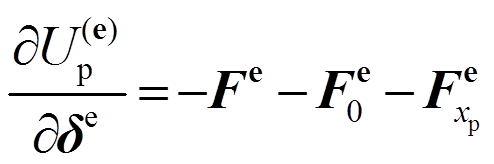 (22)
(22)根据式(20)的变分原理,推导得到基于解析形函数的总单元刚度矩阵,其具体形式可表达如下:
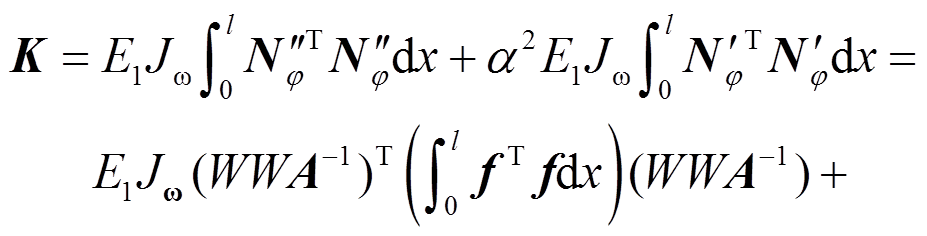
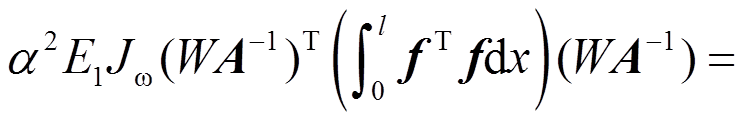
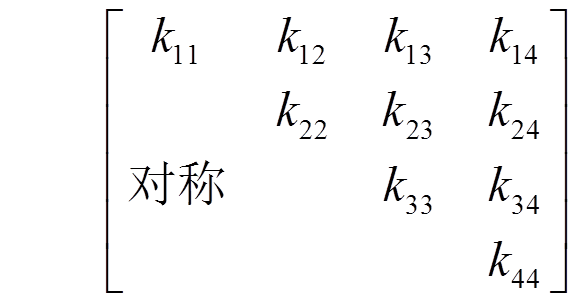 (23)
(23)
各项分列如下:
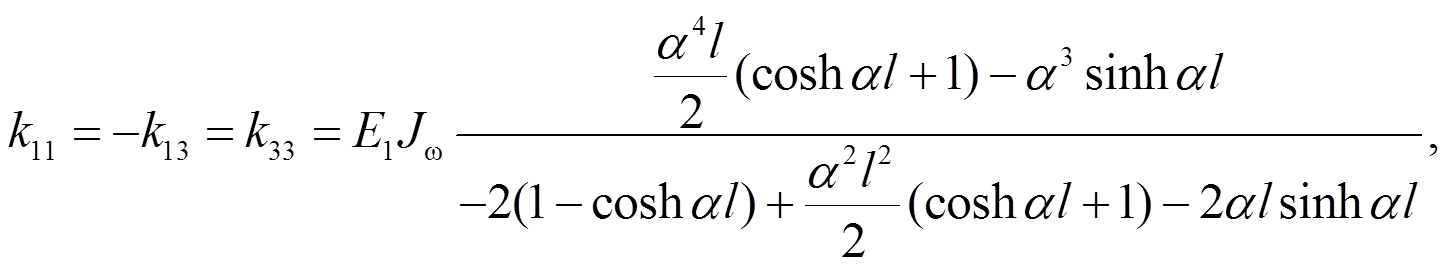
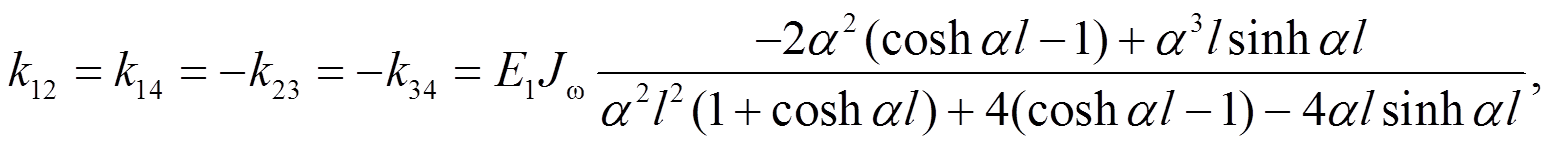

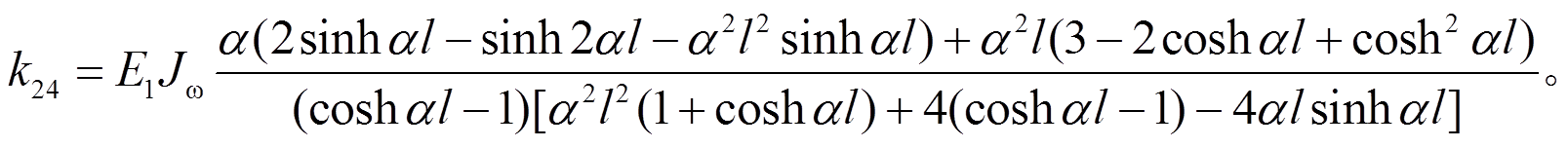
对于出现在杆件当中的沿杆件轴向均匀分布的扭矩,可作如下运算:
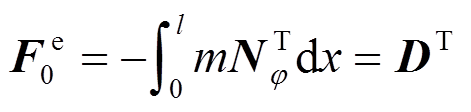 (24)
(24)式中,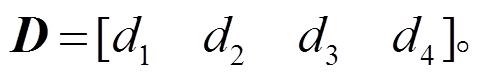
其显式形式可表示为:
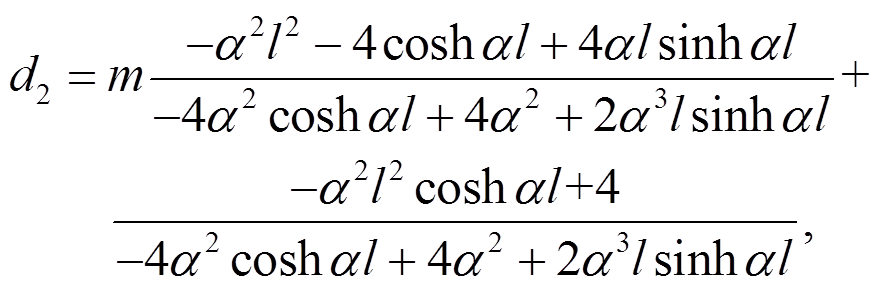
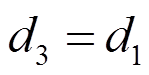 ,
,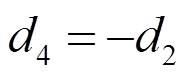 。
。
对于作用于xp处的集中扭矩,做的功为:
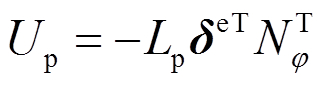 (25)
(25)对集中扭矩所做的功进行变分,可得:
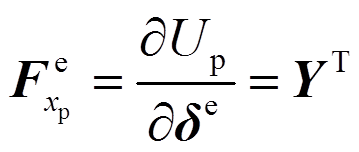 (26)
(26)
式中,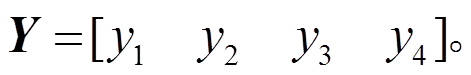
其显式形式可表示为:
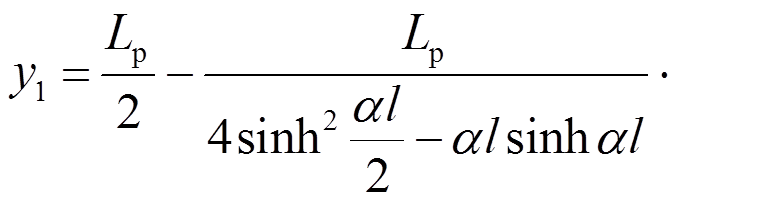
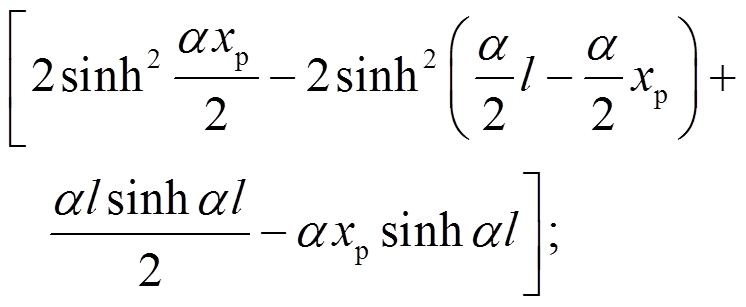
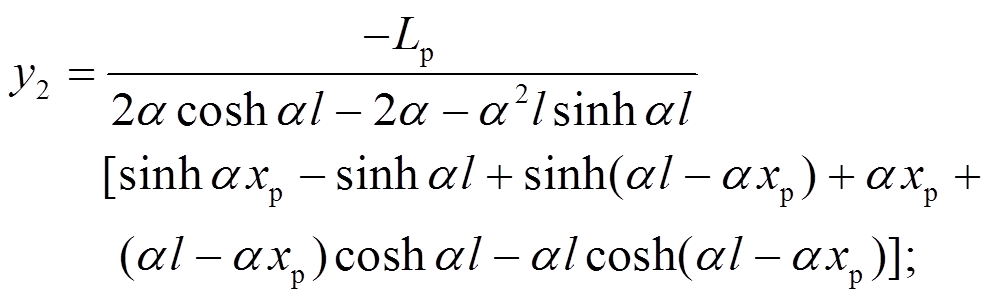
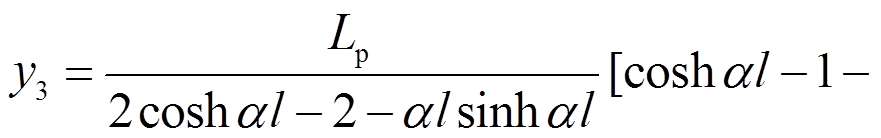
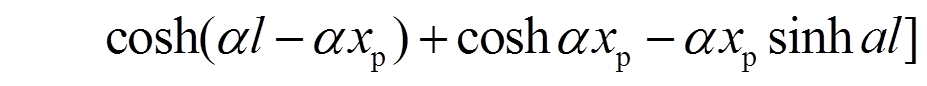
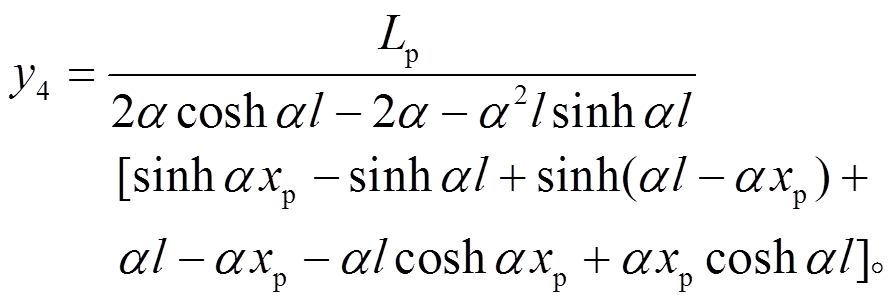
为验证解析形函数法构造的压扭杆单元精确性,分别采用解析解、插值形函数法求解压扭杆的转角及翘曲率、临界荷载,并进行对比。
4.1.1 杆件参数
如图2所示的压扭杆件,计算支座位移。杆件两端为铰支,杆长l=1 m,d1=100 mm,d2=200 mm,壁厚均匀t=10 mm,E=2.1×105 MPa,G=8.4× 104 MPa,泊松比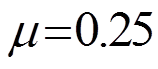 。跨端承受压力N=1.0 kN。沿杆承受均布扭矩M=0.087500 kN·m。杆件主要参数如表1所示。
。跨端承受压力N=1.0 kN。沿杆承受均布扭矩M=0.087500 kN·m。杆件主要参数如表1所示。
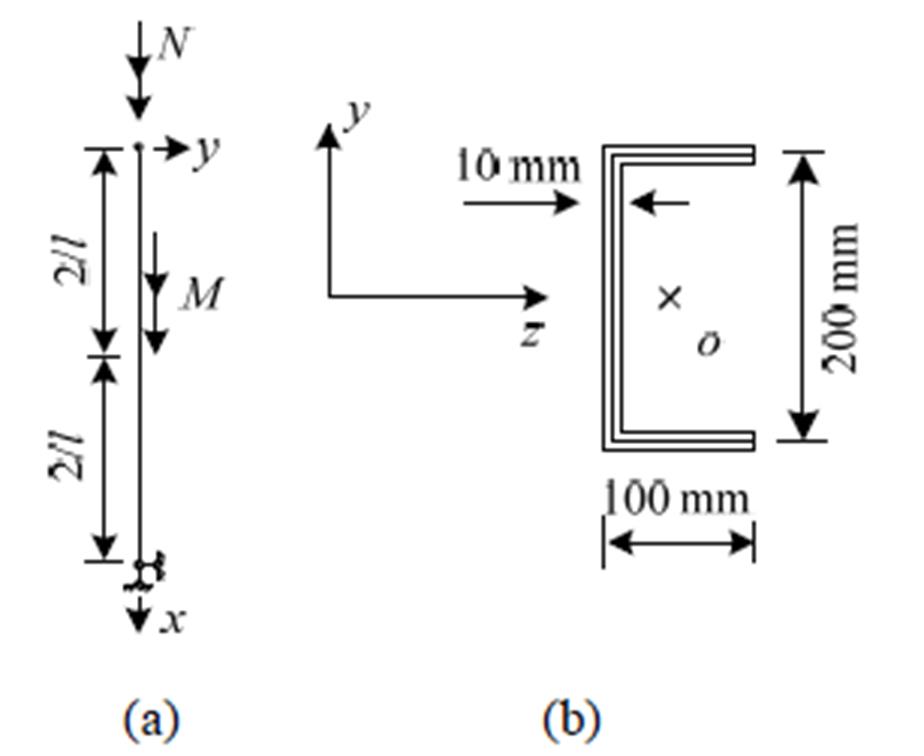
图2 杆件及截面尺寸
Fig.2 Dimension of bar and its cross section
4.1.2 结果与分析
不划分单元,采用解析形函数法计算压扭杆支座截面和跨中截面的转角和翘曲率,并与理论解、插值形函数法的计算结果进行对比,结果如表2 所示。
表1 主要参数
Table 1 Main parameters

参数Jw/mm6Jd/mm4E1/(N·mm−2)G/(N·mm−2)i0/mm2 结果1.79167×10111.333×1052.24×1058.4×1042.454856×104
表2 各种结果对比
Table 2 Comparison of different methods results

计算方法支座扭转角/(×10−6rad)支座翘曲率/(×10−6mm−1)跨中扭转角/(×10−5rad)跨中翘曲率/(×10−7 mm−1) 理论解[30]01.484263295201.43313910 有限元解插值形函数法计算值/(%)01.482342481201.24774890 相对误差/(%)00.130.090 解析形函数法计算值/(%)01.484263295201.43313910 相对误差0000
由表2可以看出,在单元数量相同时,解析形函数法所得的单元在扭转角及翘曲率计算精度上高于插值形函数法所得的单元。解析形函数法单元不需要划分单元,就能得到与理论解一致的计算结果。
产生上述结果的原因是:当计入翘曲率以及压扭大位移影响时,不同于采用插值多项式函数形式的单元,本文构造的解析型单元基于解析位移形函数模式,很大程度消除了模型误差带来的影响,将相对误差缩到最小程度。
4.2.1 杆件参数
如图2所示槽型压扭薄壁杆,计算杆的失稳临界荷载N。杆件两端为铰支,杆长l=8 m,其他参数同上4.1。
4.2.2 结果与分析
不划分单元,采用解析形函数法计算压扭薄壁杆临界荷载,并与理论解、插值形函数法的计算结果进行对比,结果如表3所示。
表3 不同方法的计算结果及精度对比
Table 3 Comparison of different methods results

计算方法失稳临界荷载N/kN 计算数值相对误差/(%) 理论解4.5612×103— 插值形函数法7.6266×10367.21 解析形函数法4.5612×1030
由表3可以看出,在单元数量相同时,解析形函数法所求得的失稳临界荷载在计算精度上远高于插值形函数单元所得的失稳临界荷载值。采用解析形函数单元不需要划分单元,就可得到与理论解一致的计算结果。
对比发现,对于压扭耦合问题,将式(1)中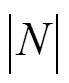 的值取为0,无论对原始位移控制方程,还是对得到的显式单元列式,都可将解析型压扭杆单元刚度矩阵完全退化为解析型约束扭转杆单元形式[29]。即本文构造的压扭耦合杆单元可退化到考虑翘曲的纯扭杆单元形式,既验证了本单元的正确性,又对文献[29]构造的纯扭杆单元进行了完善。
的值取为0,无论对原始位移控制方程,还是对得到的显式单元列式,都可将解析型压扭杆单元刚度矩阵完全退化为解析型约束扭转杆单元形式[29]。即本文构造的压扭耦合杆单元可退化到考虑翘曲的纯扭杆单元形式,既验证了本单元的正确性,又对文献[29]构造的纯扭杆单元进行了完善。
(1) 基于Vlasov杆件理论,根据压扭杆位移控制方程,得到了压扭杆单元位移解析形函数。
(2) 采用势能原理建立了势能泛函,利用势能驻值变分原理,构造了压扭杆解析型单元,并给出了解析型压扭杆单元列式。
(3) 算例表明:本文构造的解析型单元计算压扭杆位移和临界荷载的精度远高于插值形函数法,且采用一个单元即可保证计算结果与理论解一致,满足了高精度、高效率的要求。
参考文献:
[1] 韩林海. 钢管混凝土压扭构件工作机理研究[J]. 哈尔滨建筑工程学院学报, 1994, 27(4): 35―40. Han Linhai. Study on the behavior mechanism of concrete filled steel tubular (CFST) member subjected to compression and torsion [J]. Journal of Harbin Architecture & Civil Engineering Institute, 1994, 27(4): 35―40. (in Chinese)
[2] 王国周, 瞿履谦. 钢结构: 原理与设计[M]. 北京: 清华大学出版社, 1992. Wang Guozhou, Qu Lüqian. Steel structure―principle and design [M]. Beijing: Tsinghua University Press, 1992. (in Chinese)
[3] 黄宏, 郭晓宇, 陈梦成. 圆中空夹层钢管混凝土压扭构件有限元分析[J]. 建筑结构学报, 2013, 34(增刊1): 50―56. Huang Hong, Guo Xiaoyu, Chen Mengcheng. Theoretical research on concrete filled double-skin steel tubular members subjected to compression and torsion [J]. Journal of Building Structures, 2013, 34(Suppl 1): 50―56. (in Chinese)
[4] 童根树. 钢结构的平面外稳定[M]. 北京: 中国建筑工业出版社, 2013. Tong Genshu. The out–plane stability of steel [M]. Beijng: China Architecture & Building Press, 2013. (in Chinese)
[5] Cheung Y K, Zienkiewicz O C. Plates and tanks on elastic foundation : an application of finite element method [J]. International Journal of Solids & Structures, 1965, 1(4): 451―461.
[6] Timoshenko S P, Gere J M. Theory of elastic stability [M]. NewYork: McGraw-Hill, 1961.
[7] Vlasov V Z. Thin-walled elastic beams (Second edition) [M]. Jerusalem: Israel Program for Scientific Translation, 1961.
[8] 包世华, 周坚. 薄壁杆件结构力学[M]. 北京: 中国建筑工业出版社, 1991. Bao Shihua, Zhou Jian. Structural mechanics of thin walled bar [M]. Beijing: China Building Industry Press, 1991. (in Chinese)
[9] 李华煜, 辛克贵. 采用分段样条插值的半离散方法分析薄壁杆件[J]. 工程力学, 1992, 9(3): 8―22. Li Huayu, Xin Kegui. Analysis of thin-walled members by a semi-discrete method using sectional spline function [J]. Engineering Mechanics, 1992, 9(3): 8―22. (in Chinese)
[10] 杨隆宇, 李正良. 双角钢十字组合截面构件铰支轴心受压承载力研究[J]. 西南交通大学学报, 2011, 46(5): 754―759. Yang Longyu, Li Zhengliang. Bearing capacity of pinned-end built-up cruciform section members formed by two equal-leg angles under compression load [J]. Journal of Southwest Jiaotong University, 2011, 46(5): 754―759. (in Chinese)
[11] 秦剑, 万建成, 夏拥军, 等. 轴心受压开口薄壁构件弹塑性屈曲荷载的统一计算方法[J]. 建筑结构学报, 2017, 38(5): 18―23. Qin Jian, Wan Jiancheng, Xia Yongjun, et al. Integrated calculation method for elasto-plastic buckling load of thin-walled axial compression member with open cross-section [J]. Journal of Building Structures, 2017, 38(5): 18―23. (in Chinese)
[12] Yuan Z, Huo S H, Geng X L. Stability of perfect and imperfect cylindrical shells under axial compression and torsion [J]. Journal of Central South University, 2014, 21(4): 1264―1274.
[13] Rasmussen K J R, Hancock G J. Tests of high strength steel columns [J]. Journal of Constructional Steel Research, 1995, 34(1): 27―52.
[14] 聂诗东, 戴国欣, 沈乐, 等. Q345GJ钢(中)厚板H形及箱形柱残余应力与轴压稳定承载力分析[J]. 工程力学, 2017, 34(12): 171―182. Nie Shidong, Dai Guoxin, Shen Le, et al. Residual stress distribution and overall stability load-carrying capacitie of H-shaped and box section columns welded by Q345GJ structural steel plates under axial compression [J]. Engineering Mechanics, 2017, 34(12): 171―182. (in Chinese)
[15] 李国强, 王彦博, 陈素文, 等. 高强钢焊接箱形柱轴心受压极限承载力试验研究[J]. 建筑结构学报, 2012, 33(3): 8―14. Li Guoqiang, Wang Yanbo, Chen Suwen, et al. Experimental study on ultimate bearing capacity of axially compressed high strength steel columns [J]. Journal of Building Structures, 2012, 33(3): 8―14. (in Chinese)
[16] Hsu H L,Liang L L. Performance of hollow composite members subjected to cyclic eccentric loading [J]. Earthquake Engineering and Structural Dynamics, 2003, 32(3): 443―461.
[17] Hsu H L, Hsieh J C. Seismic performance of steel-encased composite members with strengthening cross-inclined bars [J]. Journal of Constructional Steel Research, 2004, 60(3): 1663―1679.
[18] Liu G R, Dai K Y, Nguyen T T. A smoothed finite element method for mechnics problems [J]. Computational Mechanics, 2007, 39(6): 859―877.
[19] Zienkiewicz O C, Taylor R L. The finite element method [M]. 5th ed. Oxford: Butterworth Heinemann, 2000.
[20] Johnson C P, Will K M. Beam buckling by finite element procedure [J]. Journal of the Structural Division, ASCE, 1974, 100(ST3): 669―685.
[21] Barsoum R S, Gallagher R H. Finite element analysis of torsional and torsional-flexural stability problems [J]. International Journal for Numerical Methods in Engineering, 1970, 2(3): 335―352.
[22] Wang Q, Li W Y. Buckling of thin-walled compression members with shear lag using spline finite member element method [J]. Computational Mechanics, 1996, 18 (2): 139―146.
[23] Liu G R, Nguyen-Xuan H, Nguyen-Thoi T. Avariationally consistent FEM (VC FEM) for solution bounds and nearly exact solution to solid mechanics problems using quadrilateral elements [J]. International Journal for Nmuerical Methods in Engineering, 2011, 85(4): 461―497.
[24] 岑松, 尚闫, 周培蕾, 等. 形状自由的高性能有限元方法研究的一些进展[J]. 工程力学, 2017, 34(3): 1―14. Cen Song, Shang Yan, Zhou Peilei, et al. Advances in shape-free finite element methods: a review [J]. Engineering Mechanics, 2017, 34(3): 1―14. (in Chinese)
[25] Cao Qiongqiong, Xu Jing, Cheng Xiaoke, Zhang Qingxia, Zhang Peng, Jiang Xiugen. Element for beam analysis based on parabolic distribution stiffness [C]. International Conference on Architectural Engineering and New Materials, Guangzhou, 2015: 131―137.
[26] Tang Lifeng, Xu Jing, Wang Hongzhi, Chen Xinghua. Accurate element of compressive bar considering the effect of displacement [J]. Mathematical Problems in Engineering, 2015, 2015: 1―8.
[27] 李潇, 王宏志, 李世萍, 等. 解析型Winkler弹性地基梁单元构造[J]. 工程力学, 2015, 32(3): 66―72. Li Xiao, Wang Hongzhi, Li Shi ping, et al. Element structure of analytical Winkler elastic foundation beam [J]. Engineering Mechanics, 2015, 32(3): 66―72. (in Chinese)
[28] 李静, 蒋秀根, 王宏志, 等. 解析型弹性地基Timoshenko梁单元[J]. 工程力学, 2018, 35(2): 221―229, 248. Li Jing, Jiang Xiugen, Wang Hongzhi, et al. Analytical element for Timoshenko beam on elastic foundation [J]. Engineering Mechanics, 2018, 35(2): 221―229, 248. (in Chinese)
[29] 夏文忠. 基于Vlasov约束扭转理论的扭杆分析单元构造[D]. 北京: 中国农业大学, 2017. Xia Wenzhong. Development of constraint torsion elements on torsion bar based on Vlasov theory [D]. Beijing: China Agricultural University, 2017. (in Chinese)
ANALYTICAL ELEMENT FOR BAR SUBJECTED TO COMPRESSION AND TORSION CONSIDERING THE LARGE DISPLACEMENT
Abstract:To improve the accuracy and efficiency in calculating the inter force and deformation of bar under compression and torsion, the shape function was determined by considering the section warping and the effect of large displacement, based on Vlasov restrained torsion theory and according to the displacement controlling equation for bar. Potential energy functional of bar subjected to compression and torsion was established by applying potential energy principle. Analytical element formulations for bar were received and element stiffness matrix was obtained via variational principle of potential energy stationary value. Comparisons among the calculation results of proposed element, theoretical solution, and interpolation polynomial element are conducted, and the results show that the solution of analytical element by one element number is in accordance with the theoretical solution. The analytical element can satisfy the high accuracy and efficiency requirement and can be applied in practice.
Key words: compression and torsion; analytical function; variation principle; finite element; element stiffness matrix
文章编号:1000-4750(2019)04-0044-08
中图分类号:TB125
文献标志码:A
Doi: 10.6052/j.issn.1000-4750.2018.03.0116
收稿日期:2018-03-01;
修订日期:2018-09-15
基金项目:国家自然科学基金项目(51279206);农业部农业设施结构工程重点实验室开放课题(201502);中央高校基本科研业务费专项资金项目(2015SY004)
夏文忠(1992―),男,浙江人,硕士,主要从事结构工程方面的研究(E-mail: xwz7298@163.com);
王宏志(1967―),男,江西人,副教授,博士,主要从事计算力学方面的研究(E-mail: climber@cau.edu.cn).