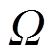 及其边界
及其边界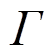 上的物理场场函数为
上的物理场场函数为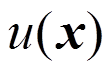 ,问题域及边界通过
,问题域及边界通过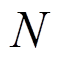 个场节点离散,假设任意点
个场节点离散,假设任意点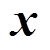 的支持域内有
的支持域内有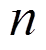 个场节点。若已知节点的场函数值为
个场节点。若已知节点的场函数值为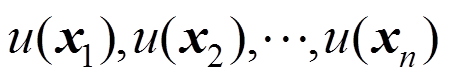 ,点
,点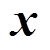 处的近似场函数可通过MLS法来逼近[21-23]。
处的近似场函数可通过MLS法来逼近[21-23]。摘 要:该文基于插值型移动最小二乘法,将无网格局部Petrov-Galerkin (MLPG)法用于二维耦合热弹性动力学问题的求解。修正的Fourier热传导方程和弹性动力控制方程通过加权余量法来离散,Heaviside分段函数作为局部弱形式的权函数,从而得到描述热耦合问题的二阶常微分方程组。然后利用微分代数方法,温度和位移作为辅助变量,将上述二阶常微分方程组转换成常微分代数系统,采用Newmark逐步积分法进行求解。该方法无需Laplace变换可直接得到温度场和位移场数值结果,同时插值型移动最小二乘法构造的形函数由于满足Kronecker delta特性,因此能直接施加本质边界条件。最后通过两个数值算例来验证该方法的有效性。
关键词:耦合热应力;移动最小二乘法;无网格局部Petrov-Galerkin法;Heaviside函数;微分代数方法
温度应力分为两类,一类是非耦合热应力问题,认为“单元体体积不变”,应力场对温度场的影响很小可忽略不计。另一类是耦合热应力问题[1-7],考虑了弹性体变形对热量传递的影响,例如结构受到热冲击这一高速热应变作用时。此时热传导方程中包含物体变形,热弹性运动方程中又包含温度,需对热传导方程与热弹性运动方程耦合进行求解。
在耦合热应力问题方面,Nowinski[3]指出,耦合作用是将施加给物体的机械能转化为热流,然后再耗散掉。Boley等[4,7]认为,耦合效应的物理实质是对热弹性波的阻尼,只要加热不太快,准静态解是足够精确的,同时其发现耦合效应会使应变-应力、温度等在波前的突变迅速衰减。随着计算机快速发展,数值计算方法在耦合热应力计算方面起着越来越重要的作用,在大多数情况下都需要借助数值计算方法。Nariboli[8]用Laplace变换法研究了球形空腔壁温度突然有跳跃的问题。Takeuti等[9]用热弹性位移势和Love位移函数法求解了轴对称有限圆柱的耦合热应力问题。Oden[10]用有限元法计算了各种物性系数下半空间的耦合问题。Park等[11]和Tehrani等[12]用边界元法计算了热冲击和机械冲击作用下耦合热应力问题。王林翔等[13]用微分代数方法求解热弹性动力学耦合问题。
上述网格类方法计算精度受网格剖分影响,当网格发生畸变时,对计算精度和效率影响很大。基于此,一些学者用无网格法来求解耦合热应力问题,无网格法是利用一组散布在问题域及域边界上的节点构造场函数近似表达式的一种计算方法,该方法不需利用预定义的网格对域进行离散,很容易实现自适应分析。Atluri等[14-15]提出了无网格局部Petrov-Galerkin法(meshless local Petrov-Galerkin method, MLPG),并将MLPG法分为6种形式。在耦合热应力计算方面,Sladek等[16]将MLPG法应用于正交各向异性材料线性耦合热应力问题的求解,同时借助Laplace变换法来消除对时间的依赖。Hosseini等[17]基于Green-Naghdi模型,将MLPG法应用于功能梯度空心圆柱耦合热应力的求解。
上述MLPG法在求解耦合热应力问题时,都是基于移动最小二乘法(moving least squares,MLS)来构造近似函数的,由于其构造的形函数不满足Kronecker delta特性,因此在本质边界条件的处理上存在困难。针对上述问题,Lagrange乘子法、罚函数法、配点法已被提出,这无疑增加了计算工作量。另外一种简便处理本质边界条件的方法就是选取具有Kronecker delta特性的形函数,例如滑动Kriging插值[18-20]、插值型移动最小二乘法[21]。插值型移动最小二乘法[22]主要对基函数进行正交化,并对权函数做奇异处理。任红萍等[23]对Lancaster提出的移动最小二乘插值法进行了改进,其形函数公式更为简单,计算效率更高。由于插值型移动最小二乘法构造的形函数具有插值性,因此方便了本质边界条件的施加,避免了利用传统Lagrange乘子法或罚函数法弱形式复杂和积分项多的问题。
本文将插值型移动最小二乘法与无网格MLPG法相结合来求解结构耦合热应力问题,Heaviside分段函数作为局部弱形式的权函数并用来推导结构动力和耦合热弹性离散方程。然后采用微分代数求解方法,将描述热耦合问题的偏微分方程组转化为二阶常微分方程组,然后对所得到的常微分代数系统采用Newmark逐步积分法进行求解。由于无需采用Laplace变换法就可以直接求解得到温度场和位移场数值结果,因此非常方便,最后通过两个数值算例来验证该方法的有效性。
设定义在问题域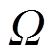 及其边界
及其边界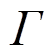 上的物理场场函数为
上的物理场场函数为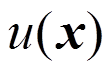 ,问题域及边界通过
,问题域及边界通过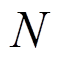 个场节点离散,假设任意点
个场节点离散,假设任意点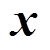 的支持域内有
的支持域内有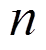 个场节点。若已知节点的场函数值为
个场节点。若已知节点的场函数值为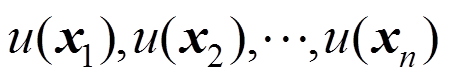 ,点
,点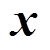 处的近似场函数可通过MLS法来逼近[21-23]。
处的近似场函数可通过MLS法来逼近[21-23]。
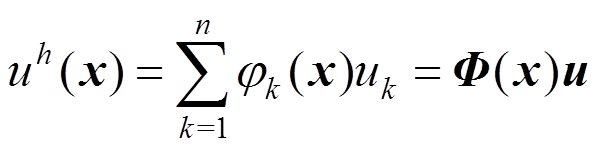 (1)
(1)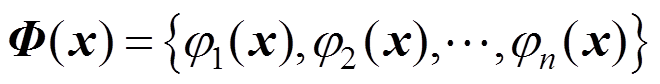 表达式如下:
表达式如下:
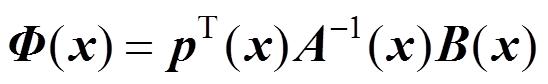 (2)
(2)
式中: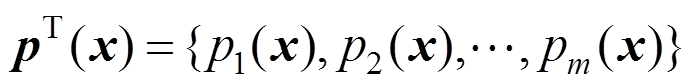 是一组完备多项式基。
是一组完备多项式基。
对于线性基:
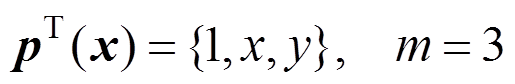 (3)
(3)二次基:
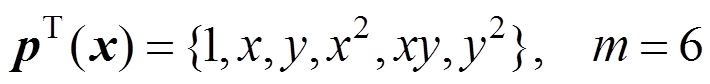 (4)
(4)
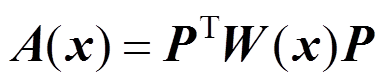 (5)
(5)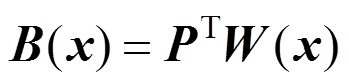 (6)
(6)
这里我们选用线性基,节点处基函数值所形成的矩阵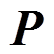 表示为:
表示为:
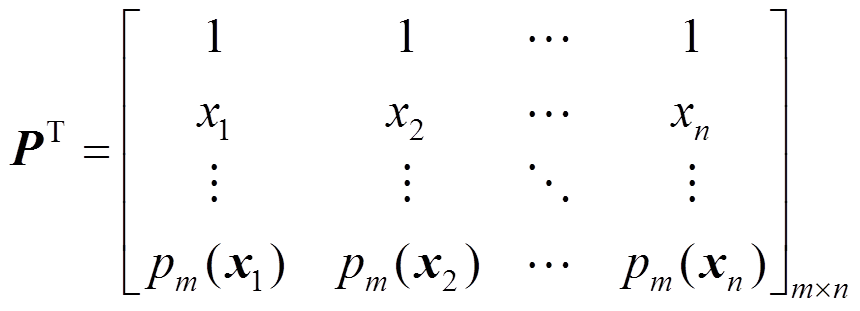 (7)
(7)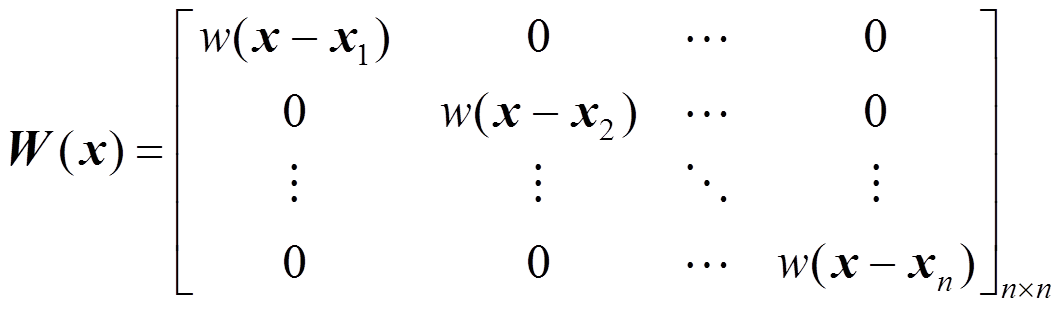 (8)
(8)
由于MLS形函数不具有Kronecker delta特性,因此不能直接施加本质边界条件。为了解决这一问题,本文按照文献[23]所示方法构造插值型移动最小二乘法(interpolating moving least squares,IMLS),即对基函数进行正交化处理。在点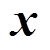 处将基函数
处将基函数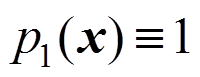 单位化为:
单位化为:
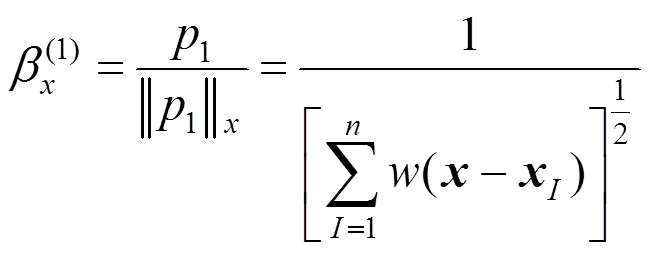 (9)
(9)再将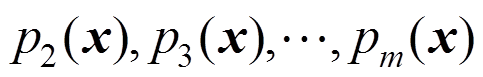 与
与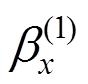 正交化为:
正交化为:
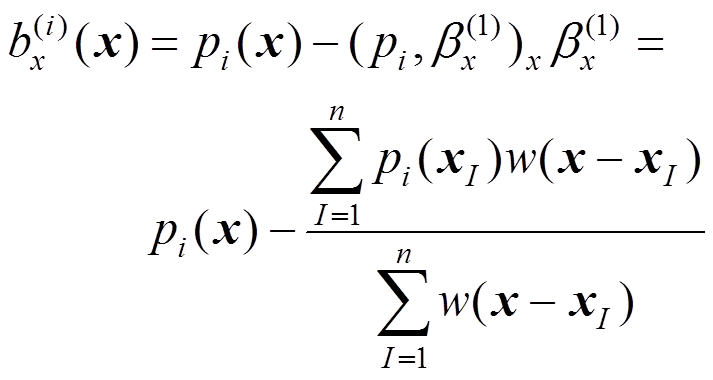 (10)
(10)
即:
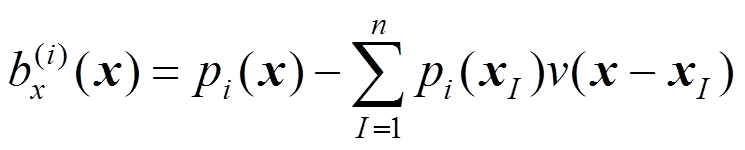 (11)
(11)其中:
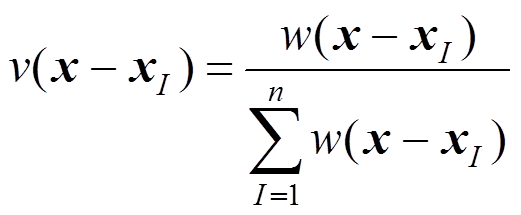 (12)
(12)
此时,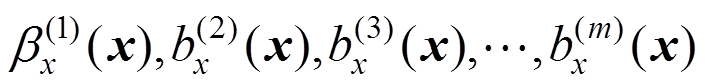 即为MLS法新的基函数,点
即为MLS法新的基函数,点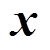 处的近似场函数变为:
处的近似场函数变为:
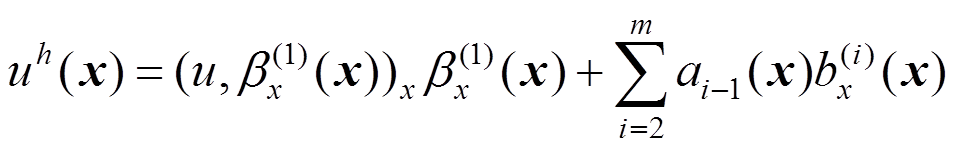 (13)
(13)即:
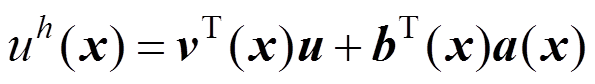 (14)
(14)
其中:
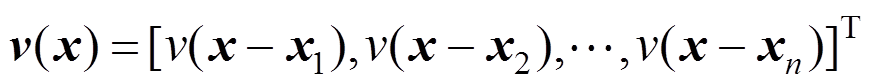 (15)
(15)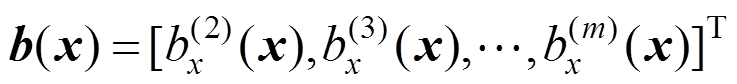 (16)
(16)
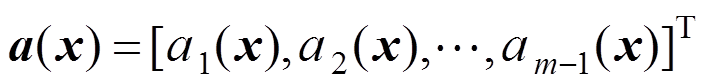 (17)
(17)
由移动最小二乘逼近法可得:
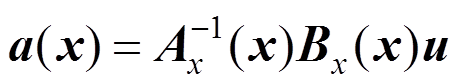 (18)
(18)即点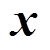 处的近似场函数变为:
处的近似场函数变为:
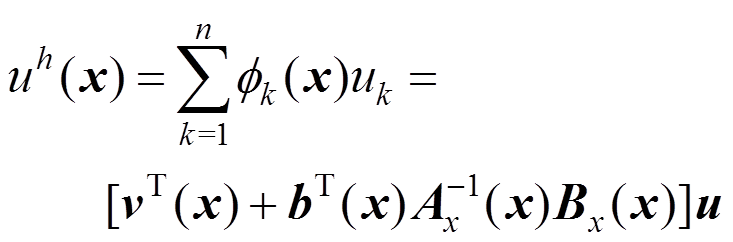 (19)
(19)
其中:
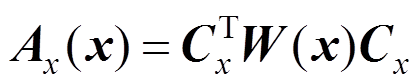 (20)
(20)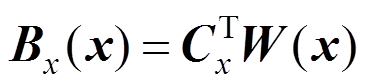 (21)
(21)
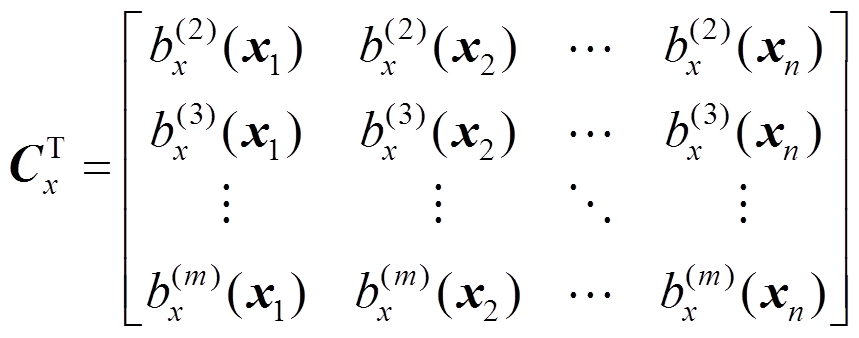 (22)
(22)
取权函数:
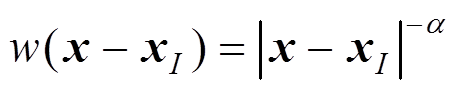 (23)
(23)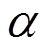 为一正偶数,此时式(19)构造的形函数满足Kronecker delta特性,并具有插值性。
为一正偶数,此时式(19)构造的形函数满足Kronecker delta特性,并具有插值性。
根据热力学第一定律,建立能量平衡方程时考虑物体变形所作的功,可推导得到修正的Fourier热传导方程。
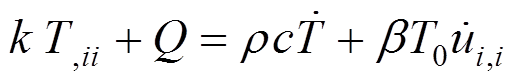 (24)
(24)运动方程为:
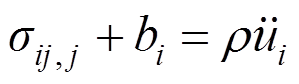 (25)
(25)
式中: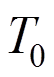 为物体的初温;
为物体的初温;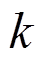 为热传导系数;
为热传导系数;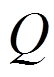 为热源密度;
为热源密度;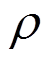 为质量密度;
为质量密度;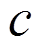 为比热;
为比热;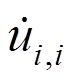 表示弹性体体积应变速率引起的热量,它是温度场和应力场的耦合项。
表示弹性体体积应变速率引起的热量,它是温度场和应力场的耦合项。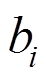 为体力分量;
为体力分量;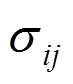 为相对于位移场
为相对于位移场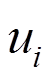 的应力张量;
的应力张量;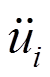 为位移
为位移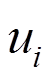 对时间
对时间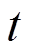 的二阶导数。
的二阶导数。
几何方程为:
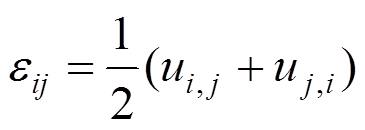 (26)
(26)物理方程为:
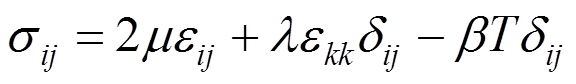 (27)
(27)
式中: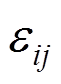 为应变张量;
为应变张量;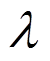 和
和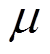 为拉梅常数;
为拉梅常数;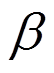 为热应力系数,这里
为热应力系数,这里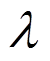 、
、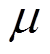 和
和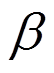 可表示如下:
可表示如下:
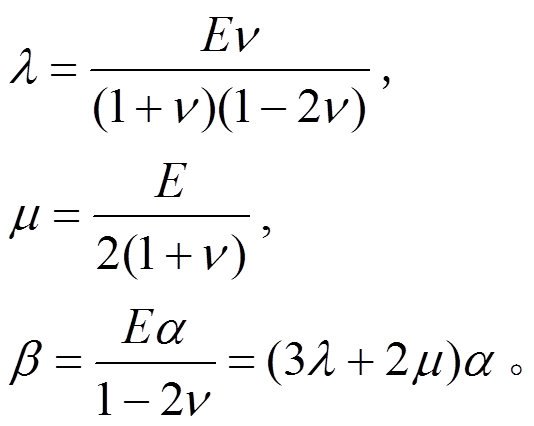 (28)
(28)式中: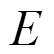 为弹性模量;
为弹性模量;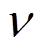 为泊松比;
为泊松比;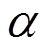 为热膨胀系数。
为热膨胀系数。
相应的边界条件为:
 当
当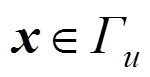 (29)
(29)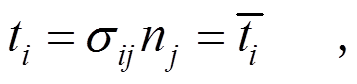 当
当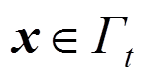 (30)
(30)
 当
当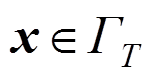 (31)
(31)
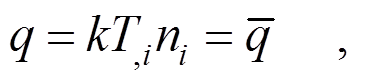 当
当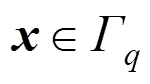 (32)
(32)式中: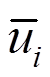 为位移边界
为位移边界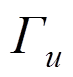 上的已知位移分量;
上的已知位移分量;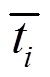 为面力边界
为面力边界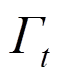 上的已知面力分量;
上的已知面力分量;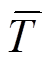 为温度边界
为温度边界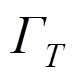 上的已知温度分量;
上的已知温度分量;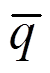 为热流密度边界
为热流密度边界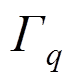 上的已知热流密度,且
上的已知热流密度,且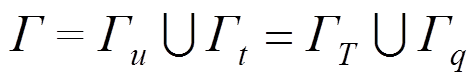 。初始条 件为:
。初始条 件为:
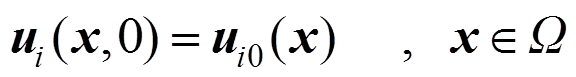 (33)
(33)
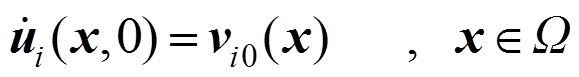 (34)
(34)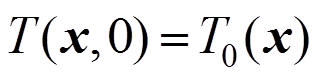 (35)
(35)
式中: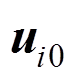 和
和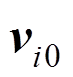 为初始位移和初始速度;
为初始位移和初始速度;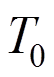 为初始温度。
为初始温度。
将问题域及边界用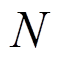 个节点离散,在任意节点
个节点离散,在任意节点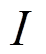 对应的子域
对应的子域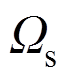 内采用加权余量法,式(24)离散为:
内采用加权余量法,式(24)离散为:
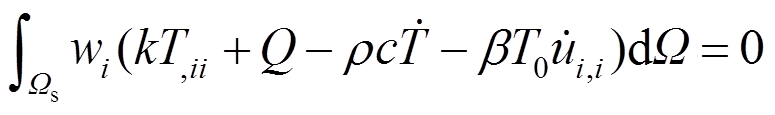 (36)
(36)采用分部积分和高斯散度定理,采用Heaviside分段函数作为权函数并施加自然边界条件式(32)可得:
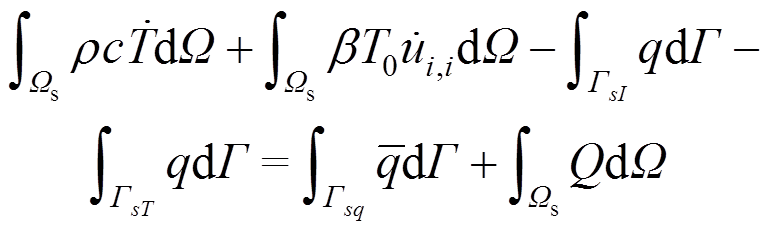 (37)
(37)
位移场近似函数可表示为:
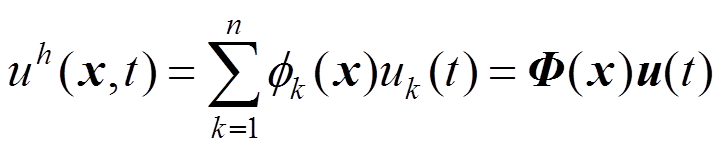 (38)
(38)温度场近似函数可表示为:
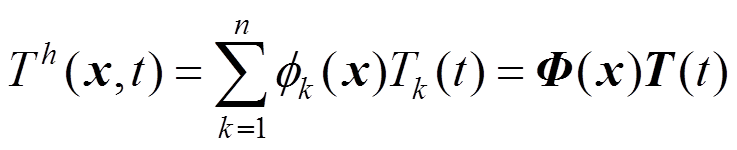 (39)
(39)
将式(38)、式(39)代入式(37),可得如下离散方程:
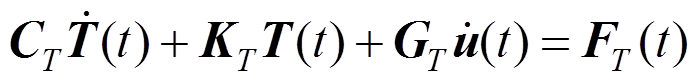 (40)
(40)式中: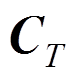 、
、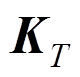 和
和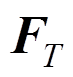 分别为热容矩阵、刚度矩阵和节点温度荷载向量。分别表示如下:
分别为热容矩阵、刚度矩阵和节点温度荷载向量。分别表示如下:
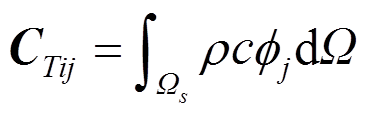 (41)
(41)
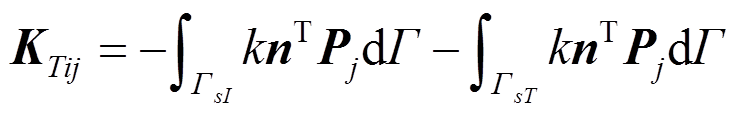 (42)
(42)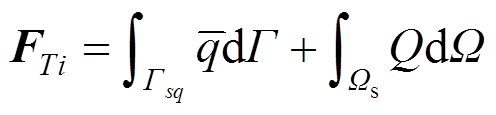 (43)
(43)
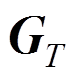 为:
为:
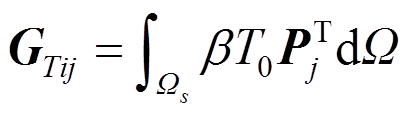 (44)
(44)式中:
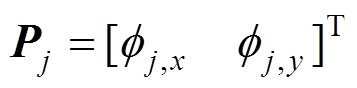 (45)
(45)
同样对式(25)离散可得:
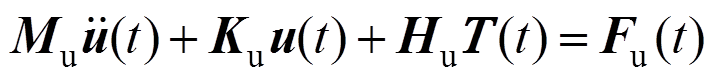 (46)
(46)式中: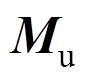 、
、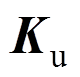 、
、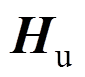 和
和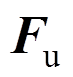 分别为质量矩阵、刚度矩阵、温度荷载矩阵和节点荷载向量。分别表示如下:
分别为质量矩阵、刚度矩阵、温度荷载矩阵和节点荷载向量。分别表示如下:
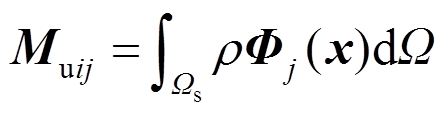 (47)
(47)
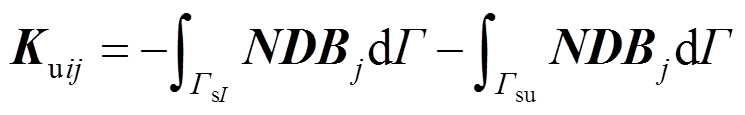 (48)
(48)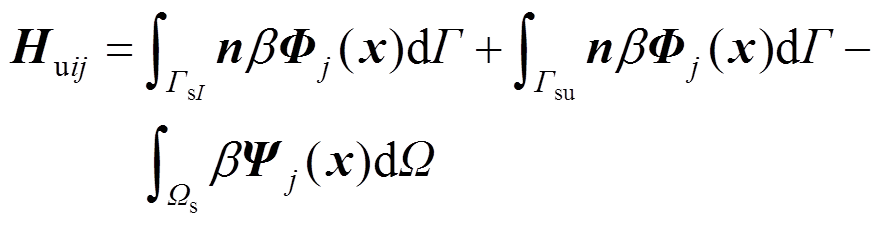 (49)
(49)
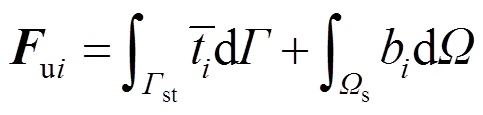 (50)
(50)
式中:
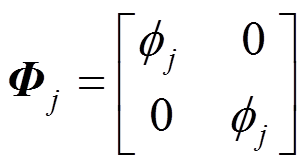 (51)
(51)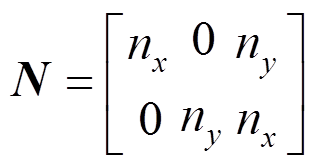 (52)
(52)
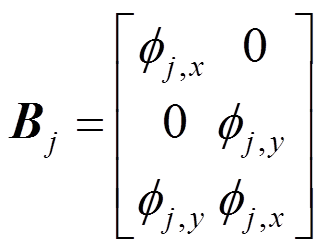 (53)
(53)
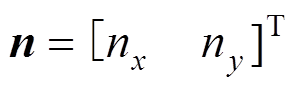 (54)
(54)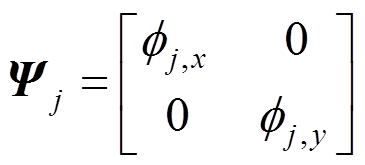 (55)
(55)
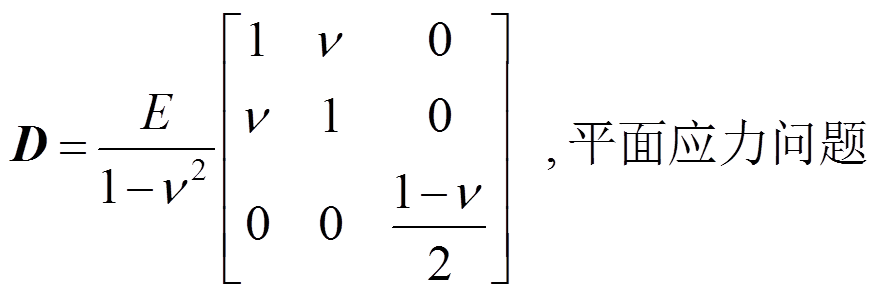 (56)
(56)
对于平面应变问题需把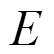 换成
换成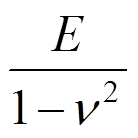 ,
,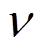 换成
换成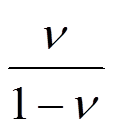 。
。
式(40)和式(46)组成的联立方程组为耦合热力学问题的基本方程,包含了双曲型方程和抛物型方程的混合型方程。应力-应变本构方程在此系统中被处理成应变-温度的代数方程,联立后的方程可改写如下:
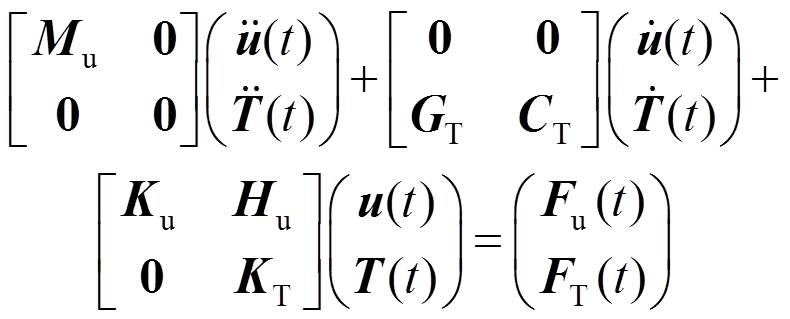 (57)
(57)令:
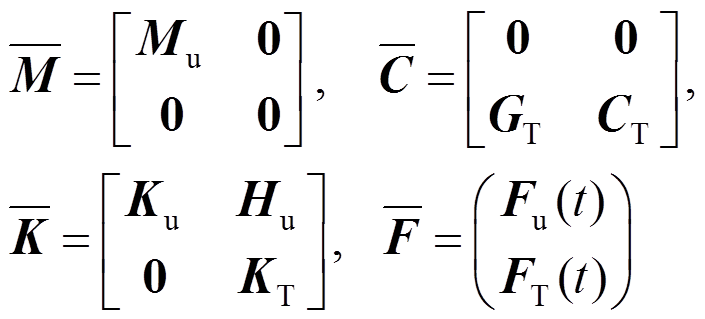 (58)
(58)
从而可得:
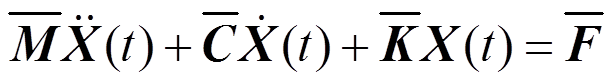 (59)
(59)式中,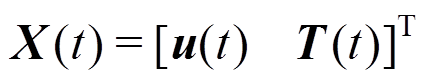 ,式(59)可采用Newmark逐步积分法来进行求解。
,式(59)可采用Newmark逐步积分法来进行求解。
为了研究耦合效应在多大程度上对问题的解产生影响,这里引入一个无量纲参数-材料的耦合系数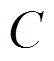 ,即:
,即:
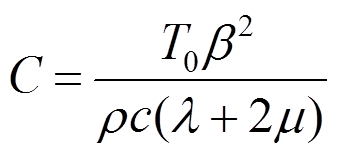 (60)
(60)为了验证本文方法的有效性,这里首先考虑一个单位面积的方形板,如图1所示,其解析解已知。板在初始时刻的温度和位移均为0,板的上端受到一突加的热荷载,板的另外其他3条边均绝热,且法向位移为0,这里假设只考虑平面应变。在不考虑内热源和体力的情况下,其解析解可以表达如 下式:
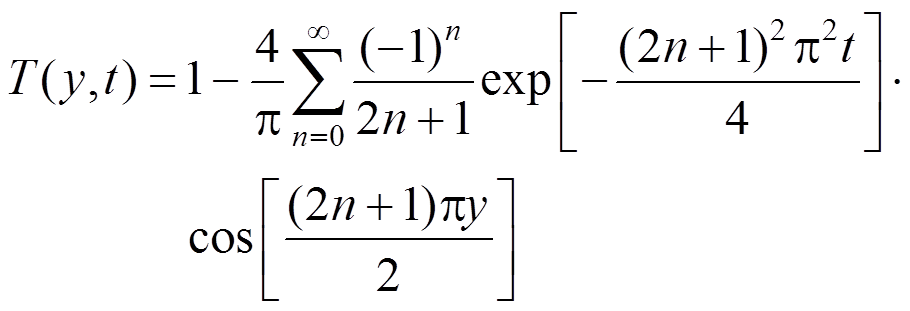 (61)
(61)
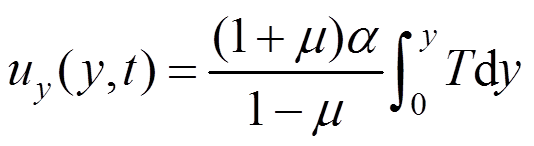 (62)
(62)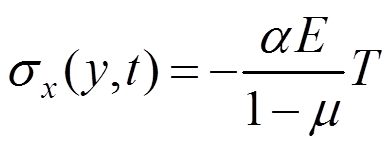 (63)
(63)
这里,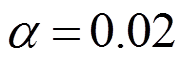 为热膨胀系数,热传导系数
为热膨胀系数,热传导系数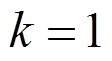 ,密度
,密度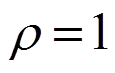 ,比热
,比热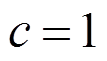 ,弹性模量
,弹性模量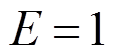 ,泊松比
,泊松比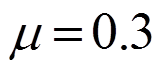 。把方形板用
。把方形板用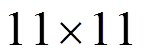 个节点进行离散,时间步取为
个节点进行离散,时间步取为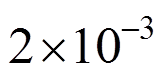 。在数值积分过程中节点支持域半径取2.0,局部积分子域半径取0.5,采用
。在数值积分过程中节点支持域半径取2.0,局部积分子域半径取0.5,采用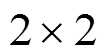 个高斯积分点。图2给出了
个高斯积分点。图2给出了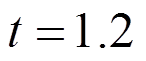 时方板温度场分布图,图3给出了
时方板温度场分布图,图3给出了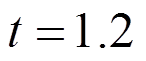 时方板
时方板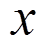 方向热应力分布图。
方向热应力分布图。
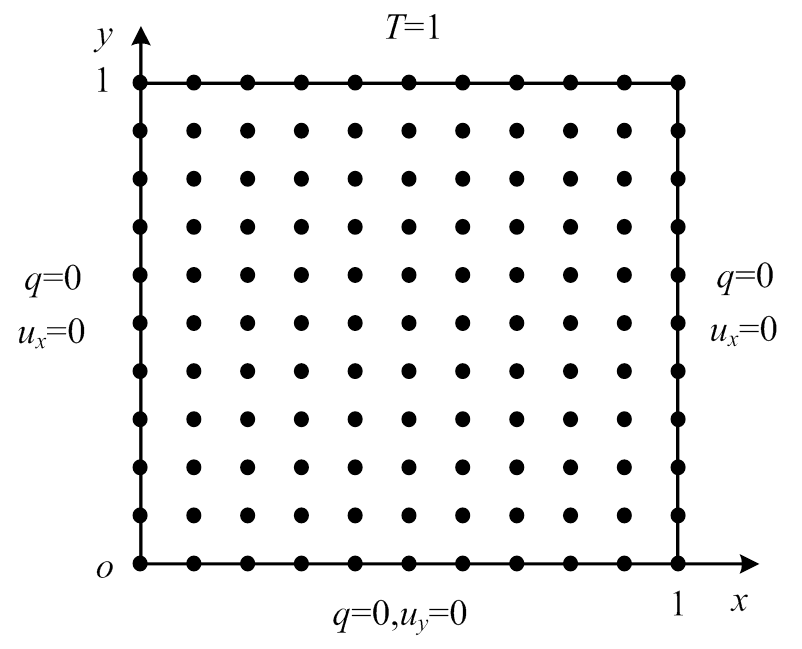
图1 突加热荷载的方板
Fig.1 A suddenly-heated unit square panel
从这些图可以看出,基于IMLS插值的无网格MLPG法计算得到的结果与解析解非常吻合。图4给出了节点尺寸相同时,MLPG法和边界元法在方板最左端底点温度、方板最左端顶点竖向位移、方板最左端中点水平向热应力相对误差比较,很明显可以看出,在节点尺寸相同时,MLPG法相对误差更小,精度更高。
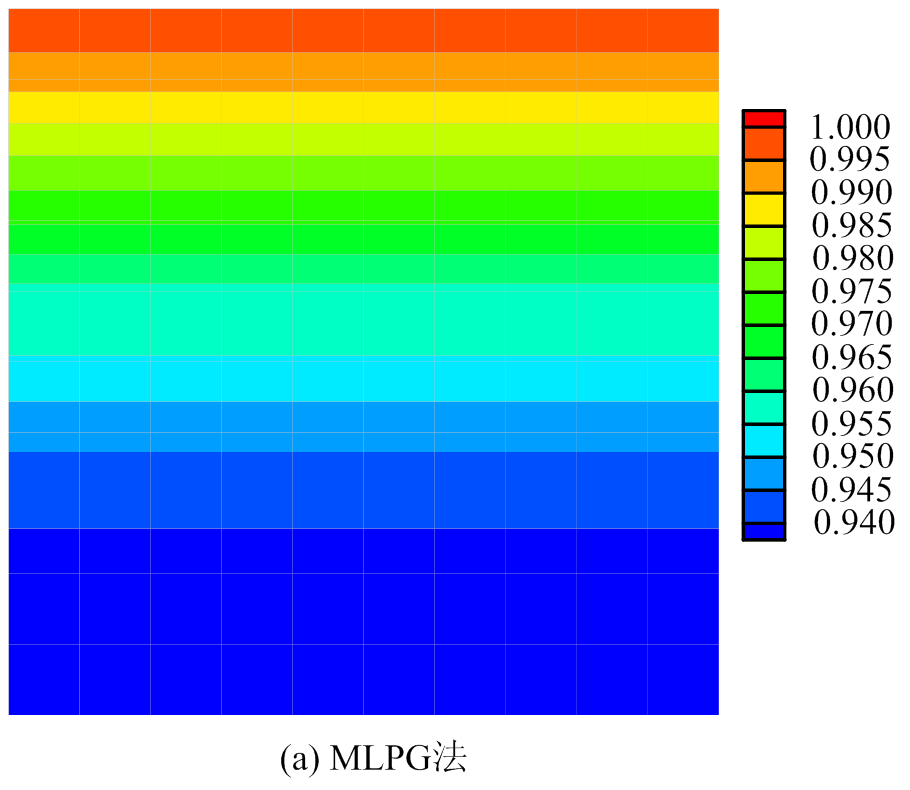
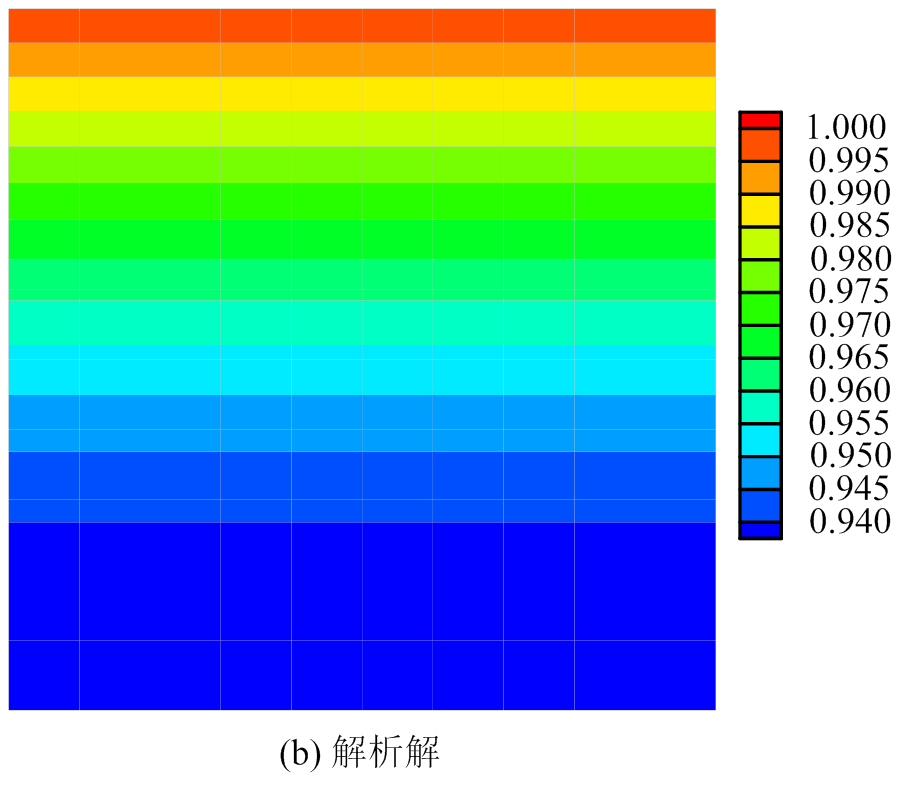
图2 t=1.2时方板温度场分布图
Fig.2 Temperature distribution for the square plate at t=1.2
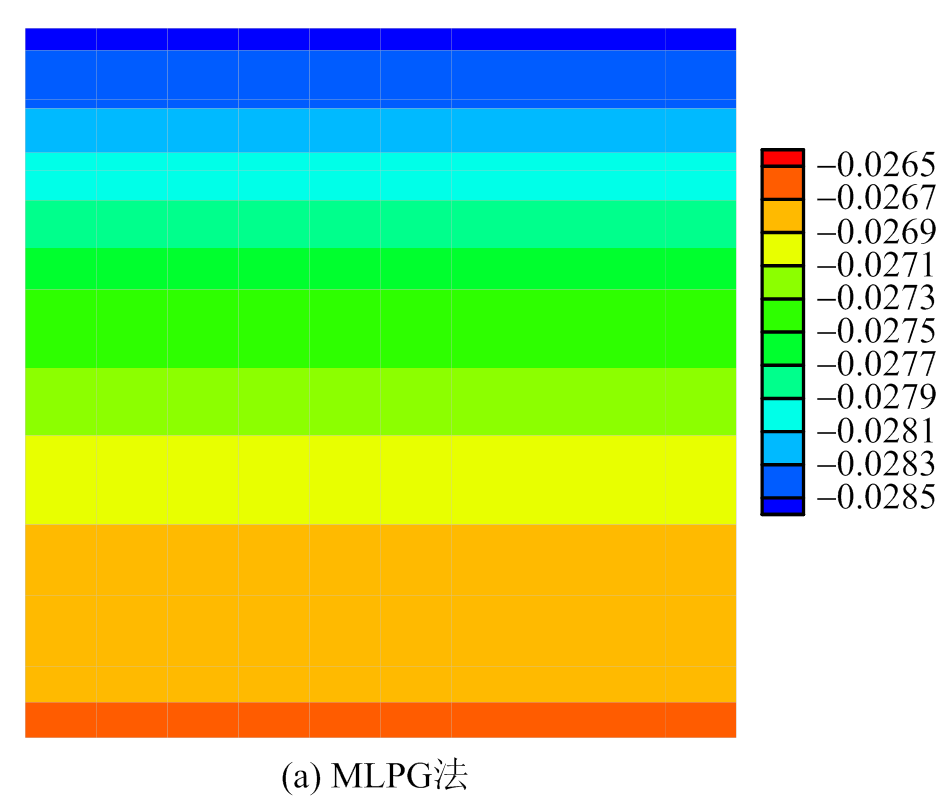
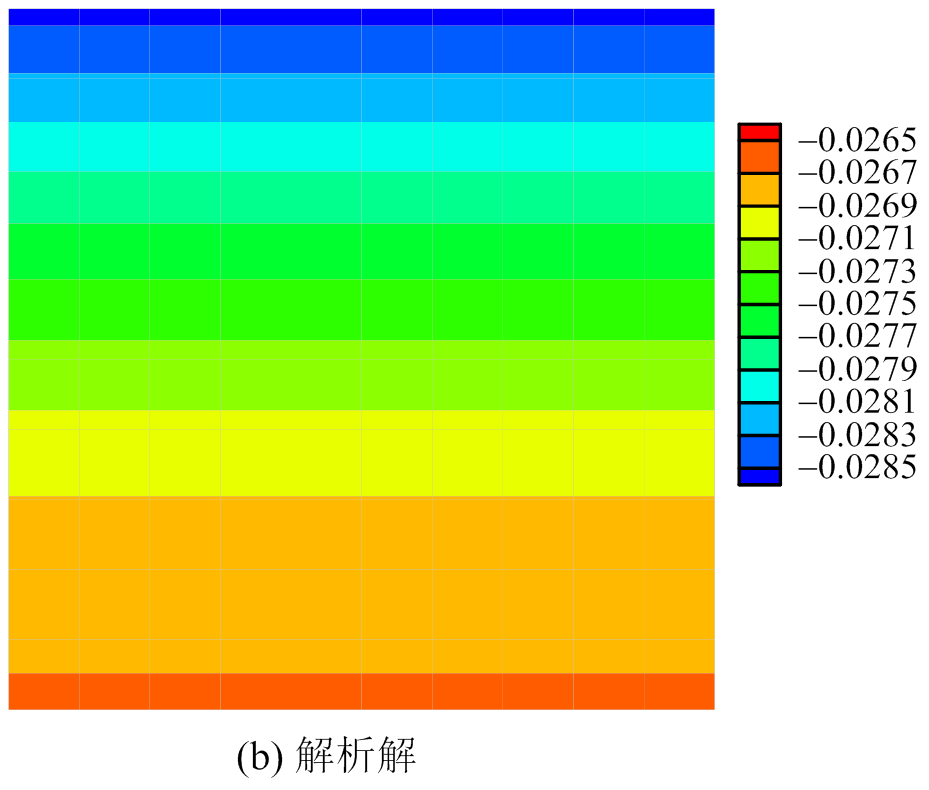
图3 t=1.2时方板水平向热应力分布图
Fig.3 Horizontal thermal stress for the square plateat t=1.2
当考虑热冲击影响时,这里假设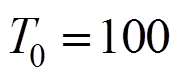 从而可得耦合系数
从而可得耦合系数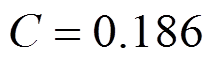 。图5给出了方板左端水平向应力随时间变化曲线图,很明显可以看出耦合项对应力的影响,此时得到的应力是波动的。
。图5给出了方板左端水平向应力随时间变化曲线图,很明显可以看出耦合项对应力的影响,此时得到的应力是波动的。
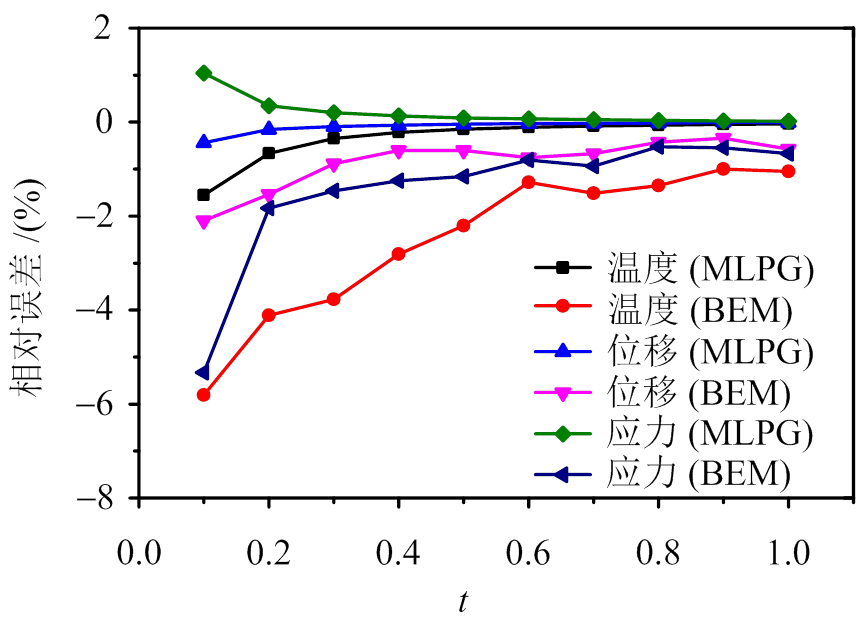
图4 MLPG法和边界元法相对误差比较
Fig.4 Comparison of relative errors between MLPG and BEM
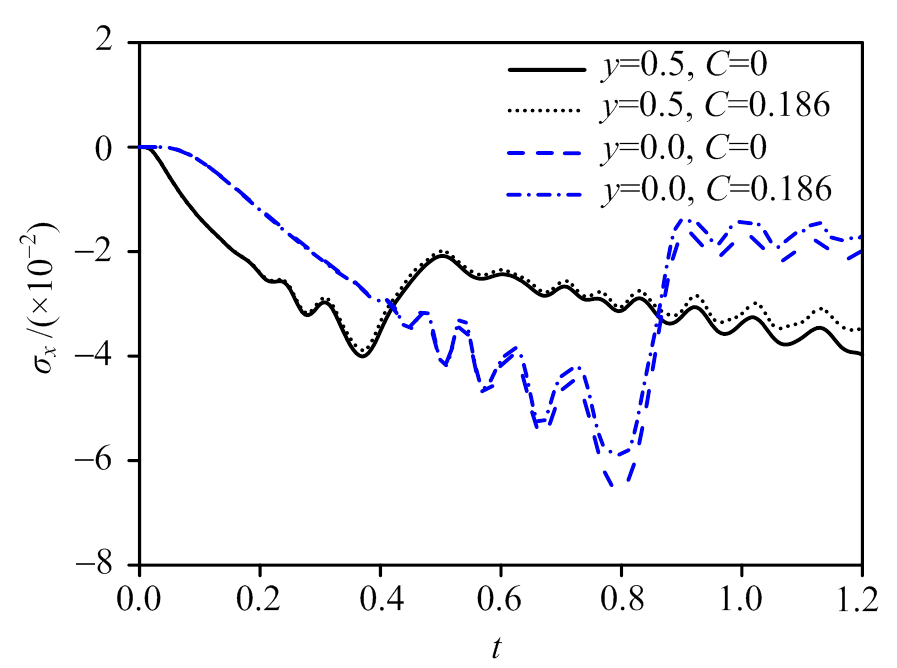
图5 方板左端水平向热应力比较
Fig.5 Horizontal thermal stress at two different points on the y-axis
考虑如图6所示的一方形板[11-12],边长为10,右端固定,其它边自由,左端受热冲击载荷,其他边绝热。材料参数:密度、比热容、导热系数和弹性模量均为1,泊松比为0.3,热膨胀系数为0.02。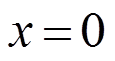 处所受热冲击荷载是时间的函数,即:
处所受热冲击荷载是时间的函数,即:
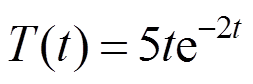 (64)
(64)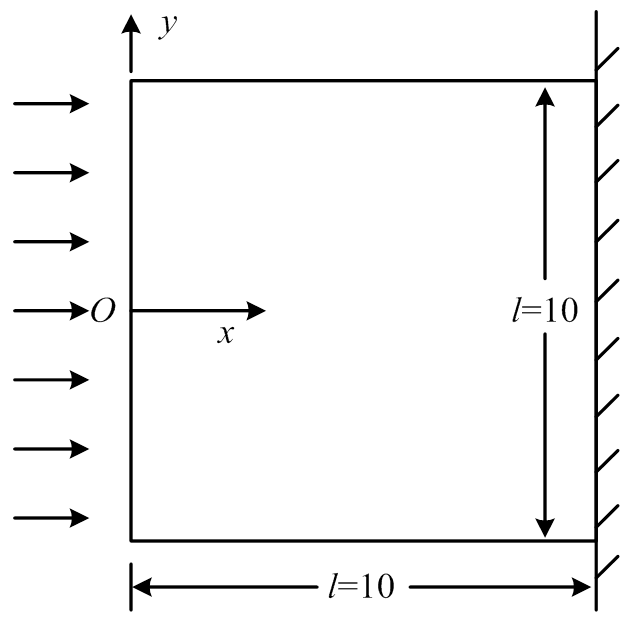
图6 受热冲击的方板
Fig.6 A square plate subjected to thermal shock loading
在数值离散之前,首先对下面的变量取无量纲量:
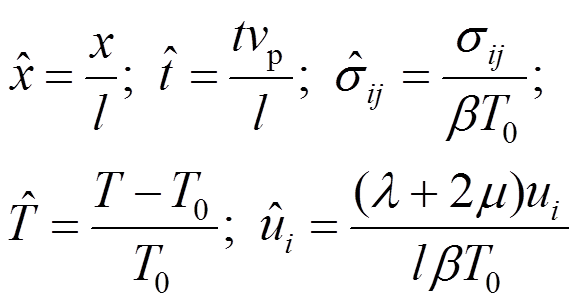 (65)
(65)本算例中都取无量纲量,并略去上标^。为了进行结果对比,这里同时用BEM进行了求解。MLPG法计算过程中,共划分为两种节点形式,一种是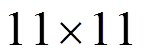 个节点,第二种是
个节点,第二种是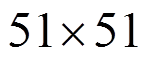 个节点。BEM求解过程中,边界共划分成20个二次单元。
个节点。BEM求解过程中,边界共划分成20个二次单元。
图7给出了无量纲时间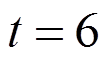 时耦合和无耦合两种情况下沿x轴的温度分布,并与BEM计算的结果作对比,很明显可以看出,由于耦合项的存在,温度分布很不相同,MLPG法相比BEM计算结果,更加逼近于
时耦合和无耦合两种情况下沿x轴的温度分布,并与BEM计算的结果作对比,很明显可以看出,由于耦合项的存在,温度分布很不相同,MLPG法相比BEM计算结果,更加逼近于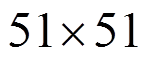 个节点时计算结果。图8给出了无量纲时间
个节点时计算结果。图8给出了无量纲时间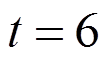 时耦合和无耦合两种情况下沿x轴的水平向位移分布,从图8可以看出热场与应力场耦合项对位移的影响,MLPG法相比BEM计算精度更高。
时耦合和无耦合两种情况下沿x轴的水平向位移分布,从图8可以看出热场与应力场耦合项对位移的影响,MLPG法相比BEM计算精度更高。
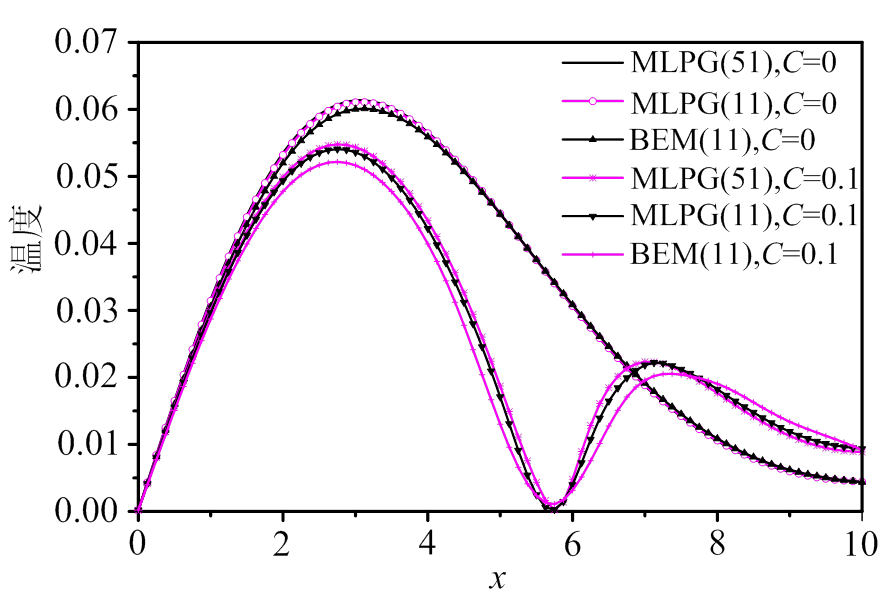
图7 t=6时沿x轴的温度分布
Fig.7 Comparison of temperature along x-axis at t=6
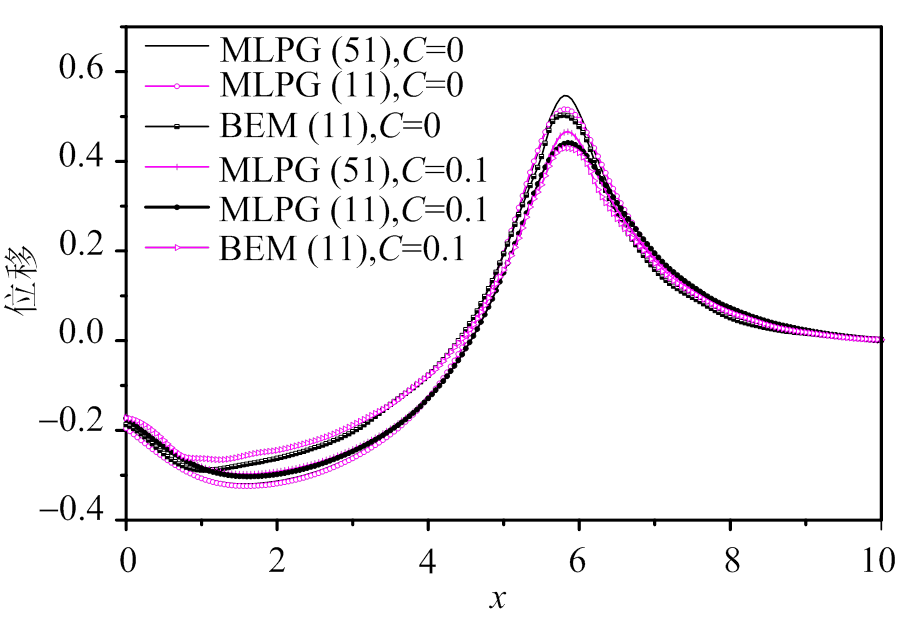
图8 t=6时沿x轴水平向位移值分布
Fig.8 Comparison of displacement 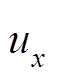 along x-axis at t=6
along x-axis at t=6
本文将插值型移动最小二乘法与无网格MLPG法结合用来求解二维结构耦合热弹性问题,Heaviside分段函数作为修正的Fourier热传导方程和弹性动力方程局部弱形式的权函数,从而可得热耦合问题的二阶常微分方程组。常微分代数系统采用Newmark逐步积分法进行求解,由于无需Laplace变换便可直接得到温度场和位移场数值结果,因此可明显减少计算工作量。
参考文献:
[1] 段进涛, 史旦达, 汪金辉, 等. 火灾环境下钢结构响应行为的FDS-ABAQUS 热力耦合方法研究[J]. 工程力学, 2017, 34(2): 197―206.
Duan Jintao, Shi Danda, Wang Jinhui, et al. A study of thermal-mechanical coupled method of analyzing steel structures’ thermal response in fire based on FDS-ABAQUS [J]. Engineering Mechanics, 2017, 34(2): 197―206. (in Chinese)
[2] Mavrič B, Šarler B. Application of the RBF collocation method to transient coupled thermoelasticity [J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2017, 27(5): 1064―1077.
[3] Nowinski J L. Theory of thermoelasticity with applications [M]. New York: Sijhoff & Noordhoff International Publishers, 1978.
[4] Boley B A, Weiner J H. Theory of thermal stresses [M]. New York: Dover Publications, 2011.
[5] 马永斌, 何天虎. 基于分数阶热弹性理论的含有球型空腔无限大体的热冲击动态响应[J]. 工程力学, 2016, 33(7): 31―38.
Ma Yongbin, He Tianhu. Thermal shock dynamic response of an infinite body with a spherical cavity under fractional order theory of thermoelasticity [J]. Engineering Mechanics, 2016, 33(7): 31―38. (in Chinese)
[6] 谷良贤, 王一凡. 几何非线性假设下温度大范围变化瞬态热力耦合问题研究[J]. 工程力学, 2016, 33(8): 221―230.
Gu Liangxian, Wang Yifan. The transient response of thermo-mechanical coupling with wide change in temperature based on the hypothesis of geometry nonliearity [J]. Engineering Mechanics, 2016, 33(8): 221―230. (in Chinese)
[7] Boley B A, Tolins I S. Transient coupled thermoelastic boundary value problems in the half-space [J]. Journal of Applied Mechanics-ASME, 1962, 29(4): 637―646.
[8] Nariboli G A. Spherically symmetric thermal shock in a medium with thermal and elastic deformations coupled [J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1959, 14(1): 75―84.
[9] Takeuti Y, Ishida R, Tanigawa Y. On an axisymmetric coupled thermal stress problem in a finite circular cylinder [J]. Journal of Applied Mechanics-ASME, 1983, 50(1): 116―122.
[10] Oden J T. Finite elements of nonlinear continua [M]. New York: Dover Publications, 2006.
[11] Park K H, Banerjee P K. Two- and three-dimensional transient thermoelastic analysis by BEM via particular integrals [J]. International Journal of Solids and Structures, 2002, 39(10): 2871―2892.
[12] Tehrani P H, Eslami M R. BEM analysis of thermal and mechanical shock in a two-dimensional finite domain considering coupled thermoelasticity [J]. Engineering Analysis with Boundary Elements, 2000, 24(3): 249―257.
[13] 王林翔, 梅尔姆克. 热弹性动力学耦合问题的微分代数方法[J]. 应用数学和力学, 2006, 27(9): 1036―1046.
Wang Linxiang, Melnik R V N. Differential algebraic approach to coupled problems of dynamic thermoelasticity [J]. Applied Mathematics and Mechanics, 2006, 27(9): 1036―1046. (in Chinese)
[14] Atluri S N, Zhu T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics [J]. Computational Mechanics, 1998, 22(2): 117―127.
[15] Atluri S N, Shen S P. The meshless local petrov-galerkin (MLPG): a simple & less-costly alternative to the finite element and boundary element methods [J]. Computer modeling in Engineering and Sciences, 2002, 3(1): 11―51.
[16] Sladek J, Sladek V, Zhang C, et al. Meshless local Petrov-Galerkin method for linear coupled thermoelastic analysis [J]. Computer modeling in Engineering and Sciences, 2006, 16(1): 57―68.
[17] Hosseini S M, Sladek J, Sladek V. Meshless local Petrov-Galerkin method for coupled thermoelasticity analysis of a functionally graded thick hollow cylinder [J]. Engineering Analysis with Boundary Elements, 2011, 35(6): 827―835.
[18] Zheng B J, Dai B D. A meshless local moving Kriging method for two-dimensional solids [J]. Applied Mathematics and Computation, 2011, 218(2): 563―573.
[19] 王峰. 改进的无网格法求解温度场和温度应力及其在水工结构分析中的应用[D]. 大连: 大连理工大学, 2015.
Wang Feng. Improved meshless method for the solution of temperature field and thermal stress and its application to hydraulic structure analysis [D]. Dalian: Dalian University of Technology, 2015. (in Chinese)
[20] Zheng B J, Gao X W, Yang K, et al. A novel meshless local Petrov-Galerkin method for dynamic coupled thermoelasticity analysis under thermal and mechanical shock loading [J]. Engineering Analysis with Boundary Elements, 2015, 60: 154―161.
[21] 程玉民. 移动最小二乘法研究进展与述评[J]. 计算机辅助工程, 2009, 18(2): 5―11.
Cheng Yumin. Advances and review on moving least- square methods [J]. Computer Aided Engineering, 2009, 18(2): 5―11. (in Chinese)
[22] Lancaster P, Salkauskas K. Surface generated by moving least squares methods [J]. Mathematics of computation, 1981, 37(155): 141―158.
[23] 任红萍, 程玉民, 张武. 弹性力学的插值型边界无单元法[J]. 中国科学: 物理学力学天文学, 2010, 40(3): 361―369.
Ren Hongping, Cheng Yumin, Zhang Wu. Interpolating boundary element free method for elasticity [J]. Chinese Science: Physics, mechanics and Astronomy, 2010, 40(3): 361―369. (in Chinese)
MESHLESS METHOD BASED ON INTERPOLATING MOVING LEAST SQUARE SHAPE FUNCTIONS FOR DYNAMIC COUPLED THERMOELASTICITY ANALYSIS
Abstract: The two-dimensional structural dynamic coupled thermoelastic problem is solved by meshless local Petrov-Galerkin (MLPG) method based on the interpolating moving least-squares (IMLS) method. The local weak forms are developed using the weighted residual method from the modified Fourier heat conduction equations and elastodynamic equations, in which the Heaviside step function is used as the test function in each sub-domain. Then the second-order ordinary differential equations describing the coupled thermoelasticity problem are obtained. Using the differential algebraic method, these second-order ordinary differential equations can be transformed into ordinary differential algebraic systems, in which temperature and displacement are chosen as auxiliary variables. The Newmark step-integration method is used to solve the ordinary differential system. The temperature and displacement numerical results can be obtained directly without the Laplace transform. Since the shape functions constructed from the IMLS method possess the Kronecker delta property, the essential boundary conditions can be implemented directly. Finally, two numerical examples are studied to illustrate the effectiveness of this method.
Key words: coupled thermoelasticity; moving least square method; meshless local Petrov-Galerkin method; Heaviside step function; differential algebraic method
文章编号:1000-4750(2019)04-0037-07
中图分类号:O343.6
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.01.0074
收稿日期:2018-01-26;
修改日期:2019-01-13
基金项目:湖北省教育厅科学技术研究项目中青年人才项目(Q20181207)
林 皋(1929―),男,江西人,教授,博导,中科院院士,主要从事核电与水工结构抗震研究(E-mail: gaolin@dlut.edu.cn);
周宜红(1966―),男,湖北人,教授,博士,博导,主要从事水工施工组织和管理研究(E-mail: zyhwhu2003@163.com);
范 勇(1988―),男,湖北人,副教授,博士,主要从事工程爆破与岩石动力学研究(E-mail: yfan@whu.edu.cn).