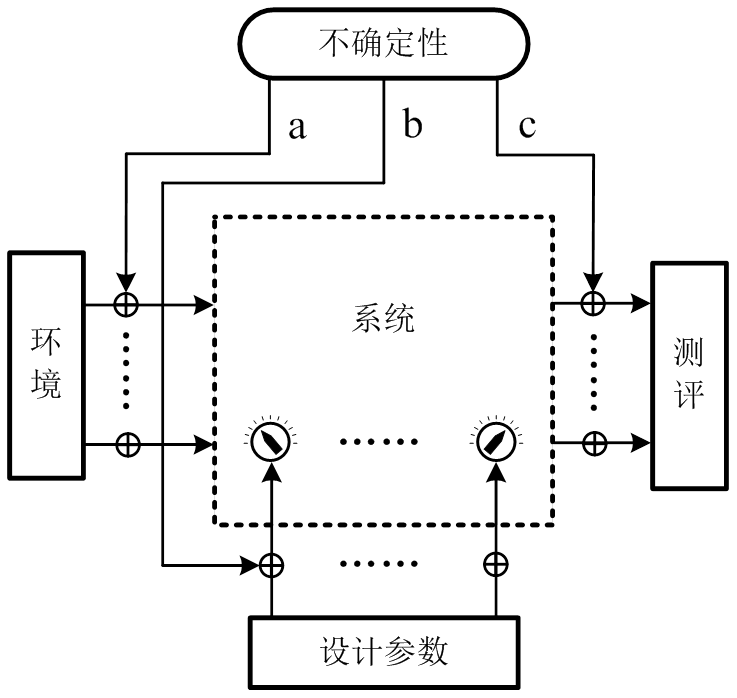
a-环境的不确定性；b-设计参数的不确定性；c-评测的不确定性
图1 工程优化问题中的不确定性
Fig.1 Uncertainties in engineering optimization problems
摘 要：如何提高结构动力学性能的鲁棒性，以减小各种不确定性因素对设计结果的影响是当前学术界和工程界研究和关注的热点问题之一。该文阐述了结构动力鲁棒优化设计的基本概念，从基于Taguchi的方法、基于多目标优化的方法和基于响应面建模的方法三个方面对结构动力鲁棒优化设计的研究进行了综述。以双转子为例，从结构的动力响应要求出发，采用响应面建模、多目标优化的方法进行了设计并与采用Taguchi方法得到的结果进行比较。结果表明，基于响应面建模、多目标优化的方法能够获得多个具有鲁棒性的设计方案，在处理具有不确定性的结构动力学问题时有着很大的应用潜力。最后，对当前方法和后续研究内容作了简要总结和展望。
关键词：结构动力优化设计；鲁棒优化；Taguchi方法；多目标优化；响应面方法
结构动力优化设计旨在根据实际问题对结构的要求来建立优化设计模型，将各种算法同动力学分析与计算相结合，对结构的设计方案包括尺寸、形状和材料等参数进行自动化的寻优[1]。作为结构动力学、有限元分析和数学规划等学科相互交叉、有机结合的产物，结构动力优化设计已成为改善结构/机械系统的动态特性、提高产品质量的一个重要手段和途径。
早期的结构动力设计，由于缺乏理论分析和计算方法的指导，不得不依靠经验，采用类比或试凑等方法。60年代以来，结构动力设计理论、有限元的创立和发展，以及高速大容量计算机的出现和普及，使得计算机化的结构动力设计成为可能。1965年，Niordson[2]采用分布参数法实现了振动梁基频的最大化，开创了结构动力优化设计的先河。分布参数法属于解析优化的方法，仅适用于简支梁、悬臂梁等简单结构的设计和优化。60年代末，出现了准则设计法和数学规划法等各种不同的优化方 法[3]。其中，准则设计法是通过基本的力学概念或实际工程经验建立优化设计准则，并进一步通过迭代算式进行优化计算；数学规划法是以规划论为基础，结合有限元来求解一个从力学现象抽象出来的数学命题。以上三种方法虽然在理论和工程方面得到广泛研究和应用，但它们忽略了各种不确定性因素对结构动态特性的影响，以确定性参数来建立优化设计模型。实际上，在工程问题中，不确定性是固有的。任何一种机械结构/产品在生产和使用过程中都会受到各种不确定性如材料分散性、加工和装配误差，以及环境温度、湿度变化等的影响，如果不考虑这些不确定性因素进行分析和设计，往往会导致相同结构、同批生产的产品具有过大的动力特性波动并影响最终产品的使用性能，严重时甚至引起产品的失效。以航空发动机为例，同一生产线上成批生产的发动机产品，零件加工、装配工艺等存在的不确定性会导致同种产品的实际动力学特性有所不同，甚至出现各个零部件均符合设计加工要求，但装配后时常出现整机振动过大的现象[4]。
考虑不确定性进行结构动力优化设计的研究始于80年代初期。1981年，Rao[5]对随机参数、随机振动结构系统进行了优化设计。此后，通过随机模拟和概率分析来处理结构的动力优化设计问题逐渐引起了人们的兴趣和关注，相关方法主要有两类：可靠性设计方法和鲁棒优化设计方法。可靠性设计方法的主要目标是针对极端情况进行安全设计。鲁棒优化设计通常被认为是源自于20世纪70年代日本学者田口博士所创立的三次设计法(也称Taguchi方法)[6]。与可靠性设计方法不同的是，鲁棒优化设计方法主要寻求合理的设计方案以最小化不确定因素变化对结构/系统响应的影响。
结构鲁棒性的概念最早由Yamakawa[7]明确提出。2005年，Zang等[8]对鲁棒性优化在结构动力学的应用作了系统回顾，并以振动吸振器鲁棒性设计为例，说明了鲁棒性设计方法应用在结构动力学中处理结构不确定性的极大潜力。至今，有关如何提高结构动力学性能的鲁棒性、减小各种不确定因素对设计方案的影响深受人们的关注和研究。本文在介绍结构动力鲁棒优化设计基本概念的基础上，从工程上常用的建模和优化方法，包括基于Taguchi的方法、基于多目标优化的方法和基于响应面建模的方法三个方面对有关结构动力鲁棒优化设计的研究进行分类叙述，并对当前方法进行总结和展望，以期为后续进一步的研究工作提供参考。
不确定性是工程设计中的一个重要概念，具体可从环境、设计参数和系统输出结果三个方面来分析，如图1所示[9]。
a-环境的不确定性；b-设计参数的不确定性；c-评测的不确定性
图1 工程优化问题中的不确定性
Fig.1 Uncertainties in engineering optimization problems
图1中，环境不确定性包括温度的改变、载荷的动态变化等。设计参数的不确定性是由制造误差如机械零件的几何形状与尺寸误差、安装误差，以及材料的老化等引起。系统输出结果的不确定性一方面是由于测量和评定误差的存在，另一方面是由环境不确定性和设计参数不确定性所导致。从设计角度看，环境的不确定性不受设计者的控制，为噪声因素；设计参数的不确定性可以通过减小零件加工误差等措施来降低，为可控因素。
鲁棒性也称作稳健性，指的是不确定因素(原因)发生微小变差对因变量(结果)影响的不敏感 性[10]。受到各种噪声因素的影响，实际结构的动力学性能表现总会与预期目标存在一定的偏差，结构动力学性能的鲁棒性可定义为机械结构/系统在输入参数存在不确定性的情形下，维持结构/系统动力学性能稳定在预期目标附近区域的能力。结构动力鲁棒优化设计实质上是在各种噪声因素客观存在且无法避免和消除的情况下，通过确定合理的设计参数值及变差范围(容差)来减少系统响应输出结果相对预期目标的偏差和波动，使得机械结构/系统的动力学性能稳定在理想值附近的区域范围内，如图2(d)所示。
图2 系统性能变化的几种情形[8]
Fig.2 Different types of system performs
图2中，大圆圈表示预期性能目标，系统的实际性能由点及相关的概率密度函数表示。
有关结构动力鲁棒优化设计的研究，以下主要从基于Taguchi方法、基于多目标优化的方法和基于响应面的方法三个方面分别进行叙述。
理想的系统动态特性y与信号因素M应具有较强的线性关系，即：
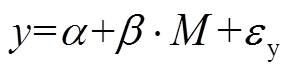(1)式中：系数β反映系统响应对信号因素的灵敏度；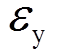
为系统响应误差。Taguchi方法引入信噪比(dynamic signal-to-noise ratio，DSN)作为设计结果鲁棒性的评价依据。动态性能的信噪比可采用下式进行计算：
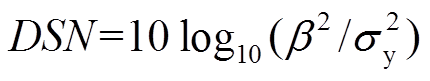(2)
式中：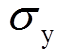
为系统动态响应的均方差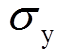，越小表明系统抗噪声的能力越强。DSN值越大，意味着系统输出波动小且对信号因素的灵敏度高。Taguchi方法采用正交试验和方差分析来估计β和DSN，通过以下两个步骤来确定控制因素最佳组合：第一步是最大化信噪比DSN得到控制因素的一个组合；第二步通过调节灵敏度高的控制因素来改变β值，使系统性能更接近目标值。
张正福等[11]为了降低有限元模型计算复杂且耗时的问题，提出了基于子结构法的微结构动态性能解析方法，在此基础上通过Taguchi方法修正音叉振动式微机械陀螺关键结构参数。谢晖等[12]以某桥车左前门为研究对象，将车门板件厚度作为控制因素，材料特性以及载荷作为噪声因素，通过正交试验、信噪比以及方差分析，找出对车门下垂刚度和一阶固有频率最敏感的最佳的控制因素水平组合。张代胜等[13]将汽车动力总成悬置结构简化为一个六自由度无阻尼振动系统，考虑关键刚度变化系数不确定性的影响，对悬置系统的隔振性能进行鲁棒设计。王淑红等[14]通过Hadamard矩阵法建立混合正交试验设计表，给出使电机效率高和转矩脉动系数小的一种方案。Cai等[15]为获得冲破性能稳定的复合材料易碎盖，比较了不同结构参数及因素水平对冲破性能的影响程度，获得了最优薄弱区结构参数组合。郭一鸣等[16]将Taguchi方法用于橡胶扭转减振器稳健性优化匹配。Song等[17]建立永久磁铁线性同步电动机的有限元模型，依据有限元分析结果进行试验设计，在保持平均推力基本不变的情况下降低其推力波动和谐波含量。孙光永等[18]为实现车门轻量化，并保证其刚度、模态及耐撞性等性能，提出了一种基于连续Taguchi 方法和TOPSIS-熵的多目标离散稳健优化算法。
Taguchi方法将产品设计分为系统设计、参数设计和容差设计三个阶段，其中容差设计的目的是通过对可控因素分配适当的容差以减少生产成本，并进一步降低产品性能的散布范围[19]。一般来说，较小的容差有助于提高产品的质量，从而减少质量损失，但容差越小会导致产品的生产成本越高。在产品的尺寸及几何容差规范设计中，采用极值法、均方根法、等精度法等方法可进行简单尺寸容差的分析和综合。随着计算机技术的发展，模拟仿真[20]、优化方法[21]也被用于尺寸以及复杂形位公差的设计。殷良伟等[22]以某发动机封严篦齿盘5参量单轴对称异型孔为研究对象，讨论了异型孔的重要结构尺寸容差对孔边应力分布及配合的影响。杨隽等[23]为减小在制造过程的设计参数不确定和安装工艺不确定影响下结构动力响应的波动，基于Taguchi方法对某型航空发动机双转子系统进行动力学容差设计。文献[24]以悬臂梁的第一阶固有频率为目标，运用正交试验设计和方差分析对悬臂梁结构进行了鲁棒优化。损失模型是Taguchi方法中的一个重要概念，岳伟等[25]通过分析止口结构刚度损失模型，以提高转子的刚度稳健性和接触状态稳健性为目的，对高速可拆卸转子止口连接结构进行稳健性设计。洪杰等[26]针对带有连接界面的航空发动机转子结构系统，分析界面损伤失效的力学特征，建立针对连接界面及结构系统力学特性的多目标、多参数稳健设计模型。
Taguchi方法虽然原理简单，但实际应用中仍然存在着一定的局限性和低效性。如难以处理具有大量设计变量和水平划分，采用内外表通常需要大量的试验、容易出现信息丢失，以及不一定能找到存在高度非线性设计问题的精确解等[27−28]。
影响机械结构/系统动力学性能的参数分为信号因素s、控制因素x和噪音因素z三种。采用容差定量描述可控因素与噪声因素的不确定性，以动力学响应为目标的鲁棒优化设计方法是同时使系统性能相对预期目标的偏差和波动最小。
令Δxi(i=1,2,…,m)和Δzj(j=1,2,…,n)分别为可控因素xi和噪声因素zj的容差，y表示系统的响应输出，y=f(s, x, z)，结构动力鲁棒优化设计本质上为一个多目标优化问题，如下[29]：
(3)式中：t为系统响应预期目标；μf和σf分别为系统性能的均值和标准差。约束条件分极限(100%满足)和统计两种情况，分别对应式(4)和式(5)：
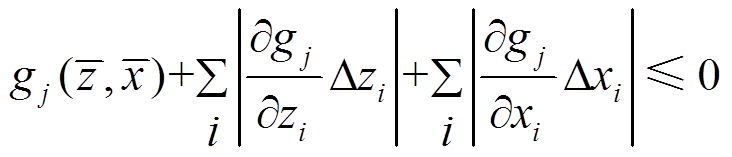(4)
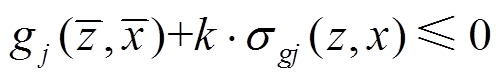(5)式中：σgj为第j个约束的标准差的近似值；k为常数，若约束服从正态分布，k=3意味当前约束满足的概率为99.865%。
Zang[30]研究了调谐质量阻尼器(tuned mass damper，TMD)的减振优化问题，考虑减震器的质量、刚度和阻尼参数的不确定性，采用一阶和二阶泰勒级数来近似计算目标函数的均值和方差，以最小化主系统在大范围内激励频率作用下位移响应的均值及标准差为目标进行优化设计。肖方豪等[31]同时考虑目标函数与约束条件的鲁棒性，对二自由度TMD进行了鲁棒优化设计。Marano等[32]将传统的TMD单目标设计和多目标鲁棒设计优化进行了比较，分析表明，多目标鲁棒设计方法在提升TMD性能稳定性方面有着显著的改进。Miguel等[33]研究将摩擦阻尼器(friction damper, FD)用于控制结构在地震激励下的位移响应，以位移响应的均值和方差为优化目标，考虑结构质量、刚度以及FD安装位置的不确定性，以一栋六层建筑为例，优化结果表明采用三个FDs就可减少结构最大响应位移约70%的均值和几乎99%的波动方差。孙晓颖等[34]采用强度Pareto进化算法(SPEA)和基于信噪比的决策方法对平流层飞艇进行了多目标优化设计。结果表明：采用的SPEA算法是合理有效的，可以得到非劣解分布较均匀的Pareto曲面；通过基于信噪比的决策方法，可从非劣解集中获得满足实际要求的最稳健设计方案。Roy等[35]考虑结构参数的不确定性，通过最小化结构最大加速度响应的期望值及其标准差，实现基础隔震系统的鲁棒优化设计。Dell’Elce等[36]提出了一种基于鲁棒等峰值概念的线性减振器调谐策略，以减小机械系统不确定的谐振。蒲利东等[37]基于多目标遗传算法研究了飞机气动伺服弹性耦合频率低且随飞机重量构型变化大的问题。陈鑫等[38]基于遗传算法，以结构响应和阻尼器行程的复合满意度作为优化目标，针对高耸结构环形TLD的多目标优化设计开展研究。
汽车发动机悬置系统的设计优化对整车减振非常重要，王歆侃[39]以悬置的主刚度值为设计变量，以发动机悬置系统能量解耦为目标，用遗传算法对系统的刚度参数进行稳健优化。陈新志等[40]以驾驶员座椅处的垂直加速度均方根值最小化为目标建立了9自由度的半挂汽车列车平顺性稳健优化模型。Loyer等[41]研究了一种被动车辆悬架系统的鲁棒设计，方法中同时考虑车辆被动悬架系统的舒适性与行驶平顺性，采用一阶泰勒级数近似获得弹簧质量的加速度、轮胎偏转以及弹簧质量的正则化绝对位移的标准偏差来进行优化设计。燕宁宁等[42]针对悬架空间结构参数的不确定性对悬架系统性能的影响，以车辆行驶中最大车身垂向加速度、最大侧倾角及最大横摆角速度3个参数为优化目标，以悬架系统的7个空间结构参数为设计变量，采用蒙特卡洛方法对悬架系统进行鲁棒优化设计。范政武等[43]以车辆平顺性和轮胎动载为优化目标，选择前后悬架弹簧刚度、减振器阻尼系数为优化参数，设计了一种基于改进多目标粒子群优化算法MDPL-MOPSO的悬架系统多目标优化策略。
转子系统是旋转机械的重要组件，转子动力学的研究中通常涉及不确定参数和随机载 荷[44－45]。Ma等[46]采用容差模型定量分析支承刚度、连接结构刚度和不平衡量这些不确定因素对转子动力响应的影响。Ritto等[47]采用坎贝尔图和罚函数对具有参数不确定性的柔性转子轴承系统进行了鲁棒优化，目的是找出一组参数的值(如轴承的刚度、直径等)，使系统的固有频率尽可能远离工作转速。Lopez等[48]提出了一种用于转子轴承系统的鲁棒优化设计方法，对于每一个给定的工作转速Ωi，以其与固有频率wij(j = 1, 2, …, nf ; nf为频率带中包含的固有频率的数量)的接近程度来定义一个相应的惩罚函数，通过最小化罚函数的期望值和方差来进行优化设计。Krack等[49]考虑连接界面上接触参数的不确定性以，提出了叶状圆盘摩擦界面设计的优化方法并应用于调谐整体叶盘的设计，提高了叶片－轮盘结构系统阻尼减振性能的稳健性。姚建尧等[50]在状态空间内建立了失谐叶盘结构的传递函数模型，以失谐传递函数矩阵的结构奇异值为指标，研究了各种失谐参数对叶盘结构鲁棒性能的影响。段勇亮等[51]研究了主动失谐叶盘的振动特性并对其随机失谐的鲁棒性进行了分析。
当设计参数与目标函数之间具有显示的数学关系且掌握了不确定性因素的统计数据时，采用概率方法进行鲁棒优化设计是一种理想的处理方法，其理论比较成熟。当不确定性参数概率分布信息较难或者无法获知的情况下，一些研究中采用非概率方法进行鲁棒设计和优化。罗佑新等[52]提出了一种基于设计变量敏感性的高维多目标稳健优化设计方法。郝芳芳等[53]建立了基于灵敏度附加目标函数及灰色关联度理论的多目标稳健优化设计模型，应用该模型进行起重机主梁的稳健优化设计。Sundaresan等[54]采用灵敏度指标来表征性能的稳健性，提出基于最差情况分析法的角空间算法来预测目标函数的稳健性，该方法不受泰勒近似所产生的误差的影响，但是计算效率较低。Petrov等[55]研究了叶盘最大响应幅值关于叶片失谐参数的灵敏度计算方法。谭元球等[56]针对失谐叶盘结构的受迫响应与叶片失谐之间的敏感性问题，提出了一种失谐叶盘最大响应幅值关于叶片频率失谐参数和叶片节点失谐质量的一阶和二阶灵敏度系数计算方法。Du等[57]提出一种实现对大型复杂结构的目标函数及约束函数变差的数值计算方法。Liu等[58]研究了结构参数和外部载荷对转子接头刚度和接触状态的动态影响，采用有限差分法对典型参数(样条接头的刚度)的临界转速和振动模式的灵敏度分析。Marano等[59]将不确定性参数均视为模糊数，在可信度理论(the credibility theory)的框架内定义了多目标函数：第一个是采用的基于性能的结构指标的模糊期望值，第二个是模糊方差。Lievens等[60]将固有频率和模态阻尼模型化为模糊数，提出了一种考虑模态参数不确定性的TMD鲁棒优化方法。
随着计算机技术的飞速发展，工程计算的模型越来越复杂，计算规模越来越大，花费的机时越来越长，例如对飞机总体结构进行优化设计，整个优化迭代过程的计算工作量非常可观，直接计算需要成百上千次的有限元分析，有时甚至无法完成。同时，许多工程问题的目标函数和约束函数对于设计变量经常是不光滑的或者具有强烈的非线性。
响应面法(response surface methodology，RSM)的基本思想是用一个简单的函数关系近似替代复杂的性能分析模型以提高优化过程的计算效率，能很好地用于解决既耗机时又非光滑的优化问题，已被广泛地用于复杂的工程优化问题中[61]。假定设计参数为n维向量x，给定一组参数值即确定一个样本点x(j)，总可以通过实体或数值的试验得到相应的性能值y=y(x(j))，对于足够多的试验，利用待定系数的方法可求出设计参数与系统响应的近似函数：
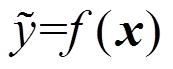(6)式中，
、f(x)为待构造的响应面函数。
刘小川等[62]基于正交设计的响应面法，采用二次多项式建立设计参数(包括空气腔初始容积、初始充气压力等)和优化目标(飞机着陆时轮胎最大垂直载荷)间的响应面模型，对飞机着陆载荷进行了优化设计。黄亚等[63]采用二次多项式响应面构造盘式制动器响应的近似模型，在此基础上对盘式制动器进行了稳定性分析。刘承杰等[64]以轻量化和第一阶固有频率为目标对V带轮进行二次优化。柯婉頔等[65]利用ADAMS/Car软件建立了某中大型SUV的前悬架装配动力学模型，以车轮相对车体上下跳动量为优化目标，分别建立了一阶、二阶和三阶多项式响应面模型，在此基础上进行前悬架性能的优化。Ghisu等[66]开发了非侵入式的多项式混沌的计算程序，生成一组正交多项式以便高精度、快速地分析系统存在不确定性情形下的鲁棒性，并将之应用于三轴燃气涡轮发动机压缩系统的设计过程，降低了系统性能对设计工况意外操作的敏感度。Tosi等[67]将正交实验设计、响应面模型和进化算法相结合，对叶片泵和齿轮泵进行鲁棒优化设计。Stocki等[68]以减小转子系统质量和提高轴的抗弯刚度为设计目标，将残余不平衡量和具有随机性的轴承刚度作为影响转子动力特性的噪声参数进行稳健设计，降低了转子的振动响应。崔杰等[69]以某轿车的前纵梁为研究对象，采用拉丁超立方抽样(latin hypercube sampling, LHS)方法和最小二乘方法创建碰撞响应的二阶多项式双响应面模型，在此基础上对峰值碰撞力响应的稳健性进行了优化。Shen等[70]提出了一种新的概率不确定非线性动力系统设计算法。陈力波等[71]针对典型公路简支梁桥提出了一种基于改进响应面方法的易损性模型建构流程。
基于RSM进行设计和优化，首先需识别影响性能的设计参数、确定各设计参数变动范围和水平值，然后利用合理的试验设计，采用回归方程拟合因素与响应值之间的函数关系，通过对回归方程的分析来寻求最优设计参数，最终目的是优化系统的输出响应。根据拟合函数形式的不同，响应面建模方法包括多项式回归法、人工神经网络法和Kriging函数法等[72]。目前常采用的响应面模型多基于多项式回归模型，以二次多项式回归模型为主。但二阶多项式本身对高阶非线性问题的描述能力不足，因此不适于拟合高阶非线性模型。Kriging和人工神经网络模型可广泛应用于拟合低阶和高阶非线性模型。陈永亮等[73]提出了基于Kriging代理模型的分析性稳健设计方法。李小刚等[74]针对现有机械结构优化设计未考虑材料特性参数的不确定性和结构动态特性对综合性能的影响、优化求解效率低下等不足，利用所构建的Kriging响应面模型代替有限元仿真分析来快速、准确地获取目标函数和约束函数值，以某型号大型汽轮发电机定子端部绕组锥环固定结构为例，以第二阶固有频率的均值及标准差最小化为目标进行优化设计。刘艳等[75]将确定性的Kriging代理模型发展到随机空间，采用随机代理模型方法对柔性机翼气动外形进行稳健性优化设计。蒙文巩等[76]针对不确定性因素引起飞机性能波动的现象，建立了面向速度和扭转角两个不确定性因素的机翼气动性能稳健性约束模型，构造基于均匀设计法的BP(back propagation)神经网络响应面，在此基础上分别进行考虑稳健性约束和不考虑稳健性约束的气动优化设计，以寻求在不确定因素干扰下机翼气动性能最优且波动较小的设计方案。
结构形状和拓扑优化的目的主要是通过调整结构内外边界形状来改善结构的动力学性能[77]。Steenackers等[78]为提高缝翼轨道在垂直方向上抵抗弯曲变形性能的鲁棒性，以飞机缝翼轨道上的筋板厚度为设计参数，采用二次多项式拟合获取缝翼轨道的垂直位移与设计参数间的函数关系，在此基础上进行设计优化。张军红等[79]采用不同阶次多项式响应面拟合对机翼结构进行颤振优化设计分析。李焦赞等[80]提出针对飞行器环境参数存在不确定性影响时的气动稳健优化设计模型，应用多目标进化算法和代理模型技术对稳健模型进行优化设计研究，以翼型为实例，通过选择合适的翼型参数化方法和CFD求解程序以及不确定性分析方法，得到了优化的Pareto前沿图。孙岩[81]采用响应面算法优化光固化树脂材料的轻质F4风洞模型构型。Jansen等[82]通过目标函数均值和标准偏差的加权和最小化，提出了一种鲁棒拓扑优化方法。邬晓敬 等[83]探讨了翼型几何形状随机不确定性对翼型气动特性的影响，采用二次多项式构建出气动力与飞机机翼几何不确定变量之间的响应面模型，在此基础上对翼型气动特性进行了鲁棒设计，相对于确定性优化结果，鲁棒优化后机翼的阻力略有增加但气动特性波动更小，气动性能的鲁棒性得以提高。何大全等[84]针对传统的基于固定设计点气动力优化设计方法中存在的非设计点性能较差的问题，依据Taguchi鲁棒性设计理论和采用共轭梯度(conjugate gradient，CG)法，以NACA0012翼型为例，以降低波阻为目标，对翼型的气动外形进行了鲁棒优化设计。Changizi等[85]采用随机扰动法计算框架结构几何不确定度对系统响应的影响，提出了一种基于应力的拓扑鲁棒优化方法。彭细荣等[86]提出应用连续体结构拓扑优化ICM法对高层建筑大型支撑体系进行拓扑优化。
以图3所示的双转子模型为例，图中低压转子(轴)的直径为30mm；高压转子(轴)的内径为50mm，外径为60mm。d1、d2、d3和d4为轮盘。b1、b2、b3和b4为轴承。弹性模量E=207 GPa，密度ρ=8300 kg/m3。在工作转速范围内，要求转子最大振动响应不超过50 mm/s。
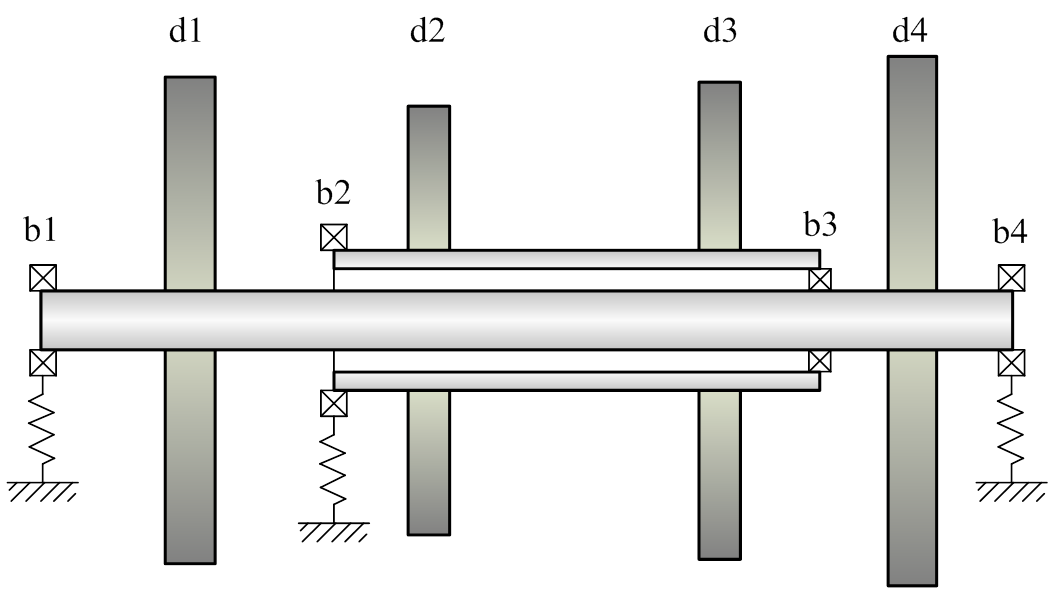
图3 双转子模型实例
Fig.3 The example dual-rotor model
转子系统在总装之前通常需完成动平衡以控制各盘的不平衡量，但由于轮盘装配工艺的不确定性，仍会出现振动过大的现象。图3中的双转子，考虑高压轮盘d2和d3的不平衡量和安装相位角进行设计。以轮盘d2和d3上不平衡量的大小和相位角差作为设计参数，各参数依次记为h2、h3和p。考虑到加工误差及装配工艺的不确定性，假定各参数的变化服从正态分布，标准差分别记为σh2、σh3和σp，且假定σh2、σh3和σp不超过各参数初始设计范围的1/6，相关数据如表1所示。
表1 各参数的初始设计范围及标准差
Table 1 Initial design range and standard deviation of each parameter
h2/(g·mm)h3/(g·mm)p/(°)σh2/(g·mm)σh3/(g·mm)σp/(°) [50, 150][50, 150][0, 180]10103
将轮盘视为集中质量、采用梁单元建立双转子的有限元仿真分析模型。在初始设计范围内，分别将h2、h3和p 10等分，取间隔Δp=20°、Δh2=10 g·mm以及Δh3=10 g·mm，在1000组不同组合下进行全因子试验，得到最大不平衡响应的统计分布图如图4所示。
由图4可看出，设计前最大不平衡响应变化具有正态分布特性，波动范围大且合格率约为50%。
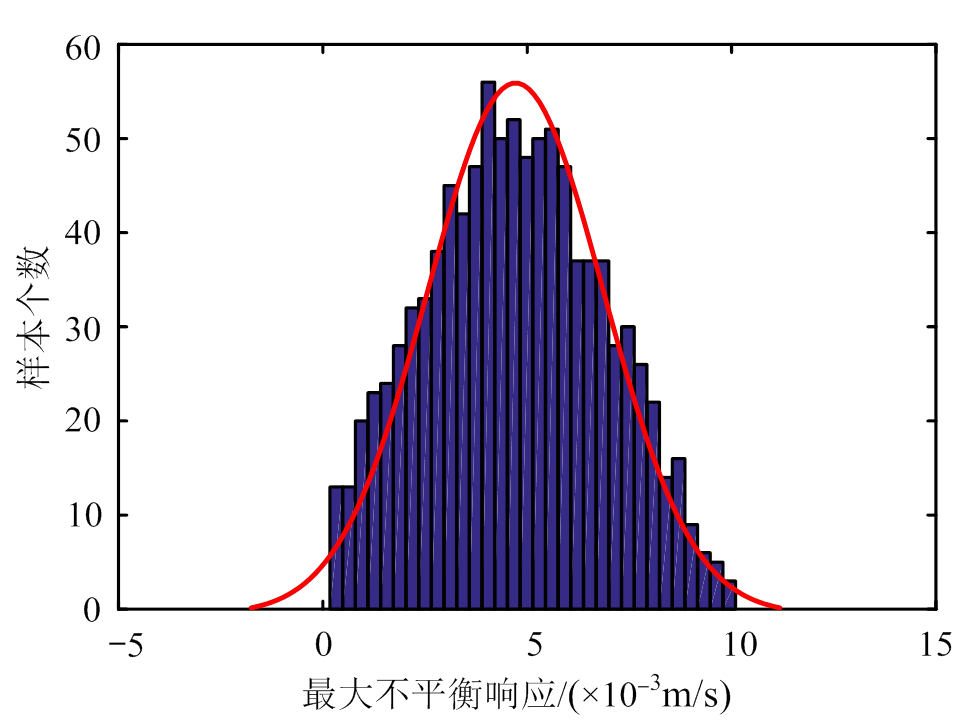
图4 最大不平衡响应的统计分布图
Fig.4 Statistical distribution diagram of the maximum unbalanced response
对于示例的双转子，基于Taguchi方法进行设计的主要思路和步骤是：首先将各设计参数在初始范围内等水平划分，并采用正交试验设计获得满足要求(振动响应均值不超过50 mm/s)的设计参数组合；其次，由标准差数据对各设计参数进行采样，得到不同参数组合下系统响应输出的波动方差；最后，以具有望小特性的信噪比即响应均值和标准差之和最小化为目标来确定各设计参数最终结果。详细方法和步骤读者可参阅文献[23]，这里不再 赘述。
基于响应面方法进行设计和优化，考虑采用如下的4次多项式来建立响应面模型：
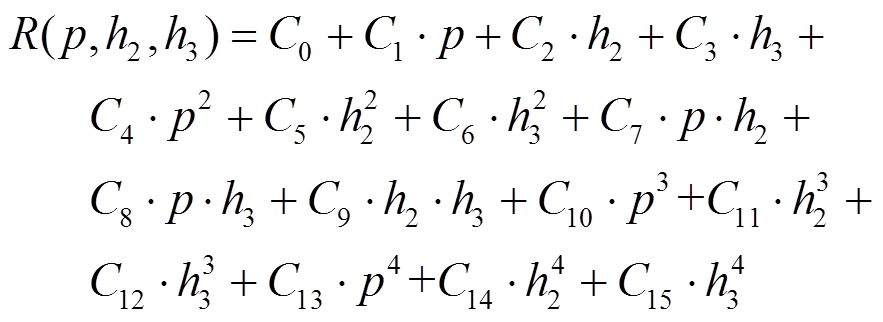(7)式(7)中：R(p,h2,h3)为最大不平衡响应与各参数间的响应面函数；Ci(i=0,1,2,…,15)为待定系数。
在初始设计范围内，分别将h2、h3和p各自10等分。采用最优拉丁超立方设计(Optimal Latin Hypercube Design, Opt LHD)进行试验设计并对试验结果进行数据拟合，整个过程在Isight多学科优化软件中进行，得到各系数的结果见表2。
通过回归分析得到的响应面模型的复相关系数为0.992，修正的复相关系数为0.991。表明响应面模型的精度达到了设计要求。
在上述建立的多项式响应面模型的基础上，采用泰勒公式将函数R(p,h2,h3)展开，取一阶和二阶来近似最大不平衡响应的均值μR和标准差 σR，有：
表2 系数C0~C12的计算结果
Table 2 Calculation results of coefficients C0~C12
系数值/(×10−3)系数值/(×10−3) C00.49585C8-60.39353 C12.77698×10−2C9-113710.45388×103 C236.71923×103C10-1.42213×10−6 C3-9.68395×103C11491595679.44602×103 C4-1.055818×10-4C12-3742965863.27641×103 C5-25406.43975×103C137.22832×10−9 C6745992.52715×103C14-1158484193641.15×103 C7-248.44622C157188444235818.88×103
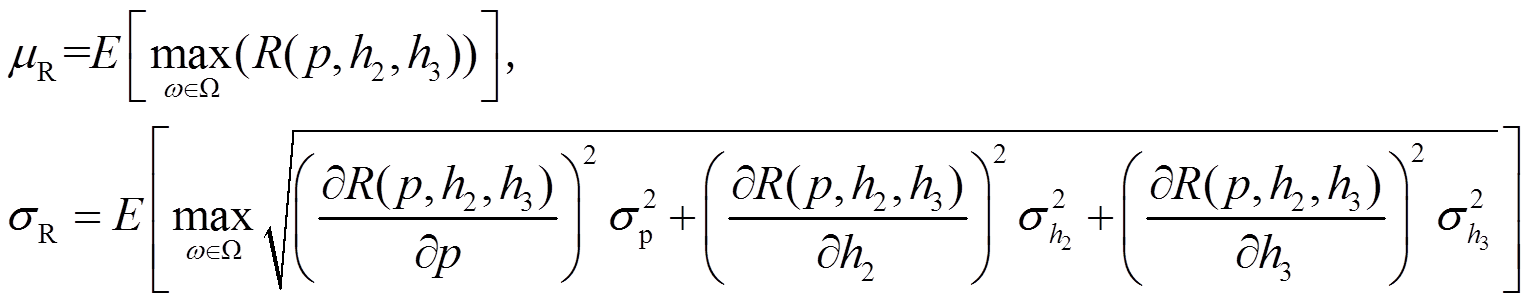(8)式中，Ω为转子的工作转速范围。以最大不平衡响应的均值和标准差最小化为目标、以设计要求和各参数的初始设计范围为约束，建立如下的多目标优化设计模型：
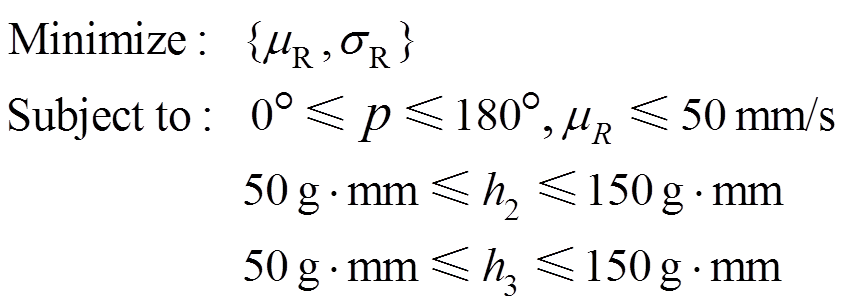(9)
采用NSGA-Ⅱ优化算法进行求解，得到式(9)对应多目标优化问题的所有可行解如图5所示。图6所示为完整的Pareto前沿。
图6中，TD为基于Taguchi方法得到的优化设计结果。为便于分析，表3给出了部分Pareto前沿和TD对应的设计参数结果。
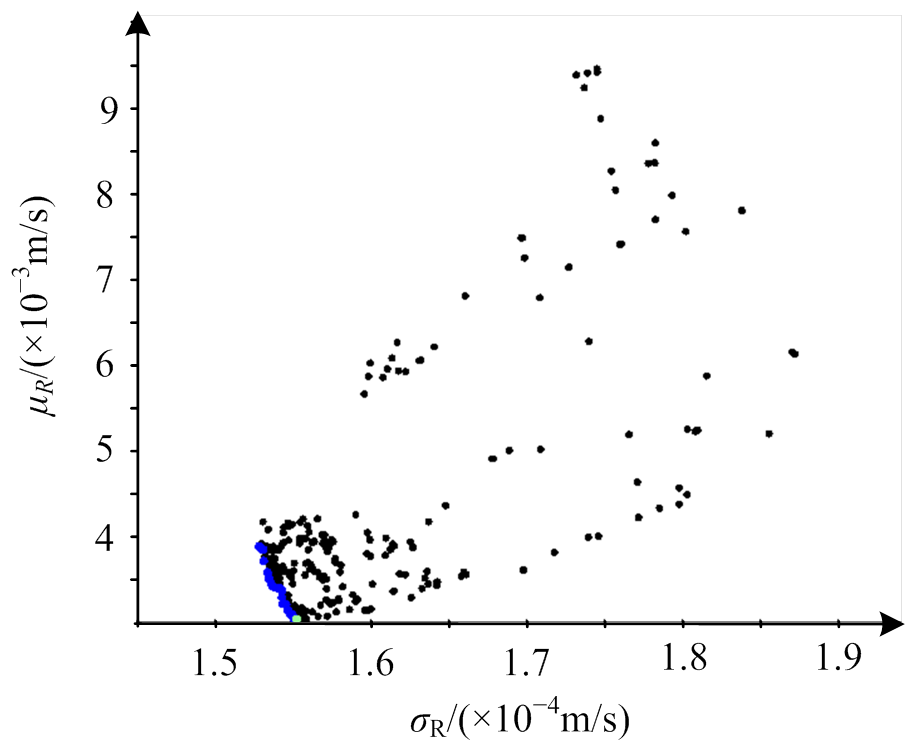
图5 可行解
Fig.5 Feasible solutions
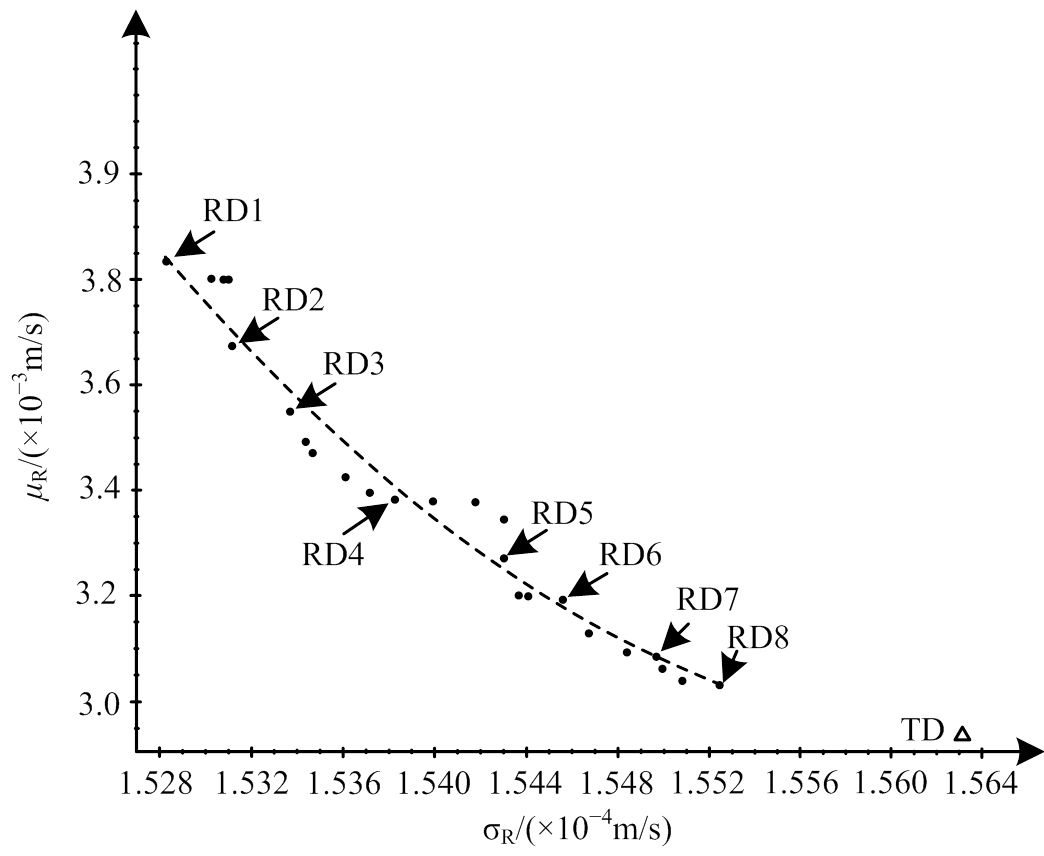
图6 Prate前沿
Fig.6 Pareto front
表3 鲁棒优化设计结果
Table 3 Robust optimal results
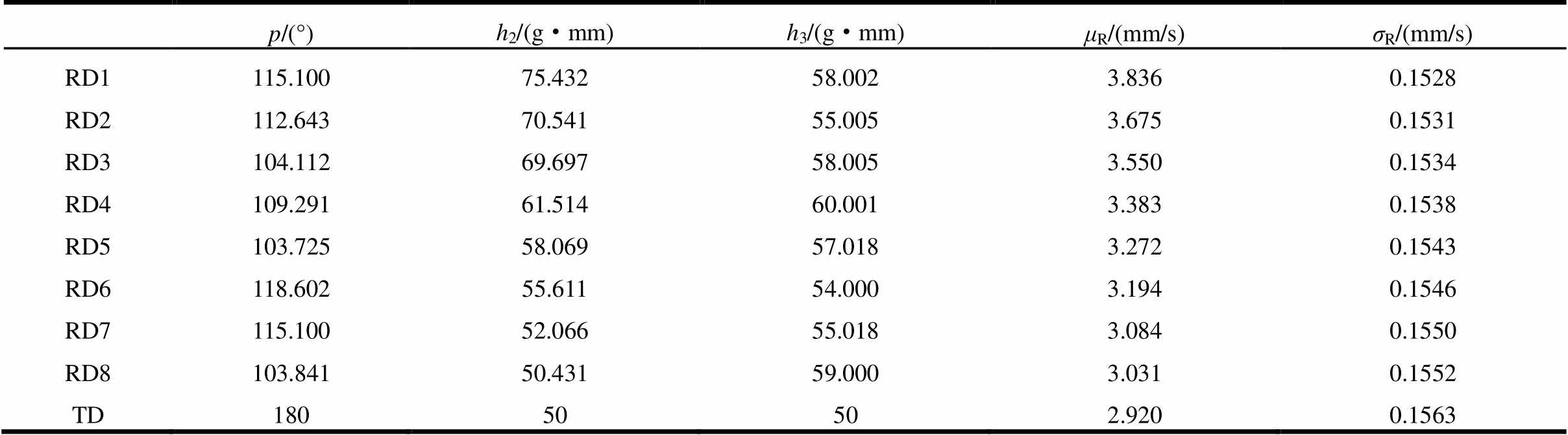
p/(°)h2/(g·mm)h3/(g·mm)μR/(mm/s)σR/(mm/s) RD1115.10075.43258.0023.8360.1528 RD2112.64370.54155.0053.6750.1531 RD3104.11269.69758.0053.5500.1534 RD4109.29161.51460.0013.3830.1538 RD5103.72558.06957.0183.2720.1543 RD6118.60255.61154.0003.1940.1546 RD7115.10052.06655.0183.0840.1550 RD8103.84150.43159.0003.0310.1552 TD18050502.9200.1563
表3中，RD1~RD8为基于响应面模型、采用多目标优化获得的部分结果。理论上，较小的不平衡量能够非常有效地降低峰值响应的幅值，但由于加工能力和工艺水平等的限制，实际中不平衡量的降低有限。σR越小意味着结果的波动也越小，即系统最大不平衡响应对由加工和装配引起的不确定性越不敏感。从表3可看出，基于响应面的方法不但能够获得多种可供选择的优化设计方案，而且在目标的方差最小化方面能够得到比Taguchi方法更好的结果。为了阐述设计结果的有效性，采用蒙特卡洛仿真方法进行验证。考虑安装工艺的不确定性，相位角差的范围为p±3°且服从正态分布。蒙特卡洛方法中，采用随机数生成器来生成相位角差的500个样本，生成的样本用于给定的一组不平衡量参数组合下计算最大不平衡响应。以RD8为例，仿真计算响应均值为2.993 g·mm，标准差为0.199 g·mm；而前述确定性优化结果响应均值为3.031 mm/s，标准差为0.1552 mm/s，与鲁棒优化结果基本相同。结果表明，基于响应面建模以及多目标优化得到不同的不平衡量的大小及初始相位角组合，不但可获得满足设计要求的不平衡响应且可以提高设计结果的鲁棒性。
结构动力优化设计是改善机械结构/系统动态性能、提高产品质量的一个重要手段和途径。作为一种先进的设计理念和方法，鲁棒优化设计理念和方法在结构动力设计问题中得到了人们的广泛关注和研究，相关方法主要有基于Taguchi的方法、基于多目标优化的方法和基于响应面的方法三种。Taguchi方法虽然原理简单、使用方便，但实际应用中存在不能处理具有约束的情形、不一定能找到存在高度非线性设计问题的精确解以及不能处理多目标问题等缺陷。相比于Taguchi方法，基于多目标优化方法的好处在于，一是能够处理有约束；二是采用遗传算法等随机最优的算法进行优化计算，不受变量的分布形式以及变量间相关性的限制。作为数值计算和统计方法相结合的产物，响应面法把系统看成一个黑匣子，用一个简单的函数关系近似替代复杂的性能分析模型，在复杂的结构动力优化设计问题中得到了非常广泛的应用。
随着机械系统结构复杂性的增加，各种不确定性因素愈为复杂，从鲁棒优化设计所涉及的建模和优化方法来看，以下研究还有待深入进行：
(1) 结构动力鲁棒优化需要同时计算实际结构动力响应相对于预期目标的偏差和波动，在迭代寻优过程，计算资源和时间通常随动力系统的复杂性而增加，因此，对不确定性参数进行灵敏度分析、寻求简便的重分析技术对于提高计算成本和优化效率非常重要。
(2) 作为一套数学与统计学相结合的方法，响应面法已经在具有多个设计变量的复杂结构动力优化问题中得到了广泛的应用。在建立的响应面模型能够捕获系统的真实物理特性以及可靠地预测系统在优化区域中各点的响应的情况下，可以通过所得方程计算出各设计参数任何一个组合的函数值，以此为基础进行后续的优化求解。值得注意的是，在建立响应面模型之前，要求在设计空间中进行样本的采集，样本数量的多少和好坏直接影响到近似模型对真实解的逼近程度，样本太少或样本不具有代表性，便不能反映出近似模型的结构映射规律，若样本太多，则又会使模型产生过拟合状态，无法建立正确的映射关系，导致模型的“泛化”能力降低，因此合理的选择样本至关重要。
(3) 对于结构复杂的装配体而言，设计变量和噪声因素的变差、装配连接的不确定性都会引起结构动力响应的波动。通过提高零件加工精度一定程度上可以减小结构动力响应的波动，但必然导致加工难度和成本的提高，且无法消除装配不确定性带来的影响。因而，考虑连接装配的不确定性，进行不确定性因素的建模和量化表示，在此基础上实现对复杂装配体结构的动力鲁棒优化设计是后续研究的重点。
参考文献：
[1] 陈建军, 车建文, 崔明涛, 等. 结构动力优化设计述评与展望[J]. 力学进展, 2001, 31(2): 181－192.
Chen Jianjun, Che Jianwen, Cui Mingtao, et al. A review on structural dynamic optimum design [J]. Advances in Mechanics, 2001, 31(2): 181－192. (in Chinese)
[2] Niordson F I. The optimum design of a vibrating beam [J]. Quarterly of Applied Mathematics, 1965, 23(1): 47－53.
[3] 林家浩. 结构动力优化设计发展综述[J]. 力学进展, 1983, 13(4): 423－431.
Lin Jiahao. Review on the development in structural dynamic optimum design [J]. Advances in Mechanics, 1983, 13(4): 423－431. (in Chinese)
[4] 刘永泉, 王德友, 洪杰, 等. 航空发动机整机振动控制技术分析[J]. 航空发动机, 2013, 39(5): 1－8.
Liu Yongquan, Wang Deyou, Hong Jie, et al. Analysis of whole aeroengine vibration control technology [J]. Aeroengine, 2013, 39(5): 1－8. (in Chinese)
[5] Rao S S. Reliability-based optimization under random vibration environment [J]. Computers & Structures, 1981, 14(5): 345－355.
[6] Ziegel E R. Taguchi techniques for quality engineering [J]. Technometrics, 1989, 39(1): 109－110.
[7] Yamakawa H, Miyashita M. A study on robust structures. 1st report: concept of robust structure and 1ts design method [J]. Transactions of the Japan Society of Mechanical Engineers Series C, 1991, 57(544): 3913－3918.
[8] Zang C, Friswell M I, Mottershead J E. A review of robust optimal design and its application in dynamics [J]. Computers & Structures, 2005, 83(4/5): 315－326.
[9] Beyer H G, Sendhoff B. Robust optimization – A comprehensive survey [J]. Computer Methods in Applied Mechanics & Engineering, 2007, 196(33/34): 3190－3218.
[10] 接婧. 国际学术界对鲁棒性的研究[J]. 系统工程学报, 2005, 20(2): 153－159.
Jie Jing. Study of robustness in the world [J]. Journal of Systems Engineering, 2005, 20(2): 153－159. (in Chinese)
[11] 张正福, 王安麟, 刘广军, 等. 基于Taguchi三次设计的微机械陀螺健壮性设计[J]. 上海交通大学学报, 2008, 42(2): 249－252.
Zhang Zhengfu, Wang Anlin, LIU GuanJun, et al. Robust design for micromachined gyroscope using Taguchi three-stage design [J]. Journal of Shanghai Jiaotong University, 2008, 42(2): 249－252. (in Chinese)
[12] 谢晖, 刘行, 洪健程. 基于Taguchi方法的车门结构稳健性优化[J]. 中国机械工程, 2013, 24(12): 1676－1681.
Xie Hui, Liu Xing, Hong Jiancheng. Robust Optimization of automotive door structure based on Taguchi's method [J]. China Mechanical Engineering, 2013, 24(12): 1676－1681. (in Chinese)
[13] 张代胜, 张旭, 王浩, 等. 基于Taguchi方法的动力总成悬置系统稳健优化[J]. 汽车工程, 2014, 36(4): 475－480.
Zhang Daisheng, Zhang Xu, Wang Hao, et al. Robust optimization of powertrain mounting system based on Taguchi's method [J]. Automotive Engineering, 2014, 36(4): 475－480. (in Chinese)
[14] 王淑红, 武潇, 高泽梅. Taguchi法在内嵌式永磁同步电动机中的应用[J]. 太原理工大学学报, 2014, 45(5): 618－622.
Wang Shuhong, Wu Xiao, Gao Zemei. Application of Taguchi method in interior permanent magnet synchronous motor [J]. Journal of Taiyuan University of Technology, 2014, 45(5): 618－622. (in Chinese)
[15] Cai D A, Xiu-Ping W U, Yang G P, et al. Design for structure parameters of composite frangible cover based on Taguchi’s method [J]. Journal of Solid Rocket Technology, 2016, 39(6): 797－802.
[16] 郭一鸣, 魏玉明, 上官文斌. 发动机曲轴橡胶扭转减振器稳健性优化匹配[J]. 华南理工大学学报(自然科学版), 2017, 45(2): 75－83.
Guo Yiming, Wei Yuming, Shangguan Wenbin. Robust optimal matching of rubber-type torsional vibration damper for engine crankshaft [J]. Journal of South China University of Technology (Natural Science Edition), 2017, 45(2): 75－83. (in Chinese)
[17] Song J, Dong F, Zhao J, et al. Optimal design of a permanent magnet linear synchronous motors based on Taguchi method [J]. Iet Electric Power Applications, 2017, 11(1): 41－48.
[18] 孙光永, 屈瑞飞, 张慧乐, 等. 基于Taguchi与TOPSIS-熵的车门多目标离散稳健优化研究[J]. 现代制造工程, 2018(3): 11－18.
Sun Guangyong, Qu Ruifei, Zhang Huile, et al. Robust optimization of automobile door structure based on Taguchi and TOPSIS-entropy[J]. Modern Manufacturing Engineering, 2018(3): 11－18. (in Chinese)
[19] Zong Y, Mao J. Tolerance optimization design based on the manufacturing-costs of assembly quality [J]. Procedia Cirp, 2015, 27: 324－329.
[20] 孙岩辉, 洪军, 刘志刚, 等. 考虑零部件制造误差的精密主轴几何回转精度计算方法[J]. 机械工程学报, 2017, 53(3): 173－182.
Sun Yanhui, Hong Jun, Liu Zhigang, et al. A calculating method for the geometric rotation accuracy of precision spindles considering the manufacturing errors of component parts [J]. Journal of Mechanical Engineering, 2017, 53(3): 173－182. (in Chinese)
[21] Mohan P, Haghighi P, Vemulapalli P, et al. Toward automatic tolerancing of mechanical assemblies: assembly analyses [J]. Journal of Computing & Information Science in Engineering, 2014, 14(4): 1－14.
[22] 殷良伟, 郭海丁. 某型航空发动机封严篦齿盘异型螺栓孔公差设计分析[J]. 航空发动机, 2017, 43(5): 85－90.
Yin Liangwei, Guo Haiding. Analysis on dimension tolerance design of non-circular hole of labyrinth disk for an aeroengine [J]. Aeroengine, 2017, 43(5): 85－90. (in Chinese)
[23] 杨隽, 臧朝平, 刘永泉, 等. 基于Taguchi方法的转子系统动力学容差设计[J]. 航空动力学报, 2014, 29(7): 1583－1590.
Yang Jun, Zang Chaoping, Liu Yongquan, et al. Taguchi-based tolerance design method for rotor dynamics [J]. Journal of Aerospace Power, 2014, 29(7): 1583－1590. (in Chinese)
[24] 杨隽, 臧朝平. 基于遗传算法的不确定性结构动力学鲁棒设计[C]// 中国力学大会2011暨钱学森诞辰100周年纪念大会, 2011.
Yang Jun, Zang Chaoping. Genetic algorithm based robust design in dynamics due to parameter uncertainty [C]// The Chinese Conference on Theoretical and Applied Mechanics-2001 in Memorial of Tsien Hsue-shen’s 100th Anniversary, 2011. (in Chinese)
[25] 岳伟, 梅庆, 张大义, 等. 高速可拆卸转子止口连接结构稳健性设计方法[J]. 航空动力学报, 2017, 32(7): 1754－1761.
Yue Wei, Mei Qing, Zhang Dayi, et al. Robust design method of Rabbet joint structure in high speed assemble rotor [J]. Journal of Aerospace Power, 2017, 32(7): 1754－1761. (in Chinese)
[26] 洪杰, 徐筱李, 梁天宇, 等. 转子结构系统界面失效分析及稳健设计方法[J]. 航空动力学报, 2018, 33(3): 649－656.
Hong Jie, Xu Xiaoli, Liang Tianyu, et al. Interface failure analysis and robust design method in rotor structural system [J]. Journal of Aerospace Power, 2018, 33(3): 649－656. (in Chinese)
[27] Tsui K L . A critical look at Taguchi's modelling approach for robust design [J]. Journal of Applied Statistics, 1996, 23(1): 81－96.
[28] Chang H H. A data mining approach to dynamic multiple responses in Taguchi experimental design [J]. Expert Systems with Applications, 2008, 35(3): 1095－1103.
[29] Parkinson A, Sorensen C, Pourhassan N. A general approach for robust optimal design [J]. Trans.asme J Mech.design, 1993, 115(1): 74－80.
[30] Zang C. Robust design of a two degree freedom system due to the parameter uncertainty [J]. Chinese Journal of Mechanical Engineering, 2008, 21(6): 30－35.
[31] 肖方豪, 蹇开林. 鲁棒优化设计方法在结构动力学中的应用[J]. 工程力学, 2007, 24(增刊1): 62－65.
Xiao Fanghao, Jian Kailin. Application of Robust Optimal Design in Structural Dynamics [J]. Engineering Mechanics, 2007, 24(suppl 1): 62－65. (in Chinese)
[32] Marano G C, Greco R, Sgobba S. A comparison between different robust optimum design approaches: Application to tuned mass dampers [J]. Probabilistic Engineering Mechanics, 2010, 25(1): 108－118.
[33] Miguel L F F, Lopez R H. Robust design optimization of friction dampers for structural response control [J]. Structural Control & Health Monitoring, 2014, 21(9): 1240－1251.
[34] 孙晓颖, 李天娥, 陆正争, 等. 平流层飞艇的多目标优化与决策[J]. 工程力学, 2015(6): 243－250.
Sun Xiaoying, Li Tian’e, Lu Zhengzheng, et al. Multi- objective optimization and decision making of stratosphere airships [J]. Engineering Mechanics, 2015(6): 243－250. (in Chinese)
[35] Roy B K, Chakraborty S. Robust optimum design of base isolation system in seismic vibration control of structures under random system parameters [J]. Structure & Infrastructure Engineering, 2016, 12(5): 592－602.
[36] Dell'Elce L , Gourc E , Kerschen G . A robust equal-peak method for uncertain mechanical systems [J]. Journal of Sound Vibration, 2018, 414: 97－109.
[37] 蒲利东, 罗务揆, 严泽洲. 气动伺服弹性系统结构陷幅滤波器优化设计[J]. 工程力学, 2018, 35(4): 235－241.
Pu Lidong, Luo Wukui, Yan Zezhou. Optimal design for notch filter of aeroservoelastic systems [J]. Engineering Mechanics, 2018, 35(4): 235－241. (in Chinese)
[38] 陈鑫, 李爱群, 徐庆阳, 等. 基于遗传算法的高耸结构环形TLD满意优化设计[J]. 工程力学, 2016, 33(6): 77－84.
Chen Xin, Li Aiqun, Xu Qingyang, et al. Satisfaction optimum design of ring-shape tld control forhigh-rise structure using genetic algorithm [J]. Engineering Mechanics, 2016, 33(6): 77－84. (in Chinese)
[39] 王歆侃. 基于容差模型的发动机悬置系统稳健优化设计[J]. 汽车科技, 2012(4): 16－19.
Wang Yinkan. Robust optimal design of engine mounting system based on tolerance model [J]. AUTO SU-TECH, 2012(4): 16－19. (in Chinese)
[40] 陈新志, 孙桓五, 刘荣, 等. 基于容差模型的半挂汽车列车行驶平顺性优化[J]. 汽车技术, 2014(4): 48－52.
Chen Xinzhi, Sun Hengwu, Liu Rong, et al. Ridie comfort optimization of semitrailer train based on tolerance model [J]. Automobile Technology, 2014(4): 48－52. (in Chinese)
[41] Loyer B, Jezequel L. Robust design of a passive linear quarter car suspension system using a multi-objective evolutionary algorithm and analytical robustness indexes [J]. Vehicle System Dynamics 2009, 47(10): 1253－1270.
[42] 燕宁宁, 董恩国. 基于多目标优化的悬架系统空间结构稳健性研究[J]. 天津职业技术师范大学学报, 2016, 26(3): 10－13.
Yan Ningning, Dong Enguo. Research on robustness of spatial structure of suspension system based on multi-objective optimization [J]. Journal of Tianjin University of Technology and Education, 2016, 26(3): 10－13. (in Chinese)
[43] 范政武, 王铁, 王永红, 等. 基于改进多目标粒子群算法的商用车悬架系统优化[J]. 振动与冲击, 2018, 37(15): 216－224.
Fan Zhengwu, Wang Tie, Wang Yonghong, et al. Commercial vehicle suspension system optimization base on improved multi-object particle swarm optimization [J]. Journal of Vibration and Shock, 2018, 37(15): 216－224. (in Chinese)
[44] 傅超, 任兴民, 杨永锋, 等. 考虑参数不确定性的转子系统瞬态动平衡研究[J]. 动力学与控制学报, 2017, 15(5): 453－458.
Fu Chao, Ren Xingmin, Yang Yongfeng, et al. Transient dynamic balancing of rotor system with parameter uncertainties [J]. Journal of Dynamics and Control, 2017, 15(5): 453－458. (in Chinese)
[45] Gan C B, Wang Y H, Yang S X, et al. Nonparametric modeling and vibration analysis of uncertain Jeffcott rotor with disc offset [J]. International Journal of Mechanical Sciences, 2014, 78(1): 126－134.
[46] Ma Y, Liang Z, Chen M, et al. Interval analysis of rotor dynamic response with uncertain parameters [J]. Journal of Sound & Vibration, 2013, 332(16): 3869－3880.
[47] Ritto T G, Lopez R H, Sampaio R, et al. Robust optimization of a flexible rotor-bearing system using the Campbell diagram [J]. Engineering Optimization, 2011, 43(1): 77－96.
[48] Lopez R H, Ritto T G, Sampaio R, et al. A new algorithm for the robust optimization of rotor-bearing systems [J]. Engineering Optimization, 2014, 46(8): 1123－1138.
[49] Krack M, Panning L, Wallaschek J, et al. Robust design of friction interfaces of bladed disks with respect to parameter uncertainties [C]// ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, 2012: 1193－1204.
[50] 姚建尧, 王建军, 李其汉. 失谐叶盘结构鲁棒性能分析[J]. 航空动力学报, 2010, 25(7): 1634－1639.
Yao Jianyao, Wang JianJun, Li Qihan. Robust performance analysis of mistuned bladed disks [J]. Journal of Aerospace Power, 2010, 25(7): 1634－1639. (in Chinese)
[51] 段勇亮, 臧朝平, Petrov E.P. 主动失谐叶盘振动特性及鲁棒性研究[J]. 航空发动机, 2015, 41(6): 6－10.
Duan Yongliang, Zang Chaoping, Petrov E P. Research on vibration performance and robustness of bladed disks with intentional mistuning[J]. Aeroengine, 2015, 41(6): 6－10. (in Chinese)
[52] 罗佑新, 车晓毅, 杨继荣, 等. 高维多目标灰色稳健优化设计及其Matlab实现[J]. 农业机械学报, 2008, 39(8): 157－160.
Luo Youxin, Che Xiaoyi, Yang Jirong, et al. Grey-robust optimal design of high-dimensional multi-objective and its achieving with Matlab [J]. Transactions of the Chinese Society of Agricultural Machinery, 2008, 39(8): 157－160. (in Chinese)
[53] 郝芳芳, 范小宁, 智博. 基于灵敏度附加目标函数的起重机主梁稳健优化设计[J]. 机械强度, 2017(6): 1385－1390.
Hao Fangfang, Fan Xiaoning, Zhi Bo. Structure and robust optimization design based on additional objective function of the sensitivity [J]. Journal of Mechanical Strength, 2017(6): 1385－1390. (in Chinese)
[54] Sundaresan S, IshiiK, Houser D R. A robust optimization procedure with variations on design variables and constraints [J]. Advances in Design Automation, 69(1): 379－386.
[55] Petrov E P, Ewins D J. Analysis of the worst mistuning patterns in bladed disk assemblies [C]. Asme Turbo Expo: Power for Land, Sea, & Air, 2003: 623－631.
[56] 谭元球, 臧朝平, 周标, 等. 失谐叶盘受迫响应的灵敏度分析方法[J]. 航空学报, 2017, 38(12): 187－197.Tan Yuanqiu, Zang Chaoping, Zhou Biao, et al. Sensitivity analysis method for forced reponse of mistuned bladed discs [J]. Acta Aeronautica et Astronautic Sinica, 2017, 38(12): 187－197. (in Chinese)
[57] Du X P, Chen W. Efficient uncertainty analysis methods for multidisciplinary robust design [J]. AIAA J, 2002, 40(3): 545－552.
[58] Liu S, Ma Y, Zhang D, et al. Studies on dynamic characteristics of the joint in the aero-engine rotor system [J]. Mechanical Systems & Signal Processing, 2012, 29(5): 120－136.
[59] Marano G C, Quaranta G. Robust optimum criteria for tuned mass dampers in fuzzy environments [J]. Applied Soft Computing Journal, 2009, 9(4): 1232－1243.
[60] Lievens K, Lombaert G, Roeck G D, et al. Robust design of a TMD for the vibration serviceability of a footbridge [J]. Engineering Structures, 2016, 12(3): 408－418.
[61] Khuri A I, Mukhopadhyay S. Response surface methodology [J]. Wiley Interdisciplinary Reviews Computational Statistics, 2010, 2(2): 128－149.
[62] 刘小川, 马晓利, 孙侠生, 等. 基于响应面方法的多支柱起落架着陆缓冲性能优化[J]. 振动工程学报, 2010, 23(3): 305－309.
Liu Xiaochuang, Ma Xiaoli, Sun Xiasheng, et al. Performance optimization of shock absorber for multi-strut landing gear based on RSM[J]. Journal of Vibration Engineering, 2010, 23(3): 305－309.(in Chinese)
[63] 黄亚, 于德介, 吕辉, 等. 含不确定参数的盘式制动器稳定性分析[J]. 机械强度, 2017(6): 1371－1378.
Huang Ya, Yu Dejie, Lu Hui, et al. Stability analysis of disc brake systems with uncertainty parameters [J]. Journal of Mechanical Strength, 2011, 47(24): 97－103. (in Chinese)
[64] 刘承杰, 李倩, 罗鹏, 等. 基于响应面法的V带轮多目标优化设计[J]. 应用力学学报, 2018, 35(1): 147－153.
Liu Chenjie, Li Qian, Luo Peng, et al. Multi-objective optimization design of V-pulley based on response surface method [J]. Chinese Journal of Applied Mechanics, 2018, 35(1): 147－153. (in Chinese)
[65] 柯婉頔, 吴婧, 杨森, 等. 基于响应面法和遗传算法的某SUV前悬优化[J]. 华中师范大学学报(自科版), 2017, 51(4): 455－460.
Ke Wandi, Wu Jing, Yang Sen, et al. Optimization of front suspension of sports utility vehicle based on response surface method and genetic algorithm [J]. Journal of Central China Normal University (Nat. Sci.), 2017, 51(4): 455－460. (in Chinese)
[66] Ghisu T, Parks G T, Jarrett J P, et al. Robust design optimization of gas turbine compression systems [J]. Journal of Propulsion & Power, 2011, 27(2): 282－295.
[67] Tosi G, Mucchi E, D’Ippolito R, et al. Dynamic behavior of pumps: an efficient approach for fast robust design optimization [J]. Meccanica, 2015, 50(8): 2179－2199.
[68] Stocki R, Szolc T, Tauzowski P, et al. Robust design optimization of the vibrating rotor-shaft system subjected to selected dynamic constraints [J]. Mechanical Systems & Signal Processing, 2012, 29(29): 34－44.
[69] 崔杰, 张维刚, 常伟波, 等. 基于双响应面模型的碰撞安全性稳健性优化设计[J]. 机械工程学报, 2011, 47(24): 97－103.
Cui Jie, Zhang Weigang, Chang Weibo, et al. Robustness optimization for crash safety based on dual-response surface model [J]. Journal of mechanical engineering, 2011, 47(24): 97－103. (in Chinese)
[70] Shen D E , Braatz R D . Polynomial chaos-based robust design of systems with probabilistic uncertainties [J]. AIChE Journal, 2016.
[71] 陈力波, 黄才贵, 谷音. 基于改进响应面法的公路简支梁桥地震易损性分析[J]. 工程力学, 2018(4): 208－218.
Chen Libo, Huang Caigui, Gu Yin. Seimic vulnerability analysis of simply supported highway bridges based on an improved response surface method [J]. Engineering Mechanics, 2018(4): 208－218. (in Chinese)
[72] 窦毅芳, 刘飞, 张为华. 响应面建模方法的比较分析[J]. 工程设计学报, 2007, 14(5): 359－363.
Dou Yifang, Liu Fei, Zhang Weihua. Research on comparative analysis of response surface methods [J]. Journal of Engineering Design, 2007, 14(5): 359－363. (in Chinese)
[73] 陈永亮, 刘双, 王汉涛, 等. 基于Kriging代理模型的主轴箱稳健设计[J]. 天津大学学报(自然科学与工程技术版), 2011, 44(12): 1111－1117.
Chen Yongliang, Liu Shuang, Wang Hantao, et al. Robust design of headstock based on kriging surrogate model [J]. Journal of Tianjin University (Science and Technology), 2011, 44(12): 1111－1117. (in Chinese)
[74] 李小刚, 程锦, 刘振宇, 等. 基于双层更新Kriging模型的机械结构动态特性稳健优化设计[J]. 机械工程学报, 2014, 50(3): 165－173.
Li Xiaogang, Cheng Jin, Liu Zhenyu, et al. Robust optimization for dynamic characteristics of mechanical structures based on double renewal kriging model [J]. Joural of Mechanical Engineering, 2014, 50(3): 165－173. (in Chinese)
[75] 刘艳, 白俊强, 华俊, 等. 基于Stochastic Kriging的柔性机翼稳健性优化设计[J]. 西北工业大学学报, 2015(6): 906－912.
Liu Yan, Bai Junqiang, Hua Jun, et al. Robust optimization of flexible wing using stochastic kriging surrogate model [J]. Journal of Northwestern Polytechnical University, 2015(6): 906－912. (in Chinese)
[76] 蒙文巩, 马东立, 楚亮. 基于神经网络响应面的机翼气动稳健性优化设计[J]. 航空学报, 2010, 31(6): 1134－1140.
Meng Wengong, Ma Dongli, Chu Liang. Wing aerodynamic robustness optimization based on neural network response surface [J]. Acta Aeronautica et Astronautic Sinica, 2010, 31(6): 1134－1140. (in Chinese)
[77] 顾松年, 徐斌, 荣见华, 等. 结构动力学设计优化方法的新进展[J]. 机械强度, 2005, 27(2): 24－30.
Gu Songnian, Xu Bin, Rong Jianhua, et al. Recent progresses on structural dynamic design methods [J]. Journal of Mechanical Strength, 2005, 27(2): 24－30. (in Chinese)
[78] Steenackers G, Guillaume P, Vanlanduit S. Robust optimization of an airplane component taking into account the uncertainty of the design parameters [J]. Quality & Reliability Engineering International, 2009, 25(3): 255－282.
[79] 张军红, 韩景龙. 考虑不确定性的机翼气动弹性优化问题研究[C]// 全国空气弹性学术交流会, 2011.
Zhang Junhong, Han Jinglong. Study on aeroelastic optimization of wing with uncertainty [C]// National Air Flexibility Academic Intercommunions, 2011. (in Chinese)
[80] 李焦赞, 高正红. 多目标进化算法和代理模型技术在气动稳健优化设计中的应用[J]. 空气动力学学报, 2012, 30(1): 46－51.
Li Jiaozan, Gao Zhenghong. The application of multi-objective evolutionary algorithm and surrogate model to aerodynamic robust optimization design [J]. Acta Aerodynamica Sinica, 2012, 30(1): 46－51. (in Chinese)
[81] 孙岩. 飞行器机翼气动/结构耦合优化设计研究[J]. 工程力学, 2012(11): 360－364.
Sun Yan. Investigation on coupling aerodynamic and structural design optimization for aircraft airfoil [J]. Engineering Mechanics, 2012(11): 360－364. (in Chinese)
[82] Jansen M, Lombaert G, Schevenels M, et al. Robust topology optimization of structures with imperfect geometry based on geometric nonlinear analysis [J]. Computer Methods in Applied Mechanics and Engineering, 2015, 285: 452－467.
[83] 邬晓敬, 张伟伟, 肖华, 等. 一种基于响应面的翼型鲁棒优化设计方法[J]. 工程力学, 2015, 32(2):250-256.
Wu Xiaojing, Zhang Weiwei, Xiao Hua, et al. A robust aerodynamic design for airfoil based on response surface method [J]. Engineering Mechanics, 2015, 32(2): 250－256. (in Chinese)
[84] 何大全, 冯爱庆, 王伟. 基于CG法及Taguchi理论的气动力鲁棒性优化方法[J]. 飞行力学, 2017(6): 25－29.
He Daquan, Feng Aiqing, Wang Wei. Robust aerodynamic optimization based on conjugate gradient algorithm and Taguchi's theory [J]. Flight Dynamics, 2017(6): 25－29. (in Chinese)
[85] Changizi N, Kaboodanian H, Jalalpour M. Stress-based topology optimization of frame structures under geometric uncertainty [J]. Computer Methods in Applied Mechanics & Engineering, 2017, 315: 121－140.
[86] 彭细荣, 隋允康. 基于ICM法的高层建筑大型支撑体系拓扑优化[J]. 工程力学, 2017, 34(5): 17－22. Peng Xirong, Sui Yunkang. Topology optimization of mega braced systems of high-rise buildings based on ICM method [J]. Engineering Mechanics, 2017, 34(5): 17－22. (in Chinese)
ROBUST OPTIMIZATION DESIGN METHODS OF STRUCTURAL DYNAMICS: A REVIEW
Abstract: How to improve the robustness of structural dynamic performance, and how to minimize the influence of various uncertainties on mean design are one of the hot issues both in academic and engineering fields. In this paper, the basic concept of structural dynamic robust optimization design is described. The robust optimization design methods of structural dynamics are reviewed from three aspects that are based on Taguchi method, multi-objective optimization and response surface methods. Taking a dual-rotor as an example, the dynamic robust optimization design is carried out by using the response surface modeling and multi-objective optimization methods. The results show that multiple robust optimization design schemes can be obtained based on response surface modeling and multi-objective optimization, and robust design methods have great potential for application in structural dynamics to deal with uncertain problems. Finally, the current research methods and future work are briefly summarized and prospected.
Key words: structural dynamic optimization design; robust optimization; Taguchi method; multi-object optimization; response surface method
文章编号：1000-4750(2019)04-0024-13
中图分类号：TU311.3
文献标志码：A
doi:10.6052/j.issn.1000-4750.2018.09.0484
收稿日期：2018-09-06；
修改日期：2018-12-07
基金项目：国家自然科学基金委员会与中国工程物理研究院联合基金项目(U1730129)；国家自然科学基金项目(11372128)；广西高校科学技术研究项目(KY2015YB344).
缪 辉(1986―)，男，江苏人，博士生，主要从事结构动力学相似性设计研究(E-mail: miaohui@nuaa.edu.cn);
张根辈(1983―)，男，河南人，博士生，主要从事结构动力学非线性参数识别研究(E-mail: zhanggb@nuaa.edu.cn)