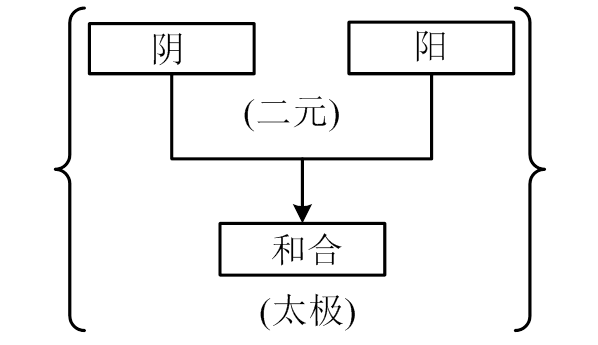
[编者按]该文是龙驭球院士几近终生讲授、研究并著述结构力学的体会和升华，可以毫不夸张地说，在这个园地他最有条件也有义务从哲学的高度来阐述这个领域的成长、过渡、变迁和生生不息之道。文风朴实简练而明晰，值此《工程力学》创刊35周年之际，龙驭球作为本刊的第一任主编，奉献此文以飨读者。
摘 要：该文对结构力学中的解法和方法从方法论的角度进行回望。提出三点认识：1) 结力方法论的文脉是“阴阳-和合系统”；2) 结力方法的特色是“成对、互补”似阴阳；3) 虚功能量法的优势是“合一、多能”成太极。此外，还在打通血脉、消除隔阂方面，提出两点看法：4) 论证能量法与虚功法之间是“殊途同归、实质相通”的关系；5) 揭示“平衡”与“几何”两个领域中存在隐晦的“互借、互伴”关系。
关键词：结构力学；能量法；虚功法；平衡；几何
教了多年的结构力学，觉得这门课程很有特点：它讲的方法多姿多彩，逻辑分析也较深入。但仍感到有些美中不足。觉得分析方法讲得多，综合方法比较少。分章分节的内部议论多，融会贯通的跨界讨论少。现借此文，谈点想法，希望在打通血脉、融会和合方面有所加强。本文曾与包世华、邢沁妍同志讨论，增添了他们的宝贵意见，在此表示感谢。
图式(a)
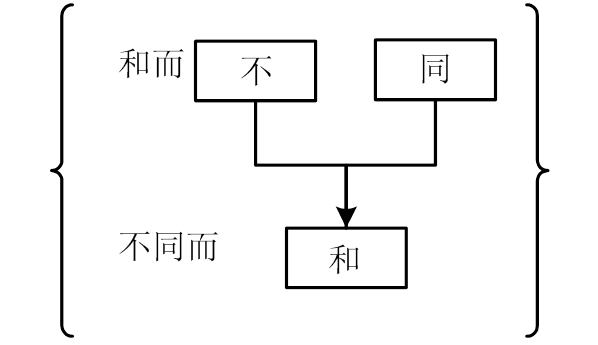
图式(b)
图式(c)
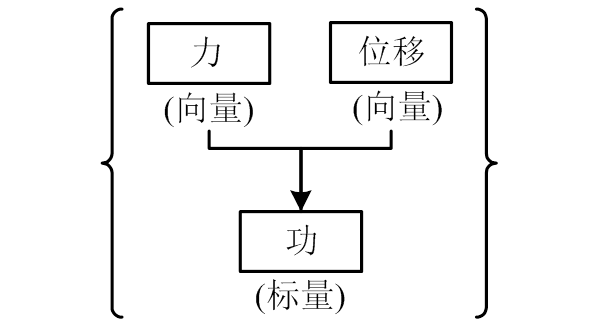
例(a) 物理量
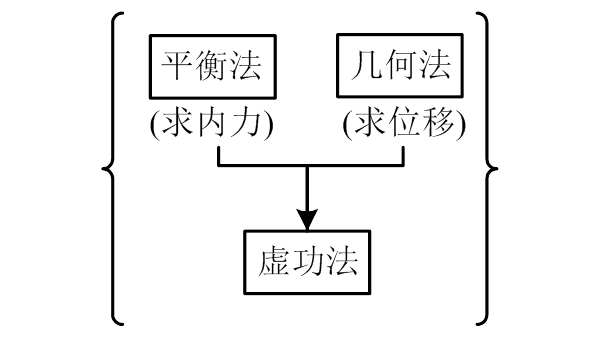
例(b) 静定结构解法
例(c) 超静定结构解法
例(a) 对联
例(b) 古代神鸟(《山海经》[1])
例(c) 合命题
冯友兰在文献[2]中谈“合命题”：“把一些反命题统一成一个合命题。这并不是说，这些反命题都被取消了。它们还在那里，但是已经被统一起来，成为合命题的整体。”
结构力学中有许多成对出现的方法。它们前呼后应，相映成趣，成为学园里一大景观。
“对联”是阴阳的范例，具有阴阳的风韵—成对相陪伴，互补相呼应：
成对陪伴—有此必定有彼。
互补呼应—由此可以知彼。
结构力学中的方法很多，如夜空群星，交相 辉映。
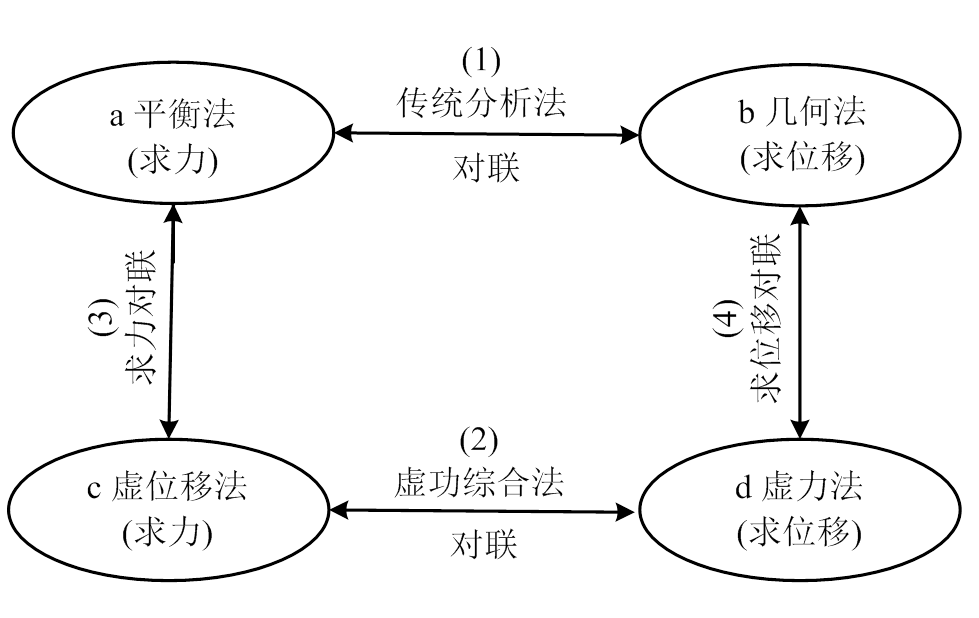
在静定结构中有四种主要解法值得特别关注。它们之间交错呼应，组成四副对联。
1) 四种解法[3－4]
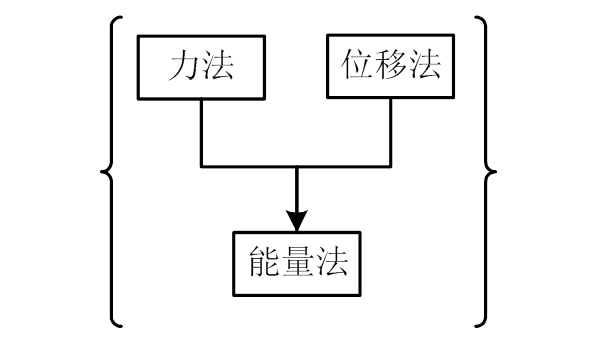
结构力学有两大主题—求力和求位移。最早采用分析法，即用平衡方程求力，用几何方程求位移。后来又提出虚功综合法，即用虚位移法求力，用虚力法求位移。因此共有四种主要解法，如下 所示。
2) 四副对联
上述四种解法可组成四副对联如下：
(1) 传统分析法对联
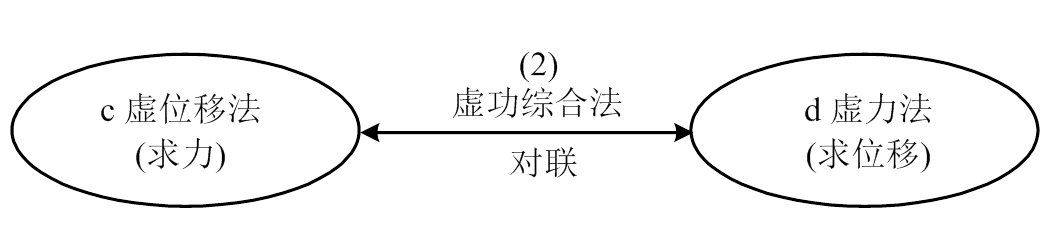
(2) 虚功综合法对联
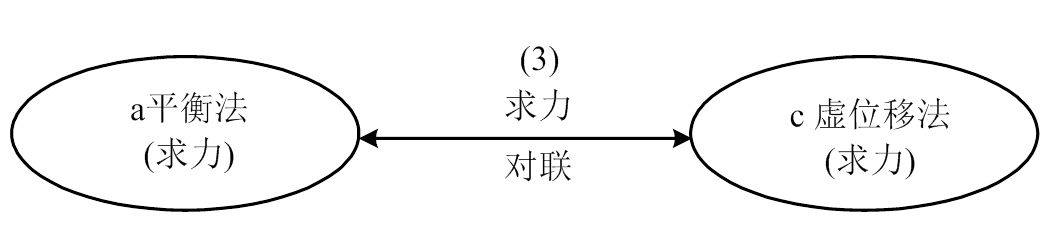
(3) 求力对联
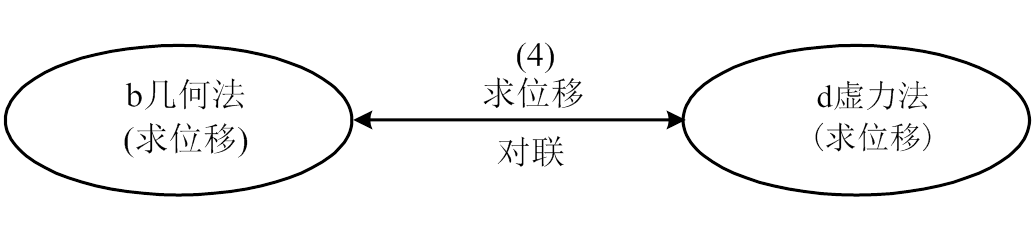
(4) 求位移对联
3) “四法四联”网络图
利用上述的四法和四联，可形成如下的网络图。四法是4个网站，四联是4条网线。
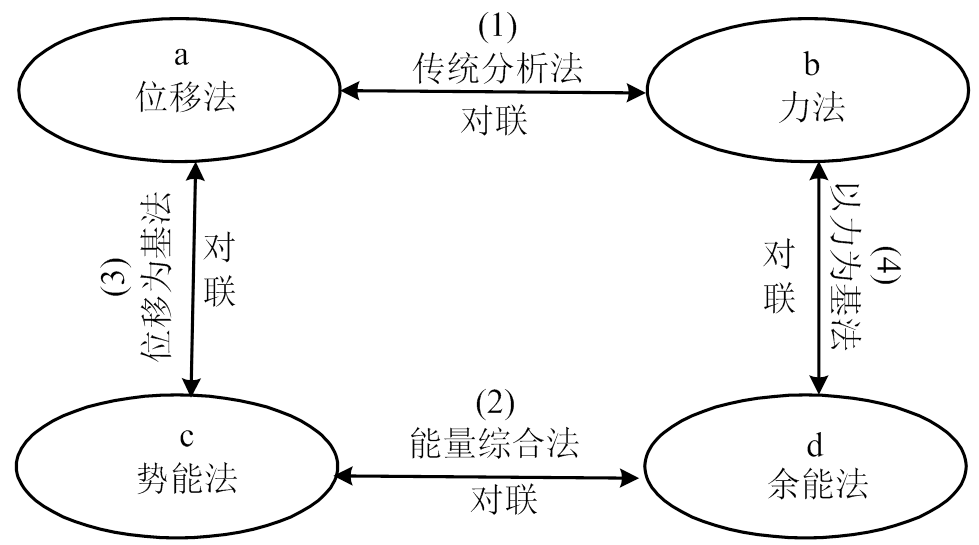
在超静定结构中也有四种主要解法，也可组成四副对联。
1) 四种解法
2) 四副对联
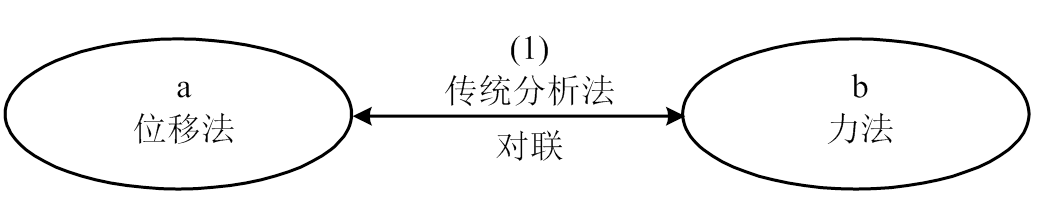
(1) 传统分析法对联
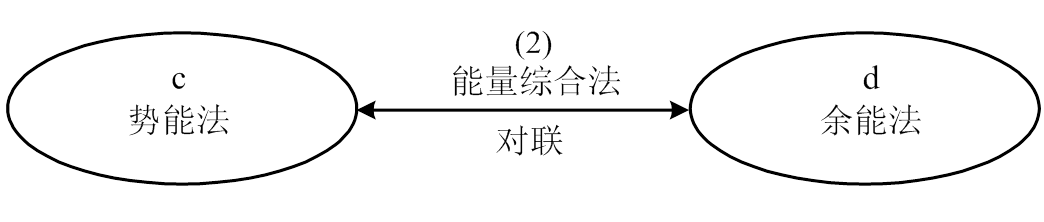
(2) 能量综合法对联
(3) “位移为基”法对联
(4) “以力为基”法对联
3) “四法四联”网络图
四法是4个网站，四联是4条网线。
结力方法往往成对出现，其特点是成对和互补。由此引出两点结论：
成对相陪伴—有此必定有彼。“二缺一”现象不会长期存在。
互补相呼应—由此可以知彼。要打通血脉，不要碎片化。
现举例分述如下：
1) 成对相陪伴。一枝独秀的局面不会长期 存在。
例1.力法最早提出，位移法较晚。现在终于成对相陪伴。
例2.计算机出现之后，矩阵位移法[5―6]应运而生。由于编程上的原因，矩阵力法却落在后面。可以预言，矩阵位移法一枝独秀的局面迟早会打破。
例3.传统的分析法最先发展，综合的虚功能量法提出较晚。是否会后来居上，且看今后发展。
2) 互补相呼应。彼此隔断的碎片化做法不 可取。
例4.碎片化的讲法不可取—把力系平衡分析与位移变形协调分析看作互不联系的两个碎片，各讲各的，互不通气。这种讲法虽仍常见，但不可取。
例5.重要定理长期埋没现象令人惊愕—平衡矩阵与几何矩阵之间的互伴定理，迟至2012年才被正式提出和严密论证[5, 7－8]。惊愕之余，不免感叹：真理深埋，发现虽晚更可贵。
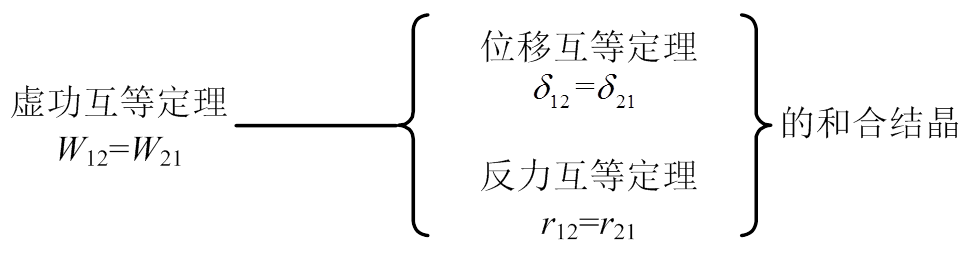
力学对联成为景观，力学学科领域成为阴阳二元争奇斗艳的园地。分久必合，虚功能量法应运而生。它是阴阳二元的和合结晶，结力方法中的太极。它的特点是“二元和合”：
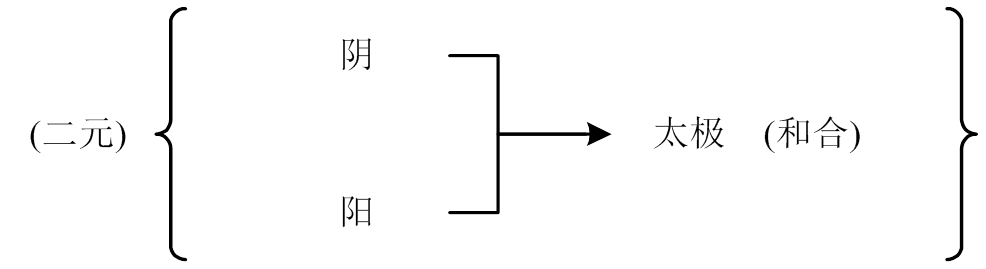
它的优势是“合一、多能”：
“合一”则简朴，“多能”则灵活。
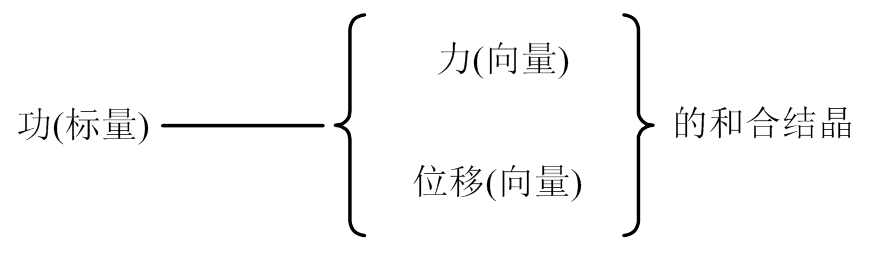
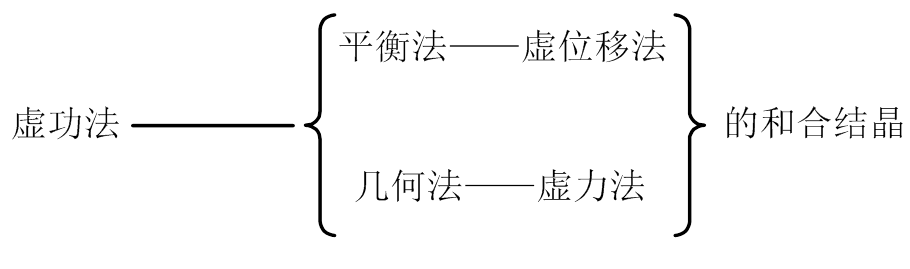
1) 合一则简朴(大道至简，易于推广)
2) 多能则灵活(能文能武，应用灵活)
能量法与虚功法的关系是：
“形式有异，实质相通。”
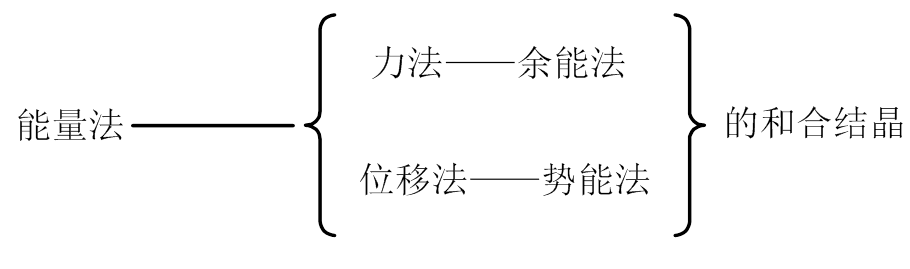
两种方法，殊途同归。不是两个碎片，而是血脉相通。下面从两个方面(势能与余能)加以论述。
先从势能法的一个主要定理—势能偏导数定理谈起[9－10]。
1) 势能偏导数定理可由虚位移原理导出
推导过程分为两步。
第一步，势能偏导数定理的表述
图1(a)所示是计算三跨连续梁时所采用的位移法基本体系。其中有受控制的可变位移Δ1、Δ2及其相应的控制约束力F1、F2。此外还有常量荷载Fp，其位移为D。现拟求控制约束力F1，并导出势能偏导数定理：
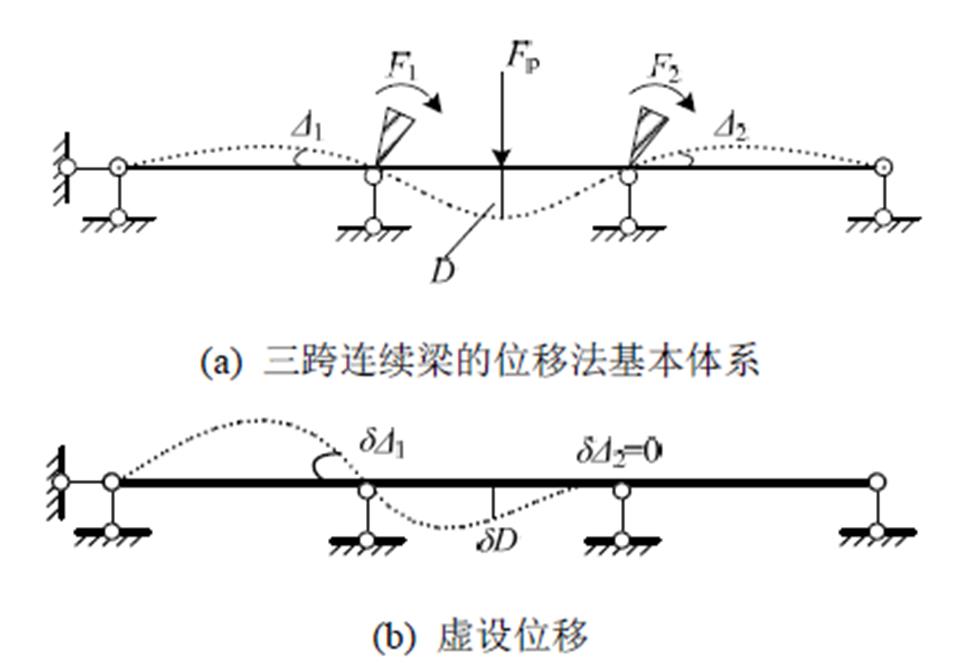
图1 三跨连续梁的位移法基本体系——求约束力F1
Fig.1 Primary system in displacement method of three-span continuous beam: solution for constraining force F1
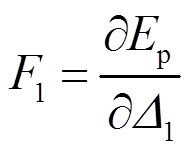(1)式中，Ep是结构势能：
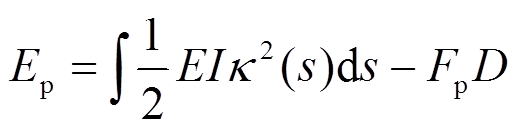(2)
式中，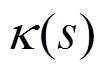
是梁的曲率。
第二步，应用虚位移原理导出式(1)
为了求F1，可虚设微量位移δΔ1(与F1相应)，并令δΔ2=0，如图1(b)所示。由此产生的微量曲率δκ与微量位移δD分别为：
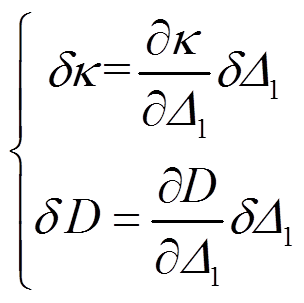(3)令图1(a)的力系在图1(b)的虚位移上做虚功，由变形体虚位移原理得：
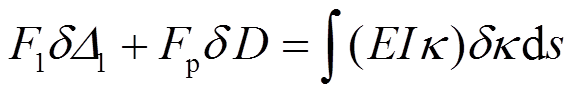(4)
除以δΔ1后，得：
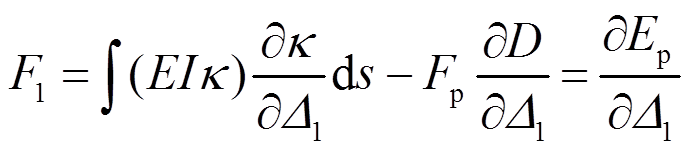(5)以上就是应用虚位移原理(式(4))导出势能偏导数定理(式(5))的过程。由此可知，二者是相 通的。
附记：两法相通，形式有异。
在式(4)中，虚位移以微分形式(δΔ1)出现，而在式(5)中，虚位移的作用则以导数形式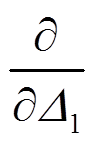
出现。
2) 两法(势能法与虚位移法)彼此相通
由势能偏导数定理还可导出下列推论：
单位位移法(求约束力的一般公式)，
势能驻值原理，
最小势能原理，
卡氏第一定理。
这些推论都可由虚位移原理导出。由此可知，势能法的各种形态都与虚位移法彼此相通。
1) 余能偏导数定理可由虚力原理导出
现结合图2所示结构和问题，说明推导过程。
第一步，余能偏导数定理的表述(参见图2)
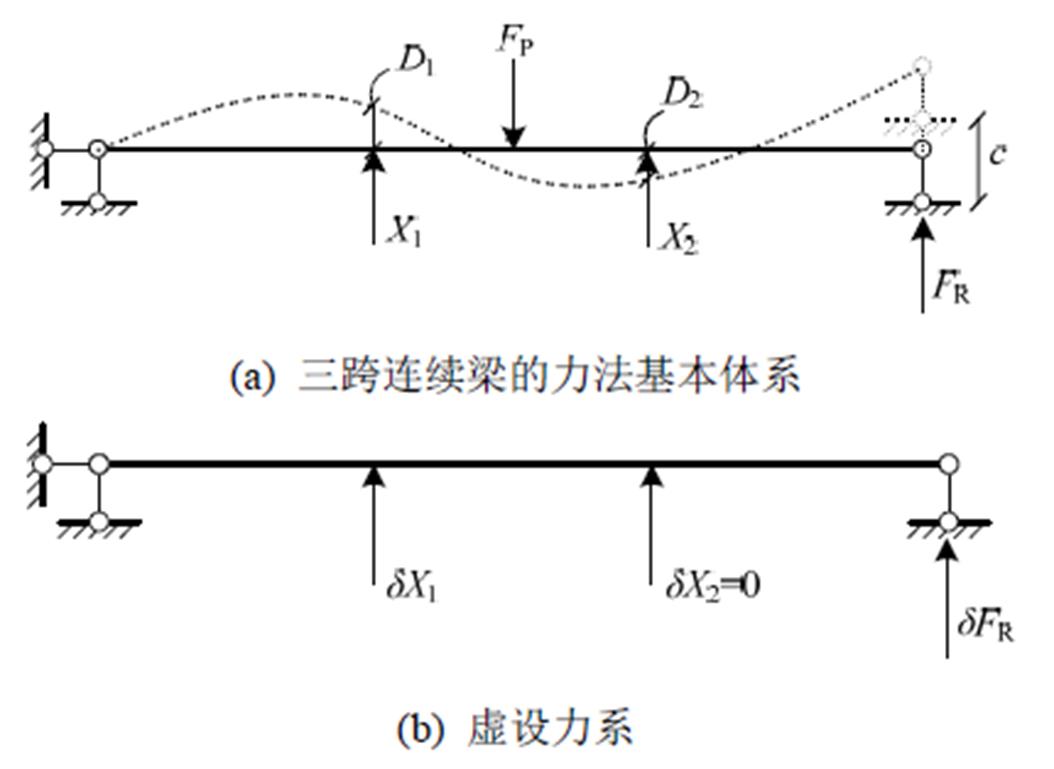
图2 三跨连续梁的力法基本体系—求位移D1
Fig.2 Primary system in force method of three-span continuous beam: solution for displacement D1
图2(a)所示是计算三跨连续梁时所采用的力法基本体系。其中有受控制的可变力X1、X2和常量荷载Fp作用，右支座有常量位移c。现拟求与可变力X1相应的位移D1，并导出余能偏导数定理：
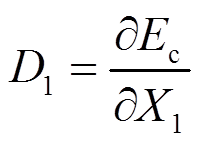(6)式中，Ec是结构余能：
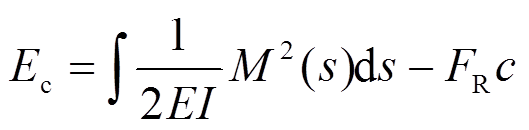(7)
式中：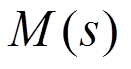
为梁的弯矩；
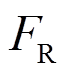为右端支座反力。
第二步，应用虚力原理导出式(6)
为了求位移D1，可虚设微量力δX1(与D1相应)，并令δX2=0。由此产生的微量弯矩δM和微量支座反力δFR分别为：
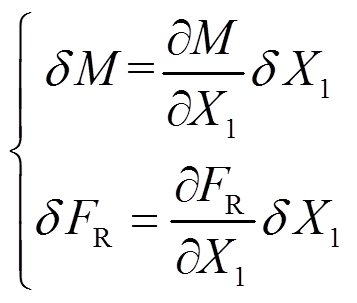(8)令图2(b)中的力系在图2(a)中的位移上作虚功，由变形体虚力原理得：
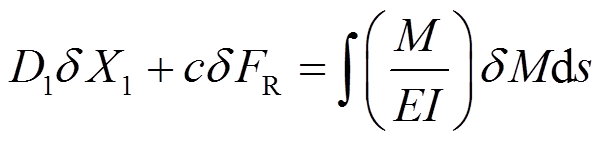(9)
除以δX1后，得：
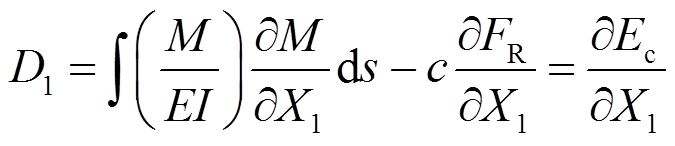(10)以上就是由虚力原理(式(9))导出余能偏导数定理(式(10))的过程。由此可知，二者是相通的。
2) 两法(余能法与虚力法)彼此相通
由余能偏导数定理还可导出如下推论：
单位荷载法(求位移的一般公式)，
余能驻值原理，
最小余能原理，
克罗蒂——恩格塞定理，
卡氏第二定理。
这些推论都可由虚力原理导出。由此可知，余能法的各种形态都与虚力法彼此相通。
在结构力学中，力系的平衡问题与位移的几何协调问题是成对的重要问题。它们之间虽然存在“成对相陪伴，互补相呼应”的紧密关系，但由于深藏隐晦，往往使人视而不见。为了打通血脉、消除隔阂，现对“平衡—几何”领域中[8]的互借图形与互伴定理等隐晦现象作进一步的揭示和论述。
在“平衡—几何”两个领域中，经常会看到同一个图形被互相借用的情况。现举三个例子如下。
例1.虚位移法作静定力影响线
对图3(a)所示简支梁，求作B点支座反力Z的影响线。
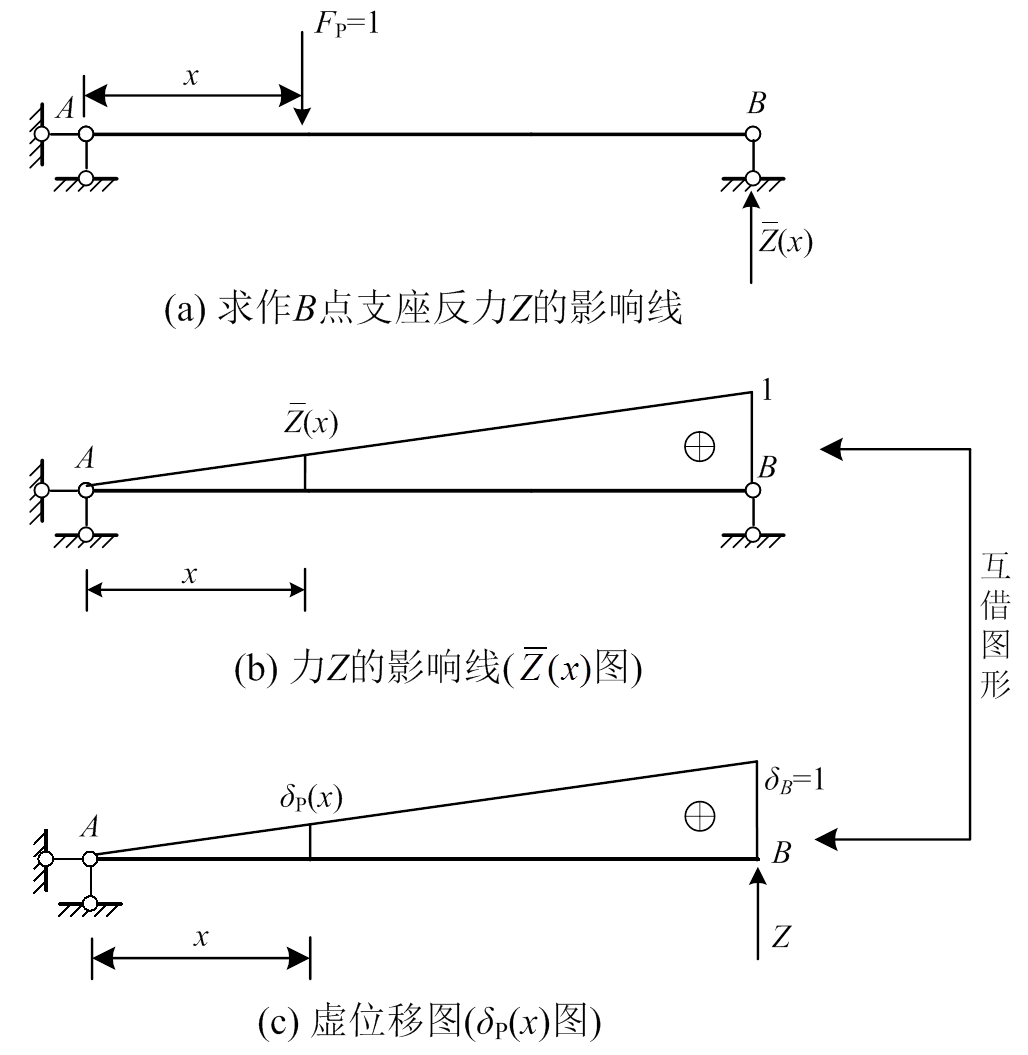
图3 虚位移法作静定力影响线
Fig.3 Solution for influence line of statically determinate force with virtual displacement method
解：当移动荷载FP=1作用于x点时，B点的支座反力为：
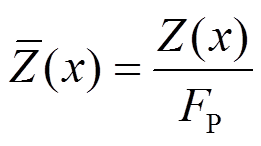(11)
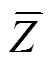称为Z的影响系数(图3(a))。
图3(b)表示Z的影响线，在x处的纵坐标为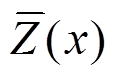
。
现应用虚位移法作影响线。其作法分为两步：
第一步，拆除B点支座，代以支座反力，使梁的B端沿Z方向产生单位位移δB=1，得到梁的虚位移图(δP(x)图)，如图3(c)所示。
第二步，应用虚位移原理，令图3(a)中的力系在图3(c)中的虚位移上作虚功，得：
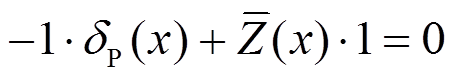(12)即：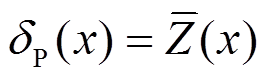
。
由此得知，图3(c)的虚位移图就是拟求的影响线(图3(b))。
余论：这里出现了互借图形的现象——同一个图形(即图3(b)和图3(c))被双方互相借用：
1) 在平衡领域，被借用来作影响线(图3(b))，用以表示两个力(FP和Z)之间的平衡关系。
2) 在几何领域，被借用来作位移图(图3(c))，用以表示两个位移(δB和δP)之间的几何关系。
这种“互借图形现象”可戏称为“一仆二主 现象”。
互借现象的出现，说明平衡规律与几何规律之间彼此相通，具有共性。如无共性，借来何用！
例2.虚位移法作超静定力的影响线(应用虚功互等定理)
对图4(a)所示超静定梁，求作B点支座反力Z的影响线。
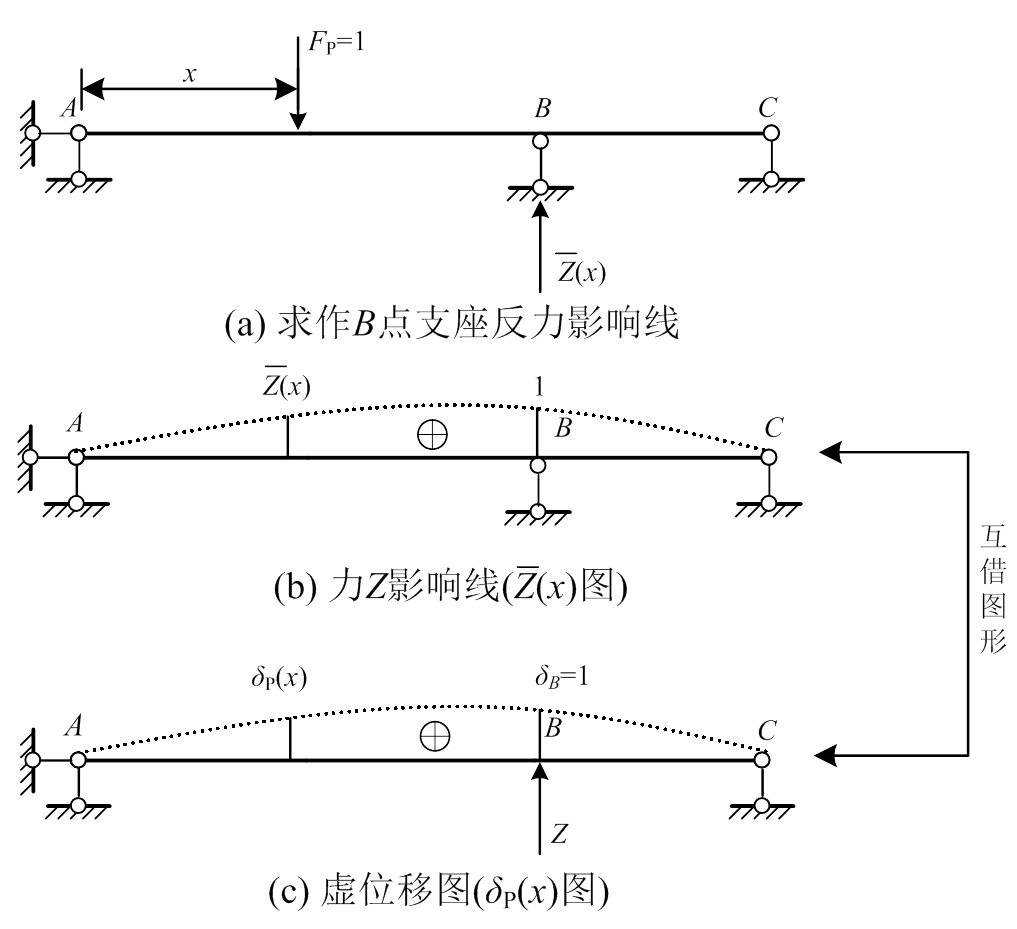
图4 虚位移法作超静定力影响线
Fig.4 Solution for influence line of statically indeterminate force with virtual displacement method
解：图4(b)表示B点支座反力Z的影响线，在x处的纵坐标为影响系数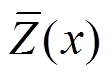
。
第一步，拆除支座B，代以支座反力Z使在B点沿Z方向产生单位位移δB=1，得到梁的虚位移图(δP(x))，如图4(c)所示。
第二步，对图4(a)和图4(c)应用虚功互等定理：
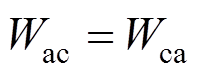(13)得：
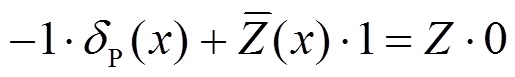(14)
即：。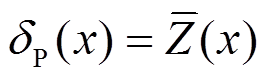
由此得知，虚位移图(图4(c))就是拟求的力Z影响线(图4(b))。这是“互借图形”现象的第二例。
例3.虚力法作位移影响线(应用位移互等定理)
对图5(a)所示梁结构，求作K点位移ΔK的影 响线。
解：图5(b)表示K点挠度ΔK的影响线，在x处的纵坐标为影响系数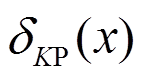
。
第一步，在K点沿ΔK方向虚设单位力FK=1，得到梁的位移图(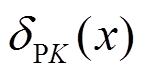
图)如图5(c)所示。
第二步，对图5(a)和图5(c)应用位移互等定理，得：
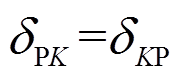(15)由此可知，由虚力产生的位移图(图5(c))就是拟求的位移影响线(图5(b))。
这是“互借图形”现象的第三例。
这里图5(b)和图5(c)虽然是同一个图形，却扮演了两个不同的角色：图5(b)表示移动荷载FP=1对固定点K产生的位移，图5(c)表示固定荷载FK=1对移动荷载点产生的位移。
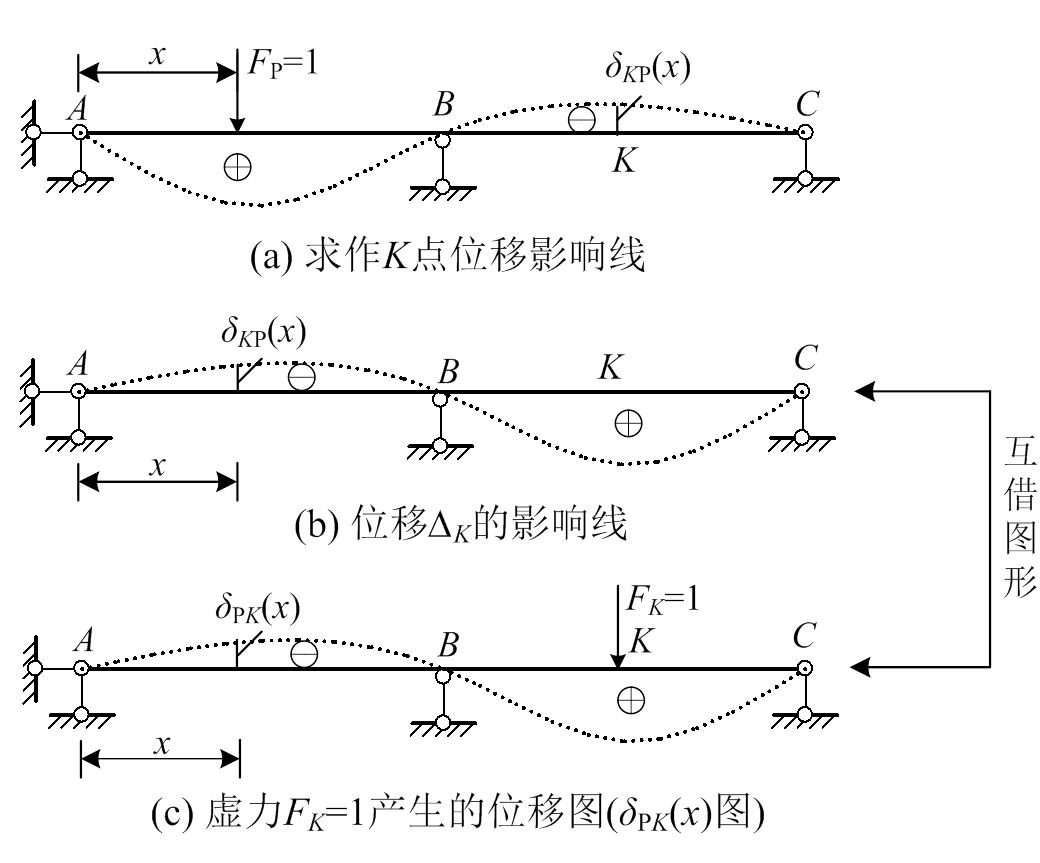
图5 虚力法作位移影响线
Fig.5 Solution for influence line of displacement with virtual force method
结构力学中有一个重要定理(“平衡—几何”互伴定理)，它长期埋没，直到2012年才被正式提出和严密论证。
在文献[5－6]《结构力学第4版》的第14章14-1节中指出：
“结构力学中有两个重要矩阵，即：
‘内力—荷载’之间的平衡矩阵H，
‘变形—位移’之间的几何矩阵G。
在本章中，将指出并论证平衡矩阵H与几何矩阵G之间的互伴定理：
H=GT
这个定理揭示了‘平衡’与‘几何’两个不同领域之间隐晦深藏的互伴关系，并用精密简洁的形式加以表述。”
“平衡—几何“互伴定理还揭示了结构的刚度矩阵和柔度矩阵为何具有对称性的秘密。
欲知详情，可读原著，这里只是发出一声长叹：
“花落梦深处，
道藏技里边。”
参考文献：
[1] 方韬, 译注. 山海经[M]. 北京: 中华书局, 2016.
Fang Tao, translation and annotation. Classic of Mountains and Seas [M]. Beijing: Zhonghua Book Company, 2016. (in Chinese)
[2] 冯友兰. 中国哲学简史[M]. 北京: 北京大学出版社, 2013.
Feng Youlan. A brief history of Chinese philosophy [M]. Beijing : Beijing University Press, 2013. (in Chinese)
[3] 龙驭球, 包世华, 匡文起, 等. 结构力学教程: I [M]. 北京: 高等教育出版社, 2000.
Long Yuqiu, Bao Shihua, Kuang Wenqi, et al. Structural mechanics: I [M]. Beijing: Higher Education Press, 2000. (in Chinese)
[4] 龙驭球, 包世华, 等. 结构力学教程: II[M]. 北京: 高等教育出版社, 2001.
Long Yuqiu, Bao Shihua, et al. Structural mechanics: II [M]. Beijing: Higher Education Press, 2001. (in Chinese)
[5] 龙驭球, 包世华, 袁驷. 结构力学II——专题教程, 第4版[M]. 北京: 高等教育出版社, 2018.
Long Yuqiu, Bao Shihua, Yuan Si. Structural mechanics II ——Adavanced course, 4th ed [M]. Beijing: Higher Education Press, 2018. (in Chinese)
[6] 袁驷. 程序结构力学[M]. 第2版. 北京: 高等教育出版社, 2008.
Yuan Si. Programming structural mechanics [M]. 2nd ed. Beijing: Higher Education Press, 2008. (in Chinese)
[7] 龙驭球, 包世华, 袁驷. 结构力学I——基础教程, 第4版[M]. 北京: 高等教育出版社, 2018.
Long Yuqiu, Bao Shihua, Yuan Si. Structural mechanics I——Fundamental course, the 4th edition [M]. Beijing: Higher Education Press, 2018. (in Chinese)
[8] 龙驭球. 结构矩阵分析中的“平衡-几何”互伴定理[J]. 工程力学, 2012, 29(5): 1―7.
Long Yuqiu. An adjoint theorem between equilibrium matrix and geometric matrix in structural analysis [J]. Engineering Mechanics, 2012, 29(5): 1―7. (in Chinese)
[9] 龙驭球, 刘光栋, 何放龙, 等. 能量原理新论[M]. 北京: 中国建筑工业出版社, 2007.
Long Yuqiu, Liu Guangdong, He Fanglong, et al. New monograph of variational principles [M]. Beijing: China Architecture & Building Press, 2007. (in Chinese)
[10] Long Yuqiu, Cen Song, Long Zhifei. Advanced finite element method in structural engineering [M]. Springer, Beijing: Tsinghua University Press, 2009.
A PHILOSOPHIC REVIEW OF STRUCTURAL MECHANICS METHODS
Abstract: The methodology of structural mechanics is reviewed. Five problems are discussed: 1) the keynote of the methodology of structural mechanics, 2) features of the structural mechanics methods, 3) the dominant features of the virtual work method and the energy method, 4) the equivalent relationship between the virtual work method and the energy method, and 5) the adjoint theorem between the equilibrium matrix and the geometric matrix.
Key words: structural mechanics; energy method; virtual work method; equilibrium; geometry
文章编号：1000-4750(2019)04-0001-07
中图分类号：TU311
文献标志码：A
doi:10.6052/j.issn.1000-4750.2019.01.ST13
收稿日期：2019-01-09