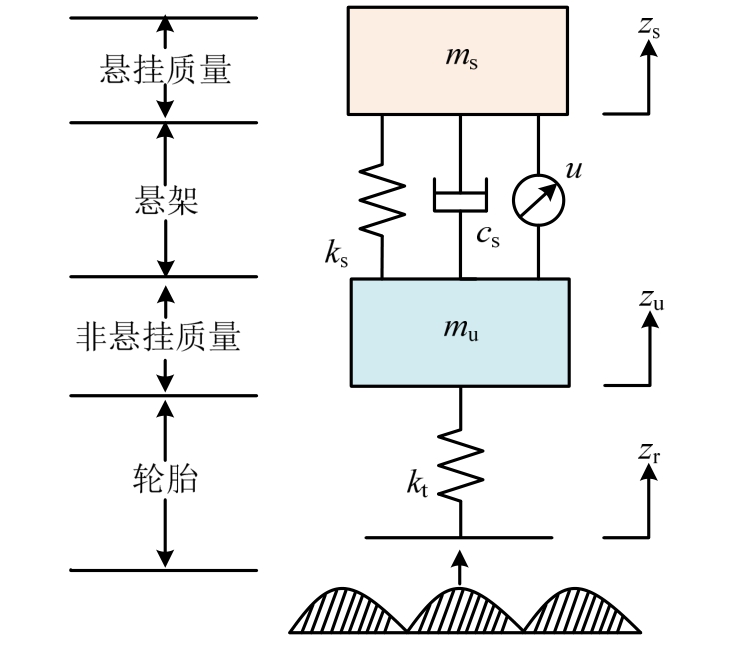
图1 1/4车辆二自由度主动悬架模型
Fig.1 Quarter-vehicle active suspension model with 2-DOF
悬架系统是指汽车车身与车轮之间所有传力连接装置的总成[1]。主动悬架控制系统的稳定性受车辆系统模型参数时变、控制时滞、行驶条件变化和外界干扰等强非线性因素影响，会对车辆乘坐平顺性、操纵稳定性及行驶安全性产生重要影响[2－4]。此外，主动悬架控制器依靠外界能源可根据路面状况的实时信号产生控制力以实现车体振动的最优反馈控制以及悬架性能和行驶工况的最佳匹配，进而使车辆悬架系统始终具有最优减振性能[5－8]。因此，主动悬架已经成为当前研究的热点之一，并且研究人员提出各种控制策略应用于主动悬架中，如模糊控制[9－11]，鲁棒控制[12]，自适应控制[13]以及神经网络控制[14]等。
在实际的控制系统中，主动悬架可能会由于种种原因导致其不能产生悬架所需的控制力，从而影响系统的性能和稳定性。然而，目前大部分主动悬架系统控制策略的研究是在假定系统完好状态下进行的，只有少数的主动悬架控制设计是考虑作动器故障的。比如：文献[15]针对作动器故障，提出一种基于故障补偿思想的主动容错控制方法。针对悬架参数摄动和作动器故障，文献[16]提出一种基于H2/H∞最优鲁棒容错控制方法。在文献[17]中，作者为改善主动悬架在传感器发生故障时悬架的控制效果，提出一种可重构的容错控制策略。在文献[18]中，针对汽车主动悬架作动器增益故障，设计卡尔曼滤波器获得状态残差，实现对故障的在线诊断，得到悬架故障增益，进而实现主动悬架作动器的容错控制。
上述文献中采用的都是线性悬架模型开展相关研究。然而悬架系统本身就存在较多的非线性因素，并且悬架参数会随着所处工况的变化而变化，因此对于悬架系统的控制而言，考虑悬架系统模型的不确定性就具有重要意义。由于T-S模糊模型结构简单，对复杂非线性系统可通过一些简单线性子系统的加权和来表示，近年来基于T-S模糊模型的控制方法受到广泛关注[19－22]。此外，文献[23]针对主动悬架作动器存在的时滞和故障问题，采用T-S模糊模型设计了一种的模糊鲁棒H∞控制器，以确保系统整体性能的稳定性。在文献[24]中考虑主动悬架的非线性和作动器时滞问题并建立T-S模型，进而设计模糊H∞控制器来保证系统渐进稳定，同时满足约束性能。上述文献所设计的T-S模糊控制在非线性模型追踪方面取得了较好控制效果，可很好地获取模型相应信息。但是，对信息简单的模糊处理容易导致控制精度降低及较差的动态品质。因而已有研究人员将模糊控制与滑模控制相结合，并应用于非线性控制系统。因为滑模控制(slidingmode control,SMC)已被公认为是设计鲁棒控制器的有效策略之一，并且适用于各种不确定条件的非线性系统，其主要优点是对系统不确定性和干扰的敏感度低，从而放宽了精确建模的必要性。在过去几年中，SMC已较为广泛应用于主动悬架系统[25－29]。
基于此，本文提出一种基于T-S模糊模型的主动悬架滑模容错控制方法，以稳定主动悬架系统并提高乘坐舒适性。首先通过T-S模糊方法建立由于车辆悬挂和非悬挂质量变化等因素引起的非线性主动悬架系统模型；接着将滑模控制与自适应理论结合设计滑模面函数和滑模容错控制律，保证系统状态的稳定性；最后讨论了该控制方法应用于不同路面激励的悬架系统仿真结果。
为简化悬架动力学分析及其控制器设计的复杂度，建立1/4车辆的二自由度的悬架动力学模型如图1所示。其中，ms为悬挂质量；mu为非悬挂质量；zs、zu分别为悬挂质量和非悬挂质量的垂向位移；zr为随机路面输入；cs、ks分别为悬架系统的阻尼和刚度；忽略轮胎阻尼，kt为轮胎刚度。
图1 1/4车辆二自由度主动悬架模型
Fig.1 Quarter-vehicle active suspension model with 2-DOF
根据牛顿第二定律建立其动力学方程为：
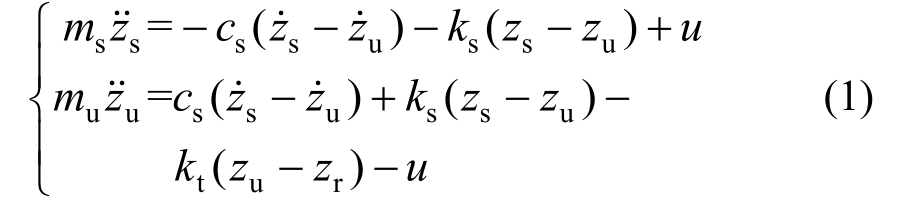
选取悬架动挠度x1=zs-zu，轮胎动位移x2=zu-zr，悬挂质量的垂向速度x3=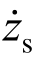
，非悬挂质量的垂向速度x4=
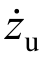分别作为系统状态变量，路面扰动w=
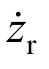与控制力u作为控制输入，定义悬架控制输出为：
则式(1)可用状态空间方程列写为：
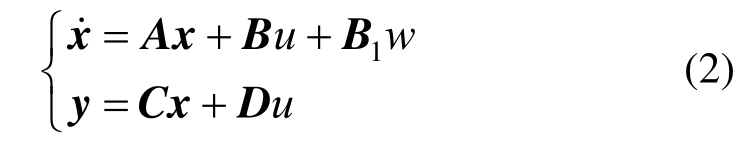
其中：
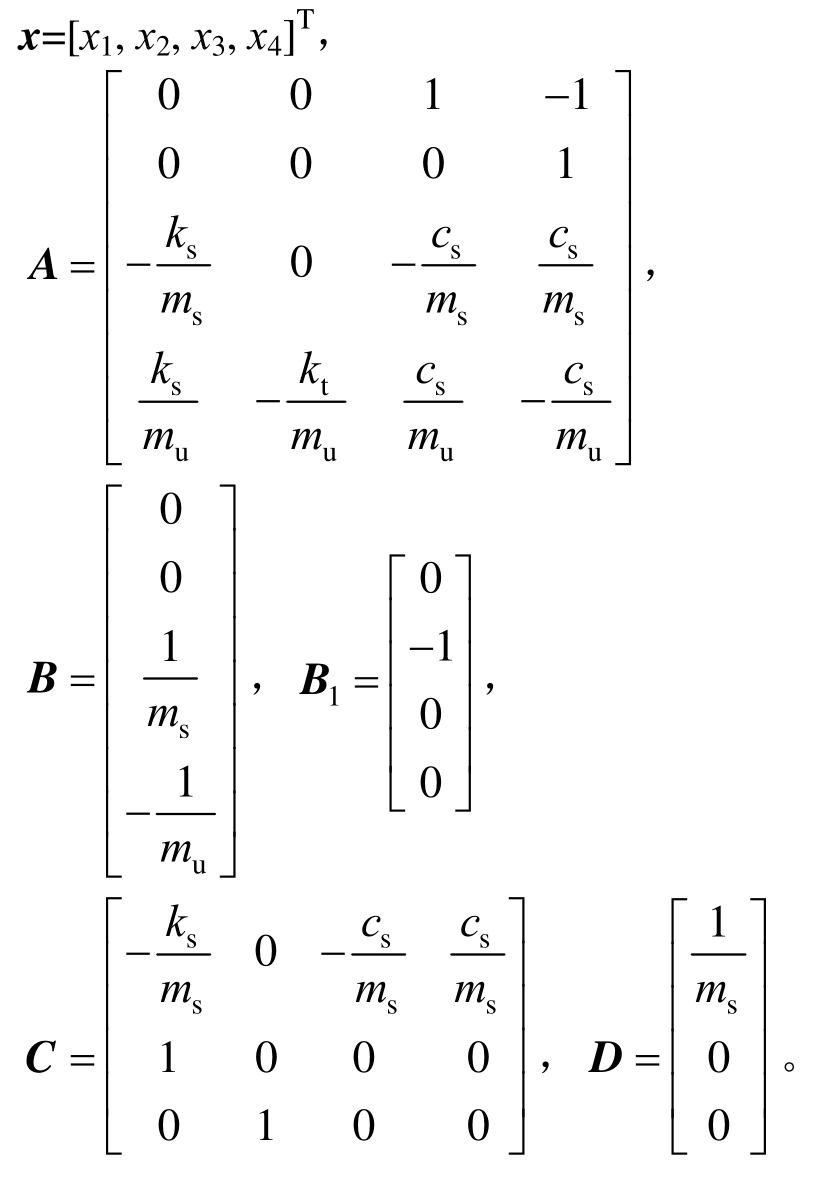
在主动悬架系统中，设计的理想控制输入u并通过作动器施加到闭环系统中，然而作动器经常会由于卡滞、增益变化、恒偏差等故障[30]，不能产生理想的控制输入u。为简化作动器故障的描述，本文引入故障调节因子δ，因此作动器产生的实际控制输入uf可以表示为：
且δ∈(0,1]。δ=1表示作动器正常工作；δ=0表示作动器完全失效；0<δ<1表示作动器部分失效，但仍可以工作。假设δ的最大值为δmax，最小值为δmin，则δ可以表示为：
其中
考虑作动器故障的主动悬架状态方程为：
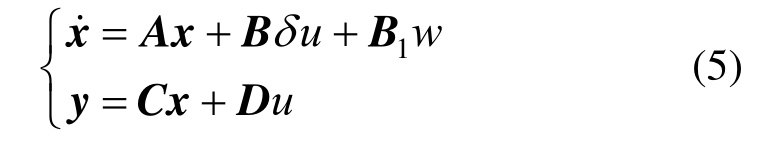
上述提到作动器故障控制输入具有一定不确定性，同时由于车身载荷或乘坐人数的变化使得悬挂质量ms和非悬挂质量mu在一定范围内变化。因此，主动悬架系统不确定性参数包括ms、mu和作动器不确定控制输入uf，且参数ms和mu应在给定载荷范围内变化，即msmin≤ms≤msmax，mumin≤mu≤mumax。定义ξ1=1/ms，ξ2=1/mu，参照文献[31]中非线性方法，可得1/ms和1/mu的值分别为：
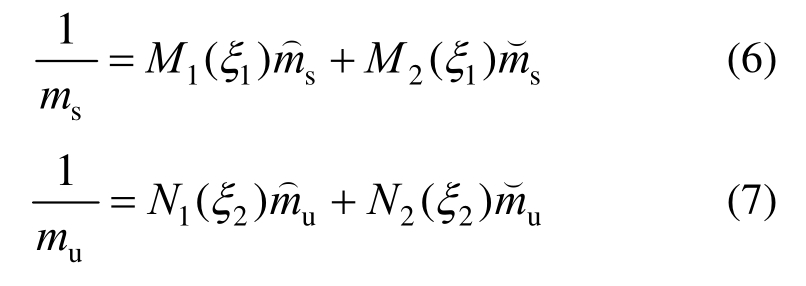
式中：
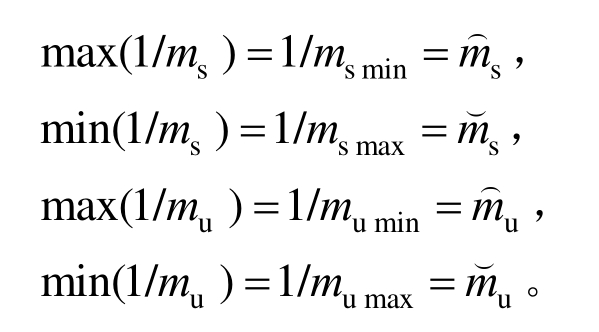
则隶属函数
可描述为：
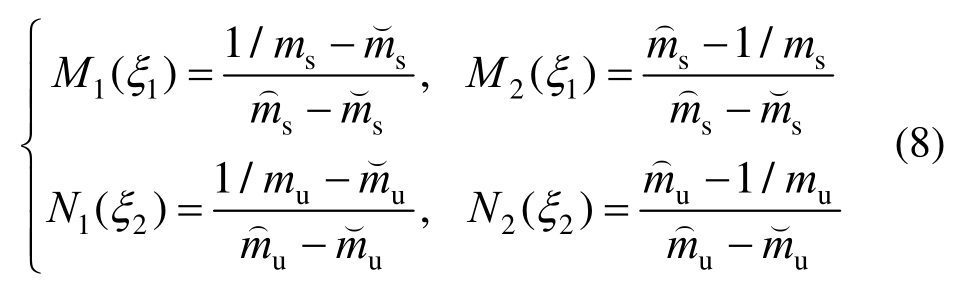
式中：
隶属函数M1(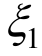
)和M2(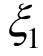
)分别定义为“Heavy”和“Light”，隶属函数N1(
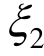)和N2(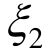
)分别定义为“Heavy”和“Light”。隶属度函数示意图如图2所示。
图2 隶属度函数
Fig.2 Membership functions
此时，考虑悬架系统质量不确定性的故障悬架系统式(5)可用如下T-S模型来描述：
规则i : 如果ξ1(t)是Mr，且ξ2(t)是Nj，
则
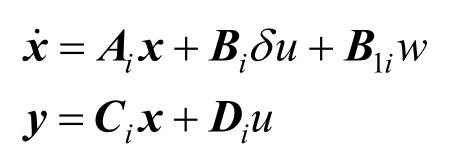
其中，r=1,2(j=1,2；i=1,2,3,4)；将矩阵A、B、B1、C、D中的1/ms、1/mu分别替换为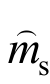
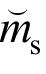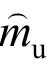(或
)、
(或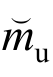
)即可得到矩阵Ai、Bi、B1i、Ci、Di。
由此，根据上述模糊规则，考虑悬架系统质量不确定性的车辆主动悬架系统可通过T-S模糊模型表示为：
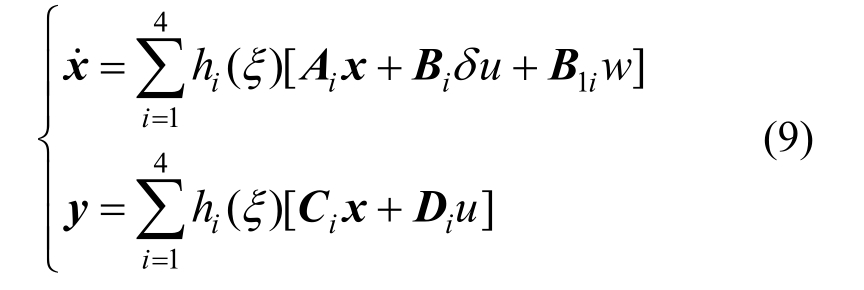
其中，hi(ξ(t))为模糊权重函数：
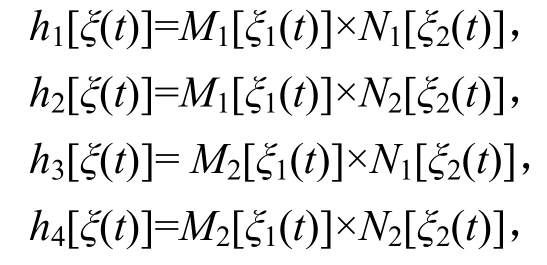
且满足
滑模切换面设计、系统稳定性分析以及安全约束性能分析是滑模容错控制器设计的主要内容。针对图1所示的1/4车辆主动悬架模型，在恶劣的路况下，车身尽可能地不产生振动是理想主动悬架控制的目标，这反映了悬架良好的隔振性能。所以悬挂质量的垂向位移和速度的期望值分别取为r1=0，r2=0。
定义e1 =zs -r1和e2 =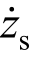
-
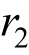分别作为悬挂质量垂向位移zs和垂向速度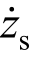的追踪误差。依据悬架动力学方程式(1)，误差动力学系统可以描述为：
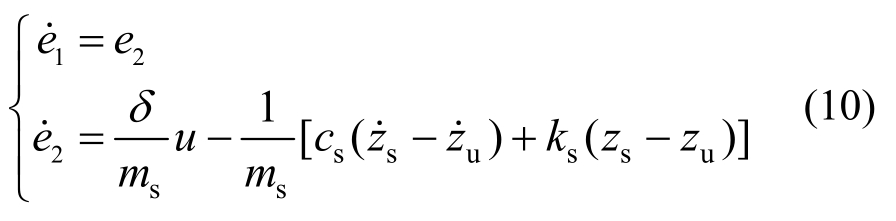
定义误差向量
则误差动力学系统式(10)的状态空间方程为：
式中：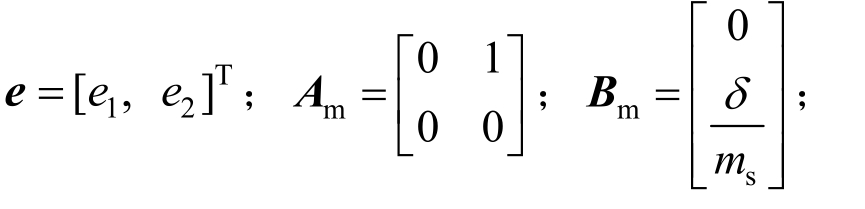
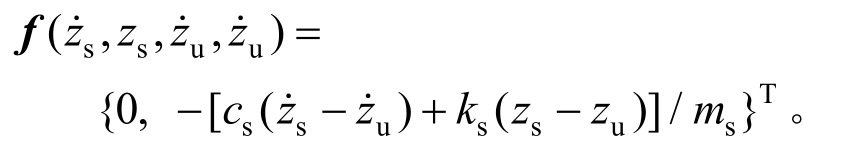
假定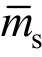
是ms的标称值，定义
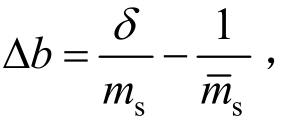则Δb的取值范围为：
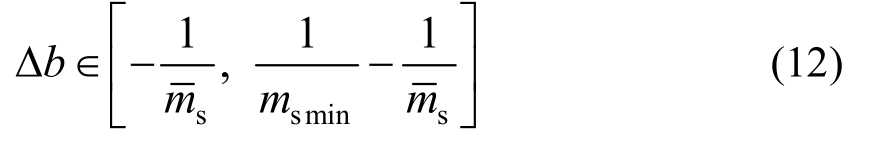
由此，式(11)可表达为：
式中，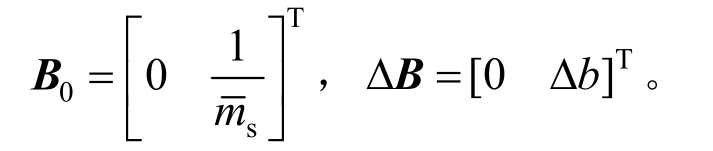
由式(12)可得：
在本研究中，通过极点配置方法设计滑模函数。
式中：s∈R1×1为滑模切面；G=[σ1 σ2]∈R1×2为系数矩阵，且σ1＞0，σ2＞0。
对滑模切换面(15)求导，可得：
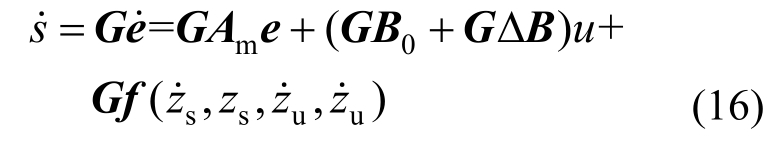
在滑模运动时，式(16)为滑动模态的运动微分方程，它决定了滑动模态的动态品质。为保证广义误差滑模面的渐近稳定性，必须使滑模运动方程的全部特征根位于复平面左半平面上。当系统状态处于滑模切换面上时，有s=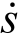
=0，则可使误差变量e1和e2都趋近于零，从而达到主动悬架理想的隔振效果。
由于悬架系统输出能量有限，因此
范数有界，即
＜L。其中，L是未知正常数；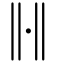
表示向量的2范数。
根据式(13)和式(15)，可以得到：
由式(12)和式(14)可得：
定义
，则：
对于主动悬架式(1)及误差动力学方程式(10)，选取滑模容错控制律如下：
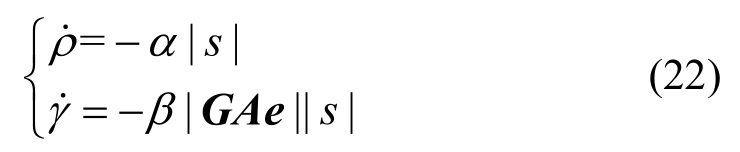
其中，α和β为自适应学习率。图3为基于T-S模糊模型的主动悬架滑模容错控制原理结构图。
图3 本文提出的滑模容错控制结构图
Fig.3 Control block of the proposed slide-mode fault tolerant control
为验证误差系统式(10)全局渐进稳定性，即当t→∞时，e→0，zs→0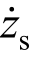，→0，作如下分析。
定义ρ～和γ～分别为：
其中：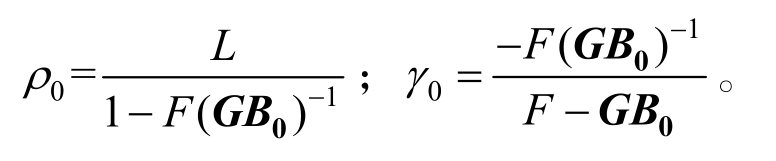
选取Lyapunov 函数为：
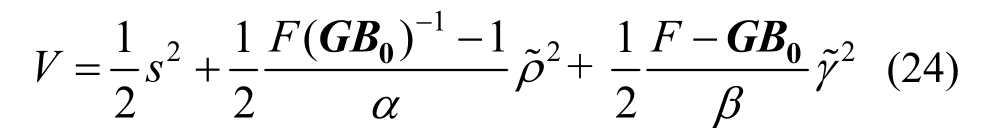
对式(24)求导，可得：
将式(26)代入(25)，则：
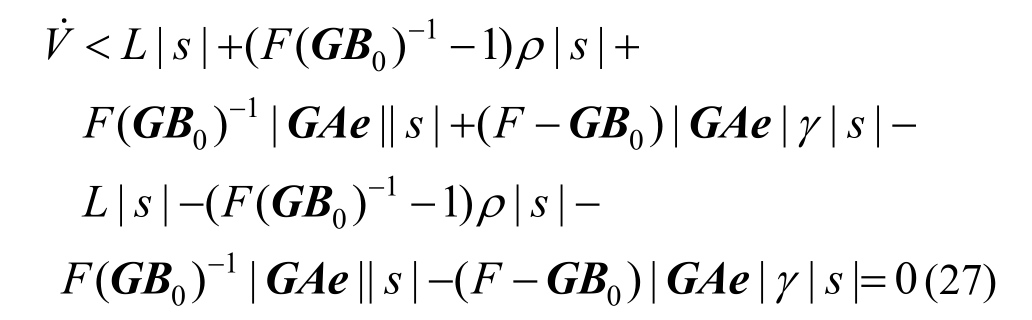
综上所述，在容错控制律式(21)和自适应律式(22)的作用下，闭环控制系统式(9)在Lyapunov理论框架下是渐近稳定的。
为了保证被控悬架系统具有良好的动态性能并满足安全约束，本文研究的悬架系统安全约束性能包括以下两个方面：
1) 由于弹簧和阻尼的机械结构限制，悬架动挠度不应超过其最大允许范围，即：
2) 为保障车辆的行驶安全性，轮胎的动载荷不可以超过其静载，即：
式中，g为重力加速度。
下面对系统的约束性能进行分析。
将容错控制律式(21)代入系统动力学方程式(1)可得：
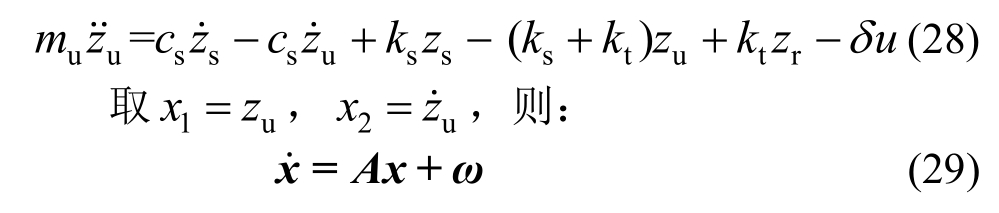
式中：
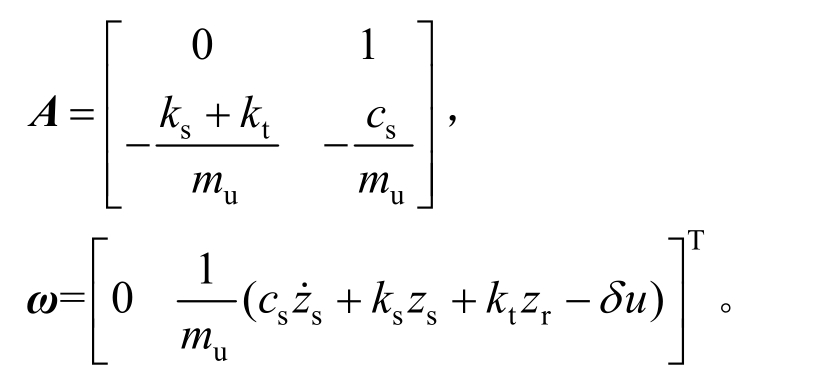
定义一个正定函数V=TxPx，其中P ＞0是一个正定矩阵，对其求导可得：
由于式(29)中的A的特征值具有负实部，因此，存在正定实对称Q满足：
另外，因为
其中μ＞0为一个可调正数，所以：
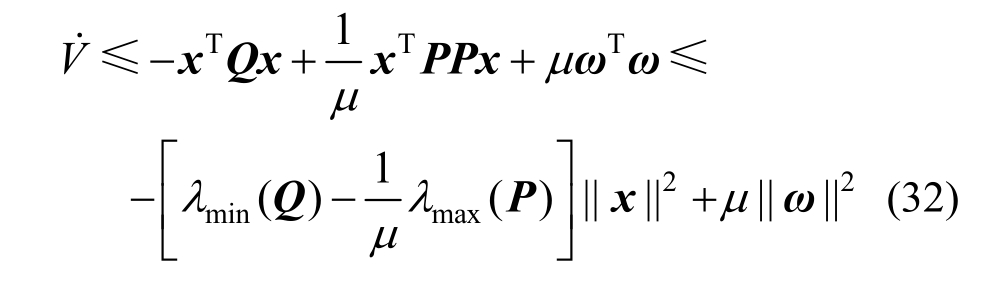
通过选取合适的参数μ，使得：
成立，即
，则：
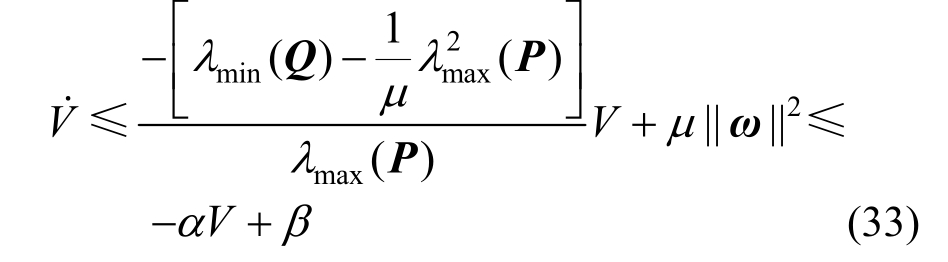
其中：
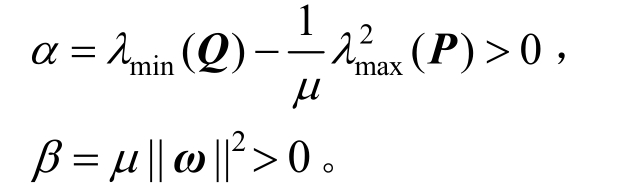
由不等式(33)可得：
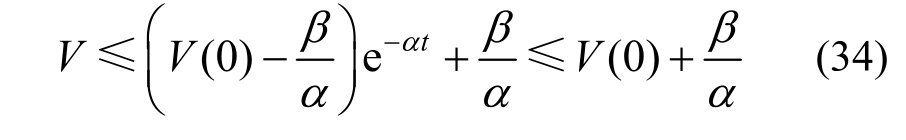
进而得到：
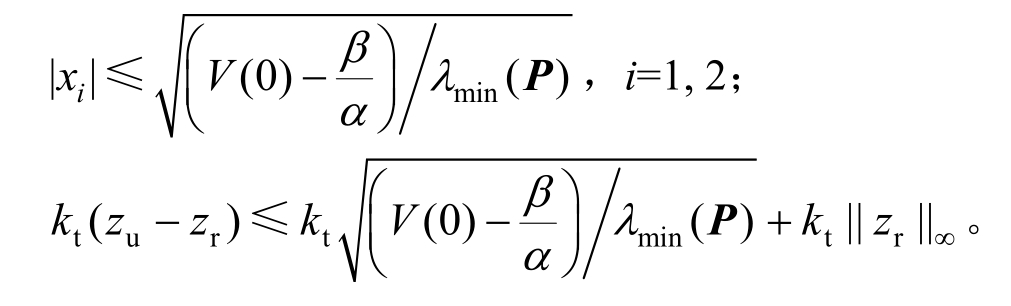
因此，通过选取适当的参数μ和矩阵P，可以使得下式成立：
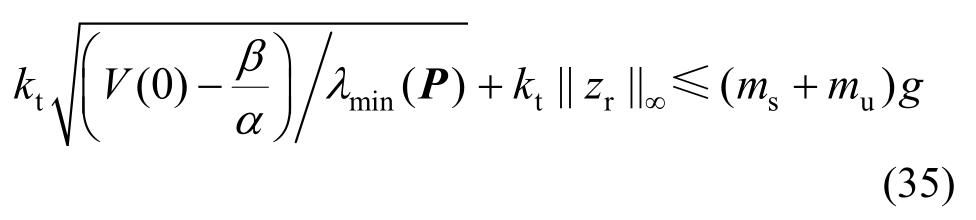
由于：
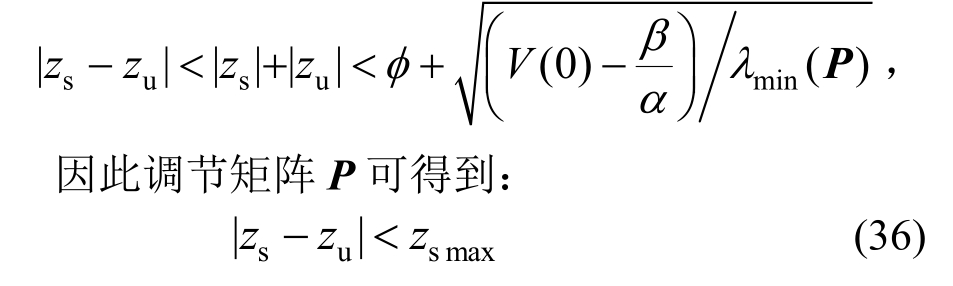
综上所述，由动力学方程式(1)设计得到的容错控制律能够满足悬架系统的安全约束条件。
本节通过数值仿真验证所设计的滑模容错控制器的有效性。首先，1/4车半主动悬架系统模型参数如表1所示。
表1 1/4车辆悬架参数
Table 1 Quarter-vehicle model parameters
参数名称 参数值ks 16000 N/m kt 200000 N/m cs 1095 N·s/m
考虑悬架系统的质量不确定性[32]，即悬挂质量为ms(t)=432+20sin(t)，非悬挂质量为mu(t)=45+0.45sin(t)。对于潜在的作动器故障，本文假设δmax=1，δmin=0.5。为保证系统的渐近稳定性，选取G=[79 1]。分别考虑以下4种情况：Case 1—被动悬架系统；Case 2—正常工作的容错控制系统，且考虑悬架系统质量不确定性ms(t)和mu(t)，设定δ=1；Case 3—发生故障的容错控制系统，且考虑悬架系统质量不确定性ms(t)和mu(t)，设定δ=0.5；Case 4—发生故障的容错控制系统，不考虑悬架系统质量不确定性，并假设ms=432 kg，mu=45 kg，δ=0.5。
为验证所设计控制器的有效性，根据ISO2361，以短时间、高强度凸块路面输入信号式(17)作为扰动输入，其数学描述为[33]：
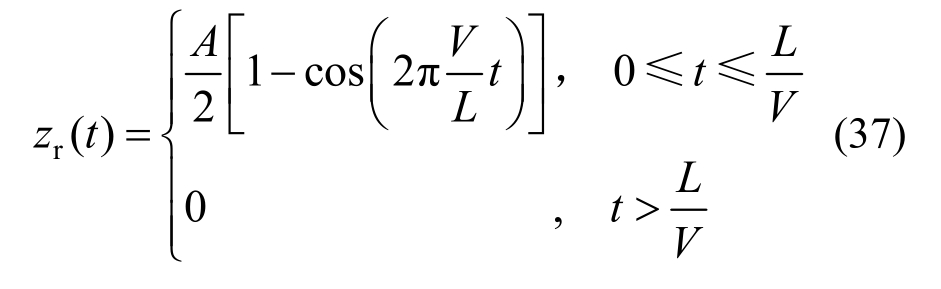
其中，A和L分别代表凸块输入的高度和长度，假定其值分别为A=50 mm，L=5 m，并且车辆以36 km/h车速匀速行驶。
图4～图6为凸块路面下四种不同案例情况下的主动悬架时域响应曲线。
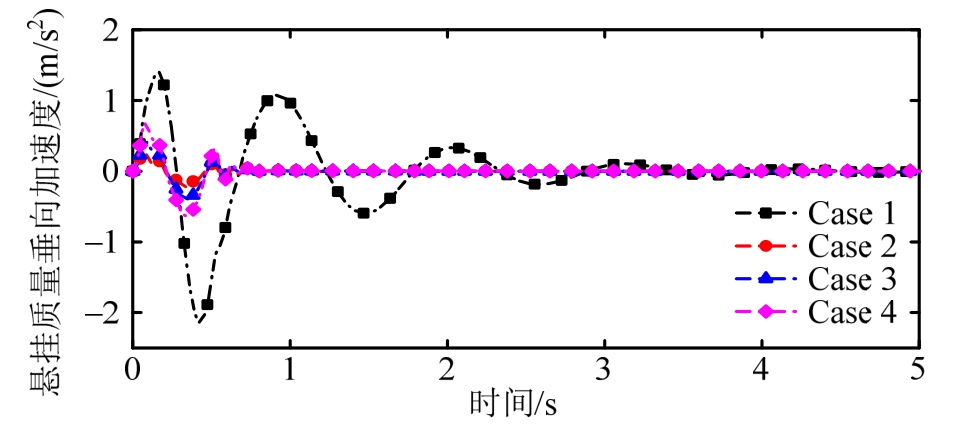
图4 悬挂质量垂向加速度
Fig.4 The vertical acceleration of the sprung mass
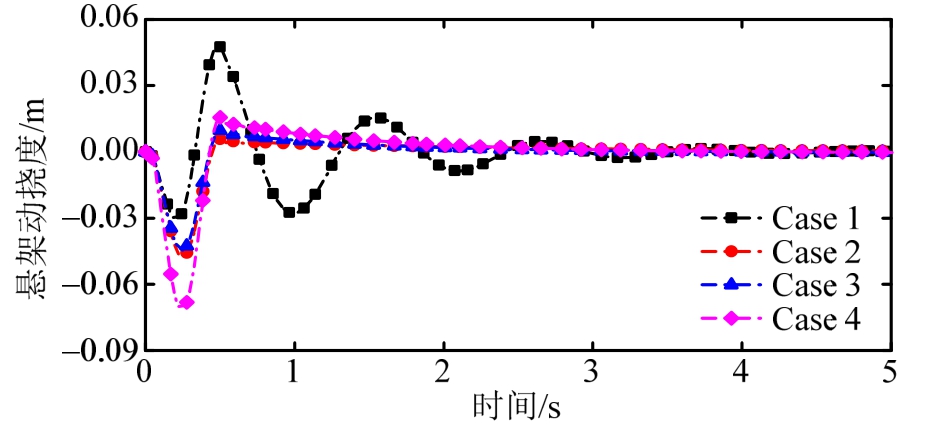
图5 悬架动挠度
Fig.5 The suspension dynamic deflection
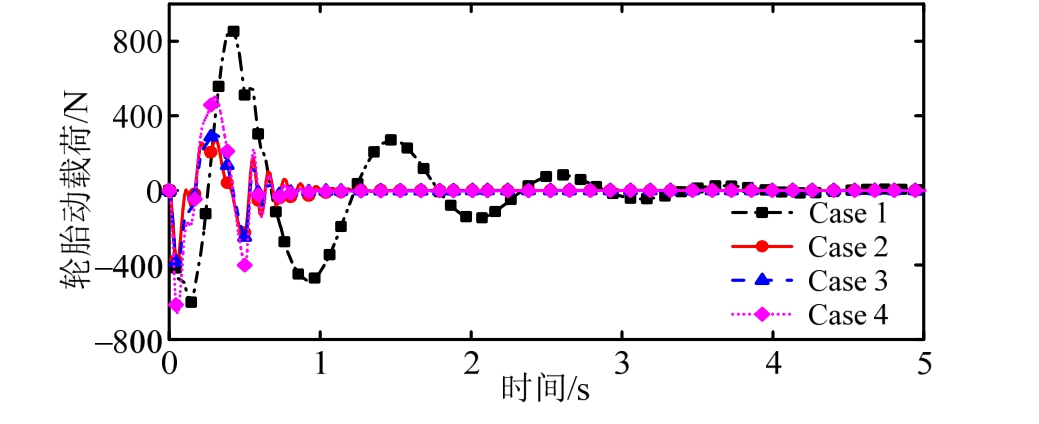
图6 轮胎动载荷
Fig.6 The tire dynamic load
首先，在Case 2和 Case 3条件下，分析其时域响应曲线可知，悬架系统响应(悬挂质量垂向加速度、悬架动挠度和轮胎动载荷)在作动器出现部分故障情况下应用本文提出的容错控制器，可使得故障悬架系统响应基本接近无故障主动悬架系统响应；其次，在Case 3和Case 4条件下，分析图4～图6相应曲线可知，若不考虑悬架系统的质量不确定性，则主动容错控制悬架出现较大的性能损失，但在本文所设计控制器作用下，即便主动悬架系统具有不确定性质量参数，其响应幅值仍会恢复至正常水平。同时，相较于被动悬架响应，不同案例(Case 2、Case 3和Case 4)条件下的主动容错控制方法都可以较好地改善主动悬架系统的性能指标。
图7为凸路面下Case 2和Case 3的主动控制力变化曲线，可以看出当车辆受到瞬态冲击时，故障悬架系统的主动控制力能够很好地跟踪正常工作条件下的悬架系统控制力，并快速做出响应。
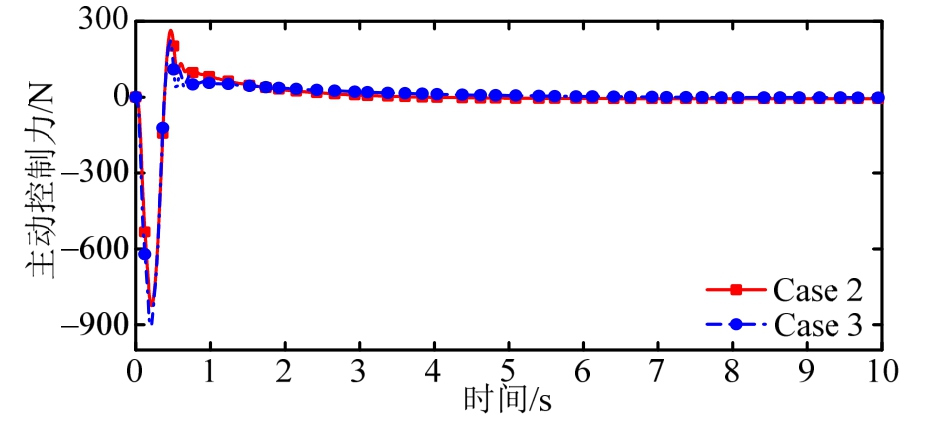
图7 凸块路面下主动控制力u的变化
Fig.7 The variation of active control forceu in Case 2 and Case 3 under bump road disturbance
为了对比分析本文所提出滑模容错控制悬架与被动悬架在凸块路面下的性能指标均方根值，经过计算给出如表2所示的性能指标均方根值表。其中az、fd和td分别代表悬挂质量垂向加速度、悬架动挠度和轮胎动载荷。分析可知，相比于被动悬架系统的Case 1，悬架系统在Case 2、Case 3和Case 4条件下，其性能指标都有较大改善。其中，悬挂质量垂向垂向加速度的优化程度最明显，达到75%以上。说明所设计的滑模容错控制器具有更好的扰动抑制能力，能够提高系统的扰动隔离能力。
表2 凸块路面激励下的悬架性能指标均方根值
Table 2 RMS lists of suspension performance indicators under bump road
控制类型 均方根值RMS az/(m/s2)fd/mtd/N Case 1 0.4088 0.0103 179.56388 Case 2 0.0395 0.0076 58.0648 Case 3 0.0697 0.0073 64.8630 Case 4 0.1004 0.0098 89.9902控制类型 变化情况/(%)(-代表改善，+代表恶化)az/(m/s2)fd/mtd/N Case 1 — — —Case 2 -90.3376 -26.2136 -67.6633 Case 3 -82.9501 -29.1262 -63.8773 Case 4 -75.4403 -4.8544 -49.8838
考虑式(38)所示的粗糙路面输入信号[34]：
路面式(38)是模拟车体共振频率(1 Hz)与高频干扰叠加的粗糙路面，图8～图10为粗糙路面下四种不同案例情况下主动悬架的时域响应曲线。
图8 悬挂质量垂向加速度
Fig.8 The vertical acceleration of the sprung mass
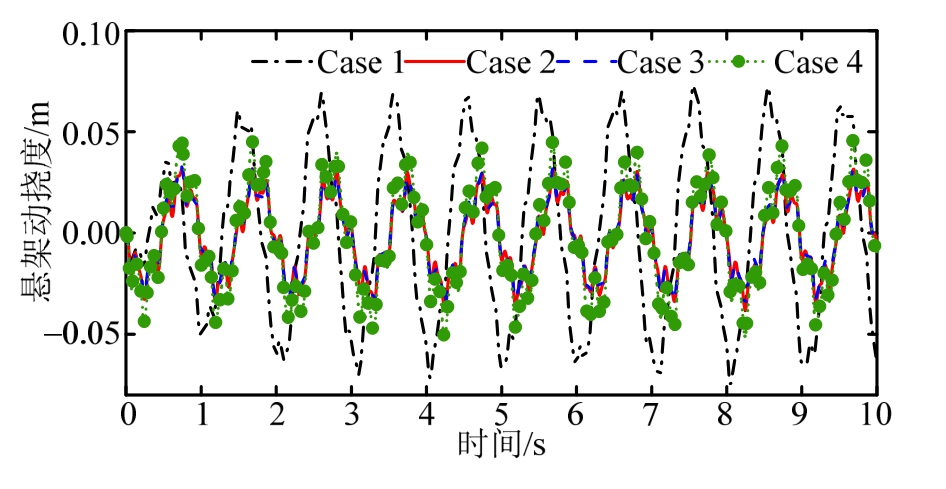
图9 悬架动挠度
Fig.9 The suspension dynamic deflection
图10 轮胎动载荷
Fig.10 The tire dynamic load
通过比较图8～图10中Case 2和Case 3下的悬架系统响应曲线可知，在悬架作动器出现部分失效故障情况下，本文设计的滑模容错控制器能够最大化地使得主动悬架系统性能指标接近无故障悬架系统响应。另外，分析Case 3和Case 4条件下的悬架系统响应可知，悬架系统质量的不确定变化会造成更大的性能损失，但在考虑悬架系统质量不确定性的主动容错控制器作用下，能够有效抑制悬挂质量垂向加速度，降低悬架动挠度和轮胎动载荷，进而改善车辆行驶平顺性。
图11为粗糙路面下主动悬架在Case 2和Case 3条件下的主动控制力变化曲线，从中可以看出，故障悬架所需的主动控制力基本与无故障悬架主动控制力基本趋势相符合，由此说明滑模容错控制器可以抑制作动器故障给系统带来的不利影响，提高乘坐舒适度。
为进一步说明所设计的控制器有效性，表3列出了不同案例条件下的滑模容错控制主动悬架与被动悬架系统在粗糙路面下的性能指标均方根值的对比分析结果。
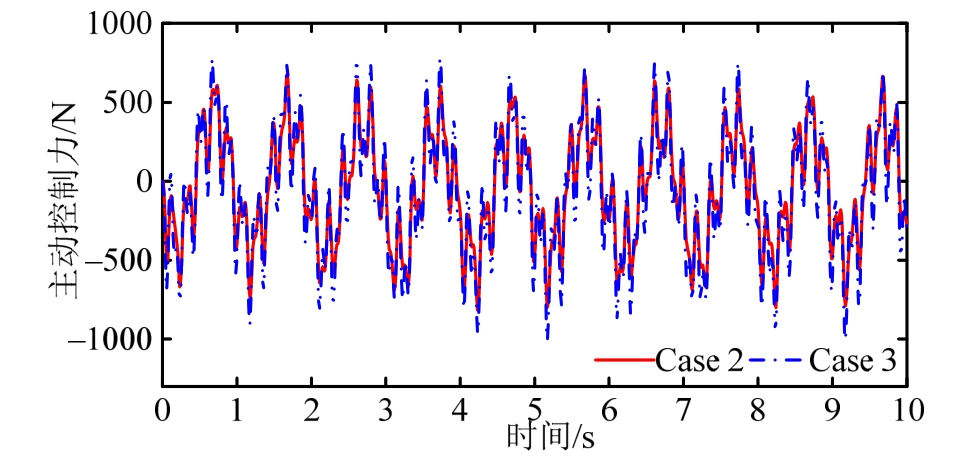
图11 粗糙路面下主动控制力u的变化
Fig.11 The variation of active control forceu in Case 2 and Case 3 under rough road disturbance
表3 粗糙路面激励下的悬架性能指标均方根值
Table 3 RMS lists of suspension performance indicators under rough road
控制类型 均方根值RMS az/(m/s2)fd/mtd/N Case 1 1.7672 0.0421 892.4720 Case 2 0.3428 0.0201 692.5553 Case 3 0.4392 0.0189 611.847 Case 4 0.5821 0.0251 748.276控制类型 变化情况/(%)(-代表改善，+代表恶化)az/(m/s2)fd/mtd/N Case 1 — — —Case 2 -80.6021 -52.2565 -22.4004 Case 3 -75.1471 -55.1069 -31.4436 Case 4 -67.0609 -40.3800 -16.1569
由表3可知，相比于被动悬架系统，在不同案例条件下的主动悬架车身加速度和悬架动挠度的改善情况均在40%以上，而由于三种性能指标之间相互矛盾，故轮胎动载荷的优化效果相对减弱，但是相比被动悬架，仍有至少16%的提升，依然能够确保汽车具有安全行驶性能。
综上所述，表明本文所提出的滑模控制器能够大幅度降低路面扰动所引起的负面影响，进而改善乘坐舒适度。
本文选取一种路面不平度系数为Gq(n0)=64×10-6 m3，车速v=72 km/h的B级随机路面，作为激励信号来验证控制器的鲁棒性，其表达式为[35]：
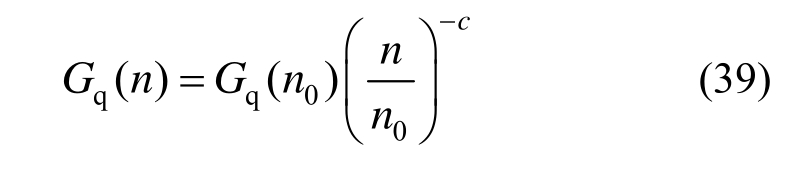
式中：n0=0.1 (1/m)是参考空间频率；c=2是道路粗糙度常数；n是空间频率，其由车辆行驶速度v与时间频率f确定，即f=nv。时间频率f随着仿真时间的变化而变化。
且考虑时变参数δ为[36]：
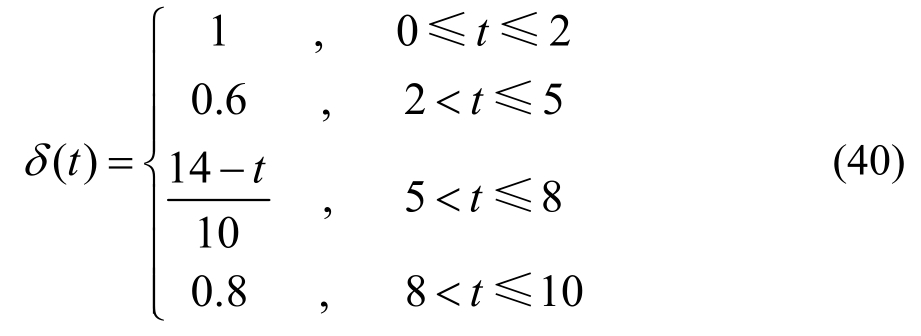
图12～图14为被控悬架模型正常工作(δ=1)和发生时变故障(δ=δ(t))的时域响应曲线。通过分析悬架动特性曲线可知，在整个时域内，故障模型的悬挂质量垂向加速度、悬架动挠度和轮胎动载荷三个指标相对于正常工作的悬架系统的跟踪精度都比较高，其中悬架动挠度的误差保持在5%以下，悬挂质量垂向加速度的误差保持在10%以下，轮胎动载荷的误差也保持在10%以下。这说明被控悬架在发生故障(δ=δ(t))情况下，仍然能够很好地跟踪正常工作(δ=1)的悬架系统，使系统具有良好的鲁棒性，从而故障模型可以较好地得到与正常工作模型一致的控制效果。
图12 悬挂质量垂向加速度
Fig.12 The vertical acceleration of the sprung mass
图13 悬架动挠度
Fig.13 The suspension dynamic deflection
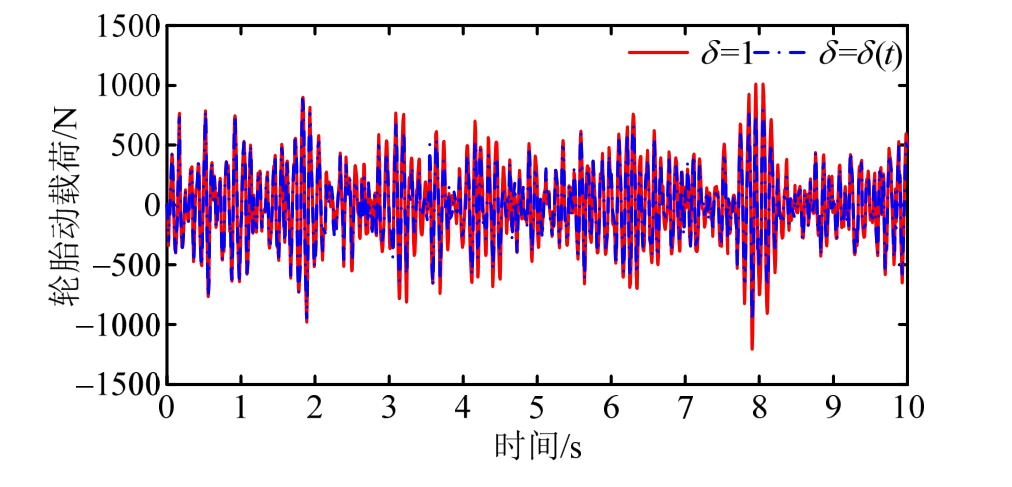
图14 轮胎动载荷
Fig.14 The tire dynamic load
本文针对悬架系统的质量参数不确定性和作动器出现的随机故障引起非线性控制稳定性问题，以某1/4车辆主动悬架为研究对象提出了一种新的基于T-S模糊模型的主动悬架滑模容错控制器设计方法，通过理论推证和仿真分析可以得出：
(1) 基于T-S模糊模型建立1/4车辆的非线性模型，可以有效描述悬架系统质量参数的不确定性，同时，利用故障调节因子描述作动器出现的随机故障大小，获得完整的考虑悬架系统质量不确定性和作动器故障的车辆主动悬架控制模型。
(2) 通过融合经典滑模控制与自适应理论设计合适的滑模面函数和滑模容错控制律，能确保闭环控制系统在有限时间内渐近稳定，降低作动器故障对悬架性能的影响以及隔离外部干扰，进而提高车辆动力学性能。
(3) 本文在两种路面扰动下对不同仿真实例进行对比分析，发现本文所设计的控制器不仅可以补偿主动悬架系统出现作动器故障后带来的性能损失，同时，有效降低了路面扰动对悬架系统带来的负面影响，改善了乘坐的舒适度。
[1] 余志生.汽车理论[M].第5版.北京: 机械工业出版社,2009.Yu Zhisheng.Automobile theory [M].5th ed.Beijing:China Machine Press,2009.(in Chinese)
[2] 周兵,赵保华.汽车主动悬架自适应模糊PID控制仿真研究[J].湖南大学学报(自然科学版),2009,36(12):27―30.Zhou Bing,Zhao Baohua.Simulation study of self-adaptive fuzzy-PID control of active suspension [J].Journal of Hunan University (Natural Sciences),2009,36(12): 27―30.(in Chinese)
[3] Li H,Yu J,Hilton C,et al.Adaptive sliding-mode control for nonlinear active suspension vehicle systems using TS fuzzy approach [J].IEEE Transactions on Industrial Electronics,2013,60(8): 3328―3338.
[4] 贾启芬,于雯,刘习军,等.汽车悬架系统的分段线性非线性振动机理的研究[J].工程力学,2005,22(1):88―92.Jia Qifen,Yu Wen,Liu Xijun,et al.Dynamiccharacteristics of bilinear suspension system of vehicles[J].Engineering Mechanics,2005,22(1): 88―92.(in Chinese)
[5] 喻凡,张勇超.馈能型车辆主动悬架技术[J].农业机械学报,2010,41(1): 1―6.Yu Fan,Zhang Yongchao.Technology of regenerative vehicle active suspensions [J].Transactions of the Chinese Society of Agricultural,2010,41(1): 1―6.(in Chinese)
[6] Sun W,Zhao Z,Gao H.Saturated adaptive robust control for active suspension systems [J].IEEE Transactions on Industrial Electronics,2013,60(9): 3889―3896.
[7] Rath J J,Defoort M,Karimi H R,et al.Output feedback active suspension control with higher order terminal sliding mode [J].IEEE Transactions on Industrial Electronics,2017,64(2): 1392―1403.
[8] Huang Y,Na J,Wu X,et al.Adaptive control of nonlinear uncertain active suspension systems with prescribed performance [J].Isa Transactions,2015,54:145―155.
[9] Huang S J,Lin W C.Adaptive fuzzy controller with sliding surface for vehicle suspension control [J].IEEE Transactions on Fuzzy Systems,2003,11(4): 550―559.
[10] Wen S,Chen M Z Q,Zeng Z,et al.Fuzzy control for uncertain vehicle active suspension systems via dynamic sliding-mode approach [J].IEEE Transactions on Systems Man & Cybernetics Systems,2017,47(1): 24―32.
[11] 高瑞贞,张京军,赵子月,等.基于改进遗传算法的半主动悬架系统模糊控制优化研究[J].工程力学,2012,29(1): 240―248.Gao Ruizhen,Zhang Jingjun,Zhao Ziyue,et al.Research on the fuzzy control of semi-active suspension systems based on improved genetic algorithms [J].Engineering Mechanics,2012,29(1): 240―248.(in Chinese)
[12] Gaspar P,Szaszi I,Bokor J.Design of robust controllers for active vehicle suspension using the mixed µ synthesis[J].Vehicle System Dynamics,2003,40(4): 193―228.
[13] Na J,Huang Y,Wu X,et al.Active adaptive estimation and control for vehicle suspensions with prescribed performance [J].IEEE Transactions on Control Systems Technology,2017,26(6): 2063―2077.
[14] Zhao F,Ge S S,Tu F,et al.Adaptive neural network control for active suspension system with actuator saturation [J].IET Control Theory and Applications,2016,10(14): 1696―1705.
[15] 高振刚,李晓雪,曹宇,等.基于作动器故障估计的汽车主动悬架容错控制研究[J].内蒙古大学学报(自然科学版),2016,47(5): 533―541.Gao Zhengang,Li Xiaoxue,Cao Yu,et al.Fault tolerant control of active suspension based on actuator fault estimation [J].Journal of Inner Mongolia University(Natural Science),2016,47(5): 533―541.(in Chinese)
[16] 杨柳青,陈无畏,汪洪波.基于H2/H∞控制的汽车主动悬架最优鲁棒容错控制[J].中国机械工程,2012,23(24): 3013―3019.Yang Liuqing,Chen Wuwei,Wang Hongbo.Optimal robust fault tolerant control for vehicle active suspension system based on H2/H∞ approach [J].China Mechanical Engineering,2012,23(24): 3013―3019.(in Chinese)
[17] 杨柳青,陈无畏.基于传感器信号重构的汽车主动悬架主动容错控制[J].汽车工程,2013,35(12): 1084―1091.Yang Liuqing,Chen Wuwei.Active fault tolerant control of vehicle active suspension based on sensor signal reconstruction [J].Automotive Engineering,2013,35(12): 1084―1091.(in Chinese)
[18] 陈双,钟孝伟.汽车主动悬架作动器故障诊断与控制补偿方法[J].汽车技术,2018(2): 40―44.Chen Shuang,Zhong Xiaowei.Failure diagnosis and control compensation of vehicle active suspension actuator [J].Automobile Technology,2018(2): 40―44.(in Chinese)
[19] Chen M C,Wang W Y,Su S F,et al.Robust T-S fuzzy-neural control of uncertain active suspension systems [J].International Journal of Fuzzy Systems,2010,12(4): 321―329.
[20] 吴忠强,陈金钉,吴云双,等.基于T-S模型的汽车主动悬架H∞控制研究[J].振动与冲击,2007,26(11):64―69.Wu Zhongqiang,Chen Jinding,Wu Yunshuang,et al.H∞control of automotive active suspension based on T-S model [J].Journal of Vibration and Shock,2007,26(11):64―69.(in Chinese)
[21] 朱芳来,蒋鹏,李晓航.基于T-S模糊模型的观测器和动态输出反馈容错控制器设计[J].西安交通大学学报,2016,50(9): 91―96.Zhu Fanglai,Jiang Peng,Li Xiaohang.Design of observer and dynamic output feedback fault tolerant controller based on T-S fuzzy model [J].Journal of Xi’an Jiaotong University,2016,50(9): 91―96.(in Chinese)
[22] 徐光智,孙秀霞,董文瀚,等.非线性系统的自适应输出反馈优化跟踪控制[J].西安交通大学学报,2017,51(1): 128―134.Xu Gaungzhi,Sun Xiuxia,Dong Wenhan,et al.Adaptive output feedback optimal tracking control for nonlinear systems [J].Journal of Xi’an Jiaotong University,2017,51(1): 128―134.(in Chinese)
[23] Li H,Liu H,Gao H,et al.Reliable fuzzy control for active suspension systems with actuator delay and fault[J].IEEE Transactions on Fuzzy Systems,2012,20(2):342―357.
[24] Li H,Liu H,Gao H.Actuator delayed active vehicle suspension control: A T-S fuzzy approach [C].IEEE International Conference on Fuzzy Systems,2011:2358―2363.
[25] Sam Y M,Osman J H S,Ghani M R A.A class of proportional-integral sliding mode control with application to active suspension system [J].Systems and Control Letters,2004,51(3): 217―223.
[26] Chen P C,Huang A C.Adaptive sliding control of non-autonomous active suspension systems with time-varying loadings [J].Journal of Sound and Vibration,2005,282(3): 1119―1135.
[27] Lin J,Lian R J,Huang C N,et al.Enhanced fuzzy sliding mode controller for active suspension systems [J].Mechatronics,2009,19(7): 1178―1190.
[28] Deshpande V S,Mohan B,Shendge P D,et al.Disturbance observer based sliding mode control of active suspension systems [J].Journal of Sound and Vibration,2014,333(11): 2281―2296.
[29] 王威,宋玉玲,王体春,等.非确定因素下汽车半主动悬架的智能控制[J].工程力学,2012,29(9): 337―342.Wang Wei,Song Yuling,Wang Tichun,et al.Intelligent control of automotive semi-active suspension with uncertain factors [J].Engineering Mechanics,2012,29(9): 337―342.(in Chinese)
[30] 张丽萍,弓栋梁.基于H2/H∞控制的汽车主动悬架被动容错控制[J].汽车技术,2017(11): 44―49.Zhang Liping,Gong Dongliang.Passive fault-tolerant control for vehicle active suspension system based on H2/H∞ control [J].Automobile Technology,2017(11):44―49.(in Chinese)
[31] Feng G.A survey on analysis and design of model-based fuzzy control systems [J].IEEE Transactions on Fuzzy Systems,2006,14(5): 676―697.
[32] Choi H D,Ahn C K,Shi P,et al.Dynamic output-feedback dissipative control for T-S fuzzy systems with time-varying input delay and output constraints [J].IEEE Transactions on Fuzzy Systems,2017,25(3):511―526.
[33] Sun W,Pan H,Gao H.Filter-based adaptive vibration control for active vehicle suspensions with electrohydraulic actuators [J].IEEE Transactions on Vehicular Technology,2016,65(6): 4619―4626.
[34] Du H,Zhang N.Fuzzy control for nonlinear uncertain electrohydraulic active suspensions with input constraint[J].IEEE Transactions on Fuzzy Systems,2009,17(2):343―356.
[35] 王威,薛彦冰,宋玉玲,等.基于GA优化控制规则的汽车主动悬架模糊PID控制[J].振动与冲击,2012,31(22): 157―162.Wang Wei,Xue Yanbing,Song Yuling,et al.Fuzzy-PID control strategy for an active suspension based on optimal control laws with genetic algorithm [J].Journal of Vibration and Shock,2012,31(22): 157―162.(in Chinese)
[36] Liu S,Zhou H,Luo X,et al.Adaptive sliding fault tolerant control for nonlinear uncertain active suspension systems [J].Journal of the Franklin Institute,2016,353(1): 180―199.
SLIDING-MODE FAULT TOLERANT CONTROLLER DESIGN FOR VEHICLE ACTIVE SUSPENSION SYSTEMS BASED ON T-S FUZZY MODEL
杨军杰(1993―)，男，山西人，硕士生，从事车辆智能控制研究(E-mail: 1282017468@qq.com).
刘 雪(1994―)，女，陕西人，硕士生，从事车辆智能控制研究(E-mail: 478896783@qq.com).