图1 空气弹簧结构示意图
Fig.1 Sketch of air spring
由于具备优良的减振降噪特性，空气弹簧(如图1所示)，广泛应用于高速铁路、地铁和干线铁路等轨道车辆的二系悬挂系统[1]。空气弹簧在使用过程中，随着刚性上盖和刚性底座在垂直方向的相互运动，其内部压缩空气的压力产生波动，因而提供抵抗振动的反力。空气弹簧上述功能特性通常用垂向刚度来表征，它是空气弹簧最重要的参数之一。
如何在设计阶段精确预测空气弹簧的力学特性，是设计者非常关注的问题。尽管研究者从解析计算的角度提出了很多空气弹簧垂向刚度的计算方法[2－7]，但这些方法仅限于定性分析。而对空气弹簧垂向刚度的准确定量预测，尚需借助有限元法。Berry和Yang[8]基于ABAQUS软件开发了一种气动单元，并使用该单元成功预测了双曲式空气弹簧的等温和绝热过程。Oman和Nagode[9]使用气动单元计算了绝热情况下气囊的受力状态。Dijk等[10]开发了一种基于壳体结构的气体单元，并使用该单元计算了空气弹簧等温过程的结构响应。Sun[11]、Liu等[12]和Wei等[13]均基于等温过程研究了空气弹簧的垂向刚度。可以发现，上述研究要么是基于目前有限元软件隐式算法的等温计算，要么就是基于显式算法的绝热计算，但空气弹簧实际的工作状态通常是多变过程。然而，目前的通用有限元计算软件不提供计算多变过程的空气单元，这也是为何将空气弹簧工作状态视为等温(频率较低时)或绝热(频率较高时)过程的原因之一。当空气弹簧的实际工作状态与等温或绝热过程差别较大时，当前的预测方法就会出现较大的误差[13]。
图1 空气弹簧结构示意图
Fig.1 Sketch of air spring
本文提出了一种适用于空气弹簧多变过程有限元计算的方法。基于ABAQUS的用户子单元UEL编写了用户子程序，实现了基于隐式算法的空气弹簧多变过程有限元计算，并与空气弹簧实验进行了对比。结果表明本文提出的方法可以准确预测空气弹簧的垂向刚度，从而证明了本文方法的有效性。与Li等[14]提出的迭代法相比，本文提出的方法更具通用性。
与固体结构的有限元基础相同，充气结构的有限单元法也可以建立在虚功原理之上。考虑内部气体的作用，充气结构平衡状态的虚功可以表示为
式中：δWstr和δWgas分别表示固体结构和内部气体的虚功。
固体结构的虚功可以表示为：
式中：ε和σ分别为功共轭的应变和应力；Vs为定义在当前构形下的固体结构体积；u为固体结构的位移；δu为u的变分；f为作用于固体结构的体力；t为作用于结构表面Γ的面力。
由式(2)可得固体结构单元刚度矩阵的一般形式：
式中：矩阵Bs表示应变和位移的关系；Ds为结构的弹性矩阵；Ves为结构单元的体积。
作用于结构单元节点上的载荷
可以表示为
式中：等号右边的三项分别表示体力f、边界面力t和初始应力σ0的贡献；N为形函数；Γes为载荷作用的单元表面积。
当不考虑空气弹簧内部空气压力梯度时，封闭腔体内气体的虚功可以表示为
式中：p和Vg分别为封闭腔体气体压力和体积。封闭气体的体积是固体结构位移的函数，式(5)可以表示为：
式中，Bg表示气体体积与结构位移的关系，其定义为：
结合式(6)，可得空气单元的刚度矩阵：
式中，Dg代表气体弹性系数，它可以表示为：
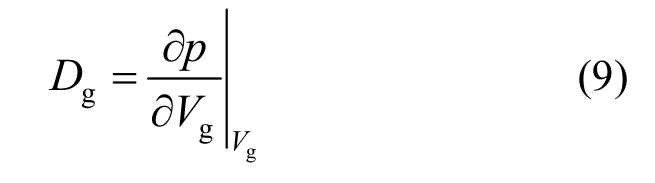
由封闭气体初始压力p0产生的单元节点作用力
可以表示为：
由式(1)，充气结构系统的整体有限元方程可以表示为：
式中，a为所有节点的位移列向量。
考虑理想气体状态方程，气体压力可以表示为：
式中：n为气体的摩尔数；Tg为气体的当前温度；R为通用气体常数。将初始的气体温度T0、压力p0和体积V0代入式(12)，可得当前气体压力的表达式：
将式(13)代入式(9)，可得气体弹性系数：
由式(14)可见气体的弹性系数取决于当前的密封空气体积和温度。
引入多变指数γ[15]，可以将式(12)中的温度消去，即：
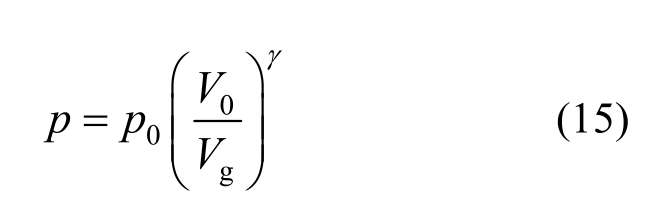
将式(15)代入式(9)，可得多变过程的气体弹性系数：
式中，1.0＜γ＜1.4。由式(16)可见，引入多变指数后，气体弹性系数仅取决于当前的空气体积。对于等温过程，即γ=1，式(16)变为：
对于绝热过程，用比热比κ(对空气来说κ=1.4)代替多变指数γ，式(16)变为：
式(17)和式(18)分别为等温和绝热过程的气体弹性系数。
式(14)和式(16)是两种表示气体弹性系数的方式，式(14)包含温度，因此在求解时必须计算体系的温度场，它的优点是可以考虑环境温度变化对充气结构响应的影响，但通常情况下在充气结构响应时间内环境温度的变化很小，因此可以忽略其变化。但由于需要计算温度场，计算复杂程度增加。而式(16)通过引入多变指数避免了温度场的求解，对有限元求解带来了便利。
本文使用ABAQUS软件的用户自定义单元二次开发程序接口UEL(User Defined Element)[16]进行多变空气单元的开发。通过UEL将充气结构内部压力等效成式(10)所示的单元节点力向量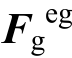
，并将其与式(4)所示结构单元节点力向量
相加，得到整体单元节点力矩阵；将式(8)所示充气结构内部气体的刚度矩阵
与式(3)所示的结构的刚度矩阵
相加，得到整体刚度矩阵。由于本文涉及大变形计算，因此上述节点力向量和刚度矩阵在每个增量步均根据新的节点位移进行更新。空气多变过程气体单元的核心是对式(16)的实施，其关系到式(8)所示充气结构内部气体的刚度矩阵
的定义，本文将多变式(16)中的多变指数γ作为变量，并根据计算工况选择γ的赋值。由于空气弹簧一般为轴对称结构，因此本文只开发了轴对称的多变空气单元UEL子程序，并首先进行了单个单元的隐式算法测试，然后再进行空气弹簧实例验证。关于UEL的变量定义、变量更新和信息传递以及编程规则等详细介绍和开发细节可参考ABAQUS帮助文档，此处不作深入介绍。本文后续的有限元计算均是在ABAQUS有限元软件平台进行。
为了验证所开发的多变空气单元的合理性，本文将计算结果与实验结果进行对比。实验使用由中车青岛四方车辆研究所开发的SYS600型空气弹簧，其相关参数见表1，相关参数的定义见图2。图3是实验照片。
表1 SYS600空气弹簧参数
Table 1 Parameters of SYS600 air spring
符号 描述 数值Ht 空气弹簧工作高度/mm 286 D0 工作高度下空气弹簧有效直径/mm 约600 V1 工作高度下空气弹簧内部体积/L 约22.2 Fz 空气弹簧载荷范围/kN 30～180
针对该空气弹簧，本文开展了两组试验。在第一组试验中，在固定附加气室内容积(选为0 L)和固定垂向静态载荷(选为120 kN)的情况下对空气弹簧施加频率为0 Hz～5 Hz，振幅为5 mm的正弦激励。在第二组实验中，在附加气室内容积为0 L～150 L范围内和垂向静态载荷为30 kN～180 kN范围内对空气弹簧施加频率为0.125 Hz，振幅为10 mm的正弦激励。
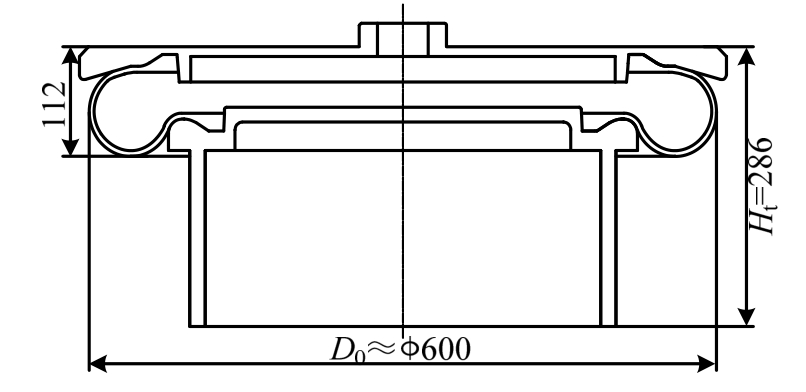
图2 SYS600空气弹簧结构与参数
Fig.2 Structure and parameters of SYS600 air spring
图3 空气弹簧垂向刚度实验
Fig.3 Experiment of vertical stiffness of the air spring
针对上述实验工况，对该空气弹簧使用本文开发的多变空气单元UEL子程序进行了有限元仿真。图4给出了有限元模型中结构部分的网格和单元类型。内部气体的单元类型指定为UEL，其网格与腔体内壁的结构单元共用节点。仿真时，首先对上盖和底座外侧单元节点施加固定约束，并设定腔体内部压力p0，使上盖或底座节点垂向反力之和达到设定值，然后将空气弹簧上盖固定，对底座施加垂向10 mm的位移，得出载荷-位移曲线，从而计算刚度。
图4 有限元模型的网格和单元类型
Fig.4 Mesh and element types of the FEM model
图5为第一组实验与有限元计算的结果对比。可以发现空气弹簧的垂向刚度随频率的增加而增加，在0.005 Hz以下空气弹簧的垂向刚度随频率增加的变化率较小，0.005 Hz到0.060 Hz间变化率较大，而超过0.060 Hz以后变化率又趋向于平缓。这说明：在0.005 Hz以下，空气弹簧的加载过程基本可以视为等温过程，在0.060 Hz以上，空气弹簧的加载过程基本可以视为绝热过程，在0.005 Hz～0.060 Hz之间，空气弹簧的加载过程为变化较大的多变过程。表2列出了具体的刚度数据，在进行有限元计算时根据经验将频率从0 Hz增加到5 Hz对应的多变指数的取值从1增加到1.4，可以发现实验结果与有限元计算结果吻合较好。在表2中的最后一列给出了动态刚度与静态刚度的比值
，根据文献[6－7]可以将
表示为：
式中：p0为空气弹簧指定工作状态的静态表压；pa为大气压力；V0为包含附加气室在内的空气弹簧内部空气总体积；(dA/dx)0定义为指定工作状态时的空气弹簧有效面积变化率，对SYS600空气弹簧来说它为正值。dS/dx表示空气弹簧气囊本体的刚度，尽管它非常小，但也是一个正值。根据式(19)，即使在高频下Cf/C0的值应该始终小于1.4，由表2可见，Cf/C0的值在5 Hz时为1.386，符合上述分析。同时，根据式(19)，可见空气弹簧垂向动态刚度与静态刚度的比值并不等于多变指数γ，因此无法通过对静态刚度的简单修正准确预测不同频率下的动态刚度。第一组实验与有限元计算的结果表明对于某个特定的频率，需要指定一个适当的多变指数从而保证仿真的精度。
图5 第一组实验与有限元结果对比
Fig.5 Comparison between experimental and FEM results of first group
第二组实验是在频率为0.125 Hz下进行的，此时实验过程显然为多变过程，根据第一组实验结果将有限元计算时的多变指数γ设置为1.349。图6给出了第二组实验与有限元计算的结果对比。可以发现，使用本文提出的方法可以精确预测空气弹簧在不同载荷和不同附加气室情况下的全部垂向刚度。第二组的所有实验和计算结果中的最大误差为4.3%，这对设计者在空气弹簧设计阶段预测垂向刚度来说已经足够精确。尽管当附加气室的体积发生变化时，相同频率下对应的多变指数会发生一定的变化，但由本文的计算结果可见，即使采用相同的多变指数，不同附加气室下的计算结果的精度也足够精确。
表2 第一组实验与有限元结果
Table 2 Experimental and FEM results of first group
频率/Hz 实验 仿真垂向刚度/(N/mm) 偏差/(%)γCf /C0 0.000 2074.01 2157.83 1.28 1.000 1.000 0.005 2216.65 2294.28 1.85 1.069 1.069 0.015 2488.42 2553.38 1.28 1.200 1.200 0.038 2720.58 2774.15 1.23 1.312 1.312 0.060 2768.83 2820.01 0.95 1.335 1.335 0.125 2796.26 2846.35 0.72 1.349 1.348 0.300 2816.55 2866.51 0.71 1.359 1.358 1.000 2841.59 2893.99 0.79 1.373 1.370 2.000 2858.32 2915.27 0.76 1.384 1.378 5.000 2874.45 2947.29 0.89 1.400 1.386
图6 第二组实验与有限元结果对比
Fig.6 Comparison between experimental and FEM results of second group
本文提出了一种计算空气弹簧等充气结构多变过程的计算方法，推导了充气结构的有限元方程，通过引入多变指数得到多变过程的气体弹性常数。基于ABAQUS的用户子单元UEL编写了用户子程序，实现了基于隐式算法的空气弹簧多变过程有限元计算，并与空气弹簧实验进行了对比。结果表明本文提出的方法可以准确预测空气弹簧的垂向刚度，从而证明了本文方法的有效性，具有较大的工程应用价值。
[1] 罗仁,曾京.空气弹簧控制的摆式列车动力学仿真研究[J].工程力学,2009,26(3): 240－245.Luo Ren,Zeng Jing.Dynamic simulation of tilting train controlled by air springs [J].Engineering Mechanics,2009,26(3): 240－245.(in Chinese)
[2] Kunieda M.Foundation of air spring [J].Machine Design,1962,6(8): 12－17.
[3] 郭荣生.空气弹簧悬挂的设计与计算[M].青岛: 交通部四方车辆研究所,1973: 50―61.Guo Rongsheng.Design and calculation of air spring suspension [M].Qingdao: Sifang Rolling Stock Research Institute,The Ministry of Communications,1973: 50―61.(in Chinese)
[4] Qing O,Yin S.The non-linear mechanical properties of an air spring [J].Mechanical Systems and Signal Processing,2003,17(3): 705－711.
[5] Prasil L,Kracik V.Frydrych,D.Shape modeling of air bellows springs [J].Vysoke Tatry,Podbanske:Proceedings of Algorithm,2005: 142－149.
[6] Li X,Li T.Research on vertical stiffness of belted air springs [J].Vehicle System Dynamics,2013,51(11):1655－1673.
[7] Li X B,He Y,Liu W Q,et al.Research on vertical stiffness of rolling lobe air spring [J].Journal of Rail and Rapid Transit,2015,230(4): 1172－1183.
[8] Berry D T,Yang H T Y.Formulation and experimental verification of pneumatic and hydraulic finite elements[J].International Journal for Numerical Methods in Engineering,1996,39(7): 1097－1114.
[9] Oman S,Nagode M.On the influence of the cord angle on air-spring fatigue life [J].Engineering Failure Analysis,2013,27(1): 61－73.
[10] Dijk R,Keulen F,Sterk J C.Simulation of closed thin-walled structures partially filled with fluid [J].International Journal of Solids and Structures,2000,37(42): 6063－6083.
[11] Sun J.Calculation of vertical stiffness of air spring with FEM [C]// Greece: 4th ANSA & μETA International Conference,Thessaloniki,Greece: BETA CAE System USA,Inc,2011.
[12] Liu Z H,Li F,Huang Y H.Finite element analysis of vertical stiffness of air spring system [J].Journal of Southwest Jiaotong University,2006,41(6): 700－704.
[13] Wei Y T,Kaliske M,Huang Y J.Advanced mechanics of tire and rubber products,proceedings of 1st Tsinghua Tire Mechanics Workshop [M].Beijing: Tsinghua University Press,2013: 195－238.
[14] Li X B,Wei Y T,He Y.Simulation on polytropic process of air springs [J].Engineering Computations,2016,33(7): 1957－1968.
[15] 朱明善.工程热力学[M].北京: 清华大学出版社,1995: 10－41.Zhu Mingshan.Engineering thermodynamics [M].Beijing: Tsinghua University Press,1995: 10－41.(in Chinese)
[16] Systèmes D.Abaqus theory manual [CP].Dessault Systémes,Providence,RI,2007,1.1.27-1－1.1.27-19.
FINITE ELEMENT MODELLING ON POLYTROPIC PROCESS OF
AIR SPRINGS
李雪冰(1983―)，男，山东人，博士生，主要从事空气弹簧和橡胶构件的研究与开发、橡胶构件的有限元仿真、橡胶材料的本构理论与测试和橡胶材料疲劳研究(E-mail: lixuebing1983@126.com; lxb16@mails.tsinghua.edu.cn);
曹金凤(1978―)，女，山东人，副教授，博士，主要从事橡胶构件的研究与开发，大型复杂结构数值模拟研究(E-mail: caojinfeng@qut.edu.cn).