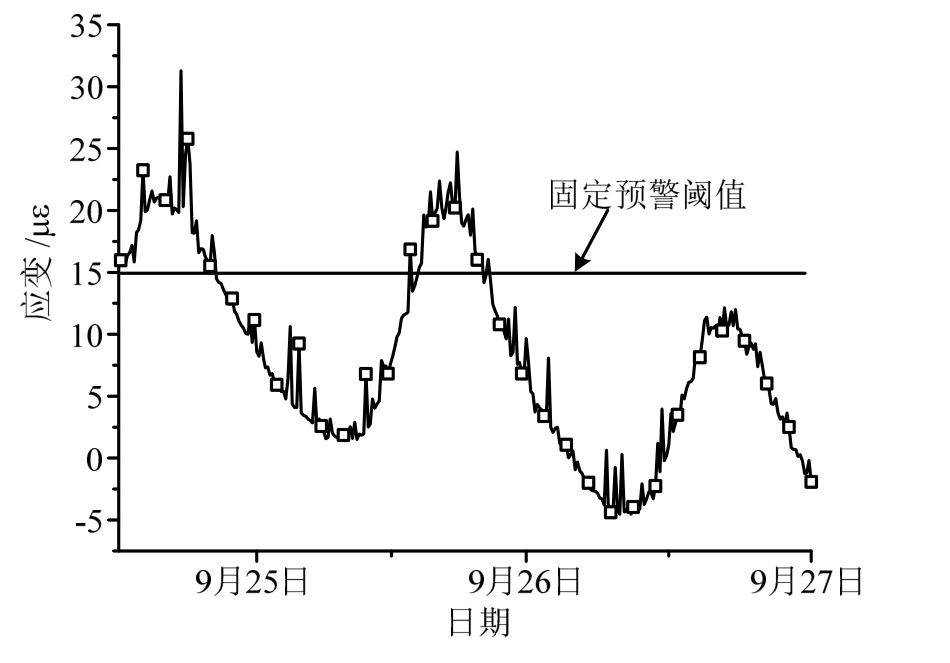
图1 桥梁结构的应变实测曲线
Fig.1 Measured strain curves of bridge
应变是桥梁结构安全监测的重要参数之一。通过应变监测,可以对桥梁结构进行安全预警和状态评估。但桥梁结构各处的应变通常会受到环境因素的影响,其中,温度是影响监测点应变的主要环境因素[1]。温度作用会产生较大的温度应力,导致恒载和车辆活载引起的结构应变信息被掩盖[2―3],同时使得桥梁在线监测系统中预先设置的固定应变预警阈值无法实现有效预警,如图1所示。因此,有必要确定结构应变监测中的温度效应,并将之从实测的总应变中分离,以便进行车辆荷载识别和安全预警;同时可将实时分离出的温度效应加入预先设置的固定应变预警阈值中,实现动态应变预警阈值的设置。
另一方面,由于大跨度桥梁结构监测系统中的传感器数量多,积累了大量的监测数据,在处理和储存这些海量数据时,要求较高的实时性[4―5],因此有必要提出一种简单有效、成本较低的温度效应实时修正方法,以便在监测系统中完成对监测数据的实时处理,及时预警、识别动荷载并进行安全状态评估。

图1 桥梁结构的应变实测曲线
Fig.1 Measured strain curves of bridge
目前,已发展了一些从桥梁结构应变响应中分离出环境温度效应成分的方法。从桥梁结构总应变响应中剔除温度效应成分可视为从时间序列中提取周期趋势项的问题,以此为基础,Bendat等[6]提出ARMA时间序列模型,可根据样本数据对平稳时间序列进行预测,从而提取出周期趋势项;陈夏春、梁宗保等[7―8]提出可以将多元线性回归模型用于提取桥梁结构中的温度效应;对于非平稳信号,由Huang等[9]提出的经验模态分解法(EMD)能够将确定温度应变与周期趋势相关的多阶本征模态函数(IMF)叠加,从而提取出温度效应成分,李苗等[10]将该方法应用于桥梁应变温度效应的提取;考虑到结构监测信号的多尺度特性,刘纲等[11]提出可采用自适应带宽滤波的方法,结合回归统计从监测信号中分离温度效应;Tang等[12]提出可以通过小波分析提取监测信号的变化趋势,涂成枫、吴佰建等[13―14]将小波分析用于提取应变监测数据中的温度效应成分。
但对于工程应用而言,已有方法的模型和操作步骤过于复杂,计算过程较为繁琐,不能简便有效地在实际监测系统中完成对监测数据的实时处理。为解决此问题,本文提出了一种桥梁在线监测数据中实时提取应变监测值中的温度效应的处理方法,有效分离了应变响应中的温度效应,并通过对实际桥梁的应变实测数据的处理,建立了动态应变预警阈值,进行了桥梁结构动荷载的识别。
合肥某斜拉桥位于合肥市内,桥长764.5 m,宽40.5 m,主桥跨径120 m+160 m,为独塔双索面塔梁墩固结体系斜拉桥,主梁为预应力混凝土双边箱梁。
主跨桥梁结构安装了在线安全监测系统,包括温度、应变、竖向挠度、加速度、索力等传感器。由于监测传感器均为桥梁投入使用一段时间后安装,传感器实测数据中不包含桥梁自重及混凝土早期收缩徐变等效应的影响,主要监测桥梁结构在正常使用条件下,在温度效应、车辆荷载等荷载或作用下的响应以及由于材料劣化或结构损伤等产生的变化。基于结构有限元模型分析,主桥应变传感器布设于靠近跨中与靠近塔柱的箱梁上与主塔的塔柱上,采用电阻式应变传感器,采样频率为9 Hz;主桥温度传感器布设于跨中(与跨中应变测点在同一截面),采用热电偶传感器,通过打孔方式安装在箱梁混凝土内,每隔10 min采样1次。主桥结构上的应变及温度传感器布置如图2所示。同时,为了测量主桥桥塔的温度变化,在桥塔靠近桥面一定高度装有4个温度传感器与应变传感器。
该斜拉桥主桥箱梁温度传感器分别布置在东西两跨跨中的南北两箱的上中下三个截面上(图2),其中T1及T6、T7及T12位于跨中截面箱梁外部的桥面上,T2、T4、T8及T10位于跨中截面箱梁的顶面内部,T3、T5、T9及T11位于跨中截面箱梁的底面内部。因各传感器所处位置不同,受日晒及温度变化的影响也均不同。取2016年9月25日至9月27日共3日中的实测温度数据进行统计,对主桥结构的温度分布进行分析。
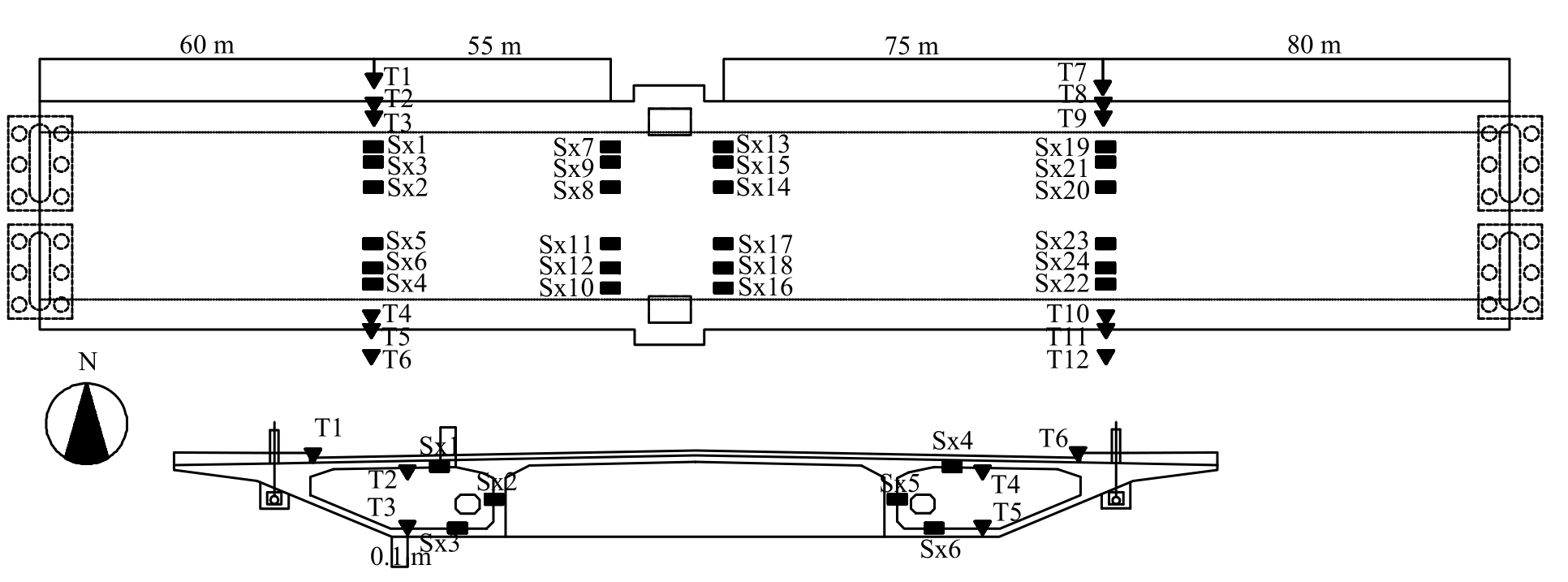
图2 应变及温度传感器布置示意图
Fig.2 Locations of strain and temperature sensors
1.1.1 同一截面实测温度的统计分析
图3给出了该斜拉桥西跨跨中截面南侧箱梁各测点在3日中的温度变化曲线。可以看出:1) 箱梁外部顶板由于直接受到日照作用,其实测温度(T6)变化幅值明显大于箱内测点,同时箱内顶板测点(T4)的温度变化幅值大于底板测点;2) 箱内测点的温度变化相对于箱梁外部顶板测点的温度变化具有明显的时间滞后效应。
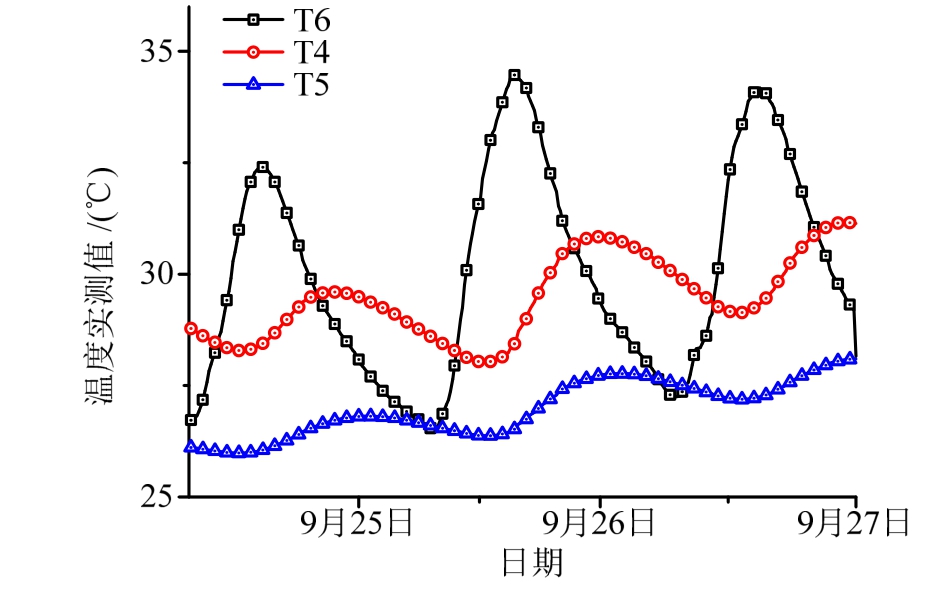
图3 主桥西跨南箱测点的温度实测曲线
Fig.3 Measured temperature curves of the south box of the west span of the bridge
1.1.2 箱梁外部顶板温度沿横向分布的统计分析
图4为该斜拉桥主桥西跨主梁外部顶板温度传感器实测的温度变化曲线。可以看出:1) 在两个截面上,南侧箱梁外部顶板测点(T6)的温度最大值和昼夜温差变化均大于北侧箱梁顶板测点(T1)处的结果,这是由于正午时太阳在南方,南侧箱梁的外部顶板测点受日晒影响大;2) 由于混凝土内热传导需要时间,因此箱梁外部顶面的温度变化趋势与大气温度的变化相比略有滞后,实测温度最大值在每天16时左右出现。
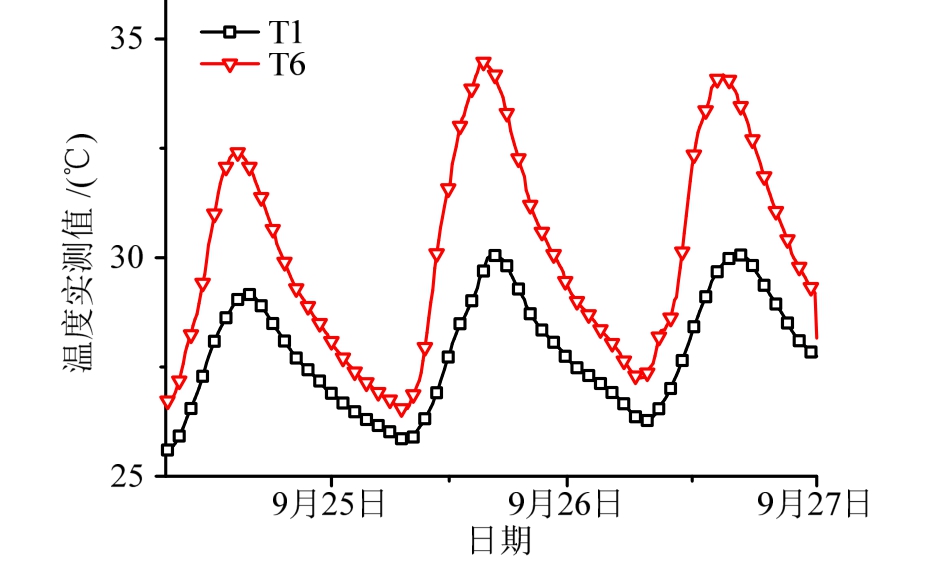
图4 主桥西跨箱梁外部顶板测点的温度实测曲线
Fig.4 Measured temperature curves of outer top plate of the west span of the bridge
1.1.3 箱内顶、底板温度沿横向分布的统计分析
图5给出了3日内该斜拉桥主桥西跨跨中主梁截面处箱内顶板测点(T2及T4)及底板测点(T3及T5)的温度变化曲线。可以看出:1) 沿桥横向方向,箱内顶板及底板测点的温度最大值和昼夜温差变化规律基本一致;2) 箱内顶板及底板测点达到温度最大值的时刻基本一致,与大气温度的变化相比滞后明显,最大值在23时左右出现。

图5 主桥西跨箱内顶、底板测点的温度实测曲线
Fig.5 Measured temperature curves of inner top and bottom plate of the west span of the bridge
1.1.4 实测温度沿桥长方向分布的统计分析
图6给出了沿该斜拉桥跨度方向南侧箱梁各测点温度传感器(T4~T6、T11~T12)在这3日中的温度变化曲线。可以看出,沿桥长方向,处于箱梁截面对应位置的温度测点的温度变化基本一致。
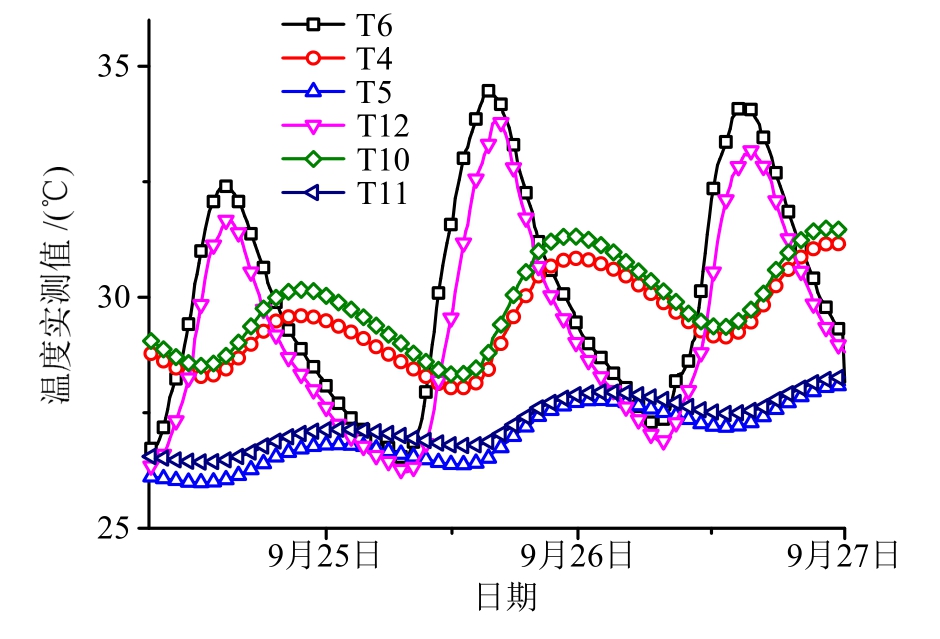
图6 沿桥长方向南箱各测点的温度实测曲线
Fig.6 Measured temperature curves of the south box along the length of the bridge
上述实测结果分析可以看出:沿桥长方向,桥梁的温度分布基本一致;沿桥宽方向,箱外测点实测温度之间有所差异,箱内实测温度分布变化规律基本一致;在同一截面箱梁的箱内及箱外、箱内顶板与底板测点之间的温度分布存在较大差异。因此,在设计钢筋混凝土箱型截面主桥结构的温度传感器布设时,可只在一个截面布置测点,该截面需监测左右两侧的箱梁外顶板、一侧箱梁内部上、中、下三个位置共五个测点处的温度。
桥梁结构的监测应变受多种因素的影响,实测结果是多因素共同作用下的结果,难以直接反应出桥梁结构在车辆荷载作用下的实际应力分布及内部受力情况。在这些影响因素中,温度是影响桥梁结构监测应变响应的主要环境因素。根据工程经验,总应变响应中的温度效应部分与各温度作用之间具有较强的线性关系,如图7所示,可用多元线性回归模型进行模拟和预测[8]。
1.2.1 温度作用自变量的确定
根据上述对该斜拉桥主桥结构温度效应分布的分析,将多元线性回归模型中的温度作用自变量设置如下:将测点温度T1、主梁日照温差T2及主塔日照温差T3作为自变量,进行多元线性回归模型的建立[8]。
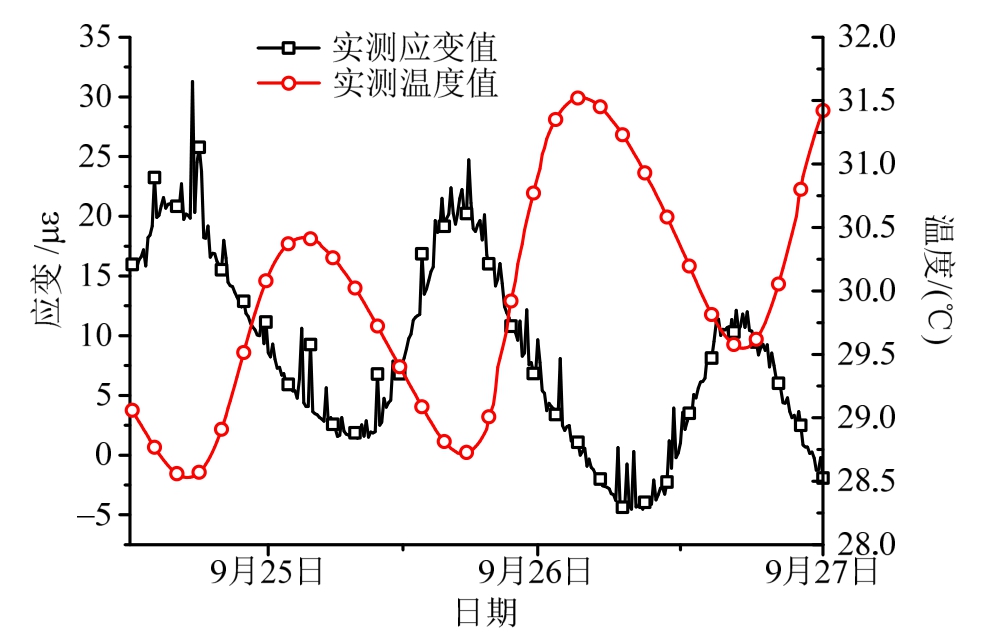
图7 桥梁结构中应变与温度之间的线性关系
Fig.7 The linear relationship of temperature and strain in the bridge
在计算各温度作用自变量的数值时:1) 在确定测点温度T1时,对于位于箱内顶板的应变测点,根据所处南北箱的不同,分别以对应的沿桥长方向的箱内顶板测点的温度平均值作为其代表值;对位于箱内底板的应变测点,根据所处的南北箱不同,分别以对应的沿桥长方向的箱内底板测点的温度平均值作为其代表值;对于位于箱内中截面的应变测点,根据所处的南北箱的不同,分别以对应的沿桥长方向的箱内顶、底板测点温度的平均值作为其代表值;2) 在确定主梁日照温差T2时,根据所处的南北箱的不同,分别以对应的沿桥长方向的箱梁外部顶板测点的温度平均值与底板测点的温度平均值之差作为其代表值;3) 在确定主塔日照温差T3时,根据所处的南北箱的不同,分布以对应方向的主塔东西两侧测点的温度实测值之差作为其代表值。
1.2.2 回归模型参数的确定及计算结果
取该斜拉桥东西两跨响应较大的跨中测点Sx1~S6、Sx19~S24这12个测点的应变S作为因变量,分别建立多元线性回归模型,见式(1):
其中:b及ai(i = 1,2,3)为多元线性模型中的回归参数,S为测点处监测应变响应,单位为με;Ti(i = 1,2,3)为各温度作用,单位为℃;tdi(i = 1,2,… ,n)为测点应变相对于各温度作用的滞后时间,采用对应变监测值与相应温度作用作相关分析计算得出,单位为10 min。
得到多元线性回归模型后,可利用多元判定系数R2来测定多元线性回归的拟合度程度。对于回归拟合而言,R2越接近1,则该回归拟合程度越高。
取2016年9月25日至9月27日三天内该斜拉桥的测量数据进行分析,计算得出各测点应变因变量与温度作用自变量之间的回归模型表达式如表1所示。
表1 主桥跨中各测点的回归模型表达式
Table 1 Multiple linear regressions of strain monitoring in mid-span sections
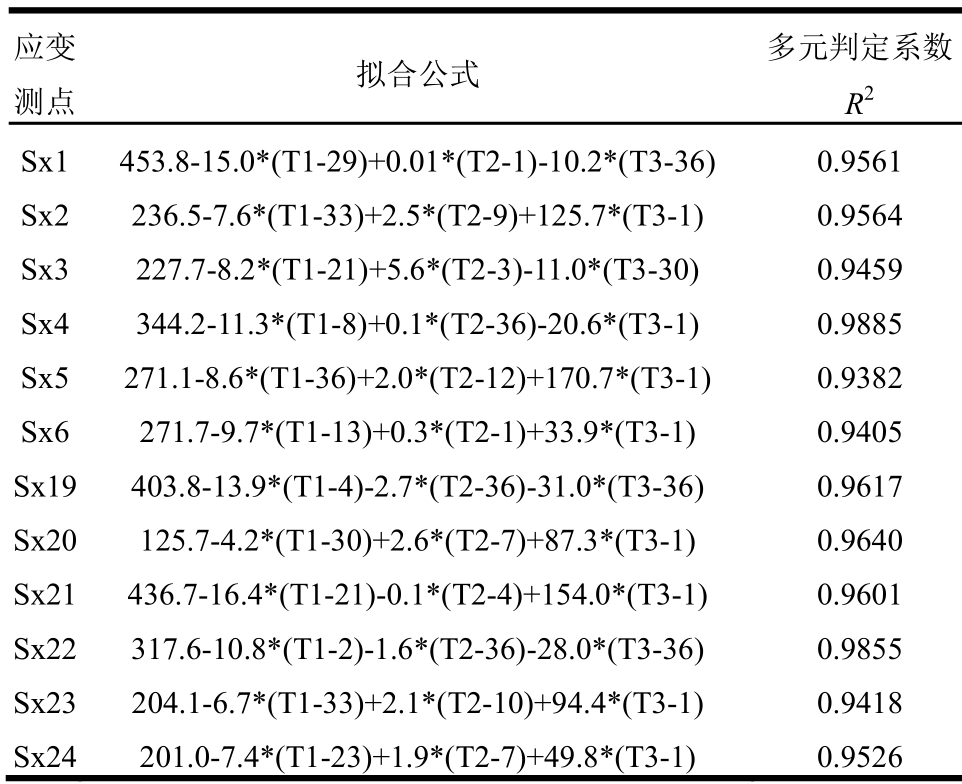
注:其中滞后效应的单位为10 min。
应变测点 拟合公式 多元判定系数R2 Sx1 453.8-15.0*(T1-29)+0.01*(T2-1)-10.2*(T3-36) 0.9561 Sx2 236.5-7.6*(T1-33)+2.5*(T2-9)+125.7*(T3-1) 0.9564 Sx3 227.7-8.2*(T1-21)+5.6*(T2-3)-11.0*(T3-30) 0.9459 Sx4 344.2-11.3*(T1-8)+0.1*(T2-36)-20.6*(T3-1) 0.9885 Sx5 271.1-8.6*(T1-36)+2.0*(T2-12)+170.7*(T3-1) 0.9382 Sx6 271.7-9.7*(T1-13)+0.3*(T2-1)+33.9*(T3-1) 0.9405 Sx19 403.8-13.9*(T1-4)-2.7*(T2-36)-31.0*(T3-36) 0.9617 Sx20 125.7-4.2*(T1-30)+2.6*(T2-7)+87.3*(T3-1) 0.9640 Sx21 436.7-16.4*(T1-21)-0.1*(T2-4)+154.0*(T3-1) 0.9601 Sx22 317.6-10.8*(T1-2)-1.6*(T2-36)-28.0*(T3-36) 0.9855 Sx23 204.1-6.7*(T1-33)+2.1*(T2-10)+94.4*(T3-1) 0.9418 Sx24 201.0-7.4*(T1-23)+1.9*(T2-7)+49.8*(T3-1) 0.9526
以测点Sx24为例,其模型拟合效果如图8所示,多元判定系数R2为0.9526,表明拟合优度高,测点应变与各温度作用之间的线性关系显著。同时可以看出,温度作用引起的应变变化较大,会导致车辆荷载引起的结构应变信息被掩盖,使预先设置的固定应变预警阈值无法有效预警。因此,在桥梁安全监测系统中必须从桥梁结构总应变响应中实时分离温度效应成分,以便实现动态预警,进行实时车辆荷载识别,并及时评估结构的安全状况。
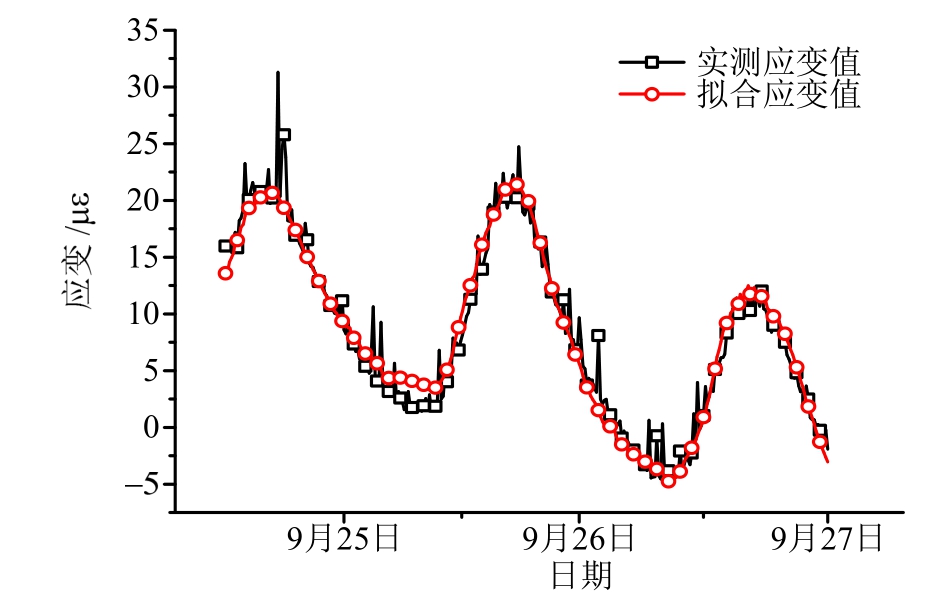
图8 测点Sx24的多元线性回归拟合结果
Fig.8 Results of multiple linear regression of Sx24
由于桥梁在线健康监测系统中对应变的采样频率较高,监测系统中需要实时储存和处理的数据量巨大,因此,如何在应变监测结果中实时剔除温度效应至关重要。但对于工程实践而言,已有方法的模型和操作步骤过于复杂,计算过程较为繁琐,不能简便有效地在线完成对监测数据的实时处理。因此有必要提出一种简单有效、成本较低的温度效应实时修正方法。
应变传感器在安装后均进行过初始值归零处理,车辆荷载等影响结束后,实测应变值会回到初始值附近。由于温度对应变的影响,实测应变数据中存在“零偏”现象,且随气温变化发生波动。在较短的一个时段内,外界温度不会发生过大的变化,因此,可假设此时段内所有应变监测数据点均较零值偏移了同一个值A[15]。图9所示为该斜拉桥位于东跨跨中南箱底部的应变测点Sx24在15 min时间段内的应变实测值,可见在15 min这一较短时间段内,应变监测曲线由于温度作用的影响而发生了整体偏移。由于外界荷载的作用是随机的,因此该时间段中的所有应变监测数据点应围绕A值波动,且由于应变指标的采样频率高(9 Hz),该历史时间段内采集的监测数据量足够多,因此可认为该历史时间段内所有应变监测数据的平均值Sa即为当前时刻的偏移值A,亦即为当前时刻应变监测数据中的温度效应值。

图9 测点Sx24在15 min时间段内的实测应变值
Fig.9 Measured strain curve of Sx24 in 15 minutes
时变平均值方法的操作步骤如下:
1) 每隔一段时间T,根据之前T时间段内的高频采样指标的实测数据,计算指标监测值的平均值Sa,见式(2)。
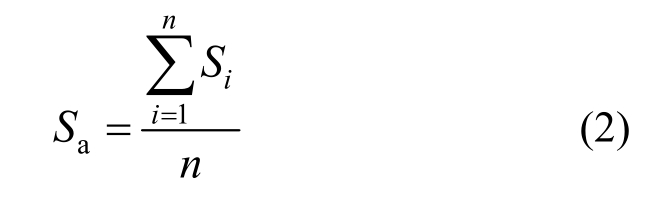
式中:Si为上一个T时间段中所测得的指标监测值。i为采样点号,n为采样点总数。该平均值Sa即为应用于当前时间段的该指标的温度效应值。
2) 从当前时刻的指标监测值S中减去该平均值Sa,公式如式(3):
由此,可实时从实测指标监测值中将温度效应分离,得到由活荷载单独引起的指标响应SΔ 。
3) 在当前T时间段结束后,根据当前T时间段中的应变实测数据,计算监测值的平均值,作为下一个T时间段的温度效应,之后以此类推。
该平均值方法计算量小,效率较高,能够简单有效地实现桥梁在线安全监测系统中实时剔除温度效应对应变监测数据的影响,用于后续的桥梁安全预警和状态评估。
在上述方法中,计算实测数据平均值所采用的时长T的选取至关重要。若T选取过短,则可能出现数据量不够、其平均值无法准确反映温度效应的情况;若T选取过长,则可能出现在该时间段内温度变化较大,其平均值无法准确反映当前时刻的温度效应的情况。因此,需要通过分析来确定一个合适的时长。
首先,使用滤波法得出温度效应计算结果,将其作为基准值,再将采用不同计算时长的平均值法计算结果与其比较,从而确定出最合理的计算时长。
在滤波法中,最重要的是截止频率合理选取。根据已有研究[11―12]得出温度效应产生的慢变部分与动荷载产生的快变成分之间的截止频率约为0.001 Hz~0.003 Hz。以此为基础,采用0.002 Hz作为截止频率,对应变时程进行分离,分离出由温度效应引起的慢变部分及由动荷载引起的应变响应快变部分。
在使用频域法得出温度效应计算结果后,将去除温度效应后的剩余应变作为基准值,之后对同样的原始监测数据应用时变平均值法,并采用不同的计算时长(15 min、10min、7 min、5 min及3 min)。将采用不同计算时长得出的剩余应变结果与基准值进行比较,结果如表2与表3所示。可以看出,当采用平均值计算时长为7 min时,其计算结果与低通滤波法所得出的基准值的均方误差较小,相关系数较高,因此可确定平均值法的计算时长取为7 min,即采取前7 min的应变监测值的平均值作为当前的温度效应值,每隔7 min更新一次。
表2 采用不同时长的计算结果与基准值间的均方误差比较
Table 2 Mean square errors between the results of different computing time ranges and the reference value
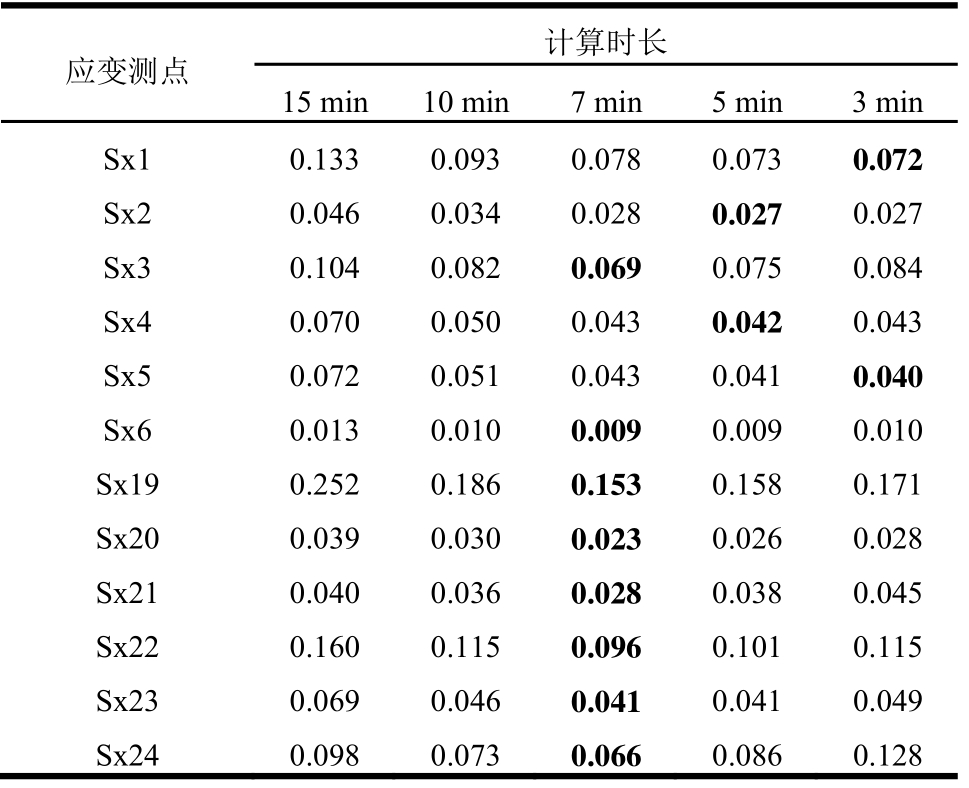
应变测点 计算时长15 min 10 min 7 min 5 min 3 min Sx1 0.133 0.093 0.078 0.073 0.072 Sx2 0.046 0.034 0.028 0.027 0.027 Sx3 0.104 0.082 0.069 0.075 0.084 Sx4 0.070 0.050 0.043 0.042 0.043 Sx5 0.072 0.051 0.043 0.041 0.040 Sx6 0.013 0.010 0.009 0.009 0.010 Sx19 0.252 0.186 0.153 0.158 0.171 Sx20 0.039 0.030 0.023 0.026 0.028 Sx21 0.040 0.036 0.028 0.038 0.045 Sx22 0.160 0.115 0.096 0.101 0.115 Sx23 0.069 0.046 0.041 0.041 0.049 Sx24 0.098 0.073 0.066 0.086 0.128
表3 采用不同时长的计算结果与基准值间的相关系数比较
Table 3 Correlation coefficients between the results of different computing time ranges and the reference value
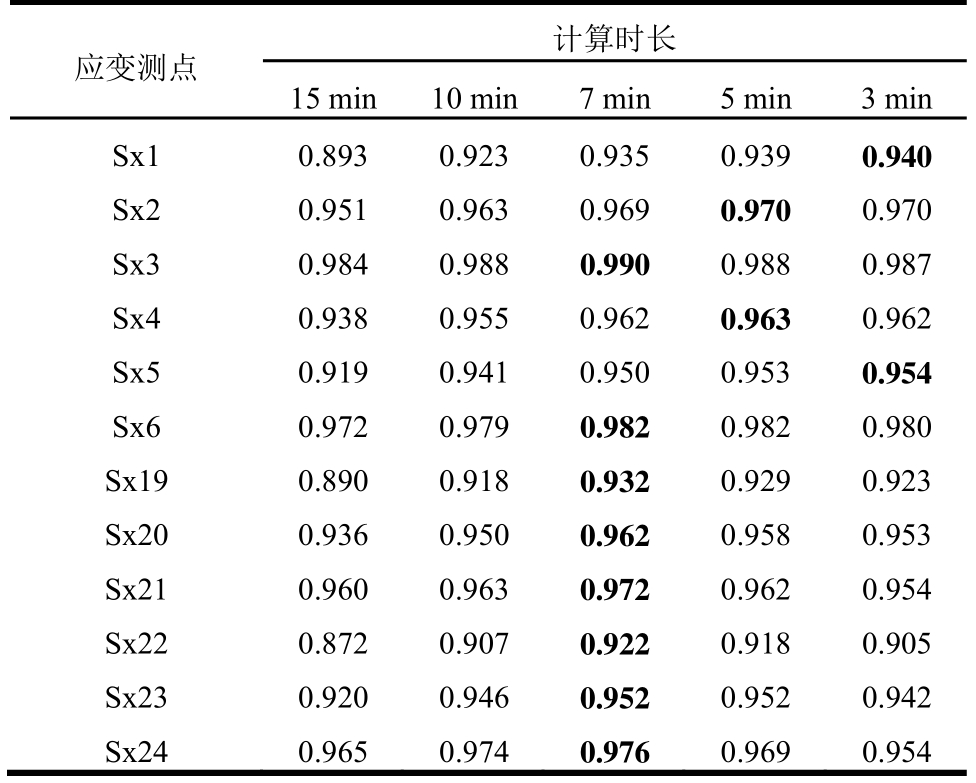
应变测点 计算时长15 min 10 min 7 min 5 min 3 min Sx1 0.893 0.923 0.935 0.939 0.940 Sx2 0.951 0.963 0.969 0.970 0.970 Sx3 0.984 0.988 0.990 0.988 0.987 Sx4 0.938 0.955 0.962 0.963 0.962 Sx5 0.919 0.941 0.950 0.953 0.954 Sx6 0.972 0.979 0.982 0.982 0.980 Sx19 0.890 0.918 0.932 0.929 0.923 Sx20 0.936 0.950 0.962 0.958 0.953 Sx21 0.960 0.963 0.972 0.962 0.954 Sx22 0.872 0.907 0.922 0.918 0.905 Sx23 0.920 0.946 0.952 0.952 0.942 Sx24 0.965 0.974 0.976 0.969 0.954
在应用平均值法得到各测点实测应变值中的温度效应部分后,将总应变实测值与其相减,即可将温度效应分离,得到的剩余应变可认为是单独由动荷载产生的应变响应。以该斜拉桥东跨跨中南箱截面的三个应变测点Sx22~Sx24为例,对去除温度效应后同一截面的各测点由动荷载产生的应变响应进行比较。选择应变响应较大的一个时段,即该桥2016年9月25日17∶28∶00~17∶43∶00的15 min监测数据进行比较分析,结果如图10所示。
可以看出,同一截面的上、中、下三个测点的应变值基本符合平截面假定,同时达到极值且大小之间基本成比例,在车辆荷载作用下该截面产生正向弯矩,位于顶板的Sx22应变响应为负向最大,位于中截面的Sx23应变响应为较小的正向值,位于底板的Sx24应变响应为正向最大。
将分离出的温度效应叠加预先设置的固定应变预警阈值,可得到随温度变化的动态应变预警阈值,结果如图11所示,由此,可以实现对考虑温度效应的实测应变值进行有效预警。
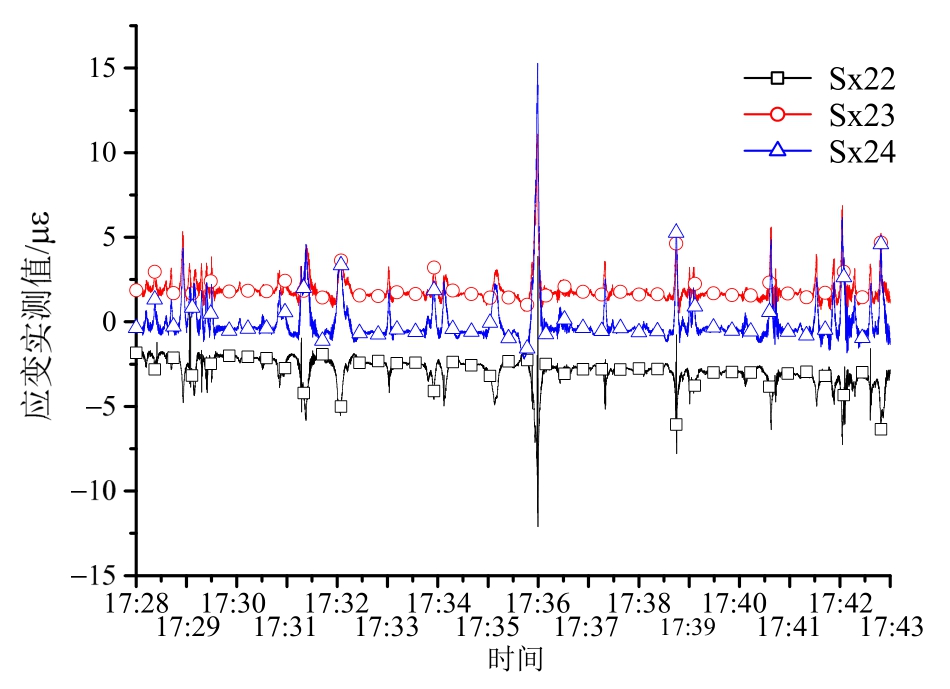
图10 15 min内的剩余应变比较
Fig.10 Residual strain variations within 15 min
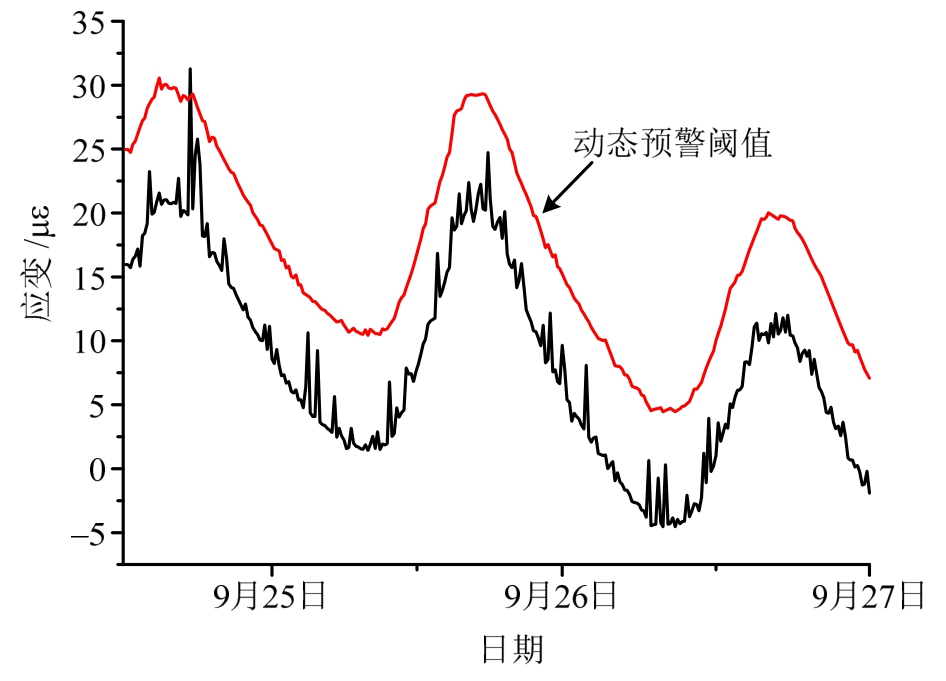
图11 动态预警阈值
Fig.11 Dynamic early-warning index
近年来,车辆超载已经成为造成我国桥梁结构损伤的一大重要原因。因此,对桥梁上通行的超载超速车辆进行监测和统计分析,对于评估桥梁结构安全状态与疲劳损伤意义重大,但传统上用来监测车辆的重量和速度的动态称重系统设备成本较高,且安装较为复杂,因此,若能通过安装于桥梁结构上的应变传感器的动态监测数据对超载超速车辆进行预警和统计,则能够以较低的成本,可靠易行地进行对车辆荷载的统计与分析评估。
由于经过时变平均值方法处理后的测点应变是由桥梁结构上的车辆荷载产生的,因此可利用分离温度效应后的各测点应变监测值,进行动荷载的识别及预警。
3.1.1 应变与动挠度监测值的比较
为了确认经过平均值法去除温度效应后的测点剩余应变值能否准确反映监测时间内的动荷载,下面将布置位置相同的应变测点Sx24及动挠度测点Dt2在同一时间段内的监测值进行比较。
取相同的15 min时间段(17∶28∶00~17∶43∶00),将布置于该斜拉桥东跨跨中南箱底板的动挠度测点Dt2与应变测点Sx24在此期间的去除温度效应的响应进行比较,结果如图12所示。由图中可见,动应变及动挠度在相同时刻达到极值,可见应用平均值方法准确地排除了应变监测数据中的温度效应,经处理后的应变值是由动荷载产生的。
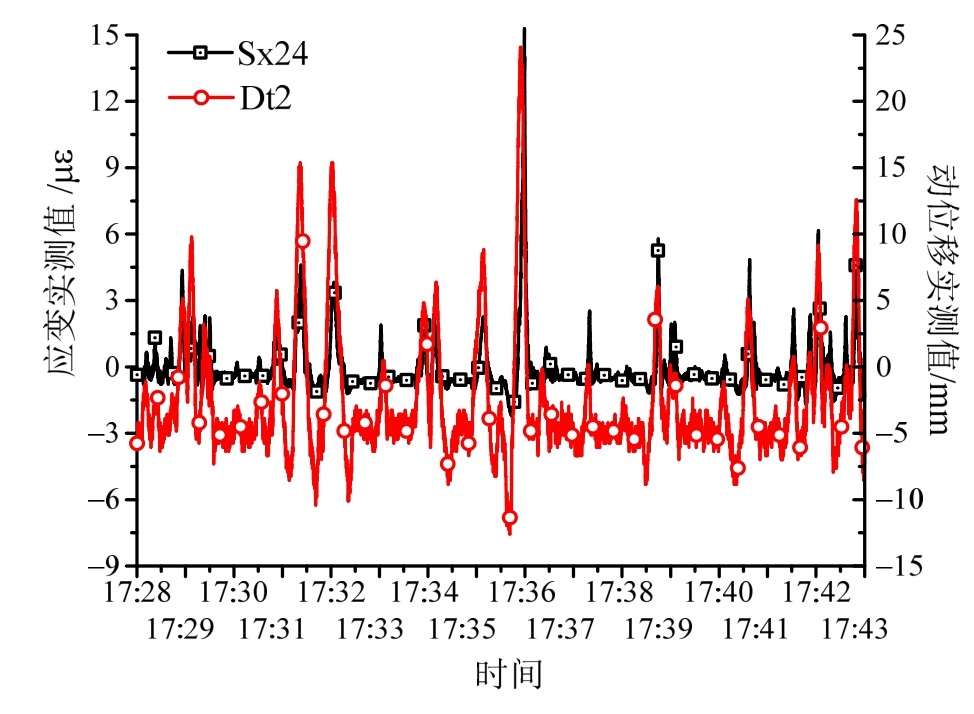
图12 剩余应变与动挠度测量值比较
Fig.12 Compare of strains and dynamic deflections
3.1.2 利用应变监测值进行动荷载识别
该斜拉桥未安装动态地磅系统。由于经过平均值方法处理后的测点应变是由桥梁结构上作用的车辆荷载产生的,因此可以利用分离温度效应后各测点的应变监测值,进行重车动荷载的识别。
1) 重车车辆速度识别
当重车经过桥梁时,沿桥长方向各应变测点去除温度效应后的的剩余应变值依次达到极值,因此可以通过找出沿桥长方向布置于不同位置应变测点达到动应变监测峰值的采样时间之差,结合应变测点间的距离估计重车荷载的移动速度,结果如图13所示。位于该斜拉桥西跨跨中的Sx6与东跨跨中的Sx24两测点在17∶36时刻依次达到极大值,二者达到峰值点的时间差约15 s,二者之间距离为140 m,由此可推算出该时段行驶的重车荷载时速约为34 km/h。

图13 车辆荷载速度识别
Fig.13 Identification of load speed
2) 可进行过桥车辆数目识别
采用统计各测点剩余应变监测值中超过一定阈值的极值数量的方式实现对一定时间内通过桥梁车辆数目的识别[13]。找出动应变时程曲线中的所有超过一定阈值的极值点的数目,由于经过处理后的动应变时程存在误差,可能存在波动,因此应合理设置阈值μ,凡大于阈值的极值点才被统计[12],如图14所示。取阈值为1 με,在Sx24的应变时程中,统计得到超过1 με阈值的极大值点为59个,即可粗略估计2016年9月25日17∶28∶00~17∶43∶00的15 min中,有约59辆车通过该桥,在该测点产生的拉应变超过1 με。根据相应时间段的监控录像,数出15 min内过桥车辆数目为61,验证了该方法的有效性。
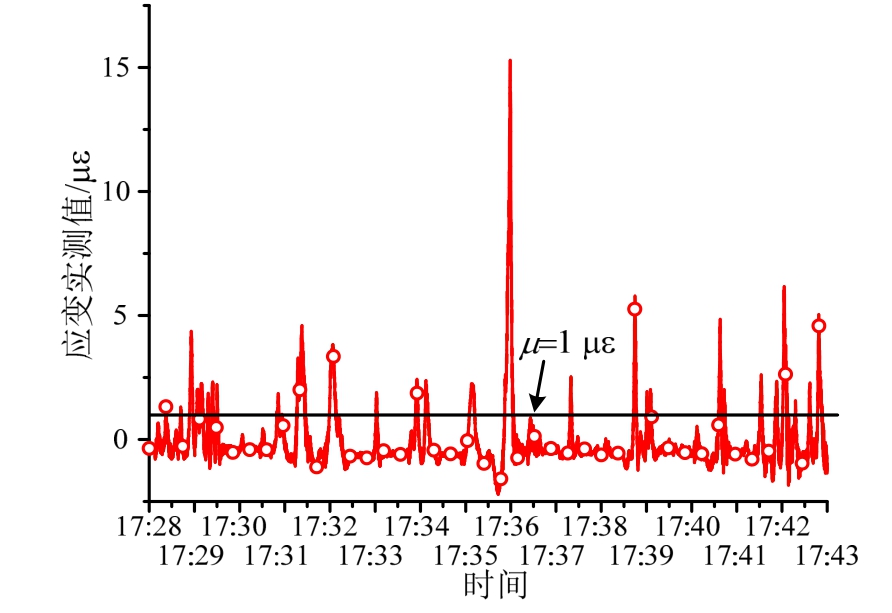
图14 车辆荷载数目识别
Fig.14 Identification of load numbers
3) 可进行车辆荷载超载超速判断
动荷载作用在桥梁结构上所产生的不同位置测点的动应变极值与车速、车重之间存在着一定的对应关系。可通过建立有限元模型,得出限速及限重车辆通过时各测点的应变响应最大值μ,凡有效应变超过此阈值说明有超载超速车辆过桥,可发出提醒警告。以该斜拉桥为例,通过有限元模拟计算,得出在Sx24位置处,重量为55 t、速度为60 km/h的重车通过所产生的应变响应为10 με,因此,从修正的实测应变结果可以得出,在2016年9月25日17∶28∶00~17∶43∶00的15 min中,有一辆超重车辆通过,如图15所示。根据相应时刻的监控录像,发现在17∶35左右有一超载的6轴重型车辆通过桥梁东跨跨中,验证了该方法的有效性。
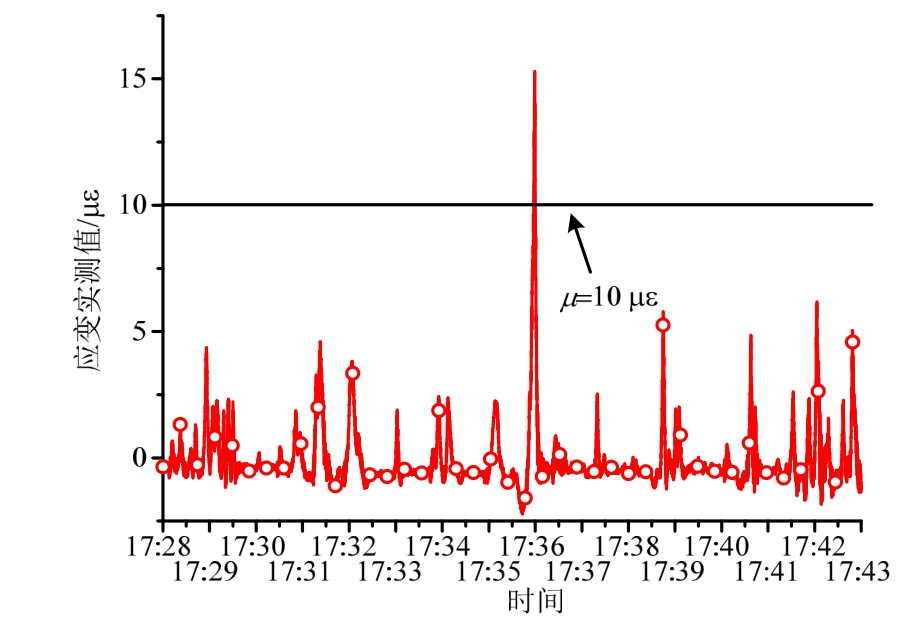
图15 超载超速车辆识别
Fig.15 Identification of overloaded/overspeed vehicles
基于合肥某斜拉桥在线监测系统实测的温度及应变监测数据,分析结果表明:
(1) 根据该桥梁结构中的温度监测结果,可得出箱梁桥温度传感器的优化布设方案:可仅在一个截面布点,该截面需监测左右两侧的箱梁外顶板、一侧的箱梁内部上中下三个位置,共五个测点的温度。
(2) 实测桥梁中的应变监测值与温度作用之间具有明显的线性关系,且温度作用引起的应变温度效应极大,会导致荷载引起的结构应变信息被掩盖。
(3) 通过选取合适的计算时长,采用平均值法可简单有效地实现对应变监测中温度效应的实时剔除,对该斜拉桥建议计算时长选取为7 min。
(4) 进行温度效应分离后,实测应变数据可用于识别过桥车辆的速度、数目,及对超载超速车辆进行预警。
[1] 陈波,郑瑾,王建平.桥梁结构温度效应研究进展[J].武汉理工大学学报,2010,32(24): 79―83.Chen Bo,Zheng Jin,Wang Jianping.State-of-the-art of the temperature effects of bridges [J].Journal of Wuhan University of Technology,2010,32(24): 79―83.(in Chinese)
[2] 王高新,丁幼亮,李爱群,等.基于长期监测数据的润扬大桥斜拉桥钢箱梁横向温差特性研究[J].工程力学,2013,30(1): 163―167.Wang Gaoxin,Ding Youliang,Li Aiqun,et al.Characteristics of transverse temperature differences of steel box girder in runyang cable-stayed bridge using long-term monitoring [J].Engineering Mechanics,2013,30(1): 163―167.(in Chinese)
[3] Ni Y Q,Fan K Q,Zheng G,et al.Automatic modal identification and variability in measured modal vectors of a cable-stayed bridge [J].Structural Engineering and Mechanics,2005,19(2): 123―139.
[4] 李惠,鲍跃全,李顺龙,等.结构健康监测数据科学与工程[J].工程力学,2015,32(8): 1―7.Li Hui,Bao Yuequan,Li Shunlong,et al.Data science and engineering for structural health monitoring [J].Engineering Mechanics,2015,32(8): 1―7.(in Chinese)
[5] 周文松,李惠,欧进萍,等.大型桥梁健康监测系统的数据采集子系统设计方法[J].公路交通科技,2006,23(3): 83―87.Zhou Wensong,Li Hui,Ou Jinping,et al.Design method of data acquisition system of health monitoring systems for long span bridges [J].Journal of Highway and Transportation Research and Development,2006,23(3):83―87.(in Chinese)
[6] Bendat J S,Piersol A G.Random data: Analysis and measurement procedures [M].New York: Wiley,2000:396―398.
[7] 梁宗保,陈伟民,符玉梅,等.混凝土桥梁结构应变监测的温度效应分离方法研究[J].混凝土,2005(12): 3―5.Liang Zongbao,Chen Weimin,Fu Yumei,et al.Method for separating by temperature effect from strain monitoring of concrete bridge structure [J].Concrete,2005(12): 3―5.(in Chinese)
[8] 陈夏春,陈德伟.多元线性回归在桥梁应变监测温度效应分析中的应用[J].结构工程师,2011,27(2): 120―126.Chen Xiachun,Chen Dewei.Application of multiple linear regression model in analysis of temperature effect on strain monitoring for bridge structures [J].Structural Engineers,2011,27(2): 120―126.(in Chinese)
[9] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proceeding of the Royal Society of London A: Mathematical,Physical and Engineering Sciences,1998,454: 903―995.
[10] 李苗,任伟新,黄天立,等.基于EMD与IMF能量的桥梁应变温度效应成分的提取[J].公路交通科技,2015,32(7): 62―68.Li Miao,Ren Weixin,Huang Tianli,et al.Extraction of bridge strain temperature effect based on EMD and IMF energy [J].Journal of Highway and Transportation Research and Development,2015,32(7): 62―68.(in Chinese)
[11] 刘纲,邵毅敏,黄宗明,等.长期监测中结构温度效应分离的一种新方法[J].工程力学,2010,27(3): 55―61.Liu Gang,Shao Yimin,Huang Zongming,et al.A new method to separate temperature effect from long-term structural health monitoring data [J].Engineering Mechanics,2010,27(3): 55―61.(in Chinese)
[12] Tang L,Liu Z,Jiang B,et al.Features of long-term health monitored strains of a bridge with wavelet packet analysis [J].Theoretical and Applied Mechanics Letters,2011,1(5): 27―30.
[13] 涂成枫,刘泽佳,张舸,等.面向桥梁长期健康监测的大数据处理技术及应用[J].实验力学,2017,32(5):652―663.Tu Chengfeng,Liu Zejia,Zhang Ge,et al.Processing technique and application of big data oriented to long-term bridge health monitoring [J].Journal of Experimental Mechanics,2017,32(5): 652―663.(in Chinese)
[14] 吴佰建,李兆霞,王滢,等.桥梁结构动态应变监测信息的分离与提取[J].东南大学学报自然科学版,2008,38(5): 767―773.Wu Baijian,Li Zhaoxia,Wang Ying,et al.Separation and extraction of bridge dynamic strain data [J].Journal of Southeast University (Natural Science Edition),2008,38(5): 767―773.(in Chinese)
[15] 周毅,孙利民,闵志华.斜拉桥主梁应变监测数据分析[J].振动与冲击,2011,30(4): 230―235.Zhou Yi,Sun Limin,Min Zhihua.Girder strain analysis of a cable-stayed bridge [J].Journal of Vibration and Shock,2011,30(4): 230―235.(in Chinese)
REAL-TIME SEPERATION OF TEMPERATURE EFFECT ON DYNAMIC STRAIN MONITORING AND MOVING LOAD IDENTIFICATION OF BRIDGE STRUCTURE