钢筋混凝土桥梁因造价低廉、刚度大等优点被广泛应用。在服役过程中同时承受荷载和环境的双重作用,随着服役时间的增长会出现锈蚀、粘结退化和疲劳等损伤现象,且各种诱发损伤的因素之间存在耦合关系,这种耦合关系进一步加速了桥梁承载力的劣化过程,一旦荷载超过其承载力将造成桥梁垮塌等重大事故。因此,对多因素作用下的桥梁时变承载力进行准确评估具有重要的理论和工程意义。
关于锈蚀对桥梁承载力的影响已有大量研究成果,并已得到了一致结论[1-3],即钢筋锈蚀会导致钢筋有效面积减少、材料性能退化以及钢筋与混凝土间粘结性能降低。粘结性能降低会影响钢筋和混凝土协同受力,常用的分析方法是通过调整截面协同工作系数来考虑粘结性能退化对承载力的影响。该方法简单易行,但不能从本质上解释粘结性能退化对承载力的影响。也有部分研究者从钢筋与混凝土粘结面的协调条件入手,试图从本质上揭示粘结性能退化对承载力的影响,但尚未得到一致结论。一种观点认为:随着锈蚀率的增加,粘结性能降低,协同工作系数和承载力均进一步下降[1―4];而另一种观点认为:当配筋指标低于某个限值时,无论钢筋锈蚀程度如何,截面协同工作系数总是等于1[5-6],即粘结性能的退化不会降低梁的承载力,只会使其刚度略有下降。可见,锈蚀后钢筋与混凝土间的粘结性能退化对承载力的影响相对复杂,目前尚无被广泛认可的机理阐释和分析方法。在疲劳对承载力的影响方面,疲劳会使混凝土的强度和弹性模量降低,并产生残余应变[7],而受拉区混凝土产生残余应变后还会对钢筋的锈蚀起到促进作用。疲劳对承载力的影响方面,一般只考虑疲劳导致的钢筋有效面积减小。
目前桥梁承载力评估方法通常只考虑锈蚀的影响,或考虑锈蚀和疲劳共同作用的影响[8-13],对锈蚀和疲劳耦合作用的影响缺乏重视。实际上锈蚀和疲劳耦合作用会加剧承载力的退化,忽视该耦合作用不能充分考虑承载力的实际下降状态,偏于不安全[14]。此外,钢筋锈蚀后,钢筋与混凝土之间粘结性能降低,传统的根据平截面假定进行承载力评估的方法不再适用。因此,在实际的桥梁承载力评估中有必要同时考虑锈蚀、粘结和疲劳损伤的影响,得到更真实的桥梁承载力状况。
鉴于目前还没有同时考虑锈蚀、粘结和疲劳综合影响的承载力评估方法,本文采用对截面协同工作系数进行修正的方法考虑以上三因素的影响。首先根据已有研究成果,阐述了锈蚀、粘结和疲劳损伤对承载力的影响机理,并以此作为时变承载力评估的基础。进而分析了锈蚀和疲劳之间的耦合作用,提出了时变耦合放大系数的计算方法,根据钢筋与混凝土间的变形协调条件,推导了考虑锈蚀、粘结滑移和疲劳损伤的锈蚀钢筋受力表达式,分析了锈蚀和疲劳对截面协同工作系数的影响,提出了同时考虑锈蚀、粘结和疲劳的桥梁承载力时变评估方法,并与有限元结果进行了对比。结果表明,本文的解析方法可以合理地反映桥梁承载力时变过程,且考虑的因素比较全面准确,更符合实际情况。
钢筋锈蚀对承载力的影响主要体现在:钢筋截面有效面积减小,屈服强度、极限强度和极限应变均发生退化,屈服平台缩短。准确评估服役期内桥梁承载力退化过程,需要确定锈蚀率随时间的变化情况,以及不同锈蚀率下钢筋的本构曲线。
对氯盐引起的钢筋锈蚀。目前一般采用Fick第二定律来描述混凝土中氯离子的扩散过程[15],其表达式为:
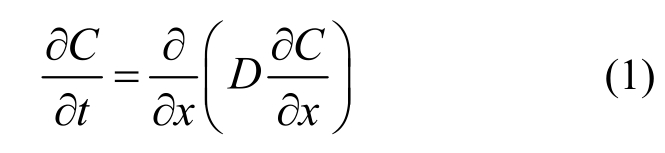
一维状态下,其解析解为:
式中:C(x,t)为距混凝土表面x处的氯离子浓度;C0为混凝土内初始氯离子浓度;Cs为混凝土表面的氯离子浓度;D为氯离子扩散系数;erf(z)为误差函数。氯离子扩散系数受温度、湿度及水灰比等因素的影响[16],其值宜根据实测数据或经验值确定。
临界氯离子浓度受较多因素影响,王伟[17]提出对于新建结构,可将0.6 kg/m3作为临界浓度;对于在役结构中的重点建筑物,可将0.6 kg/m3~0.9 kg/m3作为临界浓度;对于一般建筑物可将1.0 kg/m3作为临界浓度。
钢筋发生锈蚀后,锈蚀率的发展与环境温湿度和混凝土质量密切相关,本文选用文献[18]的模型作为常见沿海地区环境下(温度20 ℃,相对湿度75%)的锈蚀率发展公式,如下:
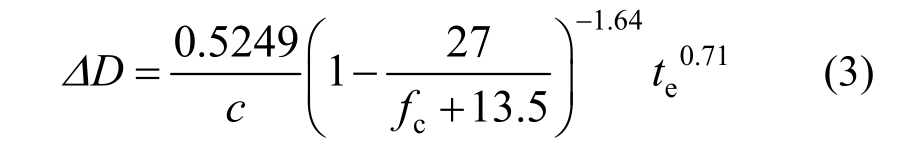
式中: 为锈蚀深度;
为锈蚀深度;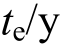 为锈蚀发展时间;
为锈蚀发展时间;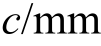 为混凝土保护层厚度
为混凝土保护层厚度 为混凝土抗压强度,As为钢筋初始截面积,
为混凝土抗压强度,As为钢筋初始截面积,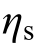 为钢筋锈蚀率。
为钢筋锈蚀率。
锈蚀钢筋本构的确定方面,本文在无锈钢筋本构模型基础上,考虑锈蚀的影响,得到锈蚀后的钢筋本构。无锈钢筋的本构如下[19]:

式中:σ、ε分别为钢筋的应力和应变;Es为钢筋的弹性模量;fy、εy分别为钢筋的屈服强度和屈服应变;k1为钢筋硬化起点应变与屈服应变的比值;k2为钢筋峰值应变与屈服应变的比值;k3为钢筋极限应变与屈服应变的比值;k4为钢筋峰值应力与屈服强度的比值。
钢筋锈蚀后,随着锈蚀率的增加弹性模量变化不大,名义屈服强度和名义极限强度相对值均近似按线性关系退化,实际工程中变形钢筋屈服平台消失的临界锈蚀率是20%,假设屈服平台长度随锈蚀的发展按线性规律退化,可计算得到锈蚀钢筋的强化应变值,锈蚀钢筋的极限应变随锈蚀的发展呈指数衰减。具体表达式如下[20]:
式中:fyc、fuc分别为锈蚀钢筋屈服强度和锈蚀钢筋极限强度;ηs为截面平均锈蚀率;fu为未锈蚀钢筋极限强度。

式中:εshc为锈蚀钢筋的强化应变;εsh0为未锈蚀钢筋的强化应变。且有![]()
根据式(5)~式(7)可得到不同锈蚀率下的钢筋本构曲线,如图1所示。
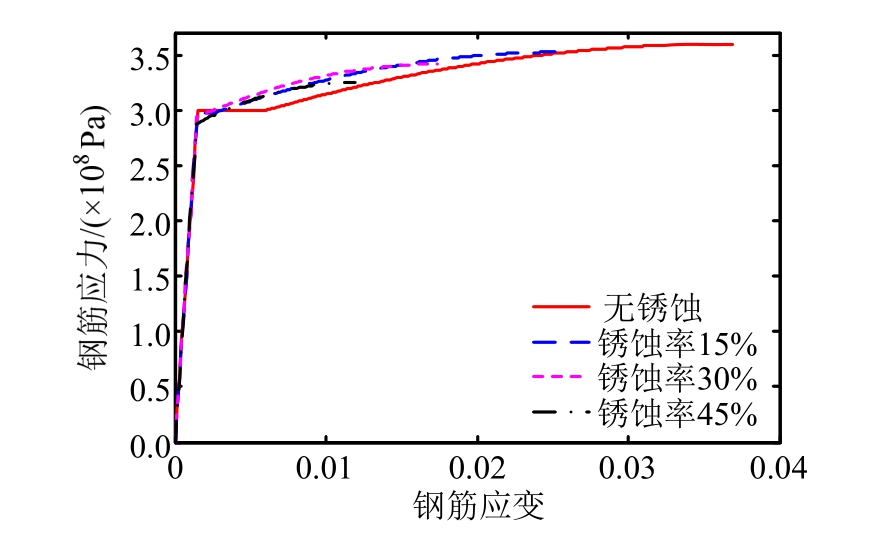
图1 锈蚀钢筋本构曲线
Fig.1 Constitutive-curve of corroded reinforcement
钢筋发生锈蚀后除了钢筋材料性能退化外,钢筋与混凝土间的锈蚀物也会影响钢筋与混凝土之间的粘结滑移性能[21],而粘结滑移性能是保证钢筋与混凝土协同受力的基本条件。为了研究锈蚀后粘结性能降低对承载力的影响,本文采用文献[22]中的无锈钢筋与混凝土的粘结滑移本构曲线形式,如图2所示,图中τs、τcr、τu和τr分别为滑移强度、劈裂强度、极限强度和残余强度,Ss、Scr、Su和Sr分别为相应的滑移量。并根据文献[23]中锈蚀对粘结强度的影响公式对相应的滑移强度、劈裂强度、极限强度和残余强度乘以一个与锈蚀率相关的折减系数λ(ηs)来考虑锈蚀的影响,λ(ηs)的表达式如下:
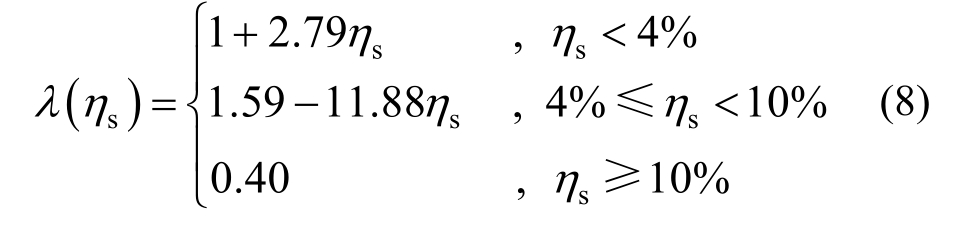

图2 粘结滑移本构曲线
Fig.2 Bond-slip curve of reinforced concrete
不同锈蚀率下钢筋与混凝土的粘结滑移本构关系,如图3所示。
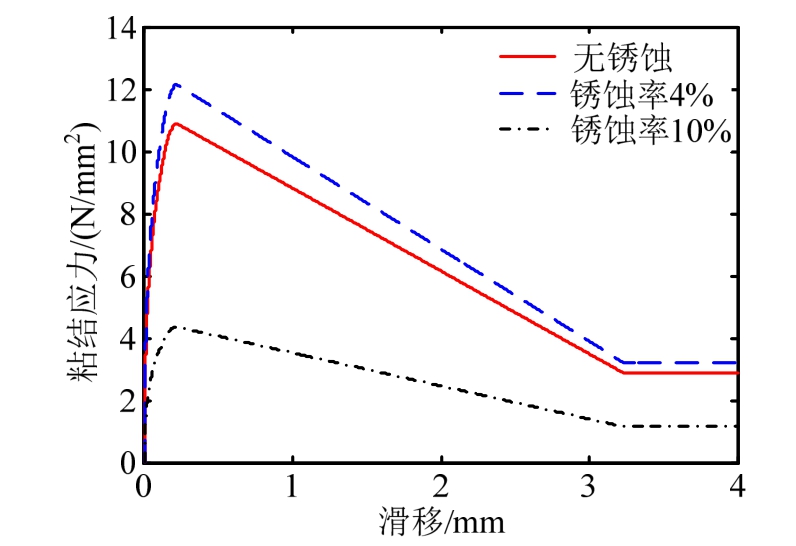
图3 不同锈蚀率下的粘结滑移本构曲线
Fig.3 Bond slip curves of different corrosion rates
通过以上理论可得到不同服役期下钢筋的锈蚀率、本构关系以及钢筋与混凝土间的粘结本构,进而考虑锈蚀和粘结对承载力的影响,但桥梁服役过程中会同时承受车辆荷载,往往存在不同程度的疲劳损伤,在承载力评估时不应忽视疲劳损伤对承载力的影响。
疲劳加载会导致混凝土的弹性模量和强度降低,并产生残余应变。在疲劳加载作用下,混凝土弹性模量退化规律为[24]:
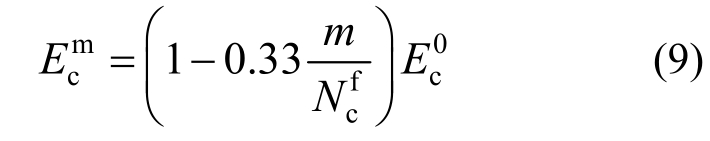
式中: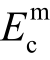 为疲劳作用m次时的混凝土弹性模量;
为疲劳作用m次时的混凝土弹性模量;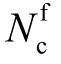 为混凝土疲劳寿命;
为混凝土疲劳寿命;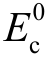 为混凝土初始弹模。
为混凝土初始弹模。
王瑞敏等[25]提出了混凝土受压疲劳后的残余应变计算公式,如下:
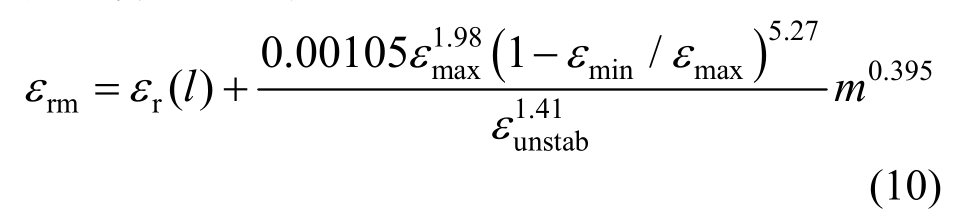
式中:εmax和εmin分别为对应的疲劳应变的上限和下限;εr(l)为第1次应力循环产生的残余应变;εunstab为不稳定状态时混凝土应变值,一般可取0.002。
在疲劳加载作用下,钢筋的最终疲劳断裂是由于剩余有效承载面积不能承担当时作用的拉伸荷载而发生的瞬时断裂[26],本文通过钢筋有效面积的减小来考虑疲劳的影响。
计算一定服役期下疲劳导致的钢筋面积减小时,应首先根据关键部位的应变信息,通过雨流计数法得到三维应力幅谱,再根据式(11)计算基于连续损伤力学的疲劳损伤模型的等效应力幅[27],进而根据式(12)和式(13)得到疲劳一定次数后的钢筋剩余有效面积[28]。
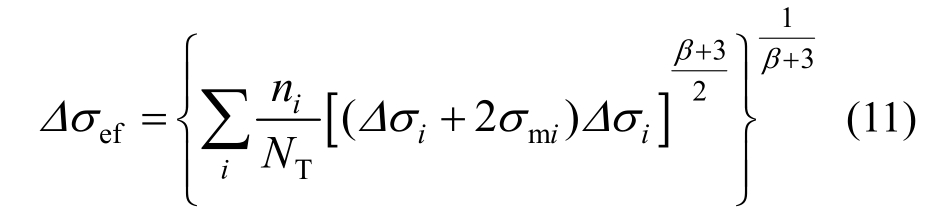
式中:Δσef为等效应力幅;ni为应力幅Δσi的循环数量;NT为循环总数量;Δσmi为第i次循环的平均应力;β为材料参数。
式中:Nf为钢筋的疲劳寿命;Δσef为钢筋的等效应力幅。
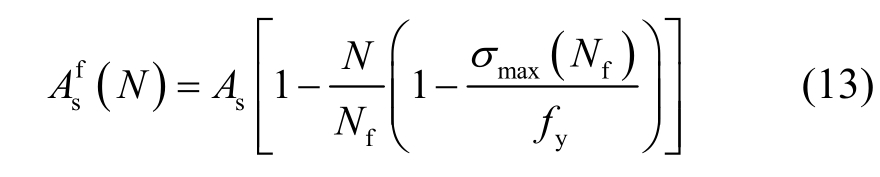
式中:As为初始钢筋面积;Nf为疲劳寿命;fy为钢筋的屈服强度;σmax(Nf)为疲劳最大应力。
通过以上分析可以看出:只要给定了桥梁的服役时间便可得到对应的锈蚀率、钢筋本构、粘结滑移本构以及锈蚀和疲劳共同作用下的钢筋剩余有效面积,进而进行承载能力退化评定。然而这样做忽视了锈蚀和疲劳耦合作用下钢筋面积加速减小的客观事实。因此,有必要对锈蚀和疲劳耦合作用下钢筋面积的退化情况进行分析与讨论。
疲劳荷载会使混凝土产生残余拉应变,裂缝存在时还会增大裂缝宽度,使氯离子、水分、氧气等更容易侵入到钢筋周围,加速锈蚀的发生和发展,研究表明混凝土受拉应力从0 MPa增大到1.6 MPa时,氯离子的扩散系数增大了25%[29],残余应变从0增大到120×10-6时,氯离子的扩散系数增大了约150%[30]。锈蚀的发展会降低钢筋的疲劳寿命[31],锈蚀和疲劳作用下钢筋的有效面积逐渐减小,其所受到的应力幅值和最大应力值均相应增大。可见锈蚀和疲劳耦合作用会加快服役期内桥梁承载力的退化。有鉴于此,本文在计算锈蚀和疲劳耦合作用时,首先分别计算锈蚀和疲劳单独作用下钢筋有效面积折减情况,再通过引入耦合放大系数θ来考虑锈蚀和疲劳耦合作用对承载力降低的促进作用,最后将锈蚀和疲劳单独作用下的钢筋面积折减乘以耦合放大系数θ得到锈蚀和疲劳耦合作用下的钢筋面积折减率,进而进行承载力评估。耦合放大系数θ根据以下步骤求得:
1) 根据式(4)和式(13)分别求得一定服役期下锈蚀和疲劳单独作用下的钢筋锈蚀率η1和疲劳后的截面面积A1,进而求出考虑锈蚀和疲劳共同作用后的钢筋剩余面积Ag。
2) 根据该服役期下疲劳次数得到受拉混凝土的残余应变,进而得到氯离子扩散系数的增大系数p,将该系数乘以由式(4)求得的锈蚀率η1,得到考虑疲劳影响下的锈蚀率η2。由于缺乏疲劳作用下受拉混凝土的残余应变和裂缝宽度计算模型,本文将p=1.4作为氯离子扩散系数增大系数的上限,并根据服役期对p进行线性折减得到不同服役期下疲劳作用对锈蚀率的影响。
3) 对该服役期下钢筋的最大应力值和应力幅值进行修正,即将初始最大、最小应力值乘以k,k为考虑锈蚀和疲劳共同作用时钢筋初始面积与所求服役期时面积的比值,得到修正后的最大、最小应力值,从而求得该服役期时的疲劳应力幅值。由于在服役过程中随着钢筋有效面积的减小疲劳最大、最小应力值是逐渐增大的,因此取该服役期时应力幅值的一半作为整个服役期内的等效应力幅Δσef。进而根据式(12)得到钢筋的疲劳寿命Nf,采用文献[31]中锈蚀对钢筋疲劳寿命的折减公式对Nf进行折减,即将Nf乘以与锈蚀率相关的系数q,![]() η2为考虑疲劳影响的该服役期下的钢筋锈蚀率,得到锈蚀影响下的钢筋疲劳寿命Nfx,将修正后的疲劳参数代入式(13)得到考虑锈蚀影响的疲劳后的钢筋面积A2。
η2为考虑疲劳影响的该服役期下的钢筋锈蚀率,得到锈蚀影响下的钢筋疲劳寿命Nfx,将修正后的疲劳参数代入式(13)得到考虑锈蚀影响的疲劳后的钢筋面积A2。
4) 根据η2和A2得到锈蚀和疲劳耦合作用后的钢筋总的有效面积Ac,![]() 即为耦合放大系数θ,式中A为初始钢筋面积。
即为耦合放大系数θ,式中A为初始钢筋面积。
在计算锈蚀和疲劳耦合作用时,可直接计算锈蚀和疲劳共同作用后的钢筋有效面积折减率![]() 再将
再将![]() 作为考虑耦合作用下的钢筋截面面积折减率。
作为考虑耦合作用下的钢筋截面面积折减率。
通过上述分析可以确定锈蚀和疲劳耦合作用下计算承载力所需参数的取值。由于锈蚀后钢筋与混凝土之间不再符合平截面假定,即钢筋位置处混凝土和钢筋的应变不再相等[32],因此在计算承载力时不能再根据平截面假定计算受拉钢筋的轴力。本节将基于前述关于锈蚀、疲劳和粘结滑移的研究成果,从锈蚀后钢筋和混凝土界面的变形协调条件入手推导截面协同工作系数的理论表达式,通过该系数来反映粘结性能退化对承载力的影响,并给出同时考虑锈蚀、粘结性能降低和疲劳损伤的承载力时变评估方法。
对在役桥梁进行承载力评估时,首先要根据桥梁所处的环境条件和荷载监测信息得到指定服役期下的锈蚀和疲劳损伤程度,进而得到钢筋面积和材性退化情况,再通过截面协同工作系数考虑粘结性能退化的影响,进行迭代求得给定服役期下桥梁所能承受的最大承载力。下文将阐述截面协同工作系数的具体推导方法。
如图4所示的钢筋混凝土截面内力平衡方程为:
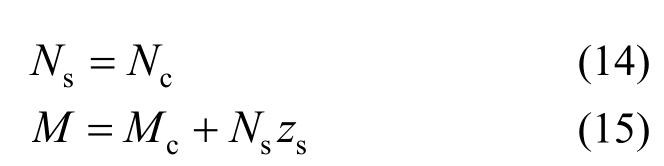
式中:Ns为钢筋所受拉力;Nc为受压区混凝土和受压钢筋共同承受的压力;M为外力作用弯矩;Mc为受压区混凝土和受压钢筋对形心轴的弯矩;zs为受拉钢筋截面中心到截面形心轴的距离。

图4 锈蚀梁正截面
Fig.4 Normal section of corroded beam
受压区内混凝土和钢筋共同承受的压力Nc为:
受压区内混凝土和钢筋对形心轴的弯矩Mc为:
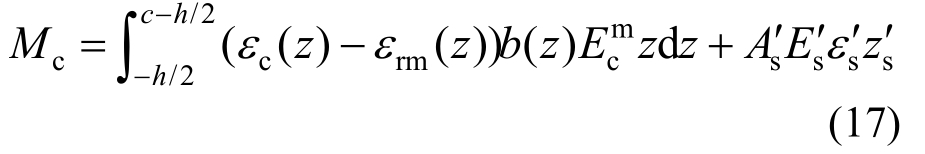
式中:εc(z)、εrm(z)分别为距截面形心z处的混凝土应变和残余应变,![]() 为疲劳作用下梁顶混凝土的残余应变;c为截面受压区高度;b(z)为距截面形心z处的截面宽度;
为疲劳作用下梁顶混凝土的残余应变;c为截面受压区高度;b(z)为距截面形心z处的截面宽度;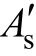 为受压纵筋截面面积;
为受压纵筋截面面积;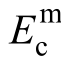 、
、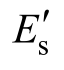 分别为疲劳后的混凝土弹性模量和受压纵筋的弹性模量;
分别为疲劳后的混凝土弹性模量和受压纵筋的弹性模量;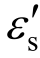 为受压纵筋应变;
为受压纵筋应变; 为受压纵筋中心到截面形心处的距离。
为受压纵筋中心到截面形心处的距离。
以截面形心为原点,z轴向下为正,混凝土受压为正,则:
式中:uc0为混凝土截面形心处的纵向位移;w为梁上x截面处的挠度。
以钢筋受拉为正,则受拉钢筋的应变εs为:
式中:Es为受拉钢筋弹性模量;As为考虑锈蚀和疲劳后的受拉纵筋截面面积。
钢筋与混凝土间单位长度的滑移量为混凝土与钢筋的应变差,因此受拉纵筋与混凝土界面处的变形协调方程为:
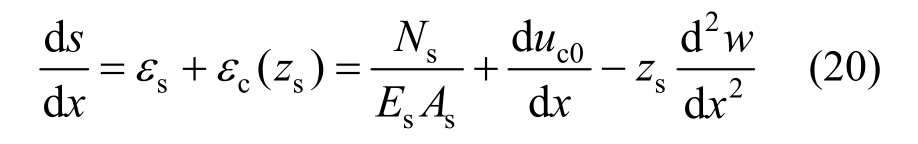
Ns与钢筋和混凝土粘结力的关系为:
式中:n为钢筋根数;di为钢筋直径。
将锈蚀后的粘结滑移曲线代入式(21),稍作变形后,等式两边对x求导,得:

引入以割线粘结滑移刚度ks表达的粘结滑移关系,并令![]() 式(22)可写为:
式(22)可写为:
根据式(15)~式(19)可以求得:
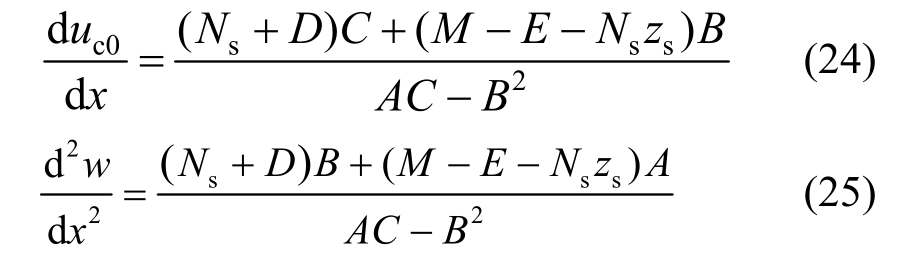
将式(24)、式(25)和式(23)代入式(20)可得到考虑锈蚀和疲劳以及钢筋与混凝土间粘结滑移的受拉钢筋的轴力微分方程:
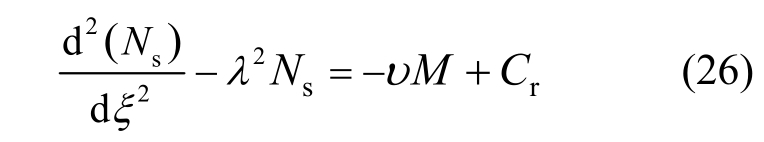
式中,ξ=x/L,L为梁长。

式(26)可以根据梁边界条件的不同求得对应锈蚀率下钢筋轴力的表达式。
不考虑粘结滑移时的纵向受拉钢筋拉力N0,可以通过界面滑移量为零求得,由式(20)得:

由截面协同工作系数的定义[4]可求得截面协同工作系数kb:
由以上分析可以看出截面协同工作系数kb与锈蚀钢筋与混凝土的粘结滑移性能、受压区高度、截面尺寸、钢筋的布置位置、钢筋和混凝土的材料性能等有关。当梁截面和配筋形式给定后,截面协同工作系数就只与锈蚀钢筋与混凝土的粘结滑移性能和混凝土的受压区高度有关。
求出截面协同工作系数后,就得到了锈蚀后的钢筋轴力与根据平截面假定计算出的钢筋轴力之间的关系,进而可以根据锈蚀后钢筋的实际轴力与混凝土截面的平截面关系列出力的平衡方程如下:
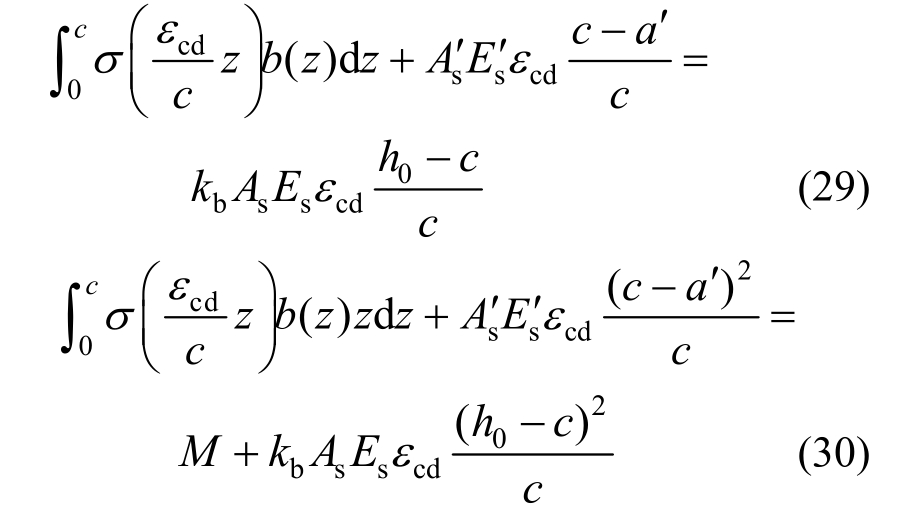
式中:![]() 为梁顶混凝土应变;εrm为疲劳后梁顶混凝土残余应变;h0为截面有效高度。
为梁顶混凝土应变;εrm为疲劳后梁顶混凝土残余应变;h0为截面有效高度。
由于适筋梁的破坏是受拉钢筋先屈服,随后受压区边缘混凝土被压坏,因此含有锈蚀钢筋的正常桥梁破坏时钢筋一般已屈服而混凝土却不一定达到极限应变,故本文将锈蚀钢筋的屈服条件作为承载力的极限状态。对于端部锚固良好的锈蚀梁,受拉钢筋在极限状态下能够发生屈服,但是由于锈蚀后钢筋与混凝土间粘结性能的降低,钢筋屈服后实际通过钢筋传导到混凝土截面应力不再是钢筋的屈服应力,而是钢筋的屈服应力与协同工作系数kb的乘积,因此本文以![]() 作为承载力极限条件。
作为承载力极限条件。
当外荷载M已知时,式(29)和式(30)中存在混凝土受压区高度c和梁顶混凝土的应变εcd两个未知数,而且锈蚀率给定时截面协同工作系数kb也只与混凝土受压区高度c有关。因此在求锈蚀梁的极限承载力时,可先给定一个外荷载M,同时假设一个截面协同工作系数kb,然后根据公式求出c和εcd,进而根据![]() 求得不考虑粘结滑移性能降低时的钢筋应力,并判断钢筋是否达到屈服。如果钢筋没有屈服则增大外荷载M直到钢筋屈服,最后将钢筋屈服状态下求得的c以及根据不同锈蚀率下钢筋与混凝土的粘结滑移本构关系得到的粘结滑移刚度ks代入式(28)中求出kb,并判断求得kb与假设的kb是否一致,如果不一致则进行迭代计算,直到计算得到的kb与假设的kb一致为止,最终得到给定锈蚀率条件下的承载力。
求得不考虑粘结滑移性能降低时的钢筋应力,并判断钢筋是否达到屈服。如果钢筋没有屈服则增大外荷载M直到钢筋屈服,最后将钢筋屈服状态下求得的c以及根据不同锈蚀率下钢筋与混凝土的粘结滑移本构关系得到的粘结滑移刚度ks代入式(28)中求出kb,并判断求得kb与假设的kb是否一致,如果不一致则进行迭代计算,直到计算得到的kb与假设的kb一致为止,最终得到给定锈蚀率条件下的承载力。
综上,对于矩形截面梁,式(29)和式(30)可写成等效矩形应力图的形式如下:

式中: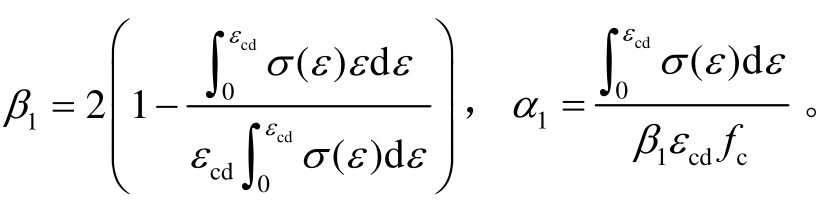
如采用规范[33]中的混凝土本构关系,α1β1、β1的积分表达式没有显示解析解,因此采用文献[34]中的混凝土本构关系,即式(33):

该混凝土本构关系对应的α1、β1为:
当ε≤ε0时![]()
![]()
当ε0<ε≤εu 时![]()
![]()
从以上分析可以看出,截面协同工作系数与梁的边界锚固条件和加载形式有关,对常见有纯弯段的简支梁其截面协同工作系数的计算过程如下。
对于图5所示的双集中对称加载简支梁,梁长为L,梁上作用两个大小为F的集中力,将沿梁长的弯矩分布公式代入钢筋轴力微分方程式(26),并求出其通解,如下:

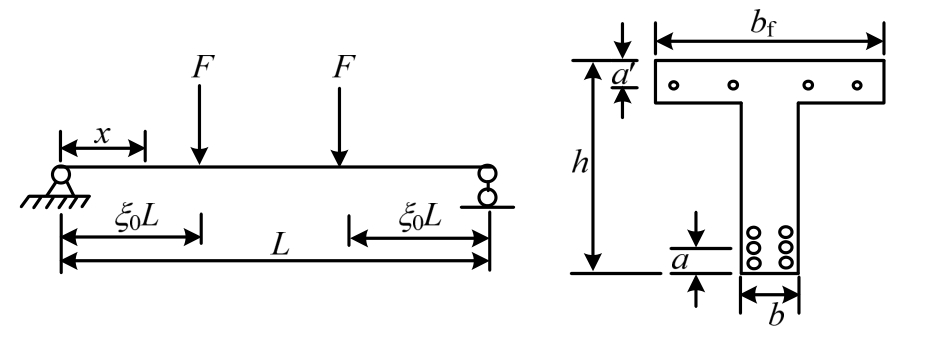
图5 梁的加载形式及截面尺寸
Fig.5 Loading form and size of beam
根据边界条件,梁端钢筋锚固良好时,端部钢筋和混凝土不产生相对滑移,考虑对称性,跨中截面钢筋和混凝土也不产生相对滑移,以及集中力作用位置截面两边钢筋轴力以及钢筋和混凝土的相对滑移量相等,有:
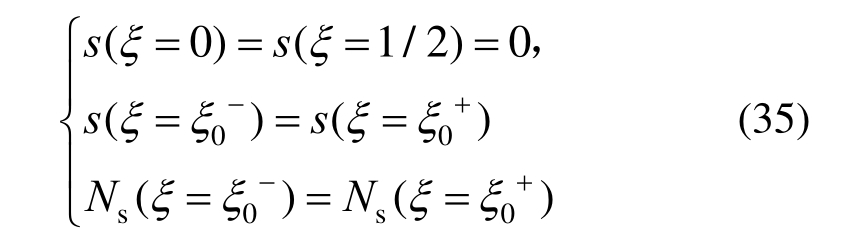
由式(21)~式(23)得到:
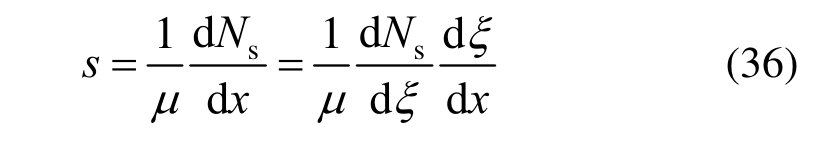
将式(34)以及ξ=x/L代入式(36)得:
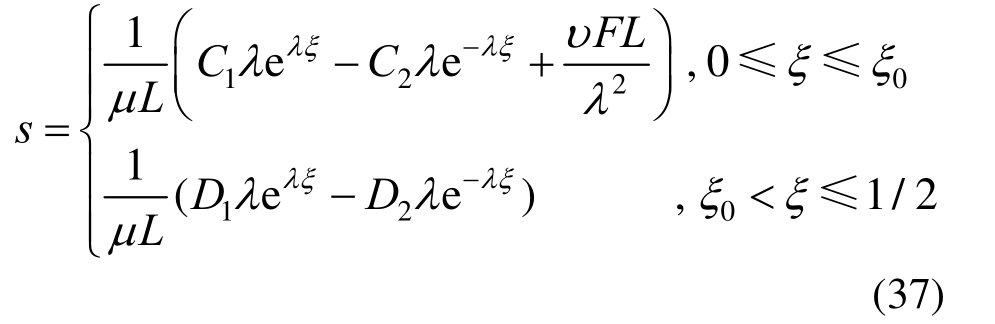
根据式(35),边界条件可以写成如下方程组:
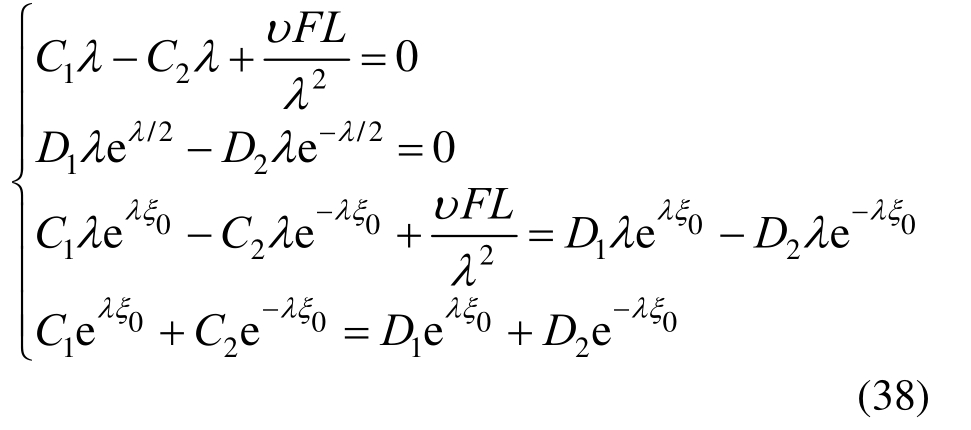
解上面方程组得:

将C1、C2、D1和D2代入式(34)便可得到粘结滑移性能降低时的锈蚀钢筋轴力。再根据式(27),可得到不考虑粘结滑移时的钢筋轴力N0,进而可以求得左侧集中力加载处的截面协同工作系数 。从上述解析式可以看出,协同工作系数主要与受压区高度c和粘结滑移刚度ks、梁长、钢筋布置位置等有关,而c和εcd又随着外荷载和材料弹模等的变化而变化。如果确定梁的尺寸和截面参数后,协同工作系数便只跟受压区高度和锈蚀程度有关。
。从上述解析式可以看出,协同工作系数主要与受压区高度c和粘结滑移刚度ks、梁长、钢筋布置位置等有关,而c和εcd又随着外荷载和材料弹模等的变化而变化。如果确定梁的尺寸和截面参数后,协同工作系数便只跟受压区高度和锈蚀程度有关。
为了验证本文提出的承载力计算方法的有效性和准确性,以及锈蚀、疲劳和粘结性能降低对承载力的影响程度,以文献[35]中的钢筋混凝土简支T形梁桥中的一片梁为例,进行理论和有限元分析。该简支T梁梁长19.96 m,计算跨径19.50 m,截面尺寸如图6所示,混凝土强度等级为C30,主筋采用HRB335钢筋,设计弯矩为2430.30 kN·m。混凝土表面氯离子浓度取为8 kg/m3,混凝土内初始氯离子浓度取0.018 kg/m3,临界氯离子浓度取为1.1 kg/m2[36],氯离子扩散系数D取为2.0×10-6 mm2/s,根据式(2)计算得到钢筋的起锈时间为3年。疲劳荷载下限取梁自重下对应的应力,其中钢筋和梁顶混凝土的应力分别为55 MPa和2.5 MPa。钢筋和混凝土等效应力幅参考文献[37]分别取为29.83 MPa和3.00 MPa,疲劳次数取为6000次/日。根据前文方法计算得到的不同服役期下混凝土的弹性模量、钢筋锈蚀率和粘结滑移刚度,以及锈蚀和疲劳导致的钢筋面积减少情况,见表1。根据这些参数可以得到锈蚀和疲劳耦合作用下的截面协同工作系数,进而求得不同服役期下的承载力。

图6 T型钢筋混凝土梁截面 /cm
Fig.6 Section of T type RC beam
表1 不同服役期下的计算参数及承载力计算结果
Table 1 Calculation parameters and bearing capacity calculation results in different service periods

服役时间/年 混凝土弹模/MPa 锈蚀率/(%) 疲劳折减/(%)耦合放大系数θ屈服强度/MPa粘结滑移刚度/(MPa/mm) 截面协同工作系数(仅锈蚀)0E0 0 0 1 300 42.43 0.99731 10 0.9948E0 4.22 1.06 1.0691 299.35 46.20 0.9978 20 0.9897E0 7.85 2.11 1.1475 298.75 27.90 0.9977 30 0.9845E0 10.82 3.17 1.2353 298.22 16.97 0.9977 40 0.9794E0 13.44 4.23 1.3341 297.72 16.97 0.9985 50 0.9742E0 15.82 5.28 1.4456 297.24 16.97 0.9996 60 0.9690E0 18.03 6.34 1.5721 296.77 16.97 0.9990

图7 梁有限元模型
Fig.7 Finite element model of the beam
图7为采用ANSYS软件建立的该梁的限元模型,建模时不考虑受压钢筋的粘结滑移,受拉钢筋截面面积、本构模型以及钢筋与混凝土间的粘结滑移曲线分别取前述理论对应输入锈蚀和疲劳后的本构曲线和截面面积。加载采用三分点加载,加载方式为位移加载,为避免出现应力集中在支座处和加载位置处分别设置了垫板。图8为考虑锈蚀和疲劳耦合作用时不同服役期下该梁加载位置处的弯矩-位移曲线,其中服役期0年时的屈服承载力为2408 kN·m,与设计值基本吻合,随着服役期的增加,该梁承载力和刚度均逐渐降低,表明本文的有限元模型合理准确。
在计算粘结滑移刚度时,取不同锈蚀率下粘结滑移本构曲线的峰值点割线刚度作为粘结滑移刚度ks,不同锈蚀率对应的粘结滑移刚度如图9所示。从中可以看出,锈蚀率较小时,粘结滑移刚度适度增大,随着锈蚀率的增加,粘结滑移刚度逐渐降低,超过一定锈蚀率后粘结滑移刚度就不再改变。

图8 不同服役期下的荷载-位移曲线
Fig.8 Load-displacement curve in different service periods

图9 不同锈蚀率下的粘结滑移刚度
Fig.9 Bond slip stiffness at different corrosion rates
图10为对应式(35)的边界条件,根据式(28)计算得到的不同服役期下的截面协同工作系数,从图中可以看出仅考虑锈蚀和同时考虑锈蚀和疲劳得到的截面协同工作系数相差不大,其值都趋近于1,这说明在梁端粘结锚固良好的情况下,梁达到极限承载力时,钢筋总能屈服,且钢筋传递到混凝土截面的应力为钢筋的屈服应力,这种情况下粘结滑移性能的降低对承载力的影响很小。
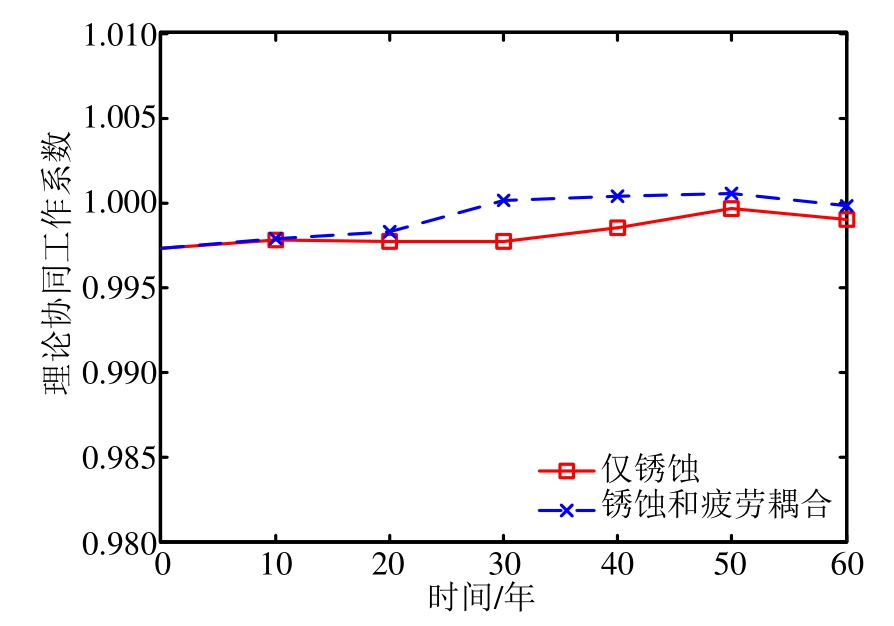
图10 不同服役期对应的截面协同工作系数
Fig.10 Cooperative work coefficient of different service periods
为了考虑极端条件下的情况,本文分别计算了锈蚀和疲劳耦合作用下服役期为60年时钢筋在端部粘结良好而中间粘结正常以及中间粘结完全失效情况下的弯矩-位移曲线,如图11所示,可以看出:中间粘结完全失效时承载力基本没有受到影响,但是刚度却明显下降。

图11 不同粘结条件下的弯矩-位移曲线对比
Fig.11 Moment-displacement curves under different conditions
图12为不同服役期下仅考虑钢筋锈蚀、考虑锈蚀和疲劳共同作用以及考虑锈蚀和疲劳耦合作用时的受拉钢筋截面折减率曲线。可见随着服役时间的增加三者之间的差值越来越大,这主要是因为随着服役时间的增长,桥梁所受的疲劳荷载逐渐增多,疲劳导致的钢筋截面减小程度和比例也逐渐增大。锈蚀和疲劳耦合作用加速了钢筋面积的退化过程。结合表1中耦合放大系数θ的变化情况也可以看出随着服役期的增加θ值逐渐增大。在服役期60年时,考虑耦合作用比不考虑耦合作用下的钢筋面积折减增大了57.21%。因此,在评估服役时间较长的桥梁承载力时,要同时考虑锈蚀和疲劳的影响,并重视耦合作用。

图12 不同服役期对应的截面折减率
Fig.12 Section reduction rate in different service periods
图13为仅考虑锈蚀、考虑锈蚀和疲劳共同作用以及考虑锈蚀和疲劳耦合作用时,该梁在不同服役期下的承载力变化曲线与根据本文理论计算结果的对比情况。可以看出:仅考虑锈蚀作用将明显高估该梁的承载力,而根据本文理论计算得到的考虑锈蚀和疲劳耦合作用下的承载力结果与有限元计算结果接近,且理论结果较有限元结果保守,有利于评估和维护。

图13 承载力退化曲线
Fig.13 Bearing capacity degradation curve
为了考察极端条件下粘结滑移性能对承载力的影响,本文对服役期为60年时的粘结滑移本构曲线分别乘以0.05、0.04、0.03、0.02的折减系数,并认为受拉钢筋通长使用同一粘结滑移本构,即不再认为端部锚固良好,在此基础上计算了粘结滑移性能降低对承载力的影响。不同情况下的弯矩-位移曲线如图14所示。
可以看出:粘结滑移本构折减到0.05倍时,锈蚀对承载力的影响仍然很小,虽然梁刚度略有降低,但钢筋的材料性能仍得到较充分发挥。粘结滑移本构折减到0.04倍时,承载力出现明显降低,此时的破坏完全是由粘结性能不足导致的,这种情况下钢筋并没有完全屈服。
本文算例中,T形梁初始受拉钢筋总面积为70.62 cm2,在锈蚀和疲劳耦合作用下,服役60年时,钢筋的总面积为43.57 cm2,此时由于锈蚀的原因,钢筋的屈服强度为296.77 MPa,根据此时的粘结滑移本构,粘结最大强度取粘结滑移曲线峰值强度4.99 MPa计算,可知只需要27.84 cm的锚固长度即可保证受拉钢筋全部屈服,在实际结构中,梁端都会有锚固加强措施,因此一般情况下由于粘结滑移失效而导致承载力降低的情况不会发生。
本文研究了锈蚀和疲劳耦合作用下锈蚀钢筋混凝土梁的承载力退化过程,分析了锈蚀、疲劳以及粘结性能退化对承载力的影响。根据受拉钢筋与混凝土接触面的变形协调方程推导了多因素影响下截面协同工作系数的表达式,给出了锈蚀和疲劳耦合作用下的锈蚀梁承载力计算方法。通过一个算例分析了锈蚀后粘结滑移性能降低、锈蚀和疲劳耦合作用对承载力的影响,得到如下结论:
(1) 锈蚀和疲劳作用下,是否考虑二者之间的耦合对承载力有明显影响,且随着服役时间的增加耦合作用的影响逐渐增大,本文算例中服役期60年时,考虑耦合时的钢筋面积折减率比不考虑耦合时的结果增大了57.21%。
(2) 对于端部锚固良好的梁,锈蚀导致的粘结性能降低对承载力的影响较小。对于端部锚固不良的情况,极端锈蚀条件下,粘结性能才会导致构件的承载力降低,此时梁的破坏是粘结不足导致的粘结滑移破坏,但这种情况在工程中一般不会出现。
(3) 对于端部锚固良好的锈蚀钢筋混凝土简支梁,导致承载力降低的主要因素是锈蚀和疲劳引起的钢筋有效面积减小,锈蚀导致的粘结性能降低对承载力影响较小。在对简支梁桥进行承载力评估时,应先判断粘结滑移强度能否提供钢筋屈服所需的粘结力,如果能,则在评估时可以忽略粘结性能降低对承载力的影响,而主要考虑锈蚀和疲劳耦合作用导致的钢筋面积减少的影响。
本文虽然提出了锈蚀和疲劳耦合作用下的钢混简支梁承载力计算方法,但对多因素下钢筋混凝土梁的承载力进行准确计算仍然比较困难,主要难点在于所提方法中的参数取值问题。针对在役桥梁进行承载力计算时,需要根据相关实测数据及理论确定出用于承载力计算的参数值,但由于锈蚀和疲劳损伤与较多因素有关,使得现场实测数据随机性较大,且缺乏为大家所广泛接受的锈蚀率发展和疲劳损伤计算模型,因此,本文计算方法中的参数在取值时如何更合理准确地反映工程实际是另一个值得思考的问题。

图14 粘结本构对荷载-位移曲线的影响
Fig.14 Influence of bonding condition on load-displacement
[1] 牛荻涛,翟彬,王林科,等.锈蚀钢筋混凝土梁的承载力分析[J].建筑结构,1998(8): 23-25.Niu Ditao,Zhai Bin,Wang Linke,et al.Analysis for bearing capacity of RC beams with rusting steel bar [J].Building Structure,1998(8): 23-25.(in Chinese)
[2] Coronelli D,Gambarova P.Structural Assessment of corroded reinforced concrete beams: modeling guidelines[J].Journal of Structural Engineering,2004,130(8):1214-1224.
[3] Francois R,Khan I,Dang V H.Impact of corrosion on mechanical properties of steel embedded in; 27-year-old corroded reinforced concrete beams [J].Materials and Structures,2013,46(6): 899-910.
[4] 赵建昌,徐宁.锈蚀钢筋混凝土梁截面协同工作系数研究[J].水利学报,2007,38(9): 1096-1102.Zhao Jianchang,Xu Ning.Studies on the section coordination coefficient of corroded reinforced concrete beam [J].Journal of Hydraulic Engineering,2007,38(9):1096-1102.(in Chinese)
[5] 孙彬,牛荻涛,王庆霖.锈蚀钢筋混凝土梁抗弯承载力计算方法[J].土木工程学报,2008,41(11): 1-6.Sun Bin,Niu Ditao,Wang Qinglin.Calculation method for flexural capacity of corroded RC beams [J].China Civil Engineering Journal,2008,41(11): 1-6.(in Chinese)
[6] 杨明.锈蚀钢筋混凝土梁受弯性能研究[D].南京: 东南大学,2006.Yang Ming.Study on flexural behavior of corroded reinforced concrete beams [D].Nanjing: Southeast University,2006.(in Chinese)
[7] 宋玉普.混凝土的动力本构关系和破坏准则(下册)[M].北京: 科学出版社,2012.Song Yupu.Dynamic constitutive relation and failure criterion of concrete: part 2 [M].Beijing: Science Press,2012.(in Chinese)
[8] Zhong X P,Jin W L,Xia J.A time-varying model for predicting the life-cycle flexural capacity of reinforced concrete beams [J].Advances in Structural Engineering,2015,18(1): 21-32.
[9] 杨良,孙立军.钢筋混凝土桥梁的钢筋锈蚀与疲劳耦合损伤[J].同济大学学报(自然科学版),2015,43(12):1784-1787.Yang Liang,Sun Lijun.Damage of steel bar of reinforced concrete bridge by the coupling effect of corrosion and fatigue [J].Journal of Tongji University (Natural Science),2015,43(12): 1784-1787.(in Chinese)
[10] Zhang W,Ye Z,Gu X,et al.Assessment of fatigue life for corroded reinforced concrete beams under uniaxial bending [J].Journal of Structural Engineering,2017,143(7): 1-14.
[11] Zhu W,François R.Prediction of the residual load-bearing capacity of naturally corroded beams using the variability of tension behaviour of corroded steel bars[J].Structure & Infrastructure Engineering,2016,12(2):143-158.
[12] Yang S,Fang C Q,Yuan Z J,et al.Effects of reinforcement corrosion and repeated loads on performance of reinforced concrete beam [J].Advances in Structural Engineering,2015,18(8): 1257-1272.
[13] 蔡健,魏沐杨,罗赤宇,等.弯曲荷载与氯盐侵蚀共同作用下的预应力混凝土梁耐久性能研究[J].工程力学,2018,35(7): 208-218.Cai Jian,Wei Muyang,Luo Chiyu,et al.Durability of prestressed concrete beams under simultaneous flexural load and chloride erosion [J].Engineering Mechanics.2018,35(7): 208-218.(in Chinese)
[14] Emilio B.Reliability of reinforced concrete structures subjected to corrosion-fatigue and climate change [J].International Journal of Concrete Structures and Materials,2018,12(1): 1-13.
[15] Fib model code for concrete structures 2010(2013) [S].Lausanne: International Federation for Structural Concrete,2013.
[16] Shafei B,Alipour A,Shinozuka M.Prediction of corrosion initiation in reinforced concrete members subjected to environmental stressors: A finite-element framework [J].Cement and Concrete Research,2012,42(2): 365-376.
[17] 王伟.氯离子环境下混凝土结构耐久性设计研究[D].合肥: 合肥工业大学,2006.Wang Wei.Research on durability design of concrete structures exposed to chloride environment [D].Hefei:Hefei University of Technology,2006.(in Chinese)
[18] 宋志刚,金伟良,刘芳,等.钢筋锈蚀率概率分布的动态演进模拟[J].浙江大学学报(工学版),2006,40(10):1749-1754.Song Zhigang,Jin Weiliang,Liu Fang,et al.Dynamic simulation method for probability evolution of reinforcement steel corrosion [J].Journal of Zhejiang University (Engineering Science),2006,40(10): 1749-1754.(in Chinese)
[19] 汪训流,陆新征,叶列平.往复荷载下钢筋混凝土柱受力性能的数值模拟[J].工程力学,2007,42(12): 76-81.Wang Xunliu,Lu Xinzheng,Ye Lieping.Numerical simulation for the hysteresis behavior of RC columns under cyclic loads [J].Engineering Mechanics,2007,42(12): 76-81.(in Chinese)
[20] 张伟平,商登峰,顾祥林.锈蚀钢筋应力-应变关系研究[J].同济大学学报(自然科学版).2006,34(5): 586-592.Zhang Weiping,Shang Dengfeng,Gu Xianglin.Stress-strain relationship of corroded steel bars [J].Journal of Tongji University (Natural Science),2006,34(5): 586-592.(in Chinese)
[21] Zandi K.Corrosion-induced cover spalling and anchorage capacity [J].Structure and Infrastructure Engineering,2015,11(12): 1547-1564.
[22] 徐有邻,沈文都,汪洪.钢筋砼粘结锚固性能的试验研究[J].建筑结构学报.1994,15(3): 26-37.Xu Youlin,Shen Wendu,Wang Hong.An experimental study of bond-anchorage properties of bars in concrete[J].Journal of Building Structures,1994,15(3): 26-37.(in Chinese)
[23] 金伟良,袁迎曙,卫军,等.氯盐环境下混凝土结构耐久性理论与方法[M].北京: 科学出版社,2011.Jin Weiliang,Yuan Yingshu,Wei Jun,et al.Durability theory and design method for concrete structures under chloride attack [M].Beijing: Science Press,2011.(in Chinese)
[24] Holmen J O.Fatigue of concrete by constant and variable amplitude loading [C]// Fatigue of Concrete Structures.Detroit America: American Concrete Institute,1982:71-110.
[25] 王瑞敏,赵国藩,宋玉普.混凝土的受压疲劳性能研究[J].土木工程学报,1991,24(4): 38-47.Wang Ruimin,Zhao Guofan,Song Yupu.Fatigue of plain concrete under compression [J].China Civil Engineering Journal,1991,24(4): 38-47.(in Chinese)
[26] 朱劲松,闫广鹏.钢筋混凝土桥面板疲劳数值分析方法[J].中国公路学报.2012,25(1): 59-66.Zhu Jinsong,Yan Guangpeng.Method of numerical simulation for reinforced concrete bridge slabs under fatigue load [J].China Journal of Highway and Transport,2012,25(1): 59-66.(in Chinese)
[27] Li Z X,Chan T H T,Ko J M.Fatigue analysis and life prediction of bridges with structural health monitoring data—Part I: methodology and strategy [J].International Journal of Fatigue,2001,23(1): 45-53.
[28] 朱劲松,朱先存.钢筋混凝土桥梁疲劳累积损伤失效过程简化分析方法[J].工程力学,2012,29(5): 107-114.Zhu Jinsong,Zhu Xiancun.Simplified method for analysis of fatigue cumulative damage failure process of RC bridge [J].Engineering Mechanics,2012,29(5):107-114.(in Chinese)
[29] Li G,Hu F,Wu Y.Chloride ion penetration in stressed concrete [J].Journal of Materials in Civil Engineering,2011,23(8): 1145-1153.
[30] 蒋金洋,孙伟,王晶,等.弯曲疲劳载荷作用下结构混凝土抗氯离子扩散性能[J].东南大学学报(自然科学版),2010,40(2): 362-366.Jiang Jinyang,Sun Wei,Wang Jing,et al.Resistance to chloride ion diffusion of structural concrete under bending fatigue load [J].Journal of Southeast University(Natural Science Edition),2010,40(2): 362-366.(in Chinese)
[31] 李士彬,张伟平,顾祥林,等.加速锈蚀钢筋的疲劳试验研究[J].铁道学报,2010,32(5): 93-97.Li Shibin,Zhang Weiping,Gu Xianglin,et al.Experimental study on fatigue properties of corrosion-accelerated steel bars [J].Journal of the China Railway Society,2010,32(5): 93-97.(in Chinese)
[32] 张建仁,张克波,彭晖,等.锈蚀钢筋混凝土矩形梁正截面抗弯承载力计算方法[J].中国公路学报,2009,22(3): 45-51.Zhang Jianren,Zhang Kebo,Peng Hui,et al.Calculation method of normal section flexural capacity of corroded reinforced concrete rectangular beams [J].Journal of Highway and Transport,2009,22(3): 45-51.(in Chinese)
[33] GB 50010-2010,混凝土结构设计规范[S].北京: 中国建筑工业出版社,2010.GB 50010-2010,Code for design of concrete structures[S].Beijing: China Architecture & Building Press,2010.(in Chinese)
[34] Ng C K,Tan K H.Flexural behaviour of externally prestressed beams.Part I: Analytical model [J].Engineering Structures,2006,28(4): 609-621.
[35] 易建国.混凝土简支梁(板)桥[M].第3版.北京: 人民交通出版社,2016.Yi Jianguo.Reinforced concrete simply supported girder(slab) bridges [M].3rd ed.Beijing: China Communications Press,2016.(in Chinese)
[36] Boulfiza M,Sakai K,Banthia N,et al.Prediction of cracking effect on the penetration of chloride ions in reinforced concrete [J].Proceedings of the Japan Concrete Institute,2000,22(1): 91-96.
[37] 赵瀚玮.钢筋混凝土简支梁桥的振动效应与疲劳特性的研究[D].重庆: 重庆交通大学,2014.Zhao Hanwei.Research on the effects of vibration and fatigue characteristics of reinforced concrete simply supported girder bridges [D].Chongqing: Chongqing Jiaotong University,2014.(in Chinese)
TIME-VARYING BEARING CAPACITY EVALUATION OF BRIDGE UNDER COUPLING ACTION OF CORROSION AND FATIGUE
杨 慧(1988―),男,河南人,博士生,主要从事结构健康监测研究(E-mail: yh198848@emails.bjut.edu.cn);
闫维明(1960―),男,黑龙江人,教授,博士,主要从事结构隔震、减震与振动控制研究(E-mail: yanwm@bjut.edu.cn).