双钢板-混凝土组合(DSCC)剪力墙是一种在双层钢板之间内填混凝土，并用栓钉等连接件将钢板和混凝土紧密组合的新型抗侧力构件。该构件以其出色的抗震性能和较快的施工速度在欧美和日本地区已有不少应用，如近海平台和核电站[1－2]。在我国，该类构件已应用于盐城电视塔、广东东塔以及千手观音像[3－5]。
国内外学者对DSCC剪力墙的抗震性能进行了较多的试验研究。Eom等[6]通过矩形和T形截面DSCC剪力墙的拟静力试验研究发现该剪力墙的抗剪承载力很高。基于拟静力试验研究，聂建国等[7－8]对比了DSCC和传统RC剪力墙以及内置钢板-混凝土组合剪力墙，结果表明DSCC剪力墙具有更好的延性和耗能能力。Ji等[9]提出了一种适用于超高层建筑底部楼层的DSCC剪力墙，其边缘构件内置了圆钢管，并通过拟静力试验发现设置圆钢管能显著增强墙体的耗能能力以及抗剪承载力。马恺泽等[10]研究了内填高强混凝土的DSCC剪力墙在高轴压比下的抗震性能，结果表明：DSCC剪力墙的滞回曲线饱满，在相同轴压力下，设置竖向加劲肋的试件较设置约束拉杆的试件具有更高的承载力。上述研究均表明这种新型抗侧力构件具有良好性能，可应用于实际工程。
在现有的DSCC剪力墙试验与分析中，主要通过式(1)计算轴压承载力[9－15]，但该公式并未考虑外侧钢板的屈曲对轴压承载力的影响。DSCC剪力墙的轴压试验研究表明：与试验结果相比，式(1)预测的误差在-7%～13%范围内，计算结果稳定性较差[16]。而JGJ 138―2016《组合结构设计规范》[17]仅提出内嵌钢板的组合剪力墙极限承载力计算公式，未对新型的DSCC剪力墙有所介绍；JGJ/T380―2015《钢板剪力墙技术规程》[18]在描述DSCC剪力墙的轴压比n时，也采用了式(1)计算轴压承载力。因此，研究DSCC剪力墙的轴压承载力非常必要。
本文首先采用非线性有限元分析得出了DSCC剪力墙中墙面钢板屈曲应力的计算方法，并将其引入DSCC剪力墙轴向承载力的计算中，提出新的轴压承载力计算方法。为验证方法的可靠性和实用性，分别采用本文提出的方法与式(1)计算现有的DSCC剪力墙试件轴压试验的承载力，并进行对比。
本文选取文献[19]的四个轴压试件作为有限元分析对象，细节构造如图1所示，试件编号为DSW-1～DSW-4，距厚比B/t分别为50、33、5、2，其中B为连接件竖向(即沿墙高方向)间距，t为钢板厚度。组合剪力墙截面总宽度700 mm，总厚度166 mm，钢板厚3 mm。栓钉为φ6×48 mm，拉杆为φ6×160 mm。试件总高度1300 mm，在基础梁和加载梁间墙体高800 mm。各试件材料性质、试验装置等详见文献[19]。
图1 试件外形及连接件布置图 /mm
(○表示栓钉，×表示对拉螺栓)
Fig.1 Layout of connectors of specimens
1.2.1 混凝土
本文采用通用软件ABAQUS提供的混凝土弹塑性损伤模型模拟DSCC墙中内填混凝土的性能。混凝土的压应力-应变关系曲线包括弹性段、塑性硬化段和软化段。弹性段应力限值fe=0.3fc，fc为峰值压应力，取
fcu为混凝土标准立方体抗压强度。弹性模量
Eci为割线模量，
混凝土的峰值应变εc0=0.002。塑性硬化段应力-应变关系采用文献[22]建议的公式，其表达式为：
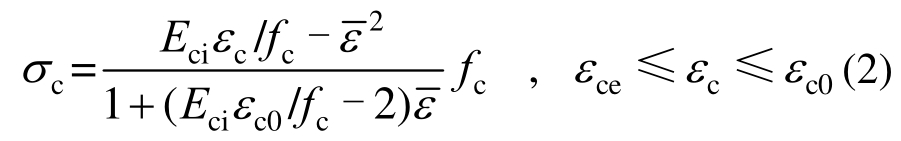
式中：
σc、εc分别为混凝土的压应力和压应变；εce=fe/Ec为弹性比例应变限值。
混凝土受压峰值后的软化曲线采用文献[22]建议的公式，其表达式为：
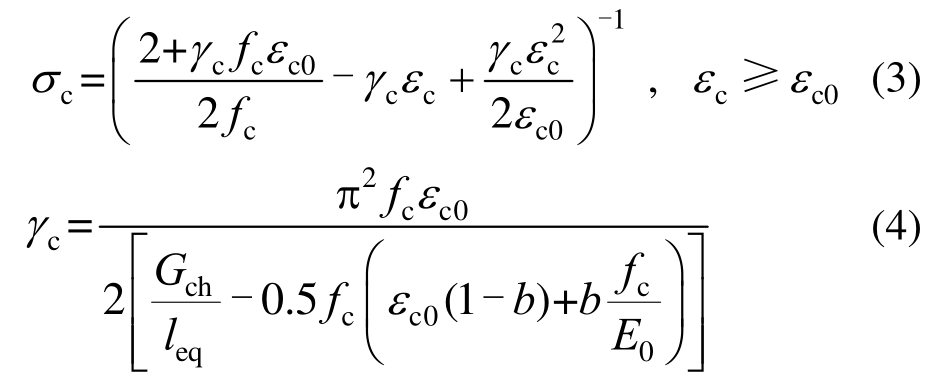
式中：γc为曲线下降段形状控制参数，考虑受压断裂能Gch和单元特征长度leq的影响；
对于实体单元；leq为单元体积的立方根；b根据文献[21]方法取值。
根据Alfarah等[21]的建议，混凝土拉应力段的表达式为：
式中：c1=3，c2=6.93；
w为裂缝宽度，wc为极限裂缝宽度，与混凝土抗拉强度ft和单位面积受拉断裂能GF有关，wc=5.14GF/ft。
考虑裂缝宽度w和单元特征长度leq的影响，混凝土拉应变的表达式为：
式中，εt0为与ft对应的拉应变。
1.2.2 混凝土的损伤变量
根据Alfarah等[21]的建议，在弹性段极限压(拉)应力后，混凝土开始产生损伤。其中，受压和受拉损伤变量(即dc和dt)分别按式(7)和式(8)计算：
式中
为非弹性应变；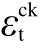
为断裂应变。
1.2.3 钢板
钢板的应力-应变关系采用三折线模型(包括弹性段、屈服平台段以及塑性硬化段)。在有限元模型中，取实际材料力学性能参数：弹性模量Es=206 GPa、泊松比μ=0.28、屈服强度fy=370 MPa、塑性硬化起始应变εsh=0.02、极限应变εu=0.15、抗拉强度fu=490 MPa。
1.2.4 栓钉和对拉螺栓
1) 抗剪性能曲线
根据Ollgaard等[23]的建议，栓钉和对拉螺栓的抗剪性能曲线按式(9)和式(10)计算：
式中：V/N和Vu/N分别为栓钉剪力和极限剪力；s/mm为滑移量；As/mm2为栓钉截面积；fc/MPa、Ec/MPa与前述定义相同。
2) 抗拔性能曲线
文献[24]表明，ABAQUS可较好模拟栓钉抗拔承载力。故采用文献[24]的方法建立了栓钉和对拉螺栓的抗拔试验模型，栓钉及混凝土采用C3D8R单元，在连接件与混凝土界面，法向采用硬接触，切向采用罚公式，获得栓钉和对拉螺栓的抗拔性能曲线，模型如图2所示，抗拔性能曲线如图3所示。
图2 栓钉抗拔有限元模型
Fig.2 Finte element model for stud pullout behavior
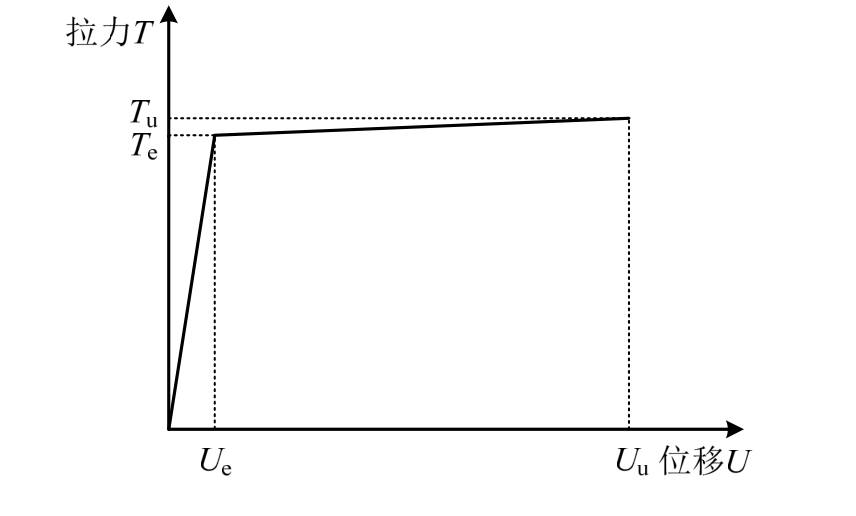
图3 栓钉抗拔性能曲线
Fig.3 Pullout curve of st uds
基于ABAQUS，建立足尺双钢板-混凝土组合剪力墙轴压性能分析模型，如图4所示。混凝土板、基础梁、加载梁均采用C3D8R实体单元，钢板采用S4R壳单元，栓钉和对拉螺栓均采用非线性弹簧单元SpringA，并考虑连接件的抗剪性能以及抗拔性能。考虑钢与混凝土的分离和抑制钢板向内屈曲，钢板和混凝土界面，采用无切向摩擦的硬接触。组合墙与加载梁、基础梁的连接采用绑定(tie)约束。为了避免由于局部荷载过大导致的单元模型局部变形过大，采用参考点与加载面耦合的方法进行竖向加载，并采用力-位移混合加载法。基础梁底面所有节点平动和转动自由度均被约束。轴压增加时，由于钢板屈曲，结构刚度可能发生剧烈变化，故，分析步采用显式动力分析(Explicit dynamics)[25]。
图4 DSCC剪力墙有限元模型
Fig.4 Finite element model of DSCC shear wall
在模拟中，提取了特征值屈曲分析中构件的屈曲模态作为钢板的初始缺陷，如图5所示。取剪力连接件间距的1/1000作为最大的侧向变形。
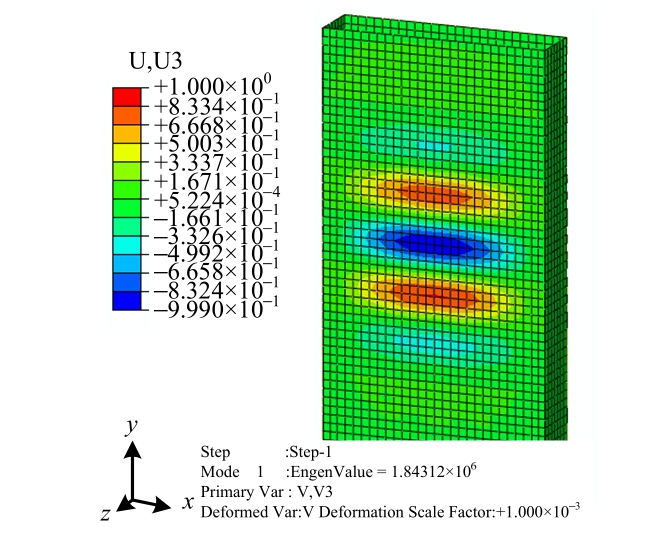
图5 DSW-1的特征值屈曲模态
Fig.5 Eigenvalue buckling mode of DSW-1
ABAQUS/Explicit应用中心差分法对运动方程进行显式时间积分，自动计算出各类含质量单元的稳定时间增量。在分析中，非线性弹簧单元SpringA只有刚度没有质量，故ABAQUS/Explicit并未对弹簧单元计算出稳定时间增量，存在潜在的不稳定性。根据文献[25―26]的建议，可通过考察能量确定模型的稳定性。图6展示了模型FE-1动能(ALLKE)、伪应变能(ALLAE)与内能(ALLIE)比值的时程图。可见，两个比值在计算时间内均小于5%，表明模型具有良好可靠性，可用于准静态分析使用。
图6 分析模型的能量比值时程图
Fig.6 Time history of energy ratios of the numerical analysis
图7展示了试验和有限元计算的荷载-位移曲线的对比。除了DSW-1和DSW-4，其他两试件在弹性受力范围内，计算结果与试验值基本重合，能较好地模拟试件的初始刚度。在非线性阶段，四个试件的极限承载力均与试验符合较好，能很好地模拟试件的极限承载力。
DSW-1试件内部混凝土可能存在孔洞缺陷，导致DSW-1的初始刚度低于模拟值。内部缺陷的存在也导致了钢板在荷载增加到500 kN时就发生局部屈曲。
造成DSW-4初始刚度较高的原因，可能是试验开始时，加载梁顶部与加载装置接触过于紧密，导致测得的初始位移偏小，初始刚度偏高，类似于文献[27]的试件DSC4-150。对比试验与模拟值的上升阶段(0.3Fu～0.8Fu)刚度，两个刚度基本接近。
图7 试验和数值荷载-位移曲线对比
Fig.7 Comparisons of experimental and numerical load-displacement curves
图8展示了试验中应变测点位置的钢板外侧应变的模拟值与试验值吻合较好，表明本文建立的有限元分析模型可靠，可用于模拟剪力墙钢板屈曲。
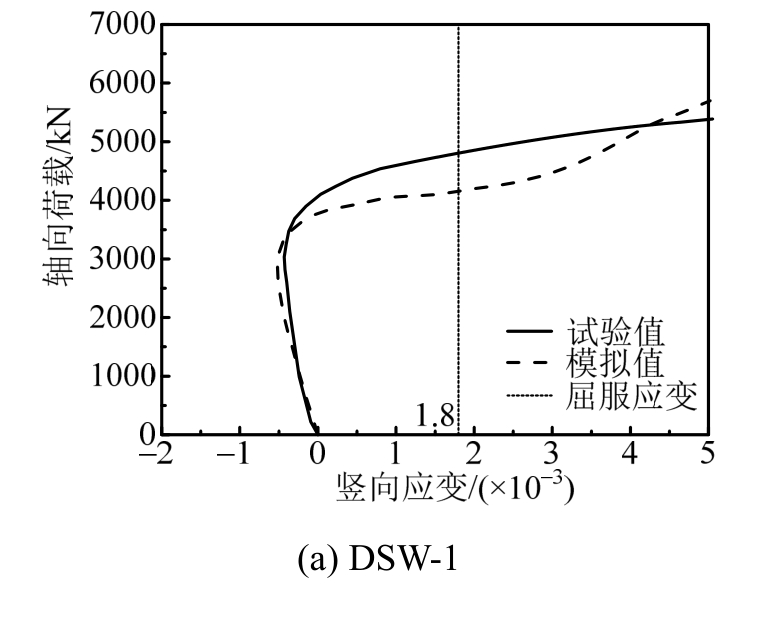
图8 试验和数值荷载-应变曲线对比
Fig.8 Comparisons of load-strain curves
图9展示DSCC剪力墙模型的位移结果以及与试验现象的对比。DSW-2未与试验现象对比是因为文献[19]未提供DSW-2的试验破坏图片。试验中，试件DSW-1～DSW-3在钢板中部出现贯通的局部屈曲。模拟结果显示DSW-1和DSW-2出现贯通的局部屈曲，钢板的最大平面外位移(U3)分别为22.8 mm、19.8 mm；DSW-3钢板的最大平面外位移为5.3 mm，也存在着出现贯通局部屈曲的趋势。由于试验中钢板缺陷的不确定性，因此无法通过有限元模拟得到具体发生最大平面外位移的位置，故模拟结果中最大位移位置与试验结果存在差异。试验中，DSW-4并未出现贯通局部屈曲，但加载梁底部发生了墙面钢板与侧面钢板交接处的焊缝拉裂，这与DSW-4构件的模拟现象类似。所以，有限元模拟结果与试验现象基本吻合。这说明较小的墙面钢板距厚比B/t可有效抑制钢板的屈曲，在相同的t下，B/t越大，墙面钢板越容易发生屈曲。
由于DSW-4的侧面钢板距厚比bs/ts为20，故本节还提取了DSW-4侧面钢板平面外位移(U1)，如图9(e)所示。可见最大位移仅为1.1 mm，故侧面钢板未出现局部屈曲，这可能是因为bs/ts较小，故需进一步研究bs/ts对侧面钢板屈曲及极限承载力的影响。
图9 钢板局部屈曲的数值结果与试验结果对比 /m
Fig.9 Comparisons of numerical and experimental results of local buckling of steel plates
图10为各试件在极限状态下的钢板与混凝土应力(S,Mises)云图，图中红色表示为钢板的屈服应力fy(370 MPa)或混凝土的轴心抗压强度fc(DSW-1、DSW-3为 41.92 MPa，DSW-2、DSW-4为37.44 MPa)，提取DSW-4的混凝土最大Mises应力为1.25fc。对比图8的结果发现，DSW-1、DSW-2试件钢板发生横向贯通屈曲的位置出现应力集中带，该位置内部的混凝土Mises应力大于混凝土轴心抗压强度fc(图中呈灰色)，两个试件的破坏模式均为钢板屈曲，混凝土压碎。
DSW-3试件的局部位置出现了钢板屈曲，剪力墙部分的钢板(不包括伸入梁内部分)受力均匀，均达到屈服应力fy，试件内多数混凝土的Mises应力仍未达到轴心抗压强度fc，该试件的破坏模式为钢板屈服。
DSW-4试件未出现钢板屈曲，钢板受力均匀，均达到屈服应力fy，多数混凝土的Mises应力高于1.25fc，该试件的破坏模式为钢板屈服，混凝土全部压碎。分析表明，较小的连接件间距及距厚比可抑制钢板屈曲，对混凝土起到约束作用，增大混凝土的极限抗压强度。同时，栓钉位置的混凝土处在较大应力状态下，也说明采用SpringA弹簧可较好地模拟栓钉在DSCC剪力墙中的作用。
图10 极限荷载下的应力云图 /Pa
Fig.10 Stress contours at the ultimate loading
当DSCC剪力墙受轴压力时,墙面钢板发生向外屈曲，降低了钢板的稳定性和剪力墙的承载力。基于试验，Akiyama等[28]提出了如下屈曲应力计算公式：
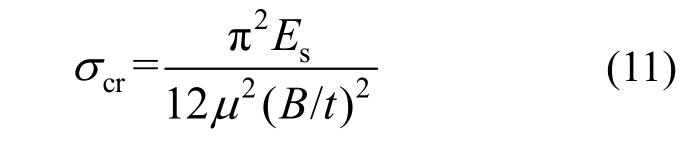
式中，μ为有效长度系数。
为验证式(11)和研究钢板初始缺陷、连接件抗拉刚度和形式以及距厚比对DSCC剪力墙屈曲性能的影响，本文建立了37个有限元模型，分析参数及模拟结果见表1。模型FEN-t3对应于文献[19]中的试件DSW-N(N=1,2,3,4)。研究距厚比的基本数值模型为四个基于试验的模型FEN-t3，而研究其余三个参数影响的基本模型均为FE1-t3，t/mm后面的数值代表钢板厚度。各设计参数均在基本模型上进行变化，变化某参数时，其余参数与基本模型中的保持一致。
DSCC剪力墙钢板的初始缺陷通常在钢板制造、连接件焊接和混凝土浇筑过程中产生。通过改变初始缺陷系数，考虑钢板表面缺陷对屈曲性能的影响。最大侧向变形Δ与连接件竖向间距B的关系如下式：
式中，αi为初始缺陷系数。
图11为钢板内侧(黑色)和外侧在不同初始缺陷情况(B/5000～B/500)下的竖向应力变化。屈曲前，初始缺陷越大，钢板内外侧的竖向应力差越大；屈曲后，内外侧应力均发生突变，且钢板凸曲使其外侧产生显著薄膜拉应力。由表1可知，初始缺陷越小，发生屈曲的轴压比越大，变化范围在0.356～0.582之间，但其对DSCC剪力墙轴压承载力的影响可忽略不计。
图11 不同初始缺陷下的墙面钢板屈曲位置竖向应力-轴压比关系曲线
Fig.11 Relationship of vertical stress and axial force ratio of steel wall plates under different initial imperfections
表1 有限元模型参数及模拟结果
Table 1 The parameters and simulation results of the finite element models
注：*表示钢板出现薄膜拉应力；ncr=
表示钢板屈曲时的轴压比，其中Ncr为钢板发生屈曲时的轴压力，NFEM为有限元模型得到的极限承载力；sd表示全栓钉连接；bt表示全对拉螺栓连接；t和ts分别为墙面和侧面钢板厚度；bs为侧面钢板的连接件间距，若侧面钢板未设置连接件，取bs为墙体厚度T；σcr,o和σcr,i分别为钢板屈曲位置的外、内侧应力。
试件编号αi/(×10-3)αstB/tbs/ts σcr/MPaNFEM/Nncr σcr,oσcr,i FE1-t3* 1 0.3 50 20 107 209 6316 0.451 FE1-t3-1* 1/5 0.3 50 20 179 223 6275 0.582 FE1- t3-2* 1/2 0.3 50 20 138 210 6323 0.498 FE1- t3-3* 2 0.3 50 20 69 177 6321 0.356 FE1- t3-4* 1 0.05 50 20 101 196 6308 0.428 FE1- t3-5* 1 0.1 50 20 103 201 6319 0.435 FE1- t3-6* 1 0.7 50 20 109 212 6312 0.460 FE1- t3-7* 1 1.4 50 20 110 217 6310 0.468 FE1-t3-sd* 1 0.3 50 20 106 204 6260 0.448 FE1-t3-bt* 1 - 50 20 112 216 6365 0.463 FE1-t2* 1 0.3 75 20 39 95 5779 0.190 FE1-t4* 1 0.3 38 20 198 348 6761 0.779 FE1-t5* 1 0.3 30 20 288 388 7202 0.923 FE1-t6* 1 0.3 25 20 321 383 7826 0.971 FE1-t7* 1 0.3 21 20 335 383 8631 0.964 FE1-t8* 1 0.3 19 20 343 380 9444 0.935 FE1-t9* 1 0.3 18 20 347 379 10025 0.937 FE2-t3* 1 0.3 33 20 287 380 6123 0.911 FE2-t2* 1 0.3 50 20 129 221 5447 0.505 FE2-t2.5* 1 0.3 40 20 218 376 5815 0.814 FE2-t4* 1 0.3 25 20 333 376 6643 0.946 FE2-t5* 1 0.3 20 20 346 375 7425 0.929 FE2-t6* 1 0.3 17 20 351 372 7973 0.933 FE2-t8 1 0.3 13 20 — — 9056 —FE3-t3 1 0.3 25 20 — — 6827 —FE3-t1.5 1 0.3 50 20 236 319 5518 0.689 FE3-t2 1 0.3 38 20 341 376 5950 0.878 FE3-t2.5 1 0.3 30 20 — — 6392 FE3-t4 1 0.3 19 20 — — 7378 —FE3-t5 1 0.3 15 20 — — 7933 —FE4-t3 1 0.3 12 20 — — 7440 —FE4-t2 1 0.3 18 20 — — 6604 —FE4-t1.8 1 0.3 20 20 — — 6415 —FE4-t1.2 1 0.3 20 30 — — 6180 —FE4-t1 1 0.3 20 36 — — 5940 —FE4-t3-ts6 1 0.3 12 28 — — 7273 —FE4-t3-ts4 1 0.3 12 40 — — 7076 —
弹簧单元的受力分析表明试件到达极限承载力前，SpringA弹簧单元均处在弹性阶段，这与文献[29]采用实体单元模拟栓钉的结果一致。
当栓钉长径比大于7.5(即，lst/d＞7.5)时，85%的试件为栓钉拉断，呈现出较好的延性[30]。文献[24]的多组试验也证实了上述观点。当lst/d≥8时，破坏为栓钉拉断，抗拔承载力主要由栓钉强度控制。
由于当前规范及研究对栓钉抗拉刚度的关注不足，本文拟研究栓钉刚度对DSCC墙承载力的影响。采用如下公式计算栓钉抗拉刚度[27]：
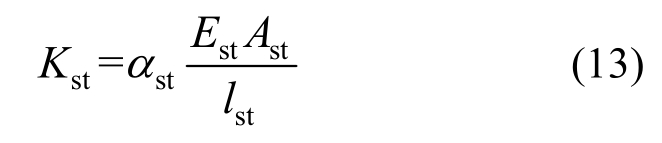
式中：αst为栓钉等效抗拉刚度系数；Est为栓钉的材料弹性模量；Ast为栓钉截面积；lst为栓钉长度。
对比FE1-t3-4～FE1-t3-7及FE1-t3的数值结果表明，当0.05＜αst＜1.4时，构件极限承载力变化微小，但对钢板屈曲应力有一定影响。
在实际工程中，常用的DSCC剪力墙连接形式有栓钉连接和栓钉-对拉螺栓连接[3－5]。栓钉通过其与周围混凝土的锚固实现钢板和混凝土的共同作用，而对拉螺栓通过自身抗拉及与周围混凝土的粘结实现共同作用。为此，本节研究了栓钉、栓钉-对拉螺栓、对拉螺栓三种连接形式对钢板屈曲的影响。
从表1可见，连接件形式对钢板屈曲应力和轴压承载力存在一定影响，屈曲应力越高，轴压承载力越大。构件的轴压承载力从大到小依次为：对拉螺栓连接的剪力墙、栓钉-对拉螺栓连接的剪力墙、栓钉连接的剪力墙。但总体来讲，连接件形式对承载力的影响较小，可忽略不计。
研究表明，墙面钢板距厚比，即连接件竖向间距B与钢板厚度t的比值是影响钢板屈曲的主要因素[27]。但目前尚无文献研究连接件竖向间距B以及侧面钢板距厚比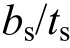
对钢板屈曲的影响。本文通过改变钢板厚度实现距厚比的变化，取
为12～75。而对
的研究仅在FE4-t3模型中展开，取为20～40。
表1结果显示
对钢板屈曲应力和极限承载力的影响均较为明显
越大，钢板屈曲应力越小，极限承载力也越小。
是影响钢板屈曲以及屈曲后强度的重要因素。FE1～FE4的连接件竖向间距B分别为150 mm、100 mm、75 mm和36 mm。在相同的
下，B越大，钢板越容易发生屈曲，对应屈曲轴压比越小；同时，当B＜100 mm时，钢板屈曲后不再产生薄膜拉应力，失去屈曲后强度，发生一定程度的卸载。当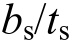
为20～40时，FE4-t3模型均未出现侧面钢板屈曲，钢板受力均匀，故
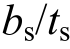不影响侧面钢板屈曲，这主要是因为侧面钢板由于其宽度较小而不会发生屈曲。故，控制连接件竖向间距B以及距厚比
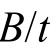可有效抑制钢板屈曲。
图12为各试件距厚比与屈曲应力的关系曲线。由于初始缺陷的存在，钢板屈曲时，其内外侧应力存在差异，取钢板的平均压应力σcr,k为钢板的屈曲应力，σcr,k=(σcr,o+σcr,i)/2。当μ=0.7时，式(11)计算结果较σcr,k偏于安全，故取μ=0.7，并认为当σcr＞fy时，取σcr=fy，进而得到适用于承载力计算的屈曲应力计算公式：
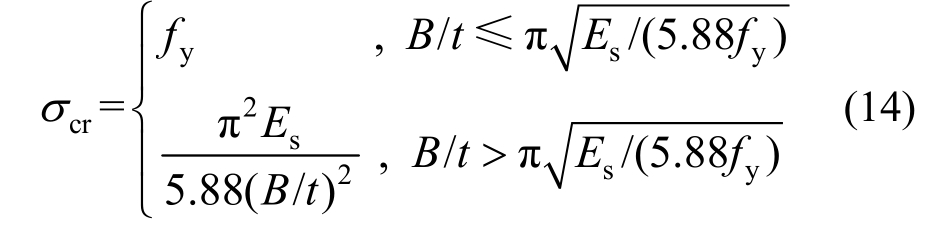
图12 各试件距厚比-屈曲应力的关系曲线
Fig.12 Relationship of buckling stress and the ratio of connector spacing to plate thickness for different specimens
由屈曲分析可知，墙面钢板距厚比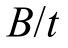
影响DSCC剪力墙的极限荷载与钢板的屈曲应力，且B影响屈曲后强度。故，考虑B及
对构件极限承载力的影响，提出了基于强度叠加理论的DSCC剪力墙轴压承载力计算公式：
式中：fc为混凝土轴心抗压强度；Ac为混凝土截面积；σcr为墙面钢板屈曲应力；fy,2为侧面钢板屈服应力；Asurf和Aside分别为墙面和侧面钢板截面积；αc为考虑钢板屈曲、B及B/t影响而对混凝土抗压强度进行调整的系数。通过表1中的极限承载力NFEM代入式(15)中得到αc，并对得到的αc进行拟合(如图13所示)，确定αc的取值表达式：
式中，
图13 参数αc的拟合过程
Fig.13 Curve fitting ofαc
当σcr＜fy且B≥100 mm时，认为钢板出现横向贯通屈曲，屈曲位置的混凝土受力迅速增大，达到抗压强度fc，故取αc=1；当σcr＜fy且B＜100 mm时，由于连接件竖向间距B较小，钢板发生屈曲但是难以形成薄膜拉应力提供屈曲后强度，可能导致构件达到极限承载力时的混凝土尚未达到fc，故通过系数β1对fc进行调整；当σcr=fy时，钢板不发生屈曲或屈曲强度接近fy，但是实际钢板由于初始几何缺陷的存在和B的差异使钢板难以保持全截面处于屈服强度fy，混凝土虽然可以继续承载，但是极限承载力难以继续提升，故通过系数β1调整这种破坏模式下的fc；当σcr=fy，且B与B/t均较小时，与钢管混凝土类似，外侧钢板对混凝土墙体形成约束效应，增大了混凝土的抗压强度，故通过系数β2对混凝土抗压强度fc进行调整。
国内外学者对DSCC剪力墙的轴压性能进行了试验研究[16,19,27,31]。将规范JGJ/T 380―2015的计算公式与本文提出的式(15)进行对比，如图14所示。本文公式计算结果与试验结果的比值Nu/Nt的平均值为1.011，标准差为0.063，均优于规范公式的结果(Nc/Nt的平均值为1.086，标准差为0.128)，表明式(15)可更准确更偏安全地计算DSCC剪力墙的轴压承载力。文献[31]的试件均未设置侧面钢板，采用本文公式计算的结果，平均值偏大3.4%，这是由于试件未设置侧面钢板，减弱了钢板对混凝土的约束。文献[32]的试件HGW-3采用竖向加劲肋连接件，采用式(15)计算的结果小于试验承载力，这是由于竖向加劲肋的设置，阻碍了墙面钢板横向贯通屈曲的形成，增大了钢板屈曲应力。除竖向加劲肋外，对其他连接形式的DSCC剪力墙均得到了较精确的计算结果，表明式(15)具有较强的适用性，可以适用于不同的连接件形式。
图14 规范公式与本文公式的计算结果对比
Fig.14 Comparision of calculation results between proposed formula and standard formula
本文首先通过数值研究得出了双钢板-混凝土组合(DSCC)剪力墙中墙面钢板的屈曲应力计算方法，并将其引入DSCC剪力墙轴向承载力的计算中，从而更加真实地考虑了墙面钢板屈曲对剪力墙轴向承载力的影响。主要结论如下：
(1) 使用ABAQUS/Explicit进行准静态分析，可较好模拟DSCC剪力墙的轴压性能。
(2) 连接件竖向间距和钢板厚度比(距厚比)是影响DSCC剪力墙钢板屈曲应力以及屈曲轴压比ncr的重要因素，但连接件形式和初始缺陷对DSCC剪力墙极限承载力的影响不大。
(3) 较小的连接件竖向间距和距厚比能使连接件对混凝土起到一定的约束作用，从而提高混凝土的抗压强度。
(4) 基于有限元计算和参数分析，提出了轴压承载力计算公式，并与试验值对比，其比值Nu/Nt的平均值为1.011，标准差为0.063，相对于规范JGJ/T 380―2015采用的计算公式能更精确稳定地计算DSCC剪力墙的轴压承载力，可为工程设计提供参考依据。
[1] Pryer J W,Bowerman H G.The development and use of British steel Bi-Steel [J].Journal of Constructional Steel Research,1998,46(1): 173―178.
[2] Takeuchi M,Narikawa M,Matsuo I,et al.Study on a concrete filled structure for nuclear power plants [J].Nuclear Engineering and Design,1998,179(2): 209―223.
[3] 祝文君,马军,黄会平,等.双层钢板组合剪力墙在异型结构中的应用及研究[J].特种结构,2010,27(2):14―16.Zhu Wenjun,Ma Jun,Huang Huiping,et al.Application and research of double-layer steel composite shear wall in the special structure [J].Special Structures,2010,27(2): 14―16.(in Chinese)
[4] 丁朝辉,江欢成,曾菁,等.双钢板-混凝土组合墙的大胆尝试——盐城电视塔结构设计[J].建筑结构,2011,41(12): 87―91.Ding Zhaohui,Jiang Huancheng,Zeng Jing,et al.An innovative application of SCS composite wall: Structural design of Yancheng TV Tower [J].Building Structure,2011,41(12): 87―91.(in Chinese)
[5] 赵宏,雷强,侯胜利,等.八柱巨型结构在广州东塔超限设计中的工程应用[J].建筑结构,2012,42(10): 1―6.Zhao Hong,Lei Qiang,Hou Shengli,et al.Engineering application of 8 columns mega frame-core wall system in Guangzhou East Tower [J].Building Structure,2012,42(10): 1―6.(in Chinese)
[6] Eom T S,Park H G,Lee C H,et al.Behavior of double skin composite wall subjected to in-plane cyclic loading[J].Journal of Structural Engineering,2009,135(10):1239―1249.
[7] 聂建国,卜凡民,樊健生.低剪跨比双钢板-混凝土组合剪力墙抗震性能试验研究[J].建筑结构学报,2011,32(11): 74―81.Nie Jianguo,Bu Fanmin,Fan Jiansheng.Experimental research on seismic behavior of low shear-span ratio composite shear wall with double steel plates and infill concrete [J].Journal of Building Structures,2011,32(11): 74―81.(in Chinese)
[8] 李盛勇,聂建国,刘付钧,等.外包多腔钢板-混凝土组合剪力墙抗震性能试验研究[J].土木工程学报,2013,46(10): 26―38.Li Shengyong,Nie Jianguo,Liu Fujun,et al.Experimental study on aseismic behavior of concrete filled double-steel-plate composite shear walls [J].China Civil Engineering Journal,2013,46(10): 26―38.(in Chinese)
[9] Ji X,Jiang F,Qian J.Seismic behavior of steel tube-double steel plate-concrete composite walls:Experimental tests [J].Journal of Constructional Steel Research,2013,86: 17―30.
[10] 马恺泽,刘伯权,鄢红良,等.高轴压比双层钢板-高强混凝土组合剪力墙抗震性能试验研究[J].工程力学,2014,31(5): 218―224.Ma Kaize,Liu Boquan,Yan Hongliang,et al.Experimental investigation on aseismic behavior of dual steel high strength concrete shear walls with high axial load ratio [J].Engineering Mechanics,2014,31(5):218―224.(in Chinese)
[11] 李健,罗永峰,郭小农,等.双层钢板组合剪力墙抗震性能试验研究[J].同济大学学报(自然科学版),2013,41(11): 1636―1643.Li Jian,Luo Yongfeng,Guo Xiaonong,et al.Experimental research on seismic behavior of double skin composite shear wall [J].Journal of Tongji University,2013,41(11): 1636―1643.(in Chinese)
[12] 刘鸿亮,蔡健,杨春,等.带约束拉杆双层钢板内填混凝土组合剪力墙抗震性能试验研究[J].建筑结构学报,2013,34(6): 84―92.Liu Hongliang,Cai jian,Yang Chun,et al.Experimental study on seismic behavior of composite shear wall with double steel plates and infill concrete with binding bars[J].Journal of Building Structures,2013,34(6): 84―92.(in Chinese)
[13] 朱立猛,周德源,赫明月.带约束拉杆钢板-混凝土组合剪力墙抗震性能试验研究[J].建筑结构学报,2013,34(6): 93―102.Zhu Limeng,Zhou Deyuan,He Mingyue,Experimental research on seismic behavior of composite concrete and steel plate shear walls with binding bars [J].Journal of Building Structures,2013,34(6): 93―102.(in Chinese)
[14] 韦芳芳,杜金娥,胡雪峰,等.单面受火双钢板-混凝土组合剪力墙的耐火性能试验研究[J].东南大学学报(自然科学版),2016,46(3): 518―522.Wei Fangfang,Du Jin’e,Hu Xuefeng,et al.Experimental research on fire performance of concrete filled doublesteel-plate composite wall exposed to one-side fire [J].Journal of Southeast University,2016,46(3): 518―522.(in Chinese)
[15] 胡红松,聂建国.双钢板-混凝土组合剪力墙变形能力分析[J].建筑结构学报,2013,34(5): 52―62.Hu Hongsong,Nie Jianguo.Deformability analysis of composite shear walls with double steel plates and infillconcrete [J].Journal of Building Structures,2013,34(5):52―62.(in Chinese)
[16] 张有佳,李小军,贺秋梅,等.钢板混凝土组合墙体局部稳定性轴压试验研究[J].土木工程学报,2016,49(1): 62―68.Zhang Youjia,Li Xiaojun,He Qiumei,et al.Experimental study on local stability of composite walls with steel plates and filled concrete under concentric loads [J].China Civil Engineering Journal,2016,49(1):62―68.(in Chinese)
[17] JGJ 138―2016,组合结构设计规范[S].北京: 中国建筑工业出版社,2016.JGJ 138―2016,Code for design of composite structures[S].Beijing: China Architecture & Building Press,2016.(in Chinese)
[18] JGJ/T 380―2015,钢板剪力墙技术规程[S].北京: 中国建筑工业出版社,2015.JGJ/T 380―2015,Technical specification for steel plate shear walls [S].Beijing: China Architecture & Building Press,2015.(in Chinese)
[19] 刘阳冰,杨庆年,刘晶波,等.双钢板-混凝土剪力墙轴心受压性能试验研究 [J].四川大学学报(工程科学版),2016,48(2): 83―90.Liu Yangbing,Yang Qingnian,Liu Jingbo,et al.Experimental research on axial compressive behavior of shear wall with double steel plates and filled concrete [J].Journal of Sichuan University,2016,48(2): 83―90.(in Chinese)
[20] GB 50010―2010,混凝土结构设计规范[S]: 北京：中国建筑工业出版社,2011.GB 50010―2010,Code for design of concrete structures[S].Beijing: China Architecture & Building Press,2011.(in Chinese)
[21] Alfarah B,López-Almansa F,Oller S.New methodology for calculating damage variables evolution in Plastic Damage Model for RC structures [J].Engineering Structures,2017,132: 70―86.
[22] Krätzig W B,Pölling R.An elasto-plastic damage model for reinforced concrete with minimum number of material parameters [J].Computers & Structures,2004,82(15): 1201―1215.
[23] Ollgaard J G,Slutter R G,Fisher J W.Shear strength of stud connectors in lightweight and normalweight concrete [J].AISC Engineering,1971,8(4): 55―64.
[24] 马原.组合结构栓钉连接件抗拔性能研究[D].北京:清华大学,2015: 85―92.Ma Yuan.Research on the uplift performance of headed studs in composite structure [D].Beijing: Tsinghua University,2015: 85―92.(in Chinese)
[25] 庄茁.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009: 209―217.Zhuang Zhuo.Finite element analysis and applications based on software ABAQUS [M].Beijing: Tsinghua University Press,2009: 209―217.(in Chinese)
[26] DS Simulia Corporation.Getting started with abaqus:interactive edition [Z].Rhode Island: DS Simulia Corporation,2012.
[27] Yang Y,Liu J,Fan J.Buckling behavior of double-skin composite walls: An experimental and modeling study[J].Journal of Constructional Steel Research,2016,121:126―135.
[28] Akiyama H,Sekimoto H,Fukihara M,et al.A compression and shear loading test of concrete filled steel bearing wall [C]// Transaction of the 11th International Conference on Structural Mechanics in Reactor Technology.Tokyo,Japan: International Association for Structural Mechanics in Reactor Technology (IASMiRT),1991: 323―328.
[29] 张有佳,李小军.钢板混凝土组合墙轴压受力性能有限元分析[J].工程力学,2016,33(8): 84―92.Zhang Youjia,Li Xiaojun,Finite element analysis of axial compressive stress performance for steel plate reinforced concrete compound walls [J].Engineering Mechanics,2016,33(8): 84―92.(in Chinese)
[30] Pallares L,Hajjar J F.Headed steel stud anchors in composite structures,Part II: tension and interaction [J].Journal of Constructional Steel Research,2010,66(2):213―228.
[31] Huang Z,Liew J Y R.Compressive resistance of steel-concrete-steel sandwich composite walls with J-hook connectors [J].Journal of Constructional Steel Research,2016,124: 142―162.
[32] Hao T,Cao W,Qiao Q,et al.Structural performance of composite shear walls under compression [J].Applied Sciences,2017,7(2): 162.
COMPUTATIONAL METHOD FOR AXIAL COMPRESSION CAPACITY OF DOUBLE STEEL-CONCRETE COMPOSITE SHEAR WALLS WITH CONSIDERATION OF BUCKLING
韦芳芳(1978―)，女，浙江人，副教授，博士，硕导，主要从事钢-混凝土组合结构研究(E-mail: ffwei@hhu.edu.cn);
郑泽军(1994―)，男，浙江人，硕士生，主要从事钢-混凝土组合结构研究(E-mail: zhengzj@hhu.edu.cn);
王永泉(1981―)，男，江苏人，副教授，博士，硕导，主要从事复杂结构施工分析研究(E-mail: wyq_hhu@hhu.edu.cn).