图1 基于混合加权法的排架结构全寿命期地震成本流程
Fig.1 Framework of SLCC estimation based hybrid weight factors
工业建筑是指供人类从事各类生产活动的建筑物和构筑物，在社会的发展和人类文明进步中占据极为重要的地位。其中以工业厂房为工业建筑的代表。工业化又直接推动了大规模的城市化发展，大量人口涌入城市，如果城市位于地震高烈度地区或沿海地区，一旦地震灾害发生将对当地的工业与民用基础设施造成严重威胁。如2008年汶川地震中大量接近震中龙门山断裂带的工业厂房倒塌损毁，这引起了人们对于满足常规抗震规范设计要求的已建传统大跨度工业建筑在面临近断层强脉冲地震波冲击时可能仍然面临抗震性能不足的担忧[1]；2018年9月28日印尼中苏拉威西省发生强烈地震(Ms7.4)并随后引发大规模海啸，这次海啸重创中苏拉威西省首府帕卢市和另一座海滨城市东加拉。据联合国难民署估计，此次地震被地震和海啸摧毁房屋2.5万座，受损6.5万座，6万人无家可归，重灾区帕卢市当地如水力、电厂、通信等工业建筑及基础设施被严重损毁，导致地震后当地电力、通信、水等供应中断[2]，由于印尼国力弱小且没有地震巨灾保险政策，灾区无法得到国家强力援助，预计完全恢复将是该地区长期面临的挑战。基于此近年来很多临近地震断裂带的地震高烈度地区都在对于当地已建建筑进行多种加固方式的研究，以期有效提高已建工程结构的抗震安全裕度，作为应对未来可能面临近断层强脉冲地震冲击巨大威胁的有效技术对策。当前国内外对于工业建筑地震易损性方面的研究较多，但基于采取有效加固措施后工程结构地震易损性并对加固结构全寿命周期地震维护成本与地震巨灾保险的相关应用性研究很少。
目前在地震灾害频发的发达国家如日本，美国加州、新西兰等国均普及地震巨灾保险，国际上地震灾害保险赔款大约占灾害损失1/3，有效分担了政府的财政负担。完善的地震保险政策的出台需要依据不同地震烈度地区建立不同的地震巨灾保险费率，而保险费率需要在工程全寿命周期研究的基础上获得。当前我国工程全寿命周期研究才刚起步，因此如何在工程全寿命周期地震成本的基础上加快推进具有中国特色的地震巨灾保险制度成为当务之急。为落实党中央和国务院关于建立国家巨灾保险制度的决策部署，2017年4月中国保监会和中国地震局共同签订了《中国保险监督管理委员会、中国地震局战略合作协议》，联合成立了中国地震风险与保险实验室，研发满足地震巨灾保险需求的地震危险性评价、地震灾害风险评估方法和技术，联合实验室的核心任务为探索建立和完善我国自主知识产权的地震巨灾模型，努力实现政府、市场、社会、企业、个人等共同承担地震灾害风险[3]。
我国地处全球两大活跃地震带之间：环太平洋地震带和欧亚地震带，历来为地震多发国家，全国大部分大中城市均处于地震区。由于地震发生具有很大的不可预测性和突然性，目前的建筑抗震技术要完全避免地震灾难还很困难，近年来随着对自然灾害灾后恢复重建研究的不断进展，明确了通过以下这三个领域的不懈努力有可能将地震等自然灾害对人类社会的不利影响消减到最小程度以期尽快恢复重建，即：
1) 减小工程结构体系的失效概率；
2) 减小体系失效后的损失值；
3) 采取措施减小灾后恢复重建的时间和费用。
工程结构全寿命周期研究从广义上而言实际上包括了所有不同风险因素对于工程结构的综合影响，其中既有人为的因素，也有自然环境的影响因素。虽然由于时间所导致的材料长期时变劣化影响针对不同地区不同环境中的工业建筑可能也是可考量的重要因素，但对于西北地震高烈度地区而言，显然将研究侧重点放在由于地震所导致的工程结构全寿命周期成本的影响更为合理。国际上由美国太平洋地震工程研究中心2000年率先提出了应用于结构损伤到损失评估的基于性能的地震工程研究方法(performance based earthquake engineering，PBEE)[4－5]，由此将工程全寿命周期地震灾害损失研究带入实用发展阶段；2001年Wen等[6]在考虑入射地震荷载随机特性(发生时间、强度、持时)基础上研究了建筑结构全寿命期成本最小化的设计优化原则，研究中全寿命周期成本包括工程建造、损伤维护、人员伤亡等成本计算，并随后以一栋九层钢筋混凝土办公楼为例基于地震和风荷载开展了优化验证；2003年Liu等[7]基于静态Pushover方法分析五层简化钢框架结构全寿命周期成本，包括起始建造成本和全寿命周期地震成本两部分，计算通过简化的基因遗传算法探测最优设计参数集，结果发现对应的有效参数解集取值范围较大；2004年Takahashi、Kiureghian等[8]通过建立综合考虑不同地区的地震断裂带类型、弹性波的传播、场地土放大效应和结构的动力特征的自更新模型来最大限度真实模拟地震发生，进一步以简化多层钢结构为例估算了预期的结构损伤和工程结构全寿命周期总成本，验证了带油阻尼器的结构可有效减小全寿命周期地震成本；由于桥梁维护从社会角度来看是有利于延长桥梁寿命的正向收益，但由于修桥有时会严重影响用户通行，耽误用户宝贵时间，所以从用户角度来看是增加了社会成本，2009年Christensen等[9]从用户和社会效益角度全面分析了桥梁的全寿命周期成本收益，从中得出了桥梁的优化维修策略；2011年Mitropoulou等[10]针对钢筋混凝土框架结构基于增量动力分析和静态Pushover法进行了全寿命周期地震成本的定量估算，研究中采用了层间最大加速度和顶层加速度指标，计算中的全寿命周期地震成本包含了结构性构件损伤维修成本和非结构性附属构件和设备的损失，进一步将结构全寿命期地震成本研究推向实用化；2013年Chiu等[11]基于Park&Ang损伤模型采用静态Pushover法对16栋低层钢筋混凝土教学楼结构的抗震加固方案进行了全寿命周期地震成本-收益分析，对台湾地区旧有教学楼的防震减灾具有积极意义；2016年Castaldo等[12]对安装不同单凹面曲率度摩擦摆隔震器的钢筋混凝土基础隔震结构全寿命周期成本和抗震可靠性进行分析，拉丁超立方样本法被用于从随机隔震周期和摩擦系数值中抽样，研究了FPS隔震摆曲率角度对于隔震结构全寿命周期地震成本的影响。
综上近年来不断有国内外学者对工程结构进行全寿命周期成本的开拓性研究，初步显现了该领域研究的广阔发展潜力和工程价值。由于工程结构全寿命周期地震成本研究涵盖了基于性能的地震工程方法(PBEE)，研究中对输入地震荷载、结构/材料、社会经济三个方面如地震震级、震中距、地震波剪切波速、场地条件、地震波作用角度、结构尺度、材料特征值、阻尼值、现金折现率等参数变量的不确定性均通过MCS法整合考虑进工程结构的全寿命周期成本分析过程中，材料时变劣化因素研究中予以了忽略，MCS法是大样本随机抽样的有效方法，研究中通过设定合理的变量区间，通过样本随机数保证了统计结果的精确性。
目前在我国西部地区，普通单层钢筋混凝土排架厂房应用广泛且大多服役年限在10年以上，汶川地震中灾区厂房曾遭受过严重的地震损毁，而CFRP碳纤维材料具有轻质高强、耐腐蚀等优点，由于前述的原因近年来采用CFRP碳纤维布对在役结构的柱、梁进行加固成为一种实用和经济性较好的做法，但目前国内外基于CFRP碳纤维布加固排架柱的厂房结构地震损伤和全寿命期地震成本分析研究成果较少，研究中通过引入CFRP加固的钢筋混凝土排架结构厂房作为分析对象，在结构的增量动力分析和全寿命期地震成本中通过蒙特卡洛随机样本法(MCS)将不确定性风险变量参数值考虑进分析中。对于推进工业建筑抗震加固和全寿命周期地震巨灾保险理论发展和应用具有重要意义。
工程结构全寿命周期地震损失成本研究(engineering seismic life-cycle cost，SLCC)是评价工程在役使用期内性能水平的长期分析研究。该研究吸收了基于性能地震工程的思想方法，将外界环境、结构/材料和社会经济方面的不确定性影响因素均考虑进SLCC方法研究中并应用于具体工业建筑工程中。
既然地震所导致的损失是由于地震造成的建筑物理损伤所导致的，而建筑的物理性损伤又分为结构性承重受力构件的损伤和非结构性附属构件设施及设备的损伤，因此，需要注意建筑的非结构性地震损伤与不同类型的建筑用途关联性较大，如工业厂房内机器设备较多，该类型建筑结构的非结构性地震损伤就与普通民用住宅内的非结构性地震损伤差异性较大。以往的国内外研究或选择以结构整体层间位移角变形(inter storey drift ratio，ISD)为主的结构性损伤指标而导致地震损失评估不全面[13－17]，或选择局部的结构性和非结构构件变形损伤指标而导致实际计算量过大[11,18]，现有计算条件下的研究中提出了综合结构性损伤和非结构性损伤的加权混合参数法工程全寿命周期地震成本研究思路，研究仅针对评估工程结构维修或更换的直接经济成本包括材料成本、建造成本、维修成本和停工导致的间接经济损失，对由于地震导致的当地建筑市场物价上涨、供应混乱、商业损失、人口失业、心理创伤、生态环境破坏等间接社会和环境成本，由于来源广泛、不确定性大暂予以忽略。研究中提出的混合加权计算流程见图1。
图1 基于混合加权法的排架结构全寿命期地震成本流程
Fig.1 Framework of SLCC estimation based hybrid weight factors
将基于一定概率的地震风险因素通过计算转化为具体可量化的工业建筑的全寿命周期地震损失成本，对于工程技术人员的决策是非常有参考价值的。工程全寿命周期地震成本CTOT一般表示为时间和设计变量的形式见式(1)[6,19－20]：
CIN为建筑起始建造成本，包括建造所需的所有建筑直接费用和间接税费总和，本次研究暂定宁夏银川为样本研究地区，计算中选取当地一般工业厂房CIN=1500 元/m2，折算CFRP加固费用CFRP=150 元/m2，并考虑±10%偏差，研究仅针对传统行业工业厂房，CIN值的确定只包含厂房本身的所有建造成本；CLC为在建筑使用年限内地震导致的不同限值损伤状态成本现值，根据地震后的维修成本、厂房内的设备和附属构件损伤恢复成本和人员伤亡的保险补偿抚恤费以及其他出租收入损失相关的成本之和来估算，厂房内设备的精密程度和价值的高低当然也会影响CLC值，个别极重要的工业厂房(如微电子无尘厂房、精密机械加工厂房、制药厂房等)需要单独计算。本文的主要目的在于验证采用CFRP碳纤维布加固对厂房全寿命期地震成本的影响程度。
厂房结构的地震损失是基于结构的量化损伤限值状态通过上面的公式转换得到的，结构的损伤限值状态(damage limit state，LS)在计算中需要尽可能考虑到厂房结构内所有结构性承重构件和非结构性附属件和设备损伤限值状态，结构的损失值是针对给定地区的工程结构每一级LS损伤级别的损伤发生超越概率来计算的。维修成本、维修持时、损毁或损坏的构件的数量都作为工程全寿命周期地震成本的一部分，同时也作为工程业主决策的依据。地震损失的结果通常表现为伤亡人数、经济损失和停工时间。而医疗费、抚恤金和停工导致的业主经营成本和承租人的经营成本均可以转化为经济损失。以上由于地震导致的直接和间接经济损失成本的不确定性研究中均通过蒙特卡洛随机样本法考虑，见式(2)。
此处p(IMm)为第m级地震振动强度IM发生的概率，
为在第m级地震振动强度IM对于第j个构件产生的第i个工程结构损伤响应参数EDPs指标，研究中采用了4个EDP损伤响应参数指标。结构层间最大位移角(ISDmax)和排架柱端最大曲率转角δc选择作为结构性响应的损伤指标[21－24]。基于文献[25]厂房最大谱加速度Sa指标作为非结构性损伤指标，由于工业厂房为大跨度单层空间结构，厂房内的很多机器设备是直接布置在地面上的，地震过程中对加速度敏感的设备将直接受到从地面传导来的地震波的冲击，因此最大地面峰值加速度PGA指标被同时引入作为非结构性构件的损伤评价，钢筋混凝土排架厂房结构PGA和Sa值与不同损伤限值状态(damage limit state,LS)之间的联系见表1。同时
为第j个构件产生的第i个工程结构损伤响应参数EDPs指标时对应的第k级损伤限值状态概率，
为分别对应于不同构件j在第k级损伤限值状态时对应的第n级经济损失率，
就为汇总后得到的结构限值状态损伤成本。研究中的限值子成本详细说明、厂房结构限值状态平均损伤百分率、经济损失百分率、延误时间、预期轻伤率、预期重伤率和预期亡故率等基础数据参见文献[19,26－28]。
表1 钢混排架厂房结构损伤响应参数EDPs指标概率损伤限值状态分级表
Table 1 Damage limit state drift ratio,peak ground acceleration,member chord rotation & spectral acceleration of industrial buildings
注：S-Slight,L-Light,M-Moderate,H-Heavy,Ma-Major,C-Collapse。
限值状态级别 max/ISD (%) /gal PGA δc/(%)Sa/gal(I)-无损伤-None(II)-微小损伤-S(III)-轻度损伤I-LI(IV)-轻度损伤II-LII(V)-中度损伤I-MI(VI)-中度损伤II-MII(VII)-重度损伤-H(VIII)-严重损伤-Ma/C θ≤0.11 0.21 0.11＜ ≤0.21 0.31 θ＜ ≤0.31 0.44 θ＜ ≤0.44 0.66 θ＜ ≤0.66 1.10 θ＜ ≤1.10 2.55 θ θ θ＞＜ ≤2.55 a≤70a 130 70＜ ≤130a 180＜ ≤180a 220＜ ≤220a 290＜ ≤290a 330＜ ≤330a 400 a＞＜ ≤400 θ≤0.03 0.09 0.03＜ ≤0.09 0.16 θ＜ ≤0.16 0.24 θ＜ ≤0.24 0.36 θ＜ ≤0.36 0.52 θ＜ ≤0.52 0.80 θ θ＞＜ ≤0.80 θ a≤34a 57 34＜ ≤57a 70＜ ≤70a 82＜ ≤82a 100＜ ≤100a 15＜ ≤1 115a 125 a＞＜ ≤125
地震风险性分析就是将地震的风险性用概率来予以解释，地震产生的效应包含场地振动、地面开裂、土壤液化、山体滑坡、海啸等，研究中主要只考虑由于地震导致的场地振动效应。选择宁夏北部银川平原为研究地区，该地区基本的地质地基特征条件参见文献[29]。依据GB 50011－2010《建筑抗震设计规范》的第5.1.4的规定[30]，整个银川平原均属于抗震设防烈度8度地区，设计基本地震分组为第二组。地震风险性分析中评价地震波的三个重要要素为：振动强度、震中距和场地土壤条件。当然建筑坐落位置是否接近地震断裂带、当地历史上地震的再发生时间间隔等也是要考虑的重要因素。
地面峰值加速度PGA和IMm可以表达地震风险性地面运动参数的地震强度指标(intensity measure，IM)[31]，但需要说明的是PGA一般并不是用来表达地震的能量等级指标，能量指标一般用里氏分级来表示。如上所述根据GB 50011－2010的规定，地震一般是通过基于水平地震影响系数αmax的反应谱分为大震、中震、小震m=3级水平见图2中的虚线反应谱曲线。
当然对于不同振动强度水平的地震时程波，工程上有不同的地震发生回归期，一般小震的地震回归期或者再发生间隔时间短，如63/50IMm小震统计概率回归期仅为50年，而大震通常再发生时间间隔长，如2/50IMm统计概率回归期长达2475年，研究中为了更加准确地基于损伤限值状态计算工业建筑的全寿命周期地震成本，突破了GB 50011－2010规定的三级抗震设防水平而采用了7级地震IMm水平。
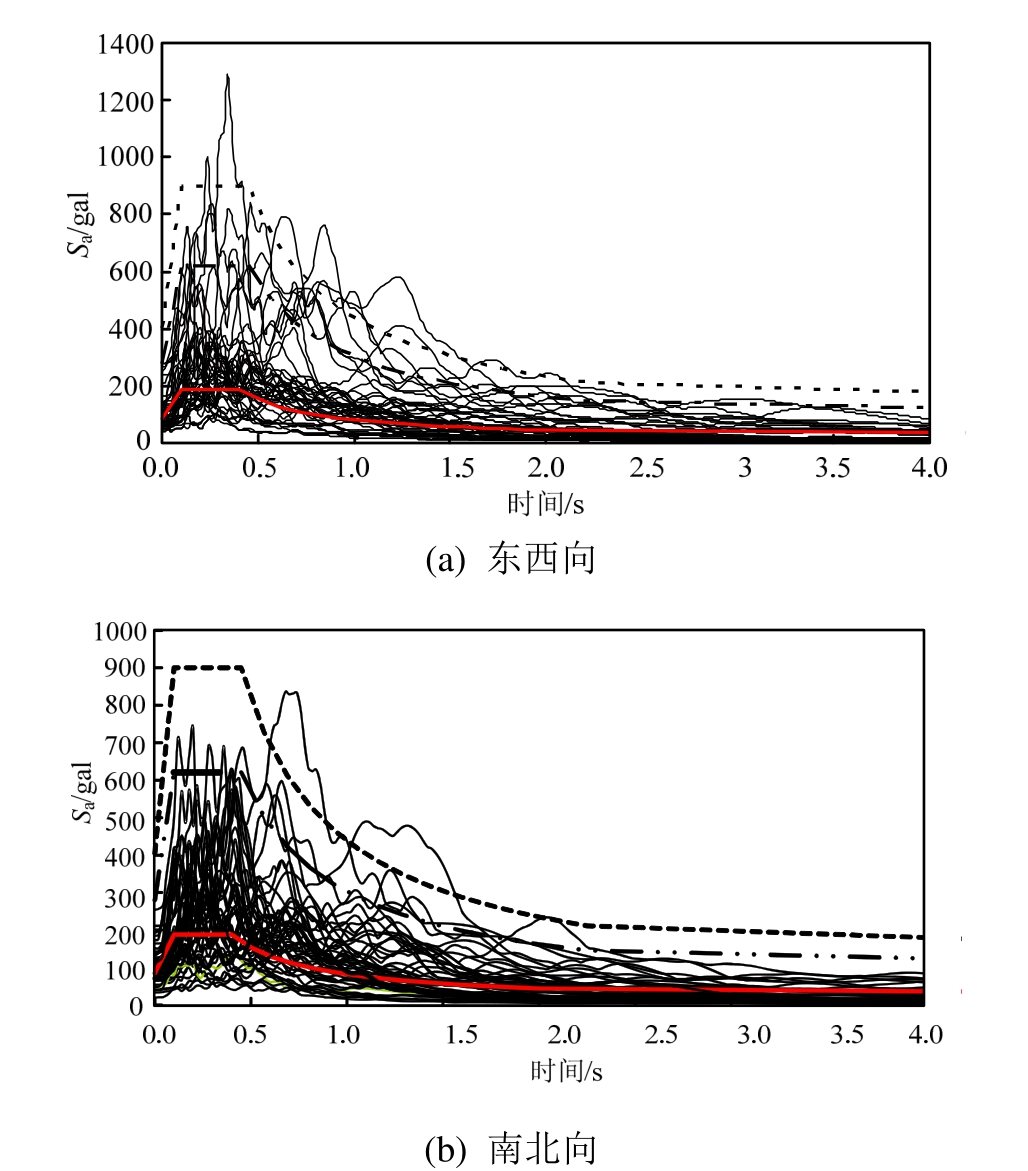
图2 实际计算使用的地震记录反应谱(虚线从上至下分别为：2/50,10/50,63/50IMm)
Fig.2 Response spectrum of selected seismic waves in calculation (chain curves: 2/50,10/50,63/50IMm)
地震风险性分析的目的在于创建与拟分析地区各级地震动强度指标相拟合的地震地面时程记录，与HL水平反应谱曲线相拟合的地震时程记录数量要达到满足工程分析的计算要求，研究中每一级筛选产生了8条地震时程记录可以满足计算精度和效率的平衡，通过PEER地面运动数据库筛选出与分析地区反应谱曲线拟合度高的地震记录数据，筛选原则包括：地震强度、场地土剪切波速、地震震中距、地震主振动持时等条件。实际计算中使用的地震记录反应谱曲线见图2。
研究中建立了两栋相同的单层钢筋混凝土排架厂房结构见图3，一栋为普通钢筋混凝土排架厂房，一栋为CFRP碳纤维布加固钢筋混凝土排架柱厂房。
图3 钢混排架厂房结构有限元模型
Fig.3 Finite element models of factory frames
计算结构为单层对称布局结构，纵向长66 m，横向24 m，顶高14.2 m，结构详细参数与配筋参见文献[19]。
混凝土选C30，钢筋选HRB335级钢筋，具体参见文献[19]。钢混框架厂房结构选取碳纤维布(carbon fber reinforced polymer，CFRP)对厂房钢筋混凝土排架柱身进行加固，碳纤维直径在5μm ～10μm ，由碳原子在晶体结构中沿长轴方向排列组成，碳纤维材料具有抗拉伸强度高、强度-重量比高的优点，对比传统钢材料采用碳纤维材料结构可以减重50%～60%，考虑原材料成本和加工费用后采用CFRP加固成本大约为同重量钢材料价格的2倍～10倍。研究中的CFRP材料采用三线型本构模型[32－37]，材料特征值包括：抗拉强度ft=3000MPa，起始刚度
后屈服刚度
弹性模量
容重
极限应变0.015。结构恒、活荷载按照
《建筑结构荷载规范》取值[30,38]。
两类厂房结构的自振周期分别为：普通厂房第一自振周期中位值T1 =1.35s ，CFRP加固后的厂房第一自振周期中位值T1 =0.99s 。厂房结构取整体阻尼率5%并考虑±10%的随机偏差。
非线性增量动力时程IDA被用于对厂房结构的有限元数字模型进行动力损伤计算，计算中使用了前述筛选得到的地震记录波，动力分析中采用FEMA350推荐的地震强度IM指标法[31]。采用100%的东西向地震波和30%的南北向地震波组合代表任意方向的地震波荷载施加于结构基础部位。结构响应的评估是通过获得的EDsP损伤响应参数指标来开展的，研究中选择了4个代表性损伤指标，遵循了基于性能的设计原理，即以基于变形/位移为基本选择原则，其中既有基于结构整体的响应指标也有基于结构重要承重构件的指标，其他一些指标如构件最大轴心压力、最大弯矩、最大剪力、最大的应力、最大的应变值等局部构件损伤指标研究中暂未考虑。
图4 厂房结构IDA增量动力分析曲线
Fig.4 IDA fragility curves of factory buildings
工业厂房结构性能的评估需要研究者基于结构全局和局部的变形损伤行为来全面地理解和评估。研究中通过前面的分析选取了56条特征地震时程波，对单层工业厂房结构开展了2000次IDA增量动力随机样本计算分析，作用于厂房结构的基于结构整体响应的IDA曲线示于图4，从结构整体位移变形结果来看，随着地震振动强度的增大，结构相应的谱加速度Sa也会增加，层间位移角变形值
随Sa增大而增加，但两种类型的厂房结构的IDA曲线斜率有很大差别，CFRP加固后的厂房结构的IDA曲线斜率明显高于普通原型结构厂房结构。如对应于同一为1%，普通厂房结构谱加速度Sa均值约在62 gal，CFRP加固厂房的Sa均值约在150 gal，CFRP加固结构对应的谱加速度值提高了1倍以上；对应于同一谱加速度Sa为100 gal，普通厂房
统计均值已经约为1.5%，而CFRP加固厂房的
统计均值约为0.5%，仅为普通厂房最大层间位移角值的1/3，从计算结果可看出，经过CFRP加固后的厂房结构地震抗易损性能得到大幅的提高。
厂房结构全寿命周期地震成本研究的目标在于，考虑多种不确定因素耦合影响的情况下，通过将作用于西部选定地区的CFRP加固厂房建筑的地震风险量化为可衡量的CFRP加固厂房结构的全寿命周期地震成本统计期望值，从而为项目业主在工程设计阶段的工程加固决策提供可靠的支持。
全寿命周期地震成本由起始建造成本CIN和损伤限值状态成本CLC组成，其中起始建造成本CIN需要研究者根据工业建筑所在地的建筑市场平均物价水平做合理的评估，研究中经过市场调研初步暂定采用CFRP加固措施后当地的工业厂房结构的起始建造成本CIN提高了150 元/m2，损伤限值状态成本CLC的计算需要基于不确定随机参数变量MCS样本法来开展计算，计算过程通过MATLAB编程从有限元动力计算结果提取数据建立MCS随机参数大样本，基于随机统计概率根据式2计算CFRP加固厂房结构全寿命周期地震损伤限值成本CLC。
研究中对地震强度IM的级数m及对应的LS损伤限值状态分级、IDA强度系数比值等详细参见文献[19]。
增量动力计算是开展工业厂房结构全寿命周期地震成本分析的基础，在结构动力计算过程中，为了完整的呈现工程全寿命周期地震成本的统计精确性，研究者不仅要关注结构性EDsP损伤指标，同时还必须关注非结构性EDPs损伤指标，研究中采用了组合加权的方法选择了4个代表性损伤指标来开展此次工业建筑全寿命周期地震成本的大样本5万次随机计算，计算中全寿命周期地震成本相关的参数服从随机变量分布，地震所导致的业主租金收入损失根据结构性损伤程度计算中服从1～6个月随机分布，工厂厂房由于地震所导致的停产时间损失根据损伤严重程度服从1～12个月之间随机分布，工人在岗率按照95%期望值随机正态分布并考虑±10%偏差，计算结果基于上述的限值状态予以分区，限于篇幅此处仅列出EDPs结构性损伤指标：基于结构层间位移角ISDmax 和柱端截面最大曲率转角δmax随机损伤散点分布见图5～图6。图中基于表1通过不同的颜色将厂房结构性损伤通过损伤限值分级进行了图形化表示，由左至右按照不同颜色区间分别表示不同IMm对应的损伤限值状态。纵坐标采用工程结构地震易损性分析中经常使用的谱加速度Sa指标可以更加直观地了解到两类工业厂房建筑的地震易损伤性能差异。从图中可见两类结构的分级损伤散点均呈现斜向喇叭状扩散分布，但两类工业建筑的喇叭状斜向分布差异性非常明显，可见CFRP加固厂房结构的随机散点损伤整体喇叭口分布斜率斜率明显高于普通结构，两类结构的均值和中位值曲线差异更加明显，如对应于ISD指标3%，普通厂房的谱加速度Sa值在192 gal，而CFRP加固工业厂房的谱加速度Sa值提高接近1倍达到约380 gal的水平，显然经过CFRP加固后的工业厂房抗震易损性得到了明显的提高。另外，对于进入最右端区域即结构进入严重损伤，从损伤散点的分布可见经过CFRP加固后的工业厂房结构进入最右端区域(严重损伤/倒塌级)的散点比例远远少于普通厂房结构，普通厂房散点损伤进入最右端区域后整体呈现水平缓慢下降屈服状态，抗震性能在逐渐降低，而CFRP加固结构损伤散点进入最右端区域后仍然保持一定的斜率，即抗震性能还有提高，并没有立刻呈现屈服状态。这一显著性差异在两类结构基于柱端截面最大曲率转角δmax承重构件结构性损伤指标分布中同样明显，普通厂房中δmax ≥ 0.08的点数超过总数的60%，而CFRP厂房结构中δmax ＜ 0.08的点数超过总数的90%，即CFRP加固后的厂房结构在IDA大样本计算中大概率保持在重度损伤及以下限值状态，体现出CFRP加固后工业厂房建筑物优良的地震抗易损伤性能。
图5 基于层间最大位移角ISDmax伤散点分区对比
Fig.5 Damage scatter distribution of industrial buildings basedISDmax
图6 基于柱端最大曲率转角δmax的损伤散点分区对比
Fig.6 Damage scatter distribution of IBs basedδmax
对各个限值状态分级内的损伤散点数量进行统计分析以柱状图进行表示，在柱状图限值损伤表示中每一级柱状图包含了4项EDPs损伤指标。可以看到基于同一个的损伤指标对应于不同LS状态级所统计得到的损伤数量的不同的，同时基于同一个LS状态级对应的4项不同损伤指标所统计得到的损伤数量也是不同的，可见不同的损伤指标对于不同的LS损伤限值状态具有不同的损伤敏感性。
具体来看从图7～图8中的基于ISDmax 损伤指标的年损伤次数统计结果来看普通厂房损伤统计数值最大在轻度损伤次数，严重损伤/倒塌次数也非常高，而CFRP加固厂房结构的严重损伤/倒塌次数仅为普通厂房的1/3，统计损伤数最大在中度损伤，其次在轻度损伤次数；而如果基于δmax来看这两类厂房结构地震易损伤差异则更为明显，普通厂房没有变化，而CFRP加固厂房损伤次数最大为轻度损伤，其次为微小损伤，而严重损伤/倒塌次数更仅为普通厂房的1/20；当然，由于非结构性损伤主要考虑对加速度敏感的机器设备和附属性构件和设施，而厂房为单层结构，两类结构所面对的地面峰值加速度PGA值是相同的，两者的最大谱加速度Sa由于这两种类型结构的自振周期不同会有所差异：1) 这两种结构的最大谱加速度Sa值的绝对差异依然是衡量厂房非结构损伤差异的重要参考指标，从PGA指标来分析看，CFRP加固厂房的微小损伤次数最多，然后为严重损伤/倒塌，而普通厂房轻度损伤次数最多，其次也为严重损伤/倒塌，这一定程度上合理反映了由于厂房排架柱被CFRP碳纤维布加固间接提高了厂房顶部部位局部非结构性构件、管件、屋顶装饰性建筑构件等的抗震易损性；2) 由于涉及非结构性地震损失主要部分的机器设备还是安装在地面上的，这部分的地震损失对于两类厂房结构是基本相同的，因此计算结果反映出来了这部分细微地差别；而基于Sa指标来看，两种类型厂房结构的前两位最大损伤次数相同，均为微小损伤次数最多，其次为严重损伤/倒塌，注意的地方在于普通厂房轻度损伤次数接近严重损伤/倒塌的次数，进一步考虑不同LS对应的年发生概率后，就可以得到对应于每一年的平均损伤发生概率。进一步厂房全寿命周期地震成本加权计算具体程序实现说明参见文献[19]。
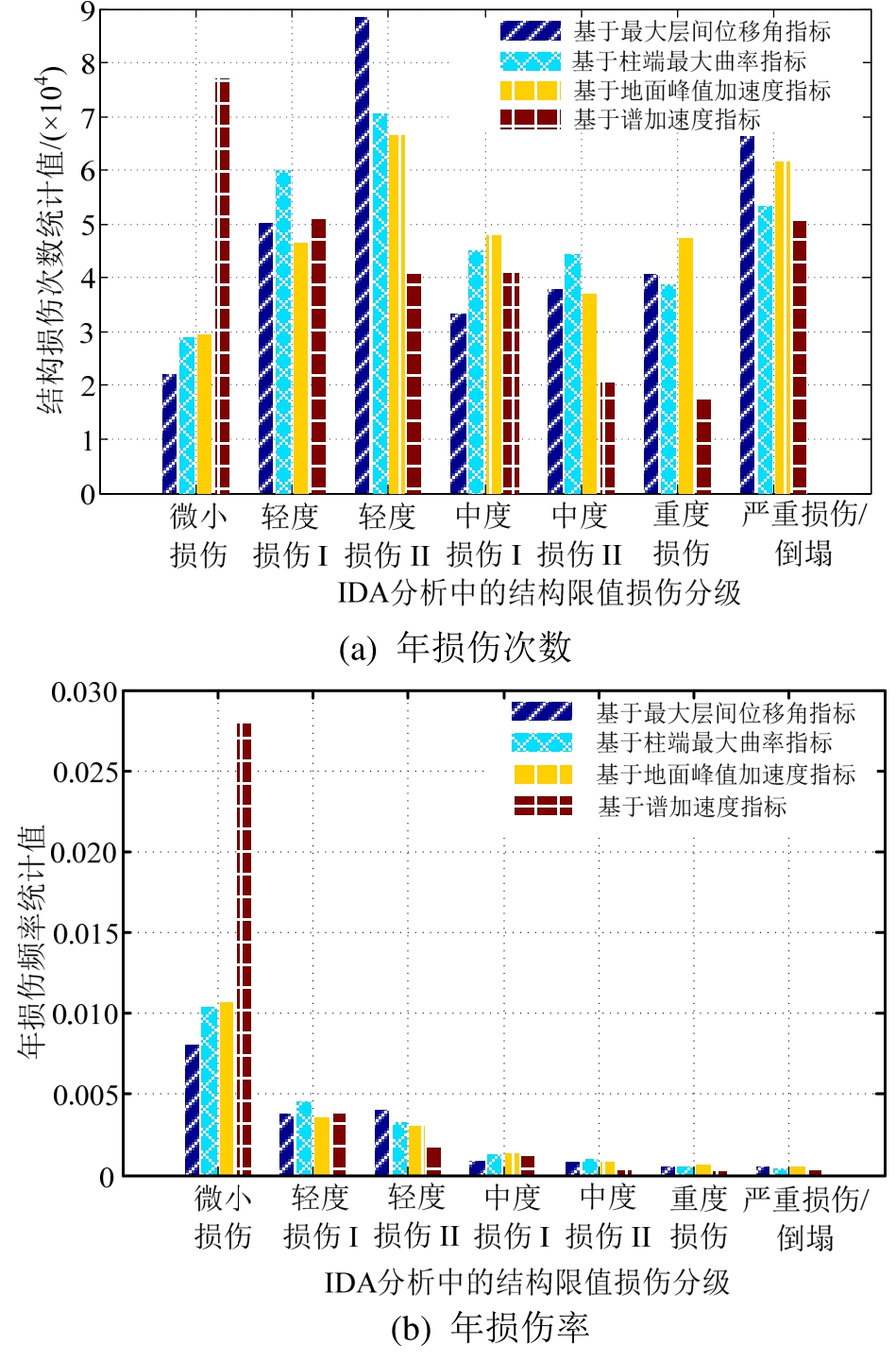
图7 普通厂房结构限值损伤柱状图
Fig.7 Damage states column distribution of original IBs
图8 CFRP加固厂房结构限值损伤柱状图
Fig.8 Damage states column distribution of CFRP reinforced IBs
两类工业厂房建筑的结构性年均地震损伤成本统计分布和厂房汇总后的年均总地震损伤成本统计随机正态分布良好，而非结构性年均地震成本统计分布效果稍差，详细如图9～图14计算结果所示。分析认为这与前述非结构性地震损失计算过程中对于各类组成子成本如业主租金收入损失、停工时间和工人在岗率等参数不确定性随机变量范围设定有关，这部分的更准确的定义需要未来进一步的深入企业和地震灾区调研补充数据后才能完善。需要说明的是，对工业建筑全寿命周期成本的计算需要根据组成地震成本的各子成本类别基础公式开展计算，这些子成本类别涵盖了地震所导致的结构性损失，机器设备和管线的非结构性损失，工人的伤亡赔偿抚恤金等费用，计算得到普通厂房的结构性年均地震损失中位值为4403元/年，平均值为4411元/年，非结构性年均地震损失中位值为4749元/年，平均值为4623元/年，CFRP加固后的厂房结构性年均地震损失中位值为3758元/年，平均值为3681元/年，非结构性年均地震损失中位值为4410元/年，平均值为4281元/年，结果发现经过CFRP加固后厂房整体全寿命期地震成本损失大幅减小了约16.5%，计算中厂房设备价值按2000元/m2考虑，其他附属构件价值按300元/m2折算考虑，这两个指标值仅作为此次研究中的参考值，实际计算中不同行业厂房的设备及附件价值差异巨大，需要根据具体行业再做详细的针对性估算。
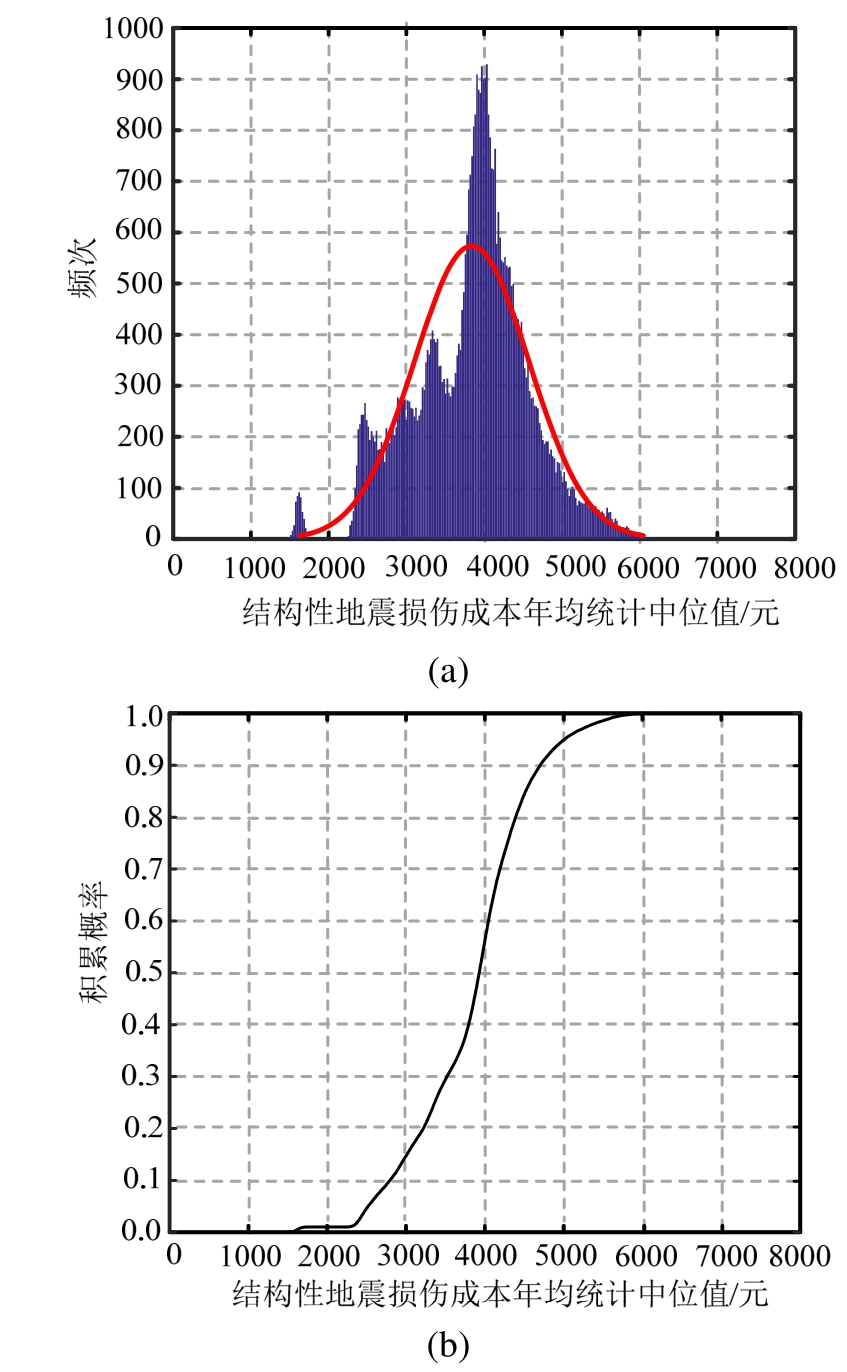
图9 CFRP厂房结构性地震成本概率统计
Fig.9 Structural annual seismic median cost of CFRP factory buildings
图10 CFRP厂房非结构性地震成本概率统计
Fig.10 Non-structural annual seismic median cost of CFRP factory buildings
图11 CFRP加固厂房总地震成本概率统计
Fig.11 Total annual seismic median cost of CFRP factory buildings
图12 普通厂房结构性地震成本概率统计
Fig.12 Structural annual seismic median cost of original factory buildings
图13 普通厂房非结构性地震成本概率统计
Fig.13 Non-structural annual seismic median cost of original factory buildings
图14 普通厂房总地震成本概率统计
Fig.14 Total annual seismic median cost of original factory buildings
两种类型工业厂房结构的全寿命周期地震损失成本对比分析见图15。
基于单位建筑面积来计算，该地区单层普通钢混排架厂房的年平均地震损失成本统计中位值7.01 元/(年·m2)，CFRP加固厂房的统计中位值5.75 元/(年·m2)，如果保险公司开征地震巨灾保险，假设最大50%的间接费和税，则该地区普通厂房地震巨灾保险参考基准费率中位值10.52元/(年·m2)，CFRP加固厂房地震保险中位值8.62元/(年·m2)，基于中位值来衡量，则采用CFRP加固技术后厂房的地震保险减小约18%，注意在计算采用CFRP加固厂房地震成本前面已经按照平米单价考虑了加固本身的材料及加工费用CFRP = 150 元 /m2，因此计算后的结果初步显示出了厂房建筑采用CFRP技术后对于钢混排架柱构造的工业建筑全寿命周期成本费用具有巨大的效益，该技术在中国西部地震高烈度广大地区的钢混排架厂房建筑具有推广的潜力。
图15 年均地震成本统计中位值及组成 /元
Fig.15 Consist of SLCC probability median values
两类结构的各项对比年均地震损失子成本统计数据见表2，初步显示非结构性设备及附件损失为最大子成本项目，其次为结构性损伤导致的地震维修成本，这两项损失占到厂房结构地震年成本的82.62%(普通厂房)和89.76%(CFRP加固厂房)。发生地震后的人员轻重伤医疗费和伤亡抚恤金均为初步估计，由于地震所导致的人员轻重伤医疗费和伤亡抚恤金总占比不大(普通厂房6.66%，CFRP加固厂房3.77%)，当然本次分析还是基于前面一系列假定的基础数据计算得来，未来更精确估算需要收集更多的来自于地震高烈度地区地震动风险性资料、工业厂房的更精确设备与非结构性构件详细成本组成、材料受长期环境影响微观力学劣化机理等基础数据支持。
表2 两类工业厂房全寿命期地震年均成本统计值对比
Table 2 SLCC of original & CFRP reinforced IBs Statistics results comparison
全寿命期地震年均成本统计中位值普通厂房/元CoVCFRP厂房/元CoV diam C 结构损伤地震成本 4403 0.02 3758 0.05 rien C 业主租金收入损失 623 0.61 355 0.53 i C 停产导致收入损失 565 0.66 237 0.57 inc Cθ附属物地震损失 4749 0.05 4410 0.03,cion iinj C 人员轻重伤医疗费 418 0.86 187 0.78 i C 伤亡保险赔偿金 351 0.91 154 0.79 fat C 地震年均成本汇总 11109 0.02 9101 0.01 tot
工业建筑加固是目前的一个研究热点，但基于加固后的工业建筑全寿命期地震成本技术与经济混合型研究成果则国内外均不多，基于此研究在以下几个方面开展了有价值的探讨：
(1) 对引入CFRP碳纤维布加固排架柱后的单层工业厂房进行全寿命期地震成本展开对比研究；两类结构的IDA增量动力分析曲线显示CFRP加固厂房结构的IDA整体曲线斜率明显高于普通厂房斜率，显示出经过CFRP加固后的厂房结构地震抗易损性能得到大幅的提高。
(2) 从随机损伤散点的分布看出，两类结构的分级损伤散点均呈现斜向喇叭状扩散分布，但两类工业建筑的喇叭状斜向分布差异性非常明显，可见CFRP加固厂房结构的随机散点损伤整体喇叭口分布斜率斜率明显高于普通结构，两类结构的均值和中位值曲线差异更加明显，普通厂房散点损伤进入最右端的严重损伤/倒塌区域后整体呈现水平缓慢下降屈服状态，抗震性能在逐渐降低，而CFRP加固结构损伤散点进入最右端的严重损伤/倒塌区域后仍然保持一定的斜率，即抗震性能还有提高，并没有立刻呈现屈服状态。体现出CFRP厂房结构优良的抗地震易损伤性能。
(3) 通过柱状统计分析来看，基于ISDmax 损伤指标，CFRP加固厂房的严重损伤/倒塌次数仅为普通厂房的1/3；基于δmax损伤指标，CFRP加固厂房严重损伤/倒塌次数更仅为普通厂房的1/20。
(4) 通过基于MCS大样本统计计算发现经过CFRP加固后单层钢混排架工业厂房建筑的年均地震统计中位值为5.75元/(年·m2)，较普通厂房地震成本减小16.5%左右，该计算已经考虑了加固本身的材料及加工费用，因此计算后的结果初步显示出了厂房建筑采用CFRP技术后对于钢混排架柱构造的工业建筑全寿命周期成本节约具有巨大的效益。
(5) 从全寿命期地震各项子成本的统计偏差分析发现，CFRP加固厂房结构性地震损失
的Cov值在4.38%～4.51%，非结构性设备及附属件地震损失
的Cov值在3.11%～3.15%，汇总后CFRP厂房结构Ctot的Cov值在1.35%～1.36%。相比普通厂房地震子成本统计偏差，计算结果显示出采用CFRP技术缩窄了损失结果的统计偏差，显示出CFRP技术有效且稳定地提高了结构的抗震性能。综上研究对我国西部具体地区CFRP加固前后的单层工业厂房全寿命期地震成本进行了技术经济混合分析，研究结果显示出采用CFRP加固后厂房结构全寿命期地震维护成本费用显著地降低，对于未来在我国西部地震高烈度地区推广工业建筑地震巨灾保险以及应用CFRP碳纤维布加固技术具有积极的促进作用。
[1] 国家减灾委员会,科技部抗震救灾专家组.汶川地震灾害综合分析与评估[M].北京: 科学出版社,2008:140－145.National Disaster Reduction Committee - Earthquake Relief Expert Group in Ministry of Science and Technology ,Wenchuan earthquake disaster comprehensive analysis and assessment [M].Beijing: Science Press,2008: 140－145.(in Chinese)
[2] 百度百科,印尼地震[EB/OL].网址http://baike.baidu.com/item/9.28 Indonesia Earthquake.Indonesia Earthquake [EB/OL].Website: http://baike.baidu.com/item/9.28 Indonesia Earthquake.(in Chinese)
[3] 中再保险公司,中国地震风险与保险实验室挂牌成立[EB/OL].网址: http://www.chinare.com.cn/zhzjt/441005.China reinsurance group,China seismic hazard &insurance laboratory [EB/OL].Website: http://www.chinare.com.cn/zhzjt/441005.(in Chinese)
[4] Porter K A.An overview of PEER’s performance-based earthquake engineering methodology [C]// Ninth International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP9),Rotterdam,Millpress,2003: 1－8.
[5] Moehle J,Deierlein G G.A framework methodology for performance-based earthquake engineering [C]// 13th World Conference on Earthquake Engineering,Vancouver,British Columbia,Canada,2004,No.679.
[6] Wen Y K,Kang Y J.Minimum building life-cycle cost design criteria I:methodology [J].Journal of Structural Engineering,2001,127(3): 330－337.
[7] Liu M,Burns S A,Wen Y K.Optimal seismic design of steel frame buildings based on life cycle cost consideration [J].Earthquake Engineering and Structure Dynamics,2003,32: 1313－1332.
[8] Takahashi Y,Kiureghian A D,Alfredo H-S.Ang,Life –cycle cost analysis based on a renewal model of earthquake occurrences [J].Earthquake Engineering &Structural Dynamics,2004,33: 859－880.
[9] Chritensen P T.Life-cycle cost –benefit (LCCB) analysis of bridges from a user and social point of view [J].Structure and Infrastructure Engineering,2009,5(1):49－57.
[10] Mitropoulou C C,Lagaros N D,Papadrakakis M.Life-cycle cost assessment of optimally designed reinforced concrete buildings under seismic actions [J],Reliability Engineering and System Safety,2011,96:1311－1331.
[11] Chiu C K,Hsiao F P,Jean W Y.A novel lifetime cost-benefit analysis method for seismic retrofitting of low-rise reinforced concrete buildings [J].Structure and Infrastructure Engineering,2013,9(9): 891－902.
[12] Castaldo P,Palazzo B,Vecchia P D.Life-cycle cost and seismic reliability analysis of 3D systems equipped with FPS for different isolation degrees [J].Engineering Structures,2016,125(15): 349－363.
[13] Rossetto T,Amr Elnashai.A new analytical procedure for the derivation of displacement-based vulnerability curves for populations of RC structures [J].Engineer Structures 2005,27(3): 397－409
[14] Jun Ji,Amr S Elnashai,Daniel A Kuchma.An analytical framework for seismic fragility analysis of RC high-rise buildings [J].Engineering Structures,2007,29: 3197－3209
[15] 朱健.结构动力学原理与地震易损性分析[M].北京:科学出版社,2013.Zhu Jian,Structural dynamics and seismic vulnerability analysis [M].Beijing: Science Press,2013.(in Chinese)
[16] 于晓辉,吕大刚.HAZUS相容的钢筋混凝土框架结构地震易损性分析[J].工程力学,2016,33(3):152－160.Yu Xiaohui,Lü Dagang.Hazus–compatible seismic fragility analysis for RC frame structures [J].Engineering Mechanics,2016,33(3): 152－160.(in Chinese)
[17] Min Liu,Baoxia Mi,Life cycle cost analysis of energy-efficient buildings subjected to earthquakes [J].Energy and Buildings,2017,154: 581－589.
[18] Porter K A,Kennedy R P,Bachman R E.Creating fragility functions for performance-based earthquake engineering [J].Earthquake Spectra.2007,23(2): 471－489.
[19] 朱健,赵均海,谭平,等.基于随机模拟的单层工业厂房全寿命期地震成本研究[J].地震工程与工程振动,2018,38(1): 51－64.Zhu Jian,Zhao Junhai,Tan Pin,et al.Seismic life-cycle loss estimation of single story factory buildings [J].Earthquake Engineering and Engineering Dynamics,2018,38(1): 51－64.(in Chinese)
[20] Wen Y K,Kang Y J.Minimum building life-cycle cost design criteria II: Applications [J].Journal of Structural Engineering (ASCE).2001,127(3): 338－346.
[21] Petrone C,Rossetto T,Goda K.Fragility assessment of a RC structure under tsunami actions via nonlinear static and dynamic analyses [J].Engineering Structure,2017,136(1): 36－53.
[22] Jinkoo Kim,Hyungjun Shin.Seismic loss assessment of a structure retrofitted with slit-friction hybrid dampers[J].Structural and Multidisciplinary Optimization,2017,130: 336－350.
[23] 徐龙河,单旭,李忠献.强震下钢框架结构易损性分析及优化设计[J].工程力学,2013,30(1): 175－179.Xu Longhe,Shan Xu,Li Zhongxian.Vulnerability analysis and optimization design for steel frame structure under strong earthquakes [J].Engineering Mechanics,2013,30(1): 175－179.(in Chinese)
[24] Ghobarah A.On drift limits associated with different damage levels [C]// Proceedings of the International Workshop on Performance-based Seismic Design:Department of Civil Engineering,McMaster University,Bled,2004: 1－12.
[25] Elenas A,Meskouris K.Correlation study between seismic acceleration parameters and damage indices of structures [J].Engineering Structures,2001,23: 698－704.
[26] Lagaros N D,Mitropoulou C C.The effect of uncertainties in seismic loss estimation of steel and reinforced concrete composite buildings [J].Structure and Infrastructure Engineering,2013,9(21): 546－556.
[27] ATC-13,Earthquake damage evaluation data for California [S].Redwood City.CA: Applied Technology Council,1985.
[28] FEMA 227,A benefit-cost model for the seismic rehabilitation of buildings [S].Washington,DC: Federal Emergency Management Agency,Building Seismic Safety Council,1992.
[29] 黄兴富,酆少英,等.银川盆地构造发展-深地震反射剖面揭示浅部地质与深部构造的联系[J].地质科学,2016,51(1): 53－66.Huang Xinfu,Li Shaoyin,et al.Development of the Yin-chuan Basin: Deep seismic reflection profile revealed the linkages between shallow geology and deep structures [J].Chinese Journal of Geology,2016,51(1):53－66.(in Chinese)
[30] GB50011－2010,建筑抗震设计规范[S].北京: 中国建筑工业出版社,2010.GB50011－2010,Code for seismic design of buildings[S].Beijing: China Construction Press Publication,2010.(in Chinese)
[31] FEMA-350,Recommended seismic design criteria for new steel moment-frame buildings [S].Washington DC:Federal Emergency Management Agency,2000.
[32] Wei H,Wu Z,Guo X and Yi F M,Experimental study on partially deteriorated strength concrete columns confined with CFRP [J].Engineering Structures,2009,31(10):2495－2505.
[33] Zhu J T,Wang X L,Xu Z D,et al.Experimental study on seismic behavior of RC frames strengthened with CFRP sheets [J].Composite Structures,2011,93(6): 1595－1603.
[34] Amran Y H M,Alyousef R,Rashid R S M,et al.Properties and applications of FRP in strengthening RC structures: A review [J].Structures,2018,16: 208－238.
[35] Grande E,Imbimbo M,Sacco E.Finite element analysis of masonry panels strengthened with FRPs [J].Engineering Structures,2013,45(1): 1296－1309.
[36] Eid R,Paultre P.Compressive behavior of FRP-confined reinforced concrete columns [J].Engineering Structures,2017,132(1): 518－530.
[37] Tabandeh A,Gardoni P.Probabilistic capacity models and fragility estimates for RC columns retrofitted with FRP composites [J].Engineering Structures,2014,74(1):13－22.
[38] GB 50009－2012,建筑结构荷载规范[S].北京: 中国建筑工业出版社,2012.GB 50009－2012,Load code for the design of building structures [S].Beijing: China Construction Press Publication,2012.(in Chinese)
SEISMIC LIFE-CYCLE LOSS ESTIMATION OF CFRP REINFORCED INDUSTRIAL BUILDINGS
赵均海(1963―)，男，陕西人，教授，博士，博导，主要从事结构力学和防灾减灾研究(E-mail: zhaojh@chd.edu.cn);
谭 平(1973―)，男，湖南人，研究员，博士，博导，主要从事结构抗震和防灾减灾研究(E-mail: ptan@gzu.edu.cn);
金建敏(1974―)，男，湖北人，高工，博士，主要从事结构抗震和防灾减灾研究(E-mail: jinjianmin152@aliyun.com).