实际工程中，由于公路交通、机场跑道、港口码头或者粮仓等构筑物、建筑物的软土地基受到一定周期振幅的循环荷载作用，在运营过程中使软土地基产生较大的沉降变形，影响上部结构正常使用，因此研究软土地基在循环荷载下的固结性状有非常重要的意义。
从Schiffman[1]对简单线性荷载作用下的固结问题进行研究以来，国内外许多学者对各种不同形式荷载作用下的固结问题进行了研究。国外学者Wilson和Elgohary[2]研究了矩形反复荷载作用下的饱和土体一维固结问题，并用分段函数表示出了加载与卸载条件下孔压与固结度的解析解；Alonso和Krizek[3]研究了随机荷载作用下弹性黏土层的沉降；Balighm和Levadoux[4]推演出了分步循环加载情况下的解析解；Favaretti和Soranzo[5]对不同形式循环荷载形式下的土体一维固结问题给出了相应的解析解；Rahal和Vuez[6]求得了正弦波荷载作用下地基的固结解析解；国内学者吴世明、杨峻等[7-8]运用荷载及微分方程的Laplace变换，对周期荷载下饱和黏土和双层地基的固结进行了求解，并对多种荷载进行了分析；蒋军和陈龙珠[9]通过可加反压的循环加载固结试验，分析不同加载波形循环荷载作用下饱和重塑粘土的沉降特性；梁旭等[10]研究了半透水边界下饱和土层在循环荷载作用下的有效应力比的变化；关山海等[11]采用分段函数的形式求得了梯形荷载下软土地基的一维固结解析解。还有许多学者[12-18]对变荷载作用和考虑其他因素下的固结理论方面做了许多的研究工作。
然而，以上研究大部分都是将土体的边界视为透水边界或者不透水边界，但以上边界在排水面上存在孔压突变为零的问题，针对这一问题，梅国雄[19]等提出了一种连续排水边界条件，该边界孔压随时间按指数函数形式变化，而且能够很好地解决边界排水面孔压突变为零的问题。
本文即是基于连续排水边界条件，推导了考虑任意荷载作用的连续排水边界条件，并在此基础上建立了一维地基固结模型，求得其无量纲化的一般解答。然后在梯形循环荷载半个周期上进行傅里叶级数的偶延拓，得到梯形循环荷载的傅里叶级数表达式，然后将其各项分别代入一般解答中，最后通过叠加原理得到梯形循环荷载作用下的固结解析解。分析了界面参数和梯形循环荷载的加载系数对土体固结性状的影响。
以Terzaghi一维固结理论为例，其求解初始条件为：
透水面z=0的边界条件为：
可以看出，透水面z=0的孔压由初始时刻的p直接突变为0，具有跳跃性。
又由Terzaghi一维固结理论给出解答如下：
可以看出，某一深度z处，当t=0时，孔压为p，当0＜t＜∞时，孔压随时间单调递减，当t=∞时，孔压为零，消散完成，又结合孔压解答式为指数型，综合这几个特点，梅国雄等[19]提出了连续排水边界条件：
式中：p为骤加荷载，b＞0且为边界上下界面参数，反映的是土体排水界面的排水性能，b越大，边界的排水性能越好。
由于荷载随时间变化，原来骤加荷载为p时的连续排水边界条件不再适用。如图1所示，为了表示变荷载作用下的连续排水边界条件，取变荷载初始值为q0，加荷时间为tc，荷载最大值为qu，在加荷时间tc段之内将其分为n段，每段取Δt，变荷载即可看作是分级瞬时加载，可得nΔt段荷载作用的连续排水边界表达式：
前(n-1)Δt段荷载作用的孔压表达式为：
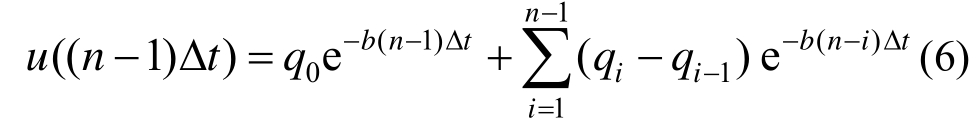
将式(5)减去式(6)，可得：
将式(7)整理可得：
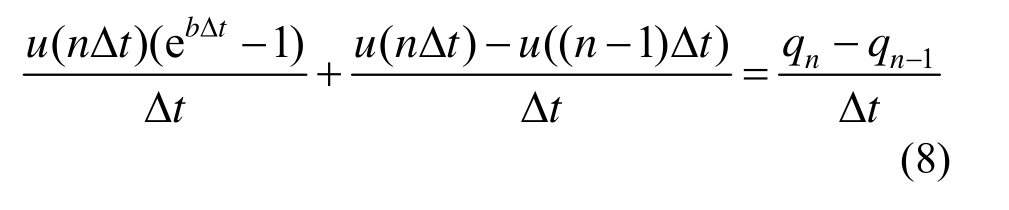
即是：
可求得任意荷载作用下的连续排水边界条件，如下所示：
图1 变荷载示意图
Fig.1 The diagram of arbitrary loadings
本文固结模型除去荷载情况外，其余假设与太沙基一维固结理论作相同的假设，计算模型如图2所示，地基只考虑双面排水条件。对于单面排水，当上下面排水性能一样时，只需要将软土厚度H调整为其一半，即可以得到单面排水条件下的解答。
图2 地基一维固结模型
Fig.2 The model of one-dimensional consolidation foundation
考虑荷载随时间变化的固结微分方程：
其求解初始条件为：
边界条件为：
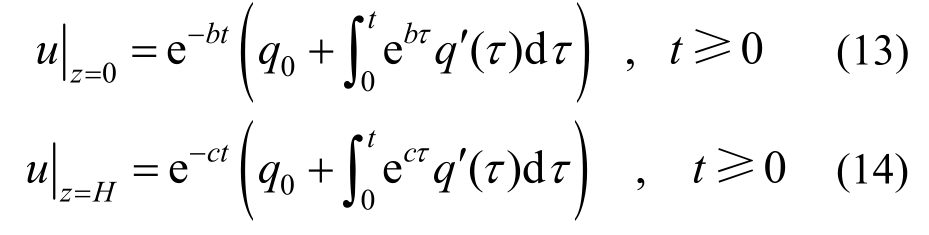
便于方程求解，将上述方程及求解条件进行参数无量纲化，无量纲化参数如下：
将上述无量纲化参数代入式(11)～式(14)中可得无量纲化后的固结方程为：
初始条件为：
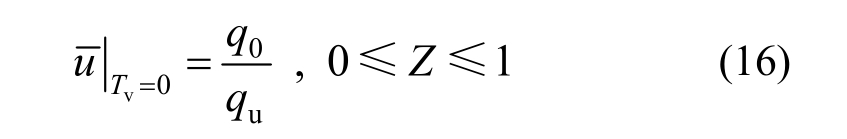
边界条件为：
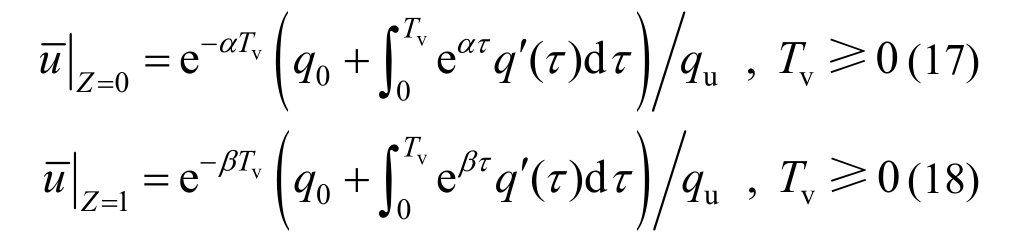
式中：
便于方程求解，将初始条件和边界条件齐次化，可令：
代入式(15)中可得：
式中：
其初始条件为：
边界条件为：
将定解问题的解
(Tv ,Z )和自由项f(Tv,Z)按关于Z的固有函数展开可得：
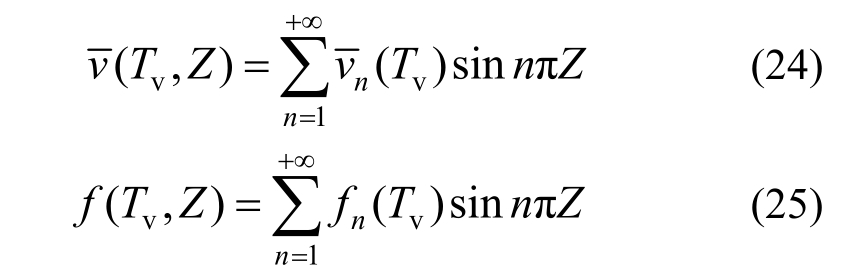
将式(24)、式(25)代入式(20)中可得：
又由初始条件可得出：
式(26) 即可求得：
对自由项f（Tv ,Z）进行傅里叶逆变换可求得：
再将式(29)代入式(28)中即可求得：
式中：
将式(30)代入式(24)中，可得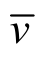
(Tv,Z)，再代入式(19)中即可以求得
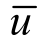Tv,Z)的一般解答:
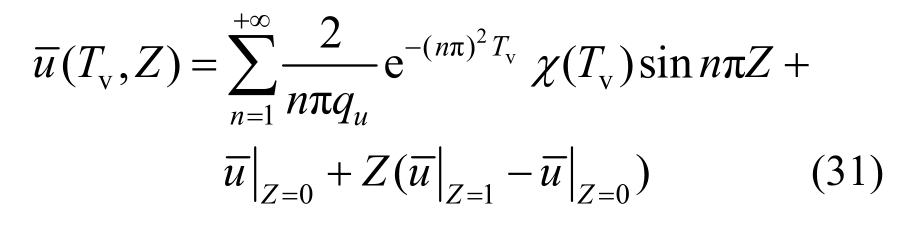
式中：
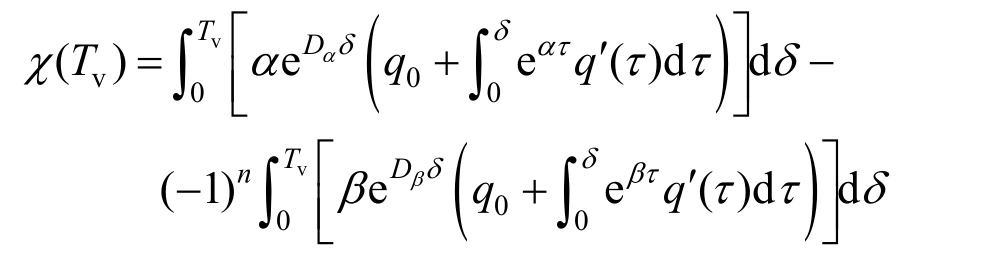
为方便梯形循环荷载的傅里叶级数展开，将其表示成关于q轴对称，第一个周期左半周期为对象的偶函数形式，如图3所示。
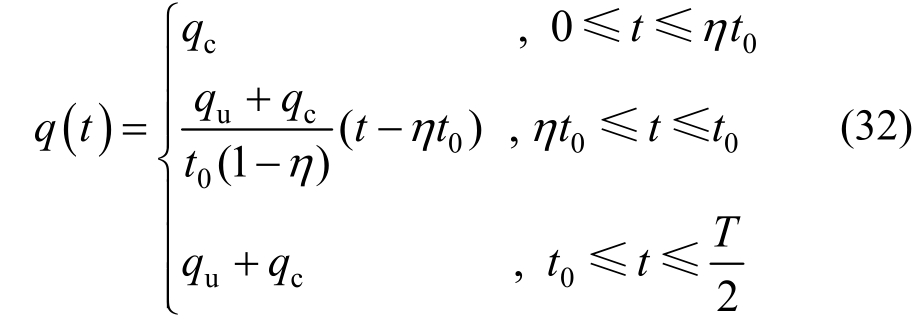
式中：qu为梯形循环荷载中荷载的波动值；η、t0为梯形循环荷载的加载系数；T为梯形循环荷载的加载周期。当t0=0时，退化为骤加荷载；当t0=T/2时，退化为三角形循环荷载；当η=1时，退化为矩形波循环荷载。
考虑梯形循环荷载的第一个左半周期，由傅里叶的余弦展开公式，得：
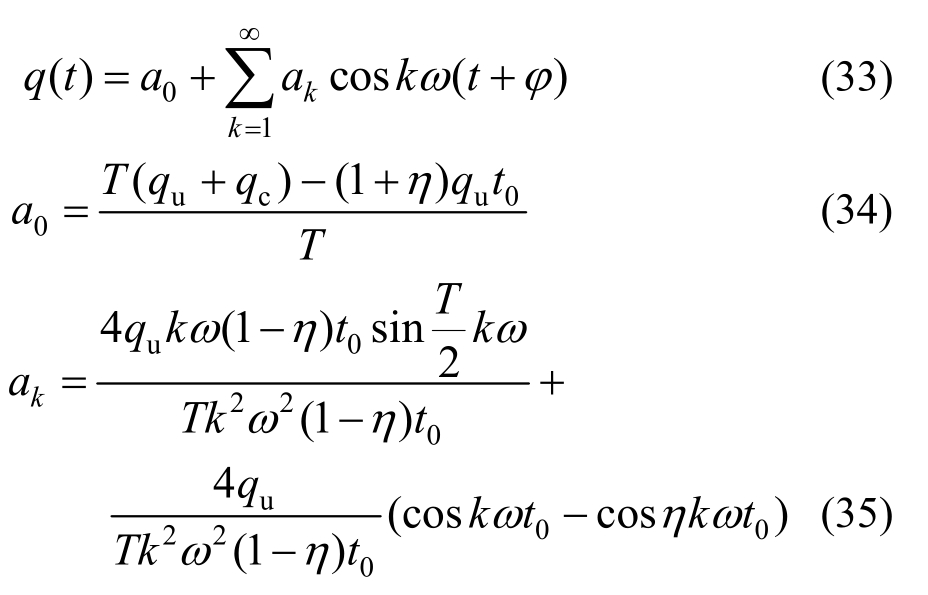
式中：
φ为初相位，控制梯形循环荷载的起始位置。
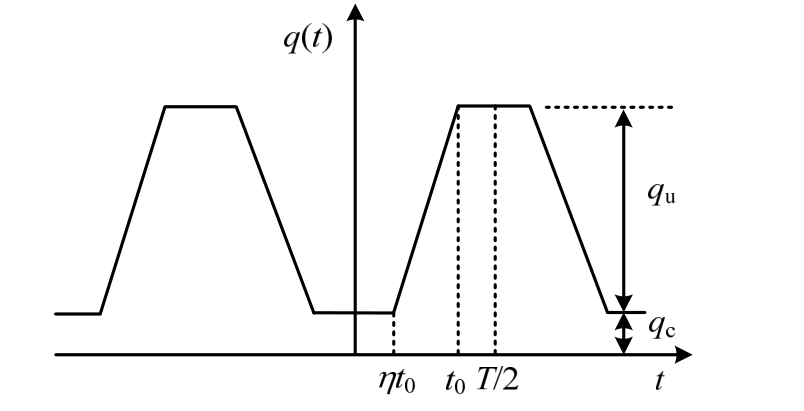
图3 梯形循环荷载示意图
Fig.3 The diagram of trapezoidal cyclic loadings
将荷载无量纲化，无量纲化参数为：
代入梯形荷载的傅里叶级数表达式可得：
便于孔压的求解，将梯形循环荷载q(Tv)看成是荷载
的叠加，又由本文求解的是均质地基固结解析解，由叠加原理可知，孔压的解答也可以看成是荷载0q、qk分别作用在土体上的孔压叠加。
将q0 =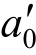
代入式(31)中，可得孔压解析解为：
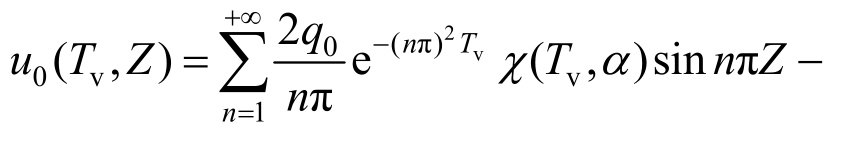
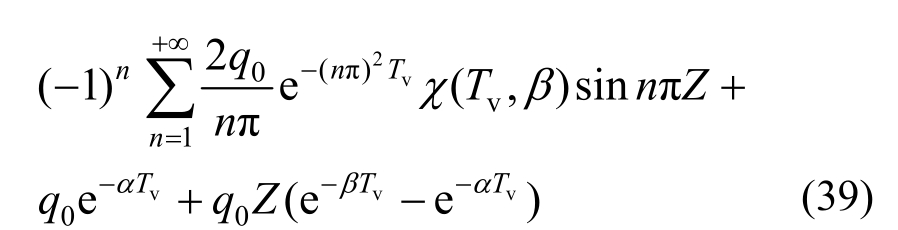
式中：
将
代入式(31)中，可得孔压的解析解为：
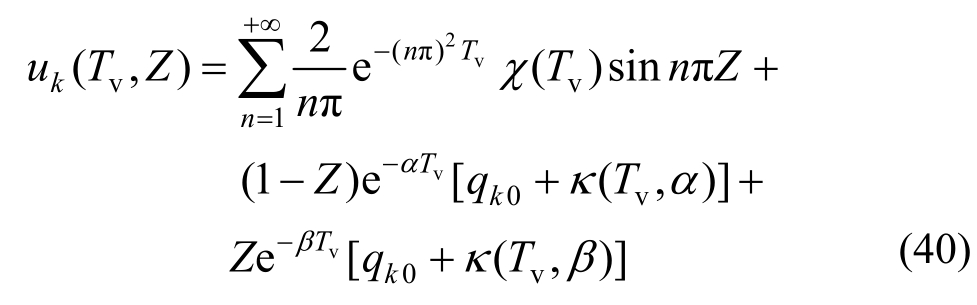
所以梯形循环荷载作用下的孔压解答可以表示为：
固结度解答为：
其中：
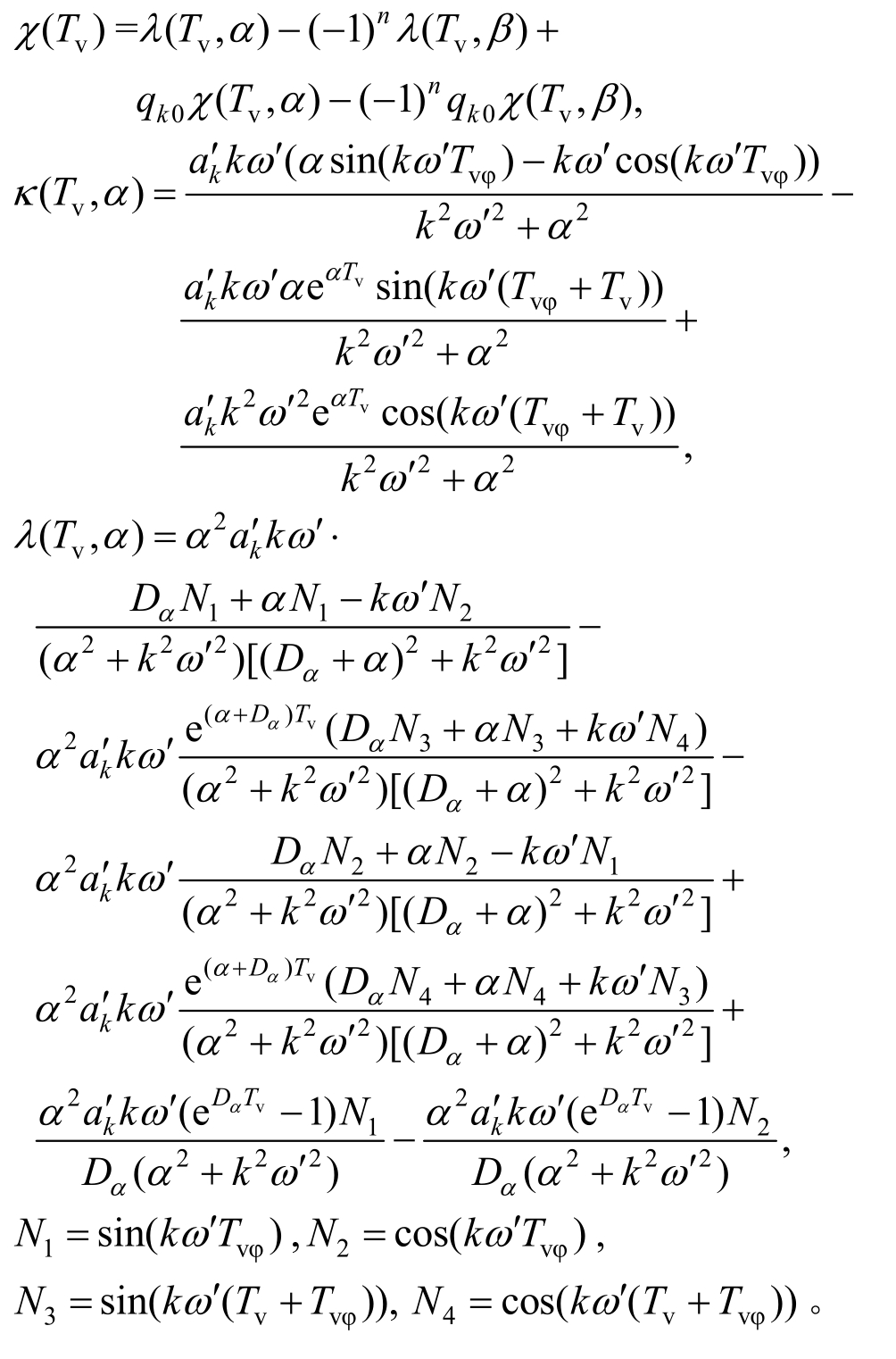
为了验证文中解析解的正确性，笔者编制了计算程序，将本文解答和梅国雄等[19]文献给出的连续排水边界下骤加荷载作用的一维固结解析解进行对比，计算结果如图4所示。
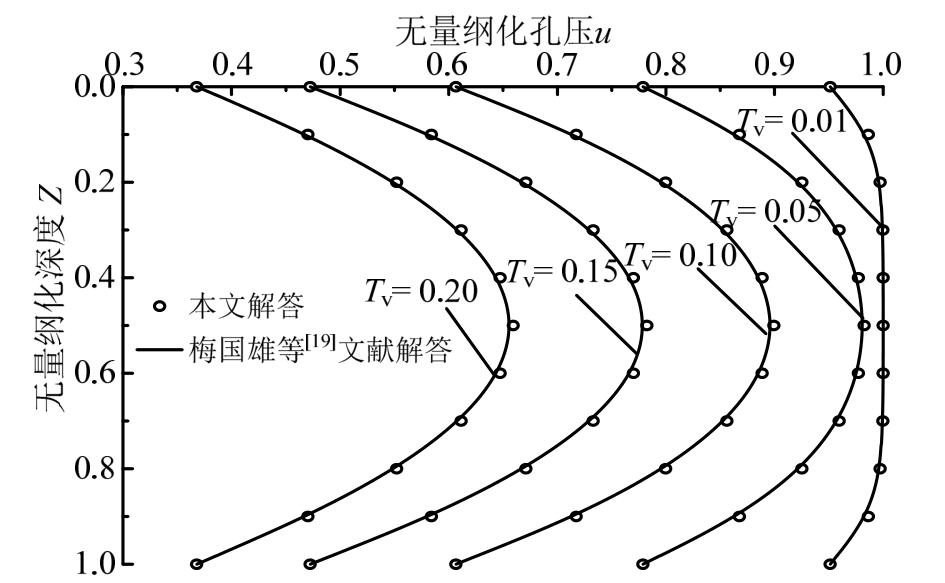
图4 本文解析解与梅国雄等[19]文献解析解比较
Fig.4 Compared with solution of Mei Guoxiong et al[19]
从图4可知，当t0取值趋向于0时，梯形循环荷载即可退化为骤加荷载，为便于编程计算，将t0取值0.0001，α、β各取值5。按照本文所求孔压解答和文献梅国雄等[19]所求孔压解答重合度非常好，初步验证了本文解答及计算程序的合理性。
为了探讨连续排水边界下梯形循环荷载作用的饱和土固结性状。本文选取梯形循环荷载的初始加荷荷载qc=30 kPa，波动荷载qu=100 kPa，加载系数η=0.25、t0=120 d，初始相位φ=30 d，加荷周期T=360 d，固结系数Cv=0.1296 m2·d-1，土层厚度H=10 m。分析了不同的界面参数α、β和梯形循环荷载的加载系数对土体固结性状的影响。
图5给出了无量纲化深度Z=0.5时，取不同界面参数，无量纲化孔压随时间因数vT的变化曲线。从图中可以看出，界面参数α越大，孔压整个固结过程消散速率也越快。在每个循环荷载作用周期内，恒载阶段孔压的最大值不断减小，最终趋向于零。
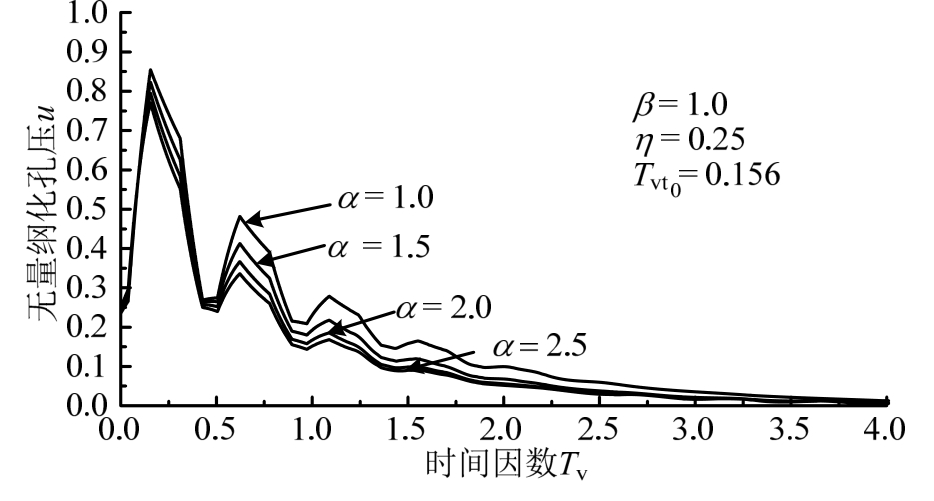
图5Z=0.5时，不同界面参数下的孔压消散曲线
Fig.5Z=0.5,the pore pressure dissipation curve of different interface parameters
图6给出了不同界面参数下的固结度变化曲线。从图中可见，经过不断地加卸载后，土体固结度最终将达到周期性稳定变化，并且界面参数越大，固结度达到稳定变化的时间越短。在每个循环荷载作用周期内，界面参数越大，恒载阶段固结度的最大值也越大。
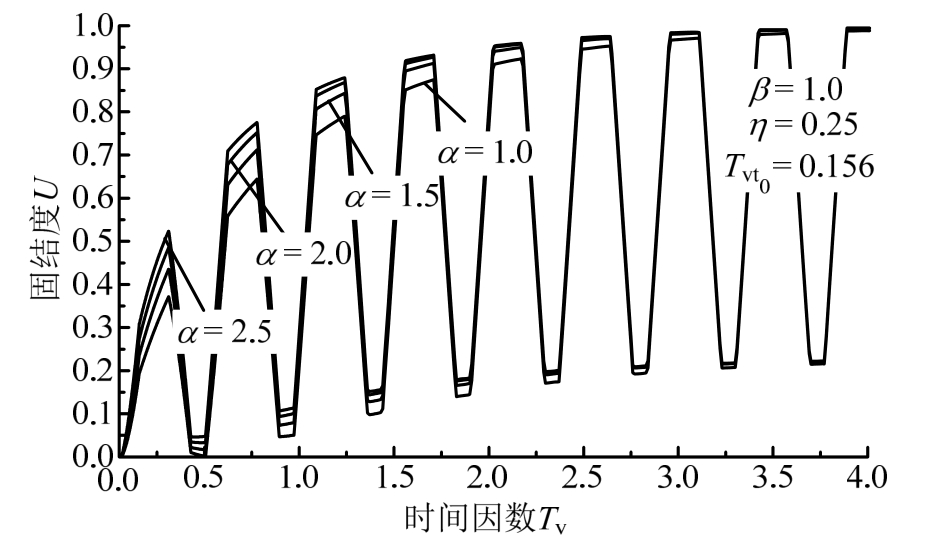
图6 不同界面参数下的固结度变化曲线
Fig.6 Consolidation curve of different interface parameters
图7给出了不同的加荷系数η下的固结度变化曲线。从图3可知，通过调节加荷系数η即可调节梯形荷载在加载和卸载阶段的速率，加荷系数η越大，在每个循环荷载作用周期内，荷载的加卸荷速率越大。从图7可见，当界面参数不变时，加荷系数η越大，在每个循环荷载作用周期内的加卸荷阶段，固结速度越快，在恒载阶段，固结度的最大值也越大。
图7 不同的加荷系数η下的固结度变化曲线
Fig.7 Consolidation curve of different loading coefficientη
图8给出了不同的加荷系数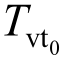
下的固结度变化曲线。从图3可知，通过调节加荷系数
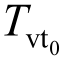即可调节梯形循环荷载恒载阶段的作用时间，加荷系数
越小，在每个循环荷载作用周期内，荷载的加卸荷速率越大，恒载作用时间越长。从图8中可见，加荷系数Tvt0越小，在加卸荷阶段，固结速度越快，在恒载作用阶段，在一个循环荷载周期内达到的最大固结度越小，而固结度变化范围越大。
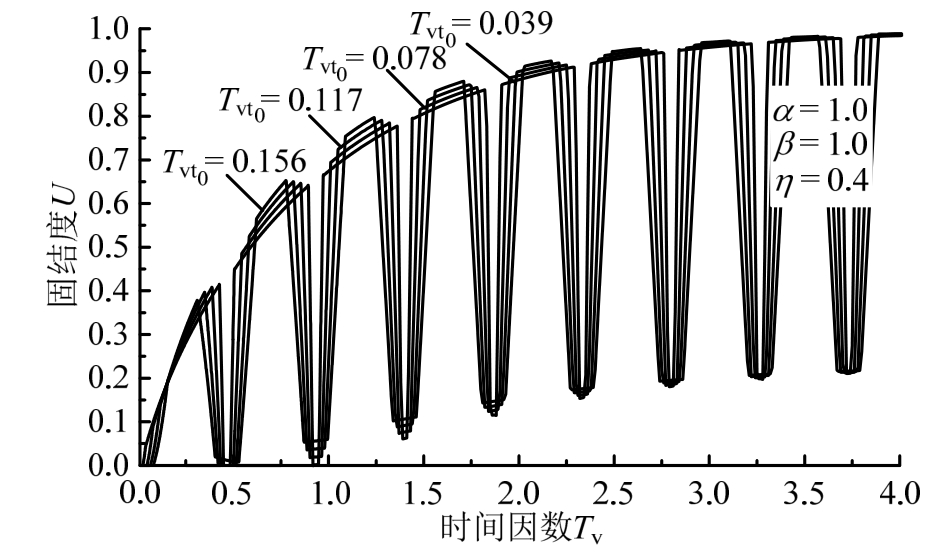
图8 不同的加荷系数Tvt0下的固结度变化曲线
Fig.8 Consolidation curve of different loading coefficient Tvt0
本文推导了基于任意荷载作用的连续排水边界条件，并在此基础上建立一维地基固结模型，给出梯形循环荷载作用下的一维固结解析解。将本文解析解退化到骤加荷载作用下的解与已有文献进行了对比，验证了本文解析解的合理性。最后通过固结性状分析，得到了以下结论。
(1) 界面参数越大，孔压消散速度越快，固结度达到稳定变化的时间越短。
(2) 界面参数不变时，加荷系数η越大，在每个循环荷载作用周期内，荷载的加卸荷速率越大，固结速度越快，在恒载阶段，固结度的最大值也越大。
(3) 界面参数不变时，加荷系数Tvt0越小，在每个循环荷载作用周期内，荷载的加卸荷阶段的加卸荷速率越大，固结速度越快，恒载作用时间越长，固结度变化范围越大。
[1] Schiffman R L.Consolidation of soil under time-dependent loadings and varying permeability [J].Proceedings,Highway Research Board,Washington,1958,37: 584－617.
[2] Wilson N,Elgohary M.Consolidation of soils under cyclic loadings [J].Canadian Geotechnical Journal,1974,11(3): 420－423.
[3] Alonso E E,Krizek R J.Randomness of settlement rate under stochastic loadings [J].Journal of the Geotechnical Engineering Division ASCE,1974,100: 1211－1226.
[4] Balighm M,Levadoux J.Consolidation theory of cyclic loadings [J].Journal of Geotechnical EngineeringDivision ASCE,1978,104(4): 415－431.
[5] Favaretti M,Soranzo M.A simplified consolidation theory in cyclic loadings conditions [C].International Symposium on Compression and Consolidation of Clayey Soils,A.A.Balkema: Rotterdam,The Netherlands,1995: 405－409.
[6] Rahal M A,Vuez A R.Analysis of settlement and pore pressure induced by cyclic loadings of Soil [J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,1998,124(12): 1208－1210.
[7] 吴世明,陈龙珠,杨丹.周期荷载作用下饱和粘土的一维固结[J].浙江大学学报: 工学版,1988,22(5):60－70.Wu Shiming Chen Longzhu Yang Dan.1-D consolidation of saturated clays under cyclic loadings [J].Journal of Zhejiang University (Engineering Science),1988,22(5): 60－70.(in Chinese)
[8] 杨峻,蔡袁强,吴世明.循环荷载作用下双层地基的一维固结[J].浙江大学学报: 工学版,1996,30(3):319－326.Yang Jun,Cai Yuanqiang,Wu Shiming.One dimensional consolidation of double-layered ground under cyclic loadings [J].Journal of Zhejiang University (Engineering Science),1996,30(3),319－326.(in Chinese)
[9] 蒋军,陈龙珠.长期循环荷载作用下粘土的一维沉降[J].岩土工程学报,2001,23(3): 366－369.Jiang Jun,Chen Longzhu.One-dimensional settlement due to long-term cyclic loadings [J].Chinese Journal of Geotechnical Engineering,2001,23(3): 366－369.(in Chinese)
[10] 梁旭,蔡袁强,吴世明.半透水边界饱和土层在循环荷载作用下的一维固结分析[J].水利学报,2002,31(7): 31－36.Liang Xu,Cai Yuanqiang,Wu Shiming.1-D consolidation analysis of saturated soil with semi-pervious boundaries under cyclie loadings [J].Shui Li Xue Bao,2002,31(7): 31－36.(in Chinese)
[11] 关山海,谢康和,胡安峰.低频循环荷载下地基一维固结性状分析[J].岩土力学,2003,24(5): 849－853.Guan Shanhai,Xie Kanghe,Hu Anfeng.Analysis of one-dimensional consolidation behavior of soils under low-frequency cyclic loadings [J].Rock and Soil Mechanics,2003,24(5): 849－853.(in Chinese)
[12] 李西斌,谢康和,王奎华,等.双面半透水边界饱和土层在循环荷载作用下的一维粘弹性固结解析解[J].工程力学,2004,21(5): 103―108,99.Li Xibin,Xie Kanghe,Wang Kuihua,et al.Analytical solution of 1-D visco-elastic consolidation consolidation of soils with impeded boundaries under cyclic loadings[J].Engineering Mechanics,2004,21(5): 103－108,99.(in Chinese)
[13] 庄迎春,胡安峰,谢康和.循环荷载下软土的一维固结分析[J].土木工程学报,2005,38(9): 109－114.Zhuang Yingchun,Hu Anfeng,Xie Kanghe.An analysis of one dimensional consolidation of soft clay under cyclic loadingsing [J].China Civil Engineering Journal 2005,38(9): 109－114.(in Chinese)
[14] 谢康和,周瑾,董亚钦.循环荷载作用下地基一维非线性固结解析解[J].岩石力学与工程学报,2006,25(1): 21－26.Xie Kanghe，Zhou Jin，Dong Yaqin,Analytical solution for one dimensional nonlinear consolidation of soil under cyclic loadings [J].Chinese Journal of Rock Mechanics and Engineering,2006,25(1): 21－26.(in Chinese)
[15] 胡亚元.梯形周期荷载作用下软基路堤的一维沉降研究[J].工程力学,2010,27(12): 114－118.Hu Yayuan.Study on the 1D settlement of road embankment on soft clay under trapezoidal periodic loading [J].Engineering Mechanics,2010,27(12): 114－118.(in Chinese)
[16] Lei G H,Fu C W,Ng C W W.Vertical-drain consolidation using stone columns: An analytical solution with an impeded drainage boundary under multi-ramp loadings [J].Geotextiles & Geomembranes,2016,44(1): 122－131.
[17] 何利军,吴立松,张涛,等.基于连续边界条件的土层厚度随时间变化的平均固结度研究[J].工程力学,2016,33(增刊1): 11－17.He Lijun,Wu Lisong,Zhang Tao,et al.The average degree of consolidation about soil layer thickness changing with time based on continuous drainage boundary [J].Engineering Mechanics,2016,33(Suppl1):11－17.(in Chinese)
[18] Ho L,Fatahi B.Analytical solution for the twodimensional plane strain consolidation of an unsaturated soil stratum subjected to time-dependent loading [J].Computers & Geotechnics,2015,67: 1－16.
[19] 梅国雄,夏君,梅岭.基于不对称连续排水边界的太沙基一维固结方程及其解答[J].岩土工程学报,2011,33(1): 28－31.Mei Guoxiong,Xia Jun,Mei Ling.Terzaghi’s onedimensional consolidation equation and its solution based on asymmetric continuous drainage boundary [J].Chinese Journal of Geotechnical Engineering,2011,33(1): 28－31.(in Chinese)
ONE-DIMENSIONAL CONSOLIDATION ANALYSIS OF THE TRAPEZOIDAL CYCLIC LOADING UNDER CONTINUOUS DRAINAGE BOUNDARY
李勇义(1990―)，男，湖北人，硕士生，主要从事软土地基处理研究(E-mail: leeyounguni@163.com);
冯健雪(1985―)，男，贵州人，博士生，主要从事软土地基固结理论研究(E-mail: fengjianxue@mail.gxu.cn).