
图1 正交异性钢桥面板的节段传力模型
Fig.1 Load-transferring model of orthotropic steel deck
正交异性钢桥面板具有自重轻、承载力高、施工快捷等特点,是现代钢桥发展最主要的成就之一;但钢桥正交异性桥面板结构(OSD结构)存在多种连接焊缝和切口,导致各板件间传力不顺畅,引起明显的应力集中,其疲劳损伤问题突出[1―7]。相关研究发现[8],正交异性钢桥面板典型疲劳易损部位主要是纵向加劲肋与横隔板交叉焊接连接(含开孔)、纵向加劲肋与顶板焊接连接、横隔板与顶板焊接连接等部位,其中发生在纵向加劲肋和横隔板交叉焊缝和开孔部位的疲劳开裂的几率最大,占总疲劳裂纹总数的38.2%,该部位是正交异性钢桥面板中应力集中程度最为明显、构造最为复杂以及焊接初始缺陷风险较高的部位。针对正交异性钢桥面板的疲劳损伤问题,国内外学者进行了深入的理论及试验研究:Tsakopoulos和Fisher[1]通过足尺模型试验对比了不同焊接方式对纵肋与横隔板疲劳应力幅的影响;Miki[9]认为顶板与加劲肋焊缝疲劳裂纹是由车轮荷载引起加劲肋腹板的局部弯曲应力造成的;Li等[10]利用弯曲疲劳试验系统模拟了临界载荷下的两种不同熔透率的顶板与纵向加劲肋的焊缝,验证了熔透率对疲劳裂纹类型及其疲劳抗力的影响;Aygül等[11]利用有限元方法结合缺口应力法对正交异性桥面板细节进行疲劳应力评估,其结果与试验吻合较好;叶华文等[12]通过数值分析和疲劳试验手段探究了横隔板厚度对开口肋正交异性钢桥面板疲劳性能的影响;朱太勇等[13]在一般全空间S-N曲线模型的基础上,考虑低应力幅造成疲劳损伤累积和高应力幅引起的塑性应变,提出了兼顾高、低水平应力幅影响的钢箱梁正交异性钢桥面疲劳评估的全空间S-N曲线模型;袁周致远等[14]对国内正交异性钢桥面板顶板竖向加劲肋焊接接头的构造细节进行研究,分析了普通角焊缝和熔透角焊缝在不同应力幅下的疲劳性能;陶晓燕[15]针对京沪高铁南京大胜关长江大桥——钢桁架拱桥的正交异性钢桥面板开展疲劳试验研究;高立强[16]针对国内首座铁路大跨度钢箱梁斜拉桥的正交异性钢桥面开展了疲劳试验研究,结果表明,铁路钢箱梁OSD结构承受典型的高周低幅疲劳作用,疲劳细节的疲劳开裂特点与公路桥梁不同。目前针对正交异性钢桥面板的疲劳特性研究大多是在公路荷载作用下进行的,针对列车荷载作用下的疲劳问题研究相对较少。
正交异性钢桥面板可视为多个由顶板与纵向加劲肋组成的闭口薄壁杆件并排固结受弯结构,国内外学者已经利用薄壁杆件理论对桥梁钢结构开展了一些研究。李国跃和吕凤梧[17]考虑断面剪力影响后将双肢缀板钢格构立柱按刚度等效的原则等效为闭口薄壁杆件,应用薄壁杆件理论分析了钢格构的整体稳定性,并验证了该方法的正确性;李翠娟等[18]通过数值模拟手段分析了轴向压力和弯矩作用下平行四边形闭口薄壁杆件的空间力学行为,结果表明,在弯矩作用下腹板倾角对截面顶、底板应力分布均有较大影响,且不均匀程度随腹板倾角增大而增大;胡启平等[19]基于薄壁杆件约束扭转一致性理论研究了组合薄壁杆件的弯-扭耦合问题,通过引入对偶变量推导出适用于开口断面、闭口断面及开闭口混合断面薄壁杆件结构的哈密顿正则方程;刘建廷[20]通过模型试验对公铁两用斜拉桥斜桁平行四边形闭口截面弦杆的受力机理进行了研究,结果表明,腹板的倾角会增大杆件截面正应力分布的不均匀程度,并导致杆件的弹性稳定系数降低;Chan和Kuang[21]基于闭口薄壁杆件理论和连续介质法提出了一种横向连接薄壁开口杆扭转的分析方法和一种利用广义扇形坐标估计薄壁杆件实际扭转刚度的方法;Mackenzie和Boyle[22]把刚度矩阵以闭口的形式给出并结合闭口薄壁曲线理论,提出了一种简单的管道弯曲有限元分析方法。
针对铁路正交异性钢桥面板的疲劳受力问题,基于弹性支撑梁理论及闭口薄壁杆件理论开展正交异性钢桥面板的传力、受力机理研究,推导了加劲肋与横隔板连接处疲劳敏感部位面内疲劳应力的解析公式,探求了影响该疲劳敏感部位面内应力的典型因素及其作用机理;根据实际桥梁正交异性桥面的受力特性进行了有限元分析,并与解析式结果进行了对比;通过对模型开展疲劳试验,系统研究了加劲肋与横隔板连接处疲劳敏感部位的疲劳受力特性。
在铁路荷载的传递中,列车轮轴荷载经过钢轨、轨枕、道砟或无砟轨道板传递至梁体顶面,已有研究表明[18],此时荷载已经相对均匀,作用于正交异性桥面的荷载由顶板与加劲肋传递至横隔板,而桥面板与加劲肋可视为“带翼缘的梁”弹性支撑于两侧横隔板上,如图1所示。鉴于顶板相对较薄,荷载通过顶板直接传递至横隔板的比例极小,可认为荷载主要通过加劲肋与横隔板的焊缝进行传递,如图2所示。

图1 正交异性钢桥面板的节段传力模型
Fig.1 Load-transferring model of orthotropic steel deck
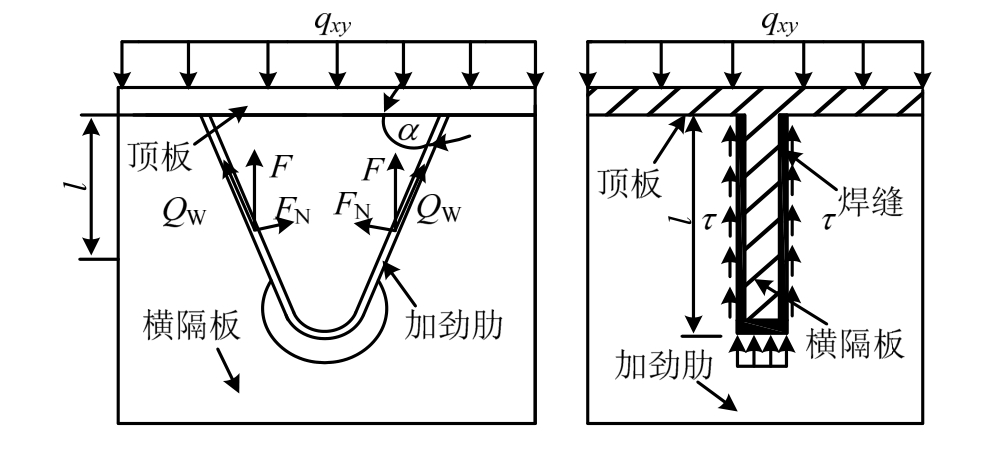
图2 横隔板与加劲肋焊接构造的传力模型
Fig.2 Load-transferring model of rib-diaphragm joints
为分析加劲肋与横隔板的传力机理,引入弹性支撑梁理论的基本假定如下:① 材料为线弹性、匀质、各向同性的假设;② 列车轮轴荷载连续分布大于3个横隔板间隔;③ 小变形假设及弯曲分析时横截面符合平截面假设;④ 加劲肋与横隔板的焊缝几何连续。则可建立传力过程的方程如下:

式中:F1、F2分别为加劲肋两侧腹板的竖向力;QW1和FN1分别为沿加劲肋一侧焊缝剪力和法向力;α为加劲肋腹板与顶板的内夹角(锐角)。沿焊缝长度的剪应力、法向应力如下:
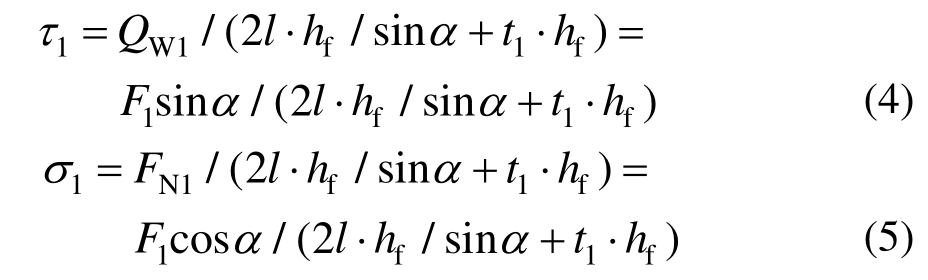
式中:τ1为一侧焊缝的剪应力;σ1为一侧焊缝的法向正应力;l为焊缝竖向投影长度;t1为横隔板厚度;hf为焊脚尺寸。在焊缝剪应力、法向正应力的基础上,可进一步计算焊缝的主拉、等效应力。
由式(1)~式(5)可见:外荷载、焊缝长度、焊脚尺寸、加劲肋腹板倾角(锐角)、横隔板厚等参数是加劲肋疲劳敏感部位面内疲劳应力的重要影响因素,并呈现规律如下:① 加劲肋疲劳敏感部位面内疲劳应力与外荷载、竖向焊缝长度、板厚直接相关;② 加劲肋疲劳敏感部位面内疲劳应力随着加劲肋与横隔板连接焊缝长度的增加而降低;③ 加劲肋疲劳敏感部位面内疲劳应力与加劲肋腹板倾角(锐角)呈负相关;④ 横隔板厚度是影响加劲肋疲劳敏感部位面内疲劳应力的重要因素之一,其应力随横隔板的厚度增加而减小。
为了分析加劲肋-横隔板焊接连接处的局部应力情况,引入闭口薄壁杆件受弯理论推导局部应力的解析公式。基于闭口薄壁理论分析薄壁杆件空间应力的基本假设有:① 由于加劲肋腹板厚度较小,沿周边切线方向的剪应力在厚度方向上均匀分布;② 由于壁厚较小,沿周边法线方向的剪应力为0。薄壁杆件空间应力分析时应确定其坐标系方向,坐标系定义如图3所示。

图3 坐标系定义
Fig.3 The definition of coordinate
由薄壁弹性分析理论可知,闭口薄壁杆件的弯曲剪应力τb计算公式如下:
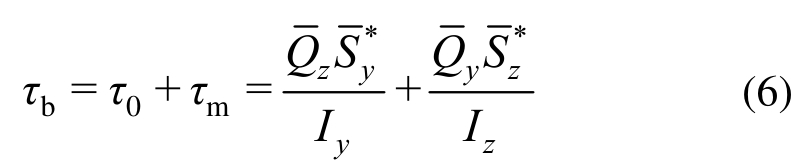
式中:τb和τ0分别为分离体顶面和底面剪力流; 和
和 为换算剪力;
为换算剪力;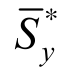 和
和 为对局部坐标系的换算静矩且:
为对局部坐标系的换算静矩且:

式中:Qy、Qz为截面剪力大小; 、
、 为对整体坐标系的截面静矩;Iy、Iz为截面抗弯惯性矩;当y和z为横截面形心主轴时
为对整体坐标系的截面静矩;Iy、Iz为截面抗弯惯性矩;当y和z为横截面形心主轴时![]() 式(6)可简化为:
式(6)可简化为:
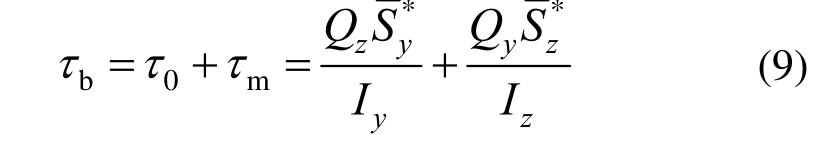
结合以上假设将加劲肋腹板受力进行一定简化,将加劲肋与顶板视为一个闭口的薄壁杆件,利用上述薄壁杆件剪应力计算式(9)求加劲肋与横隔板连接焊缝两侧加劲肋腹板上的剪力流:
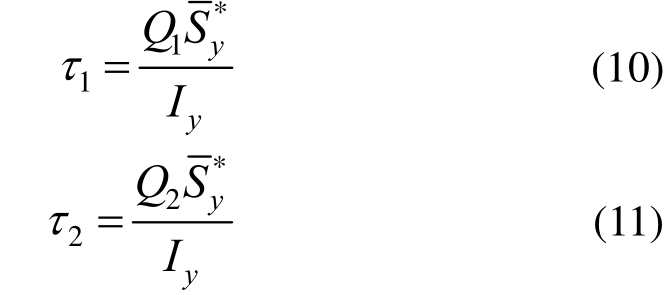
在x方向上截取dx段,如图4所示,建立z方向平衡方程式:

图4 加劲肋受剪示意图
Fig.4 Schematic diagram of stiffener withstand shear
式中:Q1、Q2分别为加劲肋与横隔板连接焊缝两侧加劲肋上的剪力大小;b为加劲肋的宽度;hc为加劲肋形心位置到顶板最上缘的垂直距离;α为加劲肋腹板与顶板的内夹角(锐角);t1为加劲肋板厚;截面静矩计算公式为 再截取ds局部作静力平衡分析,如图4所示,利用竖向平衡条件可得:
再截取ds局部作静力平衡分析,如图4所示,利用竖向平衡条件可得:
式中:![]() 为加劲肋与横隔板连接焊缝端部轴向力;σ为加劲肋与横隔板焊缝下端焊趾处竖向正应力;h为角焊缝的焊脚尺寸;Qw为加劲肋与横隔板连接焊缝竖向作用力;zc为加劲肋形心到顶板上缘的距离;l为加劲肋与横隔板连接焊缝的竖向投影长度。
为加劲肋与横隔板连接焊缝端部轴向力;σ为加劲肋与横隔板焊缝下端焊趾处竖向正应力;h为角焊缝的焊脚尺寸;Qw为加劲肋与横隔板连接焊缝竖向作用力;zc为加劲肋形心到顶板上缘的距离;l为加劲肋与横隔板连接焊缝的竖向投影长度。
将式(10)~式(12)代入式(13)中简化可得σ为:

式(14)表明,加劲肋-横隔板疲劳敏感部位面内疲劳应力还与横隔板两侧剪力、加劲肋抗弯惯性矩、加劲肋板厚等参数有关,其中:① 横隔板两侧剪力是最直接的影响因素,减小横隔板间距能大幅降低加劲肋疲劳敏感部位面内疲劳应力,能显著提高该细节的疲劳性能;② 加劲肋疲劳敏感部位面内疲劳应力随着加劲肋抗弯惯性矩的增加而降低;③ 随加劲肋厚度的增加,加劲肋的疲劳应力也会减小;④ 角焊缝焊脚尺寸的增大有利于抵抗疲劳破坏。
主跨468 m的宁波铁路枢纽甬江特大桥主桥中跨采用中部419 m钢箱梁及两侧混凝土箱梁组成的混合梁斜拉桥结构,承载双线中-活载,也是正交异性桥面钢箱梁斜拉桥在国内铁路桥梁上的首次应用。钢箱梁高4.85 m,梁宽21 m,钢材均为Q345qD;在纵桥向上每3 m设置一道横隔板,横隔板厚16 mm;顶板厚16 mm,配合间距600 mm、板厚10 mm的闭口加劲肋形成正交异性桥面板。正交异性桥面顶板采用6 mm厚甲基丙烯酸甲酯(MMA)防水防滑层,并在其上直接铺设道砟桥面。为进一步优化甬江特大桥正交异性钢桥面板的疲劳性能,比选了U、V形两种闭口加劲肋方案,两者面积及对顶板的抗弯惯性矩相近,具体的构造参数见表1。与U肋正交异性桥面相比,相同面积的V肋高度、其与横隔板焊缝长度分别增加10%、23.4%,横隔板过肋孔面积减小20.9%,且为受力合理的圆弧形。
表1 U肋、V肋构造参数表
Table 1 The structural parameters of U-rib and V-rib

加劲肋 高度/mm形心/mm焊缝高/mm腹板内倾角/(°)面积/mm2抗弯惯性矩/mm4 U肋 280 164.7 197.4 77° 1.66×104 5.646×107 V肋 307.6 161.2 243.1 69.5° 1.65×104 5.878×107
针对甬江特大桥正交异性桥面U、V两种加劲肋方案,分析实际列车荷载作用下加劲肋-横隔板受力状况。加载车辆采用实际线路中最具代表性的C64货运列车。根据C64相邻两辆车转向架之间的距离,通过计算得到最不利加载如图5所示,即相邻两辆车的2副转向架关于横隔板对称作用于四个钢箱梁节段。C64车辆轴重为210 kN,并通过双线系数和冲击系数进行修正,得到每条加劲肋上分布的荷载约为60 kN(忽略腹板的少量局部传载)。根据基于弹性支撑梁理论的加劲肋-横隔板焊缝应力计算式(1)~式(5)计算桥面道砟槽下左右各5根U、V肋共10根加劲肋在横隔板处的焊缝主拉应力结果,并与四节段的ANSYS有限元模型计算结果对比见表2。其中ANSYS有限元模型模拟中,钢箱梁纵向截取四个节段,其中采用板壳单元SHELL63模拟钢板部分,并采用实体单元SOLID45模拟道砟、轨枕和混凝土部分,利用梁单元BEAM4模拟钢轨部分,通过节点耦合实现各部分接触的相互作用,采用施加在扁平梁两侧钢锚箱上的简化横向简支约束方式,且忽略主梁体系的约束作用,各部分材料参数按实际取值,实际桥梁节段的有限元模型如图6所示。其中有限元的计算结果为加劲肋两侧腹板主拉应力的平均值。

图5 荷载纵向分布图
Fig.5 Longitudinal distribution of train load
表2 U形、V形加劲肋-横隔板焊缝主拉应力结果 /MPa
Table 2 The principal tensile stresses of rib-diaphragm joints of U-ribs and V-ribs

加劲肋 U1 U2 U3 U4 U5 V5 V4 V3 V2 V1有限元应力值 1.43 5.59 7.01 8.68 7.89 3.75 4.28 3.48 2.69 0.68解析应力值 8.56 8.56 8.56 8.56 8.56 6.99 6.99 6.99 6.99 6.99有限元值/解析式值 0.17 0.65 0.82 1.01 0.92 0.54 0.61 0.50 0.38 0.10

图6 原桥节段的有限元模型
Fig.6 Finite element model of the actual bridge segment
甬江特大桥正交异性桥面U、V两种加劲肋-横隔板焊缝主拉应力结果可见,在列车车辆荷载作用下焊缝主拉应力量值相对较小。由解析式(4)、式(5)和有限元计算结果均发现V形加劲肋腹部敏感部位的应力小于U形加劲肋的应力。结果也表明,加劲肋与横隔板连接焊缝长度的增加可以有效降低焊缝应力值,即降低了加劲肋-横隔板连接部位疲劳敏感部位的疲劳应力幅;加劲肋腹板倾角同样影响焊缝传力,焊缝剪力(切向力)将随加劲肋腹板倾角(锐角)的减小而减小,进而降低在加劲肋腹板疲劳敏感部位的疲劳应力。表2中应力的解析值与有限元计算值存在一定差距,其原因在于解析理论假定桥面荷载均由加劲肋及其上桥面传递,更符合箱梁中部加劲肋受力;而有限元模型中V1、U1加劲肋靠近箱梁两侧腹板,腹板优先传递桥面荷载并导致其附近加劲肋传递荷载显著偏小,其次是解析理论中未考虑到的横隔板剪切变形及横隔板的传递荷载作用而导致有限元计算的加劲肋-横隔板焊缝处应力相对较小。
为进一步研究正交异性钢桥面加劲肋腹板与横隔板连接焊缝处疲劳敏感部位受力状况。首先对甬江特大桥U、V肋正交异性桥面方案进行基于闭口薄壁理论的加劲肋-横隔板局部解析应力分析,根据原桥节段的几何参数和列车车辆荷载参数,通过解析式(14)对正交异性钢桥面板中U、V形加劲肋与横隔板连接焊缝焊趾敏感部位进行了应力分析。ANSYS有限元计算结果显示加劲肋与横隔板连接焊缝最不利受力位于加劲肋与横隔板过焊孔处。加劲肋与横隔板过焊孔处焊址附近(距离焊址5 mm)母材的解析计算结果及其与有限元计算结果的对比见表3。
表3 原桥节段U、V加劲肋疲劳主拉应力理论值 /MPa
Table 3 The principal tensile stresses of U-ribs and V-ribs on actual bridge

加劲肋 有限元计算值 解析计算值左侧 右侧 平均值相对误差/(%)U1 -0.45 3.30 1.43 1.59 11.19 V1 -2.08 3.29 0.61 0.68 11.48 U2 -5.11 16.28 5.59 6.26 11.99 V2 -6.13 11.51 2.69 3.03 12.64 U3 5.62 8.39 7.01 8.13 15.98 V3 1.86 5.10 3.48 3.97 14.08 U4 7.85 9.51 8.68 10.16 17.05 V4 3.58 4.97 4.28 4.92 14.95 U5 14.97 0.80 7.89 9.15 15.97 V5 10.28 -2.78 3.75 4.31 12.99
由表3可见,有限元计算结果表明,在列车荷载下U、V肋与横隔板焊缝附近母材受力较小,并存在显著的不均匀性;各疲劳敏感点由解析公式计算的疲劳应力结果与有限元计算的两侧焊缝均值结果基本吻合,各疲劳敏感部位测点应力分布规律和特性和有限元结果基本一致,表明所解析公式计算结果能够总体反映加劲肋-横隔板连接处疲劳敏感部位的力学特性与影响因素,但不能反映加劲肋两侧焊缝受力的差异;不同加劲肋的疲劳敏感点及其周围区域的应力值和分布特点均具有一定的差异,其中直接承载车辆荷载作用的中间加劲肋疲劳敏感应力值明显大于两侧加劲肋的疲劳应力值;U形加劲肋的应力稍大于同一位置的V形加劲肋应力,表明此应力与加劲肋腹板倾角以及焊缝长度有直接关系。
为验证正交异性钢桥面的实际疲劳性能,根据甬江桥正交异性桥面板参数,考虑试验场地、加载设备、运输条件等因素,优化设计出包含2个U形肋及2个V形肋的正交异性桥面足尺疲劳试验模型,试验模型的长、宽、高分别为6.0 m、3.0 m、1.386 m,在长度方向采用两个横隔板,在横向上设置四个加劲肋,模型桥面铺设道砟,并在其上设置混凝土分载板传递加载力。通过计算分析验证了该模型在加载力作用下受力与原桥正交异性桥面受力等效性良好。疲劳模型试验在考察正交异性桥面传统疲劳敏感点的基础上,重点关注加劲肋-横隔板焊缝处传力,其主要疲劳敏感点U11~U24、V11~V24及模型如图7所示。

图7 疲劳试验模型侧面图 /mm
Fig.7 Cross-sectional view of the fatigue test model
原桥正交异性桥面通过桥梁设计年运量单线2700万吨计算,通过C64列车换算运营100年的总疲劳循环次数为2934.8万次。显然,近三千万的疲劳次数难以在实验室内实现,遂利用Palmgren-Miner损伤累积定律,提升疲劳应力幅值换算至400万次疲劳循环试验,对应模型的疲劳加载力P=578.34 kN的等幅加载,其中荷载上限Pmax=619.65 kN,下限Pmin=41.31 kN。400万次后继续开展以疲劳破坏为目的160万次疲劳加载。疲劳试验过程中重点考察加劲肋与横隔板连接部位、加劲肋与顶板连接部位、横隔板开孔边缘应力集中部位等疲劳敏感区。疲劳试验及静载试验均通过液压伺服机施加荷载,经分析确定,在疲劳试验加载至1万次、2万次、5万次、10万次、50万次,之后每隔50万行进行一次静载试验直至560万次。在疲劳试验及静载试验过程中,通过动态应变仪对正交异性桥面板各测点应力进行监测与测试,并在疲劳加载循环到50万次以后每次静载测试后进行一次肉眼检视和无损探伤,检测试验模型的疲劳敏感部位是否有裂纹产生。
以铺设道砟的铁路正交异性桥面为研究对象,在理论研究的基础上开展铁路荷载高频次、较低应力幅、全寿命服役周期下的560万次的疲劳试验验证。在正交异性桥面的众多疲劳敏感区域中,加劲肋-横隔板连接处焊缝端部焊趾处加劲肋母材的疲劳问题最为显著,其主要测点的应力结果如图8所示。


图8 加劲肋疲劳敏感点主拉应力与循环次数间的关系
Fig.8 The principal tensile stress-cycle curves of sensitive rib details
U、V肋疲劳敏感部位试验测试结果表明:① 在前150万次试验荷载循环过程中,各疲劳敏感部位关注点的应力曲线保持原有线形,即各疲劳敏感部位的力学行为特性未发生明显改变;② 在疲劳荷载循环次数达到150万次后,裂缝附近测点主拉应力发生一定的变化并不断发展,并在250万次后在纵肋U1右侧腹板关注点U12焊趾处观测到约14 mm的外表层纵向微裂纹,但随着试验加载周次的累积,微裂纹长度逐渐增大,但应力测试结果保持不变,表明裂纹附近的测点应力完全释放和重分配,U1肋裂缝分布与发展见图9;③ 400万次疲劳荷载加载后V12应力发生重分布,并在500万次后采用超声波方式进行了探伤,发现V12发生疲劳微裂纹;④ 在疲劳荷载试验过程中各疲劳易损部位及其附近区域的应力量值和应力分布特性均存在较大差异,直接承受局部试验荷载作用的U2、V2加劲肋的疲劳应力大于U1、V1加劲肋的应力,横隔板与顶板焊接位置处的应力量值小于横隔板与纵向加劲肋连接切口端处的应力,表明横隔板对纵向加劲肋腹板局部支撑作用产生的应力受荷载作用位置影响显著,在铁路荷载作用下横隔板过加劲肋切口处比加劲肋与顶板焊接处更易疲劳破坏;⑤ 由加劲肋形式导致的各疲劳敏感部位的应力分布特性差异进而导致疲劳性能差异,实测U肋疲劳敏感部位疲劳应力稍大于V肋对应部位疲劳应力,表明V肋与横隔板连接具有更长的焊缝及较小的倾角能够降低疲劳敏感点的应力。

图9 加劲肋与横隔板连接的疲劳裂纹
Fig.9 Fatigue cracks at rib-diaphragm joint in U-rib
铁路正交异性桥面疲劳试验模型加劲肋与横隔板连接焊缝处的疲劳应力实测结果,及其与解析计算结果的对比见表4,表中均值为同一个加劲肋上左右侧测点测量值的平均值。可见,由于横梁的弯剪受力作用,U、V肋与横隔板连接的两侧焊缝处实测应力差异显著;在疲劳开裂前,各疲劳敏感部位测点的薄壁杆件理论计算结果与U、V肋两侧焊缝附近实测应力均值结果相符良好,其中U、V加劲肋疲劳敏感部位面内疲劳应力解析计算结果、仿真计算结果同试验结果基本吻合,而弹性支撑梁理论的计算结果与实测结果等有一定差异,表明所采用基于闭口薄壁理论的解析公式(14)能够从总体上反映加劲肋-横隔板连接处疲劳敏感部位的主要影响参数与影响程度等作用机理,但不能反映加劲肋两侧焊缝受力的差异。
表4 试验测试主应力结果同解析公式计算结果对比分析表 /MPa
Table 4 Comparison of the principal stresses for tested and from theoretical formula

注:1、560万次疲劳加载时V22测点处应变片已损坏。
位置 测点号 各疲劳荷载次数下应力测量值 有限元计算结果10万次 50万次 150万次 300万次 400万次 560万次薄杆局部应力计算值弹性支撑计算值U1肋U2肋V1肋V2肋U11 -29.02 -28.32 -28.47 -28.54 -28.37 -28.12 -28.12 — —U12 45.23 42.54 28.67 7.98 5.65 6.31 44.73 — —(U11+U12)/2 8.11 7.11 0.1 -10.28 -11.36 -10.905 8.31 8.46 11.05 U21 4.32 3.54 3.12 3.47 3.49 3.42 3.64 — —U22 36.37 36.25 36.02 36.13 35.67 35.72 37.04 — —(U21+U22)/2 20.35 19.90 19.57 19.80 19.58 19.57 20.34 22.34 11.05 V11 -24.61 -24.74 -25.54 -24.13 -23.22 -23.16 -23.88 — —V12 33.10 32.80 33.34 31.48 28.44 14.96 33.71 — —(V11+V12)/2 4.25 4.03 3.90 3.68 2.61 -4.1 4.92 4.27 8.75 V21 -2.78 -2.94 -2.74 -2.78 -2.84 -2.86 -2.93 — —V22 21.81 21.27 22.01 21.89 21.45 — 21.32 — —(V21+V22)/2 9.52 9.17 9.635 9.555 9.305 — 9.20 11.01 8.75
经疲劳试验及静载测试结果得知,加劲肋与横隔板焊接部位是铁路正交异性桥面板所有部位中最容易发生疲劳损害的关键部位,因此,选取出现开裂的U12、V12细节进行疲劳性能及寿命评估研究,探究该部位是否满足桥梁疲劳性能的要求。文中图表的相关结果以等效为欧洲规范Eurocode3中90类细节对应名义应力幅90 MPa的等效作用次数形式给出。等效荷载作用次数与加劲肋和横隔板连接焊缝处的疲劳裂纹长度关系曲线如图10所示,基于Miner准则将疲劳荷载作用下加劲肋开裂部位测点的应力幅值换算得到等效应力幅值,模型试验疲劳荷载作用次数与疲劳开裂位置等效应力的S-N曲线如图11所示。
研究表明:根据试验后横隔板与纵肋腹板连接焊缝处焊趾开裂时的荷载作用次数与应力幅间的关系,V1细节处疲劳强度大于Eurocode3中90类细节推荐的疲劳强度,等效作用次数为219万次,而U1纵肋的等效作用次数为162万次小于Eurocode3中200万次的疲劳性能要求,表明V1该部位的疲劳性能满足设计要求而U1该部位的疲劳性能不满足设计要求;U1和V1加劲肋的疲劳裂纹出现时间存在明显差异,且U1纵肋腹板敏感点在试验加载过程中应力幅始终小于Eurocode3对应的疲劳截止限但发生了开裂,开裂位置为焊缝热影响区母材,已有研究[23-24]表明焊接过程中会产生沿焊缝方向较大的残余应力,其值可能达到材料的屈服强度;说明焊接残余应力是疲劳开裂的重要影响因素。U1加劲肋开裂前期时,模型整体的承载力未发生明显改变(结构的竖向位移基本一致),仅在U1加劲肋裂纹达到最大值81 mm时,结构的竖向位移有局部加大趋势,表明在局部疲劳裂纹较多且裂纹进入后期扩张阶段之前,正交异性钢桥面板整体刚度基本保持不变并具有较大的竖向承载力。

图10 开裂长度与等效作用次数关系曲线
Fig.10 The relationship between crack length and equivalent loading cycle
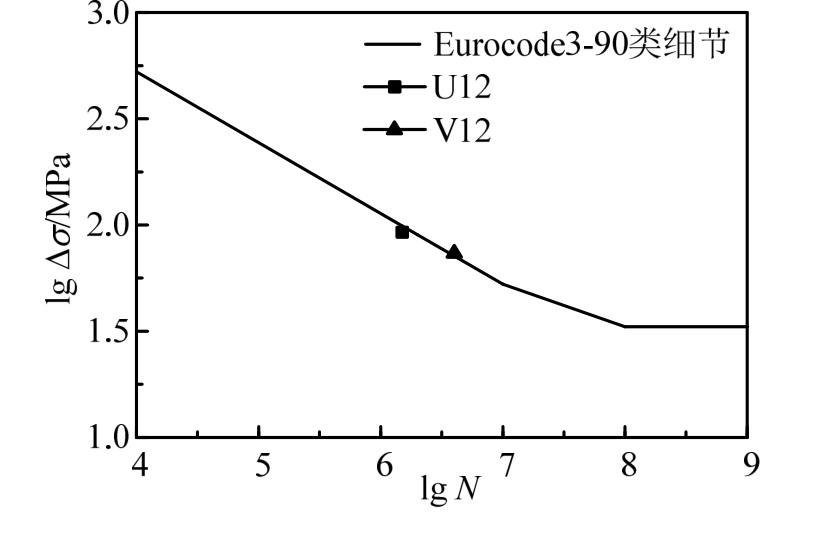
图11 加劲肋与横隔板交叉细节强度
Fig.11 Fatigue strength of rib-diaphragm joints
针对正交异性钢桥面板加劲肋与横隔板连接焊缝的构造细节,基于弹性支撑梁理论、闭口薄壁杆件理论以及有限元分析,并对试验模型进行了560万次的疲劳加载试验工作,得到如下结论:
(1) 采用弹性支撑梁理论对正交异性桥面板的传力机理进行分析,研究发现纵肋腹板与横梁腹板连接焊缝部位的疲劳应力随着纵肋腹板与横梁连接焊缝长度的增加而降低,而与加劲肋腹板倾角(锐角)呈负相关。
(2) 基于闭口薄壁杆件理论提出的应力解析公式能较为准确模拟加劲肋与横隔板连接焊缝端部疲劳敏感部位面内平均疲劳应力情况,并且可以明确该应力量值的典型影响因素如外荷载、焊缝长度、焊脚尺寸、加劲肋腹板倾角等及其作用机理,但不能反映加劲肋两侧与横隔板焊缝受力的差异。
(3) 560万次的疲劳试验结果表明,U1肋与横隔板焊趾处在设计寿命周期内发生疲劳开裂,而V形肋和U2加劲肋该部位疲劳极限大于桥梁设计年限内荷载循环次数,在运营期内具有较高的安全系数;U1肋开裂位置处于焊缝热影响区,开裂处实测应力小于对应细节的疲劳应力幅,表明焊接残余应力是疲劳开裂的重要影响因素;裂纹随着疲劳荷载循环次数的积累而加大,其效应范围也随着裂缝尺寸增大而增大,直到此处裂纹附近区域应力完全释放和重分配。
(4) 解析理论、有限元分析及模型试验测试结果一致表明,在铁路列车荷载作用下加劲肋与横隔板连接部位是正交异性桥面板中更容易发生疲劳开裂的关键部位;加劲肋与横隔板的焊缝长度和加劲肋腹板倾角的增大能够有效降低加劲肋的疲劳应力幅;铁路正交异性钢桥面板中,面积相近的V肋比U肋具有更好的抗疲劳工作性能。
[1] Tsakopoulos P A,Fisher J W.Full-scale fatigue tests of steel orthotropic decks for the Williamsburg bridge [J].Journal of Bridge Engineering,2003,8(5): 323-333.
[2] Wolchuk R.Lessons from weld cracks in orthotropic decks on three European bridges [J].Journal of Structural Engineering,1990,116(1): 75-84.
[3] Zhang Q,Cui C,Bu Y,et al.Fatigue tests and fatigue assessment approaches for rib-to-diaphragm in steel orthotropic decks [J].Journal of Constructional Steel Research,2015,114: 110-118.
[4] 王春生,付炳宁,张芹,等.正交异性钢桥面板足尺疲劳试验[J].中国公路学报,2013,26(2): 69-76.Wang Chunsheng,Fu Bingning,Zhang Qin,et al.Fatigue test on full-scale orthotropic steel bridge deck [J].China Journal of Highway and Transport,2013,26(2): 69-76.(in Chinese)
[5] Farreras-Alcover I,Chryssanthopoulos M K,Andersen J E.Data-based models for fatigue reliability of orthotropic steel bridge decks based on temperature,traffic and strain monitoring [J].International Journal of Fatigue,2017,95: 104-119.
[6] 陈斌,邵旭东,曹君辉.正交异性钢桥面疲劳开裂研究[J].工程力学,2012,29(12): 170-174.Chen Bin,Shao Xudong,Cao Junhui.Study of fatigue cracking for orthotropic steel bridge deck [J].Engineering Mechanics,2012,29(12): 170-174.(in Chinese)
[7] 曾志斌.正交异性钢桥面板典型疲劳裂纹分类及其原因分析[J].钢结构,2011,26(2): 9-15.Zeng Zhibin.Classification and reasons of typical fatigue cracks in orthotropic steel deck [J].Steel Construction,2011,26(2): 9-15.(in Chinese)
[8] 张清华,卜一之,李乔.正交异性钢桥面板疲劳问题的研究进展[J].中国公路学报,2017,30(3): 14-30,39.Zhang Qinghua,Bu Yizhi,Li Qiao.Review on fatigue problems of orthotropic steel bridge deck [J].China Journal of Highway and Transport,2017,30(3): 14-30,39.(in Chinese)
[9] Miki C.Fatigue damage in orthotropic steel bridge decks and retrofit works [J].International Journal of Steel Structures,2006,6(4): 255-267.
[10] Li M,Suzuki Y,Hashimoto K,et al.Experimental study on fatigue resistance of rib-to-deck joint in orthotropic steel bridge deck [J].Journal of Bridge Engineering,2017,23(2): 1-10.
[11] Aygül M,Al-Emrani M,Urushadze S.Modelling and fatigue life assessment of orthotropic bridge deck details using FEM [J].International Journal of Fatigue,2012,40(7): 129-142.
[12] 叶华文,徐勋,强士中,等.开口肋正交异性钢桥面疲劳设计参数研究[J] .西南交通大学学报,2012,47(3):379-386.Ye Huawen,Xu Xun,Qiang Shizhong,et al.Fatigue design parameters for orthotropic steel decks of single plane cable-stayed bridges [J].Journal of Southwest Jiaotong University,2012,47(3): 379-386.(in Chinese)
[13] 朱太勇,周广东,张欢,等.钢箱梁正交异性桥面板疲劳评估全空间S-N曲线研究[J].工程力学,2017,34(11): 210-217.Zhu Taiyong,Zhou Guangdong,Zhang Huan,et al.A full range S-N curve for fatigue evaluation of orthotropic bridge decks in steel box-girders [J].Engineering Mechanics,2017,34(11): 210-217.(in Chinese)
[14] 袁周致远,吉伯海,杨沐野,等.正交异性钢桥面板顶板竖向加劲肋焊接接头疲劳性能试验研究[J].土木工程学报,2016,49(2): 69-76.Yuanzhou Zhiyuan,Ji Bohai,Yang Muye,et al.Study on fatigue performance of welded joints for out-of-plane gusset in orthotropic steel bridge decks [J].China Civil Engineering Journal,2016,49(2): 69-76.(in Chinese)
[15] 陶晓燕.正交异性钢桥面板节段模型疲劳性能试验研究[J].中国铁道科学,2013,34(4): 22-26.Tao Xiaoyan.Experimental study on the fatigue performance of the section model of orthotropic steel bridge deck [J].China Railway Science,2013,34(4):22-26.(in Chinese)
[16] 高立强.铁路桥钢箱梁正交异性桥面板的静力行为与疲劳性能研究[D].成都: 西南交通大学,2013: 1-178.Gao Liqiang.Study on static structural behavior and fatigue performance of orthotropic deck of steel box girder for railway bridge [D].Chengdu: Southwest Jiaotong University,2013: 1-178.(in Chinese)
[17] 李国跃,吕凤梧.双肢缀板钢格构立柱的整体稳定分析[J].土木工程学报,2002(4): 17-19,35.Li Guoyue,Lü Fengwu.The overall stability of a battened plate column [J].China Civil Engineering Journal,2002(4): 17-19,35.(in Chinese)
[18] 李翠娟,卫星,强士中.平行四边形闭口薄壁杆件的空间力学行为[J].西南交通大学学报,2010,45(3):351-356.Li Cuijuan,Wei Xing,Qiang Shizhong.Spatial mechanical behavior of thin-walled members with parallelogram closed cross section [J].Journal of Southwest Jiaotong University,2010,45(3): 351-356.(in Chinese)
[19] 胡启平,涂佳黄,梁经群.组合断面薄壁杆件弯扭耦合分析[J].工程力学,2010,27(7): 52-55.Hu Qiping,Xu Jiahuang,Liang Jingqun.Bendingtorsion coupling analysis of the composite section thin-walled bar structure [J].Engineering Mechanics.2010,27(7): 52-55.(in Chinese)
[20] 刘建廷.公铁两用斜拉桥斜桁平行四边形闭口截面弦杆受力机理研究[J] .桥梁建设,2014,44(1): 50-55.Liu Jianting.Study of mechanical mechanism of parallelogram closed section chords of inclined truss of rail-cum-road cable-stayed bridge [J]. Bridge Construction,2014,44(1): 50-55.(in Chinese))
[21] Chan H C,Kuang J S.Torsional behaviour of braced thin-walled open sections [J].Thin-Walled Structures,1988,6(4): 343-354.
[22] Mackenzie D,Boyle J T.A simple pipe bend element for piping flexibility analysis [J].International Journal of Pressure Vessels and Piping,1992,51(1): 85-106.
[23] 黄永辉,王荣辉,甘泉.钢桁梁桥整体节点焊接残余应力试验[J].中国公路学报,2011,24(1): 83-88.Huang Yonghui,Wang Ronghui,Gan Quan.Welding residual stress test of steel truss bridge [J].China Journal of Highway and Transport,2011,24(1): 83-88.(in Chinese)
[24] 强斌,李亚东,顾颖,等.钢桥对接焊缝残余应力及变形场数值分析与试验验证[J].铁道学报,2017,39(9):134-139.Qiang Bin,Li Yadong,Gu Ying,et al.Numerical analysis and test verification of residual stress and deformation field of bridge butt weld [J].Journal of the China Railway Society,2017,39(9):134-139.(in Chinese)
RESEARCH ON FATIGUE PERFORMANCE OF RIB-TO-DIAPHRAGM JOINT IN RAILWAY ORTHOTROPIC STEEL DECKS
张 勇(1991―),男,山东人,硕士生,主要从事钢结构桥梁疲劳评估研究(E-mail: 422714507@qq.com);
杨仕力(1991―),男,四川人,博士生,主要从事桥梁结构动力学研究(E-mail: yangshiliswjtu@163.com);
蒲黔辉(1965―),男,四川人,教授,博士,主要从事大跨度预应力混凝土桥结构行为的研究(E-mail: qhpu@vip.163.com).