近些年随着结构全寿命设计理论的发展，余震作为一种多灾害愈发引起学者的关注[1－3]。研究主余震序列地震动作用下结构的抗震性能时，如何科学合理地选择主余震序列地震动是一个非常关键的问题。由于真实的主余震序列地震动较少，研究人员提出了生成人工主余震序列地震动的方法，其中主震和余震地震动之间的相关性需要进行合理的考虑[4－5]。
由于余震是由主震孕育而来的，因此余震和主震在震源机制、震源位置、震级等方面存在一定的联系[6]。大量统计数据显示，主震和强余震之间的震级差分布在0～3之间[7]，其平均值大约为1.2左右[8]。在此基础之上，很多学者[9－13]对余震发生率随时间的衰减过程、震级重现特征以及主震和震级最大的余震之间的震级差等方面进行了研究。除此之外，对余震震源的位置[14－15]、断层类型[12,16]以及场地条件[12]等方面也给出了相应的规律。
相对于震级以及震源机制等因素，工程人员更加关注地震动的幅值、持时与频谱特性等工程特征，因为它们对结构在地震作用下的反应有着重要且直接的影响[17－25]。由于余震和主震在震源、震级以及场地条件等方面的联系，可能会进一步导致主震地震动与余震地震动在幅值、持时以及频谱等强度参数方面也具有一定的相关性[26]。Ruiz-García和Negrete-Manriquez[27]分析了 Northridge地震和Mammoth lakes地震的主余震地震动，发现主震与其余震地震动在卓越周期和带宽方面具有较弱的相关性。同时，Ruiz-García[28]通过相关研究指出，主震地震动的卓越周期具有比余震地震动卓越周期大的趋势。此外，Ruiz-García[29]还收集了来自Imperial Valley、Chi-Chi等地震的184条主余震序列地震动，其分析结果表明：主震与余震地震动的卓越周期呈中等到偏弱不同程度的相关，而强震持时则呈弱相关。Song等[30]发现由于主震和余震在发生机制上的差异，导致在平均周期和持时方面，主震与余震地震动之间存在较大的差异。Rathje等[31]学者发现，由于震级上的差异，会导致主震地震动的平均周期往往比余震要大，而余震地震动的持时较短，且高频率成分较多。
上述研究表明，主震和余震在地震动参数方面存在一定的相关性，但是系统性的统计分析很少，基本以简单直接的对比为主。Xu等[32]利用Copula函数建立了地震动的峰值地面加速度和累计绝对速度之间的联合分布，而Tesfamariam和Goda[33]则利用Copula函数建立了主余震序列地震动作用下，结构最大位移和残余层间位移角之间的关系。Copula函数在建立不同参数之间的联合分布方面，存在天然的优势，它可以根据参数的边缘分布以及它们之间的相关系数，建立参数之间的联合分布[34]。因此借鉴上述研究方法，可以利用Copula函数来研究主震和余震地震动参数之间的相关性。
本文从PEER NGA-West2地震动数据库中挑选662条主余震序列地震动，研究它们在强度参数方面的相关性。首先对主震和余震地震动强度参数之间的相关系数和边缘分布模型进行分析，然后利用Copula函数建立主震和余震地震动强度参数之间的联合分布。在此基础之上，给出给定主震地震动强度参数条件下，余震地震动强度参数的条件分布以及条件均值等。
为了利用Copula函数建立主震和余震地震动强度参数之间的联合分布，首先要给出它们之间的相关系数，以便计算Copula函数里面的相关参数[35]。
相关系数可以直观地反映主震和余震地震动强度参数之间相关性的强弱。本文选取三种不同类型的相关系数：Pearson线性相关系数、Kendall秩相关系数、Spearman秩相关系数。它们可分别用来反映变量间线性相关程度、一致性变化程度以及单调相关程度[36]，计算公式分别为：
式中：x1i和x2i分别为主震和余震地震动强度参数的第i个观测值；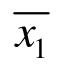
和
分别为它们的样本均值；N 为样本容量；sign[·]为符号函数，其中当
时sign=1，否则sign=0；ri和si分别为主震和余震地震动强度参数的秩，
和
分别为它们的样本均值。
得到主震和余震地震动强度参数之间的相关系数之后，需要进一步确定它们的边缘分布。首先，根据地震动强度参数的概率直方图初步选择合适的备选概率模型。然后，利用假设检验对其进行验证。如两种或者两种以上的备选概率模型通过假设检验，则利用AIC准则和BIC准则挑选出最优的概率模型，其计算公式如下：
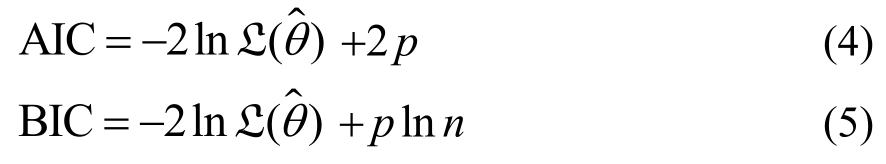
式中：
为概率模型的最大似然估计；
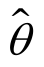为其估计参数；p为估计参数的数目；n为样本容量。
给定主震和余震地震动强度参数的相关系数以及它们的边缘概率分布条件下，可以借助Copula函数建立主震和余震地震动强度参数之间的联合分布：
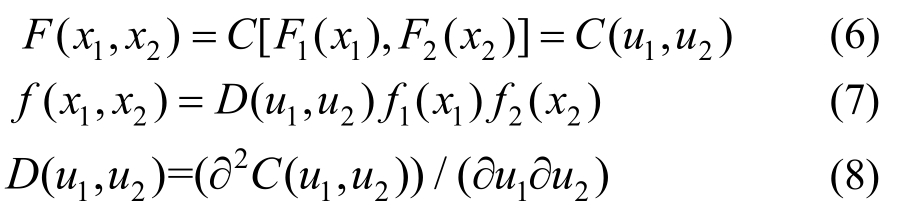
式中：
其中F1(x1)和F2(x2)分别为X1和X2的边缘累积分布函数，f1(x1)和f2(x2)分别为X1和X2的边缘概率密度函数；
为Copula分布函数，
为Copula函数的密度函数；
分别为X1和X2的联合累积分布函数和联合概率密度函数。
根据主震和余震地震动强度参数的分布特点，本文选取五种备选Copula函数：Gaussian Copula、t Copula、Frank Copula、Clayton Copula以及Gumbel Copula函数，其分布函数分别为：
式中：Φ-1(·)为一维标准正态分布函数Φ(·)的逆函数；
(·)为一维t分布函数Tν(·)的逆函数；ν为一维t分布函数的自由度；θ为Copula函数的相关参数。其中，Gaussian Copula和t Copula函数的相关参数可以按下式计算：
Frank Copula、Clayton Copula和Gumbel Copula函数的相关参数可分别按下式计算：
式中，τ为Kendall秩相关系数。
在此基础之上，可以进一步得到给定主震地震动强度参数条件下，余震地震动强度参数的条件分布和条件均值，其计算公式分别为：
式中：
和μx2|x1为给定主震地震动强度参数x1条件下，余震地震动强度参数x2的条件分布和条件均值。
PEER NGA-West2地震动数据库包含了来自世界各地的大量地震动记录，并且每条地震动记录的相关信息也很丰富，例如震级、断层距等。因此，本文以PEER NGA-West2地震动数据库作为数据来源，挑选所需的主余震序列地震动。其主要挑选原则如下：
1) 主震之后可能会伴随一系列的余震，本文只挑选主震及其震级最大的余震作为研究对象；
2) 主震地震动和相应的余震地震动记录必须来自同一记录台站；
3) 主震和余震均发生在浅层地壳结构；
4) 记录台站必须处在自由场地，排除结构对地震动记录的干扰。
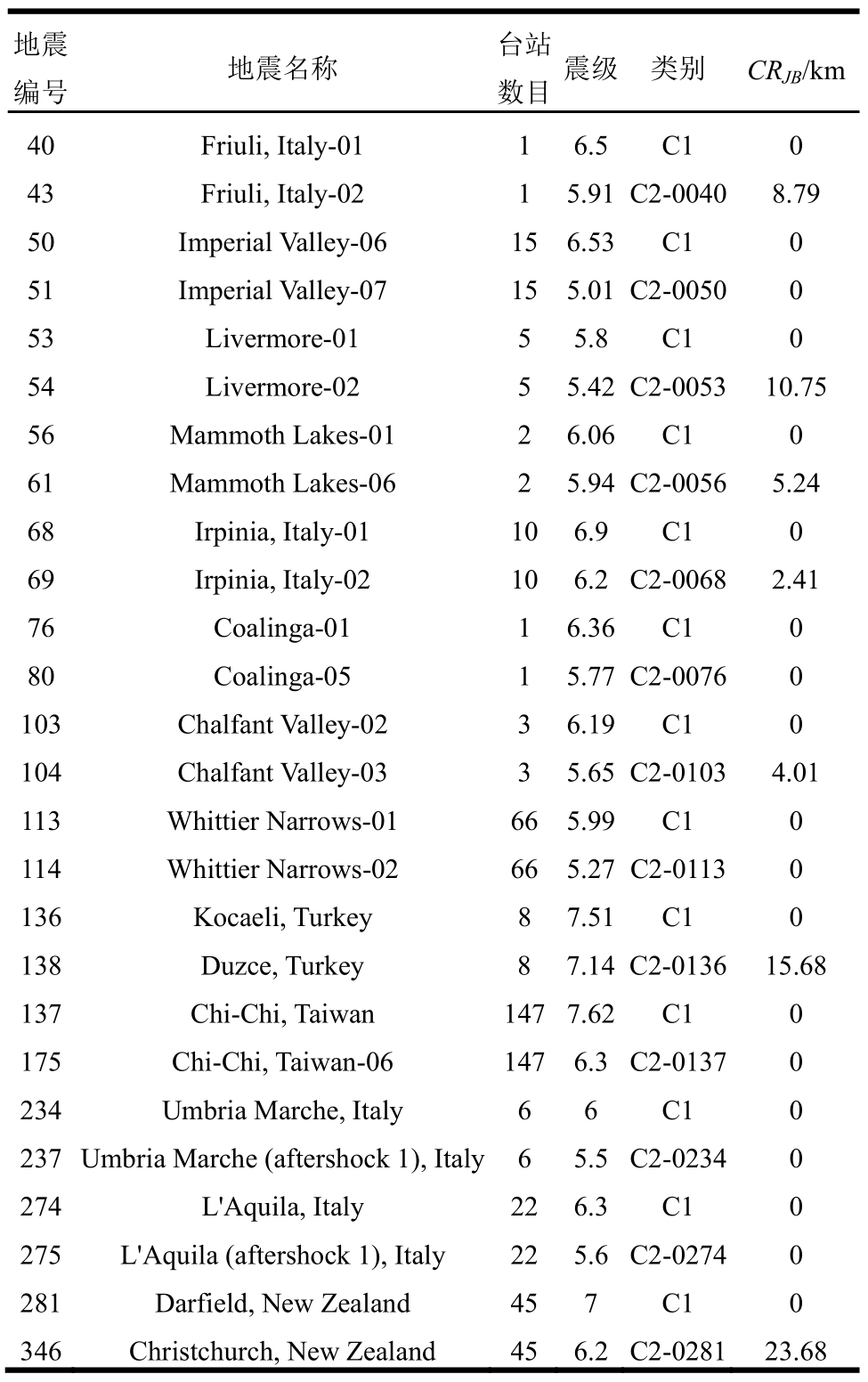
此外，排除震源深度有问题的地震事件，排除缺乏关键数据以及谱形等方面存在问题的地震动记录。考虑陈旧设备的触发阈值问题，对记录台站的断层距有一些限制，其详细信息请参考文献[37]中有关距离的限制原则。据此，本文最终挑选了662条主余震序列地震动，它们来自13次主余震事件。所选主余震地震动的基本信息如表1所示，它们的详细信息请参考文献[38]。
表1 挑选出的主余震地震序列
Table 1 List of the selected MS - AS earthquake sequences
地震编号 地震名称 台站数目 震级 类别CRJB/km 40 Friuli,Italy-01 1 6.5 C1 0 43 Friuli,Italy-02 1 5.91 C2-0040 8.79 50 Imperial Valley-06 15 6.53 C1 0 51 Imperial Valley-07 15 5.01 C2-0050 0 53 Livermore-01 5 5.8 C1 0 54 Livermore-02 5 5.42 C2-0053 10.75 56 Mammoth Lakes-01 2 6.06 C1 0 61 Mammoth Lakes-06 2 5.94 C2-0056 5.24 68 Irpinia,Italy-01 10 6.9 C1 0 69 Irpinia,Italy-02 10 6.2 C2-0068 2.41 76 Coalinga-01 1 6.36 C1 0 80 Coalinga-05 1 5.77 C2-0076 0 103 Chalfant Valley-02 3 6.19 C1 0 104 Chalfant Valley-03 3 5.65 C2-0103 4.01 113 Whittier Narrows-01 66 5.99 C1 0 114 Whittier Narrows-02 66 5.27 C2-0113 0 136 Kocaeli,Turkey 8 7.51 C1 0 138 Duzce,Turkey 8 7.14 C2-0136 15.68 137 Chi-Chi,Taiwan 147 7.62 C1 0 175 Chi-Chi,Taiwan-06 147 6.3 C2-0137 0 234 Umbria Marche,Italy 6 6 C1 0 237 Umbria Marche (aftershock 1),Italy 6 5.5 C2-0234 0 274 L'Aquila,Italy 22 6.3 C1 0 275 L'Aquila (aftershock 1),Italy 22 5.6 C2-0274 0 281 Darfield,New Zealand 45 7 C1 0 346 Christchurch,New Zealand 45 6.2 C2-0281 23.68
本文共选取34个不同的地震动强度参数，按照其定义以及计算公式分为以下四类：与加速度有关的强度参数(10个)、与速度有关的强度参数(11个)、与位移有关的强度参数(8个)以及其他强度参数(5个)。
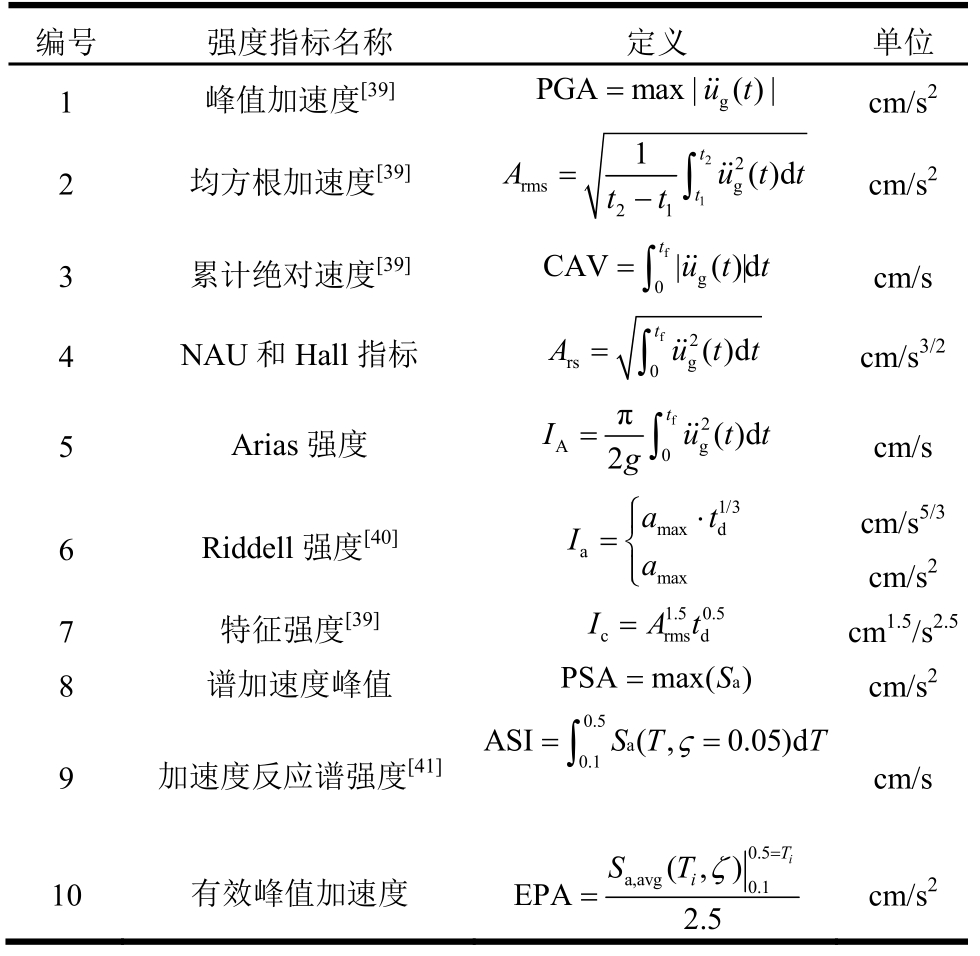
表2给出了与加速有关的强度参数，其定义均与地震动的加速度时程或者谱加速度有关。其中
为地震动的加速度时程，tf为加速度时程的总持时，amax为峰值加速度，td为5%～95%能量的卓越持时，Sa为绝对谱加速度。
表2 与加速度有关的强度参数
Table 2 Intensity measures related to acceleration
编号 强度指标名称 定义 单位PGA max|u(t)|1 峰值加速度[39] g= ˙˙ cm/s2 2 均方根加速度[39]A 1 ()d tt 2 2=- ∫˙˙ cm/s2 utt tt rms g 2 1 1 3 累计绝对速度[39]tutt=∫˙˙ cm/s f CAV |()|d 0 g t 4 NAU和Hall指标Autt f 2 rs g= ∫˙˙ cm/s3/20 ()d t 5 Arias强度f 2 A g 0 π ()d 2= ∫˙˙ cm/s Iutt g 1/3 max d a max 6 Riddell强度[40]■ ·■cm/s5/3 cm/s2 7 特征强度[39]1.50.5 at Ia=■■I=At cm1.5/s2.5 8 谱加速度峰值a c rmsd PSA max(S)= cm/s2 a ASI (,0.05)d 9 加速度反应谱强度[41]=∫0.5 0.1 STT ς=cm/s STζ==0.5 a,avg 0.1(,)EPA 2.5 iT 10 有效峰值加速度i cm/s2
表3给出了与速度有关的强度参数，其定义均与地震动的速度时程或者其谱速度有关。其中
为地震动的速度时程，υ0为加速度时程在单位时间内通过零点的次数，vmax为峰值地面速度，Sv为相对谱速度。
表3 与速度有关的强度参数
Table 3 Intensity measures related to velocity
编号 强度指标名称 定义 单位PGV max|u(t)|11 峰值地面速度[39] g= ˙ cm/s 12 均方根速度[39]V 2 1 ()d tt 2=- ∫˙ cm/s utt tt rms g 2 1 1 13 累计绝对位移[42]f CAD |()|d tutt=∫˙ cm 0 g t 14 NAU和Hall指标f 2 rs g Vutt=∫˙ cm/s1/20 ()d I I =υ cm 16 Riddell指标[40]2/31/3 15 修正的Arias强度A A,M 2 0 I=v ·t cm2/3/s1/3 17 Fajfar指标[43]0.25 v max d I=vt cm/s0.75 18 速度反应谱峰值v F maxd PSA max(S(Ti))=cm/s 19 有效峰值速度STζ==2.0 v,avg 0.8(,)EPV 2.5 iT i cm/s=∫ cm 21 速度反应谱强度[41]2.0 2.5 20 Housner谱强度SI() (,)d ζ 0.1 STT vζ VSI() (,0.05)d ζ=∫0.7 STT vζ=cm
表4给出了与位移有关的强度参数，其定义与地震动的位移时程或者其谱位移有关。其中ug(t)为地震动的位移时程，dmax为地面峰值位移，Sd为相对谱位移。
表4 与位移有关的强度参数
Table 4 Intensity measures related to displacement
编号 强度指标名称 定义 单位PGD max|u(t)|=22 地面峰值位移[39] g cm 23 均方根位移[39]D 1 ()d tt 2 2=- ∫ cm utt tt rms g 2 1 1 24 累积绝对动量[42]f CAI |()|d tutt=∫ cm·s 0 g t= ∫ cm·s1/2 26 Riddell强度[40]1/3 25 NAU和Hall指标Dutt f 2 rs g0 ()d I=d ·t cm·s1/3 27 峰值谱位移d d max d PSD max(())=ST cm 28 有效峰值位移i STζ==4.0 d,avg 2.5(,)EPD 2.5 iT i cm 29 位移反应谱强度[41]DSI (,0.05)d=∫4.0 2.5 STT dς=cm·s
表5给出了其他5个强度参数的定义。Td为地震动的卓越持时[44]，其定义为5%～95%Arias强度之间的持续时间。为了兼顾地震动速度峰值与加速度峰值的影响，本文选取了PGV/PGA和PGD/PGV两个参数[45]。Tg定义为速度反应谱中谱速度最大值对应的周期。Vanmarcke带宽可以反映地震动频率范围的宽窄，其中
、
和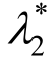
的计算公式如下[29]：
式中：Sv,i为阻尼比为0.05的弹性单自由度体系在周期Ti处的相对谱速度；ΔT为周期的时间间隔。
表5 其他强度参数
Table 5 Other intensity measures
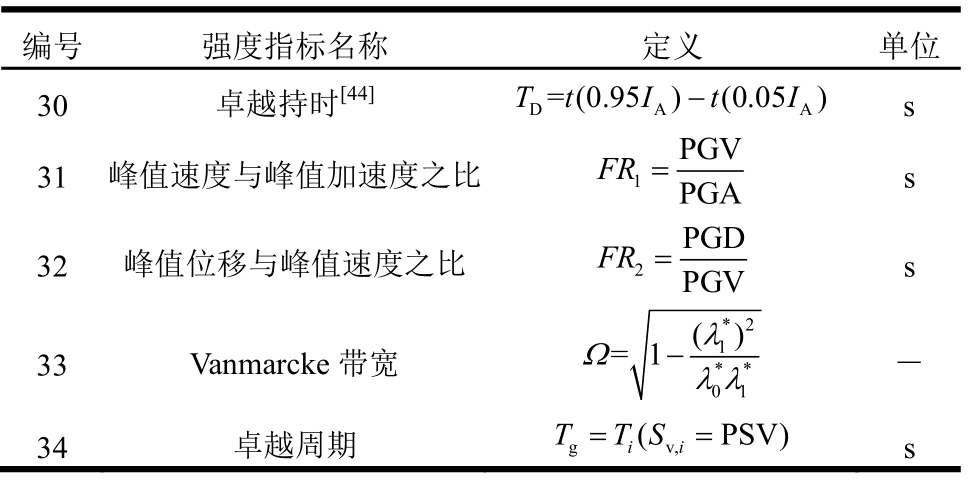
编号 强度指标名称 定义 单位30 卓越持时[44]DAA TtItI=(0.95 ) (0.05 )-s 31 峰值速度与峰值加速度之比FR= s 1 PGV PGA 32 峰值位移与峰值速度之比FR= s 2 PGD PGV 33 Vanmarcke带宽=1λ Ω -λλ －( )*2 1* *0 1 34 卓越周期 g (v, PSV)T=TS = s ii
下面对主震和余震地震动之间的相关系数进行计算，以便分析它们之间的相关性水准。此外，利用K-S检验以及AIC准则和BIC准则确定主震和余震地震动强度参数的最优的概率模型。通过上述研究，为建立主震和余震地震动强度参数之间的Copula函数奠定坚实的基础。
表6给出了34个地震动强度参数的相关系数，其中P表示Pearson线性相关系数，K表示Kendal秩相关系数，S表示Spearman秩相关系数。图1直观地展示了三种相关系数的变化趋势。
表6 主震和余震强度参数的相关系数
Table 6 Correlation coefficients of intensity measures between mainshocks and aftershocks
编号 名称 相关系数 编号 名称 相关系数P K S P K S 1 PGA 0.50 0.57 0.75 18 PSV 0.43 0.54 0.72 2Arms 0.43 0.58 0.77 19 EPV 0.42 0.55 0.74 3 CAV 0.63 0.65 0.83 20 SI 0.41 0.56 0.75 4Ars 0.51 0.60 0.78 21 VSI 0.43 0.56 0.75 5IA 0.31 0.60 0.78 22 PGD 0.20 0.50 0.70 6Ia 0.51 0.57 0.75 23Drms 0.13 0.49 0.68 7Ic 0.36 0.59 0.78 24 CAI 0.29 0.57 0.76 8 PSA 0.50 0.55 0.73 25Drs 0.20 0.54 0.73 9 ASI 0.52 0.57 0.76 26Id 0.29 0.54 0.74 10 EPA 0.51 0.58 0.76 27 PSD 0.38 0.57 0.76 11 PGV 0.30 0.51 0.70 28 EPD 0.39 0.58 0.77 12Vrms 0.22 0.51 0.70 29 DSI 0.39 0.58 0.77 13 CAD 0.53 0.62 0.81 30TD 0.80 0.58 0.76 14Vrs 0.34 0.57 0.77 31FR1 0.45 0.43 0.62 15IA,M 0.13 0.49 0.67 32FR2 0.52 0.46 0.65 16Iv 0.62 0.57 0.75 33Ω 0.68 0.49 0.68 17IF 0.36 0.54 0.73 34Tg 0.34 0.35 0.49
图1 主余震地震动之间强度参数的相关系数
Fig.1 Correlation coefficients of the selected IMs between the MS-AS ground motions
结合表6和图1可以看出，总体而言Spearman秩相关系数最大，Pearson线性相关系数最小。除了卓越持时以外，其他强度参数的Pearson线性相关系数均相对较小，说明其他强度参数的线性相关程度均相对较弱。对于与加速度、速度和位移有关的地震动强度参数：Kendall秩相关系数基本维持在0.6左右，说明主震和余震地震动强度参数之间的一致性处在中等水准；Spearman秩相关系数则稳定在0.7～0.8左右，其单调程度处在中等偏高的水准；Pearson线性相关系数呈现出中等偏弱的水准，说明它们之间的线性相关程度较差。在这三类地震动强度参数中，CAV、CAD和CAI的相关系数相对较大，主要是因为它们是地震动时程范围内的累计参数，受地震动持时影响较大。而34个所选地震动强度参数值中，主震和余震地震动在卓越持时方面的相关性最高。
图2给出了累积绝对速度(CAV)和卓越持时(Td)的散点图。从图中可以看出，对于大多数主震地震动而言，其CAV和Td要比余震地震动大。此外，随着主震地震动参数的增大，余震地震动CAV的离散性逐步增强，而卓越持时的离散性相对比较稳定。
图2 CAV和Td的散点图
Fig.2 Scatters of CAV andTd
图3给出了主震和余震地震动卓越持时的概率密度函数。根据概率直方图初步选择了三种备选概率模型，它们分别是正态分布(N)、Gumbel分布(G)和广义极值分布(Generalized Extreme Value distribution，GEV)。然后利用K-S检验对备选概率模型进行验证，其结果显示有的强度参数有两种或者两种以上概率模型通过了假设检验，例如PGV、PGD等。鉴于上述情况，则借助AIC准则和BIC准则确定最优概率模型。表7给出了所选34个强度参数的最优概率模型及其参数。为了方便讨论，后续的分布模型都是针对取自然对数之后的强度参数而言。
图3 卓越持时的概率密度函数
Fig.3 Probability density function ofTd
表7 所选强度参数的最优分布及其参数
Table 7 Optimum distributions and their parameters of the selected intensity measures
主震(lnIM) 余震(lnIM)编号名称K-S检验 最优分布类型及其参数 K-S检验 最优分布类型及其参数NGGEV类型P1P2P3 N G GEV 类型P1P2P3 1PGA10 1 G -1.760.83— 1 1 1 N -3.011.17—2Arms10 1 G -3.170.83— 1 1 1 N -4.531.14—3CAV10 0 G 6.730.74 — 1 1 1 N 5.100.96—4Ars10 1 G -1.660.71— 1 1 1 N -3.100.96—5IA 10 1 G 4.021.42 — 1 1 1 N 1.141.99—6Ia 10 1 G 6.090.76 — 1 1 1 N 4.791.07—7Ic 10 1 G 7.021.10 — 1 1 1 N 4.921.55—8PSA10 1 G -0.530.80— 1 1 1 N -1.781.13—9ASI10 1 G -1.900.81— 1 1 1 N -3.171.13—10EPA10 1 G -1.910.81— 1 1 1 N -3.181.13—11PGV00 0 G 3.190.98 — 1 1 1 N 1.501.15—12Vrms00 0 N 1.481.18 — 1 1 1 N 0.211.19—13CAD11 1 GEV-0.421.364.30 0 1 0 GEV -0.321.272.65 14Vrs11 0 GEV-0.361.252.71 0 1 1 N 1.681.16 —15IA,M01 0 N -1.191.74— 1 1 1 N -3.782.08—16IV 10 1 G -0.200.50— 1 1 1 N -1.090.69—17IF 11 0 GEV-0.361.183.05 1 1 1 N 2.181.11 —18PSV10 0 G 4.160.86 — 1 1 1 N 2.611.12—19EPV10 0 G 2.660.87— 0 1 1 N 1.171.14—20SI10 0 G 4.290.87 — 1 1 1 N 2.771.14—21VSI10 0 G 4.350.83— 1 1 1 N 2.911.11—22PGD10 0 G -0.341.621.41 0 1 0 N 0.181.38 —23Drms10 1 G 1.771.44 — 0 1 0 N -0.891.47—24CAI11 1 G 5.201.51 — 1 1 1 GEV -0.391.711.61 25Drs11 1 G 3.471.45 — 0 1 0 GEV -0.321.540.12 26Id 11 1 G 3.721.39 — 0 0 0 GEV -0.331.460.62 27PSD11 0 GEV-0.441.412.08 0 1 0 N 1.041.35 —28EPD11 0 GEV-0.461.500.80 0 1 0 N -0.291.45 —29DSI11 0 GEV-0.461.502.13 0 1 0 N 1.031.45 —30Td10 1 G 3.320.55 — 0 0 0 G 3.060.59—31FR101 0 GEV-0.330.67-2.23 0 1 0 N -2.380.49 —32FR211 1 G -0.360.63 — 1 1 1 GEV -0.400.72-1.52 33Ω110 GEV-0.500.27-0.94 1 0 0 GEV -0.490.22-0.84 34Tg11 1 GEV-0.461.070.28 1 1 0 GEV -0.250.74-0.30
表7中，如果K-S假设检验的结果为0，则表示接受之前的零假设；如果结果为1，则表示拒绝零假设。当地震动强度参数的最优概率模型为正态分布时，P1和P2分别表示均值和标准差；当地震动强度参数的最优概率模型为Gumbel分布时，P1和P2分别表示其位置参数和尺度参数；当地震动强度参数的最优概率模型为广义极值分布时，P1、P2和P3分别为形状参数、尺度参数和位置参数。对于以上三种分布模型均未通过假设检验的强度参数，本文依然给出了三个备选概率模型中的最优概率模型。对于主震地震动强度参数而言，其最优概率模型以Gumbel分布和广义极值分布为主，而余震地震动强度参数的最优概率模型则以正态分布和广义极值分布为主。主震地震动的强度参数中，大部分强度参数均有相应的概率模型通过了K-S检验。对于余震地震动的强度参数而言，与加速度有关的强度参数均未通过K-S检验，与速度有关的强度参数种仅有一部分通过了K-S检验，与位移有关的强度参数中仅CAI未通过K-S检验，其他强度参数中仅FR2未通过K-S检验。对于没有概率模型通过假设检验的地震动强度参数而言，可采用经验分布函数或者核密度估计曲线来代替相应的概率模型，用以计算其联合分布以及条件均值等。
给定主震和余震地震动强度参数的相关系数及其边缘分布条件下，可以利用AIC准则和BIC准则确定它们之间的最优Copula函数，然后利用Copula函数建立主震和余震地震动强度参数之间的联合分布。在此基础之上，可以进一步得到给定主震地震动强度参数条件下，余震地震动强度参数的条件分布。最后，将条件分布进行卷积，可以得到给定主震地震动强度参数条件下，余震地震动强度参数的条件均值。
图4给出了PGA和Td的边缘累积分布函数的散点图，从中可以看出PGA的样本点关于45°角对称并且下尾相关，而Td的样本点关于45°对称且上尾相关，它们分别符合Clayton Copula函数和Gumbel Copula函数的基本特征。根据主震和余震地震动强度参数的累积分布函数分布特性，本文选取了五种备选Copula函数，然后利用AIC准则和BIC准则从中确定最优Copula函数。
表8给出了主震和余震地震动强度参数之间的最优Copula函数及其参数。与加速度、速度和位移有关的地震动强度参数，其最优Copula函数几乎全是Clayton Copula函数，仅CAD和CAI的最优Copula函数为Frank Copula函数。其他地震动强度参数中，只有卓越持时的最优Copula函数为Gumbel Copula函数，其他地震动强度参数则全是Frank Copula函数。
图4 PGA和Td的边缘累计分布函数散点图
Fig.4 Scatter of the marginal CDF of PGA andTd
表8 最优Copula函数及其参数
Table 8 Optimum copula functions and their parameters
编号 名称 最优类型 参数(θ) 编号 名称 最优类型 参数(θ)1 PGA Clayton 2.65 18 PSV Clayton 2.33 2Arms Clayton 2.88 19 EPV Clayton 2.33 3 CAV Clayton 3.25 20 SI Clayton 2.45 4Ars Clayton 3.15 21 VSI Clayton 2.48 5IA Clayton 3.15 22 PGD Clayton 1.78 6Ia Clayton 2.73 23Drms Clayton 1.81 7Ic Clayton 3.04 24 CAI Frank 7.55 8 PSA Clayton 2.50 25Drs Clayton 1.98 9 ASI Clayton 2.80 26Id Clayton 1.92 10 EPA Clayton 2.81 27 PSD Clayton 2.30 11 PGV Clayton 2.13 28 EPD Clayton 2.19 12Vrms Clayton 2.15 29 DSI Clayton 2.19 13 CAD Frank 8.5 30Td Gumbel 2.40 14Vrs Clayton 2.37 31FR1 Frank 4.78 15IA,M Clayton 1.90 32FR2 Frank 5.23 16Iv Clayton 2.75 33Ω Frank 5.72 17IF Clayton 2.15 34Tg Frank 3.54
图5给出了给定主震地震动卓越持时条件下，余震地震动卓越持时的条件概率密度函数与条件累积分布函数。图5(a)中实线为余震地震动卓越持时的边缘概率密度函数，其他几条虚线为考虑相关性时，余震地震动卓越持时的条件概率密度函数。通过对比发现，考虑与不考虑主余震地震动强度参数的相关性条件下，它们的概率密度函数差异很大，并且随着主震地震动卓越持时的改变，其条件概率密度函数也发生了较大的变化。图5(b)、图5(c)和图5(d)分别给出了当ln(Td,MS)分别等于2.5、3.0和3.5时，余震地震动卓越持时的条件累积分布函数。与不考虑相关性的累积分布函数相比，余震地震动卓越持时的条件累积分布函数与经验累积分布函数(ECDF)更加接近。因此，Copula条件分布能够给出更加精确的结果。
图5 给定Td,MS条件下Td,AS的条件PDF与条件CDF
Fig.5 Conditional PDF and CDF ofTd,AS givenTd,MS
将Copula条件分布进行卷积，即可以得到给定主震地震动强度参数条件下，余震地震动强度参数的条件均值。图6(a)给出了给定主震地震动卓越持时条件下，余震地震动卓越持时的条件均值。从图中可以看出，Copula条件均值能够反映出给定主震地震动强度参数条件下，余震地震动强度参数的总体趋势。因此，可以利用Copula条件均值来预测给定主震地震动强度参数条件下，余震地震动参数的取值。图6(b)给出了给定主震卓越持时条件下，利用Copula条件均值预测的余震地震动卓越持时。从图6(b)中可以看出，余震卓越持时的预测值和观测值较为一致。当余震卓越持时较小时，预测值要比观测值稍微大。其主要原因是当主震地震动卓越持时较小时，余震卓越持时的Copula条件均值较大。
图6 给定Td,MS条件下Td,AS的Copula条件均值和预测值
Fig.6 Copula conditional means and predicted values ofTd,AS
givenTd,MS
本文从PEER NGA-West2地震数据库中选取了662条主余震地震动序列，并为每条地震动计算了34个强度参数，用以研究主震和余震地震动强度参数之间的相关性，得到如下结论：
(1) 对于与加速度、速度以及位移有关的地震动强度参数：Kendall秩相关系数基本维持在0.6左右，Spearman秩相关系数则稳定在0.8左右，而Pearson线性相关系数则处在0.1～0.6之间变化；CAV的相关程度最高。所选34个地震动强度参数中，主震和余震地震动卓越持时之间的相关性最高。
(2) 大部分主震地震动强度参数，均有概率模型通过K-S检验，其最优概率模型以Gumbel分布为主。对于余震地震动而言：与加速度有关的强度参数的备选概率模型均未通过K-S检验，与速度有关的部分强度参数通过了K-S检验，与位移有关以及其他强度参数大部分通过了K-S检验，且它们的最优概率模型以正态分布和广义极值分布为主。
(3) 主震和余震地震动强度参数之间，最优Copula函数以Clayton Copula和Frank Copula为主。Copula函数能够较好地建立主震和余震地震动强度参数之间的联合分布。Copula条件分布与经验累积分布函数较为接近，能够较好地反映给定主震地震动强度参数条件下，余震地震动强度参数的分布特性。在此基础之上，给定主震地震动强度参数条件下，Copula条件均值可以用来预测余震地震动强度参数的取值。
[1] Zhang Y,Chen J,Sun C.Damage-based strength reduction factor for nonlinear structures subjected to sequence-type ground motions [J].Soil Dynamics and Earthquake Engineering,2017,92(Supplement C): 298－311.
[2] Wen W,Zhai C,Ji D,et al.Framework for the vulnerability assessment of structure under mainshockaftershock sequences [J].Soil Dynamics and Earthquake Engineering,2017,101(Supplement C): 41－52.
[3] Shokrabadi M,Burton H V,Stewart J P.Impact of sequential ground motion pairing on mainshockaftershock structural response and collapse performance assessment [J].Journal of Structural Engineering,2018,144(10): 04018177(1―13).
[4] Ruiz-García J,Aguilar J D.Influence of modeling assumptions and aftershock hazard level in the seismic response of post-mainshock steel framed buildings [J].Engineering Structures,2017,140(Supplement C): 437－446.
[5] Shin M,Kim B.Effects of frequency contents of aftershock ground motions on reinforced concrete (RC)bridge columns [J].Soil Dynamics and Earthquake Engineering,2017,97: 48－59.
[6] 丁国,陈隽.序列型地震动物理随机模型研究 [J].工程力学,2017,34(9): 125－138.Ding Guo,Chen Jun.Study on physical random model of seismic sequences [J].Engineering Mechanics,2017,34(9): 125－138.(in Chinese)
[7] Helmstetter A,Sornette D.Båth's law derived from the Gutenberg-Richter law and from aftershock properties[J].Geophysical research letters,2003,30(20): SDE11.1－SDE11.4 .
[8] Båth M.Lateral inhomogeneities of the upper mantle [J].Tectonophysics,1965,2(6): 483－514.
[9] Goda K,Taylor C A.Effects of aftershocks on peak ductility demand due to strong ground motion records from shallow crustal earthquakes [J].Earthquake Engineering & Structural Dynamics,2012,41(15):2311－2330.
[10] Goda K.Nonlinear response potential of mainshockaftershock sequences from Japanese earthquakes [J].Bulletin of the seismological Society of America,2012,102(5): 2139－2156.
[11] 杨成,陈文龙,徐腾飞.余震地区桥梁施工过程易损性分析 [J].工程力学,2016,33(增刊1): 251－256.Yang Cheng,Chen Wenlong,Xu Tengfei.The vulnerability analysis of bridge construction in aftershock area [J].Engineering Mechanics,2016,33(Suppl 1): 251－256.(in Chinese)
[12] Han R,Li Y,Van De Lindt J.Assessment of seismic performance of buildings with incorporation of aftershocks [J].Journal of Performance of Constructed Facilities,2015,29(3): 04014088(1―17).
[13] 赵银刚,刘庆杰,王晨,等.基于线性回归分析的主余震相关关系 [J].地震地磁观测与研究,2017,38(2):71－76.Zhao Yingang,Liu Qingjie,Wang Chen,et al.Correlation of the minshock-aftershock based on the linear regression [J].Seismological and Geomagnetic Observation and Research,2017,38(2): 71－76.(in Chinese)
[14] Yeo G L,Cornell C A.A probabilistic framework for quantification of aftershock ground-motion hazard in California: Methodology and parametric study [J].Earthquake Engineering & Structural Dynamics,2009,38(1): 45－60.
[15] Kumitani S,Takada T.Probabilistic assessment of buildings damage considering aftershocks of earthquakes[J].Journal of Structural & Construction Engineering,2009,74(74): 459－465.
[16] 易桂喜,龙锋,张致伟.汶川M_S8.0地震余震震源机制时空分布特征[J].地球物理学报,2012,55(4):1213－1227.Yi Guixi,Long Feng,Zhang Zhiwei.Spatial and temporal variation of focal mechanisms for aftershocks of the 2008 MS8.0 Wenchuan earthquake [J].Chinese Journal of Geophysics,2012,55(4): 1213－1227.(in Chinese)
[17] Li Y,Song R,Van De Lindt J W.Collapse fragility of steel structures subjected to earthquake mainshockaftershock sequences [J].Journal of Structural Engineering,2014,140(12): 04014095(1－10).
[18] Tothong P,Luco N.Probabilistic seismic demand analysis using advanced ground motion intensity measures [J].Earthquake Engineering & Structural Dynamics,2007,36(13): 1837－1860.
[19] Baker J W,Allin Cornell C.A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon [J].Earthquake Engineering &Structural Dynamics,2005,34(10): 1193－1217.
[20] Baker J W,Allin Cornell C.Spectral shape,epsilon and record selection [J].Earthquake Engineering & Structural Dynamics,2006,35(9): 1077－1095.
[21] Bommer J J,Martnez-Pereira A.The effective duration of earthquake strong motion [J].Journal of Earthquake Engineering,1999,03(02): 127－172.
[22] Iervolino I,Manfredi G,Cosenza E.Ground motion duration effects on nonlinear seismic response [J].Earthquake Engineering & Structural Dynamics,2006,35(1): 21－38.
[23] Raghunandan M,Liel A B.Effect of ground motion duration on earthquake-induced structural collapse [J].Structural Safety,2013,41: 119－133.
[24] Kumar M,Castro J,Stafford P,et al.Influence of the mean period of ground motion on the inelastic dynamic response of single and multi degree of freedom systems[J].Earthquake Engineering & Structural Dynamics,2011,40(3): 237－256.
[25] 于晓辉,吕大刚,肖寒.主余震序列型地震动的增量损伤谱研究 [J].工程力学,2017,34(3): 47－53,114.Yu Xiaohui,Lü Dagang,Xiao Han.Incremental damage spectra of mainshock-aftershock sequence-type ground motion[J].Engineering Mechanics,2017,34(3): 47－53,114.
[26] Kim B,Shin M.A model for estimating horizontal aftershock ground motions for active crustal regions [J].Soil Dynamics and Earthquake Engineering,2017,92:165－175.
[27] Ruiz-García J,Negrete-Manriquez J C.Evaluation of drift demands in existing steel frames under as-recorded far-field and near-fault mainshock-aftershock seismic sequences [J].Engineering Structures,2011,33(2):621－634.
[28] Ruiz-García J.Issues on the response of existing buildings under mainshock-aftershock seismic sequences[C]// Proceedings of the 15th World conference on earthquake engineering,Lisboa,2012 .
[29] Ruiz-García J.Mainshock-aftershock ground motion features and their influence in building's seismic response[J].Journal of Earthquake Engineering,2012,16(5):719－737.
[30] Song R,Li Y,Van De Lindt J W.Impact of earthquake ground motion characteristics on collapse risk of post-mainshock buildings considering aftershocks [J].Engineering Structures,2014,81: 349－361.
[31] Rathje E M,Faraj F,Russell S,et al.Empirical relationships for frequency content parameters of earthquake ground motions [J].Earthquake Spectra,2004,20(1): 119－144.
[32] Xu Y,Tang X S,Wang J,et al.Copula-based joint probability function for PGA and CAV: a case study from Taiwan [J].Earthquake Engineering & Structural Dynamics,2016,45(13): 2123－2136.
[33] Tesfamariam S,Goda K.Seismic performance evaluation framework considering maximum and residual inter-story drift ratios: application to non-code conforming reinforced concrete buildings in Victoria,British Columbia,Canada [J].Frontiers in Built Environment,2015,1－18.
[34] 宋帅,钱永久,吴刚.桥梁系统地震易损性分析的混合Copula函数方法 [J].工程力学,2017,34(1): 219－227.Song Shuai,Qian Yongjiu,Wu Gang.Mixed copula function method for seismic fragility analysis of bridge system [J].Engineering Mechanics,2017,34(1): 219－227.
[35] 李典庆,唐小松,周创兵.基于Copula理论的岩土体参数不确定性表征与可靠度分析 [M].北京: 科学出版社,2015: 28－48.Li Dianqing,Tang Xiaosong,Zhou Chuangbing.Uncertainty uncertainty and reliability analysis of the parameters of rock and soil materials based on the copula theory [M].Beijing: Science Press,2015: 28－48.(in Chinese)
[36] 刘亭亭,于晓辉,吕大刚.地震动多元强度参数主成分与结构损伤的相关性分析 [J].工程力学,2018,35(8): 122－129,137.Liu Tingting,Yu Xiaohui,Lü Dagang.Analysis of correlation between principal components of multivariate earthquake intensity measures and structural damage [J].Engineering Mechanics,2018,35(8): 122－129,137.(in Chinese)
[37] Abrahamson N,Silva W,Kamai R.Update of the AS08 ground-motion prediction equations based on the NGA-West2 data set,PEER report 2013/04,pacific earthquake engineering research center [R].Berkeley:University of California,Berkeley,2013: 3―9
[38] Zhu R G,Lu D G,Yu X H,et al.Conditional Mean Spectrum of Aftershocks [J].Bulletin of the seismological Society of America,2017,107(4): 1940－1953.
[39] Riddell R.On ground motion intensity indices [J].Earthquake Spectra,2007,23(1): 147－173.
[40] Riddell R,Garcia J E.Hysteretic energy spectrum and damage control [J].Earthquake Engineering & Structural Dynamics,2001,30(12): 1791－1816.
[41] Von Thun J L,Roehm L H,Scott G A,et al.Earthquake ground motions for design and analysis of dams [J].Earthquake Engineering and Soil Dynamics II-Recent Advances in Ground-Motion Evaluation,Geotechnical Special Publication,1988,20: 463－481.
[42] Mackie K R.Fragility-based seismic decision making for highway overpass bridges [D].Berkeley: University of California,Berkeley,2004.
[43] Fajfar P,Vidic T,Fischinger M.A measure of earthquake motion capacity to damage medium-period structures [J].Soil Dynamics and Earthquake Engineering,1990,9(5):236－242.
[44] Trifunac M D,Brady A G.A study on the duration of strong earthquake ground motion [J].Bulletin of the Seismological Society of America,1975,65(3): 581－626.
[45] 褚延涵.地震地面运动加速度记录与强度参数选择的统计方法研究 [D].哈尔滨: 哈尔滨工业大学,2010.Chu Yanhan.Study on statistical methods for selection of accerelation records and intensity measures of earthquake ground motions [D].Harbin: Harbin Institute of Technology,2010.(in Chinese)
COPULA-BASED CORRELATION ANALYSIS OF INTENSITY MEASURES OF MAINSHOCK-AFTERSHOCK GROUND MOTIONS