图1 试件尺寸及配筋 /mm
Fig.1 Specimen dimensions and reinforcement details
在寒冷地区，冻融循环作用会导致混凝土材料产生物理损伤[1]，造成强度退化、弹性模量减小及其与钢筋的锚固性能下降，从而影响结构的耐久性；同时，冻融损伤后的混凝土结构仍存在经受地震作用的风险，因此，研究冻融循环作用下该类结构的抗震性能具有必要性，如何考虑冻融损伤进行结构建模成为首要问题。
目前针对冻融损伤的研究[1―6]多集中于材料层面。其中Petersen等[2―3]采用相对动弹性模量(relatively dynamic elasticity of modulus,RDME)为冻融损伤指标，通过超声波测试方法研究了冻融后混凝土的内部损伤分布，并指出随着冻融循环次数的增加，冻融损伤逐渐深入，即冻融分布具有不均匀性。Molero等[4]进一步通过超声影像观测到冻融损伤的渗透过程。
近年来，人工气候实验室的发展使构件层面的冻融循环试验成为可能，针对冻融循环作用后构件的承载力及抗震性能研究已逐步开展。Hassanzadeh和Fagerlund[7]，曹大富等[8]均通过静力试验研究了冻融损伤后梁的残余强度；郑山锁等[9]对不同冻融循环次数后的低矮RC剪力墙进行了拟静力试验。然而这些研究主要为定性分析，如何定量冻融损伤对构件力学性能的影响，尚未得到充分研究。Hanjari等[10]考虑了冻融作用对混凝土强度的折减，对文献[7]中的梁试件进行了有限元分析，指出分析结果与试验数据的误差应归因为未考虑冻融损伤的不均匀性。
综上，现有混凝土冻融损伤模型较为匮乏，尚未考虑冻融损伤的不均匀性，且没有针对抗震分析领域的应用。另一方面，诸多学者[9,11―12]指出，研究中冻融循环方案的差异造成了不同研究结果无法进行横向对比分析。故本文采用RDME作为冻融损伤参数，基于既有的冻融混凝土材性试验，提出可考虑冻融损伤不均匀性的混凝土退化模型，并建立不同冻融循环试验之间的等效循环次数，以实现数据的归纳与对比，最后根据8榀冻融后RC框架柱拟静力试验数据进行验证，并与既有冻融损伤模型进行对比分析。
试验共设计8榀尺寸及配筋相同的钢筋混凝土框架柱，如图1所示；试验变量包括冻融循环次数、混凝土强度等级以及设计轴压比(由于冻融后混凝土强度下降，实际采用轴压力为控制变量)，见表1。
图1 试件尺寸及配筋 /mm
Fig.1 Specimen dimensions and reinforcement details
表1 试件设计参数
Table 1 Design parameters of specimens
试件编号 轴压比 轴压力/kN 冻融循环次数NE 混凝土强度等级Z-C1 0.18 300.6 0 C50 Z-C2 0.18 300.6 100 C50 Z-C3 0.18 300.6 200 C50 Z-C4 0.18 300.6 300 C50 Z-C5 0.18 300.6 300 C40 Z-C6 0.18 300.6 300 C30 Z-C7 0.24 400.3 200 C50 Z-C8 0.30 486.8 200 C50
由于实际工程中的混凝土冻融条件与目前冻融循环试验多采用的“气冻水融”或“水冻水融”方法[13]有较大出入，而且构件的尺寸相对较大，难以通过这两种方法实现冻融，故采用人工气候环境试验方法，即通过控制实验室内部湿度和温度条件，放大冻融条件、缩短冻融循环周期，更为准确地模拟混凝土结构所处的实际冻融环境，并使试件尽量处于饱和水状态下以达到较好的冻融效果。为此，在试件进行冻融循环作用之前，在温度为15 ℃～20 ℃的水中浸泡一周，浸泡时水面至少高出试件顶面20 mm[13]；同时，在每个冻融循环开始前向试件表面喷水至表面混凝土不再吸收水分为止，具体操作为每次冻结前15 min对试件进行5次喷淋，喷淋1 min，间隔2 min。
试验选取ZHT/W2300气候模拟实验系统，其内部温度量程为-20 ℃～+80 ℃，温度误差控制在0.1℃，具体温度参数设置如图2所示。同时预留C30、C40和C50混凝土棱柱体试块各一组(每组3个，尺寸为100 mm×100 mm×400 mm)，用以测量冻融循环后混凝土质量、相对动弹模量和轴心抗压强度。另外，每种强度的混凝土制作立方体试块4组(每组3个，边长为100 mm)，用以测量冻融循环100次、200次和300次后的混凝土抗压强度。
拟静力试验采用悬臂柱式加载方案。在加载过程中，竖向荷载通过100 t液压千斤顶施加，并在试验过程中保持不变；水平荷载通定固定于反力架上的500 kN电液伺服作动器施加。试验加载制度为变幅值位移加载：在试件屈服前，位移增量为0.2 Δy(屈服位移按文献[14]中方法进行估算)，每级控制位移循环1次；试件屈服后，位移增量为Δy，每级控制位移循环3次。
图2 人工气候环境参数设定
Fig.2 Parameters set up in the environmental laboratory
在拟静力加载结束时，所有试件均表现出以弯曲变形为主的弯剪破坏模式，因此在本研究中冻融作用并未改变试件的最终破坏形态。对试件特征值统计如表2所示，其中屈服点根据文献[15]推荐的“能量等效法”确定，破坏荷载取为峰值荷载的85%，对应的位移为极限位移，μΔ为位移延性系数。
表2 试件特征参数
Table 2 Characteristic values of specimens
屈服 峰值 破坏试件编号Py/kNΔy/mmPc/kNΔc/mmPu/kNΔu/mmμΔ Z-C1 55.99 7.26 66.92 14.42 56.88 38.45 5.30 Z-C2 50.55 7.14 59.02 14.58 50.17 44.03 6.16 Z-C3 47.65 7.40 56.47 14.60 48.00 44.48 6.01 Z-C4 47.20 8.50 54.42 14.28 46.26 42.64 5.02 Z-C5 38.53 7.91 45.85 14.88 38.97 44.41 5.61 Z-C6 37.39 7.93 44.21 14.98 41.61 45.53 5.74 Z-C7 57.97 8.05 66.48 16.18 56.50 41.58 5.17 Z-C8 59.92 7.70 64.49 12.09 54.82 34.15 4.43
通过修正混凝土材料的本构关系，考虑冻融损伤对钢筋混凝土构件的影响，首先基于OpenSees平台、采用纤维模型提出未损伤RC柱的数值建模方法，进而提出可考虑不均匀冻融损伤的混凝土模型和可进行对比的既有冻融混凝土模型，根据等效冻融循环次数搭建不同模型之间的桥梁。
由前述试验可知，冻融后RC框架柱的破坏模式仍以弯曲破坏为主，同时为考虑冻融循环作用对混凝土材性的影响，采用基于单轴材料本构的纤维截面模型模拟RC柱的弯矩曲率关系，通过对曲率沿柱高度方向的积分即可得到柱的侧向位移。单元类型采用基于位移法的非线性梁柱单元，为得到较为精确的结果，通常需要将构件划分为若干单元，根据构件配筋及等效塑性铰高度[16]，沿柱高划分单元如图3(a)所示。为确定截面分析所需的纤维数量，进行了灵敏度分析，得到40×40个纤维可基本实现计算精度和效率的平衡。
图3 有限元模型
Fig.3 Finite element model
对于非约束混凝土本构，采用Kent-scott-park模型[17]。弹性模量Ec = 5000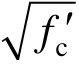
，峰值应变εc=
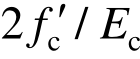，峰值后部分采用Roy和Sozen模型[18]。对约束混凝土本构进行分段表示，如图6所示：第一部分为Mander约束混凝土本构[19]；第二部分为OpenSees中的minmax材料[20]，可用来给定应变阀值，本文将其设置为在混凝土应变超过εccu时Mander本构模型失效，应力-应变关系进入第三部分，即采用OpenSees中的hysteretic材料[20]模拟约束混凝土压碎后行为，斜率计算根据Roy和Sozen模型[18]。上述本构模型如图4所示，其中损伤本构模型仅通过修改峰值应力实现。钢筋模型采用OpenSees中的Steel 02模型，即双线型强化模型，应变硬化率采用1.5%。根据试验数据，钢筋屈服强度为363 MPa，弹性模量为2.0×105 MPa。
图4 混凝土本构模型
Fig.4 Constitutive model of concrete
Petersen等[2―3]测量了冻融后混凝土棱柱体试件不同位置处的相对动弹性模量RDME与冻融循环次数N的关系，试验证明了冻融损伤在构件截面内的分布具有不均匀性。同时，诸多试验[1,5,21―23已测得混凝土强度和对应的动弹性模量数值。因此，可采用RDME作为联系混凝土强度和不同冻融损伤程度的桥梁，将构件截面按照冻融深度划分为不同部分，各部分又由不同损伤程度的混凝土纤维组成，具体计算步骤详述如下：
1) 基于2.1小节确定保护层混凝土和约束混凝
2) 根据规范[24]中的经验公式(式(1))计算未损伤的混凝土动弹性模量
：
3) 基于 Petersen试验数据[2]提出修正的Petersen模型，计算RDME随冻融循环次数的变化关系。试验数据如图5中散点所示，可以看到，对于给定深度处冻融损伤，在冻融循环次数未达到一定数值时，冻融损伤相对较小，因此提出冻融循环次数临界值参数NP′表征这一趋势；其次，当损伤开始时，RDME随着冻融循环次数的增加呈线性减小趋势，故提出线性退化模型，如式(2)所示，其中R代表RDME，并根据最小二乘法计算得模型参数如式(3)、式(4)所示(如图6所示)：
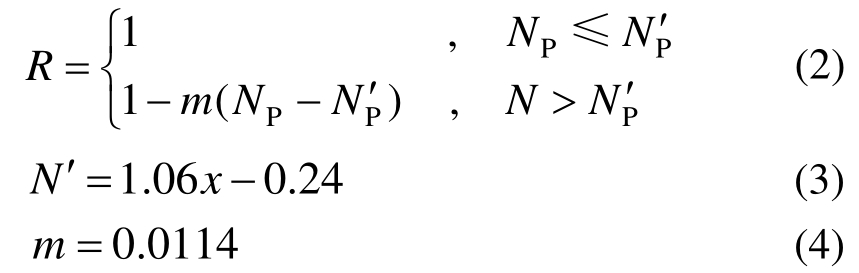
式中：NP为Petersen试验所采用的冻融循环次数；x为混凝土纤维位置与截面受冻边缘的距离，当截面受到多个方向的冻融侵蚀时取最小值，如图6所示。
4) 根据式(5)计算损伤后动弹性模量：
5) 提出经验公式，计算冻融后混凝土强度。本文收集了文献[1,5,21－23]中的试验数据，如图7所示，并对这些数据进行一元线性回归，得到式(6)，将式(5)代入，即得到损伤后冻融混凝土强度fc,d与损伤系数R和未损伤冻融混凝土强度fc，如式(7)所示：
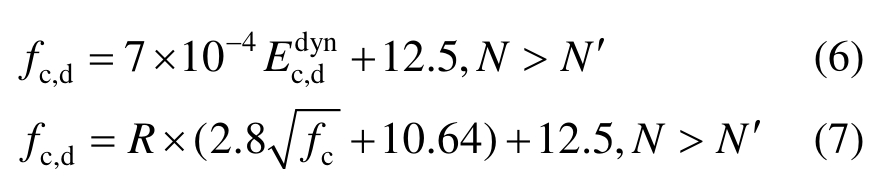
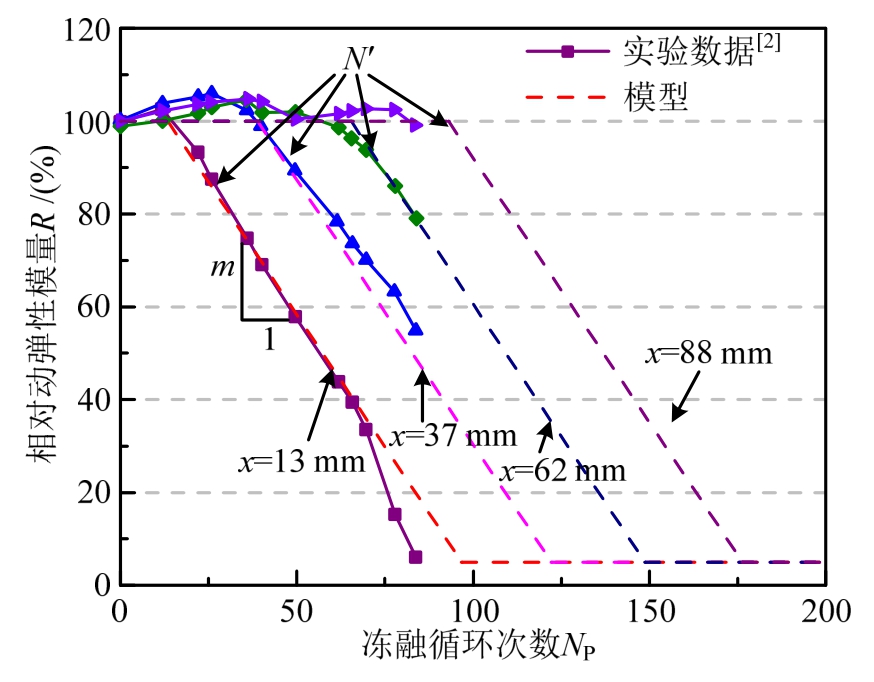
图5 修正的Petersen模型
Fig.5 Revised Petersen’s model
图6 参数x计算示意图
Fig.6 The definition ofx
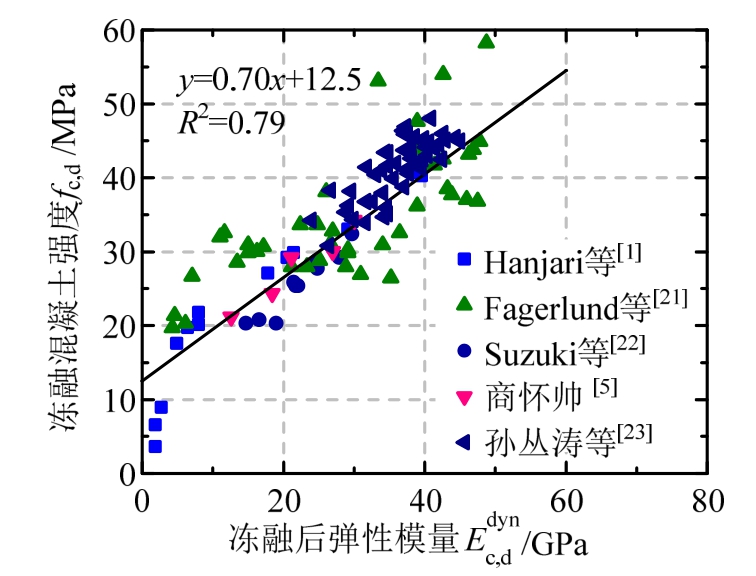
图7fc,d与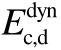
的回归公式
Fig.7 The regression formula offc,d and
6) 基于损伤后的非约束混凝土强度，根据Mander本构模型[19]计算损伤后约束混凝土强度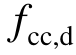
。
综上，冻融损伤后截面不同深度处的混凝土强度计算仅与冻融循环次数N和未损伤混凝土强度
相关。上述计算的流程图如图8所示。
图8 混凝土冻融损伤模型计算流程图
Fig.8 Flow chart of freeze-thaw damaged concrete model
迄今为止，国内外对受冻融损伤的混凝土应力-应变关系研究较少。Hasan等[25]通过在混凝土本构方程中引入FTC断裂系数考虑冻融损伤，并通过材性试验证明了模型的准确性，然而，FTC系数的计算需要得到塑性应变，这给模型的应用造成了一定困难。商怀帅[5]虽然对不同冻融循环次数下的混凝土立方体试件进行了受压应力-应变全曲线的测量，试验中最大冻融循环次数为100次，即使等效后亦与本文所采用的试件中最大冻融循环次数(300次)相差较远，尚不能推广应用；同时商怀帅所采用试验方法与段安[6]的试验较为一致(均参照GB/T 50082—2009[13]中的快冻法)，故选择其一作为比较已具有代表性。
段安[6]首先对不同水灰比和不同冻融循环次数下的混凝土棱柱体试件进行了轴心抗压试验，建立了混凝土本构模型中主要参数随冻融循环次数ND和立方体抗压强度fcu的变化关系，如式(8)、式(9)所示：
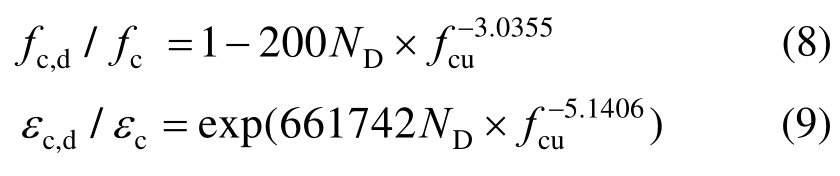
进而，段安[6]又制作了两种不同配箍系数下的混凝土试块进行试验，建立了冻融后约束混凝土峰值强度fcc,d和峰值应变εcc,d计算公式：
式中，λ为配箍特征值。
综上，本文采用段安[6]提出的冻融混凝土模型作为对比分析的基础，并记为“全截面模型”。
由于冻融循环试验参数、混凝土尺寸以及未损伤混凝土强度在内的这些因素均会导致相同冻融循环次数下的混凝土损伤程度不尽相同，因此在采用与冻融循环次数N这一参数相关的模型时，需要对不同试验条件下的该参数进行等效。为实现本文所需的不同研究之间冻融循环次数的对比，首先对本试验和段安[6]试验进行等效：根据本文试验环境下的冻融混凝土材性试验数据[9]，采用段安[6]所提出的式(8)计算导致相同混凝土强度退化程度所需冻融循环次数ND，与本试验冻融循环次数NE进行拟合，选取指数函数形式为拟合模型，得到式(12)：
随后，对Petersen试验的冻融循环次数进行等效：由于文献[3]缺乏冻融后混凝土强度数据，故可采用相对动弹性模量RDME作为等效的原则。根据本研究在前期已建立的RDME与冻融循环次数及混凝土强度的关系[26]，如式(13)所示：
计算导致相同动弹性模量退化程度所需冻融循环次数NP，与本试验冻融循环次数NE进行拟合，并采用相同拟合模型，得到式(14)：
综上，采用本文提出的等效冻融循环次数模型的计算结果如表3所示，可以看到拟合误差相对较小，具有一定的精度。
表3 等效冻融循环次数
Table 3 Equivalent numbers of freeze-thaw cycles
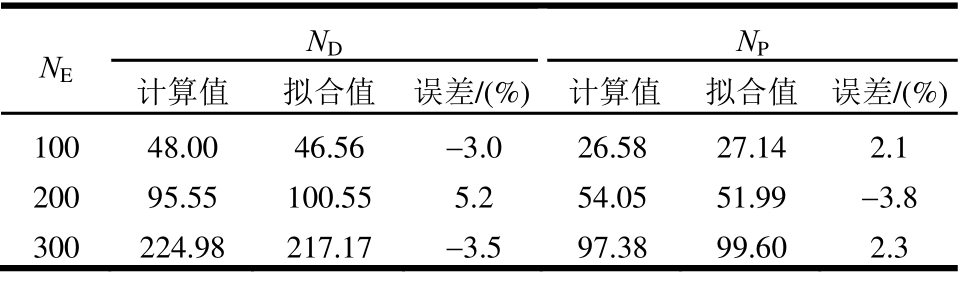
NE NDNP计算值 拟合值 误差/(%) 计算值 拟合值 误差/(%)100 48.00 46.56 -3.0 26.58 27.14 2.1 200 95.55 100.55 5.2 54.05 51.99 -3.8 300 224.98 217.17 -3.5 97.38 99.60 2.3
采用静力推覆分析方法分别对本文提出的模型和全截面模型进行计算，与试验结果进行对比，并根据不同试验参数分类详述如后文所示。
对不同冻融循环次数下的RC柱数值分析结果与试验滞回曲线对比如图9所示。由未冻融RC构件(ZC-1)的模拟结果与试验数据对比(图9(a))可看到，在负向加载阶段模拟曲线与滞回曲线的包络线吻合较好，而在正向加载阶段峰值荷载试验值大于模拟结果。由试验滞回曲线可以看出，在正向加载时，试件的初始刚度值较大，快速达到峰值荷载，同时过峰值后的退化速度也较负向更快，造成正负向明显不对称的特征，可能是由于在竖向加载时出现初始偏心造成。因此上述模拟与试验不一致的情况主要是由于试验误差产生，故本文采用的数值建模方法可作为后续冻融模型分析的前提。
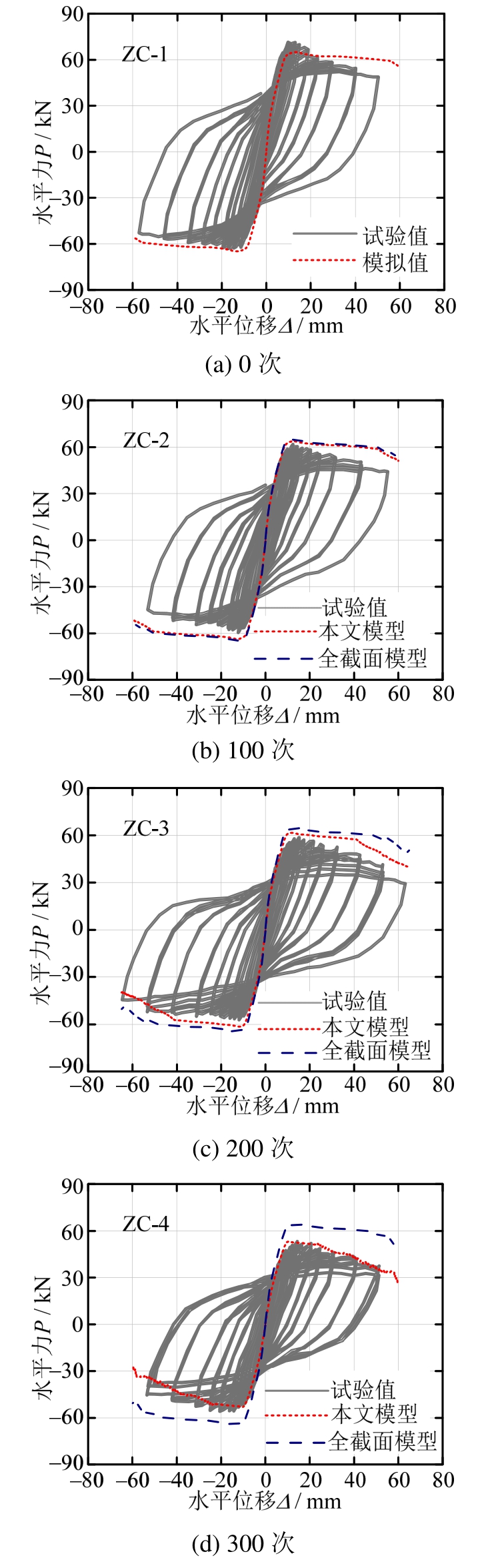
图9 不同冻融循环次数RC柱试验实测力位移曲线与数值模拟曲线
Fig.9 Force-displacement responses of RC columns of experimental results,proposed model and Duan’s model under different freeze-thaw cycles
针对全截面模型，可观察到其计算承载力均大于试验值。如前所述，全截面模型假设冻融造成的混凝土损伤呈均匀分布状态，因此导致对外侧混凝土强度值预测偏高，而对内侧混凝土强度值预测较低，在模型中体现为截面不同坐标处的混凝土纤维具有一致的损伤，由于外侧纤维对截面的弯矩贡献更大，所以该模型最终导致整体承载力偏高的结果。其次，该假设导致混凝土强度计算值相对于冻融循环次数并不敏感：其保护层混凝土强度经过300次(NE)冻融循环后由 41.86 MPa降至31.91 MPa，而其核心区混凝土强度由53.32 MPa仅降至49.53 MPa，因此在不同冻融循环次数下的全截面模型计算值相差较小(如图10所示)，并导致该模型所计算的承载力退化不明显，与试验滞回曲线中显著的强度退化相反。综上，随着冻融循环次数的增加，全截面模型的承载力计算值与试验值偏差逐渐增大。
相反地，可以观察到本文提出的模型与试验结果差值更小，特别是在冻融循环达到300次时，数值模拟与试验结果基本吻合。然而在冻融循环次数为100次时，本文模型与全截面模型计算结果相近，均大于试验承载力。其次，可以看到本文模型在过峰值后的刚度退化与试验值较为一致，即该冻融损伤模型可较好地预测峰值后的力学性能退化。
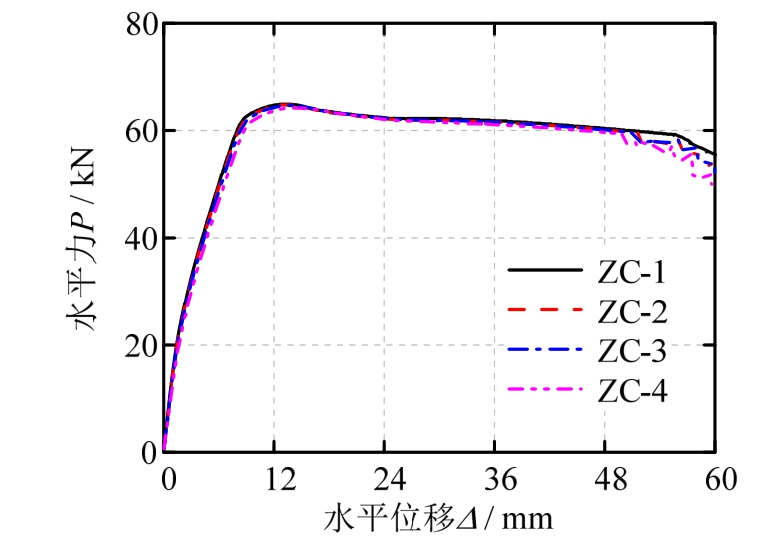
图10 全截面模型力-位移曲线
Fig.10 Force-displacement responses of Duan’s model
不同混凝土强度等级的预测结果和试验结果如图11所示。可以看到，当fc = 30.63MPa (图11(b))时，全截面模型的峰值偏大；当fc = 24.32MPa (图11(c))时，全截面模型中保护层混凝土强度在冻融循环次数达到300次后已下降至0，核心区混凝土强度仅为原强度30%，模拟误差较大，故图11(c)中没有全截面模型。这是由于在全截面模型中，混凝土强度的退化随着冻融循环次数的增加呈线性衰减，且随着混凝土强度等级的减小，衰减速率增大。值得注意的是，这与试验结果并不相符，即冻融循环作用虽会造成一定的强度退化，但是仍会保留一定的残余强度。产生该现象的原因是全截面模型采用平均强度代表冻融后的混凝土强度，同时没有考虑到构件的尺寸效应，这意味着全截面模型在结构层次上的应用具有一定的局限性。
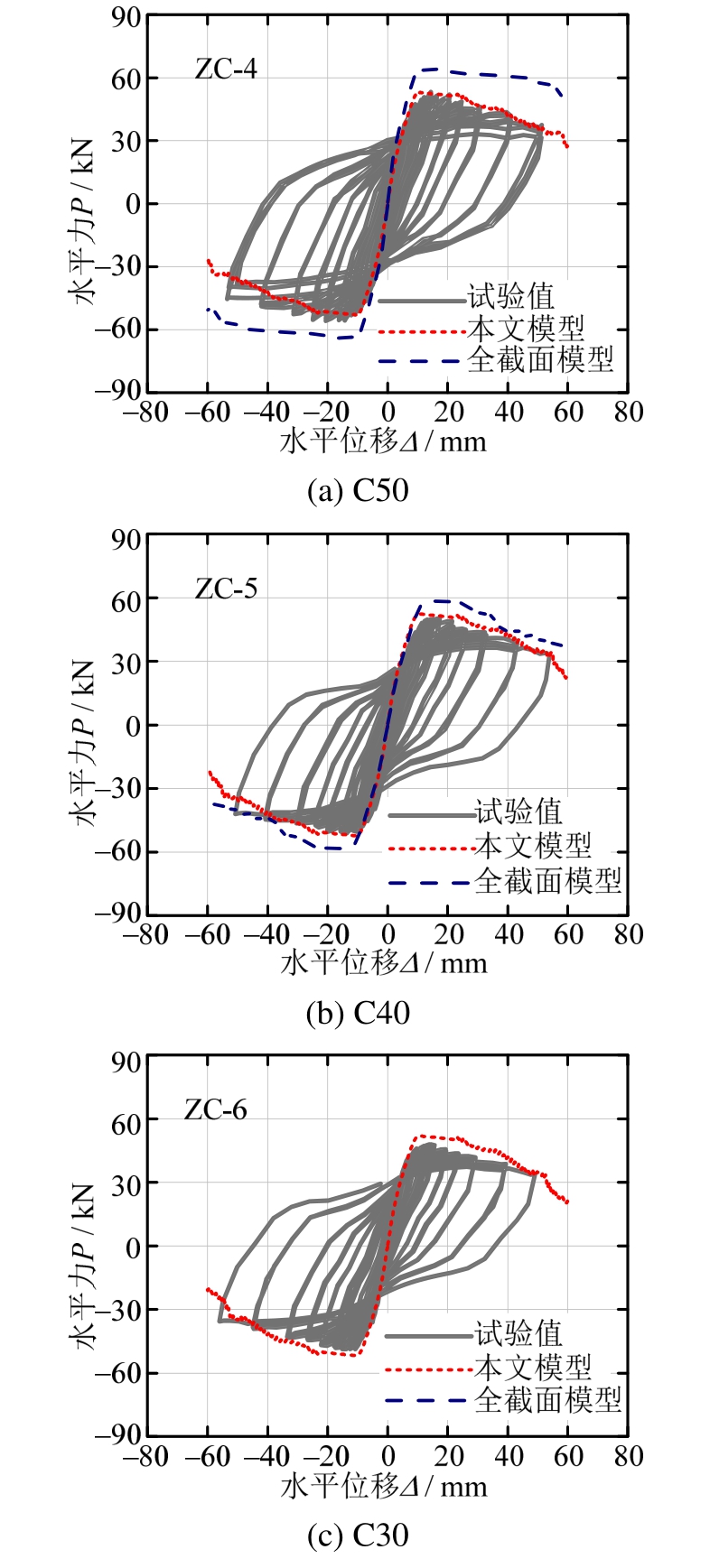
图11 不同混凝土强度RC柱试验实测力-位移曲线与数值模拟曲线(冻融循环次数均为300次)
Fig.11 Force-displacement responses of RC columns of experimental results,proposed model and Duan’s model under different concrete strength (NE=300)
同时可以看到，随着混凝土强度等级的减小，本文模型的模拟结果与试验值符合较好。与全截面模型不同，本文模型考虑了冻融损伤在截面的分布特征，并考虑了混凝土构件的残余强度。
RC柱在不同轴压下的数值模拟数据与试验数据对比如图12所示。可以看到，随着轴压力的增加，由全截面模型计算所得的承载力逐渐增加，本文模型的计算值先出现微小增加随后基本不变化，试验结果则呈现出先增加后减小的趋势。产生该现象的原因与柱的偏心受压特征相关：柱在水平力和轴向压力作用下，可等效为单独的偏心压力作用；在相同水平荷载条件下，随着轴压的增加，等效偏心距减小，柱的受压区逐渐增大，而柱的破坏形态则从大偏心受压破坏转向小偏心受压破坏。该临界状态简化计算公式可根据等效矩形应力图[27]计算，如式(15)所示：
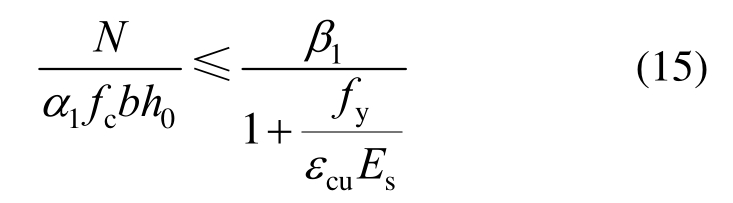
式中：α1和β1为等效矩形应力图参数；b为截面宽度；h0为截面高度，当满足该公式时为大偏心受压破坏。对不同轴压条件下的计算和分析如下。
1) 当N=400.3 kN时，临界混凝土强度fc为25.8 MPa。此时，本文模型中仅截面最外侧混凝土纤维的强度小于该临界强度，同时，如图12(b)所示，模型延性显著减小而承载力稍有增大，故从简化计算分析的角度来看，该模型即仍为大偏心破坏状态，并接近于临界破坏状态，其计算结果与负向加载数据吻合较好，在正向略小于试验数据。然而，采用全截面模型计算所得的混凝土强度最小值，即保护层混凝土强度，大于该临界值，即全截面模型仍为大偏心受压破坏，在正向加载方向与试验结果吻合较好，在负向略大于试验结果。
2) 当轴压力增大至486.6 kN时，临界混凝土强度fc随之提高到31.3 MPa。此时，本文模型中存在部分混凝土纤维强度值高于该临界值，且如图12(c)所示，模型延性进一步减小而承载力几乎维持不变，即意味着该模型已逐渐由大偏心受压破坏柱过渡至小偏心受压破坏柱，与试验数据吻合较好。同时，全截面模型中最外侧混凝土纤维强度仍大于该限值，故保持大偏心受压破坏，承载力计算值继续增大，与试验值相比过于保守。
综上，各次模拟结果(ZC2～ZC8)的峰值荷载与试验数据对比如图13所示，可以看到本文模型分布于对角线的两侧，全截面模型计算点均分布在对角线的上方，且误差总体大于本文模型。
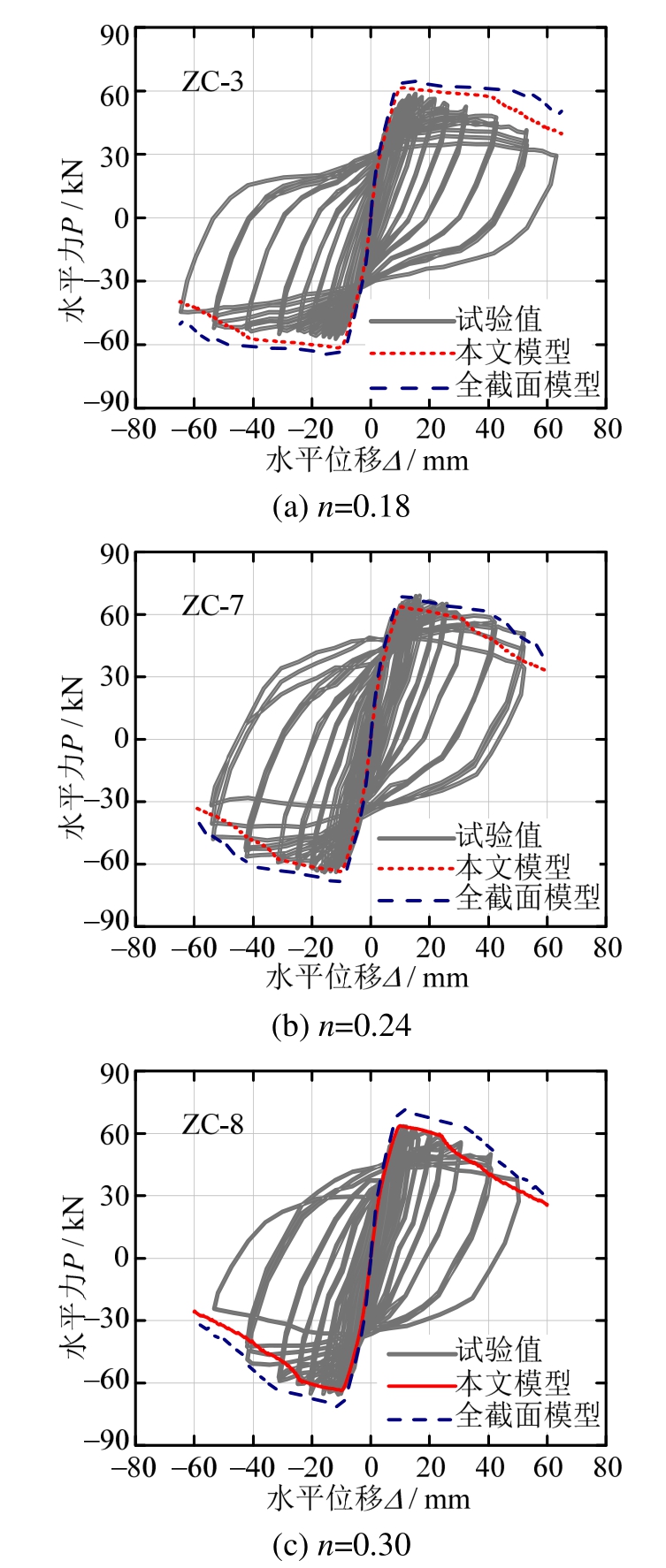
图12 不同轴压比RC柱试验实测力-位移曲线与数值模拟曲线(冻融循环次数均为200次)
Fig.12 Force-displacement responses of RC columns of experimental results,proposed model and Duan’s model under different axial load ratio (NE=200)
图13 峰值荷载模拟值与试验值对比
Fig.13 Comparison of simulation results and test data concerning peak loads
本文提出了基于纤维截面的可考虑不均匀冻融损伤分布的RC柱数值模拟方法，并建立了不同冻融循环试验次数的等效方法，对比试验结果、本文模型和既有冻融混凝土模型可以得到以下结论：
(1) 本文建立的等效冻融循环次数，可作为对比和利用不同冻融循环方案下的试验数据的基础。
(2) 采用本文提出的模型计算时，模拟结果均可基本吻合试验滞回曲线的包络线，说明该方法可应用于模拟冻融损伤后的RC柱构件地震反应。
(3) 除试件ZC-6以外，采用未考虑冻融损伤分布的全截面模型计算所得的承载力通常高于试验结果。
[1] Hanjari K Z,Utgenannt P,Lundgren K.Experimental study of the material and bond properties of frost-damaged concrete [J].Cement & Concrete Research,2011,41(3): 244―254.
[2] Petersen L.Influence of material deterioration processes on mechanical behavior of reinforced concrete structures[D].Hannover: University of Hannover,2004.
[3] Petersen L,Lohaus L,Polak M A.Influence of freezing-and-thawing damage on behavior of reinforced concrete elements [J].ACI Materials Journal,2007,104(4): 369―378.
[4] Molero M,Aparicio S,Al-Assadi G,et al.Evaluation of freeze–thaw damage in concrete by ultrasonic imaging[J].Ndt & E International,2012,52(4): 86―94.
[5] 商怀帅.引气混凝土冻融循环后多轴强度的试验研究[D].大连: 大连理工大学,2006.Shang Huaishuai.Experimental study on of air-entrained concrete under multiaxial loads after freeze-thaw cycles[D].Dalian: Dalian University of Technology,2006.(in Chinese)
[6] 段安.受冻融混凝土本构关系研究和冻融过程数值模拟[D].北京: 清华大学,2009.Duan An.Research on constitutive relationship of frozen-thawed concrete and mathematical modeling of freeze-thaw process [D].Beijing: Tsinghua University,2009.(in Chinese)
[7] Hassanzadeh M,Fagerlund G.Residual strength of the frost-damaged reinforced concrete beams [C]// III European Conference on Computational Mechanics,Springer Netherlands,2006: 366―366.
[8] 曹大富,葛文杰,郭容邑,等.冻融循环作用后钢筋混凝土梁受弯性能试验研究[J].建筑结构学报,2014,35(6): 137―144.Cao Dafu,Ge Wenjie,Guo Rongyi,et al.Experimental study on flexural behaviors of RC beams after freeze-thaw cycles [J].Journal of Building Structures,2014,35(6):137―144.(in Chinese)
[9] 郑山锁,甘传磊,秦卿,等.冻融循环后一字形短肢剪力墙抗震性能试验研究[J].工程力学,2016,33(12):94―103.Zheng Shansuo,Gan Chuanlei,Qin Qing,et al.Experimental study on the seismic behaviors of short-pier shear walls subjected to freeze-thaw cycles [J].Engineering Mechanics,2016,33(12): 94―103.(in Chinese)
[10] Hanjari K Z,Kettil P,Lundgren K.Modelling the structural behaviour of frost-damaged reinforced concrete structures [J].Structure & Infrastructure Engineering,2013,9(5): 416-431.
[11] 刘西拉,唐光普.现场环境下混凝土冻融耐久性预测方法研究[J].岩石力学与工程学报,2007,26(12):2412―2419.Liu Xila,Tang Guangpu.Research on prediction method of concrete freeze thaw durability under field environments [J].Chinese Journal of Rock Mechanics and Engineering,2007,26(12): 2412―2419.(in Chinese)
[12] Berto L,Saetta A,Talledo D.Constitutive model of concrete damaged by freeze–thaw action for evaluation of structural performance of RC elements [J].Construction and Building Materials,2015,98: 559―569.
[13] GBT 50082—2009,普通混凝土长期性能和耐久性能试验方法标准[S].北京: 中国建筑工业出版社,2009.GBT 50082—2009,Standard for test methods of long-term performance and durability of ordinary concrete [S].Beijing: China Building Industry Press,2009.(in Chinese)
[14] Watson S,Park R.Simulated seismic load tests on reinforced concrete columns [J].Journal of Structural Engineering,1994,120(6): 1825―1849.
[15] Mahin S A,Bertero V V.Problems in establishing and predicting ductility in aseismic design [C]// Proceedings of the International Symposium on Earthquake Structural Engineering,St.Louis,USA,1976: 613―628.
[16] Paulay T,Priestly M J N.Seismic design of reinforced concrete and masonry buildings [M].New York,NY,US:John Wiley & Sons,Inc.1992: 140―156.
[17] Yassin M H M.Nonlinear analysis of prestressed concrete structures under monotonic and cyclic loads[M].Berkeley: University of California,1994.
[18] Roy H E H,Sozen M A.Ductility of concrete [C]//Proceedings of the Joint ACI-ASCE International Symposium on Flexural Mechanics of Reinforced Concrete,Miami,FL,1964(12): 213―235.
[19] Mander J B,Priestley M J N,Park R.Theoretical stress-strain model for confined concrete [J].Journal of Structural Engineering,1988,114(8): 1804―1826.
[20] Mckenna F,Fenves G L,Scott M H,et al.Open system for earthquake engineering simulation [D].Berkeley,CA:Pacific Earthquake Engineering Research Center,University of California,2000.
[21] Fagerlund G,Janz M,Johannesson B.Effect of frost damage on the bond between reinforcement and report[R].Report,Division of Building Materials,Lund Institute of Technology,Lund,Sweden,1994.
[22] Suzuki T,Ohtsu M,Shigeishi M.Relative damage evaluation of concrete in a road bridge by AE rate-process analysis [J].Materials and Structures,2007,40(2): 221―227.
[23] 孙丛涛,牛荻涛,元成方,等.混凝土动弹性模量与超声声速及抗压强度的关系研究[J].混凝土,2010,246(4): 14―16.Sun Congtao,Niu Ditao,Yuan Chengfang,et al.Study on relation between dynamic modulus of elasticity and velocity of ultrasonic sound and compressive strength for concrete [J].Concrete,2010,246(4): 14―16.(in Chinese)
[24] CP110,Code of practice for the structural use of concrete[S].London,England: British Standards Institution,1972.
[25] Hasan M,Okuyama H,Sato Y,et al.Stress-strain model of concrete damaged by freezing and thawing cycles [J].Journal of Advanced Concrete Technology,2004,2(1):89―99.
[26] 郑山锁,李强强,秦卿,等.考虑冻融损伤的低矮RC剪力墙恢复力模型研究 [J].建筑结构学报已见刊,2018,39(3): 111―119.Zheng Shansuo,Li Qiangqiang,Qin Qing,et al.Restoring force model of the freeze-thaw damaged squat reinforced concrete shear walls [J].Journal of Building Structures,2018,39(3): 111―119.(in Chinese)
[27] 过镇海.钢筋混凝土原理 [M].北京: 清华大学出版社,2013: 214―233.Guo Zhenhai.Principles of reinforced concrete [M].Beijing: Qinghua University Press,2013: 214―233.(in Chinese)
RESEARCH ON THE MODELLING METHOD OF REINFORCED CONCRETE COLUMN SUBJECTED TO FREEZE-THAW DAMAGE
郑山锁(1960―)，男，陕西人，教授，博士，主要从事结构工程与工程抗震研究(E-mail: zhengshansuo@263.net);
裴 培(1992―)，女，安徽人，硕士生，主要从事结构抗震研究(E-mail: 743513468@qq.com);
李 磊(1983―)，男，湖北人，副教授，博士，主要从事结构抗震研究(E-mail: lilei1004@163.com);
秦 卿(1989―)，男，陕西人，博士生，主要从事结构抗震研究(E-mail: 495680791@qq.com);
董立国(1990―)，男，山西人，博士生，主要从事结构抗震研究(E-mail: dlg_15@163.com).