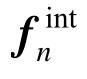基于GPU并行计算的地下结构非线性动力分析软件平台开发
曹胜涛,路德春,杜修力,赵 密,程星磊
(北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124)
摘 要:为解决地下结构隐式非线性动力分析收敛性差和计算效率低的技术瓶颈,该文建立了基于GPU并行计算的地下结构显式动力分析软件平台。在此平台中提出并实现了一种混凝土弥散开裂模型;给出并实现了一种钢筋纤维与实体单元的耦合方法;基于等参元思想,提出了人工边界节点的单元从属面积的计算方法;为实现节点不协调情况下的土与结构相互作用分析,开发实现了一种实体单元间的两节点接触单元。利用该文开发的软件对日本大开地铁站进行了重力场分析、线性和非线性动力分析。将重力场和线性动力分析结果与ABAQUS分析结果进行了对比,结果表明该文软件计算结果与ABAQUS计算结果一致,且计算效率约为ABAQUS计算效率的5.68倍,验证了软件各模块的正确性和效率。另外,通过将非线性计算结果与灾害调查结果进行对比分析,验证了软件非线性分析的稳定性和合理性。
关键词:地下结构;非线性动力分析;GPU并行计算;本构模型;软件平台
地下结构非线性动力分析需要考虑土与结构的三维空间效应、材料非线性[1]、几何非线性、土与结构相互作用[2]、模型边界条件及地震动输入[3]等问题,需解决计算规模大、非线性强等技术难点。如表1,自1996年至今,众多学者对阪神地震中发生严重损坏的大开车站进行了大量数值分析,分析能力经历了从静力到动力、从线性到非线性、从二维到三维、从简化到精细、从隐式到显式、从串行到并行的过程,取得了长足进步;但所采用分析工具均为国外程序。我国基本尚未给出专门针对地下结构工程进行精细化非线性动力计算的软件平台。国内地下结构专业的相关研究往往需要通过在国外商业软件上进行二次开发才能实现,因此这在一定程度上将会影响我国本学科的技术积累和长远发展。
表1 大开地铁车站地震分析
Table 1 Seismic analysis of Daikai subway station

学者 时间 程序 土体 结构 分析方法 分析设备Nakamura等[4] 1996 ——(日本) 三折线弹簧 塑性铰梁元 非线性静力分析 CPU An等[5] 1997 WCOMD-SJ[6](美国)路径相关的模型结合平面应变膜元弥散开裂模型结合平面应变膜元 隐式非线性动力分析 CPU曹炳政等[7] 2002 FLUSH(美国) 线性平面应变膜元 线性梁元 线性动力分析 CPU Liu等[8] 2008 MSC.Marc(美国)考虑剪切的弹塑性模型结合平面应变膜元弹性损伤模型结合纤维梁元 非线性静力分析 CPU庄海洋等[9] 2008 ABAQUS(美国/法国)非线性黏弹性动力本构模型结合平面应变膜元弹塑性损伤模型结合平面应变膜元 非线性动力分析 CPU并行杜修力等[10] 2017 ABAQUS(美国/法国)弹塑性模型结合三维实体单元弹塑性损伤模型结合三维实体单元 显式非线性动力分析 CPU并行本文作者 2017 GDA(中国)考虑塑性变形的邓肯-张模型结合三维实体单元弥散开裂模型结合三维实体单元 显式非线性动力分析 GPU并行
本文完全自主研发的地下结构动力分析软件平台(Geotechnical Dynamic Analysis Program简称:GDA)是专门针对地下结构的CAE高性能开源计算平台。基于GDA平台架构主要完成以下工作:
1) 实现了一种低阶且高精度的八节点六面体单元,并用于显式非线性动力分析;
2) 提出并实现了一种混凝土弥散开裂模型,将其与实体单元结合模拟混凝土;
3) 在显式动力分析的框架下,实现了邓肯-张模型,将其与实体单元结合模拟土体;
4) 给出了一种钢筋纤维与实体单元耦合的方法,实现了对三维钢筋混凝土构件的模拟;
5) 基于等参元思想,给出了人工边界节点的单元从属面积的计算方法;
6) 给出了用于实体单元间的一种两节点接触单元,实现了对节点不协调情况下的土与结构相互作用分析;
7) 利用显式分析中数据并行度高的特点,基于CUDA实现了GPU并行计算,大幅提高了分析效率。
本文利用GDA完成日本大开地铁车站的动力分析,并通过与ABAQUS计算结果和灾害调查结果对比,验证了GDA线性分析的正确性和非线性分析的合理性。
1 基本架构
目前GDA主要集中于计算核心的研发。前处理采用ABAQUS软件CAE模块进行几何建模,并形成有限元模型。后处理采用Tecplot软件显示计算结果。
如图1,GDA软件目前主要包括三部分:
1) 模型接口模块
模型接口主要用于读取前处理软件形成的有限元模型,对有限元模型进行预处理,形成GDA前处理文件。
2) 显式分析的最大稳定步长计算模块
GDA中动力方程求解采用条件稳定的显式格式。因此在进行显式计算前,采用波动方法[11]确定求解的最大稳定步长。
3) 显式动力分析模块
本文主要讨论此模块,包括图1中的本构模型、有限单元、动力方程求解、GPU并行计算等内容(图1中的编号对应其在本文中的章节)。在前两个模块的基础上,在此模块中采用位移约束边界,利用拟静力法完成对地下结构的重力场分析。在重力场分析的基础上,采用黏弹性边界,完成地下结构的动力分析。
2 非线性本构模型
GDA软件中混凝土采用了本文提出的一种混凝土三维正交定角弥散开裂模型;土采用了邓肯-张模型[12];钢筋采用双线性随动强化模型[13](本文不再详细论述钢筋模型)。
2.1 混凝土三维正交定角弥散开裂模型
混凝土作为准脆性材料,在外部作用下随着非线性的发展,其力学特性表现出明显的各向异性;弥散开裂模型可较好反映混凝土的这种特性[14―15]。
本文提出的混凝土三维正交定角弥散开裂模型认为混凝土应力状态未达到裂面探测面时,应力-应变关系为各项同性,遵循线性胡克定律;当应力达到或者超过裂面探测面后,混凝土形成裂面且不可恢复;而后继裂面的形成,需满足应力状态要求,还需和已存在的裂面保持正交且最多为三个。
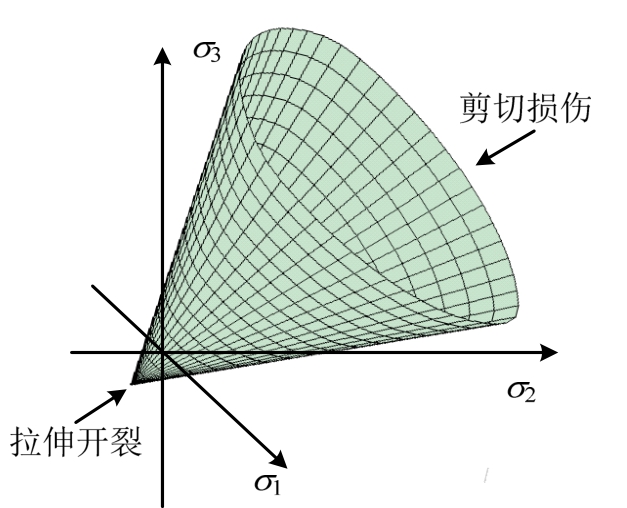
混凝土具有显著的静水压力效应[16]和中主应力效应,剪切和拉伸是导致混凝土损伤或开裂的主要原因[17]。因此,本文参考Lubliner等[18]、Lee和Fenves[19]等所给出的函数作为裂面探测面判断混凝土是否开裂,如图3所示,其表达式为:
式中:σ3、p和q分别为最小主应力、净水压力和等效剪切应力;fc和fbc分别为混凝土单轴受压强度和双轴受压强度;σt0和σc0分别为混凝土单轴受拉和受压开始进入各向异性的开裂应力;Kc为主应力空间中拉伸子午线和压缩子午线的偏应力比值,描述了偏平面中强度曲线的形状[20],反映了中主应力效应,本文取值为0.8。(注:本文应力和应变以压为正。)
开裂探测面中,最小主应力不小于0部分为剪切损伤探测面。通过观察混凝土单轴受压试验,过镇海[21]认为压应力达到单轴受压强度的0.8倍~0.9倍时,“混凝土内部裂缝有较大开展”。本文认为此阶段混凝土在最大主应力垂直方向形成裂面,所以σc0取为0.8fc。最小主应力小于0部分为拉伸开裂探测面,σt0取为单轴抗拉强度ft的0.65倍,裂面垂直于最小主应力方向。
本文模型属于定角模型,裂面形成后将不能恢复[14]。裂面法向应力-应变关系,参考《混凝土结构设计规范》GB 50010—2010[22]附录C.2(下文简称:混凝土规范)给出的单轴非线性本构模型。下文以裂面1为例阐述本文对裂面处应力-应变的处理方法。
在裂面的局部坐标系中应变矩阵为:
式中:ε为全局坐标系中单元积分点处的应变矩阵;T为裂面局部坐标系与全局坐标系的变换矩阵; 、mi、ni为裂面i开裂时主应力方向余弦(i=1,2,3)。
、mi、ni为裂面i开裂时主应力方向余弦(i=1,2,3)。
为保持和弹性阶段的连续性,在裂面局部坐标系中裂面1法向的有效正应变 取为:
取为:
式中,νc为混凝土泊松比。
裂面1法向的受压应力-应变关系采用弹性损伤模型,表达式为:
式中: 为裂面1的受压损伤;
为裂面1的受压损伤; 为
为 的历史最大值;
的历史最大值; 为裂面受压有效应变的绝对值;
为裂面受压有效应变的绝对值; 为初始达到剪切损伤面时
为初始达到剪切损伤面时 与εc,r的比值;Ec为初始弹性模量;εc,r、ρc、n和αc为模型参数,可参见混凝土规范。
与εc,r的比值;Ec为初始弹性模量;εc,r、ρc、n和αc为模型参数,可参见混凝土规范。
在单轴单调压缩过程中,混凝土应力、损伤与应变的关系,如图4所示。
在裂面局部坐标中,裂面1法向受拉应力-应变采用弥散开裂形式[23]:
式中: 为受拉作用下的开裂应变;
为受拉作用下的开裂应变; 为受拉损伤,反映了裂面1的受拉开裂程度;
为受拉损伤,反映了裂面1的受拉开裂程度; 为
为 的历史最大值;
的历史最大值; 为裂面受拉有效应变的绝对值;
为裂面受拉有效应变的绝对值;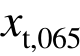 为初始达到拉伸开裂面时
为初始达到拉伸开裂面时 与
与 的比值;εt,r、ρt和αt和为模型参数,可参见混凝土规范。
的比值;εt,r、ρt和αt和为模型参数,可参见混凝土规范。
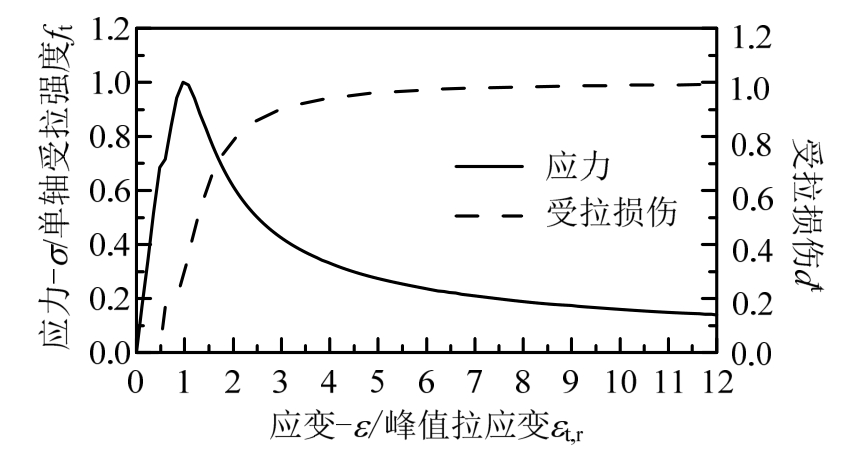
在单轴单调拉伸过程中,混凝土应力、损伤与应变的关系,如图5所示。
为考虑裂面闭合时的单边效应,裂面1整体刚度退化程度为:
H( )为Heaviside函数:
)为Heaviside函数:
裂面1局部坐标系中的剪切应力-应变关系为:
式中:Gc为初始剪切模量;将 1-d11作为剪力保持因子[24]。
采用上述方法完成局部坐标系中裂面2和裂面3处的应力更新,得到局部坐标系中应力矩阵 ,则全局坐标中应力矩阵为:
,则全局坐标中应力矩阵为:
综上,本文混凝土三维定角弥散开裂模型的应力更新算法如下:
Step1.初步开裂判断
由开裂历史量判断是否开裂,如已开裂则进入Step4;如未开裂则进入Step2。
Step2.弹性试探
式中:De为材料弹性刚度矩阵;Δε为应变增量;σtr为弹性试探应力。
Step3.开裂判断
将σtr代入裂面探测面函数判断是否开裂。如果开裂,计算变换矩阵T,更新开裂历史量,进入Step4。如果未开裂,则进入Step5。
Step4.开裂后应力计算
利用T得到裂面局部坐标系中的应变;由上文所给算法计算局部坐标系中的应力;利用T得到全局坐标系中的应力。
Step5.更新应力、损伤和相关历史量
正确性验证模型及位移荷载时程如图6所示,模型底部约束,在模型顶部进行位移加载。混凝土模型参数见表2。
表2 混凝土模型参数
Table 2 Model parameters for concrete

cE/MPacνfc/MPafbc/MPaεc,rft,r/MPaεt,r 3.25×104 0.2 40.0 46.4 1.79×10-3 3.5 1.28×10-4
图7对比了GDA软件有限元与本构模型的计算结果,两者的竖向应力-应变关系完全一致,从软件实现的角度,验证了GDA软件中三维正交定角弥散开裂模型的正确性。图7同时表明本文提出的混凝土三维正交定角弥散开裂模型反映了混凝土拉压异性、强度软化、刚度退化等力学特性;参数可由混凝土规范获取;应力更新基本无需进行迭代,易于数值实现。
2.2 邓肯-张模型
当土在加载时,邓肯-张模型[12]给出的切线弹性模量为:
式中:σ1为最大主应力;S为应力水平;pa为一个标准大气压;φ、K、n、Rf和c为模型参数。
为考虑土体在加卸载过程中产生的不可恢复变形,土体的卸载弹性模量为:
本文中邓肯-张模型的加卸载准则为:当应力偏差 (σ1-σ3 )大于历史最大应力偏差或应力水平S大于历史最大应力水平时,土体为加载状态;否则,则为卸载状态。
本文不考虑泊松比的非线性。邓肯-张模型应力更新算法采用自动控制误差的向前Euler算法[25]。
3 有限元单元
3.1 实体单元
本文在GDA中实现了Belytschko等[11,26]通过假定应变场方法提出的一种低阶且高精度的八节点六面体单元。此单元采用单点积分,有效解决了单元体积闭锁和剪切闭锁。单元积分点处的应变增量为:
式中:Δde为单元节点位移增量; 为变形矩阵,详见文献[26]。
为变形矩阵,详见文献[26]。
利用本构模型得到积分点应力增量后,积分得到单元节点力增量:
式中: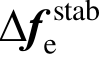 单元沙漏力增量,详见文献[26];Ve为单元体积;Δσ为积分点处应力增量。
单元沙漏力增量,详见文献[26];Ve为单元体积;Δσ为积分点处应力增量。
六面体单元的一致质量矩阵为:
式中:N为三线性差值函数矩阵;ρ为单元密度。
为保证显式动力分析中数据解耦,GDA在 的基础上得到的集中质量阵:
的基础上得到的集中质量阵:
式中: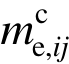 为
为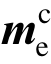 中第i行第j列的元素;me,ii为集中质量矩阵me中第i行第i列的元素,me中非对角位置元素为0。
中第i行第j列的元素;me,ii为集中质量矩阵me中第i行第i列的元素,me中非对角位置元素为0。
3.2 钢筋单元
本文参考了江见鲸[27]给出的组合式思路,假定混凝土和钢筋变形协调;同时借鉴了钢筋混凝土纤维梁元[28]和分层壳元[29]中将钢筋设置在积分点的处理方法。如图8所示,利用Belytschko等[11,26]给出的变形矩阵 ,在混凝土实体单元积分点处利用三维解耦纤维模拟钢筋,其对钢筋混凝土单元的内力增量贡献为:
,在混凝土实体单元积分点处利用三维解耦纤维模拟钢筋,其对钢筋混凝土单元的内力增量贡献为:
式中:ρrv为体积配筋率;Δσr为钢筋纤维应力增量。
3.3 三维黏弹性单元
GDA软件将杜修力等[30]给出的黏弹性人工边界单元附属于边界处单元的节点上,其单元节点力增量为:
式中:A0、Δdb和Δvb分别表示人工边界处的节点从属面积、位移增量和速度增量;kb和cb为边界处单位面积对应的人工边界单元刚度矩阵和阻尼矩阵。
在边界处的单元往往为不规则形状,如图9(a)所示。假定A点为从属此单元的人工边界点,本文利用等参元的概念将“母元”的b、o、d点坐标代入式(31)得到“等参元”中B、O、D点坐标,进而准确得到不规则边界网格中A点的从属面积 。
。
式中:xi和yi分别为“等参元”的节点坐标; 为四边形单元双线性插值函数;
为四边形单元双线性插值函数; 和η为“母元”局部坐标。
和η为“母元”局部坐标。
3.4 接触单元
本文通过两节点接触单元模拟土和结构节点非协调时的相互作用。接触单元由从节点和主节点组成,从节点位于接触面土体单元的节点上,主节点位于接触面钢筋混凝土单元的面上,如图10所示。
主节点所在面的面积为A,从节点与主节点所在面的边组成三角形面积分别为A1、A2、A3、A4。从节点和主节点所在单元形成接触对的条件为:
式中,pcTol为容差(本文取0.05)。
参考Goodman等[31]做法,采用罚函数求解接触力增量为:
式中: 为接触力增量;αst为罚参数;
为接触力增量;αst为罚参数; 为判断接触的容差(本文取0.05);
为判断接触的容差(本文取0.05); 和
和 分别为从节点和主节点的位移向量,如图10所示。
分别为从节点和主节点的位移向量,如图10所示。
 等于从节点所在单元的节点位移增量。主节点在实体单元面上,要通过主节点的母元局部坐标确定
等于从节点所在单元的节点位移增量。主节点在实体单元面上,要通过主节点的母元局部坐标确定 。利用钱向东等[32]给出的等参元逆变换算法得到主节点母元局部坐标
。利用钱向东等[32]给出的等参元逆变换算法得到主节点母元局部坐标 :
:
式中: 和
和 为第k次和第k+1次迭代得到主节点的局部坐标向量;cB为主节点的整体坐标向量;ck 为
为第k次和第k+1次迭代得到主节点的局部坐标向量;cB为主节点的整体坐标向量;ck 为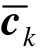 对应的整体坐标向量;
对应的整体坐标向量; 为ck处的Jacobi逆矩阵。当
为ck处的Jacobi逆矩阵。当 <10-3时,本文认为迭代收敛。
<10-3时,本文认为迭代收敛。
将主节点所在单元的节点位移增量和 代入式(35)得到主节点位移增量:
代入式(35)得到主节点位移增量:
式中,Δde为主节点所在单元的节点位移增量。
从节点位于所在单元的节点处,可以直接将接触力组装到单元节点。接触单元主节点对所在实体单元节点力增量贡献为:
3.5 几何非线性和单元失效模式
GDA采用更新的拉格朗日格式(即:UL格式)考虑几何非线性。GDA中单元节点只有3个平动自由度,因此更新每个显式分析步的节点坐标系便可更新当前时刻参考位形。
过镇海[21]根据试验指出混凝土极限压应变εc,u为6倍εc,r,超过εc,u后基本失去承载能力。同时在UL格式中,当单元急剧变形时,可能因单元体积积分为负而导致计算不稳定。因此需建立单元失效的标准,删除失效单元将有利于提高分析精度和数值稳定性。本文将εc,u推广到三维,取等效剪切应变极限值 为6倍εc,r,并作为三维混凝土单元的失效标准。本文在显式非线性动力分析中通过将失效单元节点内力和单元节点质量置零的方式实现单元删除。
为6倍εc,r,并作为三维混凝土单元的失效标准。本文在显式非线性动力分析中通过将失效单元节点内力和单元节点质量置零的方式实现单元删除。
4 动力方程求解格式
组装单元节点力可得到节点内力 和节点阻尼力
和节点阻尼力 。本文将
。本文将 和
和 代入王进廷和杜修力[33]提出的格式(简称:“王-杜”格式)中得到GDA求解动力方程的显式格式:
代入王进廷和杜修力[33]提出的格式(简称:“王-杜”格式)中得到GDA求解动力方程的显式格式:
式中:dn+1、dn和dn-1分别表示tn+1、tn和tn-1时刻的节点位移向量;vn+1和vn分别表示tn-1和tn时刻的节点速度向量;an+1表示tn+1时刻的节点加速度向量; 、
、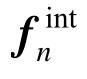 和
和 分别表示tn时刻的节点的外力向量、内力向量和阻尼力向量;Δt为动力分析时间步长。
分别表示tn时刻的节点的外力向量、内力向量和阻尼力向量;Δt为动力分析时间步长。
“王-杜”格式对于一般阻尼体系具有二阶精度,可提高人工边界阻尼单元的计算精度。
5 CPU+GPU异构并行计算程序架构
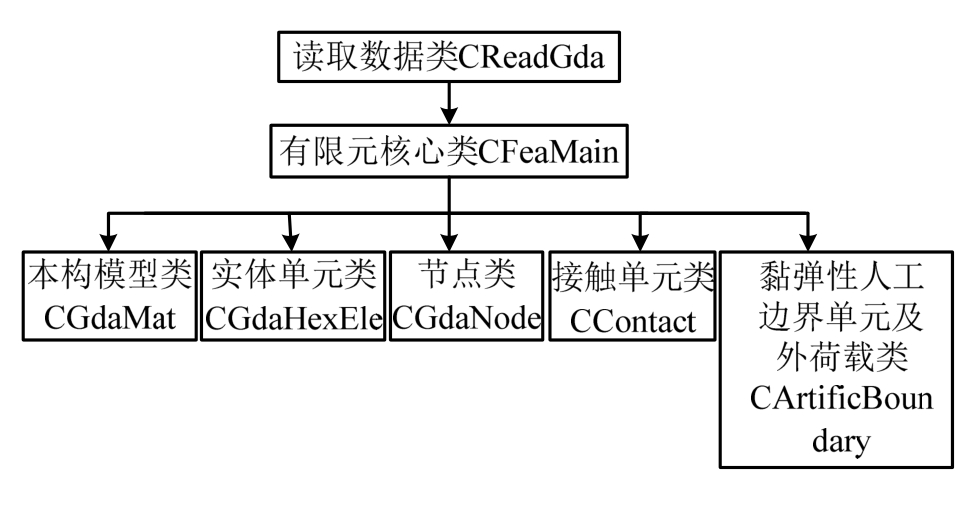
基于面向对象的程序设计,GDA通过C++类实现数据和算法的封装。如图11所示,GDA类图中包括:读取数据类CReadGda、有限元核心类CFeaMain、单元节点类CGdaNode、实体单元类CGdaHexEle、本构模型类CGdaMat、接触单元类CContact、黏弹性人工边界单元及外荷载类CArtificBoundary。
由上文计算模型、单元和方法可知,显式动力分析步长满足最大稳定步长后,非线性动力求解无需进行迭代。因此本文显式动力分析中本构模型应力更新、单元内力计算、节点力组装和动力方程求解等部分的计算特点是:1) 逻辑控制简单;2) 数据相关性低;3) 基本无需进行数据通信。GPU逻辑运算能力弱于CPU,但目前单个GPU就具有上千计算内核(Streaming Processor)更适合实现本文显式动力分析的细粒度并行。通过利用NVIDIA提供的CPU+GPU异构并行计算架构CUDA(Compute Unified Device Architecture),本文在GDA中实现了GPU并行计算,如图12所示。
6 大开车站的强震模拟
本文采用GDA软件对大开车站在地震中的动力响应进行分析,并与ABAQUS的分析结果进行对比,从而验证GDA软件中实体单元、接触单元、三维黏弹性边界单元、显式动力求解方法的正确性和精度。将GDA非线性动力计算结果与车站灾害调查结果进行对比,验证GDA非线性分析的稳定性和分析结果的合理性。
为对比计算效率,使用同一台计算机(CPU为i7-4770,GPU为NVIDIA GTX780)分别采用GDA和ABAQUS对车站进行分析。ABAQUS显式动力分析模块不支持GPU并行,因此采用8线程CPU并行;GDA采用GPU并行。
6.1 车站有限元模型
大开车站的有限元模型,如图13所示,其中:土体单元数14112,节点数16668,结构单元数1784,节点数3999,接触单元数1412,三维黏弹性边界单元数3036,模型自由度数66238。
混凝土本构模型采用本文给出的混凝土三维正交定角弥散开裂模型,参考混凝土规范、杜修力[10]和Liu等[8]的取值,模型参数如表3。结构体积配筋率为1%,钢筋的双线性随动强化模型参数如表4,屈服后刚度为初始刚度的1/50。
土的非线性本构模型及参数直接影响非线性动力计算结果,邓肯-张模型也存在参数敏感性的问题[34]。由于缺少大开车站围岩土非线性参数[7],数值模拟采用的土体参数往往需通过反演或者试验获得。本文采用GDA对大开车站进行动力分析的目的是验证GDA计算能力及非线计算结果的合理性;反演车站围岩土的邓肯-张模型非线性参数已经超出本文讨论范围。因此本文参考蒋录珍等[35]的取值,对全部土体采用一组参数如表4,将Ese和重力场土体压力代入式(23)得到参数K。
表3 混凝土弥散开裂模型参数
Table 3 Parameters of smeared crack model for concrete

Ec/MPacνfc/MPafbc/MPaεc,rft,r/MPaεt,r 密度/(kg/m3)3.25×104 0.2 25 29 1.56×10-3 2.5 1.07×10-4 2500表4 土的邓肯-张模型和钢筋的双线性随动强化模型参数Table 4 Parameters of Duncan-Chang model for soil and bilinear kinematic hardening model for rebar土体Ese/MPasν 密度/(kg/m3) 黏聚力/kPaφ/(°)n钢筋 弹性模量/MPa 屈服力/MPa 屈服应变 密度/(kg/m3)180 0.35 1900 25 30 0.5 2×105 240 1.2×10-3 7800
本文动力分析采用大开车站附近的神户海洋气象台监测到的地表水平向(x向)和竖向(y向)加速度时程,如图14所示,持时为35 s;采用波场分解法[36]确定边界处地震力输入值。
为对比计算结果,取模型中位于土体的节点1和位于结构的节点3339为监测点,如图15所示。
6.2 重力场分析
重力场分析模型的上表面为自由面,其他面取法向位移约束。GDA采用显式线性拟静力分析,质量阻尼系数取2.0,加载时程如图16所示;ABAQUS采用隐式线性静力求解。
重力场分析的竖向位移,如图17所示,ABAQUS和GDA结果一致,因结构刚度大于土体刚度,结构上方土体变形较小。如图18所示,ABAQUS监测点竖向位移分别为-0.012 m和-0.009 m;GDA在3 s时完成重力场加载,经过稍微“震荡”后,其计算结果和ABAQUS趋于一致。上述对比验证了GDA各计算模块的正确性和采用显式拟静力方法进行重力场分析的可行性。
6.3 线性动力分析
图19给出了线性动力分析中结构3339号节点x向和y向的位移时程,由图可见,两者的计算结果一致。
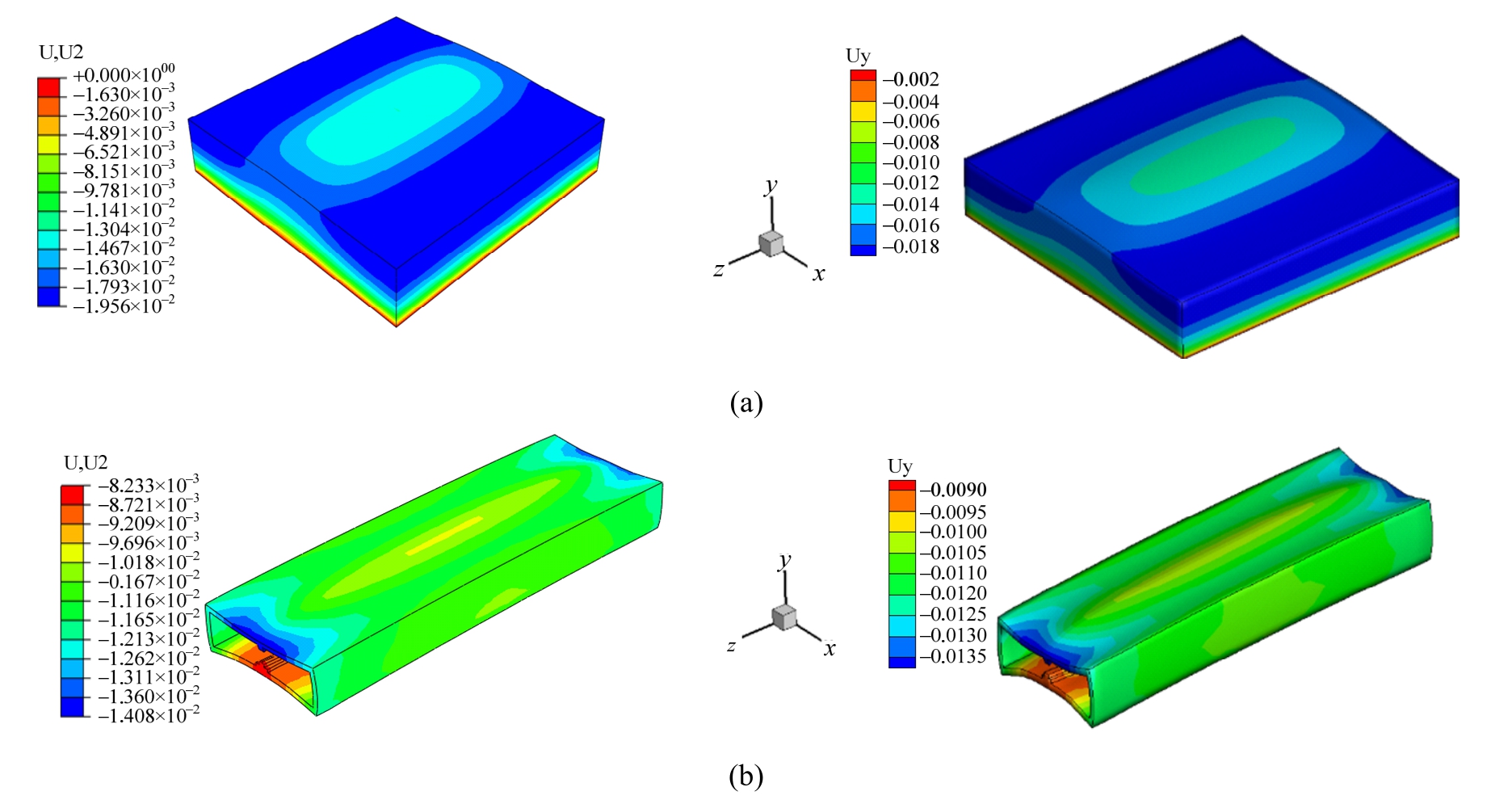
图20分别给出了两种软件计算得到的30 s时土体与结构的位移云图,由图可见,两种软件计算得到的土体和结构各个部位的变形趋势及数值都较为一致。线性动力分析过程中,GDA采用GPU并行计算,耗时35 min;ABAQUS采用8线程CPU并行计算,耗时195 min;在计算结果一致条件下,GDA的计算速度为ABAQUS计算速度的5.68倍。
通过上述对比分析,验证了GDA软件中实体单元、接触单元、三维黏弹性边界单元、显式动力求解方法的正确性和精度;也验证了GPU并行计算的速度优势。
6.4 非线性动力分析
本文主要通过与灾害调查结果对比,验证GDA非线性动力分析结果的合理性。如图21所示,GDA非线性结果中地表最终时刻沉降量明显大于线性计算结果,与灾害调查结果规律上更为接近。
图22表明GDA得到最终时刻车站混凝土损坏结果与灾害调查结果基本一致,中柱混凝土主要发生受压损坏,而结构顶部混凝土则以受拉损坏为主。
如图23所示,GDA非线性计算得到的结构变形明显大于线性计算结果。5 s时结构尚未出现明显损坏;7 s时部分中柱底部出现损坏,部分钢筋混凝土单元被删除;35 s时大量中柱损坏,车站顶板沉降明显。
如图24所示,线性计算得到的顶板和底板间变形随地震作用不断变化,最大值不超过1 mm,最终时刻未出现残余变形。相对于线性结果,非线性结果中顶板和底板间变形明显较大;随中柱损坏和失效单元的删除,变形突然增大;随着地震作用的减弱,变形趋于稳定;最终时刻相对变形约为17 cm。
以上分析结果和杜修力等[10]给出的车站损坏及变形规律基本相同,与灾害调查给出的损坏模式较为一致。
7 结论
(1) 为解决地下结构隐式非线性动力分析收敛性差和计算效率低的技术瓶颈,本文基于GPU并行计算,完全自主研发了的地下结构显式动力分析软件平台GDA。
(2) 在自主研发软件GDA中,实现了低阶且高精度的八节点六面体单元。将六面体单元与本文混凝土弥散开裂模型结合用于结构的非线性模拟。在显式动力计算框架下,实现了邓肯-张模型的应力更新,与本文六面体单元结合用于土体的非线性模拟。为实现钢筋混凝土的模拟,给出了一种钢筋纤维与实体单元的耦合方法。基于等参元思想,给出了人工边界节点的单元从属面积的准确计算方法。为实现节点不协调情况下的土结相互作用分析,开发实现了一种两节点接触单元。
(3) 为验证GDA各模块的正确性,采用GDA对阪神地震中发生严重损坏的大开车站进行了分析。将GDA的重力场和线性动力分析结果与ABAQUS结果进行对比。分析表明:GDA与ABAQUS计算结果一致,且计算效率约为ABAQUS计算效率的5.68倍,验证了GDA各模块的正确性、精度和效率。GDA非线性动力分析结果中土体和结构的变形明显大于线性结果,与现场灾害调查的损坏模式基本一致,验证了GDA非线性求解的稳定性和合理性。
参考文献:
[1] Ma C,Lu D C,Du X L,et al.Effect of buried depth on seismic response of rectangular underground structures considering the influence of ground loss [J].Soil Dynamics & Earthquake Engineering,2018,106: 278―297.
[2] 路德春,罗磊,王欣,等.土与结构接触面土体软/硬化本构模型及数值实现 [J].工程力学,2017,34(7):41―50.Lu Dechun,Luo Lei,Wang Xin,et al.Softening/hardening constitutive model for soil-structure interface and numerical implementation [J]. Engineering Mechanics,2017,34(7): 41―50.(in Chinese)
[3] 杜修力,李洋,赵密,等.下卧刚性基岩条件下场地土-结构体系地震反应分析方法研究 [J].工程力学,2017,34(5): 52―59.Du Xiuli,Li Yang,Zhao Mi,et al.Seismic response analysis method for soil-structure interaction system of underlying rigid rock base soil condition [J].Engineering Mechanics,2017,34(5): 52―59.(in Chinese)
[4] Nakamura S,Yoshida N,Iwatate T.Damage to Daikai subway station during the 1995 Hyogoken-Nanbu earthquake and its investigation [J].Japan Society of Civil Engineers,Committee of Earthquake Engineering,1996: 287―295.
[5] An X,Shawky A A,Maekawa K.The collapse mechanism of a subway station during the Great Hanshin Earthquake [J].Cement and Concrete Composites,1997,19(3): 241―257.
[6] Maekawa K,Shawky A.Computational approach to path-dependent nonlinear RC/soil interactions [J].Concrete Library International,1996,30(532): 197―207.
[7] 曹炳政,罗奇峰,马硕,等.神户大开地铁车站的地震反应分析[J].地震工程与工程振动,2002,22(4):102―107.Cao Bingzheng,Luo Qifeng,Ma Shuo,et al.Seismic response analysis of Daikai subway station in Hyogoken-Nanbu earthquake [J]. Earthquake Engineering and Engineering Vibration,2002,22(4):102―107.(in Chinese)
[8] Liu J B,Liu X Q.Pushover analysis of Daikai subway station during the Osaka-Kobe earthquake in 1995 [C] .Proceedings of the 14th World Conference on Earthquake Engineering.Beijing China,2008: No.14-0099.
[9] 庄海洋,程绍革,陈国兴.阪神地震中大开地铁车站震害机制数值仿真分析 [J].岩土力学,2008,29(1):245―250.Zhuang Haiyang,Cheng Shaoge,Chen Guoxing.Numerical simulation and analysis of earthquake damages of Daikai metro station caused by Kobe earthquake [J].Rock and Soil Mechanics,2008,29(1):245―250.(in Chinese)
[10] 杜修力,马超,路德春,等.大开地铁车站地震破坏模拟与机理分析 [J].土木工程学报,2017,50(1): 53―62.Du Xiuli,Ma Chao,Lu Dechun,et al.Collapse simulation and failure mechanism analysis of the Daikai subway station under seismic loads [J].China Civil Engineering Journal,2017,50(1): 53―62.(in Chinese)
[11] Flanagan D,Belytschko T.A uniform strain hexahedron and quadrilateral with orthogonal hourglass control [J].International Journal for Numerical Methods in Engineering,1981,17(5): 679―706.
[12] Duncan J M,Chang C Y.Nonlinear analysis of stress and strain in soils [J].Soil Mechanics & Foundation Division Journal,1970,96(5): 1629―1653.
[13] Simo J C,Hughes T J R.Computational inelasticity [M].USA: Springer,2008: 91―92.
[14] Rots J G,Blaauwendraad J.Crack models for concrete,discrete or smeared? fixed,multi-directional or rotating?[J].Heron,1989,34(1): 1―59.
[15] Vecchio F J,Collins M P.The modified compressionfield theory for reinforced concrete elements subjected to shear [J].ACI Journal,1986,83(2): 219―231.
[16] 杜修力,王国盛,路德春.混凝土材料非线性多轴动态强度准则 [J].中国科学: 技术科学,2014,44(12):1319―1332.Du Xiuli,Wang Guosheng,Lu Dechun.Nonlinear multiaxial dynamic strength criterion for concrete material [J].Scientia Sinica Technologica,2014,44(12):1319―1332.(in Chinese)
[17] 李杰,吴建营.混凝土弹塑性损伤本构模型研究 I:基本公式 [J].土木工程学报,2006,38(9): 14―20.Li Jie,Wu Jianying.Elastoplastic damage constitutive model for concrete based on damage energy release rates ,part I : basic formulations [J].China Civil Engineering Journal,2006,38(9): 14―20.(in Chinese)
[18] Lubliner J,Oliver J,Oller S,et al.A plastic-damage model for concrete [J].International Journal of Solids and Structures,1989,25(3): 299―326.
[19] Lee J,Fenves G L.Plastic-damage model for cyclic loading of concrete structures [J].Journal of Engineering Mechanics,1998,124(8): 892―900.
[20] 陈惠发,余天庆.混凝土和土的本构方程 [M].北京:中国建筑工业出版社,2004: 20―22.Chen Huifa,Yu Tianqing.Constitutive equations for materials of concrete and soil [M].Beijing: China Architecture & Building Press.2004: 20―22.(in Chinese)
[21] 过镇海.混凝土的强度和变形: 试验基础和本构关系[M].北京: 清华大学出版社,1997: 13―15.Guo Zhenhai.Strength and deformation of concrete:experimental basis and constitutive relation [M].Beijing:Tsinghua University Press,1997: 13―15.(in Chinese)
[22] GB 50010—2010,混凝土结构设计规范 [S].北京:中国建筑工业出版社,2011: 209―211.GB 50010—2010,Code for design of concrete structures[S].Beijing: China Architecture & Building Press,2011:209―211.(in Chinese)
[23] Bažant Z P,Oh B H.Crack band theory for fracture of concrete [J].Materials and Structures,1983,16(3):155―177.
[24] Suidan M,Schnobrich W C.Finite element analysis of reinforced concrete [J].Journal of the Structural Division,1973,99(10): 2109―2122.
[25] 费康,张建伟.ABAQUS在岩土工程中的应用 [M].北京: 中国水利水电出版社,2013: 146―152.Fei Kang,Zhang Jianwei.Application of ABAQUS in geotechnical engineering [M].Beijing: China Water Power Press,2013: 146―152.(in Chinese)
[26] Belytschko T,Bindeman L P.Assumed strain stabilization of the eight node hexahedral element [J].Computer Methods in Applied Mechanics and Engineering,1993,105(2): 225―260.
[27] 江见鲸.钢筋混凝土结构非线性有限元分析[M].西安: 陕西科学技术出版社,1994: 91―116.Jiang Jianjing.Nonlinear finite element analysis of reinforced concrete structures [M].Xi’an: Shaanxi Science and Technology Press,1994: 91―116.(in Chinese)
[28] Spacone E,Filippou F C,Taucer F F.Fiber beam-column model for nonlinear analysis of R/C frames [J].Earthquake Engineering & Structural Dynamics,1996,25(7): 711―725.
[29] Polak M A.Nonlinear analysis of reinforced-concrete shells [J].Journal of Structural Engineering,1993,119(12): 3439―3462.
[30] 杜修力,赵密,王进廷.近场波动模拟的人工应力边界条件 [J].力学学报,2006,38(1): 49―56.Du Xiuli,Zhao Mi,Wang Jinting.A stress artificial boundary in FEA for near-field wave problem [J].Chinese Journal of Theoretical and Applied Mechanics,2006,38(1): 49―56.(in Chinese)
[31] Goodman R E,Taylor R L,Brekke T L.A model for the mechanics of jointed rock [J].Journal of Soil Mechanics and Foundations Division,1968,94(3): 637―660.
[32] 钱向东,任青文,赵引.一种高效的等参有限元逆变换算法 [J].计算力学学报,1998,15(4): 437―441.Qian Xiangdong,Ren Qingwen,Zhao Yin.An efficient inverse transformation method of isoparametric finite element method [J].Chinese Journal of Computational Mechanics,1998,15(4): 437―441.(in Chinese)
[33] 王进廷,杜修力.有阻尼体系动力分析的一种显式差分法[J].工程力学,2002,19(3): 109―112.Wang Jinting,Du Xiuli.An explicit difference method for dynamic analysis of a structure system with damping[J].Engineering Mechanics,2002,19(3): 109―112.(in Chinese)
[34] 何昌荣,杨桂芳.邓肯-张模型参数变化对计算结果的影响[J].岩土工程学报,2002,24(2): 170―174.He Changrong,Yang Guifang.Effects of parameters of Duncan-Chang model on calculated results [J].Chinese Journal of Geotechnical Engineering,2002,24(2): 170―174.(in Chinese)
[35] 蒋录珍,陈隽,李杰.1995年阪神地震中大开车站破坏机理分析[J].世界地震工程,2015,31(3): 236―242.Jiang Luzhen,Chen Juan,Li Jie.Damage mechanism analysis of Daikai subway station caused by Kobe earthquake in 1995 [J].World Earthquake Engineering,2015,31(3): 236―242.(in Chinese)
[36] 杜修力.工程波动理论与方法[M].北京: 科学出版社,2009: 370―374.Du Xiuli.Theories and methods of wave motion for engineering [M].Beijing: Science Press,2009: 370―374.(in Chinese)
DEVELOPMENT ON SOFTWARE PLATFORM FOR NONLINEAR DYNAMIC ANALYSIS OF UNDERGROUND STRUCTURE BASED ON GPU PARALLEL COMPUTING
CAO Sheng-tao ,LU De-chun ,DU Xiu-li ,ZHAO Mi ,CHENG Xing-lei
(Key Lab of Urban Security and Disaster Engineering of Ministry of Education,Beijing University of Technology,Beijing 100124,China)
Abstract: The implicit nonlinear dynamic analysis of underground structures is of poor convergence and low computational efficiency.Based on GPU parallel computing,a software platform for the explicit dynamic analysis of underground structures was established,which can solve the technical bottleneck of the implicit method.In this platform,a smeared crack model for concrete was proposed and implemented.A coupling method for rebar fibers and solid elements was developed and implemented.Based on the isoparametric element idea,a method for calculating the element area of artificial boundary nodes was proposed.A two-node interface element for solid elements was proposed to perform the interaction analysis between soil and structure with uncoordinated nodes.The gravity field analysis,linear and nonlinear dynamic analysis of Daikai subway station in Japan were performed by the software.The results of gravity field analysis and linear dynamic analysis were compared with the results of ABAQUS.The results of the software were in an agreement with the results of ABAQUS,and the computational efficiency was about 5.68 times the efficiency of ABAQUS.Thusly,the accuracy and efficiency ofthe software modules were verified.Besides,the stability and rationality of the software nonlinear analysis were verified by comparing the results of nonlinear analysis with the disaster investigation.
Key words: underground structure; nonlinear dynamic analysis; GPU parallel computing; constitutive model;software platform
中图分类号:TU311.3;TU311.4
文献标志码:A
doi: 10.6052/j.issn.1000-4750.2017.11.0898
文章编号:1000-4750(2019)02-0053-13
收稿日期:2017-11-27;修改日期:2018-11-08
基金项目:国家自然科学基金项目(51421005,51522802,51778026)
通讯作者:杜修力(1962―),男,四川广安人,教授,博士,博导,从事地震工程领域的研究(E-mail: duxiuli@bjut.edu.cn).
作者简介:
曹胜涛(1985―),男,河北邢台人,工程师,博士,从事工程结构抗震领域的研究(E-mail: 1159563218@qq.com);
路德春(1977―),男,黑龙江兰西人,教授,博士,博导,从事土动力学与岩土地震工程领域的研究(E-mail: dechun@bjut.edu.cn);
赵 密(1980―),男,吉林公主岭人,教授,博士,博导,从事重大工程抗震领域的研究(E-mail: zhaomi@bjut.edu.cn);
程星磊(1987―),男,山西长治人,讲师,博士,从事海洋土动力学领域的研究(E-mail: chengxinglei110@163.com).









 为裂面1的受压损伤;
为裂面1的受压损伤;


 为初始达到剪切损伤面时
为初始达到剪切损伤面时 与
与






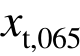


 )为Heaviside函数:
)为Heaviside函数:






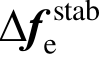 单元沙漏力增量,详见文献[26];
单元沙漏力增量,详见文献[26];
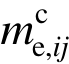
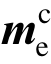










 为接触力增量;
为接触力增量;
 和
和

 等于从节点所在单元的节点位移增量。主节点在实体单元面上,要通过主节点的母元局部坐标确定
等于从节点所在单元的节点位移增量。主节点在实体单元面上,要通过主节点的母元局部坐标确定 。利用钱向东等
。利用钱向东等


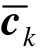





 。本文将
。本文将 和
和

 、
、