索穹顶结构[1―2]由索和杆组成,在预应力施加前没有刚度。根据结构初始几何状态、构件的关联关系,确定形成一定刚度的初始预应力形态是首先要解决的问题。确定索穹顶结构的预应力形态问题,可以分为两类:其一,结构几何给定,预应力分布未定。初始给定几何即是预应力态几何,所要求解的是在给定几何条件下的结构预应力分布。其二,结构几何和预应力分布均未定。首先假定初始几何和相应的预应力,由于为任意假定,通常情况下假定的内力不满足节点平衡条件。通过计算可求出结构各节点产生的位移分量,当各节点产生这些位移以后,体系就在新的几何位置上维持平衡,这样就达到了所求的预应力形态。此时结构几何不再是给定几何,结构预应力分布也不再是初始假定的预应力分布。
在索穹顶的预应力形态分析方面,众多专家学者已进行了较深入的研究,文献[3―4]对平衡矩阵理论做了开创性研究;文献[5―7]基于节点力平衡原理,提出了索穹顶的初始预应力分布的快速计算法,适用于单自应力模态(本文中的“模态”沿用相关参考文献中的定义,区别于动力学中的“模态”,意指分布状态),且对称的索穹顶结构;文献[8―9]充分考虑索穹顶结构的对称性及拉索受拉、压杆受压的特性,提出了整体可行预应力概念,建立了相应的判定准则,推导了二次奇异值法,适用于求解各种索穹顶的整体自应力模态,得到了广泛的认可及应用。文献[10―11]分别对力密度法[12]和动力松弛法[13]在索穹顶预应力形态确定中的应用进行了研究。
本文提出一种初始预应力分布确定的新方法,既保留了整体可行预应力概念,且实现起来更加简便,特别适用于多自应力模态结构,具有广泛的适用性。
索穹顶属于空间铰接结构体系,设有N个节点,b根杆件,则有平衡矩阵[14]:
式中:平衡矩阵A为3N×b矩阵;t为b维杆件内力矢量;f为3N维节点力矢量。假设A的秩为r,则s=b-r为自应力模态数,m=3N-r为机构位移数,可将结构分为四种类型:
s=0,m=0,静定动定体系,即静定结构;
s=0,m>0,静定动不定体系,即可变体系;
s>0,m=0,静不定动定体系,即超静定结构;
s>0,m>0,静不定动不定体系。
只有3、4类结构是可以施加预应力的,索穹顶由于没有自然刚度,需施加预应力来抵抗外荷载,故一定属于第3、4类体系。
对A矩阵进行奇异值分解:

得到结构独立自应力模态Wb-r和独立机构位移模态U3N-r。一般预应力状态X是s个独立自应力模态的线性组合:
考虑结构的对称性,并使索受拉,压杆受压,且同类杆件的预应力值相同,即满足结构的整体预应力。设分组数为n,则最终预应力X可记为:
引入基矩阵e=[e1…ei…en]b×n,基矢量ei由相应第i类压杆轴力为-1、索力为1、其余杆件轴力为0组成,则有:
则可以得到:

对W-e再次进行奇异值分解,可得整体自应力模态V:
若V为一维向量,则结构只有一组满足对称性要求的整体自应力模态,元素同号,则满足拉索受拉,压杆受压,为整体可行预应力;
若V为多维向量,需选择合适的组合系数进行优化;
若V=0,说明无满足要求的整体自应力模态,需重新调整设计结构。
以上为二次奇异值分解法的基本原理,对多自应力模态结构,该方法求得整体自应力模态后,还需对组合系数进行优化组合,优化的方法有多种,优化目标多样[15],对实际工程应用造成了一定的困难。
以一个K5型凯威特型索穹顶(图1)为例:索穹顶最外环20等分,三圈环索。跨度80 m,脊索端点均位于矢高6.5 m的球面上,凯威特脊线处斜索与水平面的夹角统一为25°,内圈拉环直径12 m。考虑结构的对称性和单元特性,将处于对称位置的同类单元设定为一组构件,则如图2所示,共有28组构件。通过二次奇异值分解法,可得其自应力模态数为35,机构位移模态数为0,独立整体自应力模态为6组,可直接使用的整体可行预应力为0组。故应该对整体自应力模态进行组合,才能求得整体可行预应力。

图1 凯威特型索穹顶模型
Fig.1 Model of Kiewitt cable dome

图2 凯威特型索穹顶构件分组
Fig.2 Member groups of Kiewitt cable dome
对尚未施加预应力的索穹顶结构施加预设荷载P(以下简称为预载),我们可以获得一组结构内力N,由力平衡关系,该组内力N恰好能抵抗预载P(图3,虚线表示变形后的结构)。考虑到索穹顶为预应力结构,其主要的承载力应由几何刚度矩阵来提供,因此,提取预载工况下的单元内力N作为预应力施加至结构上,那么结构将主要由N产生的几何刚度来抵抗预载P,这是一种充分发挥了预应力作用的状态。若撤除预载P,索穹顶将在N的作用下回弹到一个新的平衡态(图4),其刚度矩阵记为:
即:
式中,切线刚度矩阵KT可拆分为:
K0为线性刚度矩,反映的是单元材料特性、截面特性和几何特性对结构刚度的贡献;Kg为几何刚度矩阵,反映当前构件内力对结构刚度的贡献。此时的单元内力N2,对应于此时的几何刚度矩阵Kg。
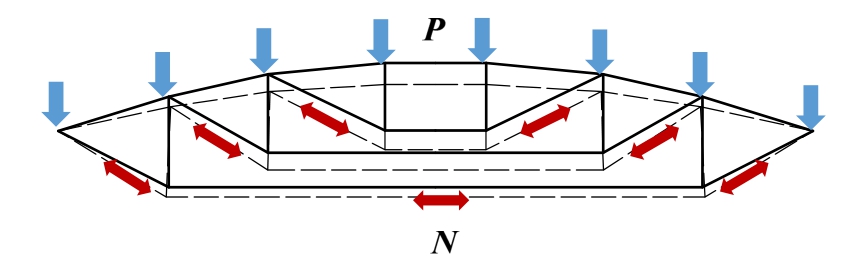
图3 预载过程
Fig.3 Preload process

图4 回弹过程
Fig.4 Rebound process
此时的状态:无外荷载,存在单元内力分布N2,此组内力利于抵抗结构主要承受的荷载P。如果施加的预载P为对称荷载,则实际上已经自动为构件的内力进行了分组,若单元内力分布N2满足拉索受拉,压杆受压,则内力分布N2就是一组有利于抵抗荷载P的较优整体可行预应力。
综上,通过两个步骤:1) 施加预载,获得初始内力分布;2) 将初始内力施加至结构上,撤除预载,结构在初始内力作用下回弹,即可能初步得到较优的索穹顶整体可行预应力。
预载过程中,求得的单元内力实际上对应于结构变形后的状态。若结构变形较大,将该内力施加至初始结构上,其实存在一定的误差;回弹过程中,若回弹的变形较大,也会使结构与初始形态差距较大,同时求得的预应力分布也是针对该状态下的预应力分布。因此,变形的控制是该方法保证精度的关键,本文采用变弹性模量法来控制求解过程中结构的变形。
在预载过程中,可将材料弹性模量放大一定的倍数,放大倍数与施加的预设荷载大小、初始设定的截面大小和材料参数有关,通常可取10倍~1000倍,使结构处于小变形状态(建议最大挠跨比小于1/500),以降低变形的影响。
针对回弹过程,引入两阶段迭代计算:第一阶段仍然保持大弹性模量,使结构处于小变形状态,只迭代预应力,将单元预应力更新为上一步回弹后的单元内力,直至内力达到收敛。需要特别指出的是,在第一步回弹过程中,由于施加的单元初始内力大部分将转化为弹性变形,故可适当等比例放大预载得到的单元初始内力,以在弹性变形发生后,尽可能多地保留产生几何刚度Kg的单元内力,放大的倍数仍以控制结构处于小变形状态来确定,建议控制最大挠跨比小于1/500。
由于大弹性模量会导致线性刚度矩阵对预应力分布存在一定影响,但其影响程度难以直接地做出判断,故当单元内力收敛后,再采用小弹性模量进行第二阶段迭代:将弹性模量缩小,使线性刚度矩阵K0对结构刚度的贡献降低至可忽略的程度,此时结构的刚度将几乎完全由预应力提供的几何刚度Kg组成。弹性模量缩小的倍数可以通过内力较大典型构件的预内力Ps与构件轴向刚度EA的比值来确定,若Ps与EA的比值大于1,则意味着预内力具有在构件上产生大于1倍构件长度变形的能力,在结构领域已属很大应变,可判定该弹性模量缩小倍数已能基本排除线性刚度的影响。由于过大的缩小倍数可能导致计算的收敛性不佳,一般情况下,取弹性模量缩小倍数使2>Ps/EA>1,可兼顾精度与收敛性。迭代计算后,如果力和位移同时满足收敛条件,则已求得目标整体可行预应力,不需再进行迭代;若不满足,则同时更新预应力与节点坐标,进行迭代。
分两阶段进行迭代有显著的优点:第一阶段内力迭代求解在给定几何条件下的结构预应力分布;第二阶段迭代排除了线性刚度矩阵的影响,得到了纯粹的预应力分布,既是对第一阶段迭代结果的复核,也可进一步对形态进行调整。
一般情况下,该方法收敛速度很快,数次迭代即可达到收敛,结构位移及内力将趋于稳定,此时再将弹性模量恢复,可进行下一步设计分析。
综合以上所述的基本原理和两阶段变弹性模量迭代计算,预载回弹法的计算流程如下(图5)。

图5 计算流程图
Fig.5 Calculation flow chart
1) 建立初始模型,设置初始的材料、截面参数。
2) 放大弹性模量,以使结构变形很小,处于小变形状态。
3) 对尚未施加预应力的索穹顶结构施加预载P(由于索穹顶结构自重轻,且重力荷载为长期的主要荷载,一般情况下,可施加1.0倍对称附加恒载),获得单元内力分布N。
4) 撤除预载P,并将单元内力N放大适当倍数作为预应力施加至结构上,结构将在N的作用下回弹到一个新的平衡态,得到此时的单元内力分布N2。
5) 内力分布判定:对内力分布N2进行判定,由于预设荷载为对称荷载,已经自动对构件的内力进行了分组,故只需判定拉杆全部受拉,压杆受压,则内力分布即为整体可行预应力,可进入下一步;若为非整体可行预应力,则调整模型,重新试算。
6) 将上一步得到的内力作为预应力施加至结构,反复迭代数次,直至满足力收敛条件。
7) 缩小弹性模量,排除线性刚度矩阵的影响。
8) 再次进行计算,若同时满足力和位移收敛条件,则证明该内力分布满足要求,已求得目标整体可行预应力,不需再进行迭代;若不满足,则同时更新预应力与节点坐标,进行迭代,直至收敛。
采用与第一小节中相同的K5型凯威特型索穹顶,由第一小节可知通过二次奇异值分解法,可得其自应力模态数为35,机构位移模态数为0,独立整体自应力模态为6组。采用预载回弹法确定初始预应力,迭代过程共进行了以下几步。
1) 预载:施加1.0倍附加恒载,同时为将结构变形控制在小变形范围内,将弹性模量放大100倍。
2) 第一次回弹:将预载获得的单元内力作为预应力施加,同时为了尽量多的保留对几何刚度起贡献的单元内力,将施加的单元内力放大50倍。
3) 第二次回弹、第三次回弹:将上一次的单元内力作为预应力施加,达到收敛。
4) 小弹性模量回弹:将弹性模量缩小为真实的1/1000,使构件预内力与刚度的比值满足2>Ps/EA>1,对预应力进行复核,结果收敛。
图6~图7分别为外圈的脊索(第9组构件)和环索(第22组构件)的内力变化过程。脊索在预载时受压,内力为-62.7 kN,回弹后受拉,经过3次回弹内力稳定在34.8 kN,小弹性模量复核时,结构内力未改变。环索预载时内力最大为700.7 kN,经过3次回弹后内力稳定在114.2 kN,小弹性模量复核时,结构内力也未改变。
图8为竖向位移最大的最内环上节点,预载时位移为-1.6 mm(向下),第一次回弹为80.5 mm(向上),然后很快收敛为0,即使采用小弹性模量,位移依然保持为0。
获得的整体可行预应力如表1所示(以内环撑杆内力绝对值为单位1),其中第24组~28组为杆单元,故预应力为负值。

图6 第9组构件内力变化过程
Fig.6 Internal force history of member group 9

图7 第22组构件内力变化过程
Fig.7 Internal force history of member group 22

图8 上内环节点位移变化过程
Fig.8 Node displacement history of upper inner ring
如图9所示的肋环型索穹顶结构,设20道径向索,三圈环索。跨度80 m,脊索端点均位于矢高6.5 m的球面上,斜索与水平面的夹角统一为25°,内圈拉环直径12 m。构件分组如图10所示,共有13个组。肋环型索穹顶较为简单,通过节点力平衡关系即可求得其预应力[5]。也可通过二次奇异值分解法,得到其自应力模态数为19,机构位移模态数为1,整体可行预应力为1组。采用预载回弹法,通过预载、三次大弹性模量回弹和一次小弹性模量回弹可求得预应力分布,结果如表2所示,与二次奇异值分解法一致,误差不超过0.02%,其中第11~13组由于为杆单元,故预应力为负值。
本节以算例1中的80 m跨凯威特型索穹顶为例,对预载回弹法求得的预应力分布在静力荷载下的性能进行验证,考察其实际工程应用价值。为尽可能地贴近实际工程应用,荷载、材料、尺寸均参考某实际工程项目,仅在荷载组合上作适当简化,并将结构受力性能与实际工程采用的具有唯一整体可行预应力分布的葵花肋环混合型索穹顶(图11,跨度、失高、撑杆高度等几何参数均相同,仅布置不同)进行对比。
表1 凯威特型索穹顶整体可行预应力
Table 1 Integrity feasible prestressing distribution of Kiewitt cable dome

注:以最内环撑杆(第24组构件)预应力大小的绝对值为单位1,拉力为正,压力为负。
单元分组 预应力模态 单元分组 预应力模态1 5.901 15 2.556 2 2.809 16 1.809 3 3.907 17 2.901 4 2.546 18 2.472 5 3.852 19 1.543 6 3.631 20 4.505 7 2.230 21 10.547 8 5.963 22 10.038 9 3.059 23 7.946 10 1.119 24 -1.000 11 0.698 25 -1.363 12 2.529 26 -1.374 13 0.433 27 -2.247 14 1.735 28 -2.089

图9 肋环型索穹顶方案模型
Fig.9 Model of Geiger cable dome

图10 肋环型索穹顶结构分组
Fig.10 Member groups of Geiger cable dome
表2 肋环型索穹顶整体可行预应力
Table 2 Integrity feasible prestressing distribution of Geiger cable dome

注:以最内环撑杆(第11组构件)预应力大小的绝对值为单位1,拉力为正,压力为负。
单元分组 预应力模态二次奇异值分解法 预载回弹法 误差/(%)1 10.817 10.817 0.000 2 13.134 13.135 0.008 3 18.756 18.756 0.000 4 2.366 2.366 0.000 5 5.664 5.665 0.018 6 12.075 12.075 0.000 7 6.854 6.854 0.000 8 16.408 16.409 0.006 9 34.978 34.979 0.003 10 34.424 34.425 0.003 11 1.000 -1.000 0.000 12 2.394 -2.394 0.000 13 5.103 -5.103 0.000

图11 葵花肋环混合型索穹顶
Fig.11 Sunflower and rib ring mixed patterned cable dome
荷载:自重按实际考虑;采用刚性屋面板,屋面板附加恒载取为0.7 kN/m2;活载取为0.5 kN/m2,分布包括全跨和半跨两种情况;升温及降温分别考虑为±30°;基本风压w0=0.35 kN/m2,体型系数μs=-1.0,风振系数βz=1.6,地面粗糙度B类,高度系数μz=1.39(高度取为30 m);荷载组合考虑正常使用极限状态组合和承载力极限状态组合,极限承载力组合考虑1.1的重要性系数。工况组合如表3所示。
材料:拉索采用高钒索,弹性模量1.6×1011 N/m2,钢丝强度1670 MPa;撑杆和刚性拉环采用Q345B圆钢管。
表3 工况组合
Table 3 Load case combinations

组合 恒载 活载(全跨、半跨) 风 温度(升温、降温)1 1.0 1.0 2 1.0 1.0 3 1.0 1.0 4 1.2 1.4 5 1.35 0.7×1.4 6 1.2 1.4 8 1.0 1.4
结构预应力度的确定:保证结构在正常使用极限状态下挠跨比小于1/250;在承载力极限状态下,为避免拉索松弛,最小应力不小于30 MPa。
拉索截面:均依据在承载力极限状态下拉索最大内力小于等于0.4倍破断力的要求选取,以确保结构的承载力。
计算表明(表4),结构在1.0恒载+1.0活载作用下,最大位移251 mm,挠跨比1/319,且变形均匀,表明结构刚度分布合理;在1.0恒载+ 1.0半跨活载作用下,最大位移256 mm,挠跨比1/313。单位投影面积用钢量仅13.0 kg/m2。实际工程采用的葵花肋环混合型方案在1.0恒载+1.0活载作用下,最大位移245 mm,挠跨比1/327;在1.0恒载+1.0半跨活载作用下,最大位移271 mm,挠跨比1/295。单位投影面积用钢量14.3 kg/m2。由此可见,采用预载回弹法求得的多自应力模态结构的整体可行预应力具有较强的实用性,结构具有较好的受力性能,能够用于实际工程。
表4 结构静力性能对比
Table 4 Structural static behavior comparison

类型 位移/mm (挠跨比) 单位投影面积用钢量/(kg/m2)全跨 半跨凯威特型 251(1/319) 256(1/313) 13.0葵花肋环混合型 245(1/327) 271(1/295) 14.3
本文提出了一种索穹顶结构初始预应力分布确定的新方法—预载回弹法。施加预设荷载,通过变弹性模量迭代计算,提取出有利于抵抗预设荷载的预应力分布,通过对该方法的研究,得到以下结论:
(1) 预载回弹法通过施加对称荷载,即可自动实现单元的分组,便于应用整体可行预应力概念。
(2) 两阶段变弹性模量迭代可保证结果的精度,获得纯粹的预应力分布。第一阶段大弹性模量迭代可确保结构处于小变形状态,获得给定几何条件下结构预应力分布;第二阶段小弹性模量迭代可排除线性刚度矩阵的影响,验证第一阶段迭代结果,并可进一步对形态行进调整。
(3) 针对多自应力模态结构,预载回弹法可直接获得对应于预载的优化预应力分布。
(4) 算例表明,预载回弹法具有高的精度、较快的收敛速度,其求得的整体可行预应力具有较好的静力性能,直接适用于实际工程应用。
[1] Geiger D H,Stefaniuk A,Chen D.The design and construction of two cable domes for the Korea Olympics[C]// Proceedings of the IASS Symposium: Shells,Membranes and Space Frame.Osaka,1986,2: 265―272.
[2] Levy M P.The Georgia dome and beyond achieving lightweight-long span structures [C]// Proceedings of the IASS-ASCE International Symposium: Spatial,Lattice and Tension Structures.New York,1994: 560―562.
[3] Pellegrino S,Calladine C R.Matrix analysis of statically and kinematically indaterminate frameworks [J].International Journal of Solids and Structures,1986,22(4): 409―428.
[4] Pellegrino S.Structural computations with the singular value decomposition of the equilibrium matrix [J].International Journal of Solids and Structures,1993,30(21): 3025―3035.
[5] 董石麟,袁行飞.肋环型索穹顶初始预应力分布的快速计算法[J].空间结构,2003,9(2): 3―8,19.Dong Shilin,Yuan Xingfei.A quick calculation method for initial prestress distribution of Geiger domes [J].Spatial Structures,2003,9(2): 3―8,19.(in Chinese)
[6] 董石麟,袁行飞.葵花型索穹顶初始预应力分布的简捷算法[J].建筑结构学报,2004,25(6): 9―14.Dong Shilin,Yuan Xingfei.A simplified calculation method for initial prestress distribution of sunflower-patterned cable domes [J].Journal of Building Structures,2004,25(6): 9―14.(in Chinese)
[7] 董石麟,王振华,袁行飞.Levy型索穹顶考虑自重的初始预应力简捷计算法[J].工程力学,2009,26(4):1―6.Dong Shilin,Wang Zhenhua,Yuan Xingfei.A simplified calculation method for initial prestress of Levy cable domes with the consideration of self-weight [J].Engineering Mechanics,2009,26(4): 1―6.(in Chinese)
[8] 袁行飞,董石麟.索穹顶结构整体可行预应力概念及其应用[J].土木工程学报,2001,34(2): 33―37,61.Yuan Xingfei,Dong Shilin.Application of integrity feasible prestressing to tensegrity cable domes [J].China Civil Engineering Journal,2001,34(2): 33―37,61.(inChinese)
[9] 袁行飞,董石麟.索穹顶结构的新形式及其初始预应力确定[J].工程力学,2005,22(2): 22―26.Yuan Xingfei,Dong Shilin.New forms and initial prestress calculation of cable domes [J].Engineering Mechanics,2005,22(2): 22―26.(in Chinese)
[10] 曾文平,王元清,张勇,等.索穹顶结构的预应力设计方法[J].工业建筑,2002,32(9): 24―26.Zeng Wenping,Wang Yuanqing,Zhang Yong,et al.The method of prestress design for cable dome [J].Industrial Construction,2002,32(9): 24―26.(in Chinese)
[11] 阚远,叶继红.动力松弛法在索穹顶结构形状确定中的应用[J].工程力学,2007,24(9): 50―55.Kan Yuan,Ye Jihong.Form finding of cable domes by modified dynamic relaxation [J].Engineering Mechanics,2007,24(9): 50―55.(in Chinese)
[12] Schek H J.The force density method for form finding and computation of general networks [J].Computer Methods in Applied Mechanics and Engineering,1974,3(1): 115―134.
[13] Barnes M R.Form finding and analysis of tension structures by dynamic relaxation [J].International Journal of Space Structures,1999,14(2): 89―104.
[14] 袁行飞,董石麟.索穹顶结构几何稳定性分析[J].空间结构,1999,5(1): 3―9.Yuan Xingfei,Dong Shilin.Analysis of geometric stability for cable domes [J].Spatial Structures,1999,5(1): 3―9.(in Chinese)
[15] 陈联盟,袁行飞,董石麟.索杆张力结构自应力模态分析及预应力优化[J].土木工程学报,2006,39(2):11―15.Chen Lianmeng,Yuan Xingfei,Dong Shilin.Selfstress mode analysis and optimal prestress design of cable-strut tension structures [J].China Civil Engineering Journal,2006,39(2): 11―15.(in Chinese)
A NEW METHOD OF DETERMINING THE INITIAL PRESTRESS DISTRIBUTION OF CABLE DOMES—THE PRELOAD AND REBOUND METHOD
董石麟(1932―),男,浙江杭州人,教授,博导,中国工程院院士,长期从事空间结构的科研、教学与工程实践工作.