的定义。该文给出的数值试验表明：采用m次单元，对于解答光滑的问题，SPR法与EEP法均可有效用于自适应求解，其位移可按最大模获得m+1的自适应收敛率；对于奇异因子为α(＜1)的奇异问题，SPR法失效，而基于EEP法的自适应求解，其位移按最大模可获得m+α 的自适应收敛率，远高于α的常规有限元收敛率。摘 要：基于EEP(单元能量投影)超收敛计算的自适应有限元法，已对一系列问题取得成功，但其自适应特性尚缺乏相关研究。该文以二阶常微分方程为模型问题，同时考察基于EEP和SPR(超收敛分片恢复)超收敛解的自适应分析方法，与有限元最优网格进行了比较分析，进而提出反映自适应有限元收敛特性的估计式，并给出了自适应收敛率的定义。该文给出的数值试验表明：采用m次单元，对于解答光滑的问题，SPR法与EEP法均可有效用于自适应求解，其位移可按最大模获得m+1的自适应收敛率；对于奇异因子为α(＜1)的奇异问题，SPR法失效，而基于EEP法的自适应求解，其位移按最大模可获得m+α 的自适应收敛率，远高于α的常规有限元收敛率。
有限元法(finite element method，简称FEM)是一种通用的数值计算方法，在工程领域应用广泛。作为一种近似的数值方法，其可靠性和计算效率的研究一直伴随着整个发展过程。自20世纪70年代以来，基于常规有限元法的后处理技术，以误差估计和自适应网格细化技术为核心，自适应有限元法(adaptive finite element method，AFEM)迅速地得到发展和应用，并成为FEM相关研究的热点问题[1]。
AFEM是现代有限元计算的新型求解方法，用户只需输入解答精度要求满足的误差限，算法即可自动生成计算网格，得到满足误差限的解答。AFEM的标准求解过程为“求解→估计→标记→细化”[2―3]，通常可基于精度更高的有限元超收敛解进行后验误差估计，对不满足误差限的网格进行标记和细化。国内外多位学者已在有限元自适应求解方面取得重要成果，并多集中在有限元超收敛解的后处理过程。Zienkiewicz和Zhu[4―7]提出了超收敛分片恢复方法(super-convergent patch recovery，SPR)，基于具有应力超收敛性的Gauss点，在若干单元构成的单元拼片上进行应力恢复，获得局部平滑应力场，并以能量模度量的应力场间差值表示离散误 差；Wiberg延续SPR法的思想，利用高次多项式，对具有位移超收敛性的Lobatto点进行拟合，得到分片的位移超收敛解[8―9]。凭借其形式简洁、计算经济的特点，基于SPR法的AFEM得到了充分发展与应用。此后，多位研究者又逐步发展出多种适用于不同数值理论及问题的后验误差估计方法[10―14]，但普遍由于复杂高、针对性强而缺乏推广的可行性。在国内，叶康生等[15―16]也提出了P型有限元超收敛算法，并将其应用于平面曲梁、结构自由振动等问题的计算中。
近些年，袁驷等[17―18]基于数学理论和力学概念，提出了基于单元能量投影(EEP)的新型有限元超收敛后处理算法，建立了完整的自适应求解策略。该算法基于EEP位移超收敛解估计误差，指导网格细分，可给出按最大模度量的、逐点满足给定误差限的解答，在多类问题中取得一系列成功[19―24]。
本文以二阶常微分方程为例，首先对有限元最优网格进行了分析，进而提出自适应有限元的收敛率指标
，给出了其定义，并分别对基于EEP和SPR超收敛解的AFEM的特性进行了数值试验，验证了自适应收敛率的合理性，展现了基于EEP超收敛解的AFEM求解奇异问题的独特性质和优势。
以一维问题为例，考虑如下两点边值问题：
其中，p＞0，r，q≥0，L为上式定义的线性微分算子，其伴随算子L*为：
定义双线性型和线性型：
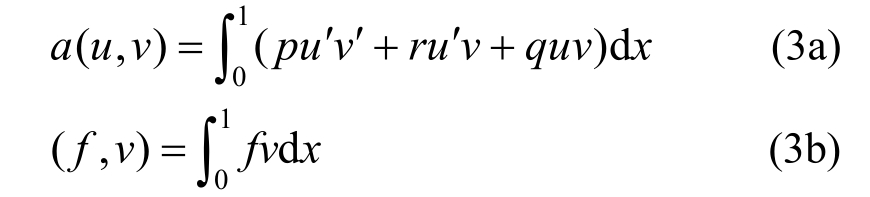
当r=0时，该问题为自伴随的，可有相应的能量泛函：
当r≠0时，该问题为非自伴随的，无相应的能量泛函形式。
记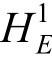
为满足本质(位移)边界条件、直到一阶导数均平方可积的函数空间，式(1)广义解归结为求u∈
使得：
对于自伴随问题，满足式(5)即满足I(u)在
上的极小化条件。
对求解域进行常规有限元离散，考虑两端结点坐标为x1、x2的标准单元e，其长度记为h。记
为有限元试探函数，相应的vh为有限元检验函数，标准单元上的试探函数和检验函数采用相同的形函数插值得到。在满足本质(位移)边界条件和单元间连续条件下，将所有单元试探函数集成，得到有限元试探解空间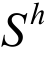
∈
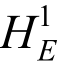。则式(1)的有限元解归结为求解uh ∈Sh，使得：
熟知，由式(6)得到的有限元解的误差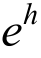
=u-
满足投影定理，即：
假定投影定理式(7)在单个单元e上仍近似成立，即：
经研究推导，得到单元上任意一点xa 
的EEP超收敛位移公式如下[17―18]：
式中：上标*表示EEP超收敛解；下标a表示xa点的值；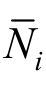
为线性形函数。类似地有EEP超收敛导数公式，这里不单独给出。
以上是EEP位移的简约格式，数学上已经证明，对于m(＞1)次单元，式(9)的EEP超收敛解u*比有限元解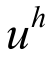
具有至少高1阶的超收敛性。此外，在计算简便的同时，EEP超收敛解还具有结点导数连续、自由端点精确等诸多优势[17]。
SPR法的基本思想是，以某结点或某单元为中心进行单元拼片，以有限元应力解或位移解具备超收敛性的点为采样点，采用高次多项式进行最小二乘拟合。
对单的个单元片e。考虑与其有公共结点的单元共同组成的单元片。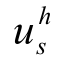
表示单元片上的超收敛点的解，np表示该单元片中具备此类性质点的个数。假设超收敛解为单元拼片上的高次多项式，即：
式中：P(x)为多项式的基；a为待定参数。
以式(10)对单元片上的超收敛点进行最小二乘拟合，即极小化下式：
极小化求出a后，便得到式(10)中的恢复解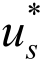
。对于高于一次的单元，以L2模度量，该
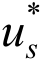具备一定的超收敛性[8]。后面可以看到，若以最大模进行度量，则对于常规问题亦有超收敛性，但对于奇异问题SPR法失效。
AFEM是一种能自动调整网格以使解答满足用户指定的误差限的数值分析方法，目前应用最为广泛的是h-加密，其策略基本上遵循“求解→估计→标记→细化”。
Babuška及Zienkiewicz等基于能量模度量的误差，提出了相应的后验误差估计及自适应策略[4]，其核心思想是通过能量模误差，估计下一步划分网格的疏密和尺寸大小。
袁驷等基于最大模度量的误差，提出了不同的自适应网格细分策略，目标是在精确解未知的情况下，事先给定误差限tol，寻求优化的有限元网格π，使得该网格上的有限元解答
按最大模度量满足误差限，即逐单元满足：
由于精确解u未知，使用比有限元解精度更高的超收敛解u*代替u进行误差估计，即要求有限元解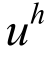
满足：
对于不满足误差限的单元，采用均差法[25]确定插入结点位置，将该单元一分为二。大量的数值试验表明，该策略自然合理、稳定通用，在本文数值试验中，将采用这一过程进行自适应网格的细分。
将自适应过程网格划分与最优网格进行对比，可对自适应方法的优劣特性进行分析。
最优网格可以抽象地表达为：在单元次数和个数给定的情况下，使有限元解的误差
=u-
最小的网格。度量误差可以采用不同的范数和方式，构成不同的优化标准。本文分析比较以下三类网格：
1) 整体能量模误差最小。对于一维自伴随问题，总势能最小等价于整体能量模误差最小。Turcke等[26]基于最小势能原理，寻求使得能量模误差最小的网格划分。此类网格是理想上的最优网格，特别是对于自伴随问题，其最优标准是天然标准。但此类网格一般只具有理论上的意义，因为要获得该网格需要同时求解所有结点的坐标位置及其结点位移，从而导致一个体系庞大而复杂的非线性系统。尽管如此，本文以下仍将此类网格称为最优网格。
2) 各单元能量模误差相等。Szabó和Babuška等[27]指出，在AFEM中，网格划分若能使各单元能量模误差近似相等，则以整体能量模衡量该网格划分将是渐近最优的。换言之，随着网格按最优网格标准自适应加密，各个单元的能量模误差将趋于相等。因此，此类优化标准提供了上述最优网格的可能实施路径。但对于非自伴随问题，由于没有直接的能量模定义，最优网格和此类网格都需要改用其他相近的范数。再者，在实际应用中，能量模也不如最大模直观。
3) 各单元最大模误差相等。若能按最大模计算误差，则此类网格体现的是一种非常实用且直观的优化标准，属于数学中的一致收敛。由于EEP超收敛解可用来估计任意一点的误差，使最大模误差估计成为可能，因此基于EEP的自适应分析便以此类优化网格为其优化目标。
传统上，对于足够光滑的问题，有限元解误差
的估计用单元长度h表示为：
式中：
表示某类范数，通常采用能量范数(能量模)或无穷范数(最大模)，β为收敛阶，同时也是均匀网格的收敛率。对于非均匀网格，各单元长度h不同，宜将h换为总自由度数N，则误差估计可表示为：
式中：k为与单元次数有关的常数。在对数坐标图中，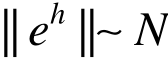
图是一条直线，β为其斜率，称为收敛率。若解答足够光滑，对于m次单元，采用能量模(或最大模)，有限元解的收敛率为β=m(或β=m+1)。可见，高次元具有更高的收敛率。
那么，自适应有限元有没有收敛率？如何定义它的收敛率？
为给自适应有限元收敛率找到合适定义，做如下分析和考虑：
1) 自适应有限元的网格往往是非均匀、非规则加密的，因而在对数坐标图中，自适应过程中的N和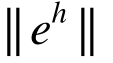
间关系不再是线性的，式(15)并不能直接套用；
2) 常规有限元的收敛率是给定N后去考察
的大小，而自适应有限元是给定
后去求取尽量小的N，即这是常规有限元的反问题；
3) 由于有多种自适应迭代路径达到最终网格，自适应有限元收敛率应该独立于自适应过程中的迭代步骤和路径，因此收敛率的定义应仅涉及自适应迭代结束后的数据和结果。
鉴于以上考虑，记
为自适应结束后有限元解的最大模误差，又记不同误差限tol(i) ，i = 1,2,3,…对应的自适应结果为
和N(i)。本文研究发现，基于EEP法的自适应有限元有如下的收敛规律估计式：
式中：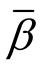
为本文定义的自适应收敛率。对比式(15)和式(16)，公式相仿，但意义并不相同。如果自适应过程就是简单地将所有单元二等分细化，则式(16)等同于式(15)。但是，由于AFEM的网格得到自适应过程的优化，一般有
≥β ，即自适应收敛率往往优于常规有限元收敛率。
本文的数值试验显示，对于足够光滑的问题，
=β=m +1；而对于奇异因子为α(＜1)的奇异问题，基于EEP法的自适应有限元收敛率
=m+α，远高于有限元收敛率β=α。这说明，即使是奇异问题，采用高次元仍具有更高的收敛率。一旦确定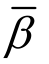
，经过一次简单试算后，式(16)还可以用来估计给定误差限下AFEM最终网格近似的自由度数(N)。
本节选择4个有代表性的问题给出数值试验结果，即自伴随常系数问题、自伴随奇异问题、非自伴随奇异问题及自伴随变系数问题。
设p=q=f=1，r=0，边界条件为u(0)=0，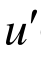
(1)= 0。微分方程及边界条件如下：
4.1.1 最优网格
将求解域划分为Ne个单元，则该问题自由度数为N=m×Ne，将结点坐标及相应结点位移均单独视为变量，求最优网格。
表1给出了具体的网格，图1给出了线性元在均匀网格和最优网格上的收敛结果，可见对于相同的自由度数，最优网格使误差变得更小。
表1 最优网格
Table 1 Optimum mesh
自由度N 结点坐标单元次数m=1 1 0，1 2 0，0.46115，1 3 0，0.29743，0.63473，1 4 0，0.21929，0.46152， 0.72438，1 5 0，0.17361，0.36196，0.56453，0.77887，1 6 0，0.14367，0.29755，0.46159，0.63489，0.81543，1 7 0，0.12253，0.25255，0.39009，0.53483，0.68586，0.84165，1单元次数m=2 2 0，1 4 0，0.39967，1 6 0，0.25233，0.55351，1 8 0，0.18451，0.39196，0.63773，1
4.1.2 自适应网格
计算中基于EEP及SPR超收敛解进行误差估计，采用均差法进行自适应网格细分。对于线性元和二次元，误差限分别设定为
= 2× 1 0-3和
=1× 10-4，对应上小节中最优网格的误差。
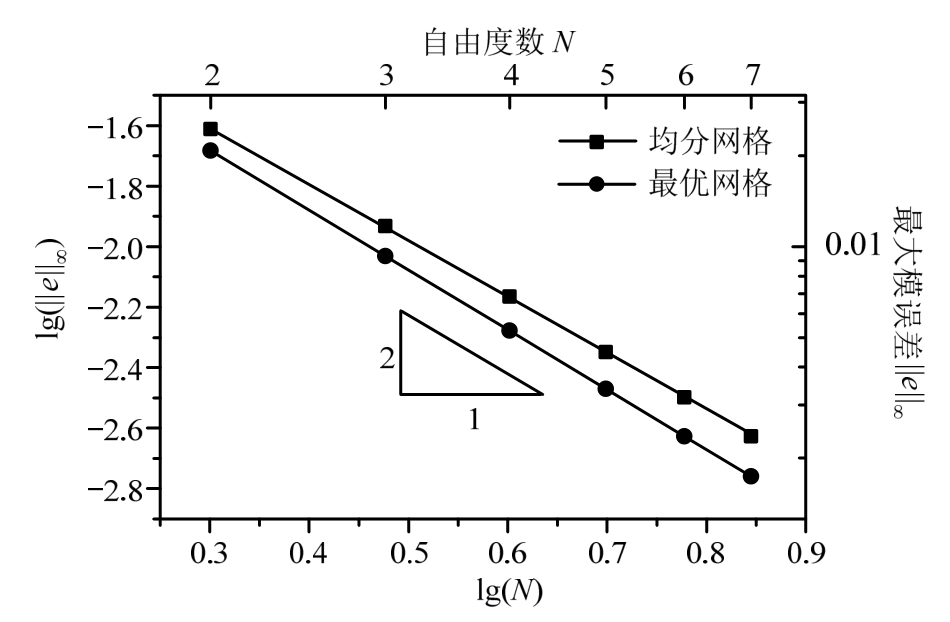
图1 最优网格与均分网格误差 (m=1)
Fig.1 Errors of optimum mesh and uniform mesh (m=1)
需要注意的是，对于SPR法，由于拼片需要多个单元(≥2)，因此其自适应分析无法从单个单元的网格开始。此处从2个均分单元开始自适应过程。
从表2可知，对该问题，两种自适应方法获得的最终网格差别较小。图2给出了最优网格和两种自适应网格上的误差比较。可见，对于最优网格，按最大模度量，各单元误差接近，精度冗余较小。亦可看到，在冗余度方面，EEP法又优于SPR法，即单元误差更为平均。
表2 自适应最终网格比较
Table 2 Comparison of AFEM final meshes
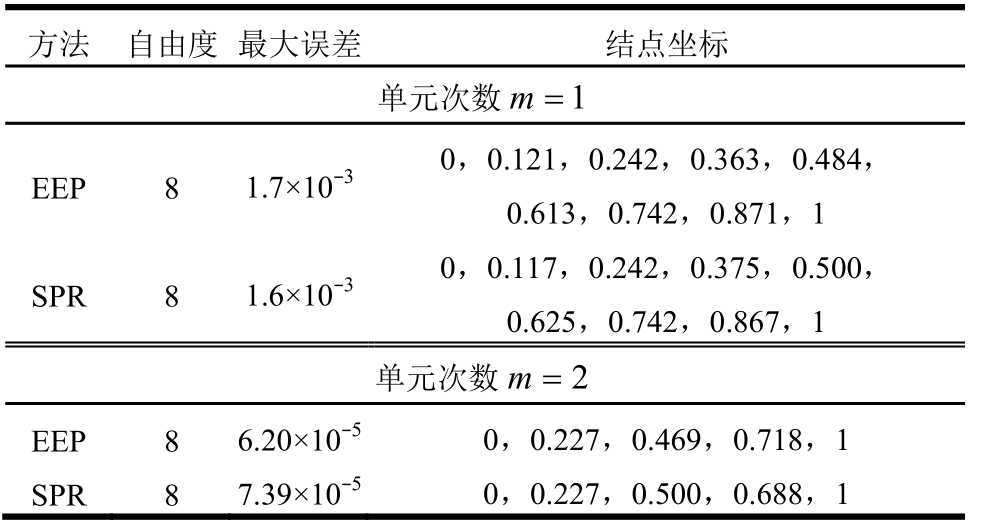
方法 自由度 最大误差 结点坐标单元次数m=1 EEP 8 1.7×10-3 0，0.121，0.242，0.363，0.484，0.613，0.742，0.871，1 SPR 8 1.6×10-3 0，0.117，0.242，0.375，0.500，0.625，0.742，0.867，1单元次数m=2 EEP 8 6.20×10-5 0，0.227，0.469，0.718，1 SPR 8 7.39×10-5 0，0.227，0.500，0.688，1
设p=q=1，r=0，u=xα-x，0.5＜α＜1，将u代入原方程定出f。微分方程及边界条件如下：
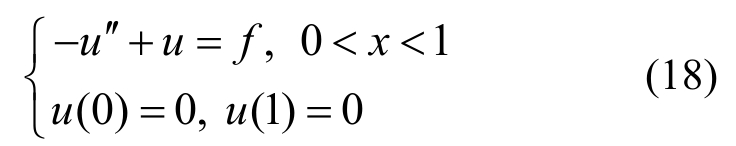
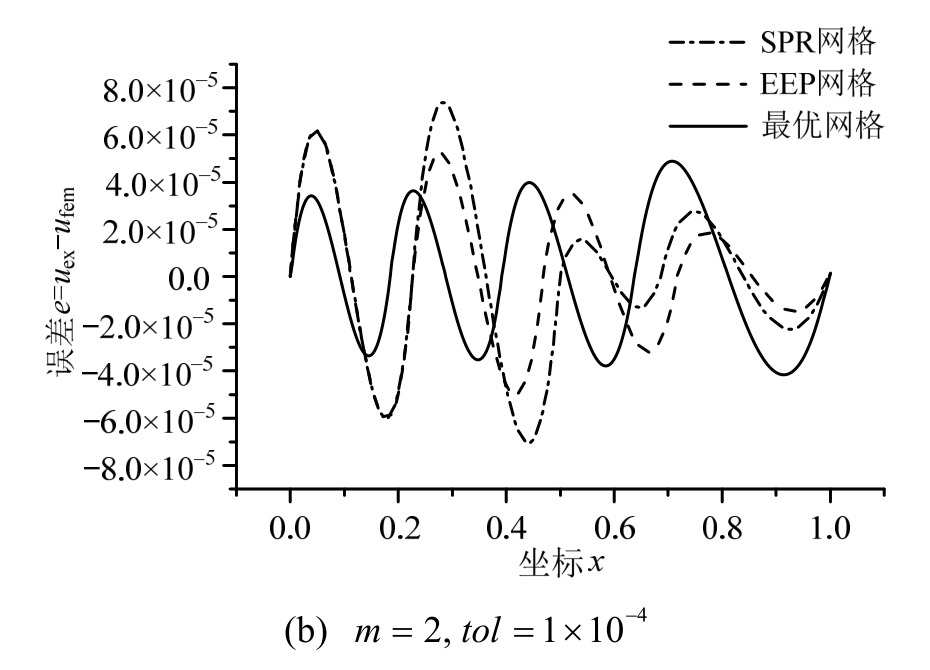
图2 各网格误差分布
Fig.2 Error distributions of corresponding meshes
4.2.1 最优网格
同4.1.1小节，求最优网格。对于本问题，精确导数u′在零点奇异，因而具有不同的性质。取奇异因子α=0.8计算。表3给出了最优网格的结点坐标。
表3 最优网格 (m= 1,α = 0.8)
Table 3 Optimum mesh (m= 1,α = 0.8)
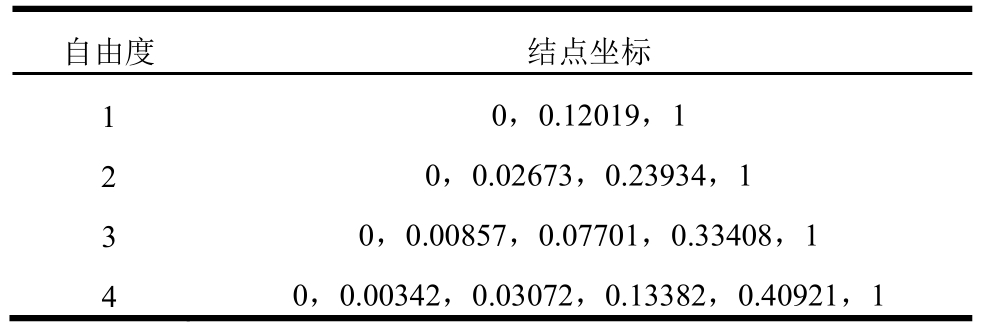
自由度 结点坐标1 0，0.12019，1 2 0，0.02673，0.23934，1 3 0，0.00857，0.07701，0.33408，1 4 0，0.00342，0.03072，0.13382，0.40921，1
图3(a)给出了网格加密后各单元能量模误差的分布。对于奇异问题，从数值试验角度进一步验证了Babuska等对最优网格的理论分析，即随网格加密，各单元误差渐近相等。图3(b)给出了网格加密后各单元误差的分布。可知，无论以能量模或最大模衡量，趋势是一致的；这也进一步说明，若自适应方法以各单元最大模相等为目标，则以能量模度量其网格划分亦是最优的。
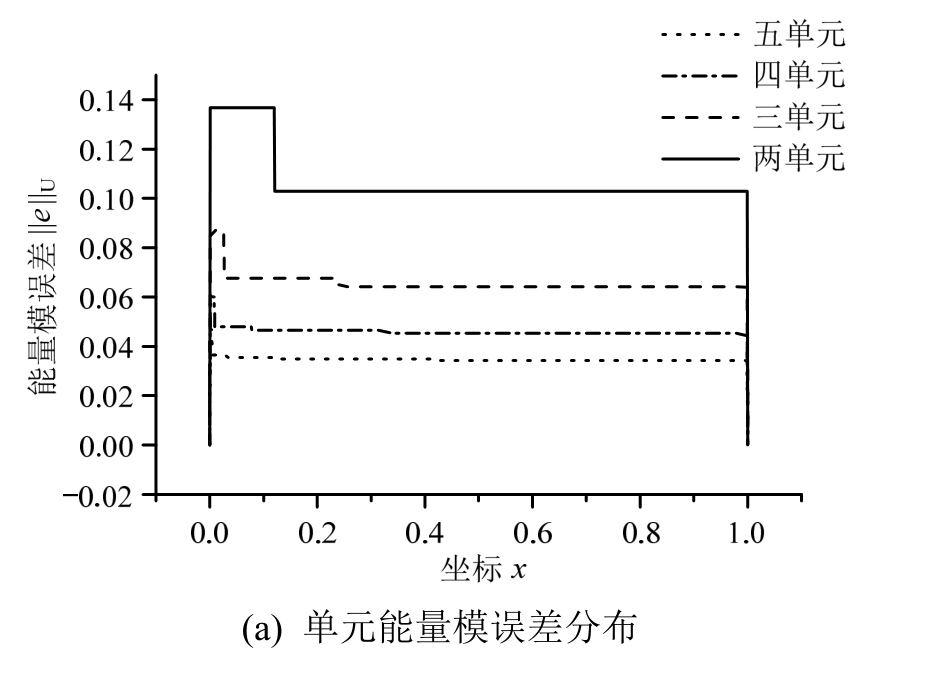
图3 最优网格误差及单元能量模误差分布(m= 1,α = 0.8)
Fig.3 Error distributions and element energy error distributions of optimum mesh (m= 1,α = 0.8)
4.2.2 自适应网格
有限元自适应的成功要求找到精度更高的解，以便进行误差估计，从理论上，该类解应具有更高的收敛阶。对于常系数等问题，相对于常规有限元解，EEP法和SPR法均可获得至少高1阶的位移超收敛解，用其指导网格细分的有效性已在4.2.1得到验证。
对于自伴随的奇异问题，有限元解、EEP解、SPR解的位移收敛阶如表4所示。可以看出，对于奇异问题，SPR法并不具备较高的收敛阶(仅精度略高)。图4给出了两种方法自适应最终网格上的误差分布，EEP法十分成功地控制了误差，而SPR法在自适应过程中实际上已失效，自适应过程停机时并未满足误差限要求。
表4 收敛阶统计
Table 4 Order of convergence
有限元 EEP法 SPR法常系数p单元端点位移 mod(,2)m+ +α m单元内点位移α min(2α,2m)+α变系数p单元端点位移m+α单元内点位移α 1+αα
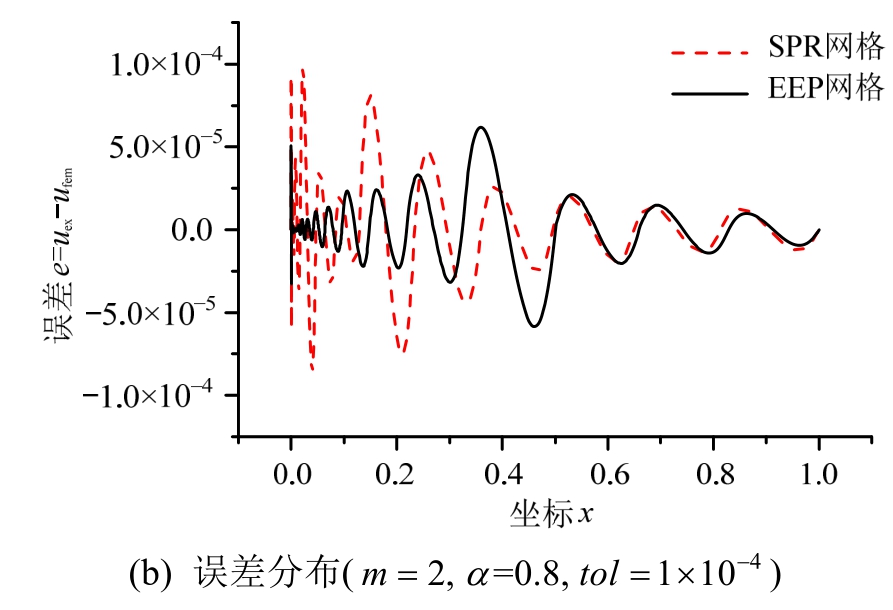
图4 SPR及EEP自适应最终网格误差分布
Fig.4 Error distributions of final meshes guided by SPR and EEP
图5给出了基于EEP法和SPR法自适应过程中误差随自由度的变化。可见，对于奇异问题，基于SPR法的误差估计失效，而基于EEP法的误差估计与真实误差吻合极好。
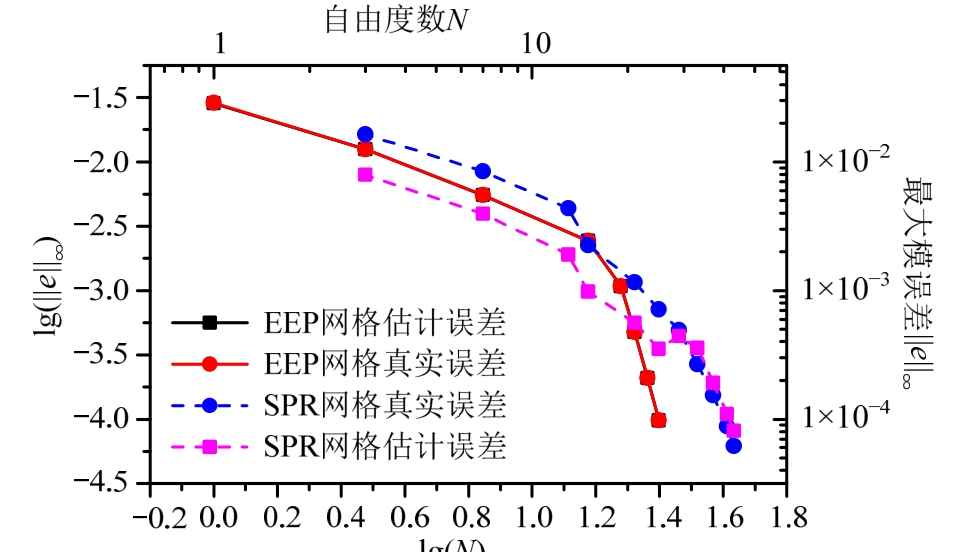
图5 自适应过程误差对比(m=2,α=0.8,
= 1× 10-4)
Fig.5 Comparison of errors between adaptive procedures(m=2,α=0.8,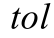
=1× 10-4)
4.2.3 自适应收敛率
对于本奇异问题，均匀网格划分的有限元法收敛率为β=α，与单元次数无关，亦即高次元也不能提高收敛率。为了检验自适应有限元估计式(16)，并确定奇异问题的自适应收敛率，取4个不同的误差限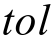
= 10-i(i = 3,4,5,6)。做如下两组试验：
1) 试验1：分4次做自适应计算，每次初始网格均为一个单元，其结果示于图6(a)；
2) 试验2：从第2次(i=4)开始，每次都采用前一次误差限的自适应网格作为初始网格来进行自适应迭代，其结果示于图6(b)。
可以看到，虽然自适应迭代的路径不同，但自适应完成时二者结果基本一致。图6(c)给出了3次元的结果。可见，对于奇异问题，尽管有限元的收敛率只有β=α，但是自适应收敛率却可以高达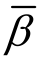
=m+α，符合式(16)显示的规律，充分体现了自适应有限元的特性和优势。
图6 EEP自适应过程误差变化
Fig.6 Error plot of adaptive procedure based on EEP
本例与4.2小节的问题唯一不同的是补充取r= 1，使问题成为非自伴随问题。解答不变，荷载项仍由方程导出。取α=0.7计算。结果示于图7～图9，可见与自伴随奇异问题的表现和结果基本一致，SPR法由于无法得到有效的超收敛解而自适应失效。
无限长薄膜大挠度是一类经典的非线性问题。问题描述如下：
其中：R =
本例无意对非线性求解进行讨论。取f=0.95，因其精确解有解析表达式，将其代入R作为变系数的考题，验证该自适应收敛特性。
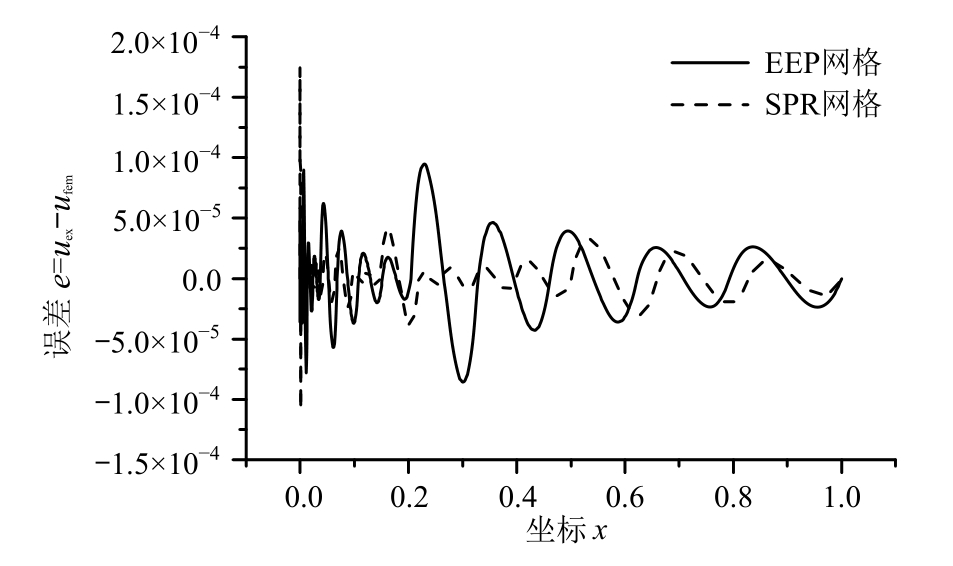
图7 自适应最终网格误差分布(
-4= × )
Fig.7 Error distributions of AFEM final meshes(m=2,=0.7,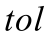
110 α m=2,=0.7,
110 α-4= × )
图8 自适应过程误差对比(m=2,α=0.7,
= 1× 1 0-4)
Fig.8 Comparison of errors between adaptive procedures(m=2,α=0.7,
=1× 1 0-4)
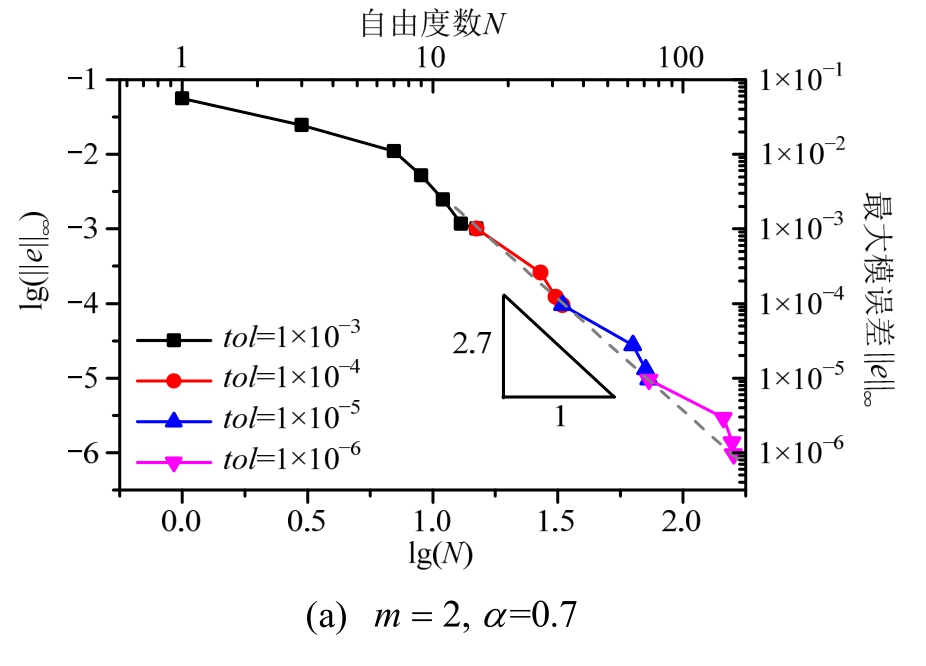
图9 EEP自适应过程误差变化
Fig.9 Error plot of adaptive procedure based on EEP
计算结果示于图10。可见，本问题虽无奇异性，但优化后的网格是极不均匀的，自适应迭代的收敛曲线呈现出与奇异问题相似的特性：“前期平缓，后期陡降”。但由于本问题无奇异性，最终的自适应收敛率为规则的
=m + 1。
图10 EEP自适应过程误差变化
Fig.10 Error plot of adaptive procedure based on EEP
此外，采用SPR法对该问题进行自适应分析，发现其获得同样的自适应收敛率，即
=m +1，再次表明问题的奇异性是SPR失效的本质原因。
图11 SPR自适应过程误差变化(m=2)
Fig.11 Error plot of adaptive procedure based on SPR (m=2)
本文对有限元最优网格划分及其性质进行了分析及数值验证，比较了基于EEP法和SPR法的自适应有限元分析的有效性，提出了反映自适应有限元收敛规律的估计式(16)，并给出了自适应收敛率
的定义，得出的主要结论有：
(1) 以能量泛函极小化为目标，在给定单元次数、单元数目情况下进行最优网格划分，随着网格加密，无论以能量模或是最大模进行度量，各单元误差均趋于相等。由此说明，有限元自适应过程以各单元误差尽可能均匀地削减是合理的。
(2) 文中提出了自适应有限元收敛规律的估计式(16)，并给出了其中自适应收敛率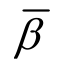
的定义，经理论分析和大量数值试验检验是正确合理的，且通用于光滑和奇异问题、自伴随和非自伴随问题。
(3) 对于光滑问题，SPR法和EEP法均可有效用于自适应分析，并获得m+1的自适应收敛率；但EEP法精度冗余更小，在停机时误差更接近误差限，各单元误差分布也更为均匀。
(4) 对于奇异问题，SPR法恢复解失去超收敛性，无法有效地用于误差估计；而EEP法超收敛解性态良好，可获得m+α的自适应收敛率，远高于α的常规有限元收敛率。
[1] Nochetto R H,Veeser A.Primer of Adaptive Finite Element Methods [M]// Multiscale and Adaptivity:Modeling,Numerics and Applications.Berlin Heidelberg:Springer,2011: 125―225.
[2] Cascon J M,Kreuzer C,Nochetto R H,et al.Quasi-optimal convergence rate for an adaptive finite element method [J].SIAM Journal on Numerical Analysis,2008,46(5): 2524―2550.
[3] Chen L,Zhang C S.AFEM@ Matlab: A Matlab package of adaptive finite element methods [R].Technique Report,Department of Mathematics,University of Maryland at College Park,2006.
[4] Zienkiewicz O C,Zhu J Z.A simple error estimator and adaptive procedure for practical engineerng analysis [J].International Journal For Numerical Methods in Engineering,1987,24(2): 337―357.
[5] Zienkiewicz O C,Zhu J Z.The superconvergent patch recovery and a posteriori error estimates.Part 1: The recovery technique [J].International Journal for Numerical Methods in Engineering,1992,33(7): 1331―1364.
[6] Zienkiewicz O C,Zhu J Z.The superconvergent patch recovery and a posteriori error estimates.Part 2: Error estimates and adaptivity [J].International Journal for Numerical Methods in Engineering,1992,33(7): 1365―1382.
[7] Zienkiewicz O C,Zhu J Z.The superconvergent patch recovery (SPR) and adaptive finite element refinement[J].Computer Methods in Applied Mechanics and Engineering,1992,101(1/2/3): 207―224.
[8] Wiberg N E,Li X D.Superconvergent patch recovery of finite-element solution and a posteriori L2 norm error estimate [J].International Journal for Numerical Methods in Biomedical Engineering,1994,10(4): 313―320.
[9] Wiberg N E,Abdulwahab F,Li X D.Error estimation and adaptive procedures based on superconvergent patch recovery (SPR) techniques [J].Archives of Computational Methods in Engineering,1997,4(3): 203―242.
[10] Creusé E,Nicaise S.A posteriori error estimator based on gradient recovery by averaging for discontinuous Galerkin methods [J].Journal of Computational and Applied Mathematics,2010,234(10): 2903―2915.
[11] Cangiani A,Georgoulis E H,Pryer T,et al.A posteriori error estimates for the virtual element method [J].Numerische Mathematik,2017,137(4): 857―893.
[12] Ainsworth M.Fully computable robust a posteriori error bounds for singularly perturbed reaction-diffusion problems [J].Numerische Mathematik,2011,119(2):219―243.
[13] Baron V,Coudière Y,Sochala P.Adaptive time discretization and linearization based on a posteriori estimates for the richards equation [J].Applied Numerical Mathematics,2017,112(2): 104―125.
[14] Čermák M,Hecht F,Tang Z,et al.Adaptive inexact iterative algorithms based on polynomial-degree-robust a posteriori estimates for the Stokes problem [J].Numerische Mathematik,2017,47(3): 1―39.
[15] 叶康生,曾强.结构自由振动问题有限元新型超收敛算法研究[J].工程力学,2017,34(1): 45―50.Ye Kangsheng,Zeng Qiang.A new superconvergent recovery method for FE analysis on structural free vibration problems [J].Engineering Mechanics,2017,34(1): 45―50.(in Chinese)
[16] 叶康生,姚葛亮.平面曲梁有限元静力分析的p型超收敛算法[J].工程力学,2017,34(11): 26―33.Ye Kang-sheng,Yao Ge-liang,A p-type superconvergent recovery method for FE static analysis of planar curved beams [J].Engineering Mechanics,2017,34(11): 26―33.(in Chinese)
[17] 袁驷,王枚.一维有限元后处理超收敛解答计算的EEP法[J].工程力学,2004,21(2): 1―9.Yuan Si,Wang Mei.An element-energy-projection method for post-computation of super-convergent solutions in one-dimensional FEM [J].Engineering Mechanics,2004,21(2): 1―9.(in Chinese)
[18] 袁驷,林永静.二阶非自伴两点边值问题Galerkin有限元后处理超收敛解答计算的EEP法[J].计算力学学报,2007,24(2): 142―147.Yuan Si,Lin Yongjing.An EEP method for post-computation of super-convergent solutions in one-dimensional Galerkin FEM for second order non-self-adjoint boundary-value problem [J].Chinese Journal of Computational Mechanics,2007,24(2): 142―147.(in Chinese)
[19] 袁驷,和雪峰.基于 EEP 法的一维有限元自适应求解[J].应用数学和力学,2006,27(11): 1280―1291.Yuan Si,He Xue-feng.Self-adaptive strategy for one-dimensional finite element method based on EEP method [J].Applied Mathematics and Mechanics,2006,27(11): 1280―1291.(in Chinese)
[20] Yuan S,Wang Y,Ye K.An adaptive FEM for buckling analysis of nonuniform Bernoulli-Euler members via the element energy projection technique [J].Mathematical Problems in Engineering,2013(2013): 544―554.
[21] Yuan S,Du Y,Xing Q,et al.Self-adaptive one-dimensional nonlinear finite element method based on element energy projection method [J].Applied Mathematics and Mechanics,2014,35(10): 1223―1232.
[22] 袁驷,刘泽洲,邢沁妍.二维变分不等式问题的自适应有限元分析[J].工程力学,2016,33(1): 11―17.Yuan Si,Liu Ze-zhou,Xing Qin-yan.Self-adaptive FEM analysis for 2D variational inequality problems [J].Engineering Mechanics,2016,33(1): 11―17.(in Chinese)
[23] 邢沁妍,杨杏,袁驷.离散系统运动方程的Galerkin有限元EEP法自适应求解[J].应用数学和力学,2017,38(2): 133―143.Xing Qin-yan,Yang Xing,Yuan Si.An EEP adaptive strategy of the galerkin fem for dynamic equations of discrete systems [J].Applied Mathematics and Mechanics,2017,38(2): 133―143.(in Chinese)
[24] 袁驷,袁全,闫维明,等.运动方程自适应步长求解的一个新进展——基于EEP超收敛计算的线性有限元法[J].工程力学,2018,35(2): 13―20.Yuan Si,Yuan Quan,Yan Wei-ming,et al.New development of solution of equations of motion with adaptive time-step size-Linear FEM based on EEP super-convergence technique [J]. Engineering Mechanics,2018,35(2): 13―20.(in Chinese)
[25] 袁驷,邢沁妍,王旭,等.基于最佳超收敛阶EEP法的一维有限元自适应求解[J].应用数学和力学,2008,29(5): 533―543.Yuan Si,Xing Qin-yan,Wang Xu,et al.Self-adaptive strategy for one-dimensional finite element method based on EEP method with optimal super -convergence order[J].Applied Mathematics and Mechanics,2008,29(5):533―543.(in Chinese)
[26] Turcke D J,McNeice G M.Guidelines for selecting finite element grids based on an optimization study [J].Computers & Structures,1974,4(3): 499―19.
[27] Szabó B,Babuška I.Introduction to finite element analysis: Formulation,verification and validation [M].Hoboken,N.J: John Wiley & Sons,2011.
PERFORMANCE OF THE ADAPTIVE FINITE ELEMENT METHOD BASED ON THE ELEMENT-ENERGY-PROJECTION TECHNIQUE
Abstract: The adaptive finite element method (AFEM) based on the element energy projection (EEP) technique has succeeded in solving a wide range of problems,while few studies have been done on its adaptive characteristics.Taking the second-order ordinary differential equation as the model problem,the adaptive methods based on both the EEP and super-convergent patch recovery (SPR) solutions were studied.The meshes generated by the two adaptive methods were compared with the optimum mesh.Furthermore,an estimate formula reflecting the characteristics of AFEM was proposed with an adaptive convergence rate
Numerical experiments show that,with the element of degreem,both SPR and EEP can be well applied for the smooth problem and the convergence rate achievedm+1.For the singular problem with a singularity factorα(＜1),SPR failed while EEP-based adaptive procedure gained the convergence rate ofm+α,a much higher rate than that of the conventional finite element methodα.