图1 不同爆炸条件下舰船整体响应及损伤模式的关系图
Fig.1 The dynamic responses and damage modes of the warship subjected to different explosion conditions
现代海战中，舰船遭受水中兵器爆炸攻击的形式多样，各种攻击方式造成的损伤效果也不尽相同。其中，鱼雷接触爆炸或直接命中将造成舰船破口，其破坏效果直接，但主要呈局部损伤特点，波及范围相对较小；鱼雷或水雷近距爆炸作用下，舰船会出现整体塑性大变形，发生中拱或中垂损伤甚至折断、沉没，影响范围广且后果严重；中远距离爆炸作用下，水下爆炸气泡多次脉动容易激起舰船低阶耦合运动，使其出现鞭状响应，造成舰船总体及大范围设备运动变形。图1给出了水下爆炸发生在舰船底部时，舰船整体响应及损伤模式与爆炸工况之间的基本关系示意图。可见，整体损伤变形不仅是水下爆炸作用下舰船的主要响应模式，且随着爆距的变化其损伤结果也不同，其相互关系及响应特性仍有待进一步研究。
图1 不同爆炸条件下舰船整体响应及损伤模式的关系图
Fig.1 The dynamic responses and damage modes of the warship subjected to different explosion conditions
关于舰船整体结构在水下爆炸冲击作用下的动态响应问题，诸多学者开展了大量的理论和试验研究工作，他们在研究该问题时通常将水面舰船视为船体梁结构。另外，为了简化问题，大多数理论研究工作通常将水下爆炸冲击波和气泡对结构的冲击作用分割开来研究，特别是在中远场爆炸条件下，往往忽略冲击波对舰船整体运动的影响，集中考虑爆炸气泡脉动和辐射压力对舰船整体的损伤作用，如爆炸气泡激起的船体梁鞭状运动[1―4]。基于球状气泡运动假设，Zong[5]理论研究了刚塑性船体梁在中远场水下爆炸气泡作用下的动态响应问题，重点关注气泡脉动过程中船体梁的刚体和塑性运动。进一步地，张弩等[6]理论研究了理想弹塑性船体梁在球状气泡运动下的响应特性，建立了梁弹性运动、刚塑性变形和回复弹性这三个运动阶段的运动模型。张阿漫等[7]、Zong等[8]、Zhu和Cheng等[9]以 ABAQUS为数值计算工具，分别研究了舰船、典型船体梁等结构在近场不同爆距条件下发生整体中拱、中垂损伤时的响应过程，并利用模型试验验证了该仿真方法的有效性。李海涛等[10―11]采用数值和模型试验方法研究了细长形船体梁在水下近场爆炸作用下的整体中垂损伤特性，揭示了船体梁发生整体中垂损伤的机理，初步提出了船体梁发生中垂损伤的条件。张振华等[12]试验研究了船体梁模型在水下近场爆炸作用下的整体塑性损伤特性，揭示了船体梁中拱损伤机理，初步提出了船体梁总体和局部变形之间的耦合力学模型。
实际上，对舰船等细长型结构而言，水下近场爆炸冲击波作为主要载荷形式，其对舰船结构造成的损伤，不仅表现为结构局部变形，还会造成结构整体弯曲[13―14]，而且该弯曲变形应作为爆炸气泡运动阶段舰船整体响应研究的初始计算条件。文献[15]将近距球面爆炸冲击波近似看作是移动的平面波，提出了一种计算船体梁在球面冲击波作用下发生整体运动的近似理论方法，并通过船体梁模型实验验证了该理论方法的合理性。
在前述工作基础上，将水面舰船简化为等截面自由船体梁，本文建立了水下爆炸冲击波和气泡联合作用下弹塑性船体梁整体运动简化理论模型，研究了船体梁分别作全弹性和弹塑性整体运动的响应模式，深入分析了不同爆炸条件下梁进入塑性运动后反复加载、卸载的响应过程及一般运动特性，并对两种不同运动模型开展了试验验证，为后续建立更加复杂的舰船整体运动响应模型奠定了基础。
前期研究工作表明，当水下爆炸发生在舰船或船体梁模型中部正下方时，爆炸造成的结构整体变形最显著。为了简化理论分析过程，同时又反映问题的本质特征，本文主要以 TNT炸药在船体结构中部正下方爆炸工况为研究对象(如图 2所示)，将船体结构简化为等截面直梁，采用理想弹塑性材料模型，忽略局部变形、剪切及应变率效应对结构总体变形的影响，重点研究爆炸冲击波和气泡联合作用下船体梁的整体运动响应过程。
图2 船体梁爆炸工况示意图
Fig.2 Sketch of hull girder subjected to underwater explosion
初始爆炸冲击波及第一次气泡脉动承载了水下爆炸的主要能量，本文拟重点研究该载荷阶段内船体梁的整体运动响应。大量爆炸试验和相似律分析表明，冲击波阶段的压力曲线可以近似用指数衰减来表示，第一次气泡脉动阶段压力可以通过求解气泡与周围流体之间的能量平衡方程来求解。本文将水下爆炸载荷压力曲线简化为如图 3所示的Ⅰ～Ⅴ共 5个阶段：第Ⅰ、Ⅱ阶段可看作冲击波载荷衰减阶段，假设其满足线性变化规律；第 III阶段为边界条件下气泡膨胀收缩运动形成的流场负压变化阶段，假设其满足正弦函数关系；第Ⅳ、Ⅴ阶段为气泡收缩产生二次脉动压力的上升、下降阶段，假设其满足线性变化规律。列出各阶段压力载荷计算公式如下[16―18]：
图3 不同阶段爆炸载荷压力曲线
Fig.3 The pressure curves of explosion load in different stages
第Ⅰ阶段：
第Ⅱ阶段：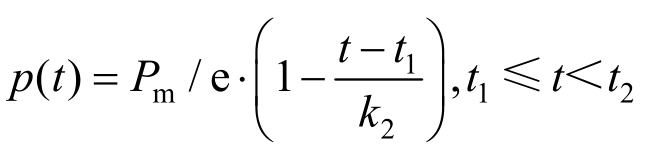
第Ⅲ阶段：
第Ⅳ阶段：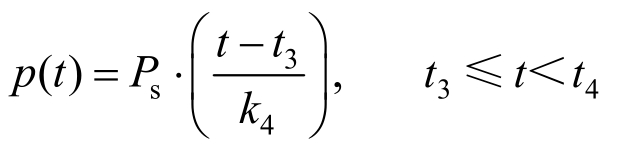
第Ⅴ阶段：
式中：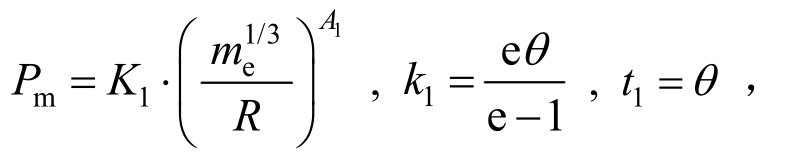
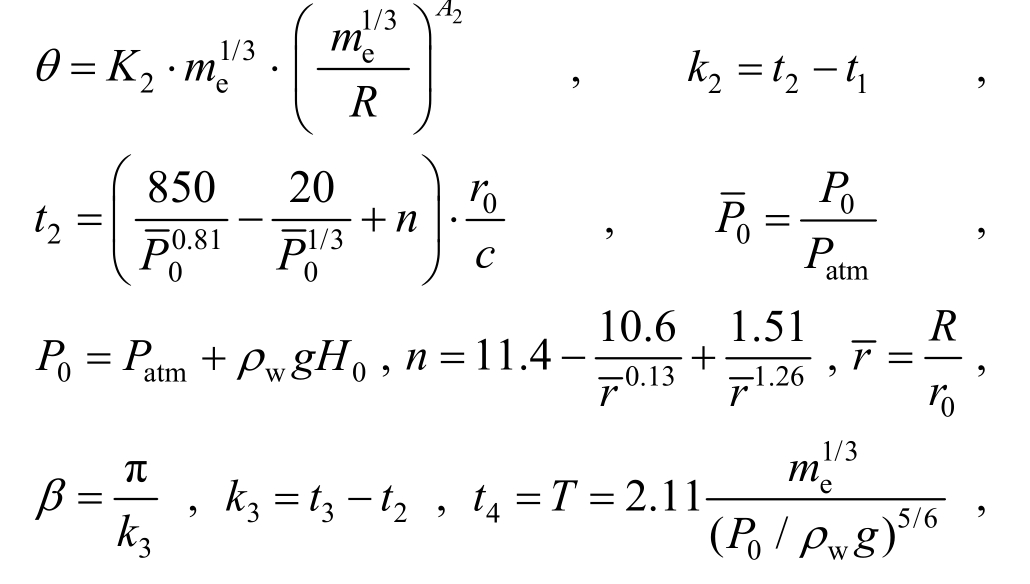
其中：me为 TNT装药当量；R为爆距；Pm为冲击波压力峰值；K1、K2、A1、A2为冲击波常数；k1、k2、k3、k4、k5分别为与五个压力阶段的持续时间相关的参数；P0为炸药处静水压力；
为无量纲压力参数；Pb为气泡脉动过程中的负压峰值；Ps为脉动压力峰值；
为表征爆炸距离的无量纲参数；θ为冲击波衰减常数；H0为装药深度；r0为装药半径；ρw为水的密度；c为水中声速；Patm为大气压；g为重力加速度；T为气泡脉动周期；β为气泡负压阶段压力函数角频率值。各物理量参数均采用国际单位制。
当水下爆炸载荷较小时，船体梁在爆炸压力P(x,t)作用下作弹性运动，其运动控制方程为[19]：
式中：w为梁运动位移函数；m为梁单位长度质量(包含附连水质量)。设其一般解为：
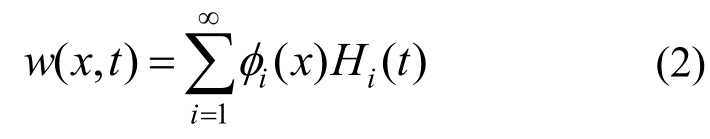
式中：φi(x)为梁第i阶固有振形；Hi(t)为梁第i阶振形对应的主坐标。为了确定梁的运动位移函数，首先应分别确定固有振形及对应的主坐标。
1) 振形函数
梁固有振形的一般表达式为：
式中：l为梁长；
为常系数；μ为与梁频率相关的常数。对于自由边界梁，两端弯矩和剪力为零，因此当x=0和x=l时满足如下边界条件：
根据式(4)列出的边界条件可以得到自由梁的固有频率ω。另外，ω满足
当μ取第一个非零解时，梁的一阶振形固有频率ω1=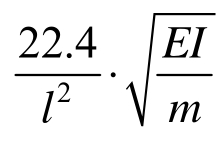
，梁的一阶振形函数可近似表示为：
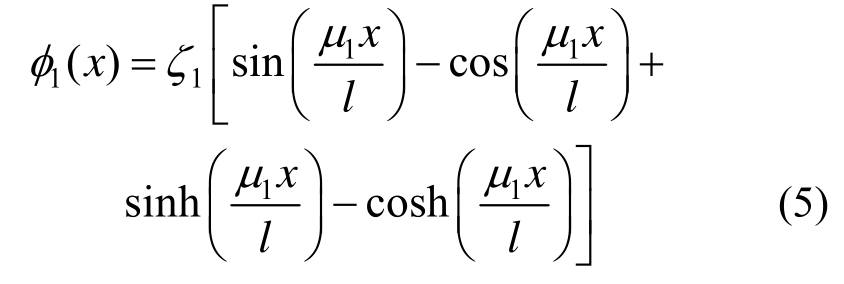
2) 主坐标函数
对于强迫振动条件下的主坐标函数Hi(t)，可以表示为：
式中：
为与广义质量对应的广义激振力；ai、bi为积分常数，由初始条件决定。
假设压力函数P(x,t)满足
其中p(t)为梁中点处压力时程衰减曲线，p(x)为相对于梁中点的爆炸载荷压力分布特征函数。
对于冲击波载荷衰减阶段(第I、II阶段)，梁上压力分布特征函数ps(x)可近似表征为：
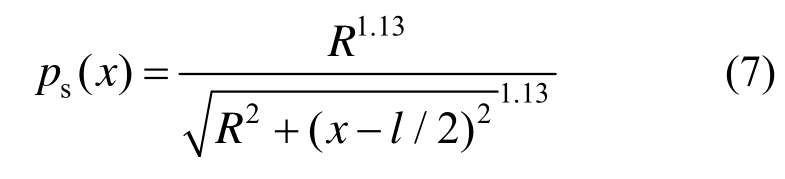
对于气泡脉动阶段(第Ⅲ～V阶段)，梁上压力分布特征函数pb(x)可近似表征为[20－21]：
分别确定冲击波和气泡阶段船体梁上的压力分布特征函数ps(x)和pb(x)后，结合5个阶段内的压力时程变化公式p(t)，即可得压力函数P(x,t)。另外，明确水下爆炸各阶段的压力分布特征函数p(x)后，为简化后续公式推导的参数表达形式，引入参数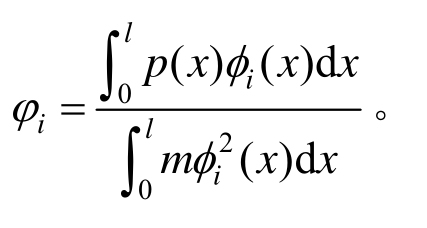
3) 位移函数
考虑到炸药在船体梁中部下方爆炸时主要激起梁低阶运动响应，此处主要选取梁的一阶模态来研究及整体运动响应。根据式(5)、式(6)分别确定振形函数φ1(x)及其对应的主坐标函数H1(t)后，可得到梁的近似位移函数为
水下爆炸五个载荷阶段所对应的梁振形函数φ1(x)保持一致，但对应的主坐标函数H1(t)不同，按照各阶段压力载荷，结合初始状态及各阶段连续运动条件，可分别推导五个阶段内梁的运动位移函数。
随着水下爆炸强度的增大，船体梁会由全弹性运动向弹塑性运动转变，可能包含如下变形过程：弹性运动→正向塑性变形→反向弹性卸载→反向塑性变形→正向弹性卸载。对于理想弹塑性船体梁而言，其运动变形过程以及应力应变关系如图4所示。
图4 理想弹塑性梁反复加载、卸载过程中的应力-应变关系
Fig.4 The relationship between stress and strain of the perfect elastic-plastic beam in the process of loading and unloading
在水下爆炸冲击载荷的某一阶段，若船体梁中部弯矩超过塑性极限弯矩时，假设其中部形成一个固定塑性铰，梁继续保持一阶运动变形的同时，两端还绕着塑性铰发生相对转动。考虑船体梁的对称性，以右半船体梁为研究对象，列出其位移函数如下：
式中：l/2＜x≤l；φ1(x)为一阶振形；H′(t)为与之对应的运动幅值；α(t)为梁两端绕着中点发生相对转动时的转角。
1) 正向塑性运动
在梁初始弹性运动过程中，其中部的弯矩最大，当其最大弯矩值超过塑性极限弯矩Ms绝对值时，中部出现固定塑性铰，梁将由弹性阶段进入塑性变形阶段，梁中点弯矩值保持为Ms不变。此时，梁的运动控制方程满足：
将式(9)代入式(10)，并对其进行一、二阶积分，结合边界条件：x=l/2时，Q=0，M=Ms，Q为梁内的剪力，M为梁的弯矩；x=l时，Q=0，M=0，可得到函数H′(t)和α(t)的方程为：
式中：
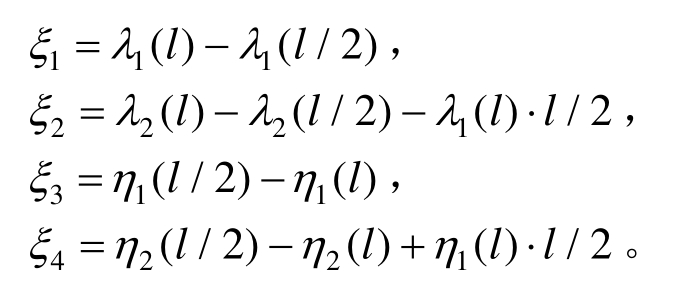
上述公式中引入了如下积分函数：
梁在弹性-塑性运动转变过程中，假设其满足动量和能量平衡条件，其中动量平衡条件为：
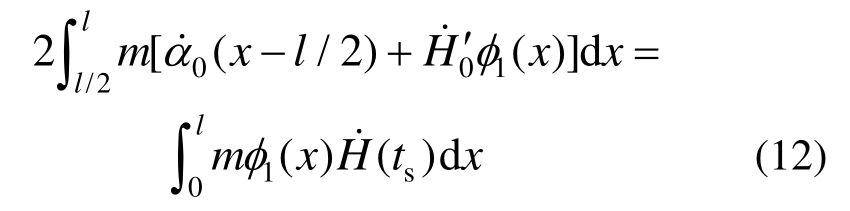
能量平衡条件为：
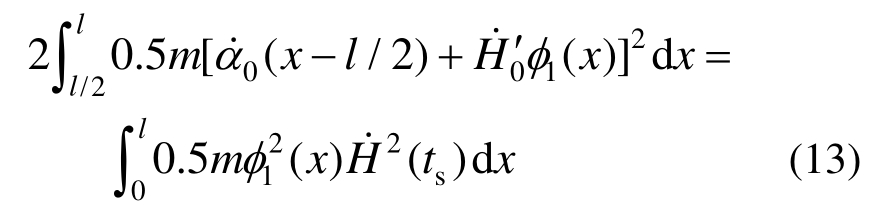
式中：ts为塑性运动发生的初始时刻；
为塑性运动发生时位移函数的初始值。
将方程组式(11)对时间t进行一、二次积分，结合梁在弹塑性运动转换时的动量和能量平衡条件，可以求出任何压力时间段内梁塑性变形阶段的位移及相对转角。
2) 反向弹性卸载
船体梁进入塑性运动后，当中部塑性变形达到最大值时，梁两端绕着固定塑性铰发生相对转动的转角α(t)也将达到最大值，此后梁开始反向运动，结构应力释放，梁中点带动两端进入弹性卸载。
假设弹性卸载过程中，梁弹性运动位移函数仍满足式(2)。根据塑性、弹性转换时刻的位移、速度连续条件，求解船体梁反向弹性卸载过程的运动幅值H(t)，方程如下：
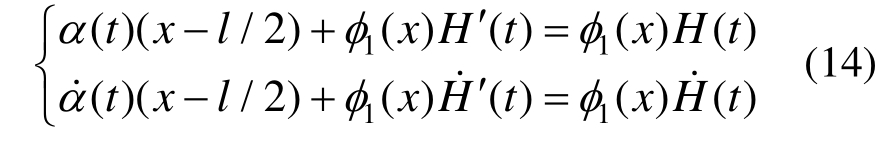
以梁中点为考察点，结合弹性和塑性阶段得到的运动方程，同时利用以上连续条件，可以得到弹性卸载阶段梁的运动方程。需要注意的是，除梁中点外，其他部分的运动位移需要在弹性变形基础上，叠加一个相对转动位移。
3) 反向塑性运动
在弹性卸载及反向运动过程中，当梁中点弯矩绝对值超过塑性极限弯矩Ms绝对值时，梁将进入反向塑性运动过程，中部出现固定塑性铰，梁在继续保持一阶变形的同时，其两端绕着塑性铰发生相对转动。假设反向塑性运动过程中，梁的位移函数及运动控制方程仍满足式(9)、式(10)的要求，保持梁中点弯矩值为-Ms不变，利用连续边界条件，可以得到梁反向塑性变形时的运动幅值H1′(t)及相对转角α1(t)：
4) 正向弹性卸载
当船体梁中部反向塑性变形达到最大值时，梁两端绕着固定塑性铰发生相对转动的转角α1(t)也将达到最大值，此后梁开始正向运动，结构应力释放，梁中点带动其他部分再次弹性卸载。
假设梁正向弹性卸载过程中，梁弹性运动位移函数仍满足式(2)。根据塑性、弹性转换时刻的位移、速度连续条件，仍可得形如式(14)的函数方程。
以梁中点为考察点，结合弹性和塑性阶段得到的运动方程，同时利用以上连续条件，可以得到正向弹性卸载阶段梁的运动方程。
试验设计的船体梁为全封闭对称结构，其内部被横隔壁分成7个小舱室，每个小舱室长度0.4 m；模型总长 2.8 m；宽 0.3 m；高 0.08 m，板厚均为1 mm；采用Q235A普通钢制造，梁结构塑性极限弯矩Ms=1.8×104N·m。利用有限元软件ABAQUS计算得到箱形梁模型的一阶理论湿模态频率为26.1 Hz，试验测得梁模型一阶湿模态频率为23.8 Hz。为了研究梁模型在水下爆炸载荷作用下的整体运动变形，沿其纵向布置加速度测点2个(A1、A2)，位于甲板边沿与舷侧连接处。船体梁模型的结构尺寸、测点布置情况如图5所示。
图5 船体梁结构尺寸及模型实物
Fig.5 Structural dimensions and models of hull girder
实验过程中，船体梁自由漂浮于水面，实验水深3.0 m，将TNT炸药置于梁中部正下方爆炸，具体实验工况如表1所示。表中参数D、W、R、rmax和fb分别为炸药深度、药量、爆距、气泡最大半径和第一次脉动频率，其中rmax和fb根据文献[22]中计算公式得到。
利用高速摄影仪记录整个水下爆炸过程，其拍摄速度为 250 f/s。参考文献[12]中采用的高速摄影图像判别法，选取固定参考点获取像高与物高的关系，根据高速摄影照片上标识点的位移判读结果获取船体梁的垂向运动位移，并将其与船体梁中点处加速度传感器采集到的位移数据进行对比。
表1 实验工况表
Table 1 Test cases
序号R/mme/gR/rmaxfb/Hz 1 1.0 5 3.83 21.9 2 0.7 5 2.66 21.5
图6给出了工况2下船体梁在水下爆炸作用下的整体运动过程，工况1与其类似。可以看出，水下爆炸过程中，梁呈现明显的一阶上下弯曲运动变形；爆距越小，梁总体弯曲运动越明显。工况2时梁的运动过程描述为：当炸药爆炸后，气泡开始快速膨胀，推动滞后流运动并以动能的形式作用于梁底部，导致其发生中拱弯曲；12 ms左右，梁中部出现最大相对中拱变形，而气泡因惯性进一步膨胀，其周围流场压力则进一步降低并逐渐低于外部大气压，导致梁中部受到流场内外压力差的作用，开始向水平状态变化；24 ms左右，气泡膨胀到最大，而梁也基本回复至水平状态，并且随着气泡的快速收缩继续向中垂弯曲状态变化；40 ms左右，梁中部出现最大相对中垂变形；48 ms左右，气泡溃灭并形成射流冲击，梁再次进入中拱弯曲状态，并随之开始自由振动。
图6 工况2下船体梁在水下爆炸作用下的整体运动过程
Fig.6 Dynamic response process of the girder subjected to underwater explosion in case 2
1) 运动模式判别
水下爆炸作用下，当爆炸强度较小时，船体梁可能仅发生弹性运动；随着爆炸强度的增大，当梁受到的总纵弯矩超过塑性极限弯矩时，其进入弹塑性变形模式。图7给出了梁全弹性运动假设条件下，两工况下船体梁中点的理论弯矩时程曲线。可以看出，工况1时，在第一次气泡脉动过程中，梁中点弯矩值未超过塑性极限弯矩Ms，梁处于整体弹性运动过程；工况2时，梁中点弯矩值超过塑性极限弯矩Ms，且梁在气泡膨胀早期就已进入塑性运动过程；梁进入塑性变形后，其后续运动变形过程需要通过卸载、加载情况来进一步判明。
图7 水下爆炸作用下船体梁中点理论弯矩时程曲线
Fig.7 Time history curve of bending moment of the hull girder at the mid-point in two cases
2) 全弹性运动
工况1条件下，船体梁发生全弹性运动，拟用上述船体梁全弹性运动理论计算结果与实验结果进行对比分析。
图8给出了工况1下船体梁中点位移wm的理论值与实验值的情况比较。可以看出，在第一次气泡脉动期间，船体梁均呈现明显的上下往复运动，整体变形的理论值和实验值基本相当，处于一个量级。就运动周期而言，梁完成一个运动周期所用的理论时间间隔AB约40 ms，与实验间隔A'B'基本相同；相比于理论曲线，实验曲线整体略有延迟。就运动幅值而言，梁往复运动的理论值略大于实验值。分析存在变形误差的可能原因为：理论模型中未考虑梁结构阻尼和流体附加阻尼对梁运动能量的损耗作用，而阻尼的存在会使结构响应幅值降低、周期增大；另外，实验水池的边界效应可能造成气泡实际脉动压力比理论值偏低，导致实验值比理论值偏小。
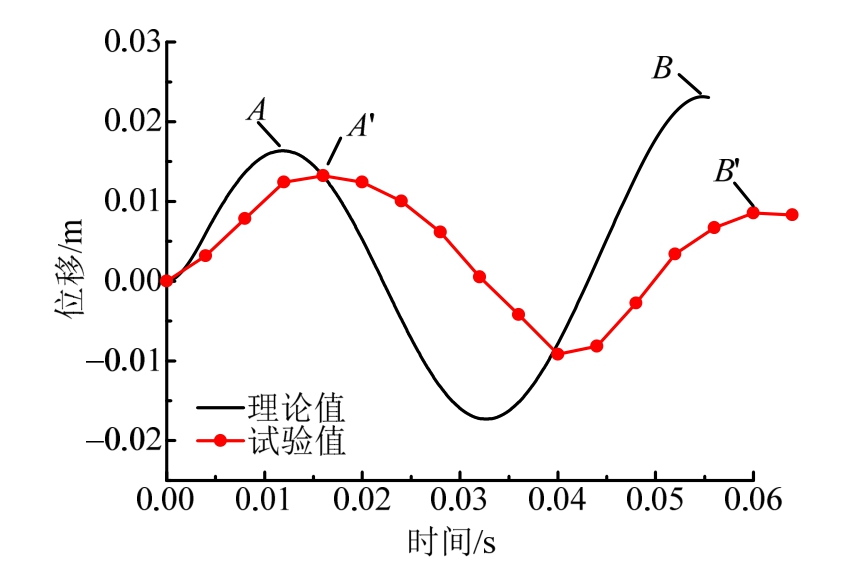
图8 工况1下船体梁中点位移理论值与实验值比较
Fig.8 Comparison of theoretical and experimental results of the girder’s midpoint displacement in case 1
图9 给出了工况1下典型时刻船体梁长度方向理论变形对比情况。可以看出，梁总体呈现一阶弹性变形，梁绕着两个驻点发生中拱、中垂弯曲；对于某一特定时刻，梁两端的运动位移甚至超过中点位移值。通过观察高速摄影获取的运动图像，船体梁模型运动变形的实验驻点距模型一端约0.68 m；通过船体梁理论变形曲线判断，理论驻点距船体梁一端约0.64 m。
图9 工况1下典型时刻船体梁长度方向理论变形
Fig.9 The theoretical deformation of the girder along longitudinal section in case 1
3) 弹塑性运动
工况2条件下，船体梁运动弯矩值超过塑性极限弯矩，梁在运动过程中进入塑性，故采用船体梁弹塑性运动理论计算结果与实验结果进行对比分析。
图10给出了工况2下船体梁中点位移wm的理论值与实验值的情况比较。与工况1情况类似，工况2下船体梁整体运动变形的理论和实验过程基本相同，理论值比实验值偏大，但处于一个量级。就运动周期而言，梁完成半个运动周期所用的理论时间间隔BD约23 ms，实验间隔B'D'约24 ms，最大误差约 5%。就运动幅值而言，梁发生弹塑性响应时，其往复运动的理论值比实验值略大，最大中拱、中垂位移理论值与实验值误差约20%。值得注意的是，工况2下，气泡收缩阶段船体梁的中垂变形均大于气泡膨胀阶段的中拱变形，表明随着爆距的降低，爆炸气泡对船体梁的中垂弯曲损伤作用越加明显[7,11]。
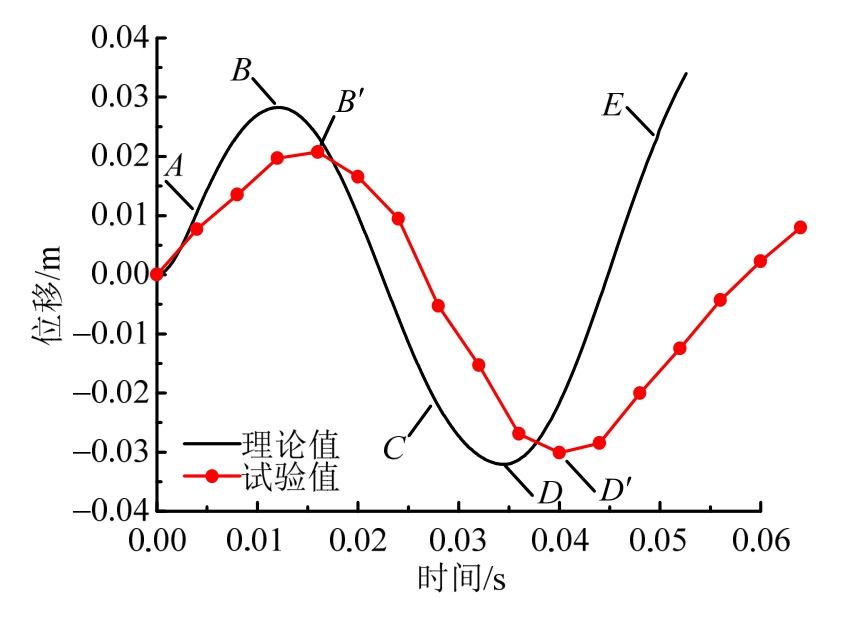
图10 工况2下船体梁中点位移理论值与实验值比较
Fig.10 Comparison of theoretical and experimental results of the girder’s midpoint displacement in case 2
从理论分析过程看，工况2下船体梁经历了中拱塑性变形→弹性卸载及反向加载→中垂塑性变形→再次弹性卸载及中拱塑性变形这一复杂运动过程。在水下爆炸初期，船体梁整体仍作弹性运动；A点时刻(约7 ms)，梁运动弯矩首次超过塑性极限弯矩，形成塑性铰，开始进入正向弯曲塑性变形阶段；B点时刻(约 12 ms)，梁最大运动位移值约2.8 cm，第一次中拱塑性变形达到最大，两端相对塑性转角α约-8.7×10-4；随后，梁向下运动并开始弹性卸载；C点时刻(约28 ms)，梁继续反向中垂运动并达到塑性极限弯矩，开始发生中垂塑性变形；至D点时刻(约 34 ms)，中垂弯曲变形达到最大值-3.2 cm，相对塑性转角α为1.9×10-3；随后，梁再次发生正向弯曲运动并开始卸载，至E点时刻(约49 ms)，梁再次发生正向中拱弯曲塑性变形，塑性铰转角α快速增大。
图11给出了工况2下典型时刻船体梁长度方向理论变形情况。可以看出，梁总体呈现一阶变形，但塑性变形的存在导致梁并不严格绕着固定的驻点发生正、反向弯曲运动；在34.3 ms时刻，梁发生最大中垂塑性变形，中部可见比较明显的塑性铰；对于某一特定时刻，梁两端的运动位移超过中点位移值。
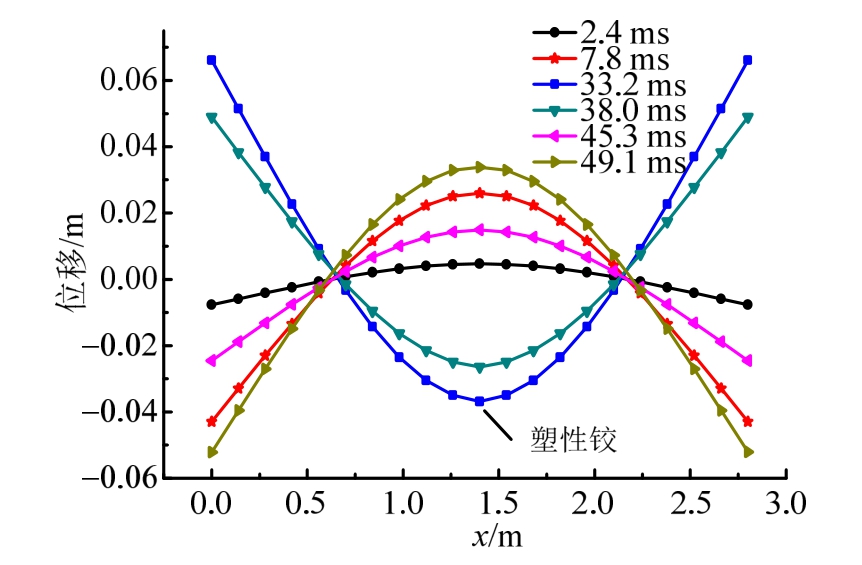
图11 工况2下典型时刻船体梁长度方向理论变形
Fig.11 The theoretical deformation of the girder along longitudinal section in case 2
为进一步分析爆距、梁长等参数变化对梁运动响应影响的一般特性，选择5g TNT炸药为基本药量，研究梁长L分别为2.4 m、2.8 m和3.2 m，爆距R在0.3 m～1.0 m范围内变化时梁的不同运动参数，包括梁典型位移wm、塑性转角α等。
图12给出了0.5 m爆距、不同R/L下梁中点处的位移时程曲线。可以看出，相同爆距下，随着梁长的增加，其运动周期和运动幅度均明显增大；在气泡运动第一周期内，梁的运动模式也由发生中拱塑性变形向中垂塑性变形转变；R/L越大，中垂塑性变形越明显，基本按倍数级增长。
图12 不同R/L下梁中点处位移时程曲线(me=5 g、R=0.5 m)
Fig.12 Effect ofR/Lon displacement of the beam’s midpoint(me=5 g、R=0.5 m)
图13 给出了0.5 m爆距、不同R/L下梁塑性转角α的时程曲线。从图中可以看出，梁在第一个气泡运动周期内大致经历Ⅰ～Ⅵ这 6个过程：Ⅰ为冲击波和气泡膨胀初期时梁的中拱弹性变形，转角α保持为零；Ⅱ为气泡膨胀过程中梁发生中拱塑性变形，转角α由零向负值方向非线性增大；Ⅲ为梁中拱塑性变形后的中垂弹性卸载，转角α保持最大中拱塑性转角不变；Ⅳ为梁在气泡收缩运动过程中由中垂弹性卸载进入中垂塑性变形，转角α由负值快速向正值转变；Ⅴ为梁最大中垂塑性变形后进入中拱弹性卸载，转角α保持最大中垂塑性转角不变；Ⅵ为气泡溃灭阶段梁由中拱弹性变形进入中拱塑性变形，转角α由正值快速向负值变化，形成中拱塑性铰。随着梁长的增加，梁第一次进入中拱塑性变形的时间相差不大，但后续中拱或中垂最大塑性转角却增加明显，塑性变形过程更加剧烈，梁也更倾向于发生最终中垂塑性变形。
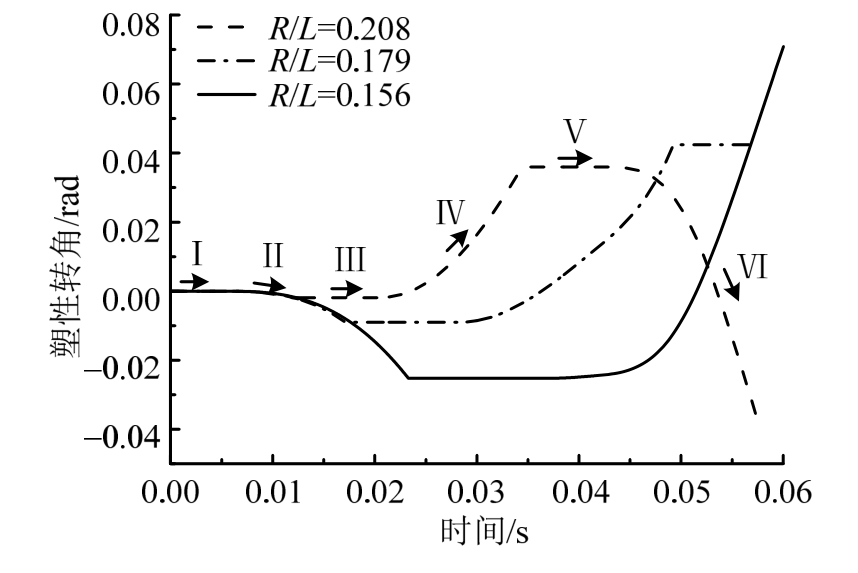
图13R/L对梁中点处塑性转角的影响(me=5 g、R=0.5 m)
Fig.13 Effect ofR/Lon plastic angleαof the beam’s midpoint(me=5 g、R=0.5 m)
设fb、fL分别表示气泡第一次脉动频率和梁的一阶湿频率，选取参数f=fb/fL。在选定爆距范围内，参数fb变化较小，基本保持在21 Hz左右；不同长度梁一阶湿频率fL可根据理论计算得到。设定wmh、wms和αh、αs分别表示气泡第一次脉动周期内，梁中点处的最大中拱、中垂塑性变形和中拱、中垂塑性转角。
图14、图15分别给出了不同f条件下wms/wmh、αs-αh与R/rmax的关系曲线。从图14、图15可以看出，在该爆径比R/rmax的变化范围内，wms/wmh比值大于 1，表明梁中垂变形均大于中拱变形；随着R/rmax的减小，wms/wmh、αs-αh的值呈现非线性增大趋势，其中在R/rmax＞2.5时，两者增大趋势均相对平缓，而当R/rmax＜1.5时，wms/wmh、αs-αh数值急速增大，该规律与文献[9－10]的结论基本一致；相比于f=0.61的情况，当参数f接近于1时，梁整体运动变形也更加明显。以上分析表明，相比中远场爆炸，水下近距爆炸会使梁发生明显的整体运动变形；近距爆炸条件下，在气泡第一次脉动周期内，梁的中垂损伤变形大于中拱变形；当爆炸气泡运动频率与梁一阶湿频率相近时，梁整体运动响应更加剧烈，也更容易出现中垂损伤模式。
引入参数T0表征梁由初始状态经历一个往复运动周期后回复到运动原点的时间，参数T表征气泡第一次脉动周期。图16给出了不同f条件下T0/T与R/rmax的关系曲线。从图中可以看出，当R/rmax较大且梁处于整体弹性运动时，参数T0/T变化不大；随着R/rmax的减小，梁发生整体塑性变形，其响应周期也随之增大；f越大，T0/T随着R/rmax减小而增大的趋势越加明显。以上变化规律也得到实验研究数据的支持[11]，即船体梁进入塑性变形后的加载、卸载过程将不同程度导致其整体响应周期增大。
图14 不同f条件下wms/wmh与R/rmax的关系曲线
Fig.14 The relationship betweenwms/wmhandR/rmaxat differentf
图15 不同f条件下αs-αh与R/rmax的关系曲线
Fig.15 The relationship betweenαs-αhandR/rmaxat differentf
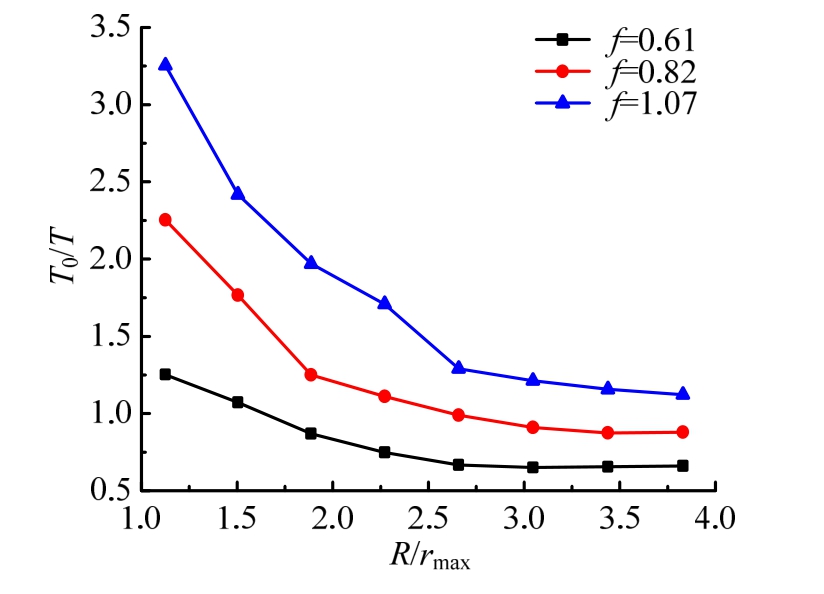
图16 不同f条件下T0/T与R/rmax的关系曲线
Fig.16 The relationship betweenT0/TandR/rmaxat differentf
最后，值得注意的是，本文将舰船简化为等截面直梁，而舰船结构在纵向上实际属于变截面框架型结构，其总纵惯性矩I(x)属于变量，并从中间向两端逐步减小。当船体梁长度保持不变，这种变化特点可能导致实际舰船低阶响应频率进一步减小，并影响爆炸响应的能量分布。另外，本文暂时忽略了结构内阻尼和流体外阻尼影响，而实际这些因素的存在也会导致船体梁响应频率的降低。
(1) 根据不同的水下爆炸强度，该理论模型能分别计算船体梁发生全弹性或弹塑性的响应过程，并对预报船体梁整体响应周期和响应幅值具有一定的精度，其中整体变形预报误差不超过30%，响应周期预报误差不超过10%。
(2) 当水下爆炸发生在船体梁中部正下方时，在第一次脉动周期内，船体梁可能发生多次加载、卸载的上下往复运动过程，且梁中垂变形大于中拱变形；随着爆径比R/rmax的减小，梁中部可能会出现一个塑性铰，其整体运动周期也将非线性增大，船体梁的最终损伤模式也由中拱损伤向中垂损伤转变。
(3) 当爆炸气泡第一次脉动频率与梁一阶湿频率相近时，梁更倾向于出现整体中垂损伤模式；当爆径比R/rmax＞2.5时，梁发生整体中垂损伤变形的趋势相对平缓，而当R/rmax位于1～1.5变化时，梁整体中垂损伤过程剧烈。
[1]Li Yujie, Pan Jianqiang, Li Guohua, et al. Experimental study of ship whipping induced by underwater explosion bubble [J]. Journal of Ship Mechanics, 2001, 5(6): 75―83.
[2]Vernon, T A. Whipping response of rhip hulls from underwater explosion bubble loading [R]. AD-A178096,1986.
[3]Stettler J W. Damping mechanisms and their effects on the whipping response of a submerged submarine subjected to an underwater explosion [R]. Lehigh University, 1983.
[4]Chen Y, Tong Z P, Hua H X, et al. Experimental investigation on the dynamic response of scaled ship model with rubber sandwich coatings subjected to underwater explosion [J]. International Journal of Impact Engineering, 2009, 36: 318―328.
[5]Zong Z. A hydroplastic analysis of a free–free beam floating on water subjected to an underwater bubble [J].Journal of Fluids and Structures, 2005, 20: 359―372.
[6]Zhang N, Zong Z. Hydro-elastic-plastic dynamic response of a ship hull girder subjected to an underwater bubble [J]. Marine Structures, 2012, 29: 177―197.
[7]Zhang A M, Yao X L, Li J. The interaction of an underwater explosion bubble and an elastic-plastic structure [J]. Applied Ocean Research, 2008, 30(3):159―171.
[8]Zong Z, Zhao Y J, Li H T. A numerical study of whole ship structural damage resulting from close-in underwater explosion shock. Marine Structures, 2013,31: 24―43.
[9]Wang H, Zhu X, Cheng Y S, et al. Experimental and numerical investigation of ship structure subjected to close-in underwater shock wave and following gas bubble pulse [J]. Marine Structures, 2014, 39: 90―117.
[10]李海涛, 朱石坚, 刁爱民, 等. 水下爆炸气泡作用下梁中垂损伤及流场变化特性. 高压物理学报, 2012,26(5): 494―500.Li Haitao, Zhu Shijian, Diao Aimin, et al. Characteristics of flow-field an sagging damage of fee-free beam subjected to underwater explosion bubbles [J]. Chinese Journal of High Pressure Physics, 2012, 26(5): 494―500. ( in Chinese)
[11]李海涛, 朱锡, 赵小龙, 等. 箱形梁在水下近距非接触爆炸作用下的整体毁伤研究. 振动与冲击, 2010,29(3): 158―161.Li Haitao, Zhu Xi, Zhao Xiaolong, et al. Study on damage mode of box-like beam as a whole subjected to underwater non-contact explosion located closely [J].Journal of vibration and shock, 2010, 29(3): 158―161.( in Chinese)
[12]Zhang Z H, Wang Y X, Zhao H F, et al. An experimental study on the dynamic response of a hull girder subjected to near field underwater explosion [J]. Marine Structures,2015, 44: 43―60.
[13]Yu T X, Yang J L, Reid S R. Dynamic behavior of elastic-plastic free-free beams subjected to impulsive loading [J]. International Journal of Solids Structures,1996, 33(18): 2659―2680.
[14]张振华, 汪玉. 近距水爆冲击波对船体梁总体毁伤的“刀锋效应”. 中国科学: 物理学 力学 天文学, 2015,48(5): 43―60.Zhang, Zhenhua, Wang Yu. “Blade effect” on the overall damage of hull girder caused by near field UNDEX shock wave [J]. SCIEN TIA SINICA Physica,Mechanica ＆ Astronomica, 2015, 48(5): 43―60. (in Chinese)
[15]李海涛, 朱锡, 张振华. 水下爆炸球面冲击波作用下船体梁的刚塑性动响应特性. 工程力学, 2010, 27(10):202―207.Li Haitao, Zhu Xi, Zhang Zhenhua. Dynamic rigid-plastic response of ship-like beam subjected to underwater spherical shockwaves [J]. Engineering Mechanics, 2010, 27(10): 202―207. (in Chinese)
[16]Zamyshlyayev B V. Dynamic loads in underwater explosion [R]. Washington D C: Naval Intelligence Support Center, 1973.
[17]Zhang Zhenhua, Wang Yu, Zhang Lijun, etal. Similarity research of anomalous dynamic response of ship girder subjected to near field underwater explosion [J]. Applied Mathematics and Mechanics, 2011, 32(12): 1491―1504.
[18]李晓杰, 张程娇, 王小红, 等. 水的状态方程对水下爆炸影响的研究[J]. 工程力学, 2014, 31(8): 46―52.Li Xiaojie, Zhang Chengjiao, Wang Xiaohong, et al.Numerical study on the effect of equations of state of water on underwater explosions [J]. Engineering Mechanics, 2014, 31(8): 46―52. ( in Chinese)
[19]刁爱民, 李海涛. 水下爆炸作用下船体梁整体运动简化理论模型[J]. 华中科技大学学报(自然科学版),2016, 44(6): 63―67.Diao Aimin, Li Haitao. Simplified theoretical model for bulk movement of hull girder subjected to underwater explosion [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(6):63―67. (in Chinese)
[20]刘巨斌, 李海涛, 王俊森. 水面无限平板下方球状爆炸气泡流场压力特性. 华中科技大学学报(自然科学版), 2013, 41(4): 119―122.Liu Jubin, Li Haitao, Wang Junsen. Characteristics of flow-field pressure of spherical explosion bubbles under an infinite plate floating on water [J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2013, 41(4): 119―122. ( in Chinese)
[21]刘巨斌, 李海涛. 水面平板下方非球状爆炸气泡运动数值模拟[J]. 海军工程大学学报, 2015, 27(2): 6―9.Liu Jubin, Li Haitao. Numerical simulation of non-spherical explosion bubble motion below plate floating on water [J]. Journal of Naval University of Engineering, 2015, 27(2): 6―9. (in Chinese)
[22]Hsu C Y, Liang C C, Nguyen A T, et al. A numerical study on the underwater explosion bubble pulsation and the collapse process [J]. Ocean Engineering, 2014, 81:29―38.
HYDRO-ELASTIC-PLASTIC DYNAMIC RESPONSE OF A SHIP HULL GIRDER SUBJECTED TO UNDERWATER EXPLOSION: A SIMPLIFIED THEORETICAL MODEL
牟金磊(1980―)，男，山东寿光人，讲师，博士，从事船舶抗爆抗冲击技术研究(E-mail: mjl1007@163.com);