图1 海冰断裂模式
Fig.1 Fracture mode of sea ice
近年来，全球气候变暖使北冰洋的海冰日益消融，北冰洋航线的开通指日可待，这一全新开辟的航线必然会对国际海洋运输格局产生重要影响，同时也给我国的经济发展带来重大机遇。破冰船是用于破碎冰层，开辟航道，引导舰船在冰区航行的勤务船。鉴于破冰船工作环境的危险性与功能使命的特殊性，对其破冰机理、运动轨迹以及所受冰载荷的研究工作显得尤为重要，这直接关系到破冰船能否安全、高效地完成破冰任务。而破冰船在层冰中的运动是破冰过程中常见的情形，也是本文研究的重点。
层冰中的连续破冰过程是指破冰船与海冰边界之间的“接触-挤压-弯曲破坏”的循环过程。Ettema等[1]、Izumiyama等[2]进行了一系列的模型试验或全尺寸试验，结果表明海冰边界的破坏与新边界的产生可以近似认为是楔形碎冰从完整冰排上脱落的连续过程。Liu等[3]将近场动力学方法应用于船-冰接触与冰载荷计算，模拟了裂纹形成与扩展的动态过程。首先，海冰边界与船艏接触并发生弯曲破坏，在船艏前方形成环向裂纹；随后，迅速从接触部位扩展出两条径向裂纹，当与环向裂纹汇合时，海冰发生初次断裂。随着破冰船的前进，初次断裂的海冰将发生二次断裂[4]，如图1所示。
图1 海冰断裂模式
Fig.1 Fracture mode of sea ice
早期由于试验数据相对匮乏、对破冰机理的认识不足，因此对破冰船在层冰中运动的研究通常采用理论分析与经验公式相结合的方法。近年来，计算力学和图形学的发展促进了数学模型的数值实现。Kashtelyan 等[5]、Lindqvist[6]、Varsta[7]早前提出的众多冰载荷模型现已被应用于数值模拟方法中。
进入21世纪，学者们对早期的模型进行了更加详细的研究，修正了其中的不合理之处，同时提出了新的数学模型。Wang[8]使用数值方法建立了船-冰接触模型，关注海冰的挤压和弯曲破坏过程，将连续破冰过程理想化为“接触-挤压-弯曲破坏”的循环过程，依据几何网格方法模拟了一个固定圆锥结构和移动海冰冰排的连续接触；Su等[9]使用有限元方法建立了一个数值模型来模拟破冰船的破冰过程，将水线和海冰边界离散化，通过检测每个时间步进入水线面内的海冰边界离散点来判断船体与海冰之间是否发生接触，依据数值积分方法在纵荡、横荡、艏摇三个自由度上建立了冰载荷与船体运动之间的耦合方程；Tan等[10]基于Su等[9]提出的三自由度模型，考虑船体的升沉、横摇、纵摇，建立了冰载荷与船体运动之间的六自由度耦合方程。到目前为止，学者们提出的众多数学模型已被广泛应用于破冰船运动的研究中，但是模型中对海冰的弹性弯曲与二次断裂、船-冰动态接触对破冰过程的影响考虑较少。
本文研究破冰船在层冰中运动的特点与海冰的破坏方式，建立了包含冰载荷、敞水阻力、螺旋桨推力与舵力的六自由度动力学方程。考虑海冰的弹性弯曲对破冰力的影响，引入海冰的二次断裂与动态弯曲破坏准则，提出了更加精确、完善的船-冰动态接触模型。对瑞典破冰船Tor Viking II在层冰中的直航与回转运动进行了数值模拟，并与全尺寸试验数据对比，验证了数值模拟结果的合理性。
层冰中的连续破冰过程是一个复杂的动力学过程，船体主要受到惯性力、恢复力与包含冰载荷、敞水阻力、螺旋桨推力、舵力在内的外载荷的叠加作用。动力学方程的建立是研究该问题的基础。
首先引入两个参考系。如图2所示，大地坐标系Oe-XeYeZe，用于表达破冰船的运动轨迹与海冰的破损形状；随船坐标系O-xyz，其中原点O为中线面、水线面、中站面的交点；x轴指向船艏；y轴指向右舷，用于表达破冰船的速度、加速度等动力学物理量。
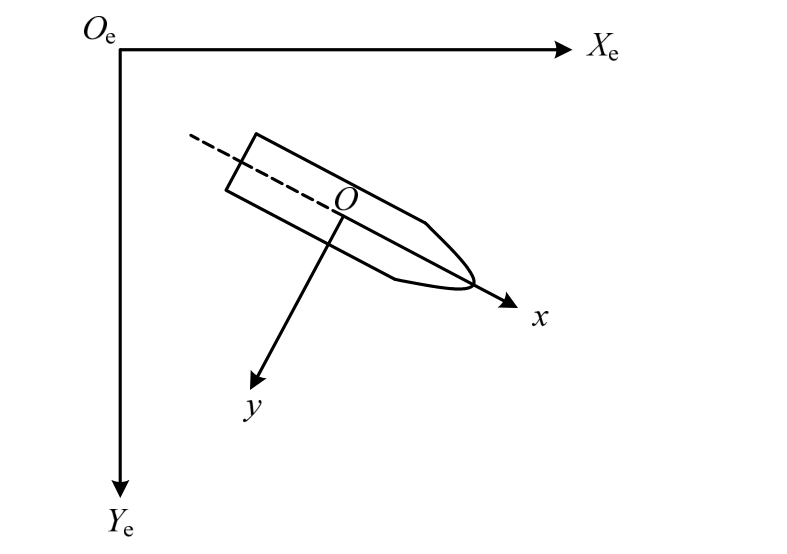
图2 大地坐标系与随船坐标系
Fig.2 Earth-fixed/ship-fixed coordinate system
破冰船在层冰中运动的六自由度动力学方程为：
式中：M为质量矩阵；A为附加质量矩阵；C为恢复力矩阵；
(t)为加速度矢量；r(t)为位移矢量；F(t)为外载荷矢量。
动力学方程的第一项为惯性力，第二项为恢复力，第三项为包含冰载荷、敞水阻力、螺旋桨推力、舵力在内的外载荷，下面将分别阐述。
1.2.1 惯性力
破冰船受到的惯性力为：
M的具体形式为：
式中：M为破冰船的质量；Ix、Iy、Iz为横摇、纵摇、艏摇转动惯量。
A的具体形式为：
式中：A1～A6为六自由度方向上的附加质量分量，可由周昭明等[11]提出的半经验公式计算得到。
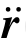(t)的具体形式为：
式中：
为六自由度方向上的加速度分量。
1.2.2 恢复力
破冰船受到的恢复力为：
C的具体形式为：
式中：ρw为海水密度；g为重力加速度；Aw为水线面面积；∇为排水体积；hx为横稳心高；hy为纵稳心高；Sy为Aw对y轴的静矩。
r(t)的具体形式为：
式中：x(t)、y(t)、z(t)、φ(t)、θ(t)、ψ(t)为六自由度方向上的位移分量。
1.3.1 冰载荷
冰载荷包含破冰力Fbrk(t)与碎冰力Fsbmg(t)。其中：Fbrk(t)为破冰船与海冰边界之间发生“接触-挤压-弯曲破坏”过程中受到的冰载荷，可由数值模拟方法得到，将在第3节中阐述。
假设楔形碎冰从完整冰排上脱落后即被立即清除，不会对后续的破冰过程产生任何影响。
sbmg(t)F为碎冰在清除过程中对船体施加的载荷，可由Lindqvist[6]提出的半经验公式得到：
式中：LWL为水线长；V为总航速；u为纵向速度；v为横向速度；Rs为淹没阻力：
式中：ρice为海冰密度；hi为海冰厚度；B为型宽；T为设计吃水；L为船长；μ为接触面摩擦系数；θ为艏柱倾角；α为水线进角；γ满足：
1.3.2 敞水阻力
敞水阻力Fow(t)由船体与海水之间的相对运动引起，主要为纵向敞水阻力，可由1957 ITTC公式近似得到：
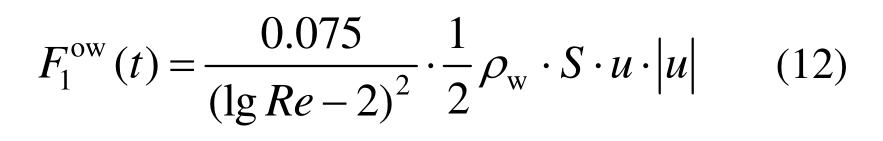
式中：Re为雷诺数；S为湿表面积。
1.3.3 螺旋桨推力与舵力
螺旋桨推力Tnet可由净推力公式[9]得到：
式中：vow为最大开阔水速；TB为系柱拉力。
螺旋桨与舵产生的力(矩)Fp(t)可表示为[9]：
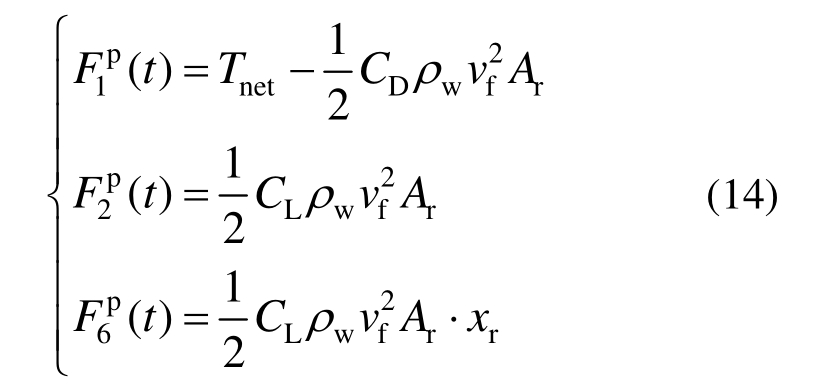
式中：CL为舵的升力系数；CD为舵的拖曳力系数；vf为流速；Ar为舵面积；xr为舵位置。上述参数的选取与计算方法参见文献[12―13]。
综上所述，F(t)的具体形式为：
式中，F1(t)～F6(t)为六自由度方向上的外载荷分量：
式(1)可由矩阵方程形式转化为关于时间的二阶常微分方程组形式，方程组中每一项均已在1.2～1.3节中阐明，将这些项代入式(1)即可得到矩阵方程的微分方程组形式。
动力学方程的求解问题实质是常微分方程组的初值问题。本文使用四阶龙格-库塔法(Runge-Kutta)求解动力学方程。二阶常微分方程组可降阶为若干一阶常微分方程的通用形式：
当x=x0时，有初值y0,y1,… ,yn。设定步长为h，当x=x0+h时，计算此时的各个函数值。四阶龙格-库塔法的迭代格式为：
假设海冰发生纯弯曲，忽略破冰船与海冰边界之间的剪切作用。理想化后的连续破冰过程为：船体先与海冰发生接触并产生挤压作用，随着破冰船的前进，船体对海冰的作用力逐渐增加，达到弯曲极限时，海冰发生弯曲破坏，楔形碎冰从完整冰排上脱落，即“接触-挤压-弯曲破坏”的循环过程。
2.1.1 水线的离散方法
为了更加精确地描述船-冰接触点的位置与海冰的破损形状，需要对水线进行精细的离散。
具体做法为：对水线型值点进行三次样条插值，在相邻型值点之间的样条曲线上取6个等间距(dWL=0.675 m)的离散点，如图3所示，“×”表示离散前的型值点，“·”表示离散后的离散点。在计算条件允许的情况下，尽量增加水线离散点的个数可以提高模拟精度。
图3 水线的离散方法
Fig.3 Discretization method of waterline
2.1.2 海冰边界的离散方法
实际上，层冰为半无限大的平面。而在本文建立的数值模拟方法中，不必建立完整层冰的数值模型，只需建立海冰边界的离散模型，即可实时模拟海冰边界在船-冰动态接触过程中的形态。本文选取的破冰船的型宽为18 m，初始海冰边界的宽度应大于型宽，因此将其设置为40 m。
具体做法为：设定初始海冰边界为与x轴垂直的线段，将其离散为若干等间距(dice=0.5 m)的离散点。随着破冰船的前进，海冰边界的形态实时变化，最终描绘出整个破冰过程中海冰边界的破损情况。
首先检测船体与海冰是否发生接触。应用Haines[14]提出的“Point-in-Polygon”法则判断离散点与封闭边界之间的位置关系。若检测到海冰边界离散点进入水线面内部，则判定船体与海冰已发生接触，如图4所示，F为首接触点，L为尾接触点。
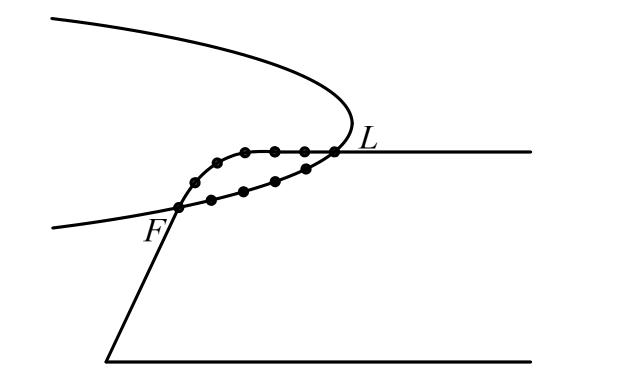
图4 接触判定
Fig.4 Contact criteria
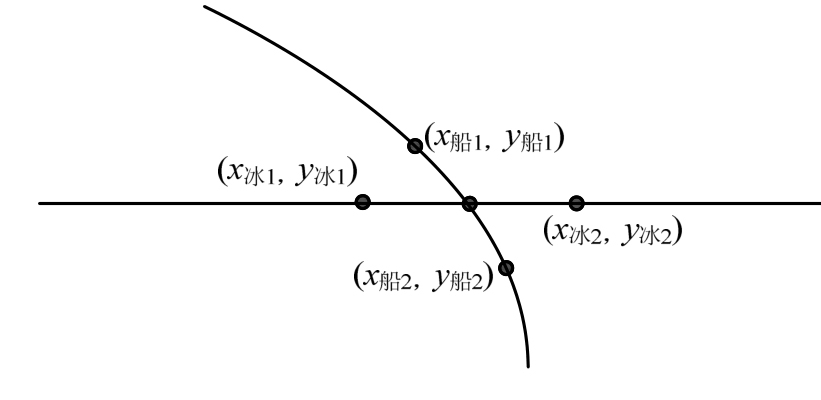
图5 接触点的确定
Fig.5 Determination of the contact point
如图5所示，当检测出船体与海冰发生接触后，可以确定刚好进入封闭边界内部的离散点
以及与其相邻的还未进入封闭边界内部的离散点
上述两个海冰边界离散点连线与两个水线离散点连线的交点即为接触点。
船体与海冰接触后产生挤压作用，船-冰接触面随即形成。假设接触面为平面，由于接触面倾角φ不同，因此将接触面分为三角形与梯形两种，如图6所示。两种接触面的面积Ac分别为：
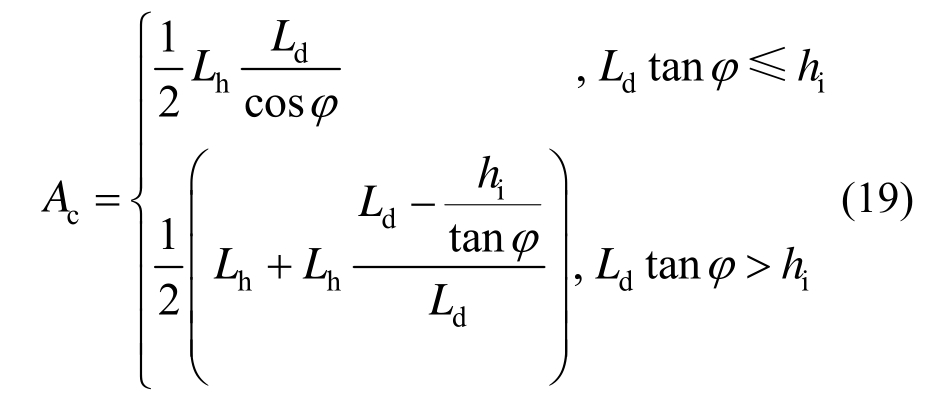
式中：Lh为F、L两点间的距离；Ld为冰楔顶点O到首、尾接触点连线
的距离。
图6 接触面积的确定
Fig.6 Determination of contact area
随着破冰船的前进，船体对海冰的作用力逐渐增加，达到弯曲极限时，海冰发生弯曲破坏，破损的海冰从完整冰排上脱落。假设海冰破损形状为圆的一部分[8]。碎冰尺寸与V成反比，与hi成正比，此外还受到船艏形状的影响。Wang[8]提出了“碎冰半径”的概念，将碎冰半径R定义为接触点与断裂点之间的距离：
式中：Cl、CV为与加载速率和海冰特征长度相关的经验常数；v2为与接触面正交的速度；l为海冰特征长度。上述参数的选取与计算方法参见文献[15]。
如图7所示，首、尾接触点F、L已在前文确定，结合碎冰半径RF、RL即可确定首、尾断裂点F1、L1，首、尾断裂点连线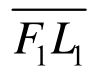
的中垂线与海冰边界的交点为冰楔顶点O，O与F1、L1连线的夹角φ为冰楔角。
由此，海冰的破损形状得以确定。其中，
为径向裂纹，弧
为环向裂纹，海冰的断裂长度
为弧
的长度：
图7 海冰破损形状的确定
Fig.7 Determination of the broken shape of sea ice
冰载荷包含
其中，
已由式(9)～式(11)得到，Fbrk(t)可由数值模拟方法得到。在破冰过程中，海冰首先发生初次断裂，随着破冰船的前进，初次断裂的海冰将发生二次断裂[4]。下面将分别阐述两次断裂过程中船体受到的Fbrk(t)。
在船体与海冰之间的接触区域内，船体受到挤压力Fcr与摩擦力μFcr的共同作用。
Fcr可由Riska[16]提出的平均挤压力公式得到：
式中：pav为海冰平均压强；k、n为经验系数。
在船-冰动态接触的过程中，由于海冰的弯曲幅度远小于l，因此将海冰的弹性弯曲简化为微幅下沉，将海水等效为弹性基础。动态过程会使Ac与Fcr减小，需对其进行修正。
如图8所示，船体侵入海冰的深度为Ld，引起海冰的下沉深度为eδ，垂向挤压高度为cδ，三者之间满足：
δe与Fcr之间的关系可由Kerr[17]提出的公式引申而来：
式中：Fcr,v为挤压力的垂向分量；D为海冰弯曲刚度。
由式(23)、式(24)可求得δe与δc。引入修正因子(δc/δv)2，则修正后的接触面积
与挤压力
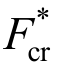为：
图8 海冰的弹性弯曲
Fig.8 Elastic bending of sea ice
如图9所示，将μFcr在接触面内分解为由水平相对速度vτ引起的水平分量fτ和由竖直相对速度v1引起的竖直分量f1，具体分解方法参见文献[18]。
图9 船体受到的局部接触力
Fig.9 Local contact forces on the ship
由文献[18]，船体受到的初次断裂破冰力在局部坐标系τnz(如图10所示)中可表示为：
式中，iφ为水线离散点i处的接触面倾角。
将其转换到O-xyz中可表示为：
式中，iα为水线离散点i处的水线进角。
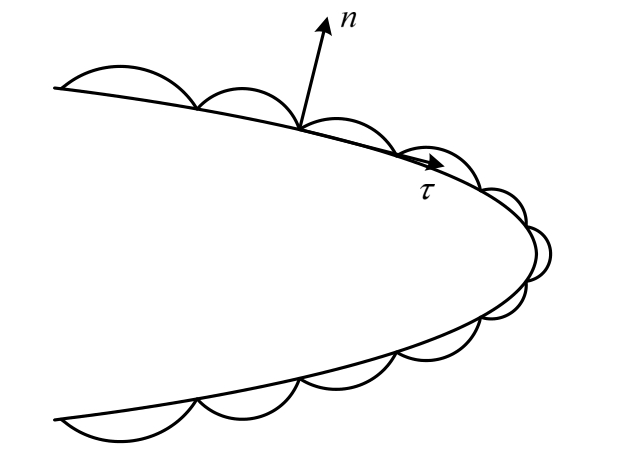
图10 局部坐标系
Fig.10 Local coordinate system
Kashtelyan等[5]通过试验观察提出了静态弯曲破坏准则：
式中：cf为经验系数；fσ为海冰弯曲强度。
由式(28)可知，静态弯曲破坏准则没有考虑到加载速率v2对海冰的弯曲破坏载荷fP的影响。然而，船-冰动态接触对破冰过程意义重大，海冰的弯曲破坏载荷、碎冰的尺寸、破冰船的动态响应都与加载速率密切相关。本文引入动态弯曲破坏准则，使海冰的断裂时机与破冰船的运动轨迹更接近真实情况。
Valanto[19]、Varsta[7]等的试验与理论研究结果表明fP与v2正相关，且受到φ的影响不大，如图11所示。
图11 弯曲破坏载荷-加载速率曲线
Fig.11 Bending failure load vs. loading rate
基于静态弯曲模型，假设动态弯曲破坏载荷
与
成正比，通过因次分析得到无量纲系数λt(v2)：
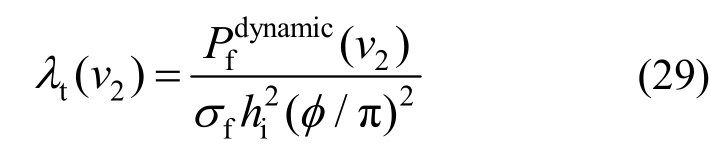
图12为无量纲系数-加载速率曲线，通过对曲线进行拟合，得到λt(v2)的近似表达式：
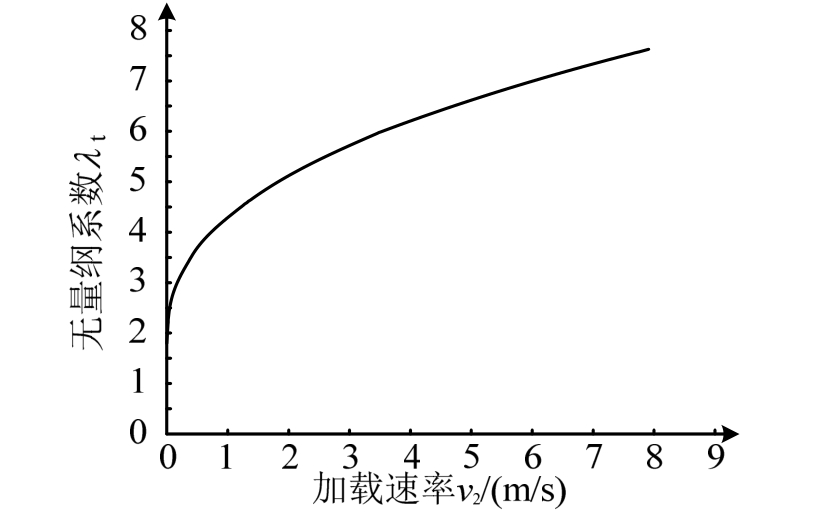
图12 无量纲系数-加载速率曲线
Fig.12 Dimensionless coefficient vs. loading rate
由式(29)、式(30)得到动态弯曲破坏准则：
当
时，海冰不会发生弯曲破坏，随着船体的前进，Fz逐渐增大，当
时，海冰就会发生弯曲破坏，楔形碎冰将从完整冰排上脱落，形成新的海冰边界。
目前，学者们对海冰初次断裂的研究比较透彻，但是海冰的二次断裂有待深入研究。二次断裂对冰载荷的作用周期影响很大，本文引入海冰的二次断裂，使破冰力的数值与冰载荷的作用周期更接近真实情况。
船艏与海冰的相互作用和倒锥体与海冰的相互作用之间的相似度很高。武文华等[20]使用显式动力分析软件LS-DYNA模拟了海冰和锥体抗冰结构相互作用的弯曲断裂过程；王刚等[21]使用三维有限元方法，对不同接触宽度的海冰与锥体相互作用过程进行了数值分析，得到了冰排环向应力和径向应力的分布规律；Di等[22]使用离散元方法模拟了层冰的破坏过程，计算了锥体结构受到的冰载荷；天津大学冰工程实验室通过倒锥体冰力学试验模拟了船艏与海冰的相互作用，黄焱等[4]在试验中发现，倒锥体前方的海冰会发生二次断裂。
图 13为破冰力的时域分析曲线，由图可知，一个大振幅的破冰力加-卸载过程总是伴随着一个小振幅的破冰力加-卸载过程。其中，F1为初次断裂时的极限破冰力；t1为破冰力达到F1时的加载时间；t2为F1的卸载时间；F3为F1卸载后的残余冰力；F2为二次断裂时的极限破冰力；t3为破冰力达到F2时的加载时间；t4为F2的卸载时间；T1为初次断裂周期；T2为二次断裂周期；T为整个海冰断裂过程的周期。
通过对曲线进行分段线性插值，得到整个海冰断裂过程中破冰力的近似表达式：
图13 破冰力的时域分析曲线
Fig.13 The time-domain analysis curve of icebreaking force
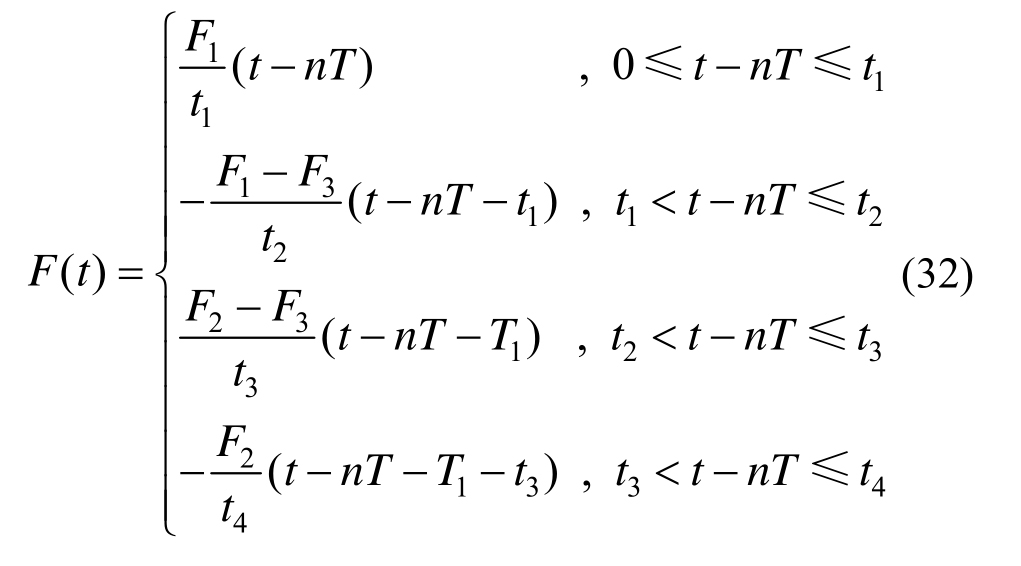
由试验可知，各个时间参数之间的比例关系为：
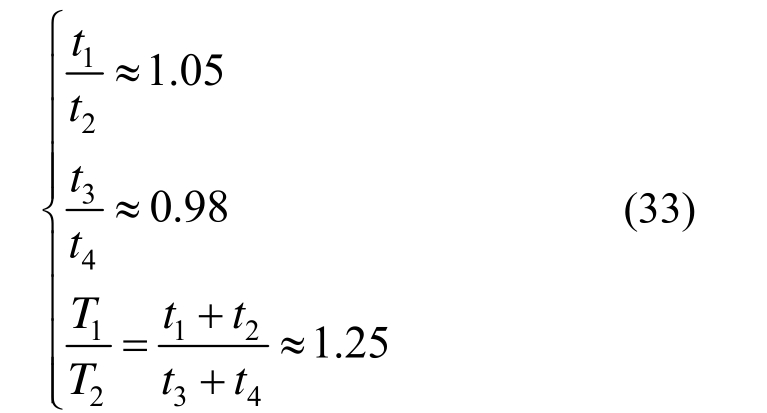
式中，t1可由3.1～3.2节确定，由式(33)可求得t2、t3、t4、T1、T2、T与t1的关系。
F1、F2、F3之间满足：
由试验可知，r与
均为φ与u的函数：
式中，F1可由3.1～3.2节确定，由式(34)、式(35)可求得F2、F3。
将上述参数代入式(32)即可求得整个海冰断裂过程中任意时刻的破冰力。
基于上述数值模拟方法，使用FORTRAN语言编写并运行数值计算程序，使用四阶龙格-库塔法求解六自由度动力学方程，模拟瑞典破冰船 Tor Viking II在层冰中的直航与回转运动，并与全尺寸试验数据[23]对比，验证数值模拟结果的合理性。
Tor Viking II的主要参数见表1，海冰的环境参数见表2。
表1 Tor Viking II主要参数
Table 1 Main parameters of Tor Viking II
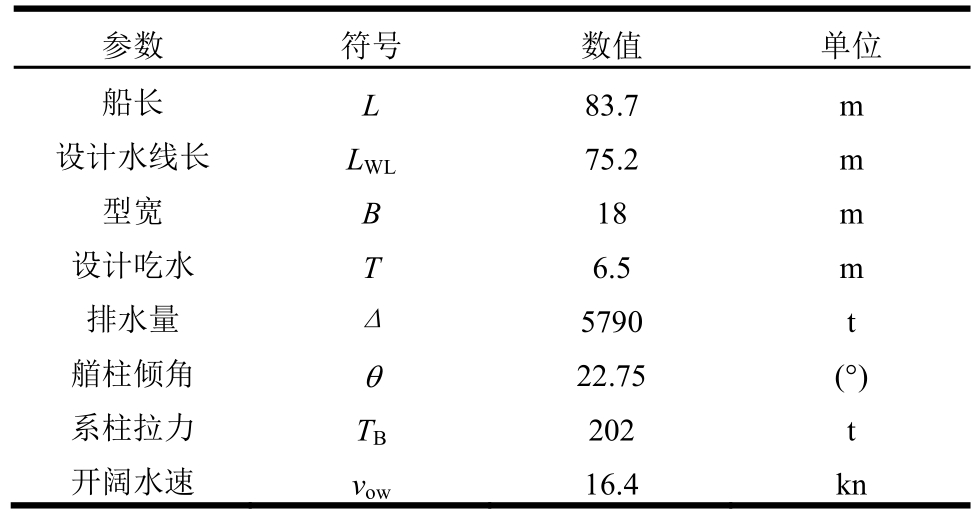
参数 符号 数值 单位船长L83.7 m设计水线长LWL75.2 m型宽B18m设计吃水T6.5 m排水量Δ5790 t艏柱倾角θ22.75 (°)系柱拉力TB202 t开阔水速vow16.4 kn
表2 海冰环境参数
Table 2 Environmental parameters of sea ice
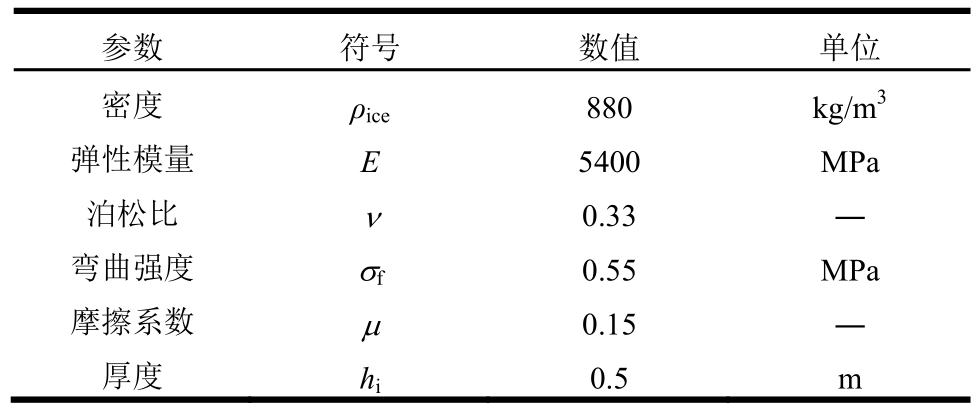
参数 符号 数值 单位密度ρice880 kg/m3弹性模量E5400 MPa泊松比ν0.33 ―弯曲强度σf0.55 MPa摩擦系数μ0.15 ―厚度hi0.5 m
本文依据Tor Viking II的全尺寸试验方案确定数值模拟方案。设定海冰的初始边界与x轴平行，hi=0.5 m，Tor Viking II的纵向初速度为 3 kn(1.5432 m/s)，横向初速度与初始回转角速度为0。首先沿y轴正向直航 50 s，然后操右舵 45°开始做回转运动。
图14为模拟Tor Viking II航行160 s后的运动轨迹。由于海冰边界对破冰船运动的阻碍作用逐渐增大，导致运动轨迹为曲率半径逐渐减小的圆弧，因此将破冰船首次回转 180 °时的回转直径定义为最大回转直径。通过统计Tor Viking II在0～160 s内每隔10-3s的大地坐标系横坐标值(Xe)，得到数值模拟中的最大回转直径为512 m。
图14 模拟运动轨迹(hi=0.5 m)
Fig.14 Simulated trajectory(hi=0.5 m)
图15 为Tor Viking II在全尺寸试验中的真实运动轨迹，通过与图 14对比可知，模拟运动轨迹与真实运动轨迹相符。表3为Tor Viking II的全尺寸试验数据，由表可知，全尺寸试验中的最大回转直径为495 m。因此，数值模拟的相对误差仅为3.32%。
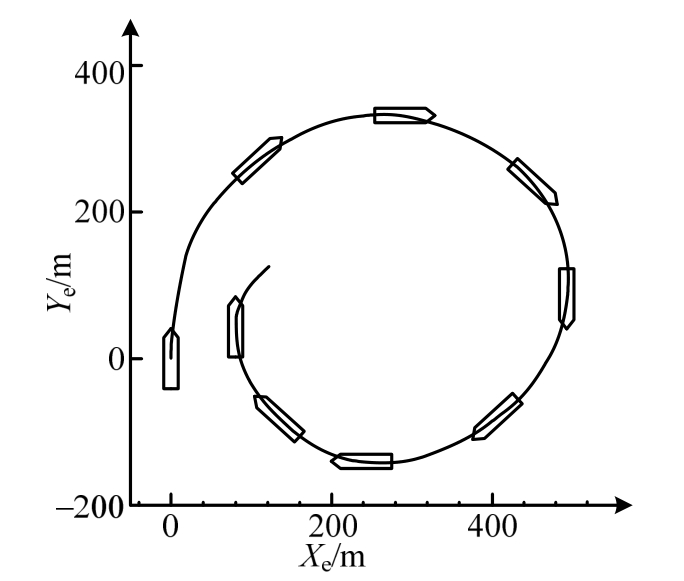
图15 真实运动轨迹(hi=0.5 m)
Fig.15 Real trajectory(hi=0.5 m)
表3 Tor Viking II全尺寸试验数据
Table 3 Full-scale trial data of Tor Viking II
ψ/(°)Xe/mYe/m 0.0 0.0 0.0 44.8 108.0 269.4 89.5 288.5 329.5 134.7 453.2 237.2 180.3 495.0 81.5 225.1 406.2 -81.8 270.2 240.8 -140.9 315.0 132.9 -80.4 359.7 79.9 42.6
图16(a)为纵向速度曲线，由图可知，Tor Viking II的纵向初速度为3 kn(1.5432 m/s)，56 s后达到峰值 6.2 m/s；121 s后减小为负值，此时纵向速度的方向变为y轴负向。图16(b)为横向速度曲线，由图可知，Tor Viking II的横向初速度为0，158 s后再次变为0，此时航向变为y轴负向。图16(c)为回转角速度曲线，由图可知，Tor Viking II的初始回转角速度为0，124 s后明显增大，此时加速回转，回转直径减小。
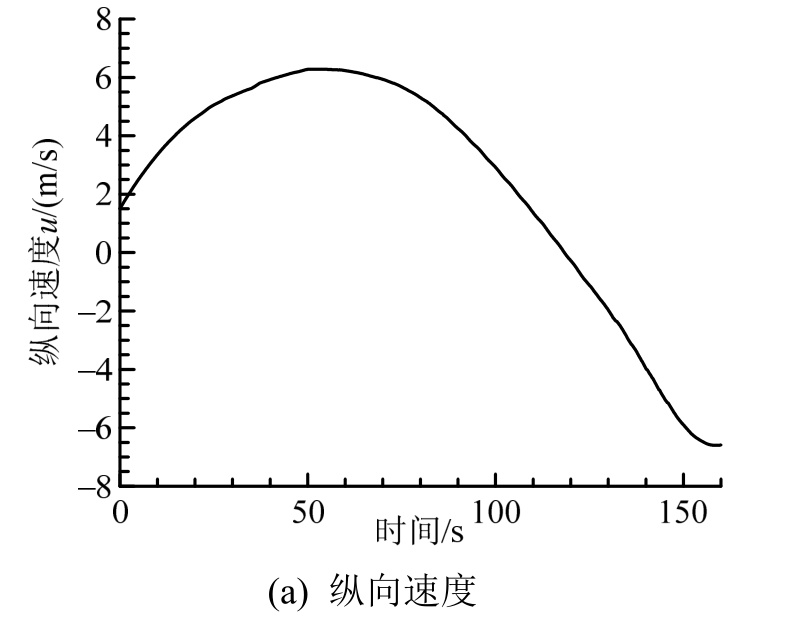
图16 航行速度曲线
Fig.16 Velocity curves
图17 (a)为纵向冰阻力曲线，由图可知，0～50 s内为直航冰阻力，通过统计Tor Viking II在0～50 s内每隔10-3s的阻力值，得到直航冰阻力的算术平均值为150.4 kN，与Lindqvist[6]提出的半经验公式的计算结果吻合。Tor Viking II的纵向冰阻力在120 s～140 s内由正值逐渐变为较大负值，此时纵向速度的方向发生反转。图17(b)为横向冰阻力曲线，由图可知，Tor Viking II的横向冰阻力在0～50 s内在0附近振荡，此时处于直航状态；在120 s～140 s内为较大负值，此时处于加速回转状态。
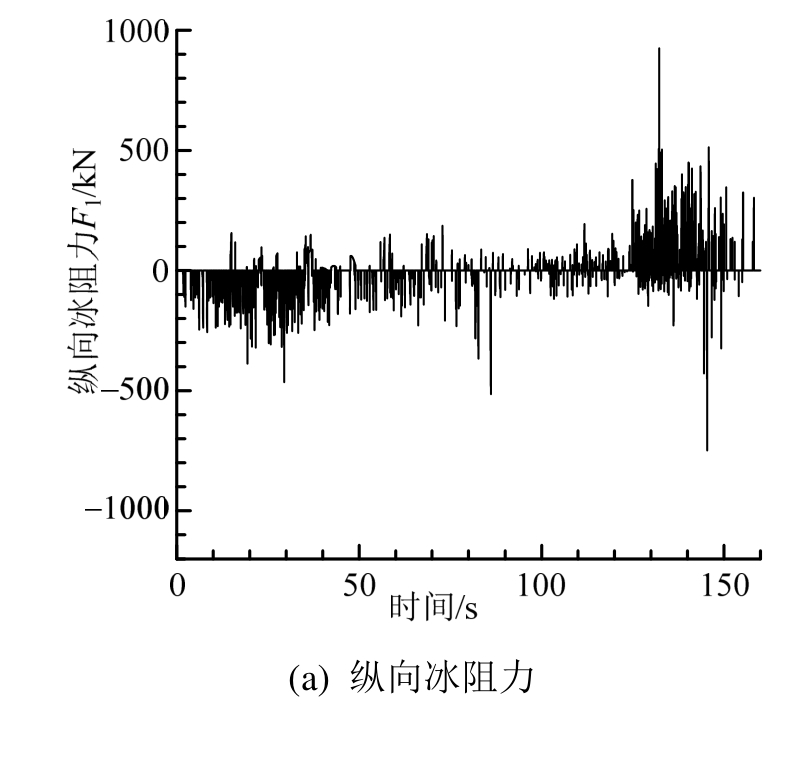
图17 航行冰阻力曲线
Fig.17 Ice resistance curves
图18 (a)为升沉运动响应曲线，图18(b)为横摇运动响应曲线，图18(c)为纵摇运动响应曲线，由图可知，Tor Viking II在升沉、横摇、纵摇三个自由度上的运动响应均在0附近呈现周期性小幅振荡。通过统计Tor Viking II在0～160 s内每隔10-3s的运动响应值，得到升沉、横摇、纵摇运动响应的算术平均值分别为0.02 m、0.0075 rad、0.001 rad，说明Tor Viking II的直航与回转运动过程比较稳定。
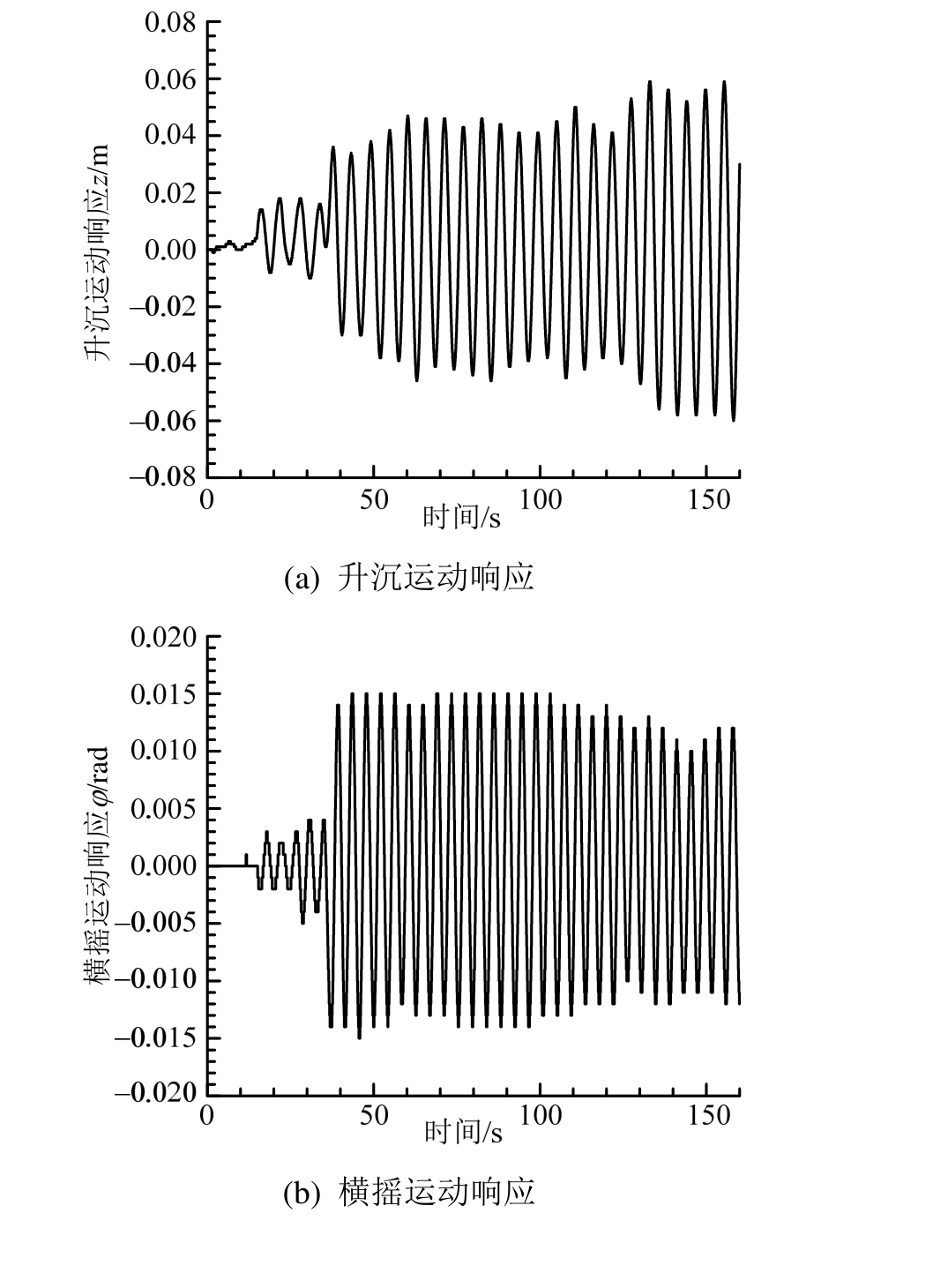
图18 运动响应曲线
Fig.18 Motion response curves
本文研究破冰船在层冰中运动的特点与海冰的破坏方式，建立了破冰船在层冰中运动的六自由度动力学方程，提出了更加精确、完善的船-冰动态接触模型，对瑞典破冰船Tor Viking II在层冰中的直航与回转运动进行了数值模拟，并与全尺寸试验数据对比，验证了数值模拟结果的合理性。得出以下结论：
(1) 模拟运动轨迹与真实运动轨迹相符，最大回转直径的相对误差仅为3.32%，说明本文建立的数值模拟方法能够真实地模拟破冰船在层冰中的运动。
(2) 虽然本文建立的数值模拟方法的精度受到理想化假设与经验公式的限制，但其优势在于：当其中的数据、公式、模型在未来得到改进时，能够很方便地对现有程序进行修改与完善，从而提高模拟精度。
为了更加精确、细致地模拟破冰船在层冰中运动，还需进一步开展以下研究工作：
(1) 考虑海冰厚度、弯曲强度等服从某种概率分布而非某一固定值。
(2) 考虑破冰船的六自由度运动对船舶各方面性能的影响。
(3) 考虑海水与海冰的相互作用及其对船舶运动的影响。
[1]Ettema R, Sharifi M B, Georgakakos K P, et al. Chaos in continuous-mode icebreaking [J]. Cold Regions Science ＆ Technology, 1991, 19(2): 131―144.
[2]Izumiyama K, Kitagawa H, Koyama K, et al. On the interaction between a conical structure and ice sheet [C]//11st International Conference on Port and Ocean Engineering under Arctic Conditions (POAC), 1991:155―166.
[3]Liu R, Xue Y, Lu X, et al. Simulation of ship navigation in ice rubble based on peridynamics [J]. Ocean Engineering, 2018, 148: 286―298.
[4]黄焱, 关湃, 禹沐. 破冰船航行状态在海冰作用下的运动响应分析[J]. 数学的实践与认识, 2015, 45(2):149―160.Huang Yan, Guan Pai, Yu Mu. Study of the sailing’s moving responses of an icebreaker in ice [J].Mathematics in Practice ＆ Theory, 2015, 45(2): 149―160. (in Chinese)
[5]Kashtelyan V I, Poznyak I I, Ryvlin A Y. Resistance of ice to ship movement [J]. Sudostroyeniye (Soviet Shipbuilding) [USSR], 1968.
[6]Lindqvist G. A straightforward method for calculation of ice resistance of ships [C]// 10th International Conference on Port and Ocean Engineering under Arctic Conditions (POAC), 1989: 722―735.
[7]Varsta P. On the mechanics of ice load on ships in level ice in the Baltic Sea [J]. 1983(8).
[8]Wang S. A dynamic model for breaking pattern of level ice by conical structures [J]. 2001(156): 2+6―94.
[9]Su B, Riska K, Moan T. A numerical method for the prediction of ship performance in level ice [J]. Cold Regions Science ＆ Technology, 2010, 60(3): 177―188.
[10]Tan X, Su B, Riska K, et al. A six-degrees-of-freedom numerical model for level ice-ship interaction [J]. Cold Regions Science ＆ Technology, 2013, 92(8): 1―16.
[11]周昭明, 盛子寅, 冯悟时. 多用途货船的操纵性预报计算[J]. 船舶工程, 1983(6): 21―29.Zhou Zhaoming, Sheng Ziyin, Feng Wushi. On maneuverability prediction for multipurpose cargo ship[J]. Ship Engineering, 1983(6): 21―29. (in Chinese)
[12]Bertram V. Practical ship hydrodynamics [M]. Oxford,UK: Elsevier/Butterworth-Heinemann, 2012: 177―203.
[13]盛振邦, 刘应中. 船舶原理. 下册[M]. 上海: 上海交通大学出版社, 2005: 304―332.Sheng Zhenbang, Liu Yingzhong. Principle of naval architecture. Vol. 2 [M]. Shanghai: Shanghai Jiaotong University Press, 2005: 304―332. (in Chinese)
[14]Haines E. Point in polygon strategies [J]. Graphics Gems IV, 1994: 24―46.
[15]Zhou Q, Peng H, Qiu W. Numerical investigations of ship-ice interaction and maneuvering performance in level ice [J]. Cold Regions Science ＆ Technology, 2016,122(1): 36―49.
[16]Riska K. Models of ice-structure contact for engineering applications [J]. Studies in Applied Mechanics, 1995,42(06): 77―103.
[17]Kerr A D. The bearing capacity of floating ice plates subjected to static or quasi-static loads [J]. Journal of Glaciology, 1975, 17(76): 229―268.
[18]Tan X, Su B, Riska K, et al. The effect of heave, pitch and roll motions to ice performance of ships [C]// Iahr International Symposium on Ice, 2012: 1080―1093.
[19]Valanto P. The icebreaking problem in two dimensions:experiments and theory [J]. Journal of Ship Research,1992, 36(4): 299―316.
[20]武文华, 于佰杰, 许宁, 等. 海冰与锥体抗冰结构动力作用的数值模拟[J]. 工程力学, 2008, 25(11): 192―196.Wu Wenhua, Yu Baijie, Xu Ning, et al. Numerical simulation of dynamic ice action on conical structure [J].Engineering Mechanics, 2008, 25(11): 192―196. (in Chinese)
[21]王刚, 武文华, 岳前进. 锥体接触宽度对冰排弯曲破坏模式影响的有限元分析[J]. 工程力学, 2008, 25(1):235―240.Wang Gang, Wu Wenhua, Yue Qianjin. FEM analysis on ice-bending failure mode with width effect of ice-cone interaction [J]. Engineering Mechanics, 2008, 25(1):235―240. (in Chinese)
[22]Di S, Xue Y, Wang Q, et al. Discrete element simulation of ice loads on narrow conical structures [J]. Ocean Engineering, 2017, 146(12): 282―297.
[23]Riska K, Leiviskä T, Nyman T, et al. Ice performance of the Swedish multi-purpose icebreaker Tor Viking II [C]//16st International Conference on Port and Ocean Engineering under Arctic Conditions (POAC), 2001:849―866.
NUMERICAL SIMULATION METHOD FOR MOTIONS OF THE ICEBREAKER IN LEVEL ICE
王永魁(1993―)，男，江苏人，博士生，主要从事结冰过程数值模拟与实验研究(E-mail: kui930927@163.com);
贾 宾(1994―)，男，山东人，博士生，主要从事船-冰作用中海冰破坏模式研究(E-mail: jiabin994830@live.cn);
王键伟(1993―)，男，黑龙江人，硕士生，主要从事破冰船运动数值仿真研究(E-mail: wangjw0519@126.com);