
图1 原型结构图
Fig.1 Prototype structure diagram
自从英国 Ronan Point公寓连续性倒塌事故[1]发生以来,多层结构的防连续性倒塌引起了工程界的关注。所谓连续性倒塌,即由初始的局部破坏,从构件到构件扩展,最终导致一部分或整个结构倒塌。一般来说结构的最终破坏状态与初始破坏状态不成比例。引起连续倒塌的因素主要为煤气爆炸、炸弹袭击、车辆撞击、火灾等意外事件。
为了研究RC框架结构体系在偶然荷载作用下发生连续倒塌破坏的可能性、倒塌过程中力的转换机制以及结构受力特性等机理,国内外学术界和工程界对倒塌破坏实例进行了大量的分析,开展了大量的抗连续性倒塌试验研究。Powell[2]利用能量平衡原理对1个一层两跨框架结构进行了抗连续性倒塌分析,在失去中柱时结构的重力势能逐渐转变为该结构的变形能和动能,当重力势能完全转化为变形能,结构的位移达到最大值,此时框架动能为零。Zdenfk[3]从能量平衡的角度阐述连续性倒塌:当结构外部受到撞击所产生的动能超过了结构自身能吸收能量限制时,结构将发生连续性倒塌。易伟建等[4]利用拟静力试验方法对1榀三层四跨钢筋混凝土平面框架进行了抗连续性倒塌试验研究。Su等[5]通过数值分析模型研究了不同梁配筋率、梁跨高比和加载速率下的钢筋混凝土框架子结构抗连续性倒塌的性能,预测模型的压拱机制与悬链线机制的能力。Lew[6]进行了 2个不同抗震等级的足尺梁柱框架子结构抗连续性倒塌试验并进行模拟分析。陆新征等[7-9]开展了 RC框架子结构拟静力倒塌的系列试验研究,包括1个三层四跨RC框架、2个关键梁柱节点和4个关键框架柱。研究表明纤维模型仍然是最适合的计算模型。Bao等[10]通过使用宏模型对 RC框架结构的连续性倒塌过程进行数值分析,利用高仿真有限元分析软件同样对这一倒塌过程进行模拟表明了宏模型是有效性。Ren等[11]和Lu等[12]通过试验研究了单向约束梁板系统移除中柱和边柱情况下楼板所起到的作用。结果表明楼板可以显著提高结构的抗连续性倒塌承载力。Jun等[13-14]利用Ls-dyna显示有限元分析了梁板子结构移除边柱过程中的荷载转化机理和承载能力,探讨了边界约束、板厚和板筋等对子结构受力机理的影响,且研究认为将楼板等效为T或L型梁的翼缘低估了大变形下结构的承载力。Pham 等[15]利用数值模拟分析了均布加载下梁板子结构移除框架柱的破坏模式和承载能力。分析发现,楼板悬膜效应对边界条件的依赖远小于梁悬链线效应,并且梁悬链线效应在梁板系统分析中可以保守的忽略。Dat等[16]通过理论和数值分析了双向约束作用下梁板楼盖系统在移除中柱情况下的荷载传递路径和承载能力,研究表明楼板可以大大提高框架结构的承载能力。刁梦竹等[17]提出将楼板沿两个平面方向离散形成一个梁网,每个方向上的网格线采用纤维梁单元来模拟钢筋和混凝土的组合受力行为的方法大大提高了整体结构运算效率。周育泷等[18]建立的压拱机制下梁板子结构系统的连续倒塌抗力分析模型,在计算梁板共同作用下的连续倒塌抗力时精度提高显著。左文武[19]通过 SAP2000软件建立空间框架结构模型,分析了楼板对框架结构倒塌性能的影响,并分析了局部楼板破坏时结构的承载能力。刘帅[20]利用ABAQUS软件中的梁单元建立空间结构的分析模型,讨论了不同层数的结构防连续倒塌的能力。李晓路等[21]建立了纵横向均为2跨的单层空间框架模型,分析了梁板柱相互作用下结构的承载能力。戎贤等[22]进行的1/3比例缩尺的两层3×2跨的空间框架底层边柱和角柱的拟静力倒塌试验表明楼板和梁的钢筋产生的悬链线效应在异形柱空间框架倒塌中发挥重要作用。
基于前述研究成果表明,对于RC框架结构,典型的替代路径法(ALP)包括弯曲作用、压拱作用和悬链线作用[23]。弯曲作用是基于RC结构构件的受弯能力而其承载力较小,压拱作用和悬链线作用承载力将会超过常规设计承载力,尤其是悬链线作用,在结构大变形下形成并且充分利用了钢筋的抗拉强度,被认为是结构抵抗连续性倒塌的最后一道防线。压拱作用和悬链线作用的发挥与周边约束密切相关,因此研究周围框架对研究子结构约束的强弱及承载力的影响很有必要。另外,楼板作为框架结构的组成构件,在框架结构防连续倒塌中常常被忽略,板在结构受力中形成压膜作用和拉膜作用,有利于结构防连续性倒塌。进一步地,研究符合实际结构的多层空间框架结构防连续倒塌承载能力很有必要。
本文利用有限元软件ABAQUS强大的非线性分析功能,建立了精细的有限元模型,对Qian等[24]做的试件进行模拟分析,模拟过程中考虑了材料非线性、边界条件非线性以及结构大变形的影响。在校准有限元计算模型的基础上,为了进一步研究框架边跨对研究子结构性能的影响,对平面框架设置了不同的边跨约束工况,分析了静力荷载下框架子结构防连续性倒塌性能的承载能力;另外建立单层空间框架模型,研究静力荷载作用下考虑楼板的 RC框架结构在框架柱失效时的防连续倒塌的能力,分析楼板在整体结构防连续性倒塌受力过程中的作用;进一步地,建立多层空间框架模型,研究其在底层不同位置处框架柱移除过程中的承载能力,分析楼层对结构防连续倒塌性能的影响。
本文研究的原型结构为1栋纵横向均为四跨层高为3.6 m的三层框架结构,如图1所示。柱截面是边长为800 mm的正方形截面,纵横向框架梁截面分别为400 mm×720 mm和320 mm×560 mm,楼板厚度为220 mm。本文按照1/4缩尺建立RC框架结构防连续倒塌有限元分析模型,见表1。

图1 原型结构图
Fig.1 Prototype structure diagram
表1 分析模型表
Table 1 Analytical models

模型编号 尺寸规格 模型信息PF1 1/4缩尺 平面框架结构,两侧无边跨约束作用PF2 1/4缩尺 平面框架结构,右侧有边跨约束作用PF3 1/4缩尺 平面框架结构,两侧有边跨约束作用SF4 1/4缩尺 单层空间框架,不考虑楼板作用SF5 1/4缩尺 单层空间框架,考虑楼板作用SF6 1/4缩尺 一层空间框架结构SF7 1/4缩尺 二层空间框架结构SF8 1/4缩尺 三层空间框架结构
利用南洋理工大学 Qian等[24]的框架子结构拟静力试验结果校验分析模型的正确性,并分别利用平面框架和空间框架模型研究其在静力荷载下防连续倒塌的承载能力。
Qian等[24]进行了 1批 1/4缩尺框架子结构试验,试件参数见表2,包括P、T和S三个系列,每个系列包括2个试件。P系列试件为平面框架,包括三根柱两根梁,T系列为十字型交叉空间框架,包括五根柱四根梁,S系列试件为考虑楼板作用的田字形空间框架,包括九根柱十二根梁。这批试件均为短柱头,且边柱柱头配筋局部加强。图2给出了试件S1的规格尺寸和钢筋布置图。试件P1和P2参数分别同S1试件B-B和A-A剖面的平面框架,试件T1参数同S1试件中十字型交叉空间框架。表3为试验材料力学性能表。
表2 试验构件信息表
Table 2 Specimen properties

构件编号试件规格 纵向钢筋 横向箍筋柱截面/mm2梁截面/mm2梁轴跨/mm 板厚/mm 柱纵筋 梁纵筋 板配筋 节点/(%) 梁截面/(%)P1 200×200 100×180 2100 — 4T13 4T10 — 0.8 0.5 P2 200×200 80×140 1500 — 4T13 4T10 — 0.8 0.6 T1 200×200 100×180/80×140 2100/1500 — 4T13 4T10 — 0.8 0.5/0.6 T2 200×200 80×140 1500 — 4T13 4T10 — 0.8 0.6 S1 200×200 100×180/80×140 2100/1500 55 4T13 4T10 R6@250 0.8 0.5/0.6 S2 200×200 80×140 1500 55 4T13 4T10 R6@250 0.8 0.6
表3 材料性能参数
Table 3 Properties of materials

项目 钢筋类型屈服强度fy/MPa屈服应变εy/µɛ极限强度fu/MPa伸长率δ/(%)R6 355 1910 465 17.5 T10 437 2273 568 13.1 T13 535 2605 611 11.6 T16 529 2663 608 14.3混凝土 圆柱体抗压强度分别为:P1:19.9 MPa P2:20.8 MPa T1:21.5 MPa S1:21.4 MPa钢筋
试验过程通过位移控制在S1试件中柱Z2上表面按比例线性施加向下的集中位移来模拟中柱移除过程,试验加载直至试件破坏失效。其余试件加载与其相同,在边柱头固定情况下,中柱上表面逐渐施加静力荷载。得到了试件的荷载位移曲线与承载能力。
1.2.1 混凝土本构
本文利用有限元软件ABAQUS模拟Qian等[24]所做的框架子结构试验的力学性能,利用损伤塑性CDP模型模拟混凝土的非线性行为。CDP模型是连续的、基于塑性的混凝土损伤模型,采用各向同性弹性损伤及各向同性拉伸和压缩塑性理论来表征混凝土的非弹性行为[25]。ABAQUS损伤塑性模型将损伤指标引入混凝土模型,对混凝土的弹性刚度矩阵加以折减,以模拟混凝土的卸载刚度随损伤增加而降低的特点,并且将非关联硬化引入混凝土塑性本构模型中,以期更好的模拟混凝土的受压弹塑性行为[26]。

图2 试件S1尺寸与配筋图
Fig.2 Dimension and reinforcement details of S1
混凝土的损伤包括受拉开裂和受压压溃两种主要的破坏模式,分别由受拉和受压的等效塑性应变控制。表4列出了定义CDP模型的五个参数。
表4 CDP模型参数[25]
Table 4 Parameter of CDP model

参数名称膨胀角Ψ流动势偏移量∈双单轴抗压强度比σb0/σc0屈服面形状参数Kc粘性系数μ数值 30 0.1 1.16 0.6667 0.0005
本文采用图 3(a)所示的混凝土单轴应力-应变关系曲线,这是我国《混凝土结构设计规范》(GB 50010-2010)[27]推荐的曲线,包括混凝土单轴受压和受拉应力-应变曲线,分别模拟混凝土受拉开裂和受压压溃过程的受力性能。
1.2.2 钢筋本构
根据表3的试验结果,纵向受力钢筋采用线性强化模型,考虑到连续倒塌过程中钢筋会发生断裂,钢筋单轴应力应变曲线采用如图3(b)所示的本构,钢筋应力达到极限值后会降为一个很小的应力值,并保持稳定,模拟中以此下降点作为钢筋断裂的依据。用理想弹塑性模型来模拟箍筋。在ABAQUS软件中用传统的金属塑性来模拟钢材的性能。
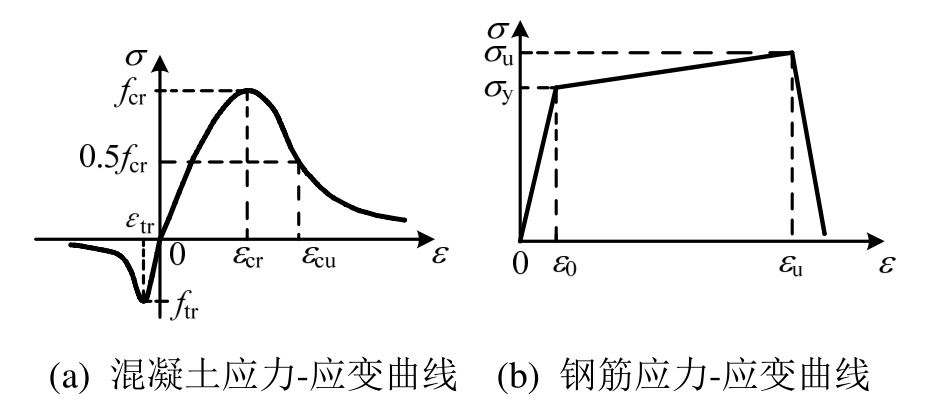
图3 材料应力-应变曲线
Fig.3 Stress-strain curve of materials
模型中混凝土采用三维六面体减缩实体单元C3D8R,钢筋采用三维二节点桁架单元 T3D2,钢筋骨架通过EMBED命令嵌入到混凝土中,这种方式能够很好的模拟钢筋与混凝土一起受力的性能。混凝土单元网格大小为 30 mm,钢筋单元大小为50 mm,网格划分采用结构化网格划分技术。图 4给出了试件S1的有限元模型图。

图4 试件S1有限元模型图
Fig.4 Finite element model of S1
为了简化计算,提高运算速度,本模型对Qian等[24]系列试验的边界条件进行了简化模拟,忽略了固定用的螺栓和钢板的影响,两个边柱头上下表面均采用完全固定约束。根据试验过程荷载的施加方式,模型采用位移控制施加集中荷载,施加点为与中柱上表面耦合在一起的参考点,约束中柱的转动,使其竖直向下运动。利用 ABAQUS/Standard通用分析模块求解。
图5为试件P1的模拟结果,从图中可以看出模拟曲线和试验曲线吻合较好,变化趋势相同。在压拱机制峰值荷载之前,试验值和模拟值基本重合,在压拱机制峰值荷载到悬链线机制峰值荷载之间,模拟曲线稍高于试验曲线。压拱机制和悬链线机制峰值荷载的模拟值稍大于试验值。图6为试件P2的模拟结果,同P1的模拟结果一样,P2试验曲线和模拟曲线吻合良好,尤其是悬链线机制的上升段,模拟曲线与试验曲线基本重合。关键节点的荷载和位移值见表5。

图5 试件P1试验与模拟荷载-位移曲线
Fig.5 Tested and simulated load-displacement carve of P1
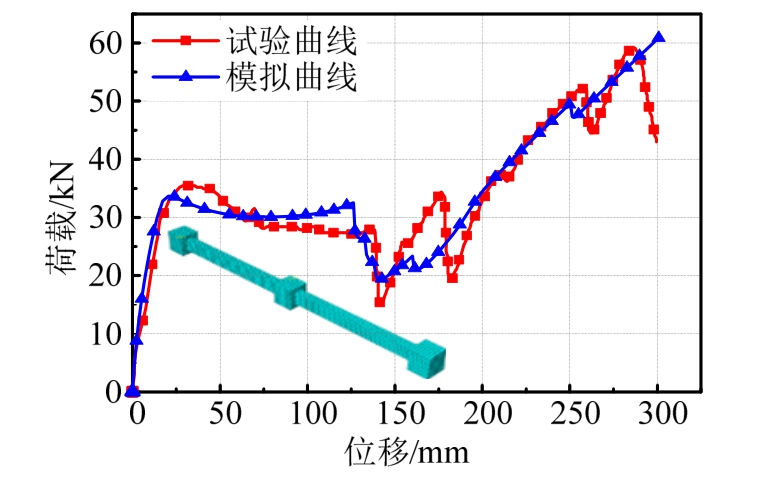
图6 试件P2试验与模拟荷载-位移曲线
Fig.6 Tested and simulated load-displacement carve of P2
图7 为试件T1的模拟结果,从图中可以看出模拟曲线和试验曲线吻合较好。在压拱机制峰值荷载之前,试验曲线和模拟曲线完全重合,在压拱机制荷载后下降段有所差异,悬链线机制上升阶段试验曲线和模拟曲线吻合良好。压拱机制峰值荷载的模拟值和试验值相差很小,悬链线机制荷载的模拟值和试验值也较为吻合。图8为试件S1的模拟结果。压拱机制峰值荷载前试验曲线和模拟曲线有所差异,悬链线机制上升段试验曲线和模拟曲线吻合很好。所不同的是试验曲线在压拱机制峰值荷载之后有所降低,而模拟曲线则没有明显下降阶段,相对变得平缓,然后继续上升。关键节点的荷载和位移值见表5。
图9~图11分别为试件P1、T1和S1试验和模拟破坏裂缝模式对比图。P1试件的试验破坏裂缝模式与模拟破坏裂缝模式相同,中柱端梁端下部混凝土受拉开裂,上部受压破坏;边柱端梁端上部混凝土受拉开裂,下部受压破坏。T1试件的试验破坏裂缝模式与模拟结果有所差异,试验试件破坏主要为一根短跨梁在靠近中柱处受剪破坏,而模拟结果为在短跨梁出现剪切裂缝,但子结构长跨方向还可以继续承载;S1试件试验与模拟破坏裂缝模式显示在楼板上表面均形成裂缝环,靠近板的外边的为受拉裂缝环,靠近中柱位置的为受压开裂环。梁的破坏为靠近中柱的梁端下部混凝土受拉开裂破坏。
表5 Qian K等系列试件试验与模拟对比表
Table 5 Comparison of tested and simulated of Qian K et al series specimens

注:系列试件的模拟悬链线峰值分别取试验悬链线位移所对应的中柱反力。
?

图7 试件T1试验与模拟荷载位移曲线
Fig.7 Tested and simulated load-displacement carve of T1
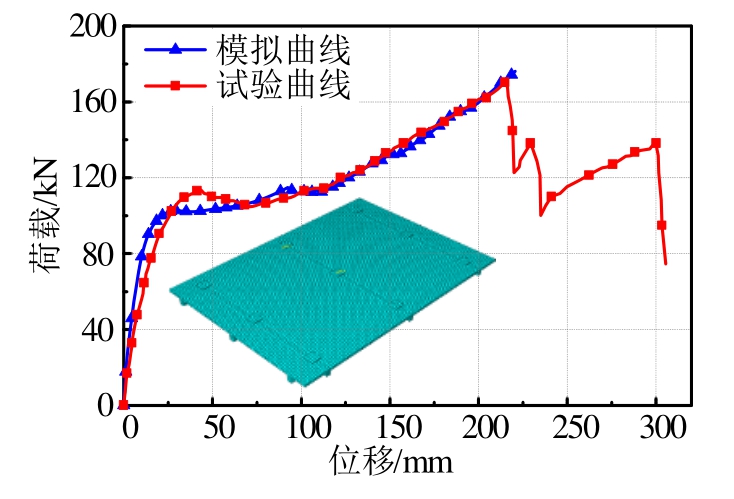
图8 试件S1试验与模拟荷载位移曲线
Fig.8 Tested and simulated load-displacement carve of S1

图9 P1破坏模式
Fig.9 Failure mode of P1

图10 T1破坏模式
Fig.10 Failure mode of T1
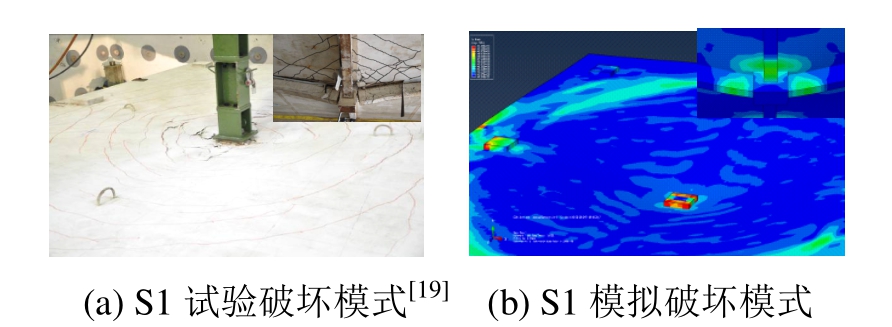
图11 S1破坏模式
Fig.11 Failure mode of S1
平面框架结构的受力性能与其周围构件的约束情况密切相关,尤其是在结构中柱失效情况下,荷载传递路径依赖于周围构件的完整性。本文根据倒塌跨受到的不同边跨约束作用,建立 ABAQUS有限元模型,分析倒塌跨在边跨约束下防连续倒塌的性能。边跨约束如图12所示,(a) PF1模型,表示倒塌跨无边跨约束作用,(b) PF2模型,表示倒塌跨右侧有边跨约束,(c) PF3模型,表示倒塌跨两侧有边跨约束。通过在中柱上表面施加静力线性位移模拟中柱移除过程,直至梁受力钢筋断裂。
图13为模型PF3在中柱移除过程中边柱节点水平位移与中柱竖向位移之间的关系曲线,负值表示节点向框架外视为位移,正值表示节点向框架内的位移。可以看出,边节点先向外移动,之后又向内移动,据此将框架结构中柱移除过程分为压拱机制和悬链线机制。
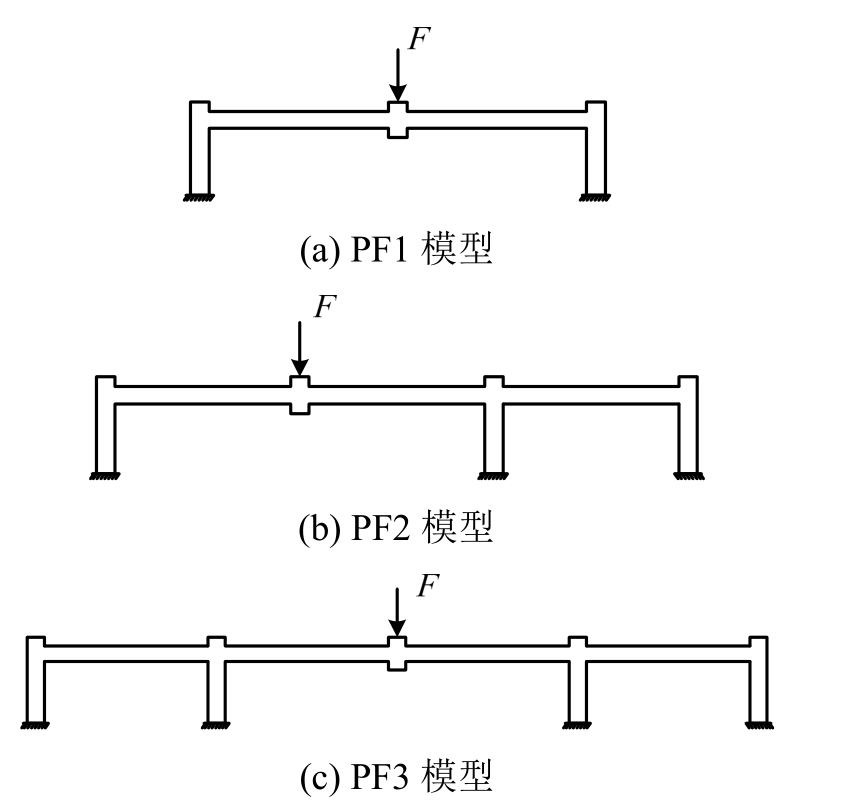
图12 平面结构模型
Fig.12 Plane structure models

图13 模型PF3边节点水平位移曲线
Fig.13 Horizontal displacement curve of model PF3 joint
图 14为不同边跨约束情况下的框架子结构移除中柱过程中荷载位移关系曲线。采用不同的约束情况,子结构荷载位移曲线发展趋势整体相同,中柱位移在150 mm之前,三条曲线基本重合,差别很小,位移150 mm之后,荷载差别逐渐变大,其中PF3子结构模型荷载下降最明显,PF1子结构模型荷载下降最少。悬链线阶段PF3子结构荷载增长速率最快,PF1和PF2子结构上升增长速率相当。
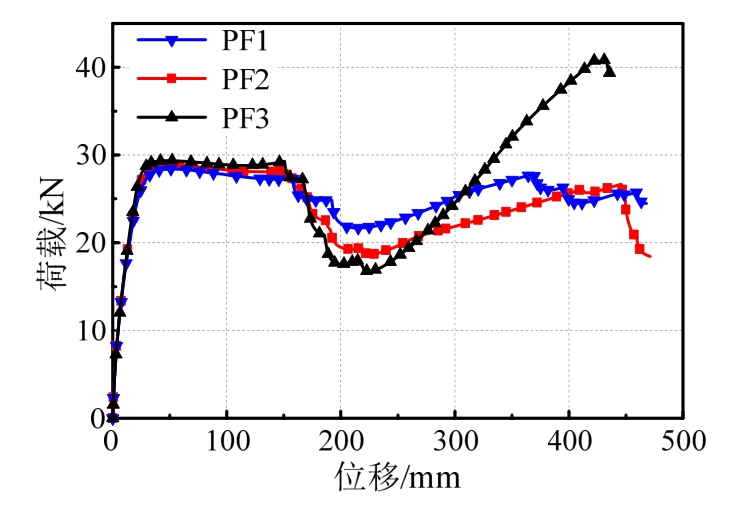
图14 不同边跨约束下荷载-位移曲线
Fig.14 Load-displacement curve under different lateral span constraints
图 15为不同边跨约束情况下边节点水平位移与中柱竖向位移之间的关系曲线。PF3子结构模型边柱节点在竖向位移为217 mm时回到初始原点,PF1子结构模型边节点在竖向位移则为137 mm时回到初始原点。PF2子结构模型左节点与右节点位移不同,右侧有边跨约束,水平位移很小,左侧无边跨约束,水平位移较大,左右节点回到初始原点的时刻也不相同,分别为131 mm和313 mm。每个子结构关键节点的具体荷载和位移见表6。

图15 不同边跨约束下边节点水平位移曲线
Fig.15 Horizontal displacement curve of joint
表6 不同边跨约束下子结构承载能力和位移表
Table 6 Capacity and displacement of substructures with different lateral span constraints

模型编号 屈服荷载Fy/kN压拱峰值Fu/kN压拱位移wu/mm悬链线峰值Ft/kN悬链线位移wt/mm边柱节点相对位移umin/mmumax/mm PF1 25.2 28.4 52.4 27.8 369.6 -2.21 65.02 PF2 25.6 28.9 51.9 26.7 445.9 -2.52 64.76 PF3 26.3 29.4 48.9 41.0 432.6 -2.80 38.64
表6为不同边跨约束下子结构关键点的荷载位移值。表中数据可以看出,子结构在弯曲阶段和压拱效应阶段的承载力差异很小,在悬链线效应阶段,子结构承载力差异较大。在悬链线阶段节点水平位移中,PF3子结构模型左右边节点相对水平位移最小,为38.64 mm,PF1和PF2模型左右边节点水平相对位移相差不大,分别为 65.02 mm和64.76 mm,是PF3模型相对位移的1.683倍和1.675倍;悬链线阶段的承载力中 PF3子结构模型为41 kN、PF1和PF2模型为分别27.8 kN和26.7 kN,是PF3模型的0.678倍和0.651倍,说明框架子结构承载能力与边跨约束密切相关。两侧均存在边跨约束时,子结构边节点水平相对位移小,边跨对倒塌跨框架梁的轴向约束大,悬链线阶段的承载能力也高。
楼板作为框架结构的组成构件,在结构受力过程中起着非常重要的作用,但在框架结构防连续倒塌中常常被忽略。以单层空间子结构为研究单元,研究不同位置处框架柱失效时框架子结构防连续性倒塌的性能,分析楼板对结构防倒塌承载力的贡献。分析模型如图16所示,(a) SF4模型,无楼板作用;(b) SF5模型,有楼板作用。对SF4和SF5模型分别进行移除中柱、长跨边柱、短跨边柱和角柱的防连续倒塌性能分析,比较不同位置处框架柱失效时框架结构防倒塌的能力。通过对比 SF4和SF5模型在同一位置处框架柱失效时防连续倒塌性能,分析楼板在结构防倒塌过程中的作用。通过在失效柱上表面施加静力线性位移来模拟框架柱的移除过程,直至梁受力钢筋断裂。

图16 单层空间框架模型
Fig.16 Single-storey spatial frame models
图17 为SF4模型不同位置处框架柱失效过程中荷载位移曲线。图中可以看出,中柱和边柱移除过程中荷载都有两个上升段,压拱效应和悬链线效应明显,角柱移除过程中荷载只有一个上升段,无悬链线效应。比较四条曲线,中柱移除过程中子结构防连续性倒塌的能力最高,拱效应峰值和悬链线效应峰值荷载达60.7 kN和90.2 kN。短跨边柱与长跨边柱在压拱效应阶段承载力相差不大,在悬链线阶段,短跨边柱移除过程承载力明显高于长跨边柱移除过程。角柱移除过程子结构防连续性倒塌能力最低,拱效应峰值约为移除中柱拱效应峰值的0.49。
图18为SF5模型不同位置处框架柱失效过程中荷载-位移曲线。不同位置处框架柱移除过程中承载力大小关系与SF4模型相似,所不同的是,由于楼板作用,移除中柱和边柱移除过程中拱效应峰值之后没有明显的下降段。中柱移除过程中的子结构防连续倒塌能力最高,拱效应峰值和悬链线效应峰值分别为146.4 kN和264.3 kN。长跨边柱和短跨边柱移除过程中拱效应峰值相差不大,约为中柱移除峰值荷载的 0.5,悬链线效应峰值长跨中柱移除过程小于短跨中柱移除过程。角柱移除过程无悬链线效应发生,拱效应峰值为 48.2 kN,为中柱移除拱效应峰值的0.33。具体承载力值见表7。
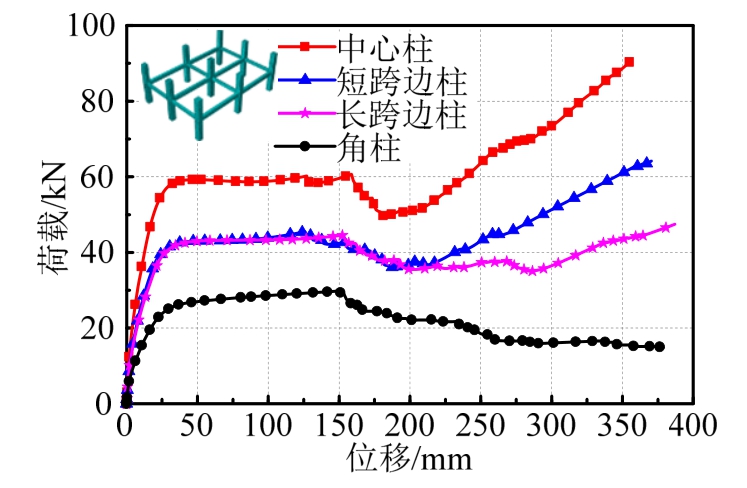
图17 SF4模型荷载-位移曲线
Fig.17 Load-displacement carve of SF4 model

图18 SF5模型荷载-位移曲线
Fig.18 Load-displacement carve of SF5 model
表7列出了空间框架SF4和SF5模型不同位置处框架柱失效的承载能力对比结果。相比于SF4模型,有楼板作用的SF5模型承载力明显更高。同一位置框架柱移除过程中,以框架子结构中柱移除过程为例,悬链线阶段承载力提高最高,SF5模型与SF4模型悬链线效应峰值比为2.92,压拱效应阶段承载力比值为2.41,弯曲阶段承载力比值为1.27。SF4和SF5模型边柱和角柱移除过程也有相同的规律,同一位置处框架柱移除过程中SF5模型承载力均明显高于SF4模型,说明楼板明显提高了框架结构防连续倒塌承载能力,最高可达2.92。并且,楼板对屈服阶段承载力提高系数最小为1.25,压拱阶段承载提高1.85,悬链线阶段提高最大,为2.65。
以1层~3层空间框架子结构为研究单元,建立有限元模型,分析多层空间框架结构防连续倒塌性能。分析模型示意如图19所示,图19(a)~图19(c)分别为1层~3层框架子结构模型。通过有限元模型对底层不同位置框架柱移除过程承载能力的分析,对比每个位置处不同楼层框架模型承载能力,得到结构承载力与楼层的关系。通过在失效柱上表面施加静力线性位移来模拟框架柱的移除过程,直至梁受力钢筋断裂。
表7 考虑楼板作用的空间框架承载力汇总
Table 7 Bearing capacity summary of space frame considering slab action

工况 模型 屈服荷载Fy/kNFF压拱峰值Fu/kN 压拱位移wu/mm y.5 y.4FF悬链线峰值Ft/kN 悬链线位移wt/mm u.5 u.4FFt.5 t.4 SF5 66.7 146.4 187.6 264.3 355.8长跨边柱失效中柱失效SF4 52.4 1.27 60.7 158.7 2.41 90.5 355.9 2.92 SF4 39.1 1.17 44.5 152.2 1.69 47.5 387.2 2.71 SF5 45.8 74.7 189.0 128.5 431.0短跨边柱失效SF4 36.5 1.23 45.5 125.9 1.68 64.2 370.5 2.35 SF5 45.9 76.4 84.83 151.1 420.9角柱失效SF4 22.2 1.53 29.8 150.4 1.62 - - -SF5 34.0 48.2 121.2 - -
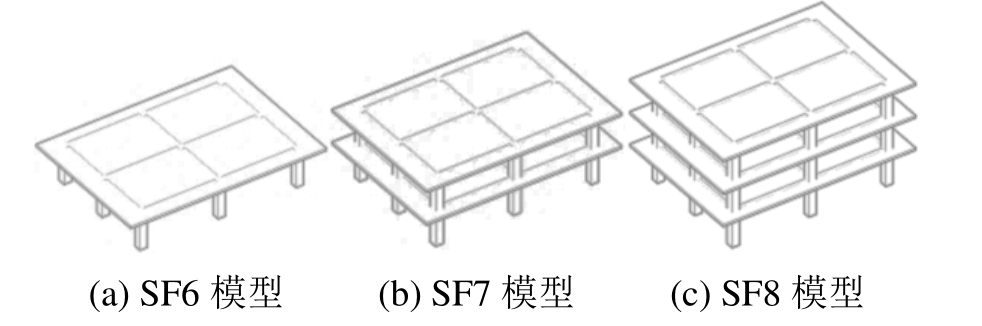
图19 多层空间框架模型
Fig.19 Multilayer spatial frame models
图20 为模型SF6框架柱移除过程荷载与中柱竖向位移的关系曲线。分别研究了移除中柱、短跨边柱、长跨边柱和角柱时结构的承载能力。图中可以看出,中柱移除过程承载力最高,悬链线效应峰值荷载达262.7 kN,长跨边柱与短跨边柱移除过程承载力相差不大,约为中柱移除过程承载力的0.39,角柱移除过程承载力最低,为 48.2 kN,且无悬链线效应阶段。
图21为模型SF7在底层框架柱移除过程中的荷载位移曲线。中柱移除过程承载力为490.8 kN,长跨边柱和短跨边柱移除过程承载力差异很小,约为中柱移除过程承载力的0.49,角柱移除过程承载力最小,为100.67 kN,且没有悬链线阶段。
图22为模型SF8在底层框架柱移除过程中的荷载位移曲线。与模型SF6和SF7有相似的规律,中柱移除过程承载力最大,为469 kN,长跨边柱和短跨边柱移除过程承载力差异很小,角柱移除过程承载力为155.36 kN。具体荷载位移值见表8。

图20 SF6模型荷载-位移曲线
Fig.20 Load-displacement carve of SF6 model

图21 SF7模型荷载-位移曲线
Fig.21 Load-displacement carve of SF7 model
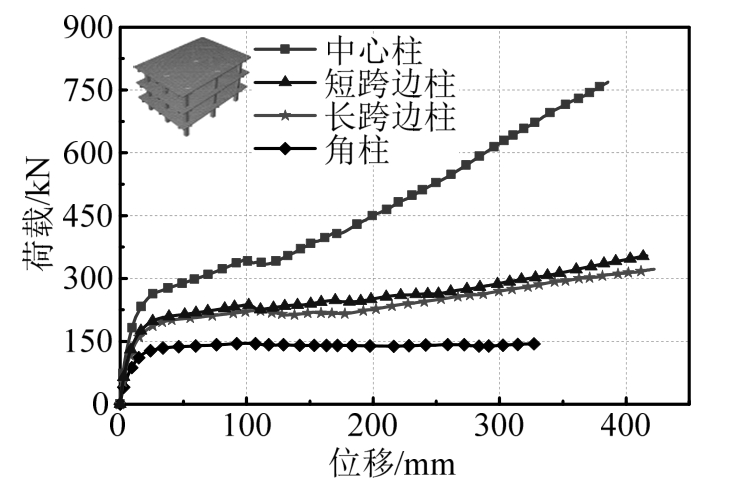
图22 SF8模型荷-载位移曲线
Fig.22 Load-displacement carve of SF8 model
表8给出了不同楼层框架结构在移除中柱、边柱和角柱过程中荷载位移对比值。中柱移除过程中,SF7框架模型和SF8框架模型的拱效应峰值荷载分别为SF6框架模型的2.17倍和3.24倍,悬链线效应峰值则分别为SF6框架模型的1.87倍和2.93倍。可以看出,随着框架结构层数的增加,结构的承载力成倍的增加,同样的规律在边柱和角柱移除过程也可以看到。说明楼层的增加,可以大幅度地提高结构防连续倒塌的能力。在相同层数分析时,中柱移除过程中,屈服阶段的承载力随楼层的增长幅度最大,压拱阶段次之,悬链线阶段最小。而边柱移除过程却有相反的规律,悬链线阶段增长幅度最大,屈服阶段增长最小。
表8 空间框架不同楼层防连续倒塌承载力汇总
Table 8 Bearing capacity summary of space frame with different stories

注:Fy,n表示编号为n框架结构的屈服荷载,n为6~8,Fu,n、Ft,n意义相同。
工况 模型编号屈服荷载Fy/kNFFy.y.6F压拱峰值Fu/kNn压拱位移wu/mmF悬链线峰值Ft/kN u.u.6n悬链线位移wt/mmFFt.t.6n中柱失效SF6 61.8 1 106.1 76.10 1 262.7 385.94 1 SF7 135.9 2.20 230.5 98.37 2.17 490.8 360.07 1.87 SF8 208.2 3.4 344.0 98.44 3.24 769.0 385.73 2.93长跨中柱失效SF6 54.4 1 71.7 160.29 1 102.3 378.27 1 SF7 96.5 1.77 158.2 220.42 2.21 230.2 457.17 2.25 SF8 143.9 2.64 233.9 214.28 3.26 342.2 422.16 3.35短跨中柱失效SF6 46.1 1 73.8 72.14 1 104.5 371.46 1 SF7 106.9 2.32 173.4 101.11 2.35 247.9 442.71 2.37 SF8 145.2 3.15 236.0 102.09 3.20 354.5 416.56 3.39角柱失效SF6 36.4 1 48.2 120.28 1 — — —SF7 71.1 1.95 97.1 100.67 2.01 — — —SF8 107.2 2.95 140.4 155.36 2.91 — — —
本文利用有限元软件 ABAQUS的强大非线性分析能力,对 Qian等[24]框架子结构拟静力试验结果进行了精细有限元模拟。在此基础上,根据框架结构周围约束的不同,分析了平面子结构在左右不同跨约束下的防连续倒塌性能;建立了单层空间框架模型,分析了楼板对空间框架防倒塌性能的影响;进一步的建立了多层空间框架模型,分析了多层框架结构的防倒塌性能。本文主要结论为以下四点:
(1) ABAQUS软件对Qian等[24]框架子结构的精细化模拟与试验结构吻合良好,S1试件拱效应峰值误差为10%,其余试件误差均在5%以内。说明塑性损伤模型能够很好地模拟混凝土的受力性能,ABAQUS对大变形下 RC框架结构的模拟是可行的。采用《规范》推荐的混凝土本构和线性强化钢筋本构是可取的。
(2) 分析了平面 RC框架子结构在受到两侧不同的边跨约束时的承载能力。两侧均有边跨约束子结构承载力最高,尤其是悬链线阶段,承载力增长明显;两侧均无边跨约束的子结构悬链线阶段承载力略高于一侧有边跨约束的子结构,但只有两侧均有边跨约束子结构承载能力的0.68。
(3) 分析了考虑楼板作用的单层空间框架结构除框架柱过程中结构防连续倒塌性能。在框架中柱、边柱和角柱移除过程中,考虑楼板作用的模型框架柱移除过程承载力均高于不考虑楼板作用的模型,且随着结构受力阶段的发展,楼板作用对屈服、压拱和悬链线各阶段的的承载力提高幅度逐渐变大,悬链线阶段最明显,楼板可将其防连续倒塌承载力提高至2.92倍,大幅度提高了结构承载力。
(4) 分析了1层~3层空间框架结构移除底层框架柱过程中结构防连续倒塌性能。RC框架结构随着楼层的增多,不同位置处框架柱除过程中承载能力都成倍的增长。相同楼层时,中柱移除过程屈服阶段承载力增长幅度最大,压拱阶段次之,悬链线阶段最小;而边柱移除过程有着相反的规律,悬链线阶段增长幅度最大,屈服阶段增长最小。
[1]Griffiths H, Pugsley A, Saunders O. Report of the inquiry into the collapse of flats at Ronan Point, canning town:presented to the Minister of Housing and Local Government [R]. London: HMSO, 1968.
[2]Powell G. Progressive collapse: Case studies using nonlinear analysis [C]. New York: Structures Congress,2005: 1-14.
[3]Zdenfk P B. Mechanics of progressive collapse: learning from world trade center and building demolitions [J].Journal of Engineering Mechanics, 2007, 133(3): 308-319.
[4]易伟建, 何庆峰, 肖岩. 钢筋混凝土框架结构抗连续倒塌性能的试验研究[J]. 建筑结构学报. 2007, 28(5):104-117.Yi Weijian, He Qingfeng, Xiao Yan. Experimental study on progressive collapse resistance of reinforced concrete frame structures [J]. Journal of Building Structure, 2007,28(5): 104-117. (in Chinese)
[5]Su Y, Tian Y, Song X. Progressive collapse resistance of axially-restrained frame beams [J]. ACI Structural Journal, 2009, 106(5): 600-607.
[6]Lew H S, Bao Y H, Sadek F, et al. An experimental and computational study of reinforced concrete assemblies under a column removal scenario [R]. Maryland, U.S.Department of Commerce, 2011.
[7]陆新征, 叶列平, 潘鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅰ: 框架试验[J]. 建筑结构, 2012, 42(11): 19-22.Lu Xinzheng, Ye Lieping, Pan Peng, et al. Pseudo static collapse test and numerical simulation competition of reinforced concrete frame structure I: frame test [J].Building Structure, 2012, 42(11): 19-22. (in Chinese)
[8]陆新征, 叶列平, 潘鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅱ: 关键构件试验[J].建筑结构2012, 42(11): 23-26.Lu Xinzheng, Ye Lieping, Pan Peng, et al. Pseudo static collapse test and numerical simulation competition of reinforced concrete frame structure Ⅱ: Key component test [J]. Building Structure, 2012, 42(11): 23-26. (in Chinese)
[9]中国建筑学会建筑结构防倒塌专业委员. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅲ: 模拟结果分析[J]. 建筑结构, 2012, 42(11): 27-30.Member of building structural collapse prevention committee of Chinese Architectural Society. Pseudo static collapse test and numerical simulation competition of reinforced concrete frame structure Ⅲ: Analysis of simulation results [J]. Building Structure, 2012, 42(11):27-30. (in Chinese)
[10]Bao Y, Kunnath S K, El-Tawil S, et al. Micromodelbased simulation of progressive collapse: RC frame structure [J]. Journal of Structural Engineering, 2008,134(7): 1079-1091.
[11]Ren P Q, Li Y, Lu X Z, et al. Experimental investigation of progressive collapse resistance of one-way reinforced concrete beam–slab substructures under a middlecolumn-removal scenario [J]. Engineering Structures,2016, 118(1): 28-40.
[12]Lu X Z, Lin K Q, Li Y, et al. Experimental investigation of RC beam-slab substructures against progressive collapse subject to an edge-column-removal scenario [J].Engineering Structures, 2017, 149(1): 91-103.
[13]Yu J, Luo L, Ge C. Numerical investigation on structural behavior of RC beam-slab assemblies under an exterior column removal scenario [J]. High Tech Concrete:Where Technology and Engineering Meet, 2018, 1(1):1252-1262.
[14]Yu J, Luo L Z, Li Y. Numerical study of progressive collapse resistance of RC beam-slab substructures under perimeter column removal scenarios [J]. Engineering Structures, 2018, 159(1): 14-27.
[15]Pham A T, Lim N S, Tan K H. Investigations of tensile membrane action in beam-slab systems under progressive collapse subject to different loading configurations and boundary conditions [J]. Engineering Structures, 2017, 150(1): 520-536.
[16]Dat P X, Hai T K. Membrane actions of RC slabs in mitigating progressive collapse of building structures [J].Engineering Structures, 2013, 55(4): 107-115.
[17]刁梦竹, 李易, 陆新征, 等. 钢筋混凝土楼板连续倒塌的一种简化模拟方法[J]. 工程力学, 2016, 33(增刊):72-78.Diao Mengzhu, Li Yi, Lu Xingzheng, et al. A simplified simulation method for continuous collapse of reinforced concrete floor [J]. Engineering Mechanics, 2016,33(Suppl): 72-78. (in Chinese)
[18]周育泷, 李易, 陆新征, 等. 钢筋混凝土框架抗连续倒塌的压拱机制分析模型[J]. 工程力学, 2016, 33(4):34-42.Zhou Yulong, Li Yi, Lu Xingzheng, et al. Analysis model of compression arch mechanism for progressive collapse of reinforced concrete frame [J]. Engineering Mechanics,2016, 33(4): 34-42. (in Chinese)
[19]左文武. 楼板对混凝土框架结构抗连续倒塌性能的影响[D]. 兰州: 兰州理工大学, 2014.Zuo Wenwu. Effect of floor slab on concrete frame structure resistance to progressive collapse [D]. Lanzhou:Lanzhou University of Technology, 2014. (in Chinese)
[20]刘帅. RC框架结构抗连续倒塌的ABAQUS仿真分析[D]. 石家庄: 石家庄铁道学院, 2012.Liu Shuai. ABAQUS simulation analysis of progressive collapse of RC frame structure [D]. Shijiazhuang:Shijiazhuang Railway Institute, 2012. (in Chinese)
[21]李晓路, 李寰, 方士超, 等. RC框架结构梁板柱空间协同抗连续性倒塌非线性有限元分析[J]. 建筑结构,2017, 47(21): 67-72.Li Xiaolu, Li huan, Fang Shichao, et al. RC frame slab column space to resist progressive collapse for nonlinear finite element analysis [J]. Building Structure, 2017,47(21): 67-72. (in Chinese)
[22]戎贤, 张健新, 李艳艳. 钢筋混凝土异形柱空间框架抗倒塌试验研究[J]. 工程力学, 2016, 33(10): 189-196.Rong Xian, Zhang Jianxin, Li Yanyan. Experimental study on progressive collapse of reinforced concrete special shaped column space frame [J]. Engineering Mechanics, 2016, 33(10): 189-196. (in Chinese)
[23]Jun Y, Tan K H. Structural behavior of RC beam-column subassemblages under a middle column removal scenario[J]. Journal of Structural Engineering, 2013, 139(2):233-250.
[24]Qian K, Li B, Ma J X. Load-carrying mechanism to resist progressive collapse of RC buildings [J]. Journal of Structural Engineering, 2015, 141(2): 4014107-1-4014107-14.
[25]刘巍, 徐明, 陈忠范. ABAQUS混凝土损伤塑性模型参数标定及验证[J]. 工业建筑, 2014, 44(增刊): 167-171.Liu Wei, Xu Ming, Chen Zhongfan. Parameter calibration and verification of damage plasticity model for ABAQUS concrete [J]. Industrial Construction. 2014,44(Suppl): 167-171. (in Chinese)
[26]江见鲸, 陆新征. 混凝土结构有限元分析[M]. 北京:清华大学出版社, 2005.Jiang Jianjing, Lu Xingzheng. Finite element analysis of concrete structure [M]. Beijing: Tsinghua University Press, 2005. (in Chinese)
[27]GB 50010-2010, 混凝土结构设计规范[S]. 北京, 中国建筑工业出版社, 2010.GB 50010-2010, Code for design of concrete structures[S]. Beijing, China Architecture & Building Press, 2010.(in Chinese)
PROGRESSIVE COLLAPSE RESISTANCE OF RC FRAME STRUCTURES CONSIDERING SURROUNDING STRUCTURAL CONSTRAINTS
胡 翔(1993―),男,湖南人,硕士生,主要从事框架结构防连续倒塌性能的研究(E-mail: 2459936667@qq.com);