钢筋混凝土框架在强震中由于节点薄弱而使结构遭受严重破坏的震害实例很多,地震双向作用下,节点核心区在两个主轴方向同时受力,使节点抗力不足,可能是导致其发生破坏的主要原因之一。现行建筑抗震设计规范对框架抗震验算主要在其主轴方向进行,但实际地震作用方向可能与框架主轴方向并不重合,框架柱和梁柱节点在两个方向同时受力,其受力性能和抗震性能均有可能较大程度降低。Kitayama 等[1]、Fujii等[2]、Li等[3]对钢筋混凝土梁柱节点的试验研究表明,与单向加载相比,双向往复荷载作用下节点的极限承载力和延性均降低。Fan等[4]进行方钢管混凝土柱-组合梁空间节点的试验研究也明确表明,双向往复荷载作用下节点的抗剪承载力与单向荷载作用相比最多降低20%,延性降低 10%。Burguieres等[5]、张连德[6]进行的钢筋混凝土空间框架节点试验研究表明,双向往复荷载作用下,节点核心区较早开裂,框架节点柱端或节点核心区更容易破坏,节点的强度和刚度均发生明显退化。
国内外学者对框架节点在往复荷载作用下的受力性能已经进行了较多研究[7-10]。但是,对于双向受力下节点核心区的抗剪承载力预测尚无具体方法。本文主要针对双向受力下钢筋混凝土框架空间节点的抗剪机理进行研究,建立双向受力下框架节点的抗剪承载力计算方法。
由Paulay等[11]学者对单向受力下钢筋混凝土平面节点的研究可知,节点在周围外部作用下,在节点核心区内部分别形成水平剪力Vh和竖向剪力Vv。贯穿节点的梁筋、柱筋在节点左、右侧梁端和上、下侧柱端分别受拉或受压,受压侧梁、柱端混凝土分别形成受压区。在节点端部梁筋所提供的拉力Tbs和压力Cbs、柱筋所提供的拉力Tcs和压力Ccs、以及梁和柱端受压混凝土分别所提供的压力Cb和Cc的共同作用下,最终在节点周围形成受拉区和受压区(如图1所示)。在受压区压力的作用下,节点核心区内部的混凝土形成斜向受压杆。核心区内混凝土斜压杆抵抗的斜向压力与Vh和Vv形成一种平衡关系,使斜压杆形成抵抗节点水平和竖向剪力的作用。
式中:Vh为节点核心区水平剪力; 和
和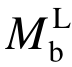 分别为节点周围左、右侧梁端的弯矩值;
分别为节点周围左、右侧梁端的弯矩值; 为上、下梁筋中心的距离;Vc为柱端剪力。
为上、下梁筋中心的距离;Vc为柱端剪力。
利用式(1)可直接通过梁、柱端内力计算节点水平剪力,按同样方法可计算节点竖向剪力。

图1 单向受力下节点的外部受力和内部剪力
Fig.1 External actions and internal shears at panel zone under unidirectional loading
双向受力下,节点在两个主轴方向同时受力,在节点核心区内x方向和y方向分别形成节点水平剪力Vhx和Vhy(如图2所示),两个方向的水平剪力可进一步合成为水平的斜向合成剪力Vh;而两个方向上的竖向剪力合成为竖向的合成剪力Vv。
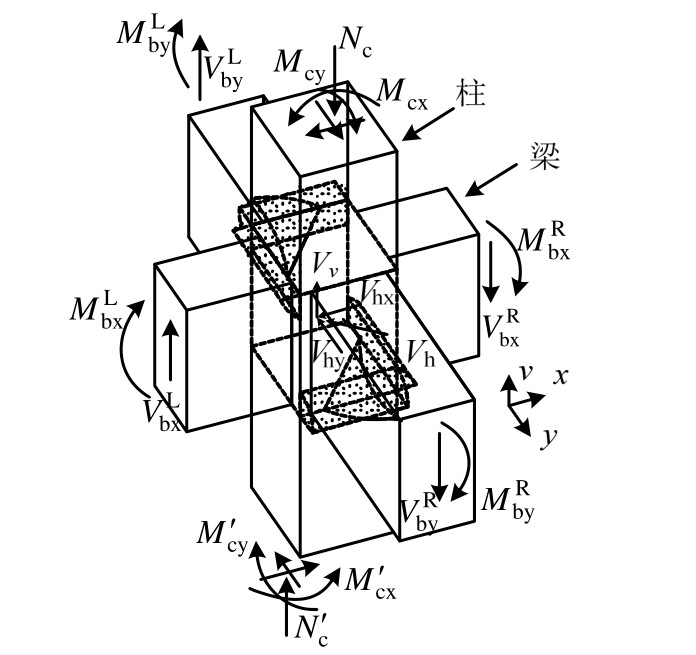
图2 双向受力下节点的外部受力和内部剪力
Fig.2 External actions and internal shears at panel zone under bidirectional loading
柱在双向受力作用下,在柱角位置形成斜向受压区,在两个方向梁端受压区的共同作用下,节点在两斜对角之间形成斜向混凝土压杆(如图3所示),这与Paulay等[12]预测的空间节点斜压杆一致。
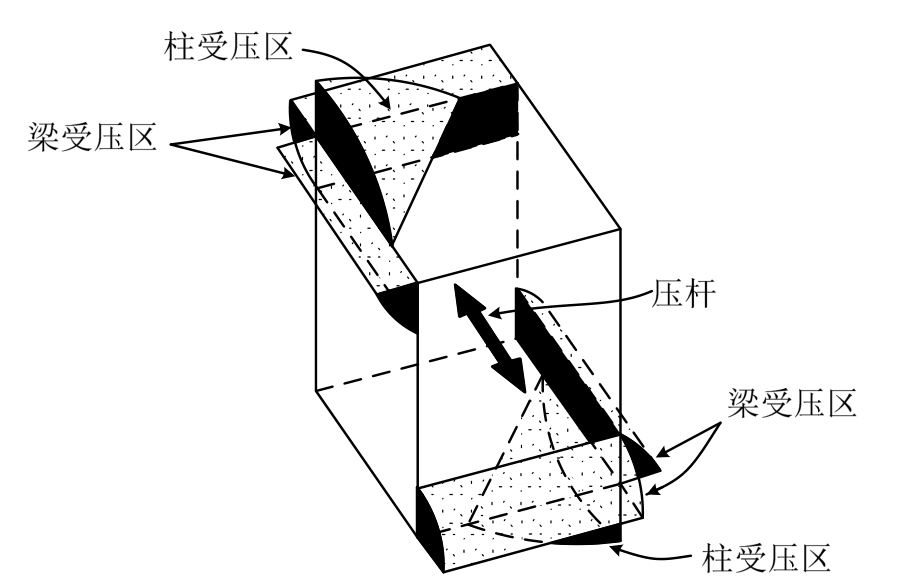
图3 双向受力下节点的端部受压区
Fig.3 End conditions for diagonal strut of panel zone under bidirectional loading
节点区域受力复杂,属于应力紊乱区(D区),Schlaich等[13]建立拉-压杆模型计算钢筋混凝土构件D区的抗剪承载力。考虑Vecchio等[14]提出的开裂混凝土的软化效应,Hwang等[15-16]建立了计算单向受力下钢筋混凝土梁柱节点抗剪承载力的软化拉压杆模型。
根据上述节点受力机理分析,水平双向受力相同时,节点上、下柱端角部形成斜向受压区,可假设在节点核心区内部斜对角线方向形成一种两头小中间大的混凝土“瓶型压杆”,如图 4中阴影部分所示。双向受力下节点核心区的混凝土斜压杆抵抗节点水平合剪力Vh和竖向合剪力Vv,核心区内混凝土形成压杆、箍筋和柱筋形成拉杆,在合剪力作用面内共同组成拉-压杆抗剪机构承担节点合剪力(如图4所示)。
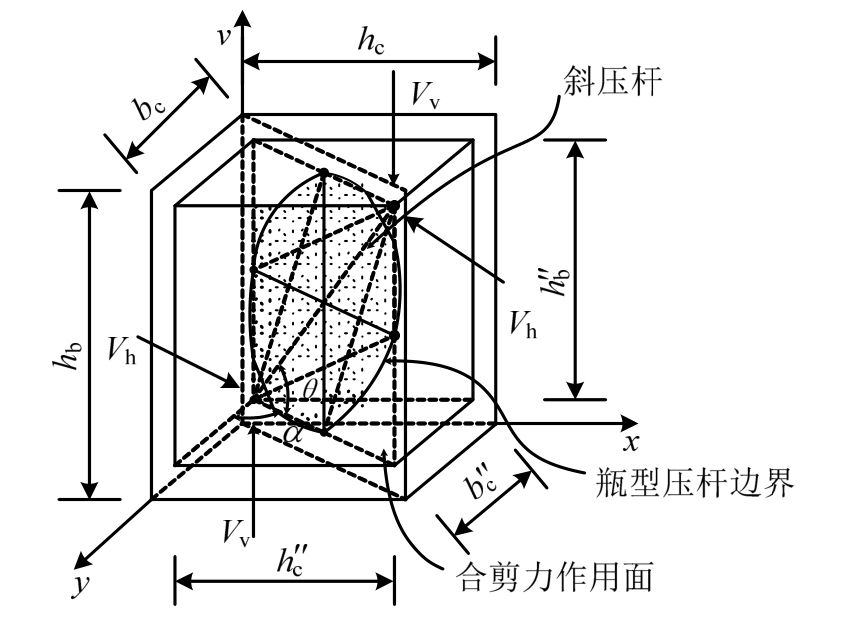
图4 双向受力下节点的抗剪机制
Fig.4 Shear-resisting mechanism of panel zone under bidirectional loading
其中:α为合剪力作用面与y向主轴的夹角;θ为斜压杆倾角;hb、bc、hc分别为梁高、柱宽和柱高;![]() 为相应侧梁筋或柱筋中心 之间的距离。
为相应侧梁筋或柱筋中心 之间的距离。
依据双向受力的不确定性,双向偏心受压矩形截面柱的混凝土受压区范围可分为5种情况[17],按柱轴力和双向受力的角度可确定矩形截面柱中和轴的角度和柱端受压区面积。为了简化研究,本文主要研究水平双向受力相同时正方形截面柱的情况,任意地震作用方向或非正方形柱截面等情况下的计算方法后文给出。图5所示为水平双向受力相同时正方形截面偏压柱的(等效)柱端受压区,中和轴与水平轴的夹角为45º。

图5 双向受力下的柱端受压区
Fig.5 Column compression zone under bidirectional loading
考虑贯穿节点的梁筋和柱筋的黏结作用影响,在节点内梁筋、柱筋之间的区域建立混凝土斜压杆。水平双向受力相同时,可将前述节点内的“瓶型压杆”理想化为棱柱形的(等效)斜压杆(如图6)。根据斜压杆斜向受压的受力特点,可假设该斜压杆的横截面与节点核心区的斜对角线AE垂直,AE与水平面的夹角θ为斜压杆的倾角。(等效)斜压杆横截面面积为Astr,由于柱端受压区面积远大于梁端受压区面积,可依据柱端受压区面积确定该斜压杆横截面面积,近似取柱端受压区面积Sc与斜压杆横截面面积Astr在水平方向的投影相等。
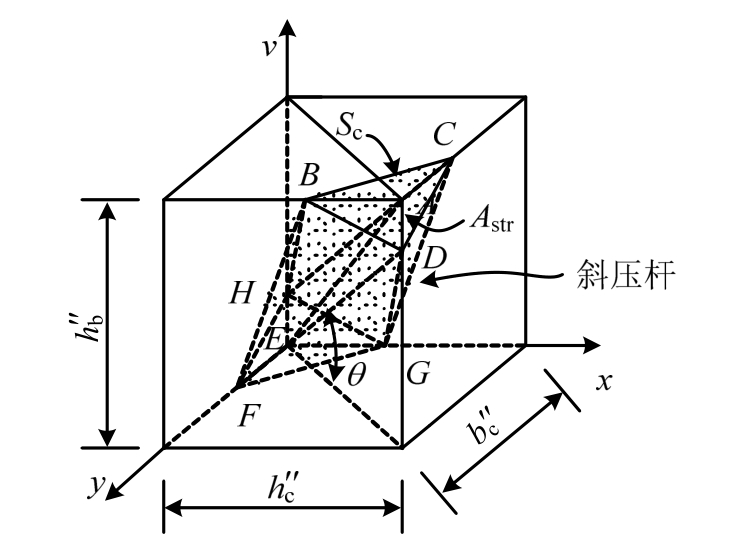
图6 双向受力下节点的斜压杆
Fig.6 Diagonal strut of panel zone under bidirectional loading
分别利用式(2)和式(3)计算双向受力下节点的斜压杆倾角θ和横截面面积Astr。
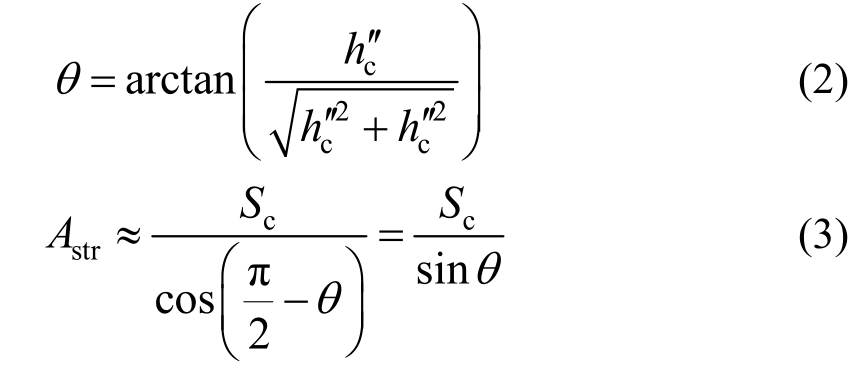
对于双向受力相同且为正方形截面柱的情况,可在节点核心区合剪力作用面内建立中节点的拉-压杆模型,如图7所示抗剪机构形式(α=45°)。其中虚线代表由混凝土形成的压杆,实线分别代表由水平箍筋形成的水平拉杆和由中间柱筋形成的竖向拉杆。节点配筋充足时,D为模型中主斜压杆(图6中所示的斜压杆简化为合剪力作用面内的主斜压杆)承担的斜向压力,Fh为节点内由水平箍筋转化成的水平拉杆中的拉力,Fv为节点内由中间柱筋转化成的竖向拉杆中的拉力。主斜压杆、水平拉杆和竖向拉杆的交点为节点核心区的中心点。

图7 双向受力下节点的拉-压杆抗剪机构
Fig.7 strut-and-tie shear-resisting mechanism of panel zone under bidirectional loading
按照节点内有无箍筋和中间柱筋的情况,可将该拉-压杆抗剪机构分为如下四种情况:第一种既无箍筋也无中间柱筋;第二种有箍筋无中间柱筋;第三种无箍筋有中间柱筋;第四种既有箍筋又有中间柱筋。
对于第一种既无箍筋也无中间柱筋的情况,可将图 7所示拉-压杆模型简化为如图 8所示机构形式,称为主斜压杆抗剪机构。仅由混凝土主斜压杆承担节点剪力,根据主斜压杆承担压力D与节点合成剪力的平衡关系,可得式(4):

图8 主斜压杆抗剪机构
Fig.8 Diagonal strut shear-resisting mechanism
对于第二种有箍筋无中间柱筋的情况,可将图7所示拉-压杆模型简化为如图9所示机构形式,称为主斜压杆和水平箍筋抗剪机构。

图9 主斜压杆和水平箍筋抗剪机构
Fig.9 Diagonal strut and horizontal reinforcement shear-resisting mechanism
这种情况的拉-压杆机构属于超静定桁架机构,可采取线弹性有限元的方法求解。根据 Schäfer[18]的研究和欧洲CEB-FIP规范[19]中给出的计算式,可得水平拉杆的拉力Fh的计算式(5)。

对于第三种无箍筋有中间柱筋的情况,可将图7所示拉-压杆模型简化为如图10所示机构形式,称为主斜压杆和竖向柱筋抗剪机构。
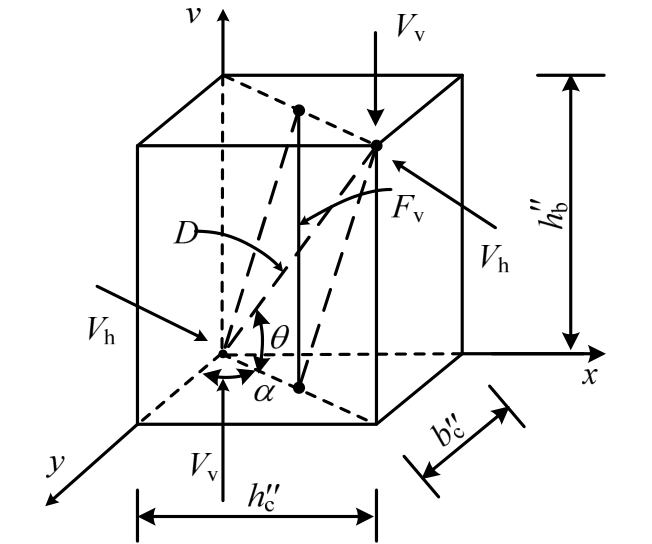
图10 主斜压杆和竖向柱筋抗剪机构
Fig.10 Diagonal strut and vertical column reinforcement shear-resisting mechanism
使用与第二种情况相同的计算方法,可得竖向拉杆的拉力Fv的计算式。
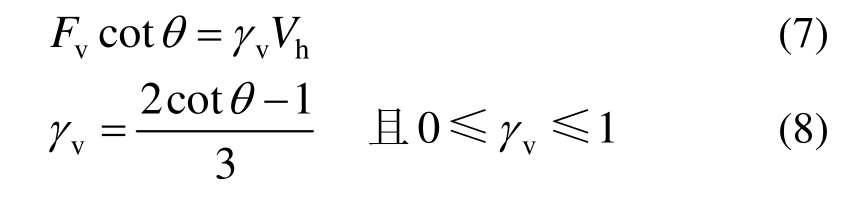
对于第四种既有箍筋又有中间柱筋的情况,即为图 7所示双向受力下节点拉-压杆抗剪模型的完整机构形式。
箍筋和中间柱筋均能提高节点抗剪能力。当节点箍筋和中间柱筋配筋充足时,主斜压杆压力D、水平拉杆拉力Fh和竖向拉杆拉力Fv之间均满足上述比例。但当节点箍筋或中间柱筋配筋不足时,箍筋或中间柱筋对混凝土的约束能力不足,节点抗剪能力相应降低,主斜压杆压力、水平拉杆拉力和竖向拉杆拉力之间则不能保持上述比例关系,而随着箍筋和柱筋的量发生变化。
节点内水平箍筋和中间柱筋的作用主要是可以使核心区内更多的混凝土形成压杆,承担部分主斜压杆方向的压力,使节点核心区在主斜压杆方向能够承担更多的压力,从而提高节点的抗剪承载力。如图9所示的主斜压杆和水平箍筋抗剪机构,由于箍筋的约束,使节点内更多的混凝土形成平缓压杆,可将其简化为如图11所示受力图。

图11 主斜压杆和水平箍筋抗剪机构受力
Fig.11 Forces in diagonal strut and horizontal reinforcement shear-resisting mechanism
在图 11中的合剪力作用面内进行受力分析,可知水平拉杆的拉力Fh越大,平缓压杆中的压力越大,这代表了有更多的箍筋提供约束能使更多的混凝土形成压杆参与抗剪。取主斜压杆的下端支座节点进行受力分析发现,核心区内主斜压杆方向的压力可由平缓压杆和主斜压杆共同承担,即增加了更多的荷载传递路径转移了主斜压杆方向的一部分斜向压力,从而减轻了主斜压杆混凝土承担的压力,这就使节点核心区能承担更大的斜向压力。这种由于箍筋的作用而使节点斜向抗压能力增大的程度,可用该机构的节点斜向抗压能力系数Kh表示,如式(9)所示。
在式(9)中,fθ为平缓压杆与水平面的夹角;分子项为双向受力下节点核心区在斜向主斜压杆方向承担的总压力(即为Vh/cosθ);分母项为主斜压杆混凝土极限受压破坏时主斜压杆两端支座(主斜压杆端部截面积Astr范围内)承受的压力,这个压力是由主斜压杆和平缓压杆共同传递的,可表示为Cmax。
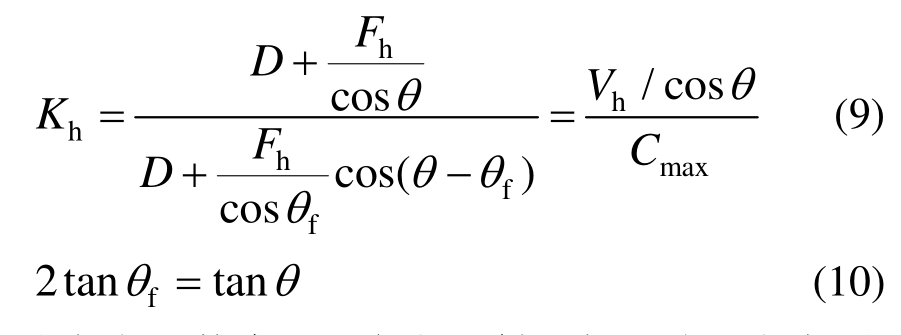
节点水平剪力Vh应由主斜压杆和水平拉杆共同承担,当节点箍筋配置充足时,水平拉杆的拉力Fh和Vh的关系满足式(5),则由式(5)及图11中节点受力平衡关系可得:
由式(9)~式(11)可得箍筋配置充足时节点的斜向抗压能力系数![]() 为:
为:

若节点箍筋配置充足,主斜压杆混凝土极限受压破坏时,由式(5)、式(9)可将水平拉杆中的拉力![]() 表示为:
表示为:
根据 Hwang等[20]的试验研究可以发现,节点的抗剪能力和箍筋配置有关,配箍越多,对节点的斜向抗压能力提高越大,二者成线性关系。但并不是箍筋越多,节点的斜向抗压能力就无限增大,如果箍筋配置充足,再增加箍筋对节点抗剪强度基本没有影响。该机构的节点斜向抗压能力系数Kh可依据节点实际配箍情况表示为:
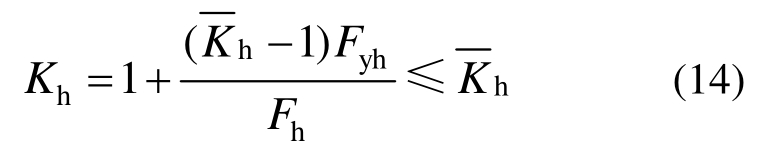
由图 12可知,双向受力下节点合剪力作用面内水平拉杆的拉力Fh平箍筋在两个主轴方向箍肢的拉力合成而得。在式(14)中,![]() 为节点水平箍筋在一个主轴平面内各肢截面积之和;fth为节点水平箍筋的屈服强度。由式(14)可见,节点的斜向抗压能力系数Kh点水平箍筋配箍量和箍筋强度有关。
为节点水平箍筋在一个主轴平面内各肢截面积之和;fth为节点水平箍筋的屈服强度。由式(14)可见,节点的斜向抗压能力系数Kh点水平箍筋配箍量和箍筋强度有关。

图12 箍筋和中间柱筋的拉杆拉力
Fig.12 Tie forces in horizontal reinforcement and vertical reinforcement
如图10所示的主斜压杆和中间柱筋抗剪机构,当节点中间柱筋配置充足时,由于中间柱筋的约束作用而使节点斜向抗压能力增大的程度可用该机构的斜向抗压能力系数 表示,使用同样的方法可得
表示,使用同样的方法可得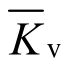 的表达式。
的表达式。

若中间柱筋配筋充足,主斜压杆混凝土极限受压破坏时,竖向拉杆中的平衡拉力![]() 可表示为:
可表示为:
与前述箍筋对节点斜向抗压能力增强的特点相同,根据中间柱筋实际配筋数量的不同,使节点斜向抗压能力增大的程度也不同,该机构的节点斜向抗压能力系数Kv可表示为:

由图 12可知,双向受力下节点合剪力作用面内竖向拉杆的拉力Fv可由全部中间柱筋的拉力合成而得。在式(17)中,![]() 为节点全部中间柱筋的截面积,中间柱筋为不在柱受压区范围内的柱筋;fyv为节点中间柱筋的屈服强度。由式(17)可见,节点斜向抗压能力系数Kv与节点中间柱筋配筋量和柱筋强度有关。
为节点全部中间柱筋的截面积,中间柱筋为不在柱受压区范围内的柱筋;fyv为节点中间柱筋的屈服强度。由式(17)可见,节点斜向抗压能力系数Kv与节点中间柱筋配筋量和柱筋强度有关。
如图7所示双向受力下节点的抗剪承载力计算模型的完整机构形式,既有箍筋又有中间柱筋,由于箍筋和中间柱筋的共同作用而使节点斜向抗压能力增大的程度用该机构的节点斜向抗压能力系数K表示。
则双向受力下节点抵抗的最大水平剪力Vh,max可表示为:
可见,节点所能抵抗的最大水平剪力Vh,max主要由主斜压杆端部所能抵抗的最大压力Cmax决定,而主斜压杆端部的抗压能力则由混凝土的抗压强度决定。根据前述等效斜压杆的特点,将主斜压杆端部截面积Astr范围内混凝土压应力达到极限抗压强度作为节点抗剪失效的标准。Hsu等[21]研究发现了开裂钢筋混凝土构件的混凝土软化效应。依据 Hwang等[16]提出的钢筋混凝土节点的抗压强度软化系数ξ,主斜压杆混凝土极限受压破坏时,斜压杆端部承担的最大压力Cmax和节点的水平抗剪承载力Vjh表示为:

式中: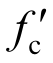 ′/MPa为混凝土圆柱体抗压强度,根据欧洲CEB-FIP规范,混凝土圆柱体抗压强度和混凝土立方体抗压强度标准值之间的换算关系为fc′=0.80fcu,k。而根据我国混凝土规范[22],fck=0.88αc1αc2fcu,k,fck为混凝土轴心抗压强度标准值。
′/MPa为混凝土圆柱体抗压强度,根据欧洲CEB-FIP规范,混凝土圆柱体抗压强度和混凝土立方体抗压强度标准值之间的换算关系为fc′=0.80fcu,k。而根据我国混凝土规范[22],fck=0.88αc1αc2fcu,k,fck为混凝土轴心抗压强度标准值。
利用式(21)计算国内外多个双向受力的钢筋混凝土框架节点试验试件,试件参数、计算结果和试验结果见表1。
由图 13可见,双向受力下节点试件的抗剪承载力计算结果与试验结果吻合较好。
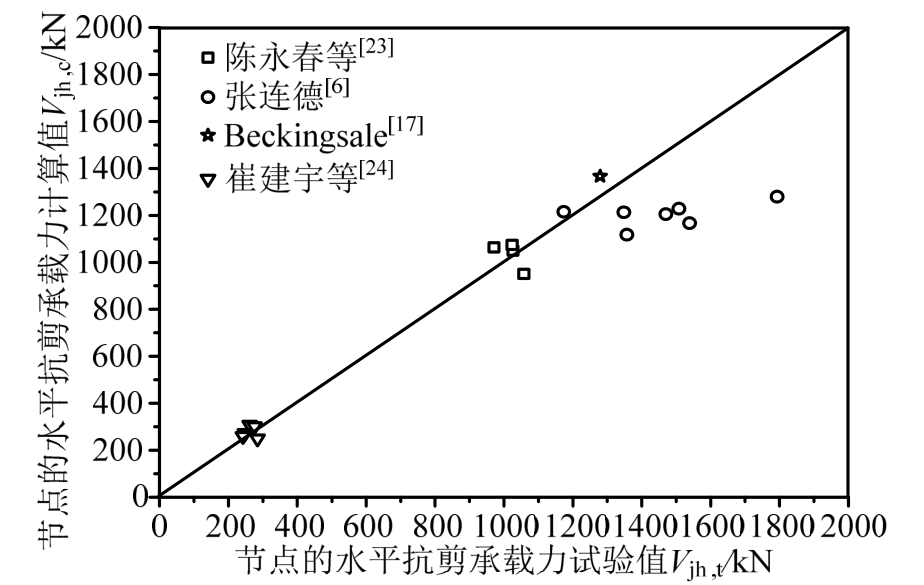
图13 双向受力下节点抗剪承载力计算值与试验值比较
Fig.13 Comparison of shear bearing capacity of panel zone between theoretical and experimental values under bidirectional loading
表1 双向受力的钢筋混凝土框架节点抗剪承载力计算值与试验值对比
Table 1 Comparison of shear bearing capacity of panel zone in reinforced concrete frame between theoretical and experimental values under bidirectional loading

注:1) BJ表示梁端屈服、节点发生剪切破坏;J表示梁端未屈服、节点发生剪切破坏;
2) 参考文献[6]中试件4为双向单调加载,其余试件均为双向低周往复加载。
参考文献试件编号bc×hc/mmbb×hb/mmfck/MPaN水平fbhckcc箍筋fy/MPa 中间柱筋fy/MPa 破坏模式计算值Vjh,c/kN试验值Vjh,t/kN BJ3 400×400 250×400 22.6 0.03 D10@100(2) 257 2D22 360 BJ 950.98 1057.57[23]BJ4 400×400 250×400 25.4 0.03 D12@100(2) 300 2D22 360 BJ 1049.68 1026.27 BJ5 400×400 250×400 25.8 0.03 D8@130(2) 272 2D22 360 BJ 1064.06 971.29 BJ6 400×400 250×400 25.8 0.03 D10@100(2) 257 2D22 360 BJ 1074.18 1023.95 2 380×380 329×455 24.1 0.38 D12@150(2) 440 2D28 480 BJ 1167.21 1539.00 3 380×380 329×455 25.8 0.36 D12@150(2) 440 2D28 480 BJ 1213.32 1348.00 4 380×380 329×455 25.5 0.36 D12@150(2) 440 2D28 480 BJ 1205.61 1470.00 5 380×380 329×455 28.1 0.33 D12@75(4) 440 2D28 480 BJ 1279.67 1793.00 6 380×380 329×455 25.5 0.00 D12@150(2) 440 2D28 480 BJ 1117.73 1357.00 9 380×380 221×455 25.5 0.36 D12@150(2) 440 2D28 480 BJ 1215.60 1174.00 10 380×380 455×455 26.4 0.35 D12@150(2) 440 2D28 480 BJ 1228.38 1508.00[17]B21 457×457 356×610 29.1 0.48 D12.7@65(4) 336 2D24 411 BJ 1366.62 1279.10[6]SP1 220×220 160×250 28.7 0.24 D6@62.5(2) 345 0 548 BJ 307.44 262.00[24]SP2 220×220 160×250 24.4 0.72 D6@62.5(2) 345 0 548 BJ 272.31 247.80 SP3 220×220 160×250 24.4 0.72 D9@62.5(2) 384 0 548 BJ 301.40 275.80[24]NB-1 220×220 160×250 22.6 0.18 D6@62.5(2) 894 0 894 J 249.74 284.00 NB-2 220×220 160×250 23.8 0.17 D6@62.5(2) 894 0 894 J 259.97 242.40
(1) 分析双向受力下钢筋混凝土框架节点的承载机理,明确节点核心区内部分别形成水平和竖向的合成剪力,根据节点的受力特点,在节点合剪力作用面内,混凝土形成斜压杆,箍筋和柱筋分别形成水平和竖向的拉杆,共同组成拉压杆机构承担节点合剪力;
(2) 依据双向受力下节点的受力机理,确定节点在双向受力下的等效斜压杆的倾角和截面面积,建立双向受力下节点的软化拉压杆模型的抗剪承载力计算方法;
(3) 采用所建立的节点抗剪承载力计算方法,对双向受力下的多组节点试验试件的抗剪承载力进行计算,计算结果与试验结果吻合较好。
由于国内外双向受力的钢筋混凝土框架节点试验资料有限,该方法仅验证了双向受力相同时正方形截面柱的节点抗剪承载力。
[1]Kitayama K, Asami S, Otani S, et al. Behavior of reinforced concrete three-dimensional beam-column connections with slabs [R]. Japan Concrete Institute(JCI). Annual Japan Concrete Institute (JCI) Meeting,Tokyo, Japan, 1986: 649-652.
[2]Fujii S, Morita S. Behavior of exterior reinforced concrete beam-column-slab sub-assemblages under bi-directional loading [R]. Pacific Conf. on Earthquake Engineering, New Zealand, New Zealand National Society for Earthquake Engineering. Wellington, New Zealand, 1987: 339-350.
[3]Li L M, Mander J B, Dhakal R P. Bidirectional cyclic loading experiment on a 3D beam-column joint designed for damage avoidance [J]. Journal of Structural Engineering, ASCE, 2008, 134(11): 1733-1742.
[4]Fan J, Li Q, Nie J, et al. Experimental study on the seismic performance of 3D joints between concrete-filled square steel tubular columns and composite beams [J].Journal of Structural Engineering, ASCE, 2014, 140(12):0401409-1-0401409-13.
[5]Burguieres S T, Jirsa J O. The behavior of beam-column joints under bidirectional load reversals [C]. Bulletin D’Information, AICAP- CEB Symposium on Structural Concrete Under Seismic Actions, RMCE, 1979(132):221-228.
[6]张连德. 钢筋砼空间框架节点抗震性能的研究[J]. 建筑结构学报, 1987, 8(2): 1-9.Zhang Liande. A study of earthquake resisting behavior of reinforced concrete space frame joints [J]. Journal of Building Structures, 1987, 8(2): 1-9. (in Chinese)
[7]闫维明, 侯立群, 陈适才, 等. 双向荷载作用下空间夹心节点受力性能试验研究[J]. 工程力学, 2016, 33(5):211-219.Yan Weiming, Hou Liqun, Chen Shicai, et al.Experimental study on the mechanical behavior of 3D sandwich joints under bi-directional loading [J].Engineering Mechanics, 2016, 33(5): 211-219. (in Chinese)
[8]王英俊, 梁兴文, 吴继伟. 纤维增强混凝土梁柱节点受剪承载力计算模型研究[J]. 工程力学, 2016, 33(3):77-86.Wang Yingjun, Liang Xingwen, Wu Jiwei. Calculation model of shear capacity of fiber-reinforced concrete beam-column joint [J]. Engineering Mechanics, 2016,33(3): 77-86. (in Chinese)
[9]Pan Z, Guner S, Vecchio F J. Modeling of interior beam-column joints for nonlinear analysis of reinforced concrete frames [J]. Engineering Structures, 2017(142):182-191.
[10]Kassem W. Strut-and-tie modelling for the analysis and design of RC beam-column joints [J]. Materials & Structures. 2016 , 49(8): 3459-3476.
[11]Paulay T, Park R, Priestley M J N. Reinforced concrete beam-column joints under seismic actions [J]. ACI Journal, 1978, 75(11): 585-593.
[12]Paulay T, Park R. Joints in reinforced concrete frames designed for earthquake resistance [R]. Department of Civil Engineering, University of Canterbury,Christchurch, New Zealand, 1984, 6: 33-34.
[13]Schlaich J, Scha ¨fer K. Design and detailing of structural concrete using strut-and-tie models [J]. The Structural Engineering, 1991, 69(6): 113-125.
[14]Vecchio F J, Collings M P. The modified compression-field theory for reinforced concrete elements subjected to shear [J]. ACI Structural Journal,1986, 83(2): 219-231.
[15]Hwang S J, Lee H J. Analytical model for predicting shear strengths of exterior reinforced concrete beam-column joints for seismic resistance [J]. ACI Structural Journal, 1999, 96(5): 846-857.
[16]Hwang S J, Lee H J. Analytical model for predicting shear strengths of interior reinforced concrete beam-column joints for seismic resistance [J]. ACI Structural Journal, 2000, 97(1): 35-44.
[17]Beckingsale C W. Post elastic behaviour of reinforced concrete beam-column joints [D]. Department of Civil Engineering, University of Canterbury, Christchurch,New Zealand, 1980, 8: 360-368.
[18]Schäfer K. Strut-and-tie models for the design of structural concrete [R]. Notes of Workshop, Department of Civil Engineering, National Cheng Kung University,Tainan, Taiwan, 1996: 140-141.
[19]CEB-FIP model code 1990 [S]. Thomas Telford services Ltd, Thomas Telford House, Comité Euro-International du Béton as Bulletins d’ Information, 1993: 216-217.
[20]Hwang S J, Lee H J. Strength prediction for discontinuity regions by softened strut-and-tie model [J]. Journal of Structural Engineering, ASCE, 2002, 128(12): 1519-1526.
[21]Hsu T T C. Toward a unified nomenclature for reinforced concrete theory [J]. Journal of Structural Engineering,ASCE, 1996, 122(3): 275-283.
[22]GB 50010-2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50010-2010, Code for design of reinforced concrete silos [S]. Beijing: China Architecture Industry Press, 2010. (in Chinese)
[23]陈永春, 高红旗, 马颖军, 等. 双向反复荷载下钢筋砼空间框架梁柱节点受剪承载力及梁筋粘结锚固性能的试验研究[J]. 建筑科学, 1995(2): 13-20.Chen Yongchun, Gao Hongqi, Ma Yinjun, et al. Study on shear capacity and bond behavior of longitudinal reinforcement of RC space frame interior beam-column joints under biaxial cyclic loading [J]. Building Science,1995(2): 13-20. (in Chinese)
[24]崔建宇, 车轶, 孙建刚, 等. 高层钢筋混凝土框架底层角节点抗震性能[J]. 重庆大学学报, 2014, 37(2): 98-105.Cui Janyu, Che Yi, Sun Jiangang, et al. Seismic performance of first floor corner joints of high-rise reinforced concrete frame structure [J]. Journal of Chongqing University, 2014, 37(2): 98-105. (in Chinese)
SHEAR CAPACITY CALCULATION METHOD OF PANEL ZONE IN REINFORCED CONCRETE FRAME UNDER BIDIRECTIONAL LOADING
马 华(1962―),女,山东人,副研究员,博士,从事工程结构抗震研究(E-mail: mahua@bjut.edu.cn);
宋 坤(1980―),女,黑龙江人,讲师,博士,从事工程结构抗震研究(E-mail: songkun_2002@163.com);