图1 人行桥横向振动模型示意图
Fig.1 Schematic diagram of models of footbridge lateral vibration
注：fp(t) 为 横向作用力；h(y,
˙,
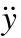)为振动相关函数；ℓby(t) 为 桥梁振动算子；Dpx(t)为行人振动算子
2000年，著名的伦敦千禧桥同样在开放当日就因为该桥发生大幅横向振动而不得不紧急关闭[1]，这一事件成为人致桥梁振动的关键性标志。伦敦千禧桥的人致大幅度横向振动事件随后引发了人们对桥梁人致振动问题的广泛讨论[2]，学者开始对大跨度人行桥中的一些深层次问题进行研究，如非线性、参数共振、人桥相互作用机理等一系列复杂问题，并提出了多种理论和模型，可总体划分归纳为以下几大类：
1) 行人激励作用与桥梁振动无关(图1(a))。这类方法一般假设行人激励与桥梁响应无关，其中具有代表性的是线性直接共振理论，将桥梁大幅度横向振动视为由行人横向步频与桥梁某阶频率共振而造成。单人横向荷载可采用简谐函数表示。日本学者 Fujino等[3－4]利用这类方法对日本户田公园T桥进行了系统研究。
图1 人行桥横向振动模型示意图
Fig.1 Schematic diagram of models of footbridge lateral vibration
注：fp(t) 为 横向作用力；h(y,˙,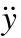)为振动相关函数；ℓby(t) 为 桥梁振动算子；Dpx(t)为行人振动算子
2) 行人激励作用与桥梁振动相关(图1(b))。这类方法或称之为自激振动方法，认为行人激励作用受到桥梁振动影响，且这种影响可用已知的模型描述。基于这类方法的模型较多，具有代表性的有：Dallard 模型[1]，Nakamura模型[5]，Piccardo 模型[6]，Ingólfsson 模型[7－8]。Dallard 模型，Nakamura 模型以及Ingólfsson模型属于考虑桥梁振动速度相关的非线性模型，认为行人激励作用受到桥梁速度响应影响(激励项包含桥梁速度)。在此类模型中，可将速度相关部分视为对结构施加负阻尼，当该项虚拟负阻尼超过结构自身阻尼时，振动将发散，并以此计算出临界桥上人数。Piccardo模型属于参数共振模型，主要是基于经典的马修参激方程，并依据稳定条件求出振动发散对应的临界人数。
3) 行人运动和桥梁振动耦合(图1(c))。此类方法同样考虑桥梁振动对行人激励的影响，但这种影响并不是通过已知的经验参数模型描述，而是通过建立行人运动和桥梁振动耦合的方程来考虑人-桥的相互作用。具有代表的有Roberts模型[9]，Newland模型[10]，混范德波尔-瑞利模型[11－12]，Macdonald模型[13－14]。其中值得注意的是Macdonald模型，其实质是一个运动倒摆模型，将行人横向力视为受人体平衡策略控制的重心惯性力。Macdonald模型与其他一般模型的不同之处在于他认为行人是依靠调节步伐位置而不是步频来维持本身的舒适和平衡。最近 Carroll等[15－16]基于Macdonald提出的运动倒摆模型框架，采用3D人体动作捕捉技术，重做了Ricciardelli等[17]的跑步机行人实验，分析了由人-结构相互作用引起的行人自激力特性。类似地，Bocian等[18]同样基于Macdonald的运动倒摆模型框架，进行了跑步机行人实验，其特色在于结合了虚拟现实模拟技术，一定程度上重现了行人实际周围环境以求减少室内试验环境对行人的影响。
以上理论模型大部分属于确定性分析方法，并未考虑到人群荷载的随机性，事实上实际观测得到的连续行人荷载并非是理想的周期力，行人在每一步的作用力都存在着变化。在谱域内，实际的谱线并没有分布在按理想周期力得到的离散频点上，而是带有一定宽度地分布在步频以及倍频附近，是一个典型的窄带激励过程。这种在步频以及倍频附近带有一定宽度离散分布的频谱意味着实际行人荷载产生的结构响应将明显不同于按理想周期考虑的结构响应。目前对行人激励的随机过程的讨论分析基本上以竖向方向为主[19－22]，横向方向的随机模型很少，影响较大的有 Ingólfsson模型[7－8]和 Racic模型[23－24]。Ingólfsson 模型的研究对象是行人横向激励，该模型基于Ricciardelli等[17]的行人横向激励模型，并将自激力中的速度同相分量和加速度同相分量的系数设为随机时间序列，属于时域内的非线性分析模型，采用数值模拟方法进行分析。Racic模型重点在于行人横向激励窄带功率谱的多高斯拟合方法研究，可有效还原实际行人横向激励的幅值以及相位变化过程，但涉及到了非常多的拟合参数。
如前文所述，人行桥的人致横向振动是一个复杂的人-桥相互作用的过程(不同于桥梁竖向振动[25－26]，也不同与车桥耦合振动[27])，其实质上是激励与振动相关的非线性随机振动过程，此时传统的线性随机振动理论将不再适用，而往往只能采用依靠大量蒙特卡罗数值模拟的离散数值计算方法[7]，考虑到精度的划分要求以及非线性动力方程的复杂性，这种计算量将是巨大而不可承受的。本文所提方法充分考虑了人行桥人致横向振动中的激励与振动相关性以及行人荷载随机性造成的激励窄带性，提出了一套能对人行桥人致横向非线性随机振动进行有效分析的非数值理论分析模型，可有效填补这方面的研究空缺。
考虑行人作用下的人行桥横向振动(图2)，忽略转动惯量，轴向力以及剪切变形影响，基于欧拉-伯努利梁的人行桥横向弯曲振动方程可表示为：
图2 人行桥横向振动示意图
Fig.2 Sketch of lateral vibration of footbridge
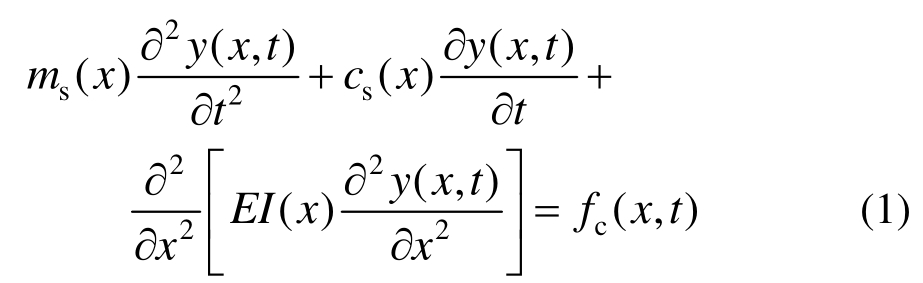
式中：ms(x)、cs(x)、EI(x)为人行桥的单位长度质量、阻尼及横向抗弯刚度；y(x,t)为人行桥的横向位移；fc(x,t)单位长度的人群横向荷载(这里假设行人在桥上均匀分布)。在人行桥横向振动中，确定行人横向作用力模型是关键。首先考虑单个行人横向荷载，一般可定义为：
式中：mps为单个行人质量；DLF为动载因子；ξ(t)为随机激励过程(考虑行人激励随机性)或者简谐荷载(确定性的理想周期荷载)。根据Ricciardelli等[17,28－29]的实验结果，可知行人横向荷载可分为与桥梁振动无关的行人荷载以及与桥梁振动相关的自激荷载，而这个划分可以动载因子的定义方式体现出来。这里自激荷载根据袁旭斌[30]的实验结果将其考虑为与桥梁横向振动幅值相关，则式(2)可写为：
式中：DLF1为桥梁静止时的行人横向动载因子；DLF2为桥梁振动时的行人横向动载因子。根据Ingólfsson等[8]以及 Brownjohn等[19]的实验结果，DLF1=d1≈ 0.04，根据袁旭斌[30]的实验结果，DLF2(A) ≈d2A=1.18A。现考虑人群荷载作用，设总人数为N。按同步与否，桥上的人群可分为两大类：未同步人群和同步人群，未人桥同步人群则视为产生振动无关的激励，其数量可采用Fujino方法[3]转换为同频率均匀相位的等效人数，同步人群视为产生振动相关激励，其数量采用与振动相关的同步系数ρ表示(这两种处理方式针对并适用于不同人群，两者的适用假定，并不冲突，可以包络在内)。基于式(3)，可得到人群的横向作用力：
同步系数ρ与振幅A以及行人步频-桥梁频率差
有关[31](当然也可以用人步频-桥梁频率比形式，如文献[32])，桥梁振幅越大，行人同步现象可能性也越大，同时，当行人步频处于桥梁基频附近较小范围内时，即Δω小于某个较小值时，才有较大可能发生同步现象。这种相关性可采用高斯曲线进行模拟[30]，ρ可写为：
根据袁旭斌实验结果[30]，这里ρ1取值0.02，ρ2ρ取值20。将式(5)代入式(4)得：
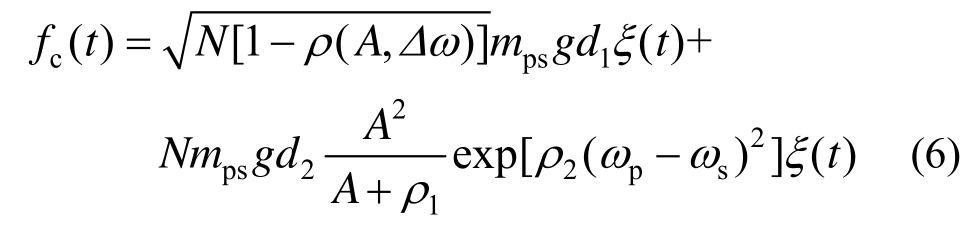
随着振动的进行，式(5)右边第一项非同步人群荷载中的ρ(A,Δω)将趋向于常数ρ0，其只对前期的非同步人群荷载引起的振动产生影响，而对后期以同步人群荷载为主的振动影响很小，且对稳定性也无影响。若假设人群在全桥长度L上均布分布，单位长度密度为mp(x)=Nmps/L，基于式(6)，单位长度的人群横向荷载为：
回到式(1)，按比例粘性阻尼考虑，采用Galerkin方法将上述人行桥横向弯曲振动方程解耦离散，其第j阶模态方程为：
式中：
分别为第j阶的模态位移、角频率、模态阻尼比、振型函数、模态质量以及模态荷载。由于人行桥横向振动主要是行人横向激励的1阶成分引起的，同时出于随机非线性动力方程推导简便的考虑，在此仅考虑人行桥横向振动第 1阶振型(略去上述各阶模态参数阶数下标)，并设定振型函数为φ(x)=sin(πx/L)。根据式(7)，模态荷载有如下表达式：
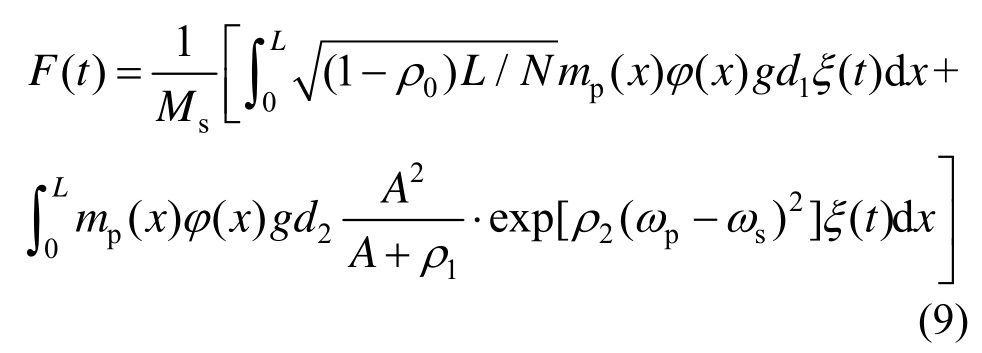
对
进行线性拟合得到
并设定：
式(9)可整理为：
现考虑行人横向荷载的随机性。Ricciardelli等[17]和Ingólfsson等[7－8]在此方面展开了细致研究，但他们实验得到的行人横向激励窄带过程的功率谱需要通过拟合以高斯形状呈现，基于 Pizzimenti根据实验结果得到的行人横向激励功率谱为：
这种形状的功率谱可采用谱展开方法[33]进行离散进而用于数值模拟，但无法用于理论推导分析。为了便于后续的非线性随机方程推导，在此将其等效转换为可由具有随机频率与相位的谐和函数产生的有理谱窄带随机过程。因此利用作者提出的一种行人横向激励功率谱等效转换方法[34]，将其等效转换为有理谱形式。具有随机频率与相位的谐和函数产生的有理谱窄带随机过程为：
式中：ξσ为激励强度；pω为行人横向激励中心频率；δ为频率随机扰动强度；B(t)为标准维纳过程；Φ为随机相位；服从[0,2π)区间上的均匀分布。采用等效转换方法，行人横向随机激励过程ξ(t)可最终表示为：
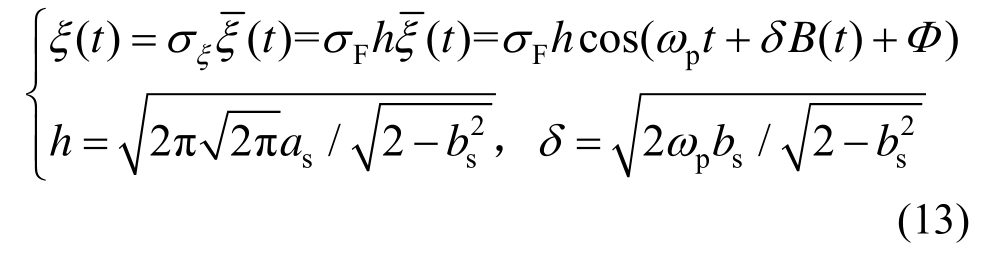
式中：σF为对应着式(15)中ξ(t)前面的乘积系数；h为等效转换产生的附加强度乘积因子；
(t)为单位强度激励的行人横向窄带随机过程；as=0.9；bs=0.043为根据Ricciardelli等[17]实验得到的1阶拟合参数。将式(13)代入式(10)，得到：
式中，
将式(14)代入式(8)，得到桥梁振动方程为：
对式(15)采用随机平均法[35－37]进行后续分析(也可采用多尺度法[38]，但随机平均法更为简捷)。引入变换：
分别代入式(14)，联立方程并整理，可得以下随机平均方程：
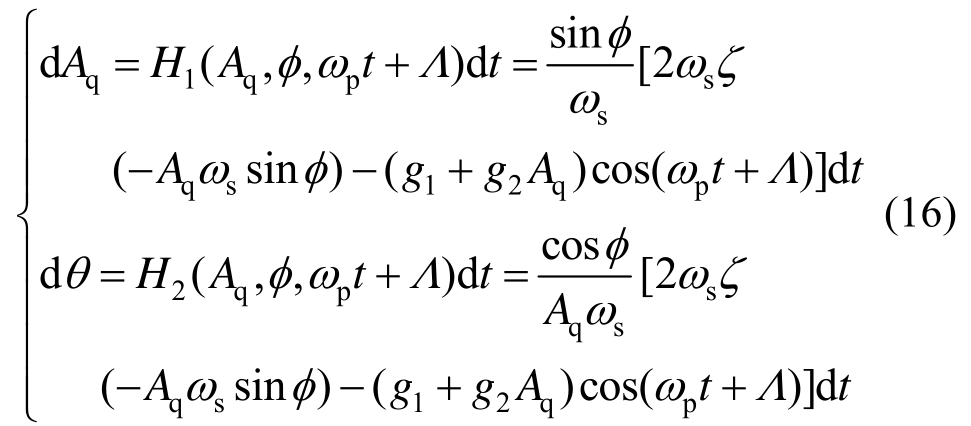
式中，Λ=δB(t)+Φ。这里考虑主共振：ωp/ωs=1+σ，σ为调谐参数。引入新变量Δ：Δ=-θ+σΨ+Λ，结合前述变换式，此时有：
应用Itô微分方程，可得到以下关于Aq、Δ和φ的Itô方程：
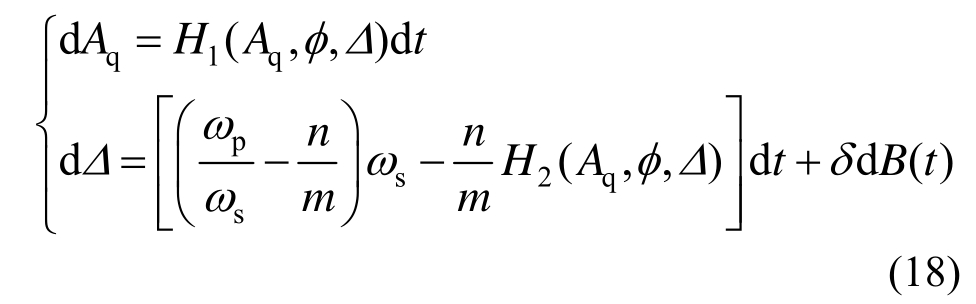
相对Aq和Δ，φ为快变量，将式(18)按φ从0到2π进行确定性平均，得到关于慢变量Aq，Δ的方程：
对式(19)的漂移和扩散系数在Aq=0处进行线性化，得到：
与式(20)对应的稳态FPK方程为：
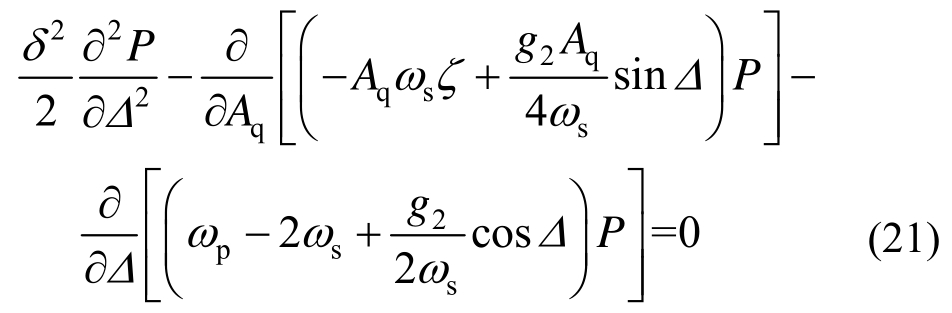
式中，P=P(Aq,Δ)为Aq和Δ的联合概率密度。可知式(21)的边界条件为：
P(Aq,Δ)的解析解形式不易得到，本文将采用采用有限4阶中心差分法求解式(21)的偏微分方程。基于求解得到的P(Aq,Δ)，可采用简单的雅克比转换得到位移和速度的联合概率密度。在后文中，基于得到的联合概率密度结果，将通过随机P-分叉分析(联合概率密度峰个数、位置及形状随参数值改变而变化)，从而得到引起振动发散的某些关键参数(如行人数、频率比)的临界区间。
引入新变量Υ=l nAq，则式(20)的 Itô 方程转为：
由于Δ(t)是[0,2π]上遍历的马尔科夫过程，其不变测度即稳态概率密度函数p()Δ满足如下的平稳FPK方程：
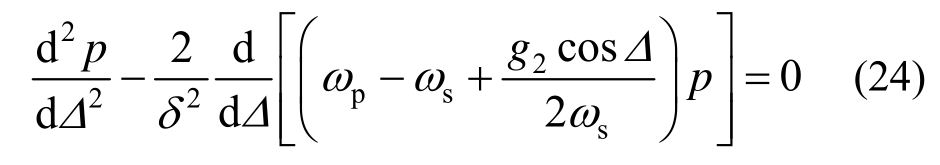
p(Δ)满足周期性条件p(Δ)=p(Δ+2 π)和概率归一化条件
其解为：
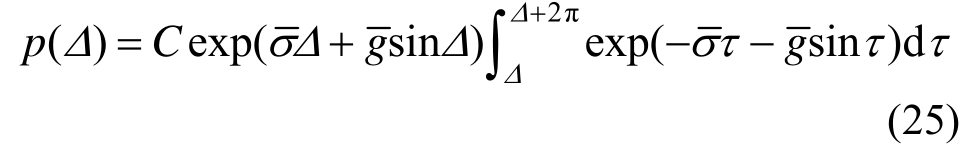
式中：
为概率归一化常数，In(x)为修正第一类贝塞尔 I 函数；
。按照Oseledec乘性遍历定理，对于式(23)，任何非零初始值对应的解的Lyapunov指数λ可定义为：
式中：w.p.1表示概率为1成立；Aq0、0Δ为初始值。由式(25)、式(26)以及Δ(t)的遍历性[39]，可求得最大Lyapunov指数λmax为：
可知式(23)平凡解的稳定性由最大Lyapunov指数λmax决定，若λmax＜0，则式(23)的平凡解以概率1渐进稳定；若λmax＞0，则该解以概率1不稳定，因此系统的稳定与不稳定的界限可由λmax=0来近似表示。这种以最大 Lyapunov指数随参数的符号变化给出的稳定定义又称之为随机D-分叉。在后文中，我们将通过随机D-分叉分析，进一步给出关键参数的具体临界值，并做比较。
英国伦敦千禧桥为浅悬索桥，跨径组成为北边跨81 m+中跨144 m+南边跨108 m。在开放日及后续的振动测试中，三跨都出现了大幅度人致横向振动。目前只有北边跨有较为完整的关于临界人数的记录，因此将千禧桥北边跨作为分析对象。在现场振动测试中，发现当桥上行人数达到166时，北边跨的横向振幅达到20 mm。根据测试结果[1]，可知北边跨基频约为 1.03 Hz，对应的模态质量约为113×103kg，模态刚度约为4730×103kg/s2，阻尼比在[0.006 0.008]之间。其他模型参数均按已有实测或理论取值[8,17,19,30]：横向桥梁静态动载因子d1取为0.04，桥梁振动相关行人横向动载因子d2取1.18，功率谱拟合参数为as=0.9，bs=0.043。每个行人质量为 70 kg。现采用上述方法对千禧桥北边跨横向振动进行分析。
根据式(21)，图 3给出了共振时(频率比fr=fp/fs=1)，不同行人数下的位移和速度的联合概率密度分布图。可知，当人数较小时，N=100，联合概率密度在幅值较小的区域内有一个尖峰，说明小幅振动的概率大。随着人数增加，中心区域内的尖峰逐渐消退并向周围转移。而当人数增长到N=180，在尖峰附近开始出现较为明显的环形峰，说明此时响应有两种较大可能性的运动状态：一种是具有小幅值的随机振动对应于尖峰，另一种是具有较大幅值的随机振动对应于环形峰，有可能从一种运动状态过度到另一种状态，即发生跳跃。当人数增加到N=190，尖峰接近消失，而环形峰则已经非常明显，意味着发生大幅振动的可能性非常大。
图3 不同人数的联合概率密度
Fig.3 Stationary joint probability density for different numbers of pedestrians
根据λmax=0，基于式(27)可得到对应的桥梁振动稳定临界人数Nlim。考虑发生共振情况(行人步频桥梁基频一致)，计算得到的禧桥北边跨最小临界人数为Nlim=174(也可见图 4(a))，这与前述基于随机P-分叉得到的结果吻合，同时也与实测结果(人数为166)相一致，验证了本文方法的有效性。图4给出了λmax-fr-N三者参数关系图。从中可知：行人步频与桥梁频率之间的分布对振动稳定性有着显著影响，当行人步频接近或等于桥梁基频时fr≈1，λmax达到顶峰(图 4(b))，此时稳定性最弱，需要引起振动发散的临界人数最少(图 4(a))，而当行人步频偏离两倍桥梁基频时，λmax迅速减少，即稳定性增大，需要引起振动发散的临界人数增加；λmax随着N的增加而增加(图 4(c))，此时人行桥横向振动稳定性随着人数增加而减弱；λmax对fr的敏感度取决于N，并随着N的增大而急剧增大。当N较少时，如N=100和N=150，无论行人步频如何变化，λmax都将不会大于零，桥梁横向振动都将处于稳定状态(图4(b))。当N较大时，如N=200和N=250，在靠近fr=1附件部分区域内，λmax开始大于零，桥梁横向振动将失稳发散。
图4λmax、fr、N不同组合等势线图
Fig.4 Contours of different combinations ofλmax，frandN
现考虑行人激励随机性对人行桥横向振动的影响。人激励随机性强弱可通过随机扰动因子δ的大小来表示。根据式(13)可知，δ又由参数bs所控制，两者为单调增长关系，因此可通过bs的变化来体现随机性强弱的变化。图5给出了N=174时，λmax-fr-bs三者参数关系图。首先从图 5(a)中可知，bs和fr组成的非稳定区域比较狭窄(灰色区域)，仅当 0.985 ＜fr＜ 1.018以及bs＜ 0.043时，桥梁横向振动才会进入非稳定状态；其次，λmax对fr的敏感度受bs影响，将随着bs的增大而减小(图5(b))，当bs较大时，即随机扰动性较强时，如bs=0.06，步频的变化将不改变λmax的符号(λmax总是小于零)，桥梁横向振动将一直处于稳定状态。当bs较小时，如bs=0.023，在靠近fr=1附近大部分区域内，λmax已大于零，桥梁横向振动处于非稳定状态；λmax对bs的敏感度同样受频率比fr影响(图5(c))。当行人步频离桥梁基频较远时，如fr=0.96，bs的变化对λmax的影响较小，λmax随着bs的增长而缓慢增长，而当行人步频接近或等于桥梁基频时，这种影响变得不可忽视：λmax随着bs的增长而急剧减小，换言之，此时稳定性将随随机扰动性增大而大幅增强。
最后，采用蒙特卡罗数值模拟对式(7)进行了仿真计算，图6为其中100个样本的模拟平均结果，计算了不同人数(阶梯递增，90～180)下的桥梁横向位移响应。从图中可知，当人数不超过150时，桥梁横向位移皆保持在有限振幅内，当人数达到 180的时候，已有发散大幅振动现象，也就是说，导致发散失稳的行人数在150～180区间，这和前面的理论结果一致。
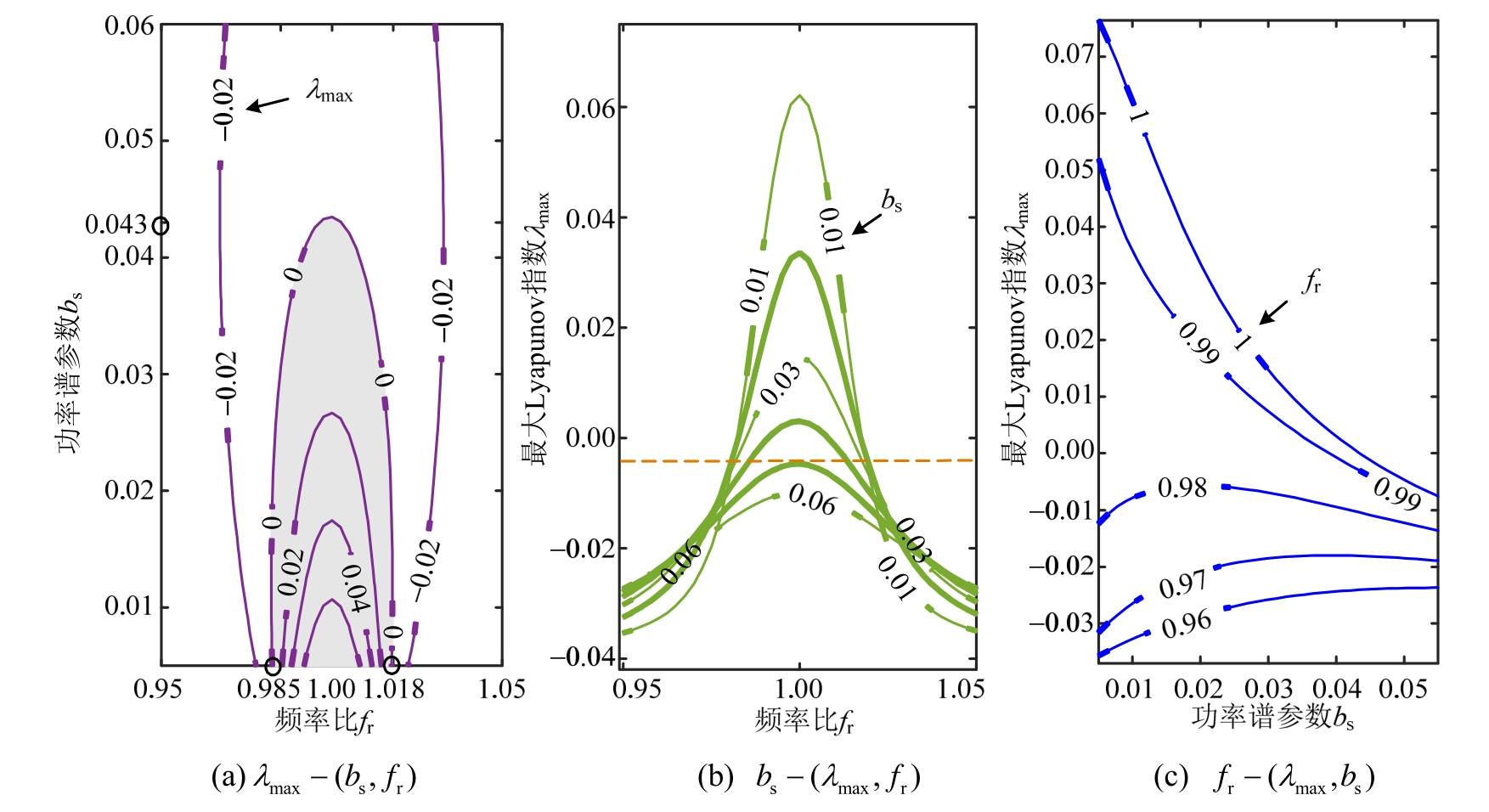
图5λmax、fr、bs不同组合等势线图
Fig.5 Contours of different combinations ofλmax，frandbs
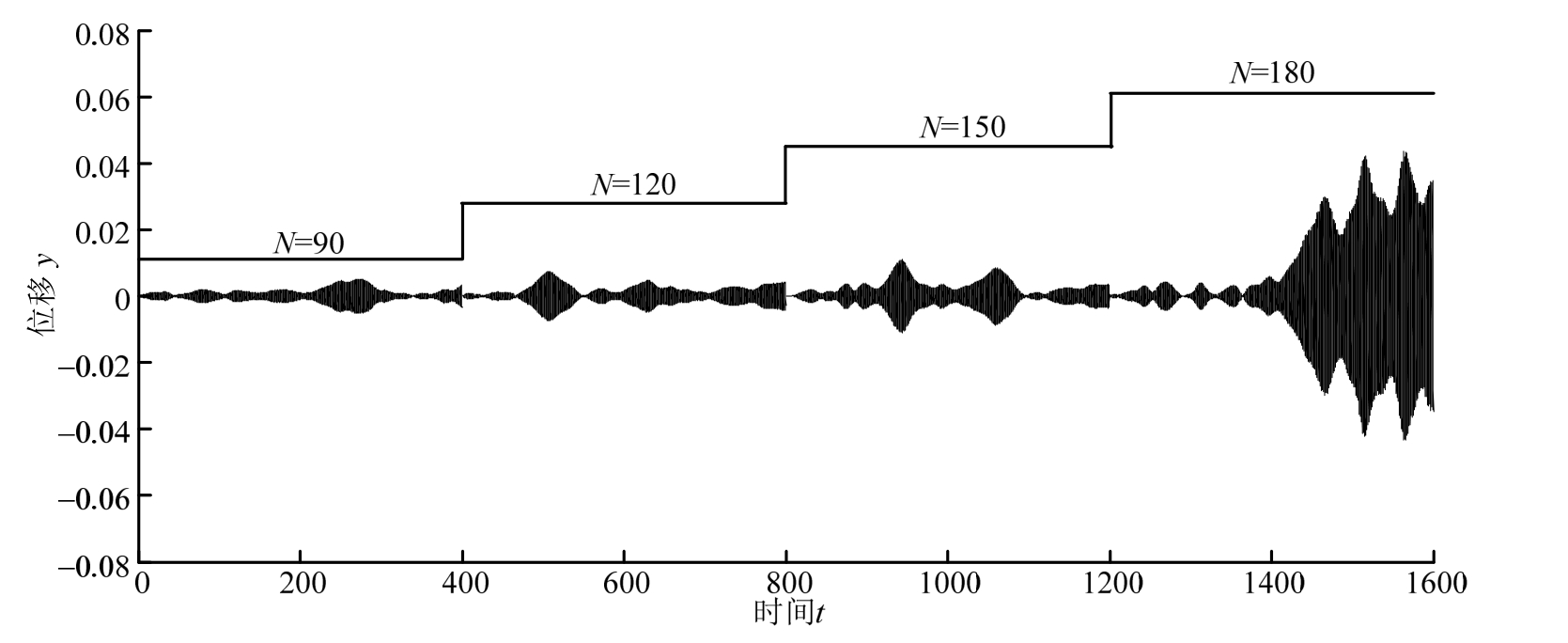
图6 不同人数作用下的随机横向振动数值模拟结果
Fig.6 Response different number of pedestrians by using numerical simulation
本文建立了振动幅值相关的人行桥横向非线性振动模型，并采用窄带随机过程考虑行人荷载的随机性，同时采用非线性随机平均法推导得到相应Itô方程，由此得到了响应的稳态概率密度及最大Lyapunov指数，并进而得到人行桥横向振动失稳发散对应的临界参数。通过千禧桥北边跨的实例分析可知：所提方法计算得到的千禧桥北边跨最小临界人数，符合现场测试结果，同时也与数值模拟计算结果一致，验证了本文所提方法的有效性。同时参数分析结果表明行人步频与桥梁频率分布、行人数以及随机扰动强度对桥梁横向振动的稳定性具有重要影响。行人数的增加将使稳定性减少，并增大稳定性对频率分布的敏感度；而随机扰动性强度对于稳定的影响取决于频率分布，在共振附近区域，稳定性随着随机扰动性强度的增长而大幅增强，但当行人步频处于距离桥梁频率一定范围外时，随机扰动性强度的增长反而会小幅减弱稳定性。
本文所提模型是在随机非线性振动理论框架下建立的，得到了人行桥横向振动稳定/非稳定边界的理论表达式，避免了数值模拟带来的巨大计算量，因此在应用方面具有一定的优势。但需要指出的是，本文并没有考虑行人之间相互作用对振动的影响，主要基于以下几点考虑：行人之间的相互作用机理复杂、不易量化，其与桥梁振动、周围环境以及个体心理及生理差异相关，目前还无法得到一个准确、可靠的描述模型；在人行桥横向大幅振动中，人-桥相互作用引起的人-桥同步被认为是影响振动的主要因素(小额人群也可能激起桥梁大幅横向振动)。尽管如此，行人之间相互作用对桥梁初始振动可能存在影响，以后需完善这方面研究工作。同时本文只考虑了行人横向荷载中第1阶成分，并没有考虑其他高阶成分，这有可能是本文计算的临界人数稍偏高于实测结果的原因。最后，本文也并没有考虑不同行人的参数随机性，如步频，体重等随机性，还有桥梁结构自身参数的随机性，这些随机性将大大增加模型的复杂度。但这些随机性对振动的影响同样有着较大的影响，需要以后展开进一步的研究工作。
[1]Dallard P, Fitzpatrick T, Flint A, et al. The London Millennium Footbridge [J]. Structural Engineer, 2001,79(171): 17－33.
[2]陈政清, 刘光栋. 人行桥的人致振动理论与动力设计[J]. 工程力学, 2009, 26(增刊2): 148－159.Chen Zhengqing, Liu Guangdong. Pedestrian-induced vibration theory and dynamic design of footbridges [J].Engineering Mechanics, 2009, 26(Suppl 2): 148－159.(in Chinese)
[3]Fujino Y, Pacheco B M, Nakamura S-I, et al.Synchronization of human walking observed during lateral vibration of a congested pedestrian bridge [J].Earthquake Engineering ＆ Structural Dynamics, 1993,22(9): 741－758.
[4]Fujino Y, Siringoringo D M. A conceptual review of pedestrian-induced lateral vibration and crowd synchronization problem on footbridges [J]. Journal of Bridge Engineering, 2016, 21(8): C4015001-1―C4015001-12.
[5]Nakamura S. Model for lateral excitation of footbridges by synchronous walking [J]. Journal of Structural Engineering, 2004, 130(1): 32－37.
[6]Piccardo G, Tubino F. Parametric resonance of flexible footbridges under crowd-induced lateral excitation [J].Journal of Sound ＆ Vibration, 2008, 311(1–2): 353－371.
[7]Ingólfsson E T, Georgakis C T. A stochastic load model for pedestrian-induced lateral forces on footbridges [J].Engineering Structures, 2011, 33(12): 3454－3470.
[8]Ingólfsson E T, Georgakis C T, Ricciardelli F, et al.Experimental identification of pedestrian-induced lateral forces on footbridges [J]. Journal of Sound ＆ Vibration,2012, 330(6): 1265－1284.
[9]Roberts T M. Lateral pedestrian excitation of footbridges[J]. Journal of Bridge Engineering, 2005, 10(1): 107-112.
[10]Newland D. Pedestrian excitation of bridges [J].Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2004,218(5): 477－492.
[11]Erlicher S, Trovato A, Argoul P. A modified hybrid Van der Pol/Rayleigh model for the lateral pedestrian force on a periodically moving floor [J]. Mechanical Systems ＆ Signal Processing, 2013, 41(1): 485－501.
[12]Kumar P, Kumar A, Erlicher S. A nonlinear oscillator model to generate lateral walking force on a rigid flat surface [J]. International Journal of Structural Stability ＆ Dynamics, 2017, 18(2): 1850020-1―1850020-31.
[13]Macdonald J H G. Lateral excitation of bridges by balancing pedestrians [J]. Proceedings of the Royal Society A Mathematical Physical ＆ Engineering Sciences, 2009, 465(2104): 1055－1073.
[14]Bocian M, Macdonald J H G, Burn J F. Biomechanically inspired modelling of pedestrian-induced forces on laterally oscillating structures [J]. Journal of Sound ＆ Vibration, 2012, 331(16): 3914－3929.
[15]Carroll S P, Owen J S, Hussein M F M. Reproduction of lateral ground reaction forces from visual marker data and analysis of balance response while walking on a laterally oscillating deck [J]. Engineering Structures,2013, 49(2): 1034－1047.
[16]Carroll S P, Owen J S, Hussein M F M. Experimental identification of the lateral human-structure interaction mechanism and assessment of the inverted-pendulum biomechanical model [J]. Journal of Sound ＆ Vibration,2014, 333(22): 5865－5884.
[17]Ricciardelli F, Pizzimenti A D. Lateral walking-induced forces on footbridges [J]. Journal of Bridge Engineering,2007, 12(6): 677－688.
[18]Bocian M, Macdonald J H G, Burn J F, et al.Experimental identification of the behaviour of and lateral forces from freely-walking pedestrians on laterally oscillating structures in a virtual reality environment [J].Engineering Structures, 2015, 105(2015): 62－76.
[19]Brownjohn J M W, Pavic A, Omenzetter P. A spectral density approach for modelling continuous vertical forces on pedestrian structures due to walking [J].Canadian Journal of Civil Engineering, 2004, 31(1): 65－77.
[20]Živanović S, Pavić A, Reynolds P. Probability-based prediction of multi-mode vibration response to walking excitation [J]. Engineering Structures, 2007, 29(6):942－954.
[21]李泉, 樊健生, 聂建国. 双向行走激励条件下人行桥的随机振动问题研究 [J]. 工程力学, 2010, 27(7): 74－81.Li Quan, Fan Jiansheng, Nie Jianguo. Random vibration of footbridge generated by crowds’ two-way walking [J].Engineering Mechanics, 2010, 27(7): 74－81. (in Chinese)
[22]朱前坤, 李宏男, 杜永峰, 等. 不同行走步速下人行桥振动舒适度定量化评估 [J]. 工程力学, 2016, 33(10):97－104.Zhu Qiankun, Li Hongnan, Du Yongfeng, et al.Quantitative evaluation of vibration serviceability of pedestrian brigde under different walking speed [J].Engineering Mechanics, 2016, 33(10): 97－104. (in Chinese)
[23]Racic V, Brownjohn J. Mathematical modelling of random narrow band lateral excitation of footbridges due to pedestrians walking [J]. Computers ＆ Structures,2011, 90/91(1): 116－130.
[24]Racic V, Brownjohn J M W. Stochastic model of near-periodic vertical loads due to humans walking [J].Advanced Engineering Informatics, 2011, 25(2): 259－275.
[25]Fernando Jimenez-Alonso J, Saez A, Caetano E, et al.Vertical crowd-structure interaction model to analyze the change of the modal properties of a footbridge [J].Journal Of Bridge Engineering, 2016, 21(8): C4015004-1－C4015004-19.
[26]Venuti F, Racic V, Corbetta A. Modelling framework for dynamic interaction between multiple pedestrians and vertical vibrations of footbridges [J]. Journal of Sound ＆ Vibration, 2016, 379(2016): 245－263.
[27]李慧乐, 夏禾. 基于车桥耦合随机振动分析的钢桥疲劳可靠度评估 [J]. 工程力学, 2017, 34(2): 69－77.Li Huile, Xia He. Fatigue reliability evaluation of steel bridges based on coupling random vibration analysis of train and bridge [J]. Engineering Mechanics, 2017, 34(2):69－77. (in Chinese)
[28]Ricciardelli F, Mafrici M, Ingólfsson E T. Lateral pedestrian-induced vibrations of footbridges:characteristics of walking forces [J]. Journal of Bridge Engineering, 2014, 19(9): 1265－1266.
[29]Ricciardelli F, Demartino C. Design of footbridges against pedestrian-induced vibrations [J]. Journal Of Bridge Engineering, 2016, 21(8): C4015003-1－C4015003-13.
[30]袁旭斌. 人行桥人致振动特性研究[D]. 上海: 同济大学, 2006.Yuan Xubin. Research on pedestrian-induced vibration of footbridge [D]. Shanghai: Tongji University, 2006. (in Chinese)
[31]Venuti F, Bruno L. Crowd-structure interaction in lively footbridges under synchronous lateral excitation: A literature review [J]. Physics of Life Reviews, 2009, 6(3):176－206.
[32]Bruno L, Venuti F. Crowd-structure interaction in footbridges: Modelling, application to a real case-study and sensitivity analyses [J]. Journal of Sound ＆ Vibration, 2009, 323(1/2): 475－493.
[33]Shinozuka M, Deodatis G. Simulation of stochastic processes by spectral representation [J]. Applied Mechanics Reviews, 1991, 44(4): 191－204.
[34]Jia B, Yu X, Yan Q, et al. Nonlinear stochastic analysis for lateral vibration of footbridge under pedestrian narrowband excitation [J]. Mathematical Problems in Engineering, 2017, 2017(22): 1－12.
[35]朱位秋. 随机振动[M]. 北京: 科学出版社, 1992.Zhu Weiqiu. Random vibration [M]. Beijing: Science Press, 1992. (in Chinese)
[36]Rong H, Wang X, Xu W, et al. Subharmonic response of a single-degree-of-freedom nonlinear vibro-impact system to a narrow-band random excitation [J]. Physical Review E, 2009, 80(2): 026604-1－026604-8.
[37]冯长水. 窄带随机激励下时滞反馈控制的强非线性系统随机动力学研究[D]. 杭州: 浙江大学, 2008.Feng Changshui. Stochastic dynamics of strongly nonlinear systems with time-delayed feedback control under narrow-band random excitations [D]. Hangzhou:Zhejiang University, 2008. (in Chinese)
[38]杨志安, 赵开元. 有界窄带激励下微梁系统主共振[J]. 工程力学, 2017, 34(增刊1): 19－25.Yang Zhian, Zhao Kaiyuan. Primary response of micro-beam system subjected to narrow-band random excitation [J]. Engineering Mechanics, 2017, 34(Suppl 1): 19－25. (in Chinese)
[39]Rong H, Xu W, Wang X, et al. Principal response of van der pol-duffing oscillator under combined deterministic and random parametric excitation [J]. Applied Mathematics and Mechanics, 2002, 23(3): 299－310.
STABILITY ANALYSIS ON PEDESTRIAN-INDUCED LATERAL VIBRATION OF FOOTBRIDGES CONSIDERING PEDESTRIAN STOCHASTIC EXCITATION
颜全胜(1968―)，男，江西人，教授，博士，博导，主要从事大跨度桥梁非线性及稳定研究(E-mail: cvqshyan@scut.edu.cn);