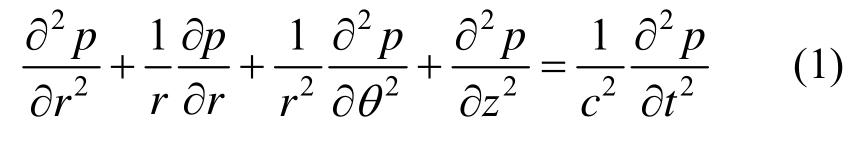
实际工程中，存在各种海上结构，如跨海桥梁、海上风电和人工岛等[1―3]；同时我国处于欧亚地震和环太平洋地震带之间，导致我国地震活动频繁，海上结构建设成本高，一旦遭受地震破坏将会导致巨大的经济损失，尤其是作为生命线工程的桥梁将会产生无法估量的后果。地震作用下水-结构相互作用会对结构产生动水压力作用，研究表明该动水压力作用会改变结构的动力特性，同时也会改变结构的动力响应[4―6]。因此，研究地震作用下水-柱体结构相互问题具有一定的工程价值。
水-柱体结构相互作用研究一般采用解析法[7―10]、解析-数值法[11―13]和数值法[14―15]。解析法是首先通过求解水-结构相互作用的定解问题构建动水压力公式，然后将动水压力公式代入结构的振动方程，从而对结构进行地震作用下的动力响应分析。解析-数值法是先求结构地震动水压力的解析公式，再采用有限元法建立结构的分析模型，从而对结构进行地震作用下的动力响应分析。解析法和解析-数值法仅能对圆形和椭圆形柱体结构进行分析。然而，实际工程中存在矩形和圆端形等截面形式的结构。对于任意截面柱体结构的动水压力可采用有限元法或边界元法等数值方法进行求解，其中有限元法是将水体和结构均采用有限元进行离散。
水-结构的动力相互作用涉及无限域介质中的波传播问题。有限元法结合人工边界条件的时域耦合算法是求解该问题的有效方法，即通过引入人工边界条件将无限域水体划分为远场无限域和近场有限域。采用动力有限元法模拟近场，通过在人工边界处施加人工边界条件模拟被截去远场对近场的影响。粘弹性人工边界[16]是常用的一种模拟无限域介质的人工边界条件，该人工边界条件是一种近似方法，相对容易实现，自身计算效率高；但为了获得充分精确的结果，人工边界需要设置于距离辐射源适当远处，显著增加了计算成本。随着计算机发展水平以及对工程分析精度要求的不断提高，无限域的精确模拟是切实可行的。精确方法本身的计算效率可能不及近似方法，但精确方法可以设置在距离结构或者辐射源较近的位置，使得总成本并一定高于近似方法。文献[17―22]建立了一套精确时域人工边界条件的系统方法，包括无限域频率响应函数有理近似的稳定性和识别、用于识别模型参数的有限函数连分式展开技术以及实现有理近似时域化的高阶弹簧-阻尼-质量模型。基于该方法，已经建立了二维出平面外域模型[21]和波导模型[22]的高精度人工边界条件。
本文针对地震作用任意截面形式柱体结构与周围水体的动力相互作用问题，根据水体控制方程和边界条件，通过分离变量法推导了三维圆柱形截断边界的频域解析人工边界条件，基于外域模型[21]和波导模型[22]人工边界条件的动力刚度关系建立了圆柱形人工边界条件动力刚度的嵌套形式，应用时间局部化方法[17]和离散人工边界条件，并将其与近场有限元方程耦合形成一种能够显式求解的时间二阶系统。
地震作用下水-柱体的动力相互作用问题如图1所示，图中圆柱形截断边界的半径为R，水深为h。假定地基为刚性，水体为无旋、无粘性、可压缩，并忽略表面重力波的影响。柱坐标系统(r,θ,z)下水体的控制方程为：
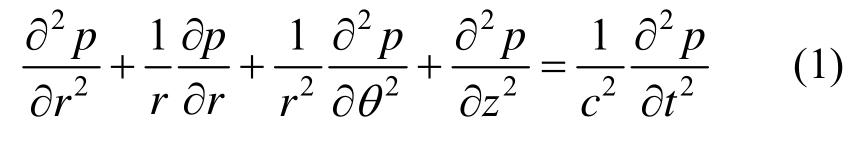
式中：p表示水体的动水压力；t表示时间；c表示水中声速。
图1 水-柱体结构相互作用模型
Fig.1 Scalar wave model in water-cylinder interaction
水底和水面的边界条件以及无穷远处的辐射条件为：
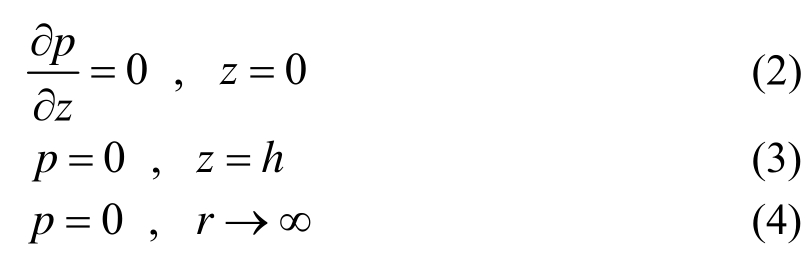
动力压力p的解可表示
为圆频率，
通过分离变量求解，并结合水底、水面和无穷远处边界条件，可求得人工边界r=R处动水压力P的解为：
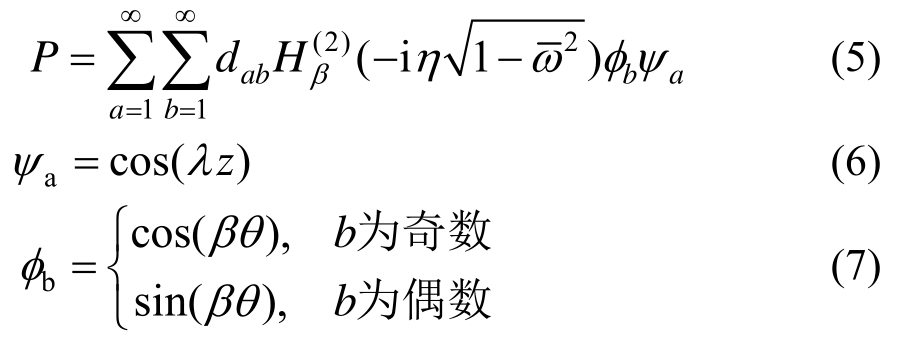
式中：
为沿深度的无量纲波数；
为无量纲频率；
为β阶第二类汉克尔函数；β取为b/2的整数部分；dab为待定系数。
对式(5)两边求坐标r的偏导数，然后将得到的结果与式(5)联立消去待定常数，得到人工边界r=R处的频域动力刚度关系为：
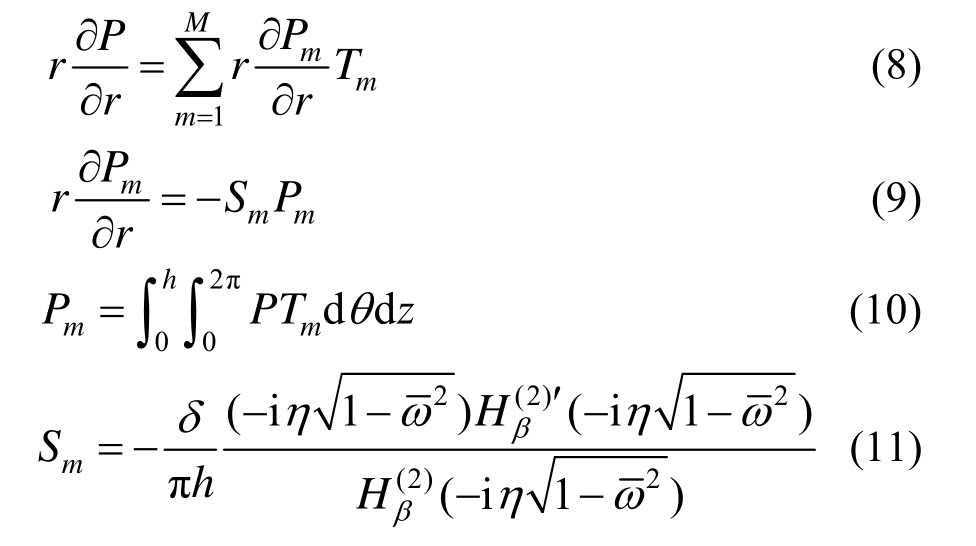
式中：M=AB，A和B分别为选取的竖向模态和环向模态阶数；
时δ=1，b＞1时δ=2；
Sm为动力刚度系数。
为了避免计算精确动力刚度人工边界条件中的全局时间卷积分，文献[18]和文献[20]提出了一套由有理函数近似和辅助变量实现构成的时间局部化方法。该方法已经应用于二维标量波外域模型[21]和波导模型[22]的人工边界条件，本节将该方法扩展应用于三维圆柱形人工边界条件。
根据文献[17]和文献[19]，动力刚度系数式(11)的有理近似为：
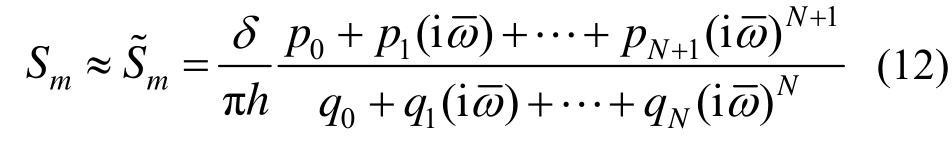
式中：N为有理函数的阶数；pn和qn为待定实值参数。
有理函数的稳定性条件是有理函数的全部极点和零点具有负实部，可以表示为：
式中：sj和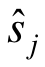
为有理函数的极点和零点；Re()为复数的实部。
为了计算有理函数的实常数，将感兴趣的频率区间进行离散，通过最小二乘拟合构建非线性优化问题，并且采用罚函数方法将稳定性约束条件强加入目标函数，形成如下优化问题。
式中：L为离散频率点的数量；
为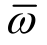
的第l个频率点；| |表示复数的模；H(y)为海维赛德函数，当x＜0时，H(x)=0，当x≥0时，H(x)=1；Dj和
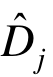分别表示零点和极点的正实数罚因子，取充分大数值时可以排除不满足稳定条件的解。采用遗传算法结合 Nelder-Mead单纯形法求解式(15)的非线性优化问题。
由式(11)可以看出，精确动力刚度系数与几何参数R/h相关。因此，直接对其进行有理函数近似需要多次识别，即对不同的R/h值和不同阶模态都要进行有理函数近似。因此，本文提出了一种有效的方法可以避免以上问题。将动力刚度系数式(11)重写为如下形式：
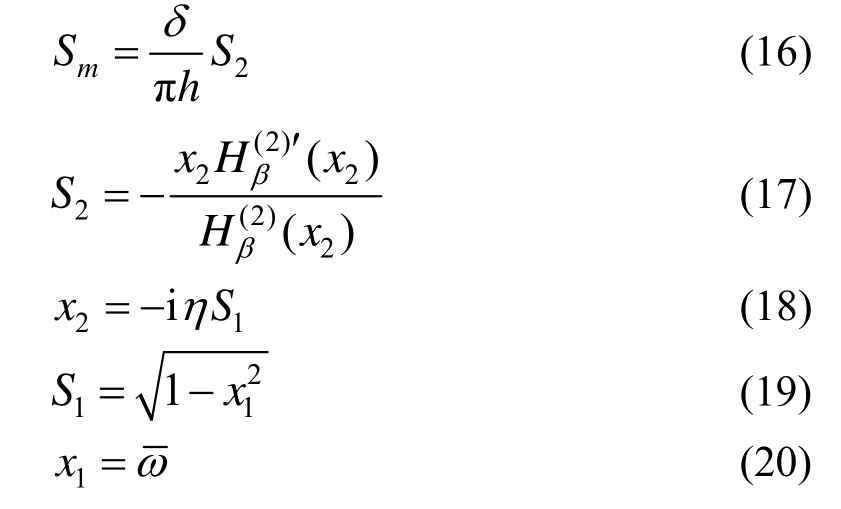
动力刚度系数S1和S2分别对应于文献[21]的外域模型和文献[22]的波导模型，S1和S2是与材料参数和几何参数不相关的。S1和S2是的有理近似分别为：
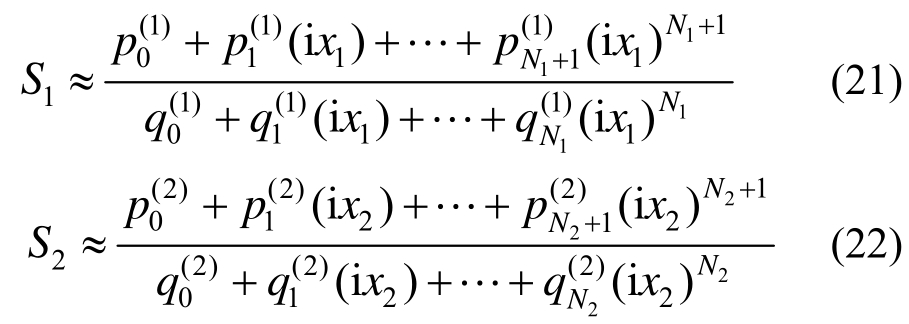
式中：N1和N2表示有理函数的阶数；
和
为待定实值参数，具体的数值见文献[23]。
因此，动力刚度系数式(11)的有理近似可通过式(16)、式(22)、式(18)、式(21)和式(20)的嵌套计算得到，有理函数的系数可由
和
计算得到，为有理函数的阶数为
数值算例表明嵌套后的有理函数精度高，并且仍满足式(13)和式(14)的稳定性条件。
通过应用有理函数的连分式展开方法并且引入辅助变量，有理近似式(12)可等价地实现为如图2所示的线性系统，即由弹簧、阻尼器、质量单元和辅助自由度构成的力学模型，模型动力方程组的矩阵形式为：
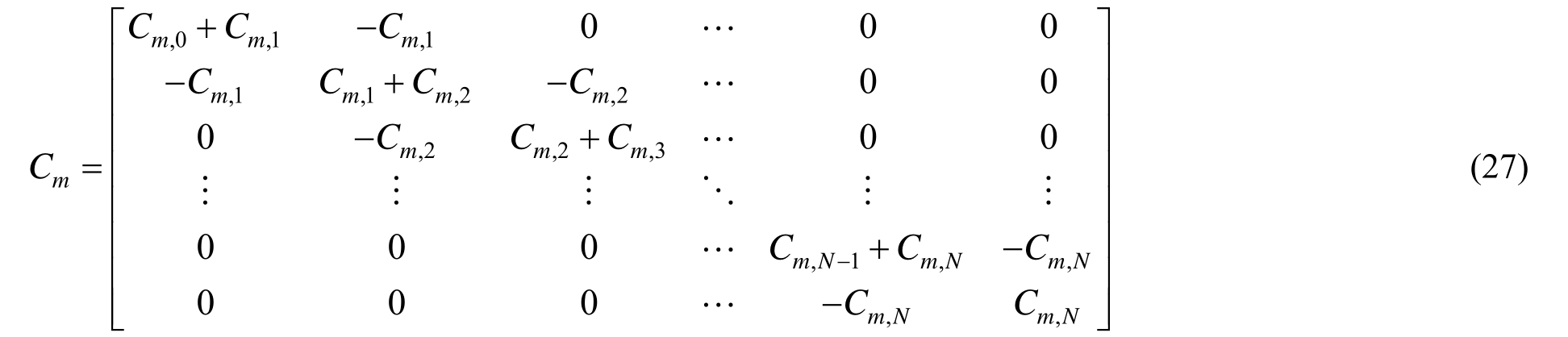
式中：Km,0、Cm,n和Mm,n分别为弹簧、阻尼和质量单元的系数。
图2 高阶弹簧-阻尼-质量模型
Fig.2 High order-spring-dashpot-mass model
模型的弹簧、阻尼和质量参数满足：
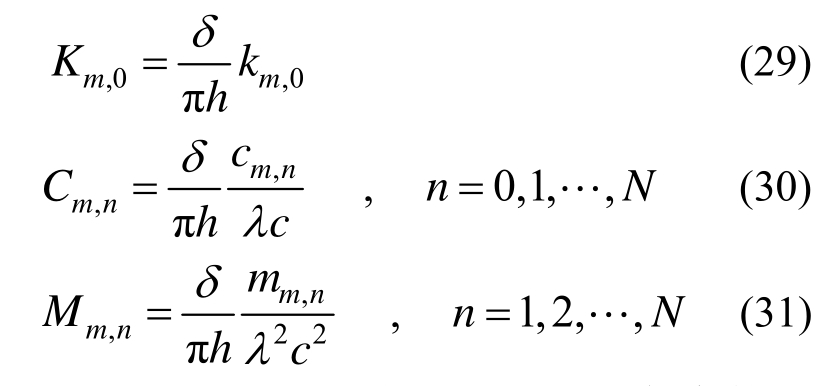
式中，km,0、cm,n和mm,n是相对于无量纲频率的无量纲参数，具体的计算程序见文献[23]。
式(8)和式(10)的时域形式为：
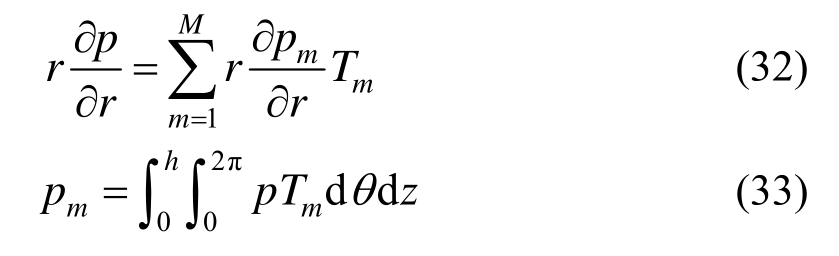
按照内域结点和人工边界结点划分，内域水体的集中质量有限元方程可以写为：
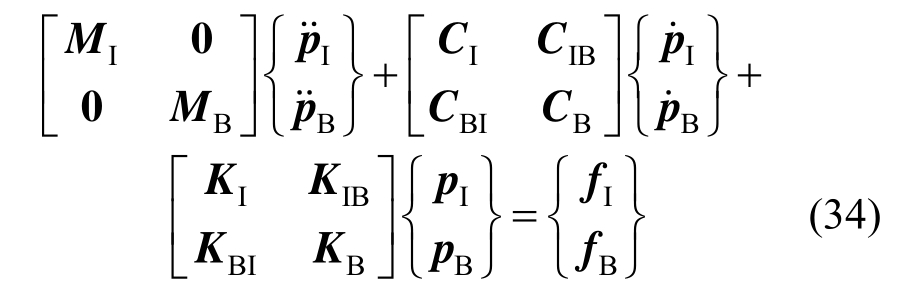
式中：下标I和下标B分别表示与内域结点相关和与人工边界结点相关；p为结点动水压力列向量；f为结点荷载列向量；M、C和K分别为质量矩阵、总阻尼矩阵分和刚度矩阵。
作用于人工边界结点的荷载列向量fB可表示为：
式中：N为与全部人工边界结点相关的全局形函数行向量；上标T表示矩阵或者向量的转置。
边界压力和模态函数可以分别离散为：
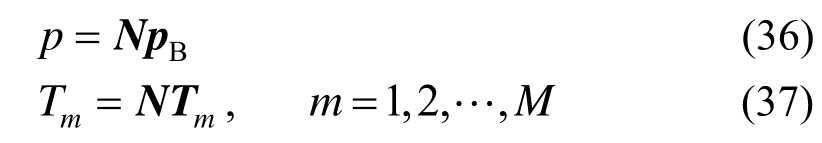
式中：Tm为人工边界结点处模态函数值的列向量。
将式(36)和式(37)代入式(33)、式(23)和式(32)，并将得到的结果代入式(34)和式(35)，整理可得到人工边界条件与近场有限元方程耦合的动力有限元方程为：
式中：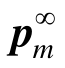
为pm去掉第一行后的列向量；
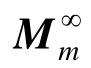为Mm去掉第一列和第一行后的矩阵；
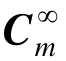为Cm去掉第一列和第一行后的矩阵；Im为第一列是Tm而其余元素为零的矩阵；
式(38)可以采用现有的隐式时间积分方法求解，如 Newmark常平均加速度法。为了提高求解大规模近场波动问题的计算效率，弥补高阶精度人工边界条件的空间全局性，本文采用文献[24]中提出的一种能够处理非角阻尼矩阵的动力学显式时间积分方法。
地震作用下柱体结构与水体动力相互作用包括地面运动引起的动水压力和结构柔性运动引起的动水压力。本文主要即通过地面运动引起的地震动水压力验证提出的高精度时域人工边界条件，即假定结构为刚性。分析如图3所示的方柱与水体动力相互作用问题。截面边长为 30 m；水深为 50 m，水体密度为1000 kg/m3，水中声速为1438 m/s2；圆柱形人工边界的半径取为30 m；水体初始静止；观测点如图3所示。地震作用沿x方向，地面加速度时程如图4所示，作用在水-结构交界面的荷载为：
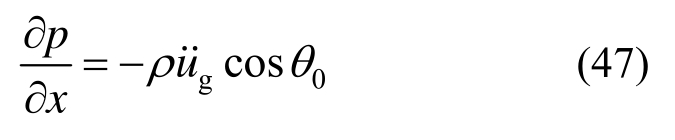
式中：θ0表示方柱截面法向与x轴正方向的夹角。人工边界条件沿深度方向和环向的模态数量分别取为A=4和B=9，总模态的数量则为M=36；有理函数式(21)和式(22)的阶数分别取为N1=5和N2=3，嵌套后有理函数式(12)的阶数为N=23。采用充分大有限元计算域得到的数值解作为参考解。图5为有理函数式(12)与精确解的比较，图 6为每阶模态下有理函数极点和零点实部的最大值。由图5和图6可以看出，嵌套后的有理函数较高的精度，并且仍满足稳定性条件。
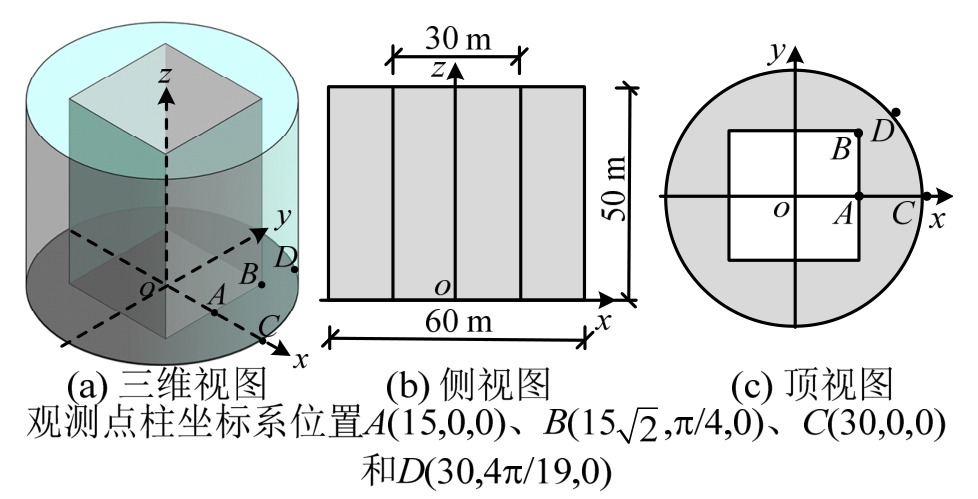
图3 数值算例有限域模型
Fig.3 Finite domain in numerical Example
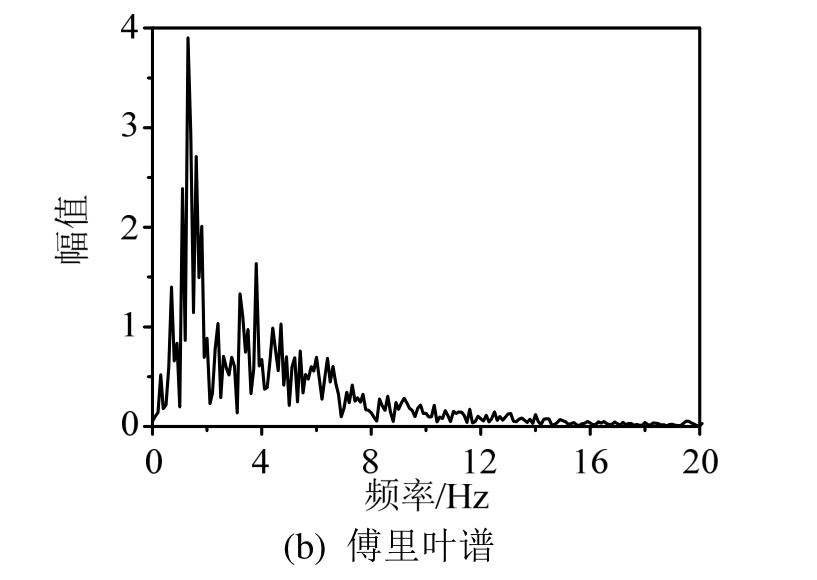
图4 地面运动加速度
Fig.4 Horizontal earthquake acceleration of water bottom
图5 动力刚度Sm有理函数近似(N=23)
Fig.5 Rational function approximations (N=23) ofSm
图7 给出观测点的动水压力时程计算结果，表给出了各观测点动水压力峰值的比较；图8和图9分别给出 3.735 s时刻方柱表面和截断边界上的动水压力云图。由图7～图9和表1可以看出，采用本文提出的高精度人工边界条件得到的计算解与参考解吻合较好。
需要指出的是，本文提出的圆柱形人工边界的模态数量的精度是与沿深度方向和环向的模态数量相关的；当圆柱形人工边界的模态数量取到高阶时，其半径取值较小时其精度也能满足工程需求。表1中观测点动水压力峰值的相对误差在5%以内，即算例中圆柱形人工边界模态阶数的取值是满足工程需求的。
图6 有理函数近似式Sm零点和极点实部的最大值(N=23)
Fig.6 Maximum real parts of poles and zeros of rational function approximations (N=23) ofSm
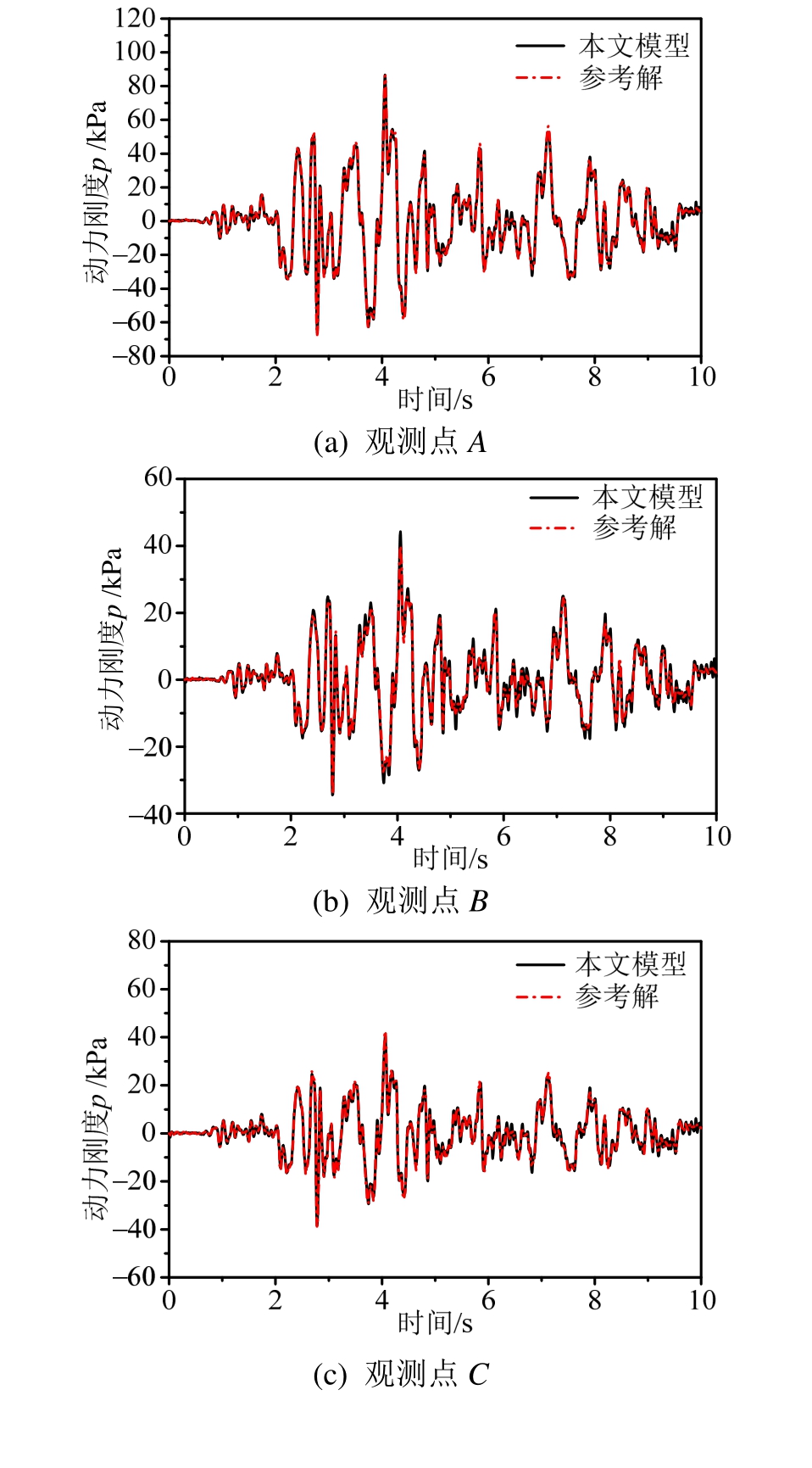
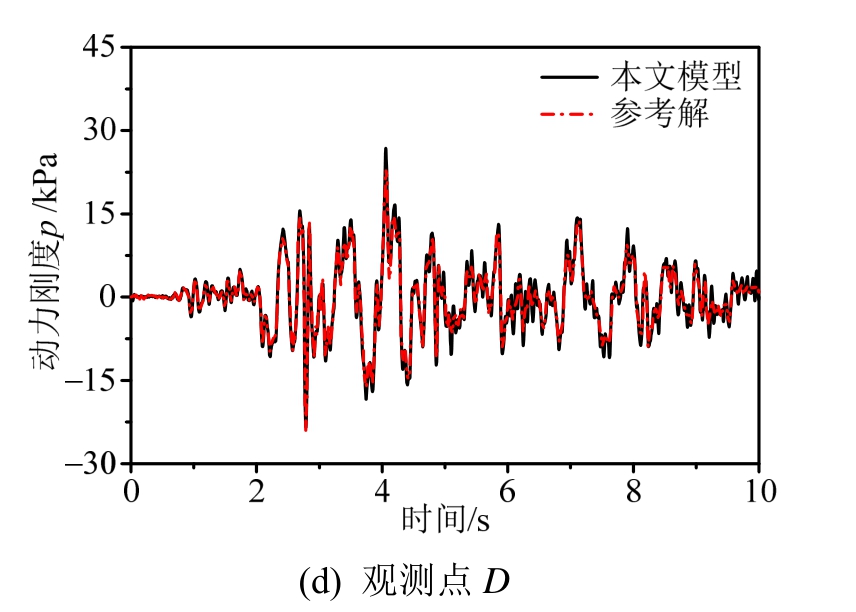
图7 观测点的动水压力时程
Fig.7 Time histories of hydrodynamic pressures at observation points
图8 3.735 s时刻方柱面x=15 ms处动水压力云图
Fig.8 Snapshots of hydrodynamic pressures at water-structure interface ofx=15 m at 3.735 s
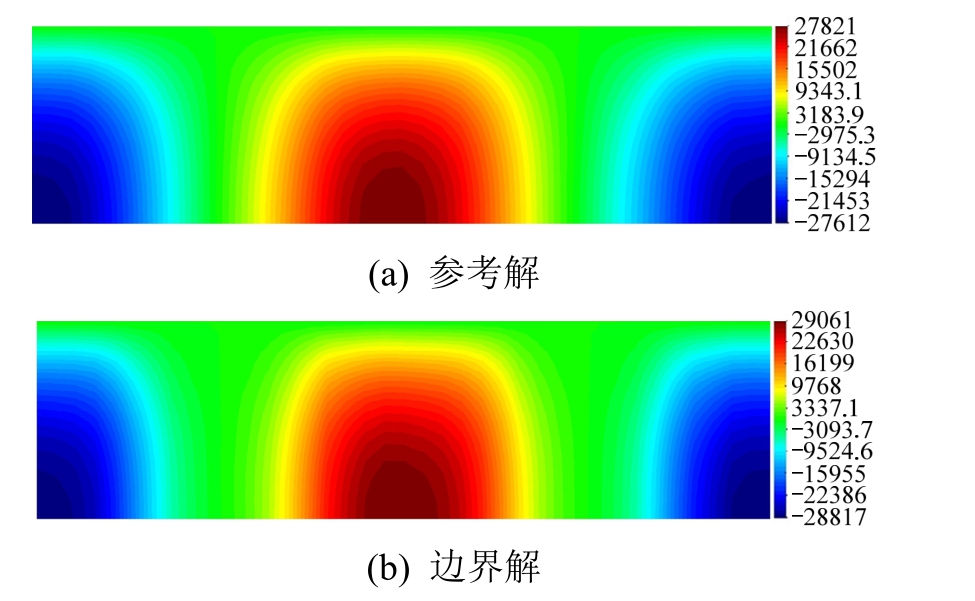
图9 3.735 s时刻截断边界上动水压力云图
Fig.9 Snapshots of hydrodynamic pressures at cylindrical artificial boundary at 3.735 s
表1 观测点动水压力峰值的相对误差
Table 1 The relative error for the peak value of the hydrodynamic pressures on the observed points
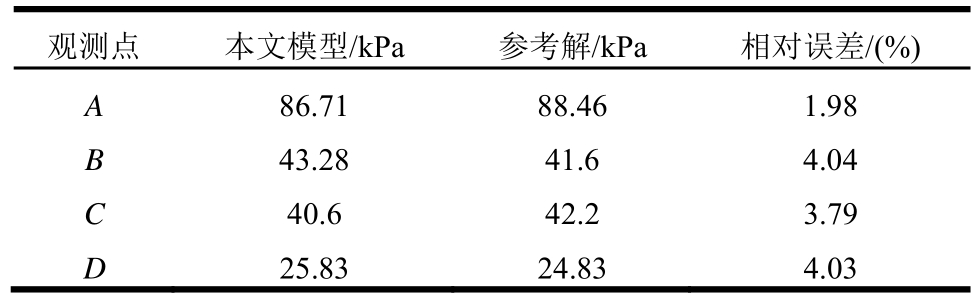
观测点 本文模型/kPa 参考解/kPa 相对误差/(%)A86.71 88.46 1.98B43.28 41.6 4.04C40.6 42.2 3.79D25.83 24.83 4.03
针对地震作用下水-柱体结构的动力相互作用问题，提出了一种三维圆柱形高精度人工边界条件。三维圆柱形人工边界条件的精确动力刚度是与边界几何参数相关，本文提出了动力刚度嵌套的方法避免了直接对其进行有理函数近似的参数识别，即通过二维外域模型和波导模型动力刚度有理近似式的嵌套计算得到三维圆柱形人工边界动力刚度式的有理近似式，该有理近似式精确、稳定。时域化的三维圆柱形精确人工边界条件能够与近场有限元法无缝结合，形成整体时域显式求解方法。数值试验表明，该方法精度高、在有限元代码中容易实现。
[1]项海帆. 21世纪世界桥梁工程的展望[J]. 土木工程学报, 2000, 33(3): 1―6.Xiang Haifan. Prospect of world’s bridge projects in 21st century [J]. China Civil Engineering Journal, 2000,33(3): 1―6. (in Chinese)
[2]Zhang D, Zhang X, He J, et al. Offshore wind energy development in China: Current status and future perspective [J]. Renewable and Sustainable Energy Reviews, 2011, 15(9): 467―4684.
[3]闫静茹, 路德春, 杜修力, 等. 港珠澳大桥工程人工岛三维非线性地震反应分析[J].世界地震工程, 2016,32(1): 161―168.Yan Jingru, Lu Dechun, Du Xiuli, et al. Threedimensional nonlinear seismic response analysis of artificial island of Hong Kong-Zhuhai-Macao bridge project [J]. World Earthquake Engineering, 2016, 32(1):161―168. (in Chinese)
[4]黄信, 李忠献. 动水压力作用对深水桥墩地震响应的影响[J]. 土木工程学报, 2011, 44(1): 65―73.Huang Xin, Li Zhongxian. Influence of hydrodynamic pressure on seismic responses of bridge piers in deep water [J]. China Civil Engineering Journal, 2011, 44(1):65―73. (in Chinese)
[5]李忠献, 黄信. 行波效应对深水连续刚构桥地震响应的影响[J]. 工程力学, 2013, 30(3): 120―125.Li Zhongxian, Huang Xin. Influence of traveling wave effect on seismic responses of continuous rigid-framed bridge in deep water [J]. Engineering Mechanics, 2013,30(3): 120―125. (in Chinese)
[6]张文学, 黄荐, 陈盈, 等. 渡槽结构考虑流固耦合的横向地震响应简化计算公式[J]. 工程力学, 2017, 34(8):69―75.Zhang Wenxue, Huang Jian, Chen Ying, et al. A simplified formula for the calculation of the transverse seismic response of aqueducts considering fluid-structure interaction [J]. Engineering Mechanics, 2017, 34(8):69―75. (in Chinese)
[7]Liaw C Y, Chopra A K. Dynamics of towers surrounded by water [J]. Earthquake Engineering and Structural Dynamics, 1974, 3(1): 33―49.
[8]Li Q, Yang W L. An improved method of hydrodynamic pressure calculation for circular hollow piers in deep water under earthquake [J]. Ocean Engineering, 2013,72: 241―256.
[9]Du X L, Wang P G, Zhao M. Simplified formula of hydrodynamic pressure on circular bridge piers in the time domain [J]. Ocean Engineering, 2014, 85: 44―53.
[10]黄信, 李忠献. 考虑水底柔性反射边界的深水桥墩地震动水压力分析[J]. 工程力学, 2012, 29(7): 102―116.Huang Xin, Li Zhongxian. Earthquake induced hydrodynamic pressure of bridge pier in deep water with flexible reflecting boundary [J]. Engineering Mechanics,2012, 29(7): 102―116. (in Chinese)
[11]赖伟, 王君杰, 胡世德. 地震下桥墩动水压力分析[J].同济大学学报, 2004, 32(1): 1―5.Lai Wei, Wang Junjie, Hu Shide. Earthquake induced hydrodynamic pressure on bridge pier [J]. Journal of Tongji University, 2004, 32(1): 1―5. (in Chinese)
[12]Williams A N. Analysis of the base-excited response of intake-outlet towers by a Green’s function approach [J].Engineering Structures, 1991, 13(1): 43―53.
[13]Jiang H, Wang B, Bai X, et al. Simplified expression of hydrodynamic pressure on deep water cylindrical bridge piers during earthquakes [J]. Journal of Bridge Engineering, 2017, 22(6): 04017014.
[14]Liaw C Y, Chopra A K. Earthquake analysis of axisymmetric towers partially submerged in water [J].Earthquake Engineering and Structural Dynamics, 1975,3(3): 233―248.
[15]刘浪, 杨万理, 李乔. 深水桥梁墩水耦合抗震分析方法[J]. 西南交通大学学报, 2015, 50(3): 449―453.Liu Lang, Yang Wanli, Li Qiao. Seismic analysis method of deep-water bridge pier and water coupling [J]. Journal of Southwest Jiaotong University, 2015, 50(3): 449―453. (in Chinese)
[16]刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6): 46―51.Liu Jingbo, Wang Zhenyu, Du Xiuli, et al. Threedimensional visco-elastic artificial boundaries in time domain for wave motion problems [J]. Engineering Mechanics, 2005, 22(6): 46―51. (in Chinese)
[17]杜修力, 赵密. 一种新的高阶弹簧-阻尼-质量边界-无限域圆柱对称波动问题[J]. 力学学报, 2009, 41(2):207―215.Du Xiuli, Zhao Mi. A novel high-order spring- dashpotmass boundary for cylindrical-symmetry wave motions in infinite domain [J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(2): 207―215. (in Chinese)
[18]赵密, 杜修力. 时间卷积的局部高阶弹簧-阻尼-质量模型[J]. 工程力学, 2009, 26(5): 8―18.Zhao Mi, Du Xiuli. High-order model of spring- dashpotmass model for localizing time convolution [J].Engineering Mechanics, 2009, 26(5): 8―18. (in Chinese)
[19]赵密, 杜修力, 刘晶波. 一种高阶精度人工边界条件：出平面外域波动问题[J]. 工程力学, 2012, 29(4): 7―14.Zhao Mi, Du Xiuli, Liu Jingbo. A high-order accurate artificial boundary condition: out-of-plane exterior wave problem [J]. Engineering Mechanics, 2012, 29(4): 7―14.(in Chinese)
[20]Du X L, Zhao M. Stability and identification for rational approximation of frequency response function of unbounded soil [J]. Earthquake Engineering and Structural Dynamics, 2010, 39(2): 165―186.
[21]Du X L, Zhao M. A local time-domain transmitting boundary for simulating cylindrical elastic wave propagation in infinite media [J]. Soil Dynamics and Earthquake Engineering, 2010, 30(10): 937―946.
[22]Zhao M, Du X L, Liu J B, et al. Explicit finite element artificial boundary scheme for transient scalar waves in two-dimensional unbounded waveguide [J]. International Journal for Numerical Methods in Engineering, 2011,87(11): 1073―1104.
[23]赵密. 近场波动有限元模拟的应力型时域人工边界条件极其应用[D]. 北京: 北京工业大学, 2009.Zhao Mi. Stress-type time-domain artificial boundary condition for finite-element simulation of near-field wave motion and its engineering application [D]. Beijing:Beijing University of Technology, 2009. (in Chinese)
[24]Wang J T, Zhang C H, Du X L. An explicit integration scheme for solving dynamic problems of solid and porous media [J]. Journal of Earthquake Engineering,2008, 12(2): 293―311.
A HIGH-ACCURACY CYLINDRICAL ARTIFICIAL BOUNDARY CONDITION: WATER-CYLINDER INTERACTION PROBLEM
李会芳(1993―)，女，河南人，博士生，主要从事人工边界方法的研究(E-mail: S201504005@emails.bjut.edu.cn);