，定义单元i的损伤指数αi为它损伤后的刚度
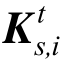与初始刚度Ks,i的比值，可以表示为：土木工程结构在服役期内因外界环境的影响或自身腐蚀、老化等原因而在结构内部发生损伤，准确而有效的识别出损伤产生的部位和程度对于维持结构后续使用阶段的安全性具有重要意义，有效的损伤识别理论可以为服役结构的使用和评估提供可靠的依据，也是健康监测领域的一项重要研究内容。近年来，国内外学者围绕损伤识别方法开展了一系列的研究工作。
依据实测数据类型的不同，通常将损伤识别方法分为以下三类：
1) 基于智能算法的损伤识别方法。该方法主要包括神经网络方法、遗传算法、小波变换、HHT变换等。近年来，这些方法发展迅速，优点也不尽相同。如李洪泉等[1]将钢筋混凝土框架结构振动信号分解为不同频段，提取各个频段的信号特征，并通过信号小波变换的尺度函数确定损伤位置，实现结构的损伤识别，试验结果表明，该方法克服了傅里叶变换不能反映结构振动信号局部特性的缺点。尽管目前智能算法在理论上已经取得了丰硕成果，但应用实际工程还有存在一定的困难。
2) 动力损伤识别方法。该方法是通过结构动力特性的改变识别结构的损伤，主要包括：基于固有频率、模态振型、柔度差、模态应变能、应变模态、灵敏度、频响函数、残余力向量等方法。如Salawu[2]通过研究固有频率与损伤之间的关系，基于自振频率的变化建立损伤指数，提出了一种确定损伤位置和估计损伤程度的方法，并通过试验验证了该方法有效性。但该类方法需要考虑阻尼，并且其动力参数易受到外界环境的影响。
3) 静力损伤识别方法。静力识别具有数据获取方式简单、精度较高、稳定性好等优点。如崔飞等[3]针对结构参数识别所需的精度和算法的稳定性，探讨了基于静态测试数据的结构刚度参数评估技术，并通过平面框架的数值模拟验证了基于静态响应参数识别具有精度高、稳定性好等特点；近年来，随着科学技术的进步，静力识别在算法实现和工程应用方面也取得了显著进展[4―5]。
此外，依据损伤识别是否依赖有限元模型，可以将损伤识别方法分为无模型损伤识别方法和有模型损伤识别方法两类。无模型损伤识别方法主要是指基于信号处理的损伤识别方法和基于智能算法的损伤识别，包括小波分析、傅里叶变换、希尔伯特黄变换、盲源分离和神经网络等[6]。无模型损伤识别方法不依赖于有限元模型，可以快速判断损伤发生的大致位置和时间，但不易实现损伤的定量分析。如李宏男等[7]综合利用小波包分析和神经网络的损伤诊断方法，并将其应用于ASCE提出的基准框架结构，成功的识别出结构损伤的发生位置和时间，且识别结果不依赖于结构有限元模型。有模型损伤识别方法一般为结构模型修正方法[8]，即利用结构的实测信息结合优化算法对有限元模型中的参数进行识别，是目前常用的方法。有模型方法一般能够定量的实现损伤识别，如向天宇等[9]以两跨预应力混凝土连续梁为例，将有限元模型修正技术运用于结构的损伤识别之中，准确的反映了静力测试数据所验证的结构损伤行为，定量的实现了连续梁的损伤识别。Bakhtiari-Nejad等[10]综述了基于有模型损伤识别方法，提出了有模型损伤方法的关键是建立有限元模型、确定待修正的参数、构造优化目标函数，同时选择好优化算法。但是，有模型方法在每一次改变结构参数进行计算时都需要进行整体刚度矩阵的更新和分解，会产生较大的数值计算成本，从而降低结构损伤识别的计算效率和精度。拟力法作为一种结构非线性新方法[11―13]，其求解思路是将构件层面的位移分解为弹性与塑性两部分。Li等[14]将拟力法的形变分解思想拓展到材料层面，通过建立单元的局部塑性机制，将本构方程中的应变隔离为弹性应变和非弹性应变，以塑性插值的形式建立单元塑性变形场，依据虚功原理及塑性插值点处的内力平衡条件，建立了隔离非线性理论，其作为一种高效数值计算分析理论，主要用于提高结构非线性求解效率。该理论在求解过程中可以保持结构整体刚度矩阵不变，其非线性状态通过局部塑性矩阵加以体现，在迭代计算时避免了结构整体刚度矩阵的实时更新和分解，提高了计算效率。
基于此，本文利用隔离非线性法的基本思想，提出了一种隔离损伤的桁架结构性态识别方法。该方法从材料层面将损伤单元截面应变分解为弹性应变和损伤应变，并以截面刚度退化定义材料损伤，把表征损伤的刚度矩阵从整体矩阵中隔离开来，实现模型中损伤隔离，避免了整体刚度矩阵的实时更新和分解，只需更新和分解规模较小表征损伤的刚度矩阵，进而提高了损伤识别的效率。
损伤指数是定量描述构件或结构状态的物理量，通常选择结构特征参数的变化来定量描述结构或构件破坏[15]，包括从变形、刚度、能量等方面定义损伤指数。对于土木工程结构而言，结构进入非线性往往伴随着结构刚度的降低，即表明结构发生了损伤，本文以桁架结构为研究对象，从整根杆件截面刚度退化角度定义损伤。设第i单元的初始刚度为Ks,i，损伤后的单元刚度为，定义单元i的损伤指数αi为它损伤后的刚度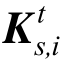与初始刚度Ks,i的比值，可以表示为：
由式(1)可知，若单元i没有发生损伤，损伤指数为1；若单元i完全失效时，损伤指数为0。实际损伤往往只发生在单元i的某个断面，但这将会引起整根杆件单元刚度降低。为了模拟整根杆件的刚度降低，以及便于数值计算，本文假定杆件刚度降低沿单元长度是一致的，将损伤表征为全长范围内的杆件截面或者弹性模量发生缩减。此近似处理方式在低频结构的健康监测和损伤识别领域是可行的，Friswell等[16]和张青霞[17]对此进行了论述，并证明了这种近似处理方式的可行性。
以平面杆单元i的损伤为例，如图1所示。单元节点位移为：
单元中任意一点的位移u分布可表示为：
图1 平面杆单元
Fig.1 Plane link element
N(x)为表征位移模式的插值形函数。考虑单元i的位移-截面应变关系，利用几何方程，推导出截面轴向应变的分布函数为：
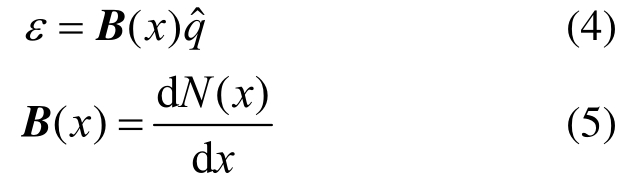
其中，B(x)为应变矩阵。
基于隔离非线性理论，当单元i发生损伤时，将截面应变分解成弹性应变和损伤应变。图2给出了平面杆单元模型截面轴向应变的分解示意，OC段表明单元i处于未损状态，B点表示单元i发生损伤的最终状态，其截面轴向应变分解可表示为：
其中：ε为B点截面的总轴向应变；ε′为弹性轴向应变；ε′为损伤轴向应变。
图2 截面轴力-应变关系曲线
Fig.2 Section axial force-strain relationship
假定损伤后单元i的刚度降低，其截面面积不变，弹性模量发生缩减。定义图2中OC段所在直线的斜率为单元i的初始弹性模量Ee，定义直线OB的斜率为单元i损伤后弹性模量Et，此时，B点状态下单元i的损伤指数αi可表示为：
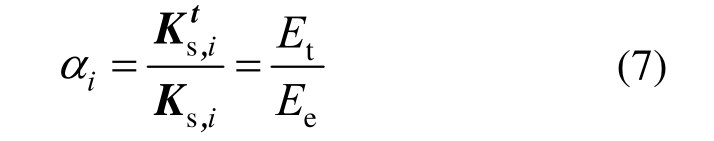
由图2中几何关系可知：损伤状态B的截面应力-应变关系可以表示为：
联立式(6)～式(9)可以得到单元i的损伤指数αi与截面损伤轴向应变和总轴向应变之间的关系为：
单元弹性模量不变时，截面面积的缩减同样也符合式(7)，式(10)，此时只需将弹性模量换为截面面积，并采用相同的推导步骤即可。由式(10)可以看出：一旦给出了单元i截面损伤轴向应变分布形式，便可推导出单元的损伤指数。损伤轴向应变在单元中的分布也可采用插值形函数表示，单元中的损伤应变分布通过若干个损伤插值节点处的损伤应变插值得到，此时截面损伤应变表示为：
式中，C(x)为插值形函数，其中，对于桁架结构而言，由于单元所有截面的应变相等，可以假定损伤应变的分布形式为等值分布，在高斯积分点处引入损伤插值节点，即C(x)=1。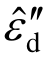
′为插值点处的损伤轴向应变。
基于虚功原理可知：单元i节点力ˆF所做的虚功等于单元的虚应变能，即：
将式(4)、式(6)、式(8)、式(11)代入式(12)得：
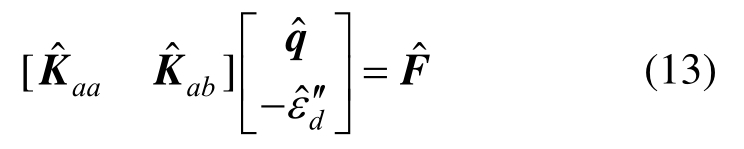
式中，
均为单元i相关的矩阵和向量。其中：
由上式可知：
是常数矩阵，均不含损伤指数，即与单元是否发生损伤无关，在计算过程中只需计算一次，不需要实时更新计算。上式中
为待求未知量，由于未知量的数量多于方程数量，求解过程需要构建补充方程。
为了建立补充方程，考虑损伤插值点处的内力平衡条件，联立式(4)和式(10)可得：
将式(11)式代入式(16)，可得：
整理可得：
其中：
联立式(13)和式(18)，隔离损伤法的控制方程为：
式中，
均为在整体坐标系下的整体矩阵和向量。其中，q为损伤结构的节点位移，矩阵Kbb为分块对角阵，由对角元素的Kˆbb集成得到，由于Kˆbb和损伤指数密切相关，且在优化过程中损伤指数不断变化，所以在求解过程中，仅需要更新表征损伤的刚度矩阵Kbb即可。此外，表征损伤的刚度矩阵Kbb可以从整体矩阵中隔离开来，实现模型中损伤隔离，
与损伤无关，均为常数矩阵。
式(21)可以利用Wood-burry[18]公式进行求解，即：
式中：
式中，q1为初始结构位移，由式(22)可知，损伤后的结构位移可以隔离成初始结构的位移和损伤引起的位移，此外，引入的未知量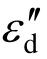
在求解节点位移过程中被消去，并未增大方程的求解规模。Kb与损伤指数有关，而Ka、Kba是常数矩阵，与损伤无关。因此，当给定损伤指数α时，可以利用隔离损伤控制方程快速求解损伤结构的响应。
由式(25)可知，求解过程中同样需要求逆的相关计算，需要求逆的矩阵Kb的规模与损伤单元的数目相关，若结构只有少数单元发生损伤，矩阵Kb规模较小，此时对Kb求逆的运算量较小。如果某单元没有发生损伤，此时，该矩阵是奇异矩阵，即
中没有该单元对应位置。因此，正确的求解方式是先求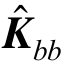
的逆，进而判断
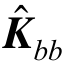是否存在。假定结构中所有单元都未发生损伤时，式(22)退化为：
当给定结构单元的损伤指数α，则可以利用式(22)快速求解出损伤结构的位移；反之，假设给定损伤结构的响应，也可通过优化算法识别出单元损伤的位置和程度，即通过使目标函数最小化的方法求解单元的损伤指数。对一般的结构损伤识别问题，目标函数的选取恰当与否会直接影响到其结果的准确性。利用静力有限元模型修正方法实现结构损伤识别时，一般选取结构的响应作为建立目标函数的依据，本文选用结构静力位移相对残差向量的二范数作为优化目标函数[10]，选用自然对数。目标函数如下：
式中：XM为实测结构响应；X(α)为隔离损伤法求解结构响应；f(α)为目标函数；α为优化求解变量。
损伤识别问题实质为求解目标函数最小值的数学问题，此数学问题属于有约束的非线性规划问题，其具体形式如下：
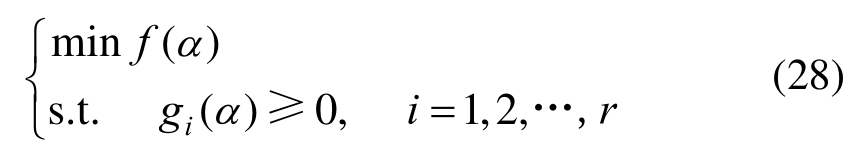
式中：α为损伤指数；gi(α)为不等式约束函数；r为优化变量个数。
求解式(28)常用的优化计算方法主要包括直接搜索法、线性搜索法、多目标优化法和序列二次规划(SQP)法。直接搜索法一般广泛适用于约束条件不断变化的目标函数；线性搜索法在优化求解时需要对目标函数求导，但是直接对对数型目标函数求导比较困难；多目标优化法通常用于求解多目标问题；而SQP算法作为一种高效的约束非线性规划算法[19]，其求解过程无需考虑模型的精确导数信息，具有收敛性好、计算效率高等优点，本文将SQP算法用于该目标函数的优化求解。其求解步骤如下：
1) 利用 SQP算法将式(28)转化为求解一般约束二次规划子问题(p为搜索方向，Hk为海赛矩阵)。
2) 采用有效集法对上式进行迭代求解，其迭代步长公式为：
式中：αk为第k次迭代的损伤指数；pk为指αk向αk+1的搜索方向；λk为搜索步长。
综上所述，其求解算法流程图如图3所示。
当目标函数收敛时，最终求解出桁架结构单元的损伤指数α，实现了结构的损伤识别。
算法时间复杂度理论是一种算法效率定量评价方法，其本质是统计计算过程中的计算量。时间复杂度大，表示计算量大，计算效率低。因此被广泛应用于计算效率评价，如Deng等[20]利用时间复杂度理论比较分析了传统变刚度法和虚拟荷载法的计算效率。本文将时间复杂度理论应用于结构损伤识别，从数学角度揭示隔离损伤法实现结构局部损伤识别的高效性。
图3 有约束最优化问题求解流程
Fig.3 Flow chart for constrained optimization
对于一个位移自由度为n的桁架结构体系，当结构有d个单元发生了损伤，分别采用传统变刚度法和隔离损伤法进行优化求解，其迭代次数均为w，下面利用两种方法分别计算结构损伤识别的算法时间复杂度。
1) 隔离损伤法。
式(22)中，Kaa在迭代过程中只需求解进行一次，其复杂度为O(n3)，其余迭代步只需进行回代计算，其复杂度为O(n2)[21]。选用自右向左的顺序求解KaKb-1Kbaq1。此时，可以得到基于隔离损伤法实现结构损伤识别的时间复杂度为：
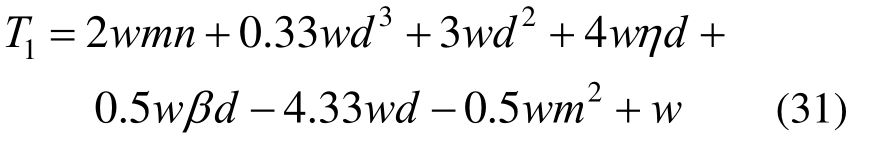
式中：m为矩阵Kaa的带宽；η、β是与所选单元类型有关的常数。
2) 变刚度法。
在利用传统变刚度法求解损伤结构的位移时，在每个优化迭代步中都需要重新合成和分解结构的刚度矩阵，对该方法总计算量约为m2n+8mn+n次浮点运算[22]，进而可以得到基于传统变刚度法实现损伤识别的时间复杂度为：
3) 对比分析。
若令T1<T2，即：
当桁架结构发生损伤的单元个数d满足式(33)时，隔离损伤法实现结构损伤识别的效率高于传统变刚度法，其中d越小，此方法识别效率越高。因此，本文所提出的隔离损伤法对于高效地实现结构局部损伤识别具有重要意义。
某曲弦钢桁架桥，桥梁总长55 m，宽14.5 m，节间长5 m，高为6.5 m～8.5 m，上部为下承式钢桁架结构，下部结构由桥面板、支座、联结系、桥面系、主桁五大部分组成。主桁架是桥的主要承重结构，包括上弦杆、下弦杆、竖杆、端斜杆、斜腹杆，其中，端斜杆截面为箱形体系，其他杆件截面为工字型体系。随着桥梁服役年限的增加，主桁杆件可能由于疲劳老化或者腐蚀而产生损伤。
在ANSYS软件平台建立平面有限元模型，如图4所示，模型中每榀桁架共有22个节点、44个单元，11个节间，两端铰接。材料的弹性模量为206 GPa，上弦杆、下弦杆、竖杆、端斜杆、斜腹杆截面积分别为 0.0512 m2、0.03984 m2、0.01514 m2、0.05645 m2、0.02432 m2，钢材密度7.85 g/cm3，泊松比取0.2。在主桁杆件损伤识别之前，依据现场实测结果，将初始模型修正为符合现阶段桥梁真实情况的有限元模型，保证数值模拟结果和实测结果一致[23]。
图4 钢桁架桥有限元模型
Fig.4 Finite element model of steel truss bridge
采用数值模拟的方法来验证隔离损伤识别方法对主桁杆件的损伤识别效果，杆件单元编号如图4所示。在外界环境作用下，设只有杆件单元10、单元 14发生损伤，用杆件弹性模量的缩减模拟单元的损伤，损伤指数分别为0.8和0.6，单元的损伤指数如图5所示。假设已知损伤发生在结构中部的5个单元(单元 10、11、12、13、14)中，但不知损伤的数量、位置和程度。下面通过本文所提出的方法对这5个单元进行损伤识别。
图5 损伤指数
Fig.5 Damage index
为了识别结构损伤，设计两种静荷载工况，工况1：载货车辆静荷载。选取4重车(单辆重420 kN)作为荷载，车轮距和平面布置如图6所示，加载布置如图4所示，其中，P1为280 kN，P2为560 kN。工况2：自重荷载。
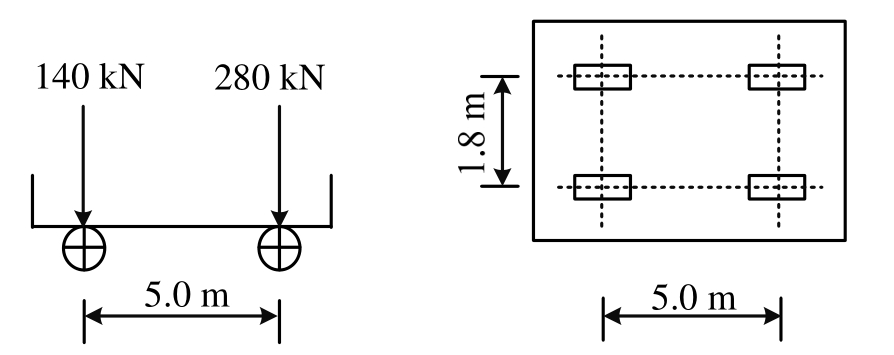
图6 加载车辆轮矩和平面布置图
Fig.6 Wheel base of loading vehicle and floor plan
计算两种荷载工况作用下，主桁杆件的初始位移和损伤结构位移。主桁结构为等截面杆单元，只有一个轴向应变，且杆内应变相等，因此，插值形函数C(x)=1，利用有限元基本理论求出Kaa、Kab、Kba，将损伤指数作为未知数代入式(20)，并集成Kbb，建立隔离损伤的控制方程，并利用式(22)求解损伤结构的位移为uSDM。对于损伤结构重新建立有限元模型并计算其位移为uFEM。
采用数值模拟的方法，把结构位移uFEM作为实测结构位移XM，把隔离损伤法求解的位移uSDM作为X(α)，代入目标函数式(27)，利用SQP算法进行两种工况下目标函数的优化迭代，最终求解出结构中部5个单元的损伤指数。两种静荷载工况作用下，隔离损伤法目标函数的迭代情况如图7。由图7可知，SQP算法优化目标函数的收敛速度快，这说明SQP算法能够快速准确的优化建立的目标函数。目标函数收敛时，隔离损伤法求解出桁架中部5个杆单元的损伤指数。
图7 目标函数迭代
Fig.7 Iteration of objective function
在两种工况作用下，隔离损伤法和传统方法的损伤识别结果如图8所示，可知，隔离损伤法和传统方法均能够精确地识别出结构的损伤指数，5个单元中只有单元10和单元14发生了损伤，损伤指数分别为0.8和0.6，其物理意义为单元损伤前后弹性模量的比值，例如损伤指数为0.8表示单元10损伤后弹性模量是未损伤的0.8倍，即弹性模量下降了20%。此外，隔离损伤法和传统方法分别与真实损伤相比，其识别结果的最大的相对误差分别为0.62%和0.58%，可以忽略。表明了隔离损伤法能够精确地进行结构损伤识别。
图8 损伤工况的识别结果
Fig.8 Identification results of damage cases
从算法时间复杂度方面评价传统变刚度法和隔离损伤法实现结构损伤识别的计算效率，算例中有5个杆单元可能发生损伤，即d=5，满足式(33)，且在两种荷载工况作用下，两种方法实现损伤识别的时间复杂度，见表1。
表1 损伤识别的时间复杂度
Tabal 1 Time complexity of damage identification
识别方法 时间复杂度 工况1 工况2变刚度法 7.31×1059.31×105隔离损伤法 7.16×1049.09×104
从表1可知，两种工况作用下，在整个损伤识别过程中，传统方法的时间复杂度约是隔离损伤法复杂度的10倍，所以当进行结构局部损伤识别时，与传统变刚度法相比，隔离损伤法显著地提高了损伤识别的计算效率。
而如果没有预判损伤杆件的大致位置，所有单元都参与损伤识别，即d=42，则隔离损伤法实现结构损伤识别的时间复杂度高于传统变刚度法。此种情况采用传统变刚度法进行损伤识别效率更高。
因此本文方法一般需要根据经验、结构分析或者信号处理的方法预先确定或估计损伤的范围，然后对结构局部进行识别。
本文基于隔离非线性理论，提出了一种隔离损伤的桁架结构性态识别方法。并通过一个桁架桥梁结构模型验证了该方法的有效性。并得到如下结论：
(1) 基于隔离非线性变量分离的思想，实现桁架结构的损伤识别，拓展了隔离非线性的应用范围。
(2) 通过对截面应变进行分解，将结构中表征损伤的刚度矩阵从整体矩阵中隔离开来，可以实现模型中损伤隔离。
(3) 在桁架结构的损伤识别过程中，避免了整体刚度矩阵的实时更新和分解，只需对规模较小表征损伤的刚度矩阵进行更新和分解，可以快速实现结构局部损伤识别，较传统模型修正法可大幅提高工程损伤识别的效率。
[1]李洪泉, 董亮, 吕西林. 基于小波变换的结构损伤识别与试验分析[J]. 土木工程学报, 2003, 36(5): 52―57.Li Hongquan, Dong Liang, Lü Xilin. Identification of structural damage and test study based on wavelet transform [J]. China Civil Engineering Journal, 2003,36(5): 52―57. (in Chinese)
[2]Salawu O S. Detection of Structural Damage Through Changes in Frequency: A Review [J]. Engineering Structures. 1997, 19(9): 718―723.
[3]崔飞, 袁万城, 史家钧, 等. 基于静态应变及位移测量的结构损伤识别法[J]. 同济大学学报, 2000, 28(1): 5―8．Cui Fei, Yuan Wancheng, Shi Jiajun, et al. Damage detection of structures based on static response [J].Journal of Tongji University, 2000, 28(1): 5―8. (in Chinese)
[4]Sanayei M, Onipede O. Damage assessment of structures using static test data [J]. Aiaa Journal. 2012, 29(7):1174―1179.
[5]Banan M R, Hjelmstad K D. Parameter estimation of structures from static response. I. Computational aspects[J]. Journal of Structural Engineering, 2015, 120(11):3243―3258.
[6]姜绍飞. 结构健康监测-智能信息处理及应用[J]. 工程力学, 2009, 26(5): 487―490.Jiang Shaofei. Structural health monitoring-intelligent information processing and application [J]. Engineering Mechanics, 2009, 68(5): 487―490. (in Chinese)
[7]李宏男, 孙鸿敏. 基于小波分析和神经网络的框架结构损伤诊断方法[J]. 地震工程与工程振动, 2003,23(05): 141―148.Li Hongnan, Sun Hongmin. Damage diagnosis of framework structure based on wavelet packet analysis and neural network [J]. Earthquake Engineering ＆ Engineering Vibration, 2003, 23(05): 141―148. (in Chinese)
[8]郭彤，李爱群，韩大章. 基于灵敏度分析与优化设计原理的大跨桥梁动力模型修正[J]. 桥梁建设. 2004(6):20―23.Guo Tong, Li Aiqun, Han Dazhang. Updating of dynamic model for long-span bridges based on structural sensitivity analysis and optimization design principle [J].Bridge Construction, 2004(6): 20―23. (in Chinese)
[9]向天宇, 赵人达, 刘海波. 基于静力测试数据的预应力混凝土连续梁结构损伤识别[J]. 土木工程学报.2003, 36(11): 79―82.Xiang Tianyu, Zhao Renda, Liu Haibo. Damage detection of prestressed concrete continuous beam from static response [J]. China Civil Engineering Journal,2003, 36(11): 79―82. (in Chinese)
[10]Bakhtiari-Nejad F, Rahai A, Esfandiari A. A structural damage detection method using static noisy data [J].Engineering Structures. 2005, 27(12): 1784―1793.
[11]Lin T H. Theory of inelastic structures [M]. New York:John Wiley ＆ Sons, 1968: 43―55.
[12]李钢, 余丁浩, 李宏男. 基于拟力法的纤维梁有限元非线性分析方法[J]. 建筑结构学报, 2016, 37(9): 61―68.Li Gang, Yu Dinghao, Li Hong Nan. Nonlinear fiber beam element analysis base on force analogy method [J].Journal of Building Structures, 2016, 37(9): 61―68. (in Chinese)
[13]Li G, Zhang Y, Li H N. Nonlinear seismic analysis of reinforced concrete frames using the force analogy method [J]. Journal of Bridge Engineering, 2015, 43(14):2115―2134.
[14]Li Gang, Yu Dinghao. Efficient inelasticity-separated finite-element method for material nonlinearity analysis[J]. Journal of Engineering Mechanics, 2018, 144(4):1―11.
[15]刘海卿, 陈小波, 王学庆. 基于损伤指数的框架结构倒塌分析综述[J]. 自然灾害学报, 2008, 17(1): 186―190.Liu Haiqing, Chen Xiaobo, Wang Xueqing. Overview of damage index-based analytical method for collapse of frame structure [J]. Journal of Natural Disasters, 2008,17(1): 186―190. (in Chinese)
[16]Friswell M I, Penny J E T. Crack modeling for structural health monitoring [J]. Structural Health Monitoring,2002, 1(2):139―148.
[17]张青霞. 基于虚拟变形法的动态荷载与结构损伤识别方法研究[D]. 哈尔滨工业大学, 2010: 46―48.Zhang Qingxia. Dynamic load and structural damage identification using virtual distortion method [D].Harbin Institute of Technology, 2010: 46―48.
[18]Hager W W. Updating the inverse of a matrix [J]. Siam Review. 1989, 31(2): 221―239.
[19]Nocedal J, Wright S J. Numerical optimization [M].Springer, 2006: 29―76.
[20]Deng L, Ghosn M. Pseudoforce method for nonlinear analysis and reanalysis of structural systems [J]. Journal of Structural Engineering, 2001, 127(5): 570―578.
[21]Golub G H, Van Loan C F. Matrix computations [M].JHU Press, 2012.
[22]Golub, Gene H. Matrix computations (Forth Edition)[M]. Beijing: Posts ＆ Telecom Press, 2014: 12―13.
[23]Liu Y, Ma J, Nie J, et al. Virtual distortion method-based finite element model updating of bridges by using static deformation [J]. Journal of Engineering Mechanics,2015, 143(3): 1―9.
A STRUCTURAL STATE IDENTIFICATION METHOD FOR TRUSS STRUCTURES WITH SEPARATED DAMAGE
靳永强(1990―)，男，甘肃人，博士生，主要从事结构非线性分析等研究(E-mail: jinyqlut@163.com).