图1 改进的SHPB装置示意图
Fig.1 Schematic diagram of improved SHPB
砂土作为一种典型的松散颗粒物质，得益于其松散、多孔、易压缩的特性，使得应力波在其中传播时表现出较显著的衰减特性[1－3]。作为消波材料，砂土常常被用于构筑防护工程的消波分配层，用以吸收、耗散爆炸波的巨大能量。因此，定量地量测爆炸应力波在砂土中传播衰减规律，为防护工程选型和设计施工提供理论依据，显得至关重要。
现有的研究砂土中一维应力波衰减的实验加载方法多种多样，如激波管[4－5]、落锤[6]、摆锤[7]等。这些方法一般通过在砂土中埋置应力计来获取试件中的应力波信号，但由于波阻抗的差异，应力计很难准确反映砂土中的实际应力状态，且应力计的存在，必然会对试件中波的传播造成影响。有结果表明，埋置应力计的方法对峰值应力的测试误差甚至高达20%[4]。
由Hopkinson[8]提出，并经Kolsky[9]改进后，分离式霍普金森压杆(split hopkinson pressure bar,SHPB)[10]已广泛地应用于测量各种材料(金属[11－12]、混凝土[13－14]、岩石[15]、陶瓷[16]、泡沫与孔隙材料[17]、复合材料[18]、生物材料[19]等)在高应变率下的力学性质，其最大的优点在于，能够通过测量两弹性长杆中的应力波，通过时域平移，间接而准确地反映试件两端面的应力状态。正是基于这一特点，Ross等[20]采用SHPB研究了受侧限的不同长度的砂土试样中应力波的传播规律，然而，不同于传统 SHPB材料实验，为探究应力波在试件中单程的传播规律，在所试时间内，不允许应力波在试件内部的多次反射，试件两端不存在应力平衡。并且，砂土试样的波阻抗并非恒值，无法直接通过透射杆中的透射波精确且直接的计算得到试件尾部的应力状态，故Ross等[20]仅通过比较了两杆中入射波与透射波，讨论试件中应力波的衰减，赵凯[21]也采用同样的方式研究了分层防护层对爆炸波的衰减作用。然而，杆中的入射波与透射波并不能准确代表试件两端的应力状态，这一方法只能在一定程度上得到定性的结论。
本文基于SHPB装置并对其进行改进，设计了一种钢制长套管，在其中充填松散介质形成一维应变状态的长试件，用以量测松散介质中应力波的定量传播规律。提出了一种通过杆中三波(即入射杆中的入射波和反射波、透射杆中的透射波)，准确地计算试件两端峰值应力的方法，也为定量研究松散介质一维应变波峰值应力的衰减提供理论基础。并针对珊瑚砂开展了一系列静压和冲击实验，验证了实验技术和计算方法的可靠性。
该实验方法以如下4项基本假定为前提。
1) 材料均匀性假定。实验目的是研究砂土介质中应力波的衰减，将它宏观上当作一种材料研究，但由于其本身的细观上的颗粒大小不均匀性，这就需要将试件在各维度上的尺寸设计得足够大(一般为最大颗粒10倍)，以保证试件各轴向截面的应力均匀性。
2) 长试件假定。试件长度L需足够长，以保证在实验时间t内，应力波在试件内无反射叠加，如试件中波速为C，则可表示为t＜2L/C，即应力波在试件中传播一个来回的时间大于实验有效量测时间。
3) 一维应变状态假定。实验目的是模拟应力波在半无限松散介质中的衰减规律，可以简化为一维应变条件。因此专门设计了钢制长套管，近似为径向刚性约束，使得试样只存在轴向应变，而径向与环向应变可以忽略，满足一维应变假定。通过改变套筒的材料和套筒内外半径也可以调整约束条件，具体可见参考文献[21]。
4) 在冲击实验的应变率范围内(约1～102s-1)，忽略试样的应变率效应。有研究表明，在一维应变的条件下，砂土介质不存在应变率效应[22－24]，或应变率效应不明显，可以忽略[25]。基于这一假定，可推导出砂土介质的波阻抗与其轴向应力的单变量函数关系。
借助SHPB加载装置和测试系统，并改进设计了钢制长套筒试件，对一维应变状态下的砂土长试件进行冲击加载实验，实验基本装置如图1所示。
图1 改进的SHPB装置示意图
Fig.1 Schematic diagram of improved SHPB
不同于传统 SHPB实验，应力波衰减实验在冲击加载过程中不需要试件达到应力平衡，且必须满足“长试件假定”。如图2所示，由于杆件材料与试件波阻抗的不同，当杆中入射波σBI通过界面1时，一部分透射进入试件，称为试件中的入射波σBI，一部分反射回入射杆，称为杆中反射波σBR。基于“长试件假定”，量测时间内，应力波在试件内单程传播，因此，由界面1进入试件的入射波σRI，在传播经过整个试件后，由于试件中的衰减与弥散效应，到达界面2时，波形已完全改变，称之为试件中的透射波σST。在界面2上，同样由于波阻抗的不同，σST一部分透射进入透射杆，形成杆中透射波σBT，另一部分反射回试件，称为试件中的反射波σSR。
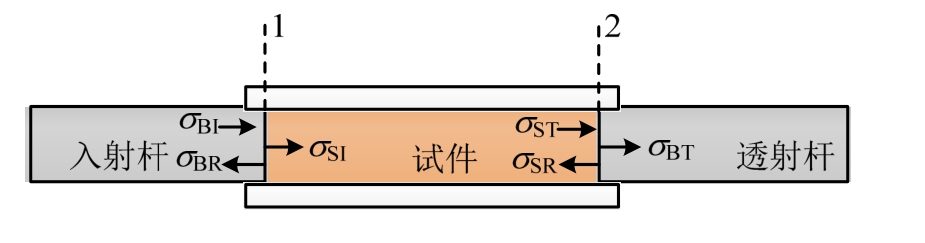
图2 一维应变状态下的松散介质长试件
Fig.2 Long specimen of loose porous media under one-dimensional state
通过杆中获取的杆中三波(即入射杆中的入射波σBI和反射波σBR、透射杆中的透射波σBT)计算试件两端的峰值应力σSI-peak和σST-peak，通过比较二者的值，得到这一长度试件(即应力波传播距离)的峰值应力衰减率(σST-peak/σSI-peak)%。通过改变试件的长度，便可得到峰值应力衰减率随应力波传播距离的改变而变化的规律。另外，试样中的弹性波速C0(初始应力波速)、峰值应力速度Cpeak、应力波前沿升时tr均可通过计算得到。
实验过程中，试件的轴向受力状态如图2所示(图中，定义入射杆与试件的接触面为界面 1，试件与透射杆的接触面为界面2；应力符号角标B代表杆件，S代表试件，I代表入射波，R代表反射波，T代表透射波)。入射杆中的入射波σBI和反射波σBR，以及透射杆中的透射波σBT，这三个波可以由示波器记录的杆上的应变信号换算得到，为已知量。而研究应力波在试件中的衰减规律，必须得到应力波在进入试件时的入射波峰值应力σSI-peak和传播经过试件到达末端的透射波峰值应力σST-peak。这两个量无法直接测量，需通过σBI、σBR和σBT计算。
1) 试件中的入射峰值应力σSI-peak
如图2所示，在界面1上，σBI、σBR已知，σSI-peak可通过应力平衡直接得到：
2) 试件中的透射峰值应力σST-peak
在界面2上，如图2所示，由于实验只能测得杆中透射波σBT，为了计算珊瑚砂中透射峰值应力σST-peak，需借助应力波在不同介质面的传播公式[26]：
式中，T2为界面2的透射系数：
式中，nSB为试件的波阻抗Sλ与杆的波阻抗Bλ之比：
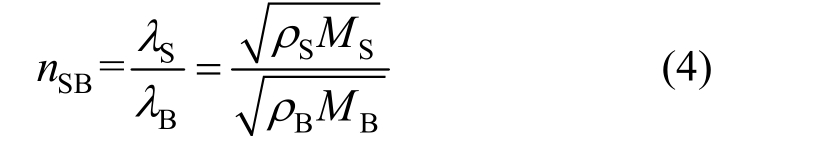
式中：杆件的密度Bρ和弹性模量EB，由于杆件始终为弹性变形，二者是恒值。但是，试样的密度Sρ与侧限切线模量MS(即一维应变状态的切线模量)则非恒定值。这是因为，试样受力过程中发生的并非弹性变形，其侧限切线模量MS也会受到影响而变化，并且，砂土材料具有多孔特性，受力过程中具有大变形的特点，变形对于密度Sρ的影响必须考虑。
Kondner[27]提出用双曲线拟合三轴实验数据，即：
式中，p、q为实验常数。对于侧限单轴受压的情况，试样的轴向应力与径向应力之比始终为常数[28－29]，即
，代入式(5)，得到：
对于同一种材料，只要初始状态(包括颗粒级配、初始密度、初始受力状态)和侧限条件(套筒材质、内外半径)一定，式(6)的m和n是恒定的。也有研究表明，在一维应变的压缩条件下，砂土介质加载段的切线模量与卸载段的切线模量是不同的；加载段曲线基本不受加载路径、加载速率的影响，而卸载曲线更为复杂，虽然仍可采用双曲线方程表示，但m和n却与卸载曲线的起始点的有效应力和应变相关[30]。本文的研究重点是峰值应力(即加载段的顶点)的衰减规律，通过加载曲线的表达便可满足要求，对卸载段的切线模量不做考虑。因此，下文论述的侧限切线模量MS均是加载段之值。式(6)也可以表示为：
式中：a、b为常数。将式(7)对应变ε求导，得到侧限砂土试件在处于某轴向应力下的切线模量：
这说明，侧限切线模量可以表示为轴向应力σ的函数。其次，考虑冲击加载对砂土试样密度Sρ的影响。在砂土试件中取一个极短微元，如图3所示，试件的初始密度为0ρ，微元受轴向应力σ压缩时，微元厚度由初始的h0变为h，则受压缩的砂样密度变为：
图3 试件微元的受力状态
Fig.3 Stress state of specimen element
式中：m为微元质量；r为微元半径。将式(7)代入式(9)，得到：
结合式(8)和式(10)，可以得到一维应变状态砂样的波阻抗与轴向应力σ的关系式：
即：
以上对于试样的侧限切线模量与密度的讨论并未考虑应变率的影响。这是因为，已有很多学者证明，一维应变状态下的砂土材料不存在应变率效应[22－24]，或应变率效应不明显，可以忽略[25]。因此，本文忽略冲击实验的应变率范围内(1～102s-1)试样的应变率效应，认为一维应变状态下，砂土材料的波阻抗仅由其所受轴向应力决定。
考虑图2，界面1的反射系数F1可表示为：
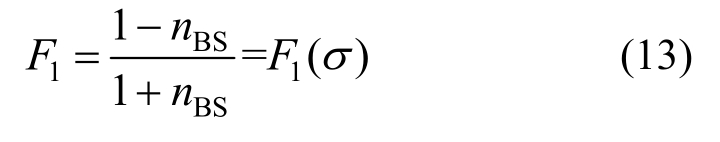
式中：
，σ为试件端部轴向应力，在界面1上，其值等于试件中的入射波σSI。
界面2的透射系数T2对应的式(3)可表示为：
式中：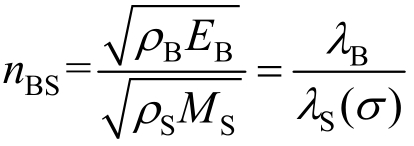
。同样，σ为试件端部轴向应力，界面2上，其值等于杆中透射波σBT，这是因为，试件端部同时受试件中的透射波σST与反射波σSR共同作用，由应力平衡可知，二者之和等于σBT。
显然，对于同一种介质有：
因此有：
由于在界面1上，σBI和σBR是已知的，通过实验结果，可以很容易地得到不同应力σSI对应的F1之值，将二者数据拟合，便可得到拟合的F1(σ)函数式。再结合式(16)，可得到拟合的T2(σ)函数式，即界面2上试样端部应力σBT与T2的关系，既而联立式(2)，便可计算得到σST-peak的真实值，表示为：
基于应力波在不同介质面上传播原理[26]，杆中入射波σBI的前沿升时与试件前端面入射波σSI的前沿升时是一样的，同理，杆中透射波σBT的前沿升时与试件后端面透射波σST的前沿升时是一样的。因此，将杆中两波经时域平移能够计算出试件中的弹性波速(初始应力速度)、峰值应力速度，如图4所示。具体公式如下：
弹性波速：
式中：t0为杆中入射波与透射波起始点的时间差；tI为波从入射杆应变片传播到界面1所需时间，可由该段距离除以杆中弹性波速计算；tT为波从界面2传播至透射杆应变片所需时间，同样可由该段距离除以杆中弹性波速计算；L为试件长度。
峰值应力速度：
式中，tp为杆中入射波与透射波峰值点的时间差。
试件前端与末端的应力波前沿上升时间，分别与杆中入射波、透射波一致，可直接从实验数据中读取。
图4 试件的波速、峰值应力速度和应力波前沿上升时间的计算示意图
Fig.4 Schematic diagram on calculation of wave velocity,peak stress velocity and rise time of stress wave front
本节以干燥的珊瑚砂为实验材料，对其中应力波的衰减进行了初步实验。实验共进行了 33次，长度75 mm的试件12次，长度150 mm、225 mm和300 mm的试件各7次。
实验珊瑚砂颗粒级配如图5所示，原始砂样烘箱经烘干后，放入标准筛由振筛机筛分，再按原始级配，以50%的相对密实度，即相对密度1.464 kg/m3，配置实验所需试件。
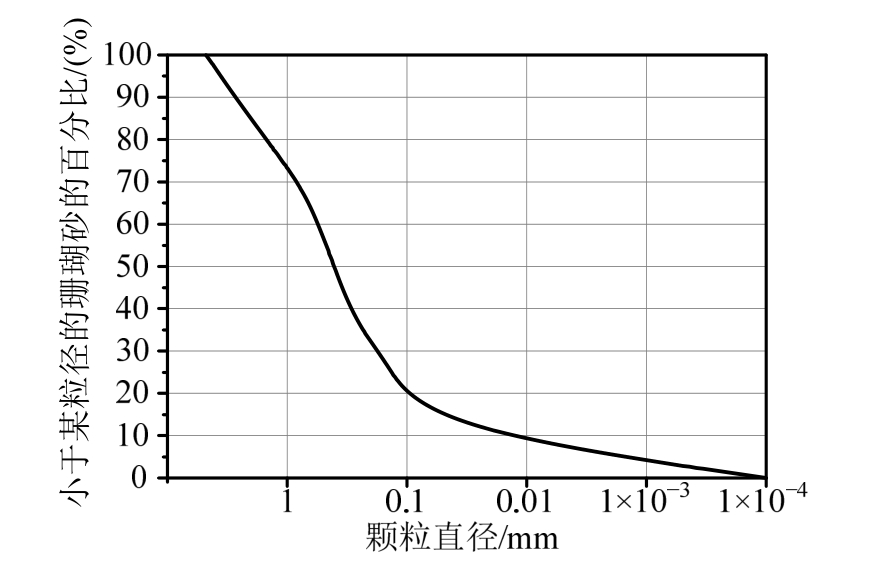
图5 珊瑚砂的颗粒级配
Fig.5 Particle size distribution of coral sand
实验中，珊瑚砂试样通过一个套筒和两个圆饼状垫块装配，如图6所示。套筒内径75 mm、壁厚10 mm，垫块直径75 mm、厚度10 mm，加工材料选用 45号钢，以保证试样径向位移近似为零。沿轴向套筒对称开5对通孔，通孔直径5 mm，对应的，垫块侧面对称的开一对 5 mm直径深度 5 mm的螺孔，通过5 mm螺栓配合，可固定垫块在套筒中的位置，从而控制试件长度，试件的可控长度为75 mm、150 mm、225 mm、300 mm。将装配好的试件配置于SHPB装置上后，需将螺栓卸除，保证试件轴向位移不受限制。SHPB装置材料为钢，直径为75 mm，如图7所示，子弹长度200 mm，入射杆长 5500 mm，透射杆长 3500 mm，吸收杆长1000 mm。
图6 套筒与垫块
Fig.6 Sleeve and cushion block
图7 SHPB装置
Fig.7 Photo of SHPB
图8 为75 mm实验的典型波形，可以看出，由于试件的波阻抗与杆件相差较大，大部分的入射波反射回了入射杆。为尽量减小误差，本文只选用入射波与反射波的峰值对F1()σ进行拟合，结果如图9所示。图中散点为实验结果，实线是线性拟合的曲线，其表达式为：
图8 杆中三波波形
Fig.8 Three waves in the bars
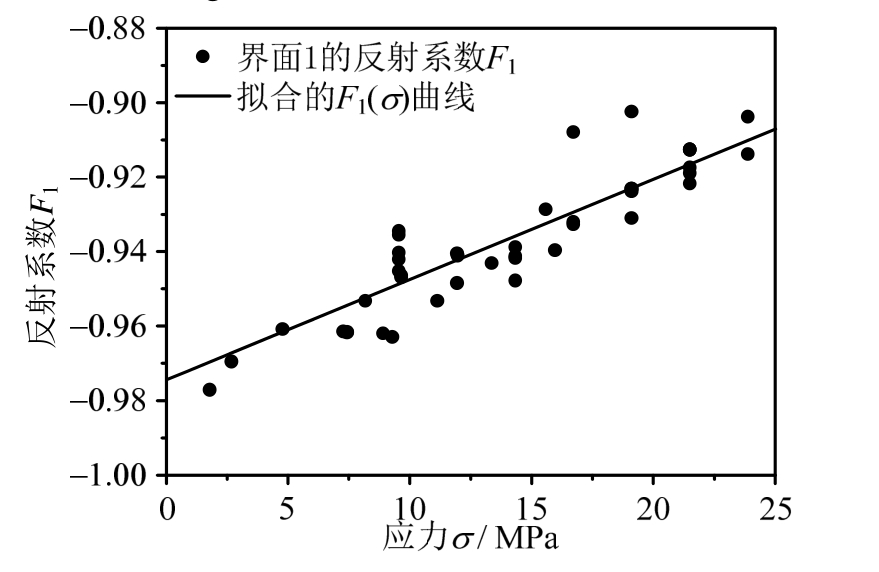
图9F1函数的拟合
Fig.9 The fitting curve ofF1
式(20)线性拟合的皮尔森相关系数(Pearson correlation coefficient[31])为 0.7610，调整决定系数(adjusted determination coefficientR2[31])为 0.5690。σ的定义域由实验中界面 1试件的峰值应力σSI-peak所能取到的值决定，本文σSI-peak最大取到23.9 MPa，故定义域取[0,23.9]。结合式(20)与式(16)，得到：
因此，在[0,23.9]，T2的变化范围是 1.974～1.908。
如前文所述，虽然试样应力-应变曲线加载段的切线模量可通过本文的方法计算，但卸载段的切线模量则十分复杂，本方法不再适用。因此，很难通过简单的计算，由透射杆中透射波σBT定量准确地反演试件中完整的透射波σST。虽然如此，σBT仍然相似于σST，能够定性地反映σST的特点，而定性的讨论不同长度试件中(或不同传播距离上)透射端的应力波形具有重要的实际意义。因此，总结绘制了对应75 mm、150 mm、225 mm、300 mm四种试件的透射杆中典型的透射波σBT(以实测珊瑚砂平均波速 158 m/s，经时域平移，将波头对应于图中位置)，如图10所示，此外，图中还绘制了试件左端(0 mm)的入射波σSI，作为比较。可以得到以下几个结论：1) 应力波的峰值应力随传播距离的增大而不断减小；2) 应力波的升压时间和脉冲长度随传播距离的增加而明显增加；3) 传播距离越远，波形越平滑。这是因为，在应力波传播经过珊瑚砂试件过程中，珊瑚砂颗粒间不完全充分的接触以及颗粒的滑移、变形或破碎，对应力波中的高频部分产生了过滤作用。
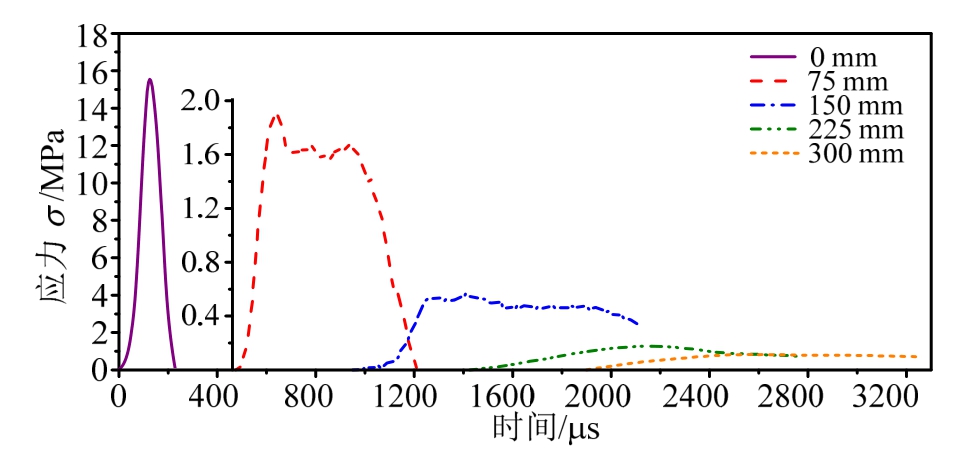
图10 不同传播距离上的应力波形
Fig.10 Stress wave at different propagation distances
值得注意的是，图中的四个透射波σBT，仅绘出前 1163 μs的波形，而超过这一时间后的波形将面临着波形叠加，叠加后的波形不再准确，故不予绘出。这是因为，应变片张贴于透射杆上距试件0.5 m位置，钢杆中实测波速5157 m/s。因此，σBT由透射杆远端返回到达应变片位置所需的时间间隔为ts=2×(3.5-0.5)/5157=1163 μs。
结合式(17)与式(21)，得到试件末端的透射波峰值应力σST-peak。试件前端的入射波峰值应力σSI-peak由式(1)计算。定义无量纲的峰值应力σST-peak/σSI-peak，表示应力波在一定长度的试件中传播时，峰值应力的衰减情况，由此得到无量纲的峰值应力与应力波传播距离的关系，实验结果如图 11所示。不难看出，随着传播距离的增加，峰值应力衰减明显，当传播至 75 mm处时，衰减至 10%左右，传播至150 mm处时，衰减至2%左右，继续传播至225 mm处时，仅剩余不到1%，到达300 mm处，剩余已不足0.5%。采用指数与一次函数的线性关系式，拟合无量纲的峰值应力与传播距离x的关系，可表示为：
式中，A=0.023，B=0.977，β=27.08×10-3m，C=-6.24×10-2m-1。x的单位取m。式(22)拟合曲线的调整决定系数R2为0.9995。拟合曲线同样绘于图11中。
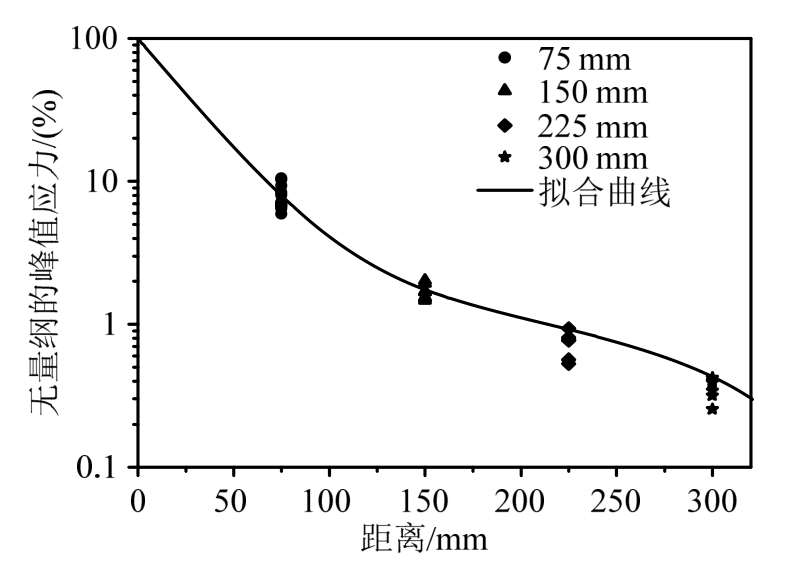
图11 峰值应力随传播距离的衰减曲线
Fig.11 Curve of peak stress attenuation with propagation distance
为验证方法和实验结果的可靠性，本节就实验所计算的峰值应力σST-peak/σSI-peak衰减率进行讨论。实际上，由式(1)的应力平衡关系知，σSI-peak是可以通过量测结果准确计算的，而σST-peak是由式(17)计算得到的，它的准确与否由拟合的T2(σ)决定，须讨论关键参数T2(σ)的误差影响。因此，进行了一组对比实验，目的是通过测试珊瑚砂试样的单轴应力-应变曲线，结合式(11)、式(13)和式(16)，拟合准确的T2(σ)。
对比实验选择进行珊瑚砂的准静态实验，在MTS液压伺服实验机上进行，如图12所示。珊瑚砂的颗粒级配、初始密度与上述应力波的传播实验完全一致，试件长度75 mm，套筒壁厚10 mm，实验时，在套筒内涂油以消除摩擦力的影响。
图12 一维应变状态下珊瑚砂的准静态实验
Fig.12 Quasi-static test of coral sand under quasi-one-dimensional strain state
需要说明的是，对比实验没有选择SHPB进行材料的高应变率加载的原因是：一方面是因为砂土介质波速极低(一般为102m/s量级，较杆件波速低一个量级)，试件的应力平衡很难在极短的时间内达到，使得应力-应变曲线的上升段的相当一段长度内并不可靠，对应计算的T2()σ有相当一段长度是不可靠的；另一方面，是因为实验材料颗粒较大，最大颗粒达 4.8 mm，无法实现试件两端部的应力平衡，不能进行SHPB实验。
尽管对比实验中计算的T2()σ没有计及材料的应变率效应，并且，应力-应变曲线也是通过实验数据平均拟合得到的，但准静态实验过程更稳定、整个实验过程试件受力状态均匀，因此，认为对比实验计算得到的T2()σ更接近真实值，称之为T2()σ真。
准静态压缩实验共进行 4次，实验应变率0.001s-1。应力-应变曲线如图13所示，几次实验结果重复性相对较好，对应力-应变曲线采用式(7)数据拟合，得到关系式：
即a=50.95 MPa，b=3.37。式(23)拟合曲线的调整决定系数R2为0.9916。将参数代入式(23)，并结合式(13)、式(16)绘制应力σ与透射系数T2真(σ)的关系，如图14中虚线所示。在0～23 MPa，T2真(σ)的变化范围是1.986～1.961。
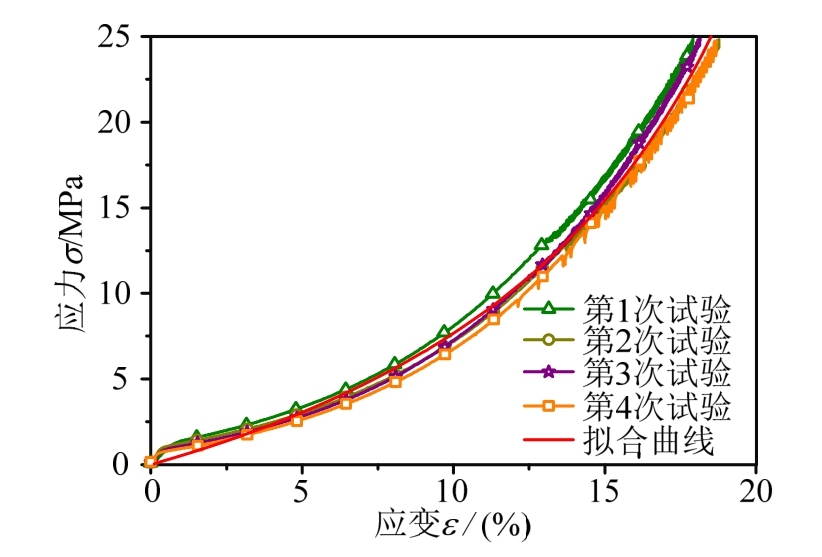
图13 一维应变状态下珊瑚砂试件的应力-应变曲线及其拟合曲线
Fig.13 Stress-strain curve and fitting curve of coral sand specimen under one-dimensional strain state
图14T2函数的真实值与拟合值对比
Fig.14 The true value and fitted value comparison ofT2
对比图 14中的两条曲线，不难发现，虽然T2(σ)与T2真(σ)的变化趋势基本一致，但由于实验误差、数据处理误差的存在，二者不可避免地存在一定误差。定义误差δ：
由式(17)知：
将式(25)和式(26)代入式(24)，得：
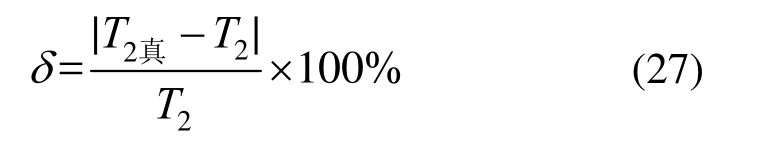
因此，结合T2()σ真与T2()σ曲线，可绘制δ(σ)曲线，如图15所示。结果表明，当σ在0～23.9 MPa变化时，δ的最大值仅为 2.83%，可以忽略。说明本文提出的，量测松散介质中峰值应力衰减效应的实验方法是可靠的。
然而，图 15中的绝对误差值虽然不大，但却存在一个显著的倾向，即误差随应力增加而显著增加。笔者推测，造成这一现象的主要原因可能来自于材料的侧限切线模量在动态与静态加载情况下的差别。
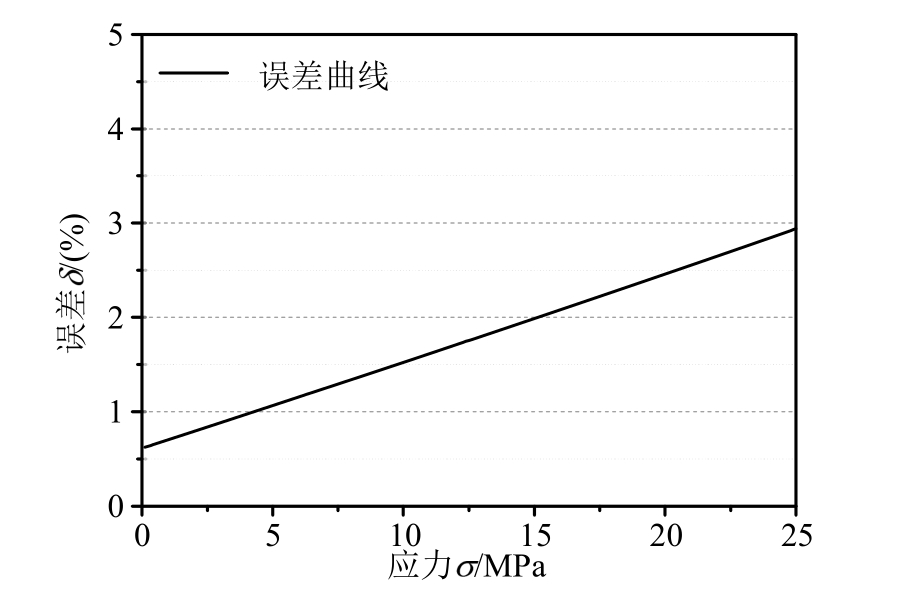
图15 误差曲线
Fig.15 The error curve
有研究表明，砂土材料在高应变率下的侧限切线模量与静态存在差异(约0.8倍到3倍不等，视材料的颗粒级配、矿物组分、相对密实度等初始条件而定)[32－34]。在初始应力下，二者区别不大，但超过 1%应变之后，高应变率下的试件则表现出更高的刚度[32]。密度一定，静态情况下，更低的刚度对应更低的波阻抗，对应T2更大，因此将明显放大绝对误差，且应力越大，绝对误差被放大得越多，在图中表现为绝对误差随应力的增加而增加。
将静态曲线拟合式(23)中参数b放大1.5倍(即b=5.055，a不变)，以模拟动态情况下，实际材料增加了的侧限切线模量。图 16为对应各应力值下侧限切线模量的放大系数(侧限切线模量放大系数定义为MSD/MS。其中，MSD为预估的动态侧限切线模量，对应b=5.055；MS为静态的侧限切线模量，对应b=3.37)。在初始应力状态下(0 MPa)，放大系数为1；25 MPa时，放大系数为1.72。
图16 侧限切线模量的放大系数
Fig.16 The increase factor of the confined tangent modulus
计算得到拟合的T2与预估的动态情况下T2的误差曲线，与原误差曲线对比如图17所示。显然，较之于静态的误差曲线(b=3.37)，预估的动态情况下(b=5.055)，绝对误差随应力增大而增大的倾向明显降低，显然更加合理。当然，这一预估的动态情况下的侧限切线模量并不准确，笔者推测，实际情况下，珊瑚砂的侧限切线模量可能更高，才能能够使得误差曲线趋于恒值(不随应力变化存在明显趋势)。
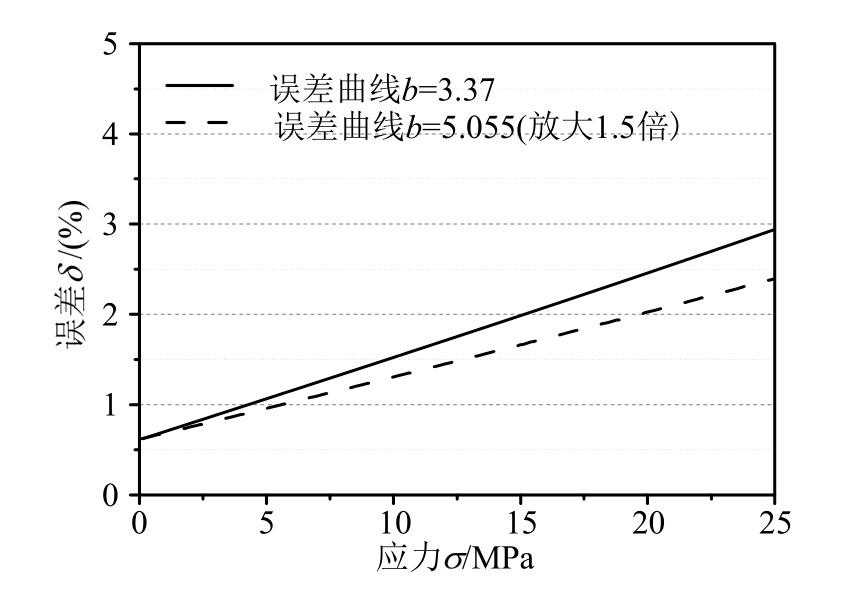
图17 误差曲线的对比
Fig.17 The comparison of the error curves.
借助已有的SHPB装置并稍作改进，提出了一种研究松散介质中一维应变状态下应力波衰减的新方法，并对干燥珊瑚砂进行了应力波传播衰减效应实验。主要结论可总结为以下几点。
(1) 提出了一种借助 SHPB装置，通过两杆中三波(入射波、反射波、透射波)计算试件两端峰值应力，从而定量地讨论应力波在试件中衰减的方法。该方法的基础在于，所试松散介质在冲击荷载的应变率范围内(约 1～102s-1)，应变率效应不明显。方法的创新之处在于：将试件前端面的反射系数F1与后端面的透射系数T2表示成试样端部所受应力的函数，通过拟合F1(σ)可得到T2()σ，从而通过T2()σ与杆中透射波计算试件中的透射峰值应力。
(2) 除了峰值应力衰减，该方法还可以测量试件的弹性波速、峰值应力速度、试件端部应力波的前沿升时等关键参数。
(3) 利用提出的方法，对干燥珊瑚砂进行了实验，发现随着传播距离的增大，珊瑚砂中峰值应力的衰减特别明显，应力波升压时间与脉冲长度均明显增加，波形变平滑。并由试验结果拟合了无量纲峰值应力随传播距离衰减的公式。
(4) 参数讨论表明，试件应力为0～23.9 MPa时，实验结果误差不超过2.83%，实验方法较为可靠。
[1]Li X M, Wang M, Guo X, et al. Measurement of stress attenuation effect in the sand under explosion wave [J].Applied Mechanics ＆ Materials, 2014, 556-562: 3187－3190.
[2]Li J C, Ma G W. Experimental study of stress wave propagation across a filled rock joint [J]. International Journal of Rock Mechanics ＆ Mining Sciences, 2009,46(3): 471－478.
[3]Luo H, Cooper W L, Lu H. Effect of moisture on the compressive behavior of dense eglin sand under confinement at high strain rates [J]. International Journal of Impact Engineering, 2014, 65(65): 40－55.
[4]Hampton D, Wetzel R A. Stress wave propagation in confined soils [R]. Chicago: IIT Research Institute Technology Center, 1966: 3.
[5]Akai K, Hori M, Ando N, et al. Shock tube study on stress wave propagation in confined soils [C]//Proceedings of the Japan Society of Civil Engineers.Japan Society of Civil Engineers, 1972(200): 127－141.
[6]Seaman L. One-dimensional stress wave propagation in soils [R]. Washington: Defence Atomic Support Agency,1966: 3.
[7]Akai K, Tokuda M, Kiuchi T. Experimental study on the propagation of stress wave in cohesive soils [C]//Proceedings of the Japan Society of Civil Engineers.Japan Society of Civil Engineers, 1969(161): 59－67.
[8]Hopkinson B. A method of measuring the pressure produced in the detonation of high explosives or by the impact of bullets [J]. Philosophical Transactions of the Royal Society of London, 1914, 213(612): 437－456.
[9]Kolsky H. An investigation of the mechanical properties of materials at very high rates of loading [J]. Proceedings of the Physical Society. Section B, 1949, 62(11): 676.
[10]Chen W W, Song B. Split Hopkinson (Kolsky) bar:Design, testing and applications [M]. New York:Springer Science ＆ Business Media, 2010: 1－3.
[11]Zhao H, Gary G. On the use of SHPB techniques to determine the dynamic behavior of materials in the range of small strains [J]. International Journal of Solids and structures, 1996, 33(23): 3363－3375.
[12]田杰, 胡时胜. G50钢动态力学性能的实验研究[J]. 工程力学, 2006, 23(6): 107－109.Tian Jie, Hu Shisheng. Research of dynamic mechanical behaviors of G50 steel [J]. Engineering Mechanics, 2006,23(6): 107－109. (in Chinese)
[13]Grote D L, Park S W, Zhou M. Dynamic behavior of concrete at high strain rates and pressures: I.Experimental characterization [J]. International Journal of Impact Engineering, 2001, 25(9): 869－886.
[14]方秦, 洪建, 张锦华, 等. 混凝土类材料SHPB实验若干问题探讨[J]. 工程力学, 2014, 31(5): 1－14.Fang Qin, Hong Jian, Zhang Jinhua, et al. Issues of SHPB test on concrete-like material [J]. Engineering Mechanics, 2014, 31(5): 1－14. (in Chinese)
[15]夏昌敬, 谢和平, 鞠杨, 等. 冲击载荷下孔隙岩石能量耗散的实验研究[J]. 工程力学, 2006, 23(9): 1－5.Xia Changjing, Xie heping, Ju yang, et al. Experimental study of energy dissipation of porous rock under impact loading [J]. Engineering Mechanics, 2006, 23(9): 1－5.(in Chinese)
[16]Chen W, Ravichandran G. Dynamic compressive failure of a glass ceramic under lateral confinement [J]. Journal of the Mechanics and Physics of Solids, 1997, 45(8):1303－1328.
[17]Yu J L, Li J R, Hu S S. Strain-rate effect and micro-structural optimization of cellular metals [J].Mechanics of Materials, 2006, 38(1): 160－170.
[18]Luo Y, Lü L, Sun B, et al. Transverse impact behavior and energy absorption of three-dimensional orthogonal hybrid woven composites [J]. Composite Structures,2007, 81(2): 202－209
[19]Song B, Chen W, Ge Y, et al. Dynamic and quasi-static compressive response of porcine muscle [J]. Journal of Biomechanics, 2007, 40(13): 2999－3005.
[20]Ross C A, Nash P T, Friesenhahn G J. Pressure waves in soils using a split-Hopkinson pressure bar [R]. San Antonio: Southwest Research Institute, 1986: 42－49..
[21]赵凯. 分层防护层对爆炸波的衰减和弥散作用研究[D]. 合肥: 中国科学技术大学, 2007.Zhao Kai. The attenuation and dispersion effects on explosive wave of layered protective engineering [D].Hefei: University of Science and Technology of China,2007. (in Chinese)
[22]Bragov A M, Lomunov A K, Sergeichev I V, et al.Determination of physicomechanical properties of soft soils from medium to high strain rates [J]. International Journal of Impact Engineering, 2008, 35(9): 967－976.
[23]Felice C W, Brown J A, Gaffney E S, et al. Investigation into the high strain-rate behavior of compacted sand using the split-Hopkinson pressure bar technique [R].Los Alamos: Los Alamos National Laboratory, 1985: 6－7.
[24]郑文, 徐松林, 胡时胜. 侧限压缩下干燥砂的动态力学性能 [J]. 爆炸与冲击, 2011, 31(6): 619－623.Zheng Wen, Xu Sonnglin, Hu Shisheng. Dynamic mechanical properties of dry sand under confined compression [J]. Explosion and Shock Waves, 2011,31(6): 619－623. (in Chinese)
[25]Song B, Chen W, Luk V. Impact compressive response of dry sand [J]. Mechanics of Materials, 2009, 41(6): 777－785.
[26]王礼立. 应力波基础 [M]. 北京: 国防工业出版社,1985: 45－47.Wang Lili. Foundation of stress waves [M]. Beijing:National Defense Industry Press, 1985: 45－47. (in Chinese)
[27]Kondner R L. Hyperbolic stress-strain response:Cohesive soils [J]. Journal of the Soil Mechanics and Foundations Division, 1963, 89(1): 115－144.
[28]Bragov A M, Lomunov A K, Sergeichev I V, et al.Determination of physicomechanical properties of soft soils from medium to high strain rates [J]. International Journal of Impact Engineering, 2008, 35(9): 967－976.
[29]Ravi-Chandar K, Ma Z. Inelastic deformation in polymers under multiaxial compression [J]. Mechanics of Time-Dependent Materials, 2000, 4(4): 333－357
[30]鲁晓兵, 谈庆明, 俞善炳, 等. 饱和砂土在往复荷载作用下有侧限的本构关系实验研究 [J]. 岩石力学与工程学报, 2001, 20(6): 859－863.Lu Xiaobing, Tan Qingming, Yu Shanbing, et al.Experimental study on constitutive relation of laterally constrained saturated sand under cyclic compressive loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 859－863. (in Chinese)
[31]User guide for Origin 8.1 [M]. Northampton, USA:OriginLab Corporation, 2009: 365.
[32]Omidvar M, Iskander M, Bless S. Stress-strain behavior of sand at high strain rates [J]. International Journal of Impact Engineering, 2012, 49(49): 192－213.
[33]Whitman R V, Miller E T, Moore P J. Yielding and locking of confined sand [J]. Journal of the Soil Mechanics and Foundations Division, 1964, 90(90):57－84.
[34]Akers S A. Uniaxial strain response of Enewetak Beach sand [M]. Vicksburg: US Army Engineer Waterways Experiment Station, 1986: 85.
A TESTING METHOD ON THE ATTENUATION OF STRESS WAVES IN LOOSE POROUS MEDIA AND ITS APPLICATION TO CORAL SAND
方秦(1962―)，男，福建人，教授，博士，博导，主要从事结构抗爆研究(E-mail: fangqinjs@139.com).