翟金金,董 胜
(中国海洋大学海洋工程系,山东,青岛 266100)
摘 要:夏威夷群岛因其特殊的地理位置及周围海底地形,长期遭受太平洋地震带和近岸地震带产生的海啸影响,如何准确地确定夏威夷群岛沿岸的海啸爬高对海洋结构设计具有重大意义。基于非线性浅水方程建立的NEOWAVES模型包含非线性静水压力项和垂向动量方程,用于描述海底的动态变形和弱频散波的传播过程,它能够模拟海啸的整个生命过程,包括产生、传播、爬高和淹没。以对夏威夷地区影响比较严重的1946年Aleutian历史海啸为例,采用NEOWAVES模型模拟其产生、传播以及在夏威夷欧胡岛沿岸地带的爬高。计算结果表明,NEOWAVES模型计算得到的欧胡岛沿岸(北部、西部和南部)的爬高与历史记录的爬高数据接近,验证了NEOWAVES模型的合理性和可靠性,同时也为夏威夷地区海洋结构物的设计提供合理的参考意见。
关键词:地震海啸;数值模拟;NEOWAVES模型;夏威夷欧胡岛;海啸波高;海啸波振幅
海啸是海平面的巨大扰动引起的破坏性海浪,是一种毁坏性极其严重的海洋灾害。引发海啸的原因有几种:天体作用(陨石坠落);地球外动力作用(海岸或海底滑坡);而灾难性的海啸多是地球内动力作用于海底的地震和火山爆发引起的[1―3]。自2004年印度洋大海啸和2011年日本大海啸后,全世界对海啸灾害的关注度达到前所未有的高度。数值模拟方法是模拟和预报海啸灾害的有效手段之一。它不仅可以模拟地震、海啸波浪传播以及近岸爬坡的全过程,而且可以为海啸预警系统提供大量的数据,为准确模拟和评估海啸灾害,建立海啸预警系统提供必要的支撑[4]。
目前海啸的数值模拟主要基于两种类型的控制方程,其中一类是基于非线性浅水方程建立的,主要包括:康奈尔大学的 Liu等[5-6]开发的可采用双向嵌套网格的 COMCOT (Cornell Multi-grid Coupled Tsunami Model)、美国国家海洋和大气管理局(NOAA)[7―9]的 MOST (Method of Splitting Tsunami)模型和日本东北大学[10]研制的 TUNAMI模型。上述的数值模型忽略了水质点的垂直运动对水压力的影响,计算过程中采用数值色散部分代替物理色散,从而使得计算时间和计算机储存减少[11―12]。另一类模拟方法考虑更高阶的Boussinesq类型方程来模拟海啸的非线性项和频散项,主要包括:美国德拉瓦大学的 Kirby[13]根据 Wei等[14]提出的非线性Boussinesq模型开发的 FUNWAVE模型。Watts等[15―18]基于FUNWAVE模型开发的GEOWAVE模型,适用于浅水区域海啸的传播和上岸,滑坡引起的海啸初始波动由TOPICS模型得到。康奈尔大学[19]的CULWAVE (Cornel University Long and Intermediate Wave Modeling Package)采用aka Boussinesq方程作为控制方程来进行非线性弱频散的海啸数值模拟,并应用到 1998年巴布亚岛新几内亚海啸,与实测数据的比较表明模型较准确。而Yamazaki等[20―21]提出了一种基于非线性浅水方程建立的NEOWAVE (Non-hydrostatic Evolution of Ocean Wave)模型,它包括垂向动量方程以及非线性浅水方程组中的非线性静水压力项,被用来描述由于海底地震引发的海啸以及弱频散波的传播过程[22]。
夏威夷群岛处在太平洋盆地,因其特殊地理位置,长期遭受从太平洋地震带和近岸地震带产生的海啸灾害,是世界上最容易遭受海啸危害的地区之一。根据美国国家气象局地理物理数据中心(National Geophysical Data Center)发布的资料可知,自 20世纪以来远场地震所产生的海啸造成夏威夷地区超过200人死亡。Walker[23]指出对夏威夷地区产生最具破坏力的海啸事件主要有五场:1946年Aleutian海啸,1952年 Kamchatka海啸,1957年Aleutian海啸,1960年Chile海啸和1964年Alaska海啸。本文以1946年Aleutian群岛地震源所产生的海啸为研究对象,采用NEOWAVES模型模拟其产生、传播以及在夏威夷欧胡岛的爬高,为夏威夷欧胡岛地区的防灾减灾提供合理的参考意见。
NEOWAVES模型能够模拟海啸的整个生命过程,包括产生、传播、爬高和淹没。它采用非线性静水压力和垂向动量方程描述海底的动态变形和弱频散波的传播过程。NEOWAVES模型采用球形坐标系统(λ,φ,z)下的动量方程和连续方程作为控制方程模拟海啸的产生、传播和淹没。
动量方程:
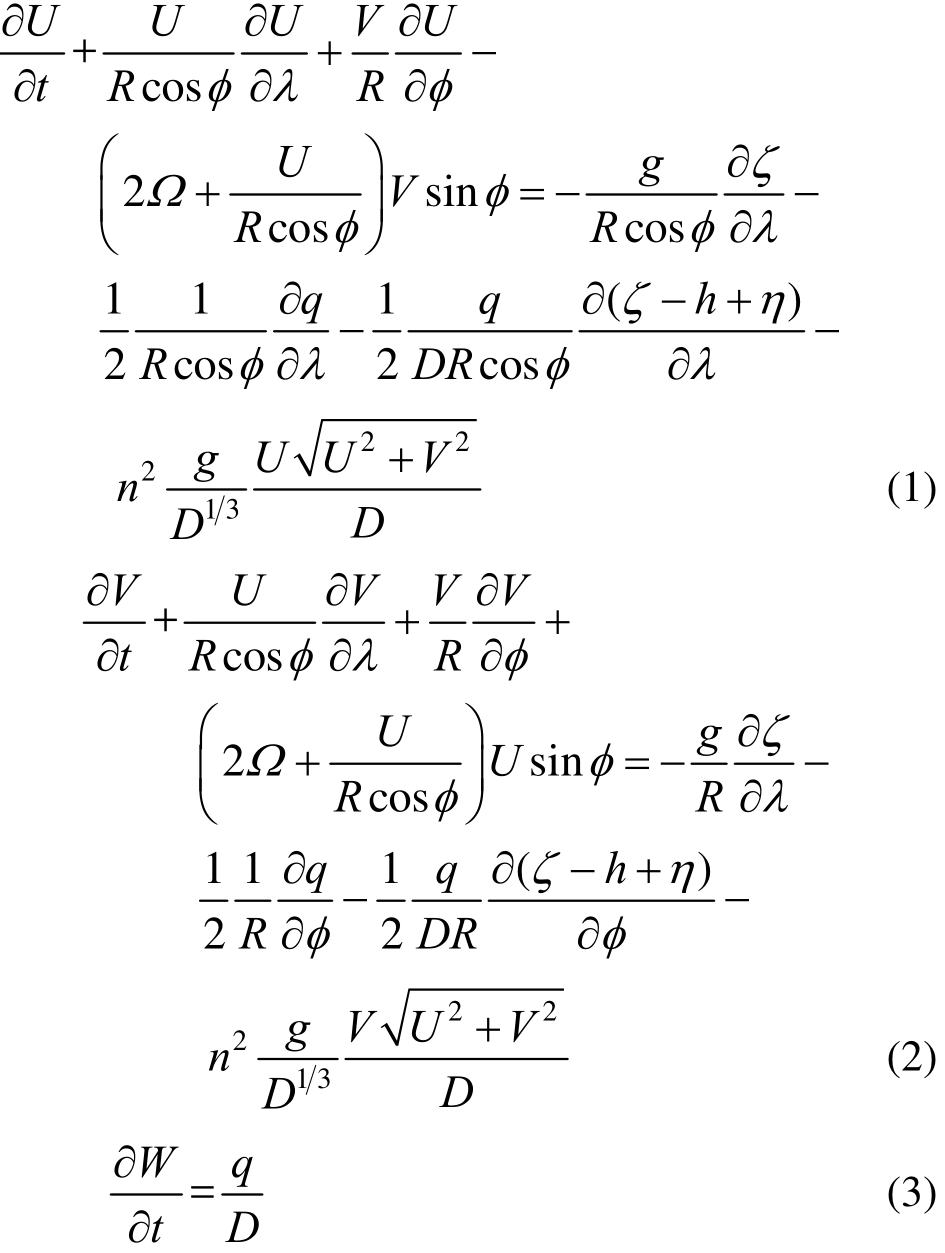
连续性方程:

式中:λ、φ和z分别表示经度、纬度和海面高度;U、V和W分别表示λ、φ和z三个方向的速度分量;R和Ω分别表示地球半径和角速度;ζ、η、h和D分别表示海面高度、海底竖向位移、水深和流速;q表示海底的非静水压力;g表示重力加速度;n表示曼宁粗糙系数。由于假定竖向速度为线性分布,W为自由表面和海底的竖向速度的平均值,可由简化的运动学边界条件给出:
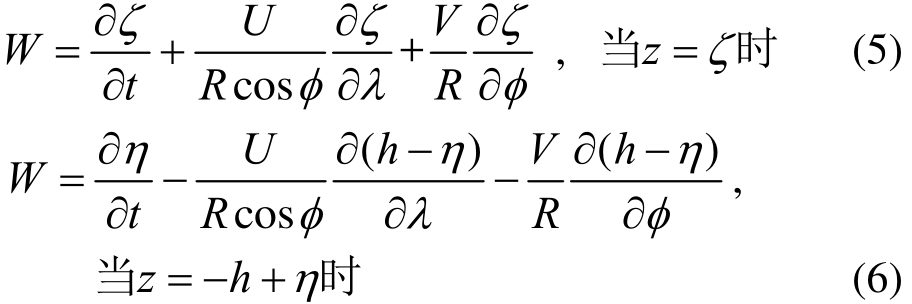
NEOWAVES海啸数值模型的地震断层模型采用USGS的有限断层模型,本次地震过程的地震参数参考文献[24]得到,具体见表1。
表1 1946年Aleutian海啸数值模拟震源各参数
Table 1 The earthquake source parameters of 1946a Aleutian tsunami numerical simulation
根据表1的地震参数对这次大海啸事件进行数值模拟,并将模拟的夏威夷欧胡岛沿岸的爬高与美国National Centers for Environmental Information(NCEI)所记录的爬高进行对比,验证 NEOWAVES数值模型的合理性。数值模拟采用三层嵌套网格(如图1),第一层网格区域为太平洋地区,第二层网格区域包含整个夏威夷群岛,第三层网格区域为欧胡岛地区,具体经纬度范围和分辨率如表2。根据CFL稳定条件,一层、二层和三层网格的时间步长分别设置为1.0 s、0.5 s和0.1 s,如表2。同时,整个模型的计算时间为 30600 s (8.5 h),二层嵌套网格从12600 s (3.5 h)开始计算。

图1 三层网格的计算区域
Fig.1 The computed regions of three levels grid
表2 计算网格设置
Table 2 The setup of computed grids

图2给出了地震的滑移模型和地震断层所造成的海底初始变形。

图2 地震断层滑移与海底初始变形
Fig.2 The fault dislocation and the initial seafloor displacement
由图2(a)可知,本次地震模型仅包含一个断层。同时,图2(b)可以看出该断层模型引起海底拱起变形大约 20 m,且海啸变形方向集中指向夏威夷群岛。通过NEOWAVES模型的计算,可以得到欧胡岛地区的海啸爬高,如图 3。图 3(a)表示欧胡岛的最大海啸波震幅,图3(b)、图3(c)和图3(d)分别表示欧胡岛北岸、西岸和南岸的NEOWAVES模型计算得到的爬高值(实线)与调查结果(NCEI)得出的爬高数据(虚线)的对比图。由图 3可知,计算得到的欧胡岛地区的爬高与调查结果得到的爬高都比较接近。此外,Walker[23]和美国NCEI总结得到的欧胡岛 1946年、1952年、1957年、1960年、1964年和2011年的海啸爬高记录,对比图3和Walker[23]中欧胡岛爬高图,可以看出NEOWAVES模型计算得到的爬高分布与 NCEI所记录数据趋势基本一致,说明NEOWAVES模型能较好地模拟海啸的爬高。

图3 欧胡岛海啸爬高对比结果
Fig.3 The comparison results of tsunami runup in Oahu Island
图4给出了太平洋区域、夏威夷群岛和欧胡岛的最大海啸波震幅分布图。对于太平洋区域的海啸波振幅分布图来说,由于断层的走向和滑移,1946年Aleutian海啸的能量向S和SE方向传播,导致了海啸能量在夏威夷群岛区域集聚,对夏威夷群岛产生严重的破坏。这也再次说明 1946年 Aleutian海啸是对夏威夷群岛地区破坏严重的海啸之一。
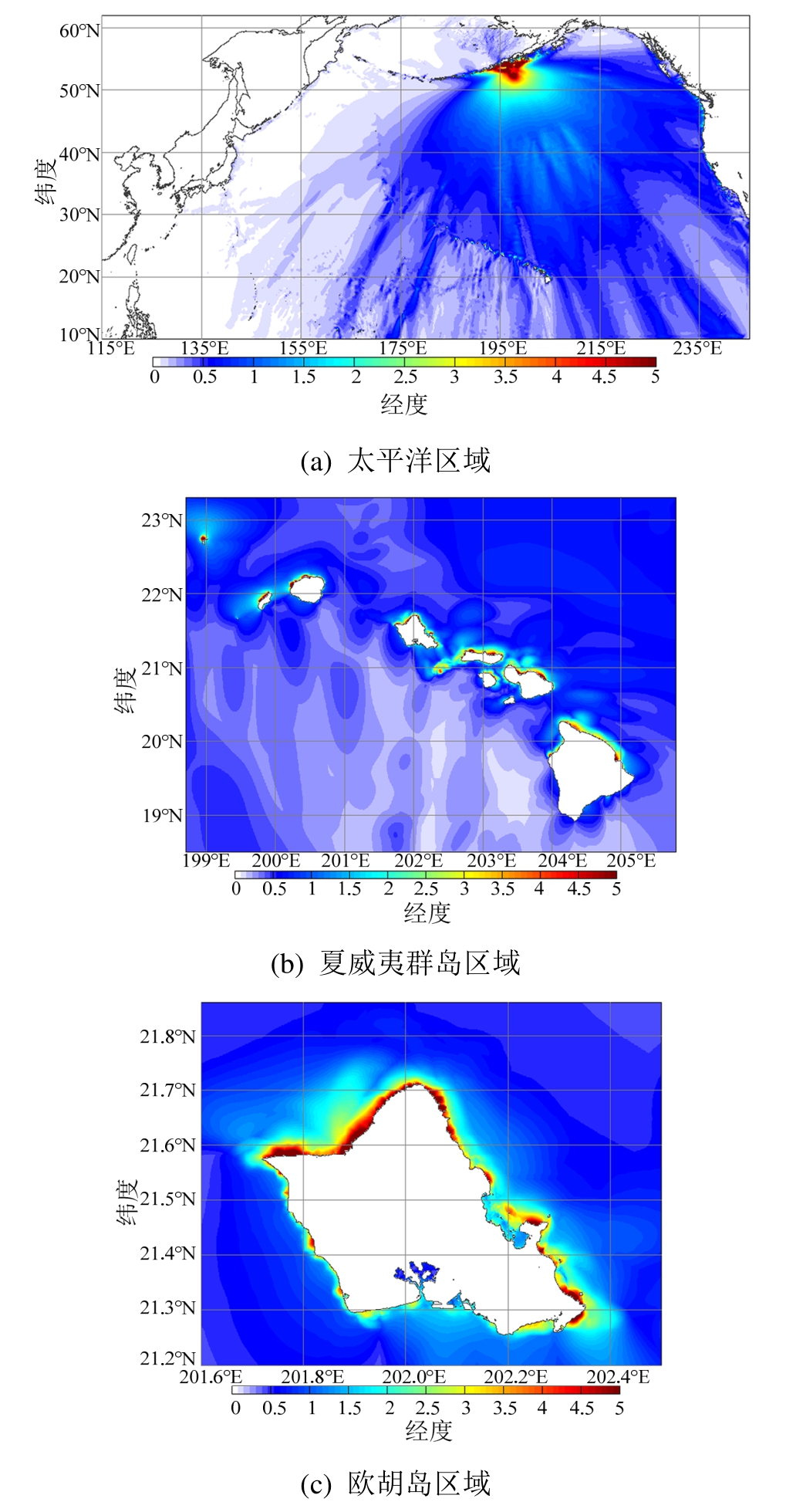
图4 最大海啸波震幅图
Fig.4 The maximum tsunami amplitude
本文采用 NEOWAVES数值模型对 1946年Aleutian海啸的产生、传播和爬高进行模拟计算,结果表明:
(1) 通过对比 NEOWAVES模型得到的欧胡岛地区的爬高与调查结果得到的爬高数据,发现两者比较接近,验证了模型的合理性和准确性。
(2) 最大海啸波震幅分布图表明 1946年Aleutian海啸能量集中向夏威夷群岛方向传播,该海啸事件对夏威夷群岛影响较大。
本文仅采用 NEOWAVES模型对 1946年Aleutian海啸进行了模拟,为了得到太平洋地震带所产生的远场海啸对夏威夷群岛的影响,还需要更多的海啸事件来验证。
参考文献:
[1]Dawson A G, Stewart I. Tsunami deposits in the geo-logical record [J]. Sedimentary Geology, 2007,200(3/4): 166―183.
[2]于福江, 原野, 赵联大, 等. 2010年2月27日智利8.8级地震海啸对我国影响分析 [J]. 科学通报, 2011,56(3): 239―246.Yu Fujiang, Yuan Ye, Zhao Lianda, et al. Evaluation of potential hazards from teletsunami in China: Tidal observation of a teletsunami generated by the Chile 8.8 Mw earthquake. Chinese Sci Bull, 2011, 56(3): 239―246. (in Chinese)
[3]Ammon C J, Ji C, Thio H K, et al. Rupture process of the 2004 Sumatra-Andaman earthquake [J]. Science, 2005,308(5725): 1133―1139.
[4]王培涛, 于福江, 原野, 等. 海底地震有限断层破裂模型对近场海啸数值预报的影响 [J]. 地球物理学报,2016, 59(3): 1030―1045.Wang Peitao, Yu Fujiang, Yuan Ye, et al. Effects of finite fault rupture models of submarine earthquake on numerical forecasting of near-field tsunami [J]. Chinese Journal of Geophysics, 2016, 59(3): 1030―1045. (in Chinese)
[5]Liu P L F, Cho Y S, Yoon S B, et al. Numerical Simulations of the 1960 Chilean Tsunami Propagation and Inundation at Hilo, Hawaii [M]// Tsuchiya Y, Shuto N, eds Tsunami: Progress in Prediction, Disaster Prevention and Warning. Advances in Natural &Technological Hazards Research, 1995, 4: 99―115.
[6]Wang X M, Liu P L F. Numerical Simulations of the 2004 Indian ocean tsunami-coastal effects [J]. Journal of Earthquake & Tsunami, 2007, 1(3): 273―297.
[7]Titov V V, Synolakis C E. Modeling of Breaking and Nonbreaking Long-Wave Evolution and Runup Using VTCS-2 [J]. Journal of Waterway Port Coastal & Ocean Engineering, 1995, 121(6): 308―317.
[8]Titov V V, Gonza’lez F I. Implementation and testing of the method of splitting tsunami (MOST) model [R].NOAA Seattle, Washington, USA: U.S. Department of Commerce, National Oceanic and Atmospheric Administration, Environmental Research Laboratories(ERL PMEL-112), NOAA/Pacific Marine environmental Laboratory, 1997: 1―11.
[9]Tang L, Titov V V, Bernard E N, et al. Direct energy estimation of the 2011 Japan tsunami using deep-ocean pressure measurements [J]. Journal of Geophysical Research Oceans, 2012, 117(C8): 72―82.
[10]Imamura F. Review of tsunami simulation with a finite difference method [M]// Liu P L F, eds Long-wave Runup Models. Friday Harbor, USA: World Scientific Publishing, 1995: 25―42.
[11]Shuto N. Numerical simulation of tsunamis - Its present and near future [J]. Natural Hazards, 1991, 4(2/3): 171―191.
[12]Burwell D, Tolkova E, Chawla A. Diffusion and dispersion characterization of a numerical tsunami model[J]. Journal of Shenyang Agricultural University, 2007,19(5): 10―30.
[13]Grilli S T, Ioualalen M, Asavanant J, et al. Source constraints and model simulation of the December 26,2004, Indian Ocean Tsunami [J]. Journal of Waterway Port Coastal & Ocean Engineering, 2007, 133(6): 414―428.
[14]Wei G, Kirby J T. Time-dependent numerical code for extended boussinesq equations [J]. Journal of Waterway Port Coastal & Ocean Engineering, 1995, 121(5): 251―261.
[15]Watts P, Grilli S T, Kirby J T, et al. Landslide tsunami case studies using a Boussinesq model and a fully nonlinear tsunami generation model [J]. Natural Hazards& Earth System Science, 2003, 3(5): 391―402.
[16]Watts P, Imamura F, Grilli S T. Comparing model simulations of three benchmark tsunami generation cases[J]. Science of Tsunami Hazards, 2000, 18(2): 107―124.
[17]Grilli S T, Watts P. Modeling of waves generated by a moving submerged body. Applications to underwater landslides [J]. Engineering Analysis with Boundary Elements, 1999, 23(8): 645―656.
[18]Watts P. Tsunami Features of Solid Block Underwater Landslides [J]. Journal of Waterway Port Coastal &Ocean Engineering, 2014, 126(3): 144―152.
[19]Roddis W M K. Community Workshop on Computational Simulation and Visualization Environment for the Network for Earthquake Engineering Simulation (NEES) [R].Davis, California, USA: University of California, 2003:10―15.
[20]Yamazaki Y, Cheung K F, Kowalik Z. Depth-integrated,non-hydrostatic model with grid nesting for tsunami generation, propagation, and run-up [J]. International Journal for Numerical Methods in Fluids, 2011, 67(67):2081―2107.
[21]Yamazaki Y, Kowalik Z, Cheung K F. Depth-integrated,non-hydrostatic model for wave breaking and runup [J].International Journal for Numerical Methods in Fluids,2009, 61(5): 473―497.
[22]Cheung K F, And Y B, Yamazaki Y. Surges around the Hawaiian Islands from the 2011 Tohoku Tsunami [J].Journal of Geophysical Research Oceans, 2013, 118(10):5703―5719.
[23]Walker D A. Regional tsunami evacuations for the state of hawai‘i: a feasibility study based on historical runup [J]data. Science of Tsunami Hazards, 2004, 22(1): 3―22.
[24]Cheung K F. Hawaii Tsunami Mapping Project: Data Sources, Procedures, and Products - Final Report for Hawaii Inundation Maps (FOUO) [R]. Honolulu, Hawaii,USA: University of Hawaii, 2010: 6―20.
SIMULATION OF ALEUTIAN TSUNAMI BY NEOWAVES MODEL
ZHAI Jin-jin , DONG Sheng
(Department of Ocean Engineering, Ocean University of China, Qingdao, Shandong 266100, China)
Abstract:Hawaiian Islands have long been impacted by tsunamis caused by the Pacific seismic zone and near-field seismic zone, largely attributed to its special geographical location and its offshore geography. How to accurately calculate the tsunami runup along the coast of Hawaiian Islands is of great significance on the design of marine structures. Based on the nonlinear shallow water equation, NEOWAVES is a shock-capturing, dispersive wave model for tsunami generation, basin-wide evolution, and run-up. It utilizes non-hydrostatic pressure and vertical velocity terms to describe dispersion and time-varying seafloor deformation. In this study, the NEOWAVES model is applied to the simulation of generation, propagation and runup of the 1946a Aleutian historical tsunami at Oahu Island. The result shows that the tsunami runup data at Oahu Island (North, West and South) calculated by NEOWAES model are similar to the historical recorded runup data, which proves that the NEOWAVES is rational and reliable to simulate tsunami, and offers reasonable reference on design of marine structure.
Key words:earthquake tsunami; numerical simulation; NEOWAVES model; Oahu Island at Hawaii; tsunami runup; tsunami wave amplitude
中图分类号:P731.25
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.06.S053
文章编号:1000-4750(2018)Suppl-0359-06
收稿日期:2017-06-01;修改日期:2017-12-27
基金项目:国家自然科学基金委员会-山东省人民政府联合基金项目(U1706226);国家自然科学基金项目(51479183)
通讯作者:董 胜(1968―),男,山东青岛人,教授,博士,博导,从事海洋工程环境及其与结构相互作用研究(E-mail: dongsh@ouc.edu.cn).
作者简介:翟金金(1990―),女,河南商丘人,博士生,主要从事海岸工程及其与海洋环境的相互作用研究(E-mail: zhaijinjin.good@163.com).