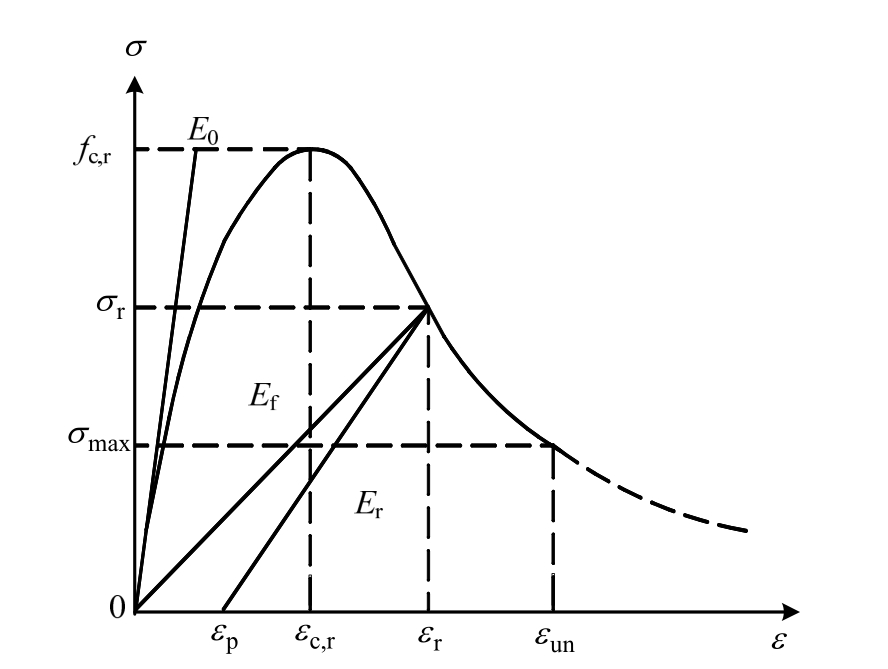
图1 混凝土单轴受压应力-应变曲线
Fig.1 Concrete stress-strain relations under axial compression
钟 铭1,2
(1. 北京市市政工程研究院,北京 100037;2. 地下工程建设预报预警北京市重点实验室,北京 100037)
摘 要:为实现对长期承受疲劳作用的混凝土桥梁进行原位评估,该文提出了基于实测弹性模量的结构混凝土累积损伤评估方法。首先根据损伤力学的定义讨论了混凝土弹性模量的取值,建议混凝土的初始无损弹性模量采用静力弹性模量;然后根据混凝土应力-应变曲线和残余应变与累积应变的统计关系,提出混凝土静力等效应变和残余应变计算方法,以及混凝土损伤后强度的估算方法,给出了混凝土结构现场测试与分析的详细步骤和弹模比、残余应变的阶段特征值。在以上研究基础上,比较分析了混凝土变形模量、静力等效应变和残余应变损伤指标的应用效果,结果表明残余应变损伤指标的适用性最好,因此根据残余应变的实用限值将混凝土损伤程度划分为4个等级。最后,为了简化评估过程,提出了一种根据混凝土实测强度和弹模比的快速查表评估方法,直接得出混凝土的剩余强度和损伤等级,对工程实践具有参考价值。
关键词:桥梁工程;混凝土累积损伤;原位评估;弹性模量;残余应变;剩余强度
混凝土桥梁、刚性混凝土路面与机场跑道、轨枕、吊车梁、海洋平台和核反应堆压力容器安全壳等混凝土结构长期承受疲劳作用,这些结构的可靠性与混凝土结构疲劳损伤的实际状态有关,从这些承受重复荷载作用的老龄混凝土结构严重损伤的现状表明,疲劳累积损伤对结构的使用寿命和安全性产生了严重影响,工程实践中迫切需要对这些长期承受疲劳作用的混凝土有损结构进行评估和维修决策。目前,各国学者通过试验和理论研究,建立了Miner准则、Corten-Dolan模型、P-M准则、Shah模型等疲劳累积损伤准则,为有效预测混凝土累积损伤程度与疲劳寿命奠定了基础。然而目前的疲劳损伤研究有优点也有局限性,局限性主要体现在以下特征中的一个或多个[1]:1) 按混凝土的应力幅来计算疲劳损伤度,没有从本质上考虑混凝土疲劳损伤;2) 准则中的参数值较多,其取值不仅与材料特性有关,而且与荷载特性有关;3) 没有考虑荷载加载次序的影响,所以很难通过疲劳累积损伤准则准确判断既有结构混凝土的累积损伤程度。近年来,一些学者通过疲劳试验统计[2―6]或数值分析的方法[7-8]研究混凝土的疲劳累积损伤问题,根据明确的荷载作用历程,获取了混凝土总应变、残余应变、刚度和强度与加载应力幅、疲劳次数等相关参量的关系,得出了混凝土弹性模量退化、残余应变增大及强度衰减规律,大大推进了混凝土累积损伤分析和寿命预测问题的研究。但是,实际混凝土结构的作用历程往往不知,损伤后的应力重分布,以及在服役过程中受疲劳、徐变、温度和收缩等多种时变效应的非线性耦合影响,使得既有结构混凝土的累积损伤程度评估更为复杂,采用简化的疲劳累积损伤分析方法预测结果往往与实际相差很大。因此,亟需一种能够直接判明既有结构混凝土累积损伤程度的原位评估方法。
许多疲劳试验结果表明[2―5],混凝土的损伤和破坏是内部微裂纹的扩展直至产生宏观裂缝,当裂纹长度达到某一临界长度后,将发生不稳定扩展直至破坏。而且在各种时变效应下,混凝土损伤的统一内因也是混凝土内部微裂纹的扩展造成混凝土力学性能的劣化[9]。文献[10]提出了基于微裂纹扩展机理的损伤混凝土强度和临界裂纹长度实用评估方法,但是由于混凝土材料组成不均匀,除微裂纹外还存在随机分布的微空隙等初始缺陷,单从细观机理评估混凝土损伤过于复杂且难以达到高的精度。弹性模量和残余应变能够宏观反映混凝土的细观损伤机制,而且与加载历程无关,是混凝土原位评估很好的选择。基于残余应变定义的损伤物理意义明确,然而残余应变在现场还无法直接测试;弹性模量虽然是可测试的参量,但其应用范围有一定局限性[11],导致结构混凝土累积损伤原位评估始终是一个难题。为此,本文基于“变形唯一性”假定和混凝土材料在静态荷载与疲劳荷载作用下破坏的相似性,以混凝土实测弹性模量为评估参量,提出混凝土损伤后静力等效应变和残余应变计算方法,以及混凝土损伤后强度的估算方法。然后讨论了混凝土各损伤阶段的弹模比限值与静力等效应变、残余应变特征值的关系,提出了一种根据混凝土实测强度和弹模比的快速查表评估方法,直接得出混凝土的残余应变和损伤等级,并用已有试验结果进行了验证。
混凝土在疲劳荷载作用下的应力-应变包络线与单调应力-应变曲线基本一致[12],因此,混凝土受压疲劳包络线可采用单轴受压应力-应变曲线表示,如图1所示。

图1 混凝土单轴受压应力-应变曲线
Fig.1 Concrete stress-strain relations under axial compression
根据损伤力学的定义,混凝土内部微裂纹扩展宏观上表现为弹性模量的退化,受力方向的混凝土损伤可用变形模量与基体弹性模量表征:
式中:Ef为混凝土变形模量,定义为从原点出发的割线模量;E为混凝土基体弹性模量。
在多次加卸载的疲劳裂纹扩展过程中,由于混凝土内部残余应力释放、裂纹尖端的微塑性和损伤以及受压混凝土微空隙压密、裂纹摩擦滑移等损伤机制[13],造成了混凝土卸载后产生残余应变,使得变形模量在疲劳损伤后难以直接测试。谢和平等[11]对式(1)进行了改进,提出了考虑不可逆残余应变影响的弹塑性材料损伤定义。
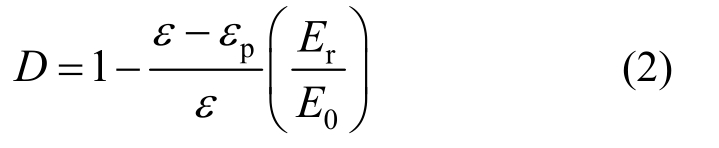
式中:ε为材料的总应变;εp为残余应变;E0为无应力状态下的切线模量;Er为卸载弹性模量。
应用式(2)计算时需要获知混凝土的疲劳累积应变和残余应变,但当混凝土结构应力状态已知或现场采用应力释放法仅可以得到混凝土的弹性应变,即使采用混凝土长期应变监测方法,并设置无应力计消除温度变化、收缩变形的影响,测试应变中还包含了徐变应变,由于混凝土徐变的影响因素复杂,其计算结果与实际往往差距很大,混凝土的疲劳累积应变的误差就会很大,更不用说残余应变。由于残余应变产生的机理非常复杂,不少研究者基于混凝土的疲劳破坏和静载破坏两者的破坏机理一致和“变形唯一性假设”,建立了混凝土疲劳损伤时的应变发展公式[5,14],以及混凝土结构疲劳损伤等效静力分析方法[7-8]。这些公式和方法从初始状态研究混凝土的疲劳累积损伤过程,在一定条件下揭示了混凝土累积损伤的机理,但是考虑实际混凝土结构加载历程不明确、应力重分布和时变效应影响,这些公式和方法显然不适用于混凝土残余应变的现场确定。基于以上原因,混凝土损伤评估中常采用卸载后实测弹性模量与初始无损伤弹性模量的比值来度量其弹性损伤程度,损伤指标可用式(3)表示。
一些学者通过试验研究,认为混凝土残余应变εp与卸载弹性模量损伤指标Dr是等比例的线性关系[15],遗憾的是现在还没有明确给出不同强度等级的混凝土比例因子。而且式(3)在实际应用中,初始弹性模量的定义也存在争议,若取混凝土初始切线模量E0作为初始值,则计算中可能出现负损伤,这也偏离了对损伤的定义,并且初始缺陷损伤难以考虑;以静力受压弹性模量Ec为初始值,也很难区分初始缺陷损伤和受力损伤。但是根据损伤力学的定义,初始无损弹性模量是混凝土基体的弹性模量,所以从简化分析和实用评估的角度,初始弹性模量应选择与定义最接近的模量参数。
静力受压弹性模量Ec可能比初始切线模量E0更接近于基体弹性模量,参照《普通混凝土力学性能试验方法标准》(GB/T 50081―2002),弹性模量Ec是在1/3混凝土轴心抗压强度作用下,经过3次反复预压得到的试验值,在混凝土裂纹基本不扩展的情况下消除了大部分内部初始微缺陷的影响。例如根据我国《混凝土结构设计规范》(GB 50010―2010)(以下简称《规范》)规定的应力-应变曲线,初始切线模量可按式(4)计算,与《规范》表 4.1.5中的弹性模量统计值Ec比较结果如表1所示。
式中:fc,r为混凝土抗压强度标准值;εc,r为峰值压应变;n为形状系数,fc,r≤50 MPa时,n=2;fc,r>50 MPa 时,n=2-(fc,r-50)/60。
由表1可以看出,按《规范》规定的应力-应变曲线计算的E0值均小于静力受压弹性模量Ec。混凝土强度等级小于或等于C50情况下,随强度等级增大,E0 /Ec比值从 C20的 0.715升高至 C50的0.980;混凝土大于C50时,E0/Ec比值从C55的0.970减小至C80的0.885。
表1 受压混凝土初始切线模量E0与弹性模量Ec比较 /(×104N/mm2)
Table 1 The comparison between initial tangent modulusE0and elastic modulusEcfor compressive concrete

因此,混凝土初始弹性模量宜选用弹性模量Ec,式(3)可变更为:
王时越等[4]通过对C15混凝土静载及等幅循环荷载疲劳试验得出,当混凝土接近疲劳破坏时,卸载弹性模量Er与静力弹性模量Ec的比值在0.474~0.757之间,平均为 0.63。疲劳破坏时的弹模比离散性较大,主要原因在于混凝土材料本身的离散性,即使是同强度等级、同龄期的混凝土,由于成型工艺、养护条件等方面的原因,其静力弹性模量Ec也有较大的差异[16]。所以在既有结构混凝土损伤测试评估中,弹性模量Ec应采用实测值。
混凝土累积损伤破坏从力学意义上讲,是材料的微观变形达到了变形承载能力极限,这与Holmen[2]给出的“可以利用混凝土极限应变作为混凝土疲劳破坏的准则”相吻合,大量的疲劳试验结果也验证了这一点;而且对于各种强度的混凝土,疲劳残余应变的发展较为稳定且具有代表性[1,3]。因此,如何获取残余应变就成为结构混凝土累积损伤现场评估的关键。基于混凝土疲劳包络线的Berkeley加卸载模型[17]中给出了式(6)所示的残余应变εp与静力等效应变εr关系,过镇海等[18]根据试验研究也得出了式(7)所示的统计公式。Berkeley加卸载模型计算的残余应变值与过镇海模型计算值比较接近,总体稍微偏大一些。

现有研究表明[7,19],混凝土在疲劳荷载作用下疲劳破坏时的最大应变与单调加载软化段最大应力所对应的应变相当,如图1中的εun,但是此值与混凝土所受的软化段最大应力σmax有关,不易准确确定。现在一般采用“疲劳残余应变εp=0.4εc,r”作为疲劳破坏实用失效准则[5,20]。实际结构中混凝土受力不均匀,发生损伤的部位往往是局部的,但超过此限值时结构通常严重开裂,承载力下降,不能再有效使用。因此,本文也采用了这个失效准则,并提出此准则下如式(8)所示的残余应变与静力等效应变的实用关系式,与Berkeley加卸载模型和过镇海模型的比较见图 2。可以看出本文关系式计算的残余应变曲线处于Berkeley加卸载模型和过镇海模型曲线之间,更接近于过镇海模型曲线,也验证了本文关系式的合理性。当残余应变εp=0.4εc,r时,按式(8)计算的静力等效应变为1.3εc,r。
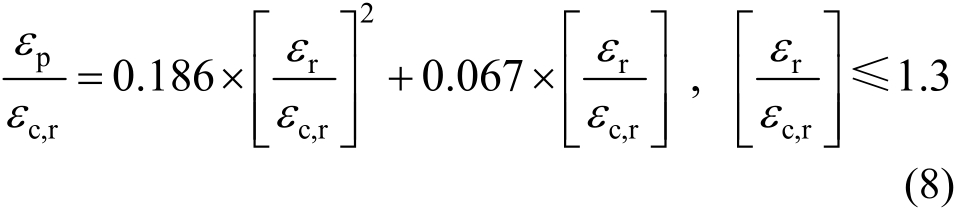

图2 混凝土残余应变与静力等效应变的关系曲线
Fig.2 Concrete residual strain and static equivalent strain relationship
为了在现场得到混凝土的残余应变,本文提出一种基于混凝土卸载弹性模量的静力等效应变和残余应变的分析方法。根据Sinha等[12]提出的混凝土变形唯一性假设:不管以前承受的重复荷载历程如何,只要残余变形相同,则在此基础上施加相同的重复荷载,其荷载与变形的关系将保持不变,而与以前的荷载变形历程无关。这一假设目前已被许多试验所证实,因此以残余应变为等效参量,可以得出疲劳荷载与静载分析的等效关系。在《规范》给出的单轴受压混凝土本构关系的基础上,摒弃荷载循环能量耗散规律的复杂性,假定混凝土损伤后加卸载的弹性模量采用如图 1所示的线性发展模式,即混凝土实测弹性模量与加卸载弹性模量相等,结合式(8)建立了受压混凝土累积损伤的静力等效应变分析方法,由计算的静力等效应变和应力得出受压混凝土的残余应变,进一步可以推定混凝土损伤后的强度。具体测试与分析步骤如下:
步骤 1:利用超声波、冲击波等无损检测方法或取芯法,在有代表性的混凝土构件或部位测试与分析无损伤混凝土的力学参数,包括混凝土抗压强度fc,r、混凝土的弹性模量Ec和峰值压应变εc,r;
步骤2:根据混凝土实际抗压强度fc,r和弹性模量Ec作出单轴受压应力-应变全曲线,计算公式见下式;
式中:σ、ε分别为混凝土的压应力和压应变;dc为混凝土受压损伤演化参数,详见《规范》第C.2.4条。
步骤 3:利用无损检测方法或静力加载及应变测试系统现场测量结构混凝土关键测点(一般为主要受力构件的最不利受力截面受压区边缘)的弹性模量Er;以静力加载为例,通过对结构混凝土施加弹性范围内的静力荷载,由静力平衡条件得出混凝土应力增量和实测的应变增量,按式(10)计算卸载弹性模量Er;
式中,Δσ、Δε分别为静力加载下的混凝土应力增量和应变增量。
步骤4:根据式(7)或式(8)给出的残余应变与静力等效应变的关系,与式(11)联立求解静力等效应变εr;
步骤 5:按式(12)计算εr对应的静力等效应力σr,混凝土残余应变值εp由式(13)求得;
步骤6:根据混凝土应力-应变曲线和静力等效应变εr推断混凝土损伤后剩余强度:εr≤εc,r时,混凝土强度不下降,剩余强度仍为fc,r;εr>εc,r时,混凝土强度下降,按式(12)计算的静力等效应力σr即为混凝土损伤后剩余强度。
需要指出的是,以混凝土疲劳包络线为基础的加卸载弹性模量线性假设,对于评估混凝土大应变低周疲劳效应是合理的,而与实际混凝土的随机疲劳滞回曲线及高周疲劳损伤后再加载曲线发展模式[21]不完全相符,导致高周疲劳损伤后的混凝土实测弹性模量往往大于按此假设确定的卸载弹性模量,计算的静力等效应变偏小,不利于结构安全评估。鉴于不同加载方式下,相同静力等效应变或残余应变对应的损伤弹性模量实际是一个变化值,卸载弹性模量与静力弹性模量的比值(简称弹模比)的取值宜以区间来表征。因此,对于混凝土累积损伤评估,由疲劳包络线确定的线性加卸载弹模比仅可看作是下限值,而对于高周疲劳作用下的混凝土弹模比则需要确定上限值。
在疲劳包络线的上升段,静力等效应变在0<εr≤εc,r范围内,无论是高周疲劳还是低周疲劳,损伤后的混凝土强度基本不变。此阶段静力等效应变对应残余应变特征点的确定如下:当εr=εc,r时,按式(8)计算的残余应变为 0.253εc,r,Berkeley加卸载模型和过镇海模型的计算结果分别为 0.275εc,r和0.247εc,r,统一取为 0.25εc,r,与《规范》方法计算结果相等;根据混凝土在静力应力≤0.75fc,r作用下宏观弹性工作[22],计算出 C20~C80混凝土的应变在0.75fc,r时介于 0.45εc,r~0.55εc,r之间,统一取为 0.5εc,r,相应的残余应变近似等于 0.08εc,r。由此可以得出εr=0.5εc,r和εr=εc,r卸载后的弹性应变分别为 0.42εc,r和 0.75εc,r,对应的静力等效应力分别用σ0.5εc,r和fc,r表示,所以混凝土静力或低周疲劳弹模比的下限值,εr=0.5εc,r或εp=0.08εc,r时可取为σ0.5εc,r/(0.42εc,r),εr=εc,r或εp=0.25εc,r为fc,r/(0.75εc,r)。
混凝土高周疲劳则不同,试验研究表明混凝土初期的弹性模量降低和残余应变增大较快[3―5],但从试验数据来看,混凝土卸载弹性模量的降低量小,疲劳累积应变超出静力弹性应变就会对混凝土强度有降低影响[8,11,23]。因此,根据混凝土高周疲劳损伤后的强度变化特征,在εr=0.5εc,r或εp=0.08εc,r时的弹模比上限值可取为1;而取εp=0.08εc,r时的静力弹模比 下 限 值σ0.5εc,/(0.42εc,r)作为高周疲 劳εr=εc,r或εp=0.25εc,r的弹模比上限值。由于在少量疲劳作用后,弹模比的降低量就超出此限值,这也解释了混凝土高周疲劳为什么总是造成强度下降的原因。
在疲劳包络线的下降段,当残余应变εp=0.4εc,r时,按式(8)计算的静力等效应变为 1.3εc,r,直接反映了残余静载强度降低量,同样可取σ1.3εc,r/ (0.9εc,r)作为εr=1.3εc,r或εp=0.4εc,r时的弹模比下限值。混凝土高周疲劳性能更复杂,试验研究表明[1,3,5]:εp=0.4εc,r时的混凝土疲劳总应变稳定地近似静力峰值应变值εc,r,疲劳寿命接近90%;而实测的混凝土弹模比一般大于按fc,r/(0.75εc,r)确定的弹模比下限值fc,r/(0.75εc,r),更接近于fc,r/(0.6εc,r),因此近似取此值为εp=0.4εc,r时的弹模比上限值。此外,混凝土的初始缺陷也能造成残余应变的变化,但此值很难准确计算,本文计算约等于0.02εc,r。
根据以上分析,将基于残余应变特征值的混凝土弹模比上限值和下限值分别列于表2、表3中,可以分别在混凝土高周疲劳和低周疲劳后评估时采用。可以看出C20~C80混凝土的弹模比随残余应变的增大而逐渐减小,平均弹模比上限值从 1.000减小至 0.810,平均弹模比下限值从 0.943减小至0.517;混凝土强度对弹模比的影响较大,随混凝土强度越低弹模比降低量越大。
本文重点讨论混凝土高周疲劳后损伤评估问题,当εp=0.4εc,r时,C20~C60混凝土的弹模比上限值降低为 0.596~0.877,而 C60以上的混凝土弹模比最大只减小了 0.092,说明弹性模量对较低强度等级混凝土的损伤较为敏感,而对于高强混凝土则不太理想。
表2 受压混凝土卸载弹性模量(上限值)与静力弹性模量的比值
Table 2 The ratio of unloading elastic modulus (upper limit value) and static modulus for compressive concrete

表3 受压混凝土卸载弹性模量(下限值)与静力弹性模量的比值
Table 3 The ratio of unloading elastic modulus (lower limit value) and static modulus for compressive concrete

将静力等效应力σr和静力等效应变εr代入式(1),并用Ec代替E,按式(14)可以计算出以变形模量表征的混凝土累积损伤指标。
分别计算混凝土强度等级 C20~C80的变形模量损伤指标D20~D80,如图3所示。
变形模量损伤指标总体随应变增大近似线性发展,但是混凝土强度不同时的指标发展趋势不一致:低强度混凝土(小于C50)表现为“前快后慢”,高强度混凝土(大于C50)“前慢后快”。在应变特征点处的指标也较为离散,峰值应变εc,r时的损伤指标在 0.41~0.64 之间,1.3εc,r时介于 0.64~0.74 之间。因此,以变形模量评估混凝土累积损伤时必须考虑混凝土强度的影响。

图3 混凝土变形模量损伤指标
Fig.3 The concrete damage index of deformation modulus
为了使变形模量损伤指标最大值为1,并考虑高周疲劳破坏实用失效准则,将其归一化处理为:
式中,Efz为混凝土失效(ε=1.3εc,r)时的变形模量。
以混凝土残余应变和静力等效应变计算的实用损伤指标可分别表示为:
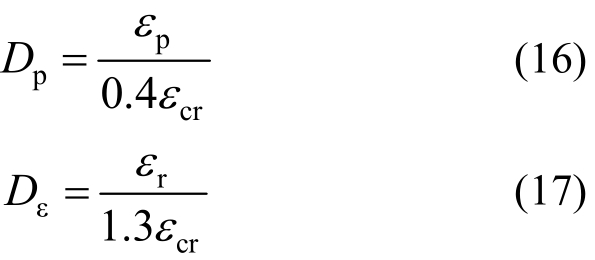
式中:Dp为混凝土残余应变表征的损伤指标;Dε为混凝土静力等效应变表征的损伤指标。残余应变损伤指标Dp与归一化后的变形模量损伤指标Df以及静力等效应变损伤指标Dε的比较如图4、图5所示。可以看出,Df与混凝土强度相关,而且不同强度的发展趋势不一致,Dp和Dε与混凝土强度无关;Df平均值和Dε随着应变增大而线性增大,只有Dp能够体现随应变增大各阶段损伤加速发展的特征。因此,在混凝土累积损伤评估中采用残余应变损伤指标Dp更合理,与静力等效应变的统计关系可表示为:
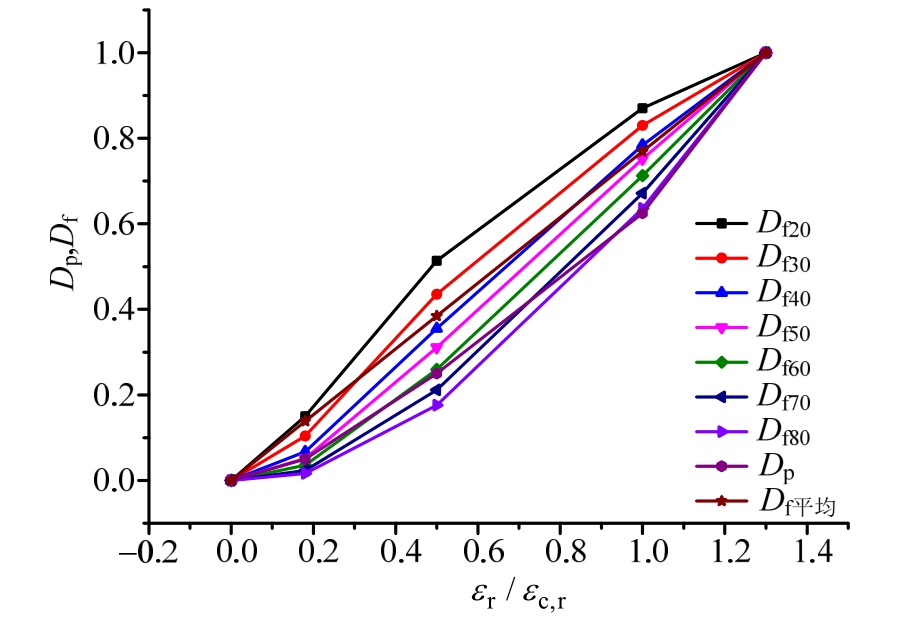
图4 残余应变损伤指标Dp与变形模量损伤指标Df的比较
Fig.4 A comparison for concrete damage index between residual strain and deformation modulus
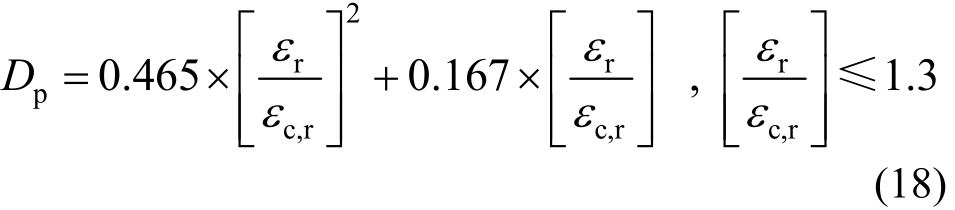
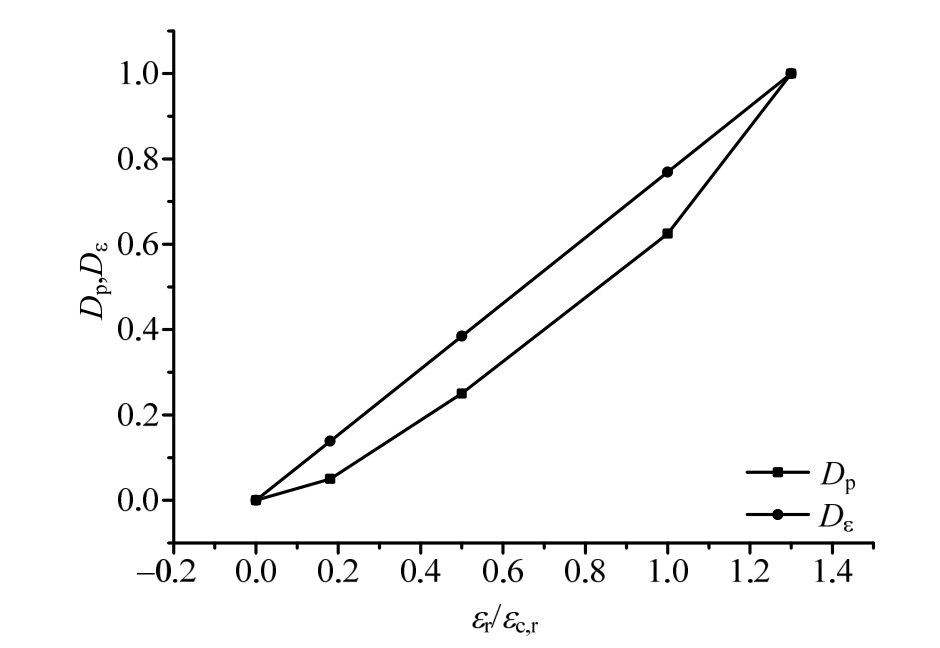
图5 残余应变损伤指标Dp与静力等效应变损伤指标Dε的比较
Fig.5 A comparison for concrete damage index between residual strain and static equivalent strain
混凝土结构损伤评估往往需要分等级评定,根据第4节损伤阶段特征值的分析,将高周疲劳受压混凝土累积损伤程度划分为良好、中等、严重和失效4个等级,相应的评定标准如表4所示。
表4 受压混凝土累积损伤程度评定
Table 4 Cumulative damage degree evaluation for compression concrete

弹模比虽然仅能反映混凝土的弹性损伤程度,不同混凝土强度的弹模比发展规律也不一致,但是对于混凝土高周疲劳情况,根据结构混凝土的实测强度和弹模比查表 2中对应的残余应变值(中间数值可以近似直线内插),由表4可以对混凝土累积损伤程度快速评估,直接判别混凝土高周疲劳的累积损伤程度和损伤后强度。为验证方法的可靠性和实用性,选择孟宪宏[6]的受压混凝土疲劳试验第4组和第 7组数据进行分析,试验混凝土初始强度在C35~C40之间,分别在最大应力水平 0.75和 0.85的情况下进行了2万次和1千次等幅加载,然后测试了剩余弹性模量和剩余强度。根据试验数据计算出弹模比和剩余强度与初始强度比,与评估值的对比列于表 5,可以看出,采用弹模比的上限值能较好地评估高周疲劳后混凝土的剩余强度,而且得到了以残余应变表征的损伤指标,直接评判混凝土已经进入了严重损伤状态。
表5 受压混凝土疲劳损伤后的等级评定和剩余强度评估
Table 5 Cumulative damage degree and residual strength evaluation for compression concrete after fatigue loading

评估结果还可以揭示高周疲劳累积损伤对未发生疲劳破坏的混凝土桥梁受弯极限承载力降低影响不显著[24]的原因:当混凝土残余应变εp≤0.25εc,r时,混凝土材料强度不变,而纵筋基本弹性工作,则受弯极限承载力基本不变;0.25εc,r<εp<0.4εc,r时,从表 5中的试验数据可知混凝土材料强度下降量很少,即使εp=0.4εc,r时剩余强度与初始强度比评估值还可以达到0.88,而且截面受压区损伤仅在边缘部分,所以受弯极限承载力下降很少,仍然保持了95%左右的受弯极限承载力。因此,残余应变 εp=0.25εc,r及对应的弹模比上限值可作为混凝土桥梁受弯极限承载力是否降低的界限。
此外,获取实际结构的混凝土残余应变或静力等效应变,可进一步对损伤混凝土桥梁的恒载应力状态、正常使用承载力下降值和时效变形中的应力相关变形等进行具体分析,限于篇幅将另文论述。
(1) 既有结构混凝土弹性损伤评估中,为避免混凝土初始缺陷造成的评估误判,建议混凝土初始无损弹性模量采用静力弹性模量Ec,并宜采用实测值。
(2) 根据《规范》混凝土应力-应变曲线和残余应变与累积应变的实用关系式,提出了基于卸载弹性模量的混凝土静力等效应变和残余应变的计算方法,给出混凝土结构现场测试与分析的详细步骤和弹模比与残余应变的相关特征值,适用于现场获取结构混凝土的残余应变。
(3) 通过比较混凝土变形模量、静力等效应变和残余应变表征的损伤指标,发现残余应变损伤指标能够体现随应变增大的各阶段损伤加速发展特征,因此建议采用残余应变损伤指标,并给出了残余应变损伤指标与静力等效应变的关系式。
(4) 将受压混凝土累积损伤程度划分为良好、中等、严重和失效4个等级,给出了各等级的残余应变损伤指标、静力等效应变和残余应变范围,以及推定混凝土损伤后强度的方法。提出了根据结构混凝土实测强度和弹模比的快速查表评估方法,大大简化了评估过程,可应用于结构混凝土损伤的实用评估。
(5) 直接基于弹模比和残余应变的混凝土累积损伤评估方法,避免了复杂的加载历程和时变效应分析,进一步可对既有损伤混凝土结构的现存应力应变状态、剩余承载能力和变形能力等进行评估。
参考文献:
[1]刘国军, 杨永清. 一种基于残余应变的混凝土疲劳损伤模型 [J]. 材料导报 B: 研究篇, 2014, 28(3): 141―144.Liu Guojun, Yang Yongqing. A fatigue damage model for concrete based on residual strain [J]. Materials Review B: Research, 2014, 28(3): 141―144. (in Chinese)
[2]Holmen J. Fatigue of concrete by constant and variable amplitude loading [J]. ACI Special Publication, Fatigue of Concrete Structures 1982, 75(4): 71―110.
[3]李朝阳, 宋玉普, 赵国藩. 混凝土疲劳残余应变性能研究[J]. 大连理工大学学报, 2001, 41(3): 355―358.Li Chaoyang, Song Yupu, Zhao Guofan. Study of residual strain of concrete under fatigue loading [J].Journal of Dalian University of Technology, 2001, 41(3):355―358. (in Chinese)
[4]王时越, 张立翔, 徐人平, 等. 混凝土疲劳刚度衰减规律试验研究[J]. 力学与实践, 2003, 25(5): 55―57.Wang Shiyue, Zhang Lixiang, Xu Renping, et al.Deterioration laws of concrete elastic modulus under fatigue loading [J]. Mechanics in Engineering, 2003,25(5): 55―57. (in Chinese)
[5]王瑞敏, 赵国藩, 宋玉普. 混凝土的受压疲劳性能研究[J]. 土木工程学报, 1991, 24(4): 38―47.Wang Ruimin, Zhao Guofan, Song Yupu. Study on concrete compressive fatigue performance [J]. China Civil Engineering Journal, 1991, 24(4): 38―47. (in Chinese)
[6]孟宪宏. 混凝土疲劳剩余强度试验及理论研究[D]. 大连: 大连理工大学, 2006.Meng Xianhong. Experimental and theoretical resear ch on residual strength of concrete under fatigue loading[D]. Dalian: Dalian University of Technology, 2006.(in Chinese)
[7]朱劲松, 朱先存. 钢筋混凝土桥梁疲劳累计损伤失效过程简化分析方法 [J]. 工程力学, 2012, 29(5): 107―121.Zhu Jinsong, Zhu Xiancun. Study on simplified method for the analysis of fatigue failure process of RC bridges[J]. Engineering Mechanics, 2012, 29(5): 107―121. (in Chinese)
[8]王青, 卫军, 刘晓春, 等. 钢筋混凝土梁疲劳损伤过程的等效静力分析方法[J]. 中南大学学报(自然科学版),2016, 47(1): 247―253.Wang Qing, Wei Jun, Liu Xiaochun, et al. Equivalent static analysis method for fatigue cumulative damage process of reinforced concrete beam [J]. Journal of Central South University (Science and Technology),2016, 47(1): 247―253. (in Chinese)
[9]刘国军, 杨永清, 魏召兰. 时变效应导致的混凝土损伤研究进展[J]. 材料导报 A: 综述篇, 2014, 28(5):92―96.Liu Guojun, Yang Yongqing, Wei Zhaolan. Research progress of concrete damage caused by time-varying effects [J]. Materials Review A: Review, 2014, 28(5):92―96. (in Chinese)
[10]钟铭, 徐骋. 基于裂纹扩展机理的损伤混凝土强度预测方法研究[J]. 建筑科学, 2015, 31(7): 6―11.Zhong Ming, Xu Cheng. Research of damage concrete intensity forecast method Based on concrete crack evolvement mechanics [J]. Building Science, 2015,31(7): 6―11. (in Chinese)
[11]谢和平, 鞠杨, 董毓利. 经典损伤定义中的“弹性模量法”探讨[J]. 力学与实践, 1997, 19(2): 1―5.Xie Heping, Ju Yang, Dong Yuli. Discussing ‘elastic modulus method’ in the classic damage definition [J].Mechanics in Engineering, 1997, 19(2): 1―5. (in Chinese)
[12]Sinha B P, Gerstle K H, Tulin L G. Stress-strain relations for concrete under cyclic loading [J]. J Proc , 1964,61(2): 195―212.
[13]冯西桥, 余寿文. 准脆性材料细观损伤力学[M]. 北京:高等教育出版社, 2002.Feng Xiqiao, Yu Shouwen. Quasi brittle material microscopic damage mechanics [M]. Beijing: Higher Education Press, 2002. (in Chinese)
[14]王瑞敏, 宋玉普, 赵国藩. 混凝土疲劳破坏的概率分析[J]. 大连理工大学学报, 1991, 31(3): 331―336.Wang Ruimin, Song Yupu, Zhao Guofan. Fatigue strength of concrete under repeated stress amplitude [J].Journal of Dalian University of Technology, 1991, 31(3):331―336. (in Chinese).
[15]易成, 朱红光, 王青, 等. 疲劳荷载下混凝土梁弯曲损伤指标的探究[J]. 应用力学学报, 2009, 26(1): 71―75.Yi Cheng, Zhu Hongguang, Wang Qing, et al. Damage index for concrete beam under fatigue loading [J].Chinese Journal of Applied Mechanics, 2009, 26(1):71―75. (in Chinese)
[16]王时越, 张立翔, 徐人平. 弹性模量对混凝土疲劳性能的影响[J]. 昆明理工大学学报, 2001, 26(5): 18―20,25.Wang Shiyue, Zhang Lixiang, Xu Renping. Effect of modulus on fatigue behaviors of concrete [J]. Journal of Kunming University of Science and Technology, 2001,26(5):18―20, 25. (in Chinese)
[17]Blakely R W G, Park R. Prestressed concrete sections with cyclic flexure [J]. Journal of the Structural Division,ASCE, 1973, 99(8): 1717―1743.
[18]过镇海, 张秀琴. 混凝土在反复荷载作用下的应力-应变全曲线[J]. 工业建筑, 1981, 18(9): 14―17.Guo Zhenhai, Zhang Xiuqin. Stress-strain relations for concrete under cyclic loading [J]. Industrial Construction,1981, 18(9): 14―17. (in Chinese)
[19]朱劲松, 肖汝诚, 宋玉普. 混凝土疲劳特性与疲劳损伤后的等效单轴本构关系[J]. 建筑材料学报, 2005,8(5): 484―489.Zhu Jinsong, Xiao Rucheng, Song Yupu. Fatigue behavior and damaged equivalent constitutive law of plain concrete [J]. Journal of Building Materials, 2005,8(5): 484―489. (in Chinese)
[20]混凝土疲劳专题组. 混凝土受弯构件疲劳可靠性验算方法的研究[R]. 北京: 中国建筑工业出版社, 1994.Special Group on Concrete Fatigue. Study on fatigue reliability checking method of concrete beams [R].Beijing: China Building Industry Press, 1994. (in Chinese)
[21]雷兵, 宋玉普. 基于 ANSYS 的部分预应力混凝土梁疲劳性能模拟[J]. 工业建筑, 2013, 43(9): 71―76.Lei Bing, Song Yupu. Fatigue performance simulation of partially prestressed concrete beams based on ANSYS[J]. Industrial Construction, 2013, 43(9): 71―76. (in Chinese)
[22]过镇海. 钢筋混凝土原理[M]. 北京: 清华大学出版社,2012.Guo Zhenhai. Principle of reinforced concrete[M].Beijing: Tsinghua University Press, 2012. (in Chinese)
[23]欧进萍, 林燕清. 混凝土高周疲劳损伤的性能劣化试验研究[J]. 土木工程学报, 1999, 32(5): 15―22.Ou Jinping, Lin Yanqing. Experimental study on performance degradation of plain concrete due to high-cycle fatigue damage [J]. China Civil Engineering Journal, 1999, 32(5): 15―22. (in Chinese).
[24]张建仁, 彭晖, 张克波, 等. 锈蚀钢筋混凝土旧桥超限及极限荷载作用的现场破坏性试验研究[J]. 工程力学,2009, 26 (增刊 II): 213―224.Zhang Jianren, Peng Hui, Zhang Kebo, et al. Test study on overload and ultimate behavior of old reinforced concrete bridge through destructive test of corroded bridge [J]. Engineering Mechanics, 2009, 26 (Suppl II):213―224. (in Chinese)
AN IN-SITU EVALUATION METHOD FOR CUMULATIVE DAMAGE OF STRUCTURAL CONCRETE
ZHONG Ming1,2
(1. Beijing Muntcipal Engineering Research Institute, Beijing 100037, China;2. Beijing Key Laboratory Underground Construction Forecasting and Warning, Beijing 100037, China)
Abstract:In order to realize the in-situ evaluation of concrete bridges subjected to fatigue for a long time, an evaluation method for cumulative damage of concrete structures is proposed, based on unloading elastic modulus.First, the value of elastic modulus is discussed by the definition of damage mechanics and the concrete initial condition is suggested using the static elastic modulus. Then, according to the concrete stress-strain curve and the statistical relationship between residual strain and cumulative strain, the calculation method of static equivalent strain and residual strain concrete are proposed by unloading elastic modulus and the method for estimating the strength of concrete after damage. The detailed steps of field test and analysis and the phase characteristic value of elastic modulus ratio and residual strain are developed. Based on the above research, the indicator of residual strain is compared with the indicators of modulus of deformation and static equivalent strain to indicate the most effective for damage evaluation of concrete. Therefore, the concrete damage degree is divided into four grades by the practical limiting value of residual strain. Finally, according to the measured concrete strength and elastic modulus ratio, a look-up table assessment method is put forward to evaluate the concrete residual strength and damage degree so as to simplify the evaluation process and it can be used as a practical evaluated method for cumulative damage of concrete.
Key words:bridge engineering; concrete cumulative damage; in-situ evaluation; elastic modulus; residual strain; residual strength
中图分类号:U441+.4
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.02.S054
文章编号:1000-4750(2018)Suppl-0278-09
收稿日期:2017-05-28;修改日期:2018-02-07
基金项目:北京市财政专项资金项目(科-J-15066);北京市西城区优秀人才骨干个人项目(科-J-17047)
作者简介:钟铭(1972―),男,山东人,研究员,博士,主要从事桥梁结构抗震及损伤评估研究(E-mail: zhongm2005@sina.com).