半开式桁架桥结构稳定性分析

岳子翔，温庆杰，卓 涛

(中国矿业大学力学与土木工程学院深部岩土力学与地下工程国家重点实验室，江苏，徐州 221116)

摘 要：半开式桁架桥无上部联系，其上弦杆易发生平面外屈曲。在上弦杆屈曲后的整桥体失稳模态中，存在明显的横向弯曲与扭转变形，上弦杆屈曲临界力和屈曲模态与理论结果有一定差异。该文使用有限元软件对一定数量的半开式桁架桥进行分析，通过有限元结果对影响桁架桥稳定性的因素进行了探讨，发现影响半开式桁架桥稳定性的尺寸参数是宽跨比，对这一桥型而言，稳定性与其宽跨比有正比关系；宽跨比对稳定性的影响来自其对整桥横向刚度和扭转刚度的影响，两种刚度共同决定整桥稳定性，但横向刚度是决定性因素；横向刚度会影响整桥失稳模态，若失稳模态产生突变，稳定性能随之产生巨大变化；对单座桥梁而言，若要通过增大宽跨比来提高稳定性，必须使两榀主桁建立有效联系，否则会起反作用；加装风撑能有效联系主桁，加强整桥横向刚度，进而提升整桥稳定性，但风撑无法加强抗扭刚度。

关键词：桥梁工程；半开式桁架桥；稳定性；横向刚度；扭转刚度；宽跨比；风撑

半开式桁架桥由上下弦杆、腹杆、横梁构成，由于无上部联接系，其上弦杆易发生平面外屈曲，上弦杆屈曲临界力是决定桥梁整体稳定性能的关键参数。

目前关于半开式桁架桥上弦杆屈曲临界力的计算理论，有Timoshenko等[1－2]国外科研人员和我国科研人员[3－4]进行的研究。这些研究均假定只有桁架桥上弦杆及横梁顶面以上竖腹杆能发生横向位移，同时各构件均不发生扭转，本文将这一状态称为“理想模型”。显然，理想模型与实际情况不符。目前国内半开式桁架桥的设计主要参照《水运工程钢结构设计规范(JTS 152―2012)》[5]、《港口工程钢结构设计规范(JTJ 283―99)》[6]和《铁路桥梁钢结构设计规范(TB 100091―2017)》[7]中的相关条文规定，三个规范吸取了相关研究结论，按理想假定为基础推导求解上弦杆面外屈曲临界力。工程人员与学者[8－9]在半开式桁架桥的设计与施工中发现了理论结果与实际运用的偏差，但是并未针对相关问题展开系统论证。

实际上，在试验[10－11]和有限元结果[12]中，由于上弦杆侧向屈曲导致的桁架失稳模态中，一定存在桁架整体的横向弯曲或扭转变形。本文在大量工程实例有限元结果中发现，半开式桁架桥上弦杆屈曲会引起全桥发生兼有横向弯曲与扭转的整体失稳，各实例的上弦杆屈曲临界力和屈曲模态分析结果与理想模型假定下的有限元分析结果有不同程度的差异，加装风撑可以减小这一差异。上述说明半开式桁架桥稳定性与桥梁自身横向抗弯刚度和抗扭刚度等结构参数存在联系，而风撑加强稳定性的作用机理也应进行研究。本文通过整理各实例结构参数与有限元分析结果，得到了影响桥梁稳定性的尺寸参数，分析了桁架桥横向刚度与扭转刚度对桥梁稳定性的影响，研究了两种刚度与结构尺寸参数间的联系，探究了风撑对两种刚度及桥梁稳定性的作用关系，并结合上述，分析了半开式桁架桥的失稳特点和规律。

1 半开式桁架桥失稳模态分析

既有半开式桁架桥上弦杆屈曲的理论研究中，假定各构件除上弦杆与横梁顶面以上腹杆外不发生横向位移，且不发生扭转变形，即理想模型，此时有限元分析的整桥失稳模态只有上弦杆的屈曲变形，如图1。此时，图1中例举3个实例的上弦杆屈曲临界力分别为：模型a：9824 kN、模型b：3102 kN、模型c：5515 kN；屈曲半波数为：模型a：3；模型b：3；模型c：2。

图1 理想模型失稳模态
Fig.1 Instability modes of ideal models

实际状态下，半开式桁架桥并无横向位移与扭转的限制，上弦杆屈曲会带动其他构件产生横向弯曲与扭转。在实际状态下进行有限元分析，上弦杆屈曲后的整桥失稳模态带有明显的扭转与横向弯曲，如图2。与理想模型分析结果不同，此状态下所得上弦杆屈曲临界力较理想模型分析值下降，此时模型的上弦杆屈曲临界力分析值分别为：模型 a：5183 kN；模型b：1844 kN；模型c：3782 kN；屈曲半波数为：模型a：1；模型b：1；模型c：1。

图2 无风撑时桥梁失稳模态
Fig.2 Instability modes of bridges without wind braces

在布置风撑后，整桥稳定性有所提高，屈曲临界力与失稳模态分析结果会向理想模型分析结果靠近，如图 3，此时模型的上弦杆屈曲临界力分析值分别为：模型a：8958 kN、模型b：2805 kN、模型c：4870 kN；屈曲半波数为：模型a：3、模型b：3、模型c：2。

由上述数据可得，未加装风撑时3个模型的上弦杆屈曲临界力分别为理想模型的 52.8%、59.4%和68.6%，加装风撑后3个模型屈曲临界力为理想模型的91.2%、90.4%和88.3%，未加装风撑时，上弦杆屈曲模态半波数均为1，加装风撑后上弦杆屈曲半波数则与理想模型相等，且整桥弯扭变形明显减小。可知，实际有限元结果与理想状态下有限元结果差异极大，不同实例的差异大小也不同，加装风撑可大幅提高屈曲临界力并减小弯扭变形，加装风撑前后屈曲模态半波数也明显不同。本文依托大量工程实例进行有限元分析后，发现该现象是半开式桁架桥所共有的。本文使用的实例参数见表1和表2，表1中tan α和横向位移的计算、意义与作用见本文第2节，由于实例较多，本文不对各实例结果进行展示。

图3 安装风撑后桥梁失稳模态
Fig.3 Instability modes of models with wind braces

表1 算例结构参数
Table 1 Structural parameters of calculation examples

算例 跨径/m 宽度/m 宽跨比 tan α 横向 桁架榀数位移/m 1 38.1 8.7 0.228 0.00057 0.056 2+3中纵梁2 23.68 3.38 0.143 0.00325 0.069 2 3 42.25 3.9 0.0923 0.003070.125 2+1中纵梁7 4 40.8 5.86 0.144 0.00171 1.673 2 5 21.2 3.2 0.151 0.00344 0.19 2 6 21.38 4.8 0.225 0.00104 0.324 2 7 26 3.9 0.150 0.003070.321 2 7 8 29.736 4.6 0.155 0.00109 0.433 2 9 42.863 4.9 0.114 0.00163 0.387 2 10 30.6 3 0.098 0.006 0.318 2 11 23 6.38 0.277 0.00078 0.039 2+2中纵梁12 35 5.4 0.154 0.00148 0.114 2+1中纵梁13 38 4.6 0.121 0.0013 0.865 2 14 32.29996 8.6 0.266 0.00023 0.045 2+3中纵梁

根据上述：1) 各实例稳定性各异，而桁架桥根本的不同是结构几何参数与构件截面参数的不同，故需研究影响半开式桁架桥稳定性的结构参数；2) 桁架桥稳定性显然受整桥横向抗弯刚度和扭转刚度的影响，故需研究两种刚度、稳定性和结构参数之间的关系；3) 加装风撑前后，屈曲临界力、屈曲半波数、弯扭变形均有极大变化，故需对风撑的影响和作用原理进行研究。下文研究内容即围绕这3点展开。

表2 算例构件截面参数
Table 2 Section parameters of components of calculation examples

算 上/下弦杆 上/下弦杆 上/下弦杆 斜/竖腹杆 斜/竖腹杆 斜/竖腹杆例 截面惯性 截面惯性 截面面积/截面惯性 截面惯性 截面面积/矩Ix/m4矩Iy/m4m2矩Ix/m4矩Iy/m4m21 1.50×10-42.22×10-42.06×10-21.58×10-53.638×10-57.104×10-32 1.50×10-42.22×10-42.06×10-28.173×10-62.129×10-55.2×10-33 1.50×10-42.22×10-42.06×10-21.58×10-53.638×10-57.104×10-31.50×10-42.22×10-42.06×10-249(上.93弦×1杆0-)51(上.30弦×1杆0-)41(上.54弦×1杆0-)21.58×10-53.638×10-57.104×10-3(下弦杆)(下弦杆)(下弦杆)5 9.933×10-51.304×10-41.538×10-25.313×10-67.148×10-63.636×10-36 9.933×10-51.304×10-41.538×10-25.313×10-67.148×10-63.636×10-37 1.50×10-42.22×10-42.06×10-28.173×10-62.129E-5 5.2×10-38 1.50×10-42.22×10-42.06×10-22.425×10-54.328×10-58.164×10-39 1.50×10-42.22×10-42.06×10-21.58×10-53.638×10-57.104×10-310 9.933E-5 1.304×10-41.538×10-21.137×10-51.809×10-55.2×10-311 1.50×10-42.22×10-42.06×10-28.173×10-62.129×10-55.2×10-312 1.50×10-42.22×10-42.06×10-21.58E-5 3.638×10-57.104×10-313 1.50×10-42.22×10-42.06×10-22.425×10-54.328×10-58.164×10-314 1.50×10-42.22×10-42.06×10-21.58×10-53.638×10-57.104×10-3

2 影响稳定性的因素

本文有限元分析采用商业有限元软件 Midas Civil进行，有限元模型均使用梁单元建立。

为研究横向刚度与扭转刚度对桁架桥稳定性的影响，本文通过在各算例有限元模型横梁上施加等大小、等偏心距的竖向集中荷载使各算例受到相同的扭转作用，以结构扭转角α的正切值tan α衡量各算例抗扭刚度大小，即扭转刚度与 tan α成反比；通过在各算例有限元模型跨中施加等大小横向集中力，使桥梁发生横向变形，并以跨中横向位移大小衡量桥梁横向刚度大小，即横向刚度与横向位移成反比。

通过有限元分析，本文得到各桁架桥算例在理想状态、实际状态、只限制下弦杆侧向位移(对应加装风撑)3种情况下的上弦杆屈曲临界力有限元分析值，记这3个分析值为P1、P2、P3，并以此对各类结构参数与半开式桁架桥稳定性的关系进行了分析。

本文选取 14个国内半开式桁架桥作为分析算例，各算例结构参数如表 1，影响整桥稳定性的主要构件截面参数如表2。

2.1 影响半开式桁架桥稳定性的结构尺寸参数

本文研究的稳定性并非单纯评价不同算例承载力大小，而是指结构在实际状态下承载力与理想状态保持一致的能力，故而算例稳定性越高，则实际状态下的上弦杆屈曲临界力分析值 P2应与理想状态下的屈曲临界力分析值P1越接近，故本文使用P2/P1的大小衡量算例的稳定性能。

本文发现影响半开式桁架桥稳定性的结构尺寸参数是宽跨比，随着宽跨比的增大，P2/P1随之增大，不断向1靠近，见图4。

图4 宽跨比对桥梁稳定性影响
Fig.4 Relation between width span ratio and stability

图4 中与拟合曲线偏离较大的3个算例按宽跨比递增分别为算例7、算例12、算例1。波动较大的原因为，算例 7：无中纵梁且上弦杆呈拱形，导致稳定性较差；算例12：中纵梁为两榀桁架，而非大多桁架桥的一榀或无中纵梁，稳定性相对较高；算例 1：中纵梁为三榀桁架，即有五榀桁架构成，稳定性相对较高。剔除上述3个数值点，本文采用幂函数拟合宽跨比与稳定性的关系，曲线函数见式(1)，式中y为P2/P1，x为宽跨比，相关系数R2为0.945。

2.2 扭转刚度/横向刚度与尺寸参数的关系

通过对比 tan α与各尺寸参数的关系，本文发现 tan α随桥梁宽跨比增大而减小，即扭转刚度随宽跨比增大而提高，见图5。

图5 抗扭刚度与宽跨比关系
Fig.5 Relation between width span ratio and torsional stiffness

图 5中与拟合曲线偏差较大的 4个算例分别为：算例 10、算例 2、算例 7、算例5。其中算例10各截面参数在各算例中最小，且无中纵梁，同时宽跨比较大，算例7与算例5上弦杆截面尺寸同样为各算例中最小，且同时没有中纵梁，算例2与算例12均为拱形上弦杆且无中纵梁。剔除上述4个数值点，本文采用幂函数拟合宽跨比与抗扭刚度的关系，曲线函数见式(2)，式中y为tan α，x为宽跨比，相关系数R2为0.843。

对于横向刚度，本文并未发现其与各结构参数之间存在特定关系。

2.3 扭转刚度/横向刚度与稳定性的关系

本文在上文中阐述了稳定性随宽跨比增大而增强的关系，虽然抗扭刚度同样和宽跨比成正比，但本文发现随 tan α增大(抗扭刚度减小)，P2/P1的下降趋势存在较大波动，即对半开式桁架桥而言，抗扭刚度并非影响其稳定性的决定性因素，但抗扭刚度的提高有利于桥梁稳定，tan α与P2/P1的关系见图6。

图6 抗扭刚度与稳定性关系
Fig.6 Relation between torsional stiffness and stability

本文对半开式桁架桥稳定性与其横向刚度之间的关系进行了分析，发现随整桥横向位移增大(横向刚度减小)，各算例P2/P1值呈下降趋势，说明横向刚度增大有利于提高稳定性，但这一趋势存在较大波动，即对半开式桁架桥而言，横向刚度亦非影响其稳定性的决定性因素，但横向刚度的提高有利于桥梁稳定性，横向刚度与稳定性关系如图7。

基于桁架桥稳定性并非由扭转刚度或横向刚度其中一个因素决定，本文一起比较两种刚度与稳定性的关系。如图 8，桁架桥稳定性提高伴随着扭转刚度与横向刚度同时增大的趋势，当桁架桥稳定性极高时，其扭转刚度与横向刚度同时达到较大值，但两种刚度的增大趋势均存在一定波动，说明两种刚度共同决定桁架桥稳定性，而非其中一种。

图7 横向刚度与稳定性关系
Fig.7 Relation between lateral stiffness and stability

图8 两种刚度与稳定性关系
Fig.8 Relation between stability and two kinds of stiffness

3 风撑对桥梁稳定性影响

通过上文有限元分析结果，本文发现加装风撑对桥梁稳定性存在有利影响。就此，本文对加装风撑与桥梁稳定性、抗扭刚度、横向刚度的关系进行了分析，研究了风撑对稳定性提高的作用原理。

3.1 加装风撑对半开式桁架桥稳定性的影响

本文通过比较加装风撑前后算例P2/P1值与宽跨比之关系，发现加装风撑对桁架桥稳定性有提高作用，但加装风撑无法使桁架桥稳定性完全达到理想状态，各算例P2/P1虽有提高，但多数算例P2/P1未能提高至0.9以上，如图9。

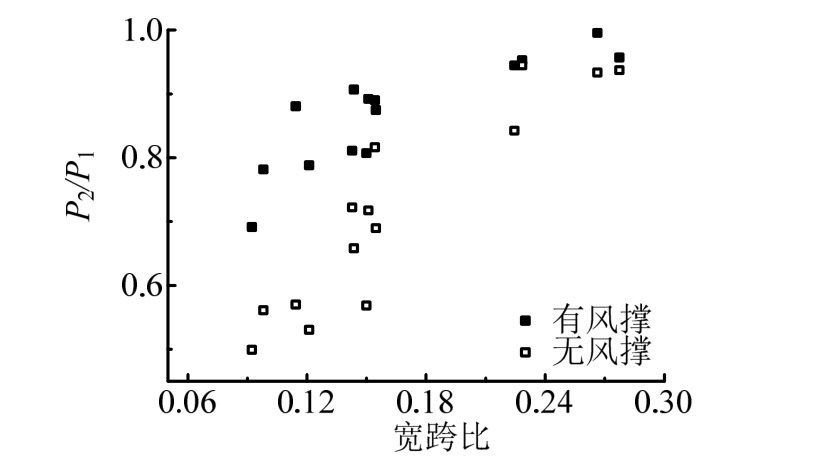
图9 风撑对桥梁稳定性影响
Fig.9 The strengthening effect of wind brace on stability

风撑是加强两下弦杆之间联系的结构，其作用相当于限制下弦杆的侧向位移，本文通过比较加装风撑前后算例P2/P3值与宽跨比之关系发现，加装风撑后除宽跨比最小的两个算例，其余算例P2/P3值均提高至0.9以上，即加装风撑能有效的联系下弦杆，能起到约束下弦杆侧向位移的作用，如图10。

图10 风撑对下弦杆联系作用
Fig.10 The link effect of wind brace on bottom chords

3.2 加装风撑对扭转刚度的影响

本文对比各算例扭转角正切值 tanα在加装风撑前后与宽跨比关系之变化，发现加装风撑前后tanα几乎不变，即加装风撑对提高抗扭刚度作用不大，如图11。

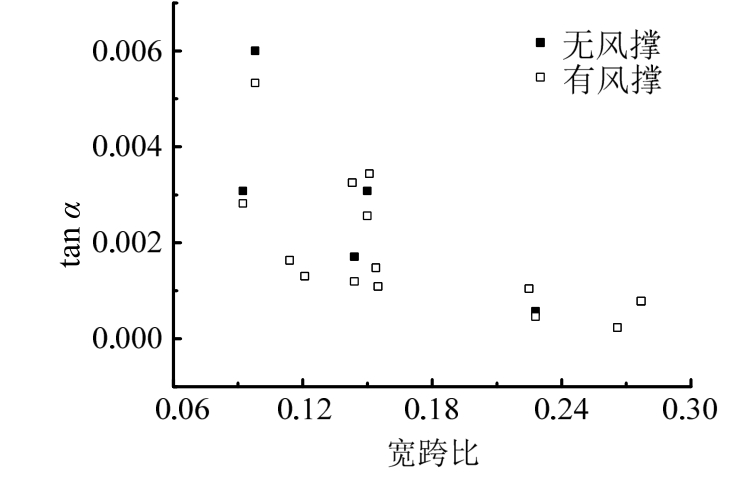
图11 加装风撑对抗扭刚度影响
Fig.11 The effect of wind brace on torsional stiffness

3.3 加装风撑对横向刚度的影响

本文通过对比加装风撑前后各算例横向位移的变化，发现加装风撑前后横向位移大幅度减小，即加装风撑能有效提高桁架桥横向刚度，如图12。

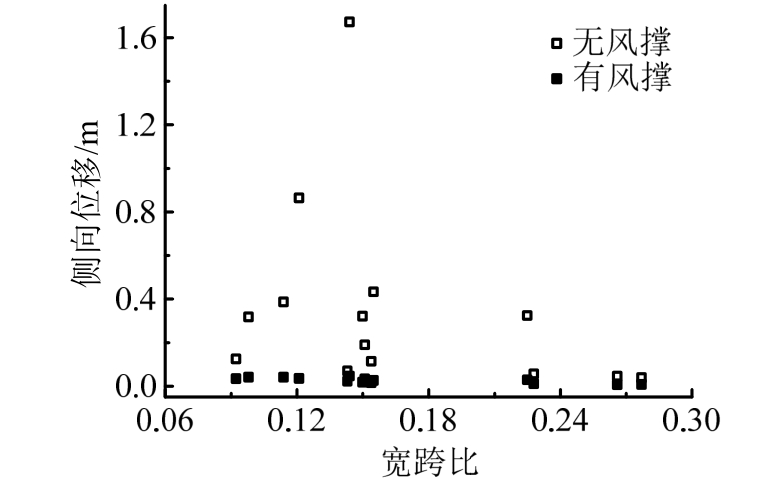
图12 加装风撑对横向刚度影响
Fig.12 The effect of wind brace on lateral stiffness

3.4 小结

基于本节和第2节分析结果，可知宽跨比和加装风撑对半开式桁架桥稳定性有很大影响，这一影响来自两者对整桥抗扭刚度与横向抗弯刚度的影响，而两种刚度、整桥稳定性、宽跨比、风撑作用机理这四者之间的关系至此仍不明确，故仍然需要选取单一算例对风撑作用和宽跨比进行参数分析，以确定半开式桁架桥稳定性中存在的规律和风撑的作用原理。

4 半开式桁架桥失稳特性

本节使用单一算例进行基于宽跨比和风撑尺寸的参数分析，以研究宽跨比、整桥抗扭刚度、横向抗弯刚度、稳定性四者之间的关联以及风撑的作用原理。本节分析采用上文算例 10进行，算例结构参数见表1与表2。

4.1 基于宽跨比的分析(无风撑)

改变分析模型的宽跨比，在宽跨比为0.025/0.05/0.075/0.1/0.15/0.20/0.25/0.30时依照上文方法计算不同宽跨比模型对应的P1、P2、结构扭转角α正切值和横向位移，不同宽跨比下P1/P2、tanα值和横向位移见图13。

图13 不加装风撑模型分析结果图
Fig.13 Analysis results of model without wind brace

如图13，侧向位移随宽跨比增大而增大，即宽跨比增大，整桥横向刚度下降；tanα随宽跨比增大而下降，即宽跨比增大，整桥抗扭刚度增大。在宽跨比从0.025到0.1变化的区间内，随宽跨比增大，tanα减小幅度极大(对应抗扭刚度增大)，P1/P2随之大幅提高。在宽跨比从0.1到0.3变化的区间内，tanα减小幅度趋于缓和，P1/P2随侧向位移的增大(对应横向刚度降低)而快速减小。

上述说明，当半开式桁架桥下部未加装风撑时，在抗扭刚度较小的情况下，随宽跨比增大，即使横向刚度下降，若抗扭刚度能获得较大幅度增强，整桥稳定性仍会有所提高，但是当抗扭刚度增大达到一定数值后，整桥稳定性会随横向刚度的不断降低而降低。可以看出，半开式桁架桥稳定性并非由抗扭刚度与侧向刚度中的一种决定，而是由两者共同影响。但除去宽跨比较小的情况，在大部分宽跨比区间内，决定半开式桁架桥稳定性的因素是整桥横向刚度。与一般桥梁不同，半开式桁架桥在未加装风撑时，横向刚度随宽跨比增大而减小，这一现象的原因将在下文中进行分析。

4.2 基于风撑作用的分析

在桁架桥底部加装风撑，不改变原算例宽跨比，仅改变风撑截面尺寸，计算加装不同尺寸风撑时的P2/P1、结构扭转角α正切值和横向位移，同时记录加装不同尺寸风撑时的上弦杆屈曲半波数，并与未加装风撑和理想假定下的分析结果进行对比，结果见表3。

表3 加装风撑后有限元分析结果
Table 3 Analysis results when bridge are installed with different wind braces

风撑尺寸/mmP2/P1屈曲模态半波数 侧向位移/m tanα无风撑 0.56 1 0.216 0.0053□30×30×3 0.67 介于 1～3 0.071 0.0053□50×50×5 0.82 3 0.039 0.0053□70×70×6.5 0.87 5 0.028 0.0053□70×100×8 0.89 5 0.023 0.0053□120×160×10 0.92 5 0.020 0.0053理想状态(限制横1 5 / /梁侧向位移)

如表 3，在桁架桥底部加装风撑后，横向刚度增大，P2/P1提高，屈曲模态半波数增加，但抗扭刚度未出现变化，即加装风撑能有效提高半开式桁架桥横向刚度与稳定性，但无法提高其抗扭刚度。

在加装风撑并持续提高风撑尺寸的过程中，当横向刚度出现大幅度提升时，上弦杆屈曲半波数会增多，P2/P1会大幅提升，当横向刚度提升幅度趋于缓和时，屈曲半波数不产生变化，P2/P1仅小幅提升。可见，整桥横向刚度对上弦杆屈曲模态影响很大，而屈曲模态对屈曲临界力会产生很大影响，即整桥侧向刚度对上弦杆屈曲临界力的影响是由于其对上弦杆屈曲模态的影响而产生的。同时可知，风撑对半开式桁架桥的作用之一是提高桁架桥横向刚度，从而加强稳定性。

4.3 基于宽跨比的分析(有风撑)

为进一步研究半开式桁架桥受力特性及风撑的作用，本节在模型底部加装□120×160×10尺寸的风撑后，依照4.1节的分析方法对模型进行有限元分析并同时记录屈曲模态半波数的变化情况，分析结果见图14和表4。

图14 加装风撑模型分析结果图
Fig.14 Analysis results of model with wind brace

表4 模型屈曲模态随宽跨比变化情况
Table 4 Half-wave number of buckling waveform at different width-span ratio

宽跨比 半波数(有风撑) 半波数(无风撑)0.025 1 1 0.050 介于 1～3 1 0.100 5 1 0.150 5 1 0.200 5 1 0.250 5 1 0.300 5 1

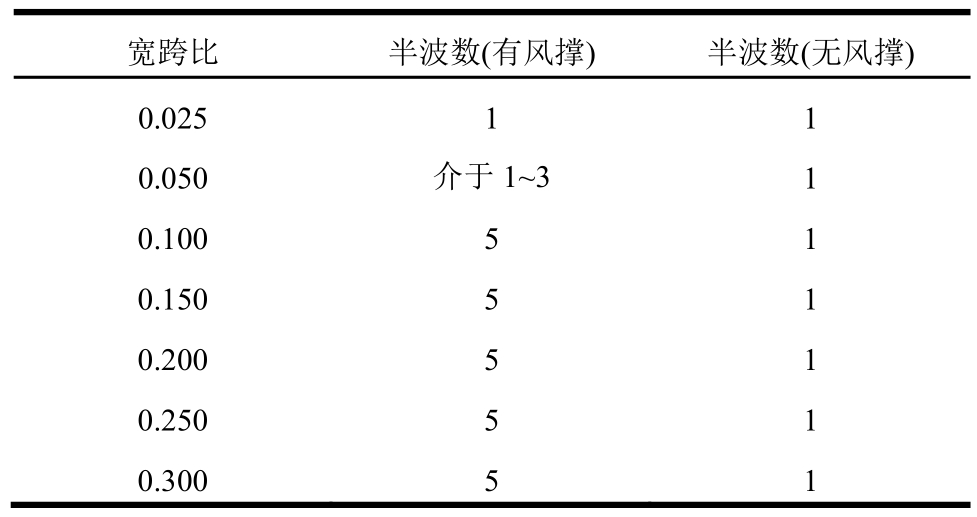
结合图 14与表 4分析，在模型宽跨比从0.025～0.100变化的区间内，随宽跨比增大，抗扭刚度与横向刚度均急剧增大，屈曲半波数同时增大，P2/P1大幅提升。在宽跨比0.1～0.3的区间上，横向刚度与抗扭刚度只有小幅提高，屈曲半波数不再变化，此时P2/P1只有小幅提升。

在加装风撑后，随宽跨比增大，横向刚度随之提高，P2/P1只升不降，这与无风撑时进行的宽跨比参数分析情况相反，造成这一现象的原因为：加装风撑前下弦杆之间无联系，两榀主桁不能协同受力，增加桥梁宽度只会使联系主桁的横梁结构刚度下降，两榀主桁之间的联系变得更弱，进而导致横向刚度与稳定性被削弱，由3.1节可知，加装风撑后，两榀主桁得到有效联系，此时增大宽跨比自然会提高横向刚度与稳定性。

4.4 小结

结合第4节与前文内容，可知：1) 抗扭刚度与横向刚度共同影响整桥稳定性，但横向刚度起决定性作用；2) 横向刚度会影响失稳模态，失稳模态对稳定性能有重要影响；3) 在保证两榀主桁得到有效联系的前提下，提高宽跨比可有效提高桁架桥的刚度与稳定性，若无法保证有效联系，提高宽跨比反而对稳定性有不利影响；4) 风撑的作用为加强两榀主桁的联系与提高整桥横向刚度，进而加强桁架桥稳定性。

5 结论

本文对大量半开式桁架桥工程实例进行有限元分析，发现半开式桁架桥上弦杆屈曲后的桥梁失稳模态有显著的横向弯曲与扭转变形，各算例实际状态下的上弦杆屈曲临界力、屈曲模态分析结果与理想模型分析结果存在不同程度的差异，通过分析各算例结构尺寸参数、扭转刚度、横向刚度、风撑尺寸与这一差异的关联，得到以下结论：

(1) 影响半开式桁架桥稳定性的结构尺寸参数是宽跨比，对这一桥型而言，随宽跨比增大，稳定性有增大的趋势；

(2) 宽跨比对稳定性的影响源自其对整桥横向刚度与扭转刚度的影响，两种刚度共同决定整桥稳定性，但横向刚度起决定性作用；

(3) 横向刚度的变化会影响失稳模态(上弦杆屈曲半波数)，当失稳模态发生突变时，整桥稳定性会发生巨大变化，若失稳模态不发生变化，两种刚度的改变对稳定性影响较小；

(4) 对于单座半开式桁架桥，如能保证两榀主桁得到有效联系，则提高宽跨比可有效提高桁架桥的刚度与稳定性，若无法保证有效联系，提高宽跨比反而对稳定性有不利影响；

(5) 加装风撑能有效联系两榀主桁，并加强整桥横向刚度，进而提高整桥稳定性，但风撑对扭转刚度没有影响。

参考文献：

[1]Timoshenko Gere. Theory of elastic stability [M]. 2nd ed. New York: McGraw- Hill, 1961: 107―113.

[2]小西一郎. 钢桥(第九分册) [M]. 北京: 中国铁道出版社, 1981: 87―90.Konishi Ichiro. Steel bridge (9th) [M]. Beijing: China Railway Press House, 1981: 87―90. (in Chinese)

[3]段明德, 黄耀怡. 对铁路 《桥规》 关于半穿式梁计算的建议 [J]. 铁道标准设计通讯, 1984, 27(4): 1―5.Duan Mingde, Huang Yaoyi. Suggestions on the calculation of the semi-dressed beam of railway bridge code [J]. Railway Standard Design, 1984, 27(4): 1―5.(in Chinese)

[4]张方银, 黄剑源. 半穿式桁架桥上弦杆侧向稳定性计算方法的研究[J]. 宁波大学学报(理工版), 1998, 11(2):62―68.Zhang Fangyin, Huang Jianyuan. Study of calculation method on lateral stability of top chord of half-through truss bridge [J]. Journal of Ningbo University (Natural Science & Engineering Edition), 1998, 11(2): 62―68. (in Chinese)

[5]JTS 152―2012, 水运工程钢结构设计规范[S]. 北京:人民交通出版社, 2012.JTS 152―2012, Code for design of steel structures in port and waterway engineering [S]. Beijing: China Communications Press, 2012. (in Chinese)

[6]JTJ 283―99, 港口工程钢结构设计规范[S]. 北京: 人民交通出版社, 2000.JTJ 283―99, Code for design of steel structure in port engineering [S]. Beijing: China Communications Press,2000. (in Chinese)

[7]TB 100091―2017, 铁路桥梁钢结构设计规范[S]. 北京: 中国铁道出版社, 2017.TB 100091―2017, Code for design of steel structure of railway bridge [S]. Beijing: China Railway Publishing House, 2017. (in Chinese)

[8]胡汉舟, 叶梅新. 桥梁事故及教训[J]. 桥梁建设，2002,32(3): 71―75.Hu Hanzhou, Ye Meixin. Bridge accidents and lessons[J]. Bridge Construction, 2002, 32(3): 71―75. (in Chinese)

[9]宋宁, 尹越, 邓楠. 铝合金桁架步行桥设计及侧向稳定性分析[J]. 沈阳理工大学学报, 2011, 30(4): 87―90.Song Ning, Yin Yue, Deng Nan. Design and lateral stability analysis of an aluminum alloy through truss footbridge [J]. Journal of Shenyang Ligong University,2011, 30(4): 87―90. (in Chinese)

[10]张文元, 麦浩, 于海丰. 板式连接中心支撑钢框架结构推覆试验研究[J]. 工程力学, 2017, 34(10):128―138, 167.Zhang Wenyuan, Mai Hao, Yu Haifeng. Pushover tests of steel concentrically braced frameswith gusset plate connections [J]. Engineering Mechanics, 2017, 34(10):128―138, 167. (in Chinese)

[11]Jankowska-Sandberg J, Kołodziej J. Experimental study of steel truss lateral–torsional buckling [J]. Engineering Structures, 2013, 46(46): 165―172.

[12]Biegus A. Trapezoidal sheet as a bracing preventing flat trusses from out-of-plane buckling [J]. Archives of Civil& Mechanical Engineering, 2015, 15(3): 735―741.

STABILITY ANALYSIS OF HALF-THROUGH TRUSS BRIDGE

YUE Zi-xiang , WEN Qing-jie , ZHUO Tao
(School of Mechanics and Civil Engineering , State Key Laboratory for Geomechanics and Deep Underground Engineering,China University of Mining & Technology, Xuzhou, Jiangsu 221116, China)

Abstract:Half-through truss bridges without upper lateral members are vulnerable to out-of-plane buckling of the upper chords. The instability modes caused by upper chords buckling involve obvious lateral bending and torsional deformation. The observed critical buckling load and buckling modes of upper chords are different with theoretical results. Based on FEA analysis, we analyzed some half-through truss bridges, and found that the stability is proportional to the width-span ratio. For those bridges, stability is directly proportional to its width-span ratio. The influence of the width span ratio on the stability was investigated by considering its influence on lateral stiffness and torsional stiffness. The influence of lateral stiffness is more significant, which affects the instability mode of the whole bridge. If the instability mode suddenly changes, the stability performance will change greatly. It is necessary to set effective link between the two main trusses of a bridge.Installing wind braces can effectively link the two main trusses, increase the lateral stiffness, and thus improve the stability, but the wind brace can not increase the torsional stiffness.

Key words:bridge engineering; half-through truss bridge; stability; lateral stiffness; torsional stiffness;width-span ratio; wind braces

中图分类号：TU311.2

文献标志码：A

doi:10.6052/j.issn.1000-4750.2017.04.S052

文章编号：1000-4750(2018)Suppl-0270-08

收稿日期：2017-04-22；修改日期：2017-12-13

基金项目：中国工程建设标准化协会标准《铝合金人行天桥技术规程》编制项目(2013)；中国矿业大学青年科研基金项目(2012QNB28)；国家自然科学基金项目(51108452)

通讯作者：温庆杰(1978―)，男，河南西平人，副教授，博士，硕导，从事高强铝合金桥梁与结构设计理论研究(E-mail: cumtwenqingjie@126.com).

作者简介：岳子翔(1992―)，男，江苏新沂人，硕士生，从事桥梁结构稳定性与可靠性研究(E-mail: 827511232@qq.com);

卓 涛(1994―)，男，江苏新沂人，硕士生，从事BIM在桥梁工程中应用的研究(E-mail: 704107252@qq.com).