图1 车辆-轨道耦合模型侧视图
Fig.1 Side view of vehicle-track coupling model
李林峰，马 蒙，刘维宁，杜林林
(北京交通大学土木建筑工程学院, 北京 100044)
摘 要：为了研究不同激励作用下钢弹簧浮置板轨道的减振效果，该文建立了二维车辆-轨道耦合动力有限元模型，考虑了普通整体道床和钢弹簧浮置板轨道两种轨道型式，对比和分析了在冲击荷载、移动常力和移动列车荷载作用下，两种轨道结构的振动响应，并通过插入损失评价不同荷载作用下钢弹簧浮置板轨道的减振效果。结果表明：① 与移动常力作用相比，冲击荷载会高估钢弹簧浮置板轨道的减振效果。② 与移动单节车辆作用相比，冲击荷载在钢弹簧浮置板轨道自振频率以下频段会低估其减振效果，在125 Hz～400 Hz频段内会高估减振效果。
关键词：减振性能；钢弹簧浮置板轨道；车-轨耦合模型；冲击荷载；列车荷载；插入损失
随着城市轨道交通不断深入人们的生活，车辆运行所带来的环境振动问题也愈加突出[1]。为削弱其影响，常常采用多种减隔振措施，而且对于不同的减隔振措施，也有不同的评价方法[2]。对于轨道减振措施，通常采用两种激励方法来评价轨道减振效果。其一，是采用落锤、落轴等设备施加冲击荷载[3－5]，通常用于实验室试验；其二，是采用移动列车荷载[6－8]，通常用于在线测试评价。插入损失作为轨道减振效果的评价量，并非轨道的固有特性，而是与轨道所受激励条件密切相关的物理量。因此，即使是同一种减振轨道，采用定点冲击荷载和移动列车荷载其插入损失是不同的。这必将导致实验室测试结果与真实在线测试结果之间存在差异。然而目前，尚鲜有文献对这种差异进行定量研究。
本文建立了二维车辆-轨道动力耦合模型，考虑了钢弹簧浮置板轨道和整体道床轨道两种轨道型式，施加了冲击荷载、移动常力、移动列车荷载等3种不同类型的激励，对比分析了冲击荷载和列车荷载作用下两种轨道的动力性能和钢弹簧浮置板轨道的减振效果。
依据文献[9]，将车辆-轨道耦合系统分解成车辆和轨道两个子系统，利用轮轨关系作为两个子系统间的纽带，建立数值模型。车辆系统为包含车体、二系悬挂、转向架、一系悬挂、轮对的 10自由度多刚体系统。轨道系统通过有限元法建立两种模型，分别为整体道床轨道(普通轨道)模型和钢弹簧浮置板轨道模型。整体道床轨道模型视道床与隧道结构为一整体，分为4层，如图1(a)、图2(a)所示，从上至下依次为钢轨、扣件、隧道结构(道床)和围岩；钢弹簧浮置板轨道模型分为6层，如图1(b)、图2(b)所示，从上至下依次为钢轨、扣件、浮置板、钢弹簧、隧道结构和围岩。两种轨道模型的奇数层采用 Timoshenko梁单元模拟，偶数层采用弹簧阻尼单元模拟。
图1 车辆-轨道耦合模型侧视图
Fig.1 Side view of vehicle-track coupling model
轮轨关系采用赫兹接触理论，第j个轮对承受的轮轨相互作用力可表示为：
式中：Z w j (t)为第j轮对的竖向位移；wr j(x,t)为接触点处钢轨的竖向挠度；δ(x)为接触点处钢轨不平顺；K H为赫兹弹簧刚度，可表示为：
式中：E为钢轨弹性模量；ν为钢轨泊松比；Q为垂直轮荷载；R w为车轮半径；R r为接触点处钢轨踏面曲率半径。
综上，车辆-轨道耦合系统动力平衡方程可表示为：
式中：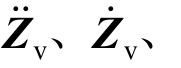
Zv分别为车辆模型的加速度向量、速度向量和位移向量；
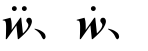w分别为轨道模型的加速度向量、速度和位移向量；M v、C v、Kv分别代表车辆模型的质量矩阵、阻尼矩阵和刚度矩阵；M r、C r、K r分别代表轨道模型的质量矩阵、阻尼矩阵和刚度矩阵。
图2 轨道模型正视图
Fig.2 Front view of track model
依据北京地铁6 m直径标准区间盾构隧道及典型地层情况，对模型计算参数进行设计。在参数确定前，说明以下几点：1) 为准确比较不同激励作用下钢弹簧浮置板轨道的减振效果，钢弹簧浮置板轨道道床与普通轨道道床所采用基底回填混凝土的截面相同(图 2)；2) 因计算模型为假设仅考虑竖向振动的二维平面模型，轨道模型材料参数对应于两股钢轨；3) 将道床及隧道结构横截面等效为矩形截面，在保证其截面几何参数(惯性矩)不变的情况下，对材料参数(密度)进行补偿。另外，车辆模型参考地铁B型车的标准参数，如表1所示。根据以上说明计算得到的整体道床轨道参数如表2所示，钢弹簧浮置板轨道参数如表3所示。
表1 地铁车辆参数
Table 1 Metro vehicle parameters
表2 整体道床轨道参数
Table 2 Parameters of monolithic track
表3 钢弹簧浮置板轨道参数
Table 3 Parameters of steel-spring floating slab track
由表2、表3中的参数，参照文献[10]，计算得到两种轨道模型的基本动力特性：由浮置板及钢弹簧构成的下部体系所决定的特征频率(一阶自振频率)fL=6.476 Hz和由钢轨及扣件系统构成的上部体系所决定的特征频率fU=208.429 Hz。
对于钢弹簧浮置板轨道模型，拾振点选取在模型中部道床板中心位置对应的隧道单元处(图3(a))；对于整体道床轨道模型，拾振点选取在与钢弹簧浮置板轨道模型拾振点相同位置所对应的隧道(道床)单元处(图3(b))。
采用插入损失来评价不同激励作用下钢弹簧浮置板轨道的减振效果[11]，定义为：
式中：Ib e fore为没有采用减隔振措施的振动响应；Ia f ter为采用减隔振措施的振动响应。当IL>0时，说明隔振措施起到了减振的效果；当IL≤0时，说明隔振措施没有起到隔振的效果，反而放大了体系的振动。
图3 拾振点及冲击荷载作用点示意图
Fig.3 Schematic diagram of receiver point and impact loading point
首先分析考虑一个轮对质量的冲击荷载(17 kN)作用下整体道床轨道和钢弹簧浮置板轨道在 1/3倍频程分析域内的动力响应，并将式(4)计算所得的插入损失曲线与现场实测情况进行比对校核，如图4、图5、图6所示。分析可知：1) 由数值模型计算得到的轨道下部体系决定的特性频率f1=5.85 Hz和上部体系决定的特征频率fu=243.652 Hz与2.2节中通过参照文献[10]计算得到的主要特征频率(fL和fU)基本一致。2) 整体道床轨道模型振动加速度级曲线在fu附近达到最大值；浮置板轨道模型振动加速度级曲线分别在f1和fu附近达到最大值和极小值；两者间的插入损失曲线在f1和fu附近分别出现明显的转折，在f1附近达到最小值，且小于0，fu附近达到最大值。3) 现场实测的基底处插入损失曲线与数值模拟拾振点处的插入损失曲线变化情况基本一致。
图4 冲击荷载作用下整体道床轨道与钢弹簧浮置板轨道的加速度级
Fig.4 Acceleration level curves of monolithic track and steel-spring floating track under impact load
图5 测点布置示意图
Fig.5 Schematic diagram of the sensor layout
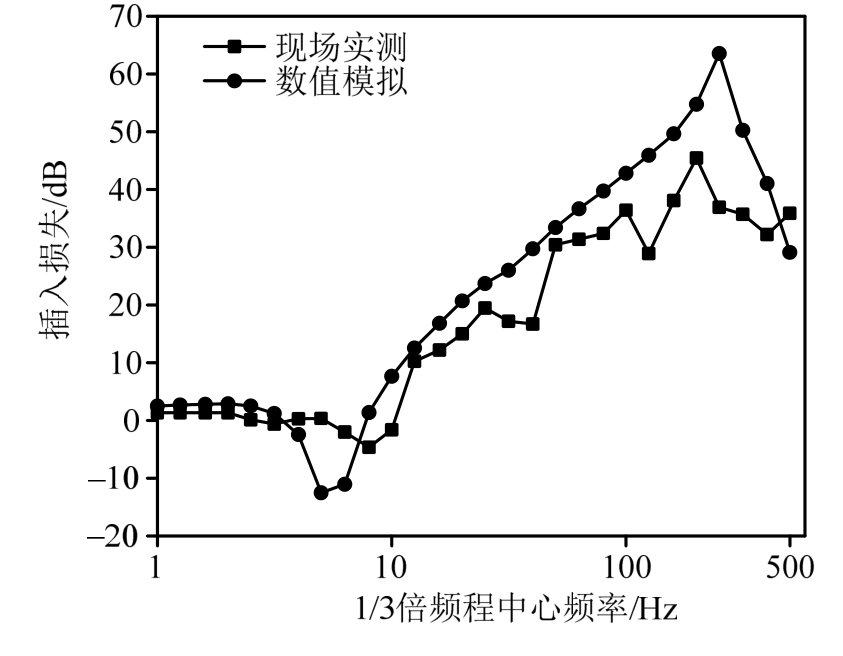
图6 数值模拟与现场实测插入损失曲线对比图
Fig.6 Comparison of insert loss curves between numerical simulation and field measurement
综上，可认为本文中建立的两种轨道模型是准确的。另外由于本文中将冲击荷载作为参与对比分析的两类激励之一，因此在分析中将轨道上部体系的特征频率fu和下部体系的特征频率f1作为重要的频率参考值。
考虑 20 km/h、40 km/h、60 km/h、80 km/h、100 km/h五种移动速度情况，分析移动常力(17 kN)作用下两种轨道模型的动力响应(图7、图8、图9)。其中计算加速度级的参考加速度取10-6m/s2。
由图7可知，整体道床轨道模型中，与移动速度和扣件间距相关的1阶特征频率随速度的增加而增长，其对应的加速度级也随速度的增加而增大。即加速度级曲线随车速的增大具有较为明显的“右移”特性。
由图8可知，钢弹簧浮置板轨道模型中，与轨道下部体系相关的1阶特征频率f1不随速度的变化而发生改变，但对应的加速度级随速度的增加而增大。
图7 移动常力作用下整体道床轨道的加速度级
Fig.7 Acceleration level curves of monolithic track under moving constant force
图8 移动常力下钢弹簧浮置板轨道的加速度级
Fig.8 Acceleration level curves of steel-spring floating slab track under moving constant load
由图9可知，不同速度移动常力作用下的插入损失曲线，其第1个波谷与钢弹簧浮置板轨道的1阶特征频率值f1有关，位置不随速度的增大而改变，其第 1个波峰与整体道床轨道的 1阶特征频率有关，位置随速度的增大而向右移动；另外，在全频段内冲击荷载作用下的插入损失大于移动常力作用下的插入损失，即冲击荷载作用与移动常力作用相比，会高估钢弹簧浮置板轨道的减振效果。
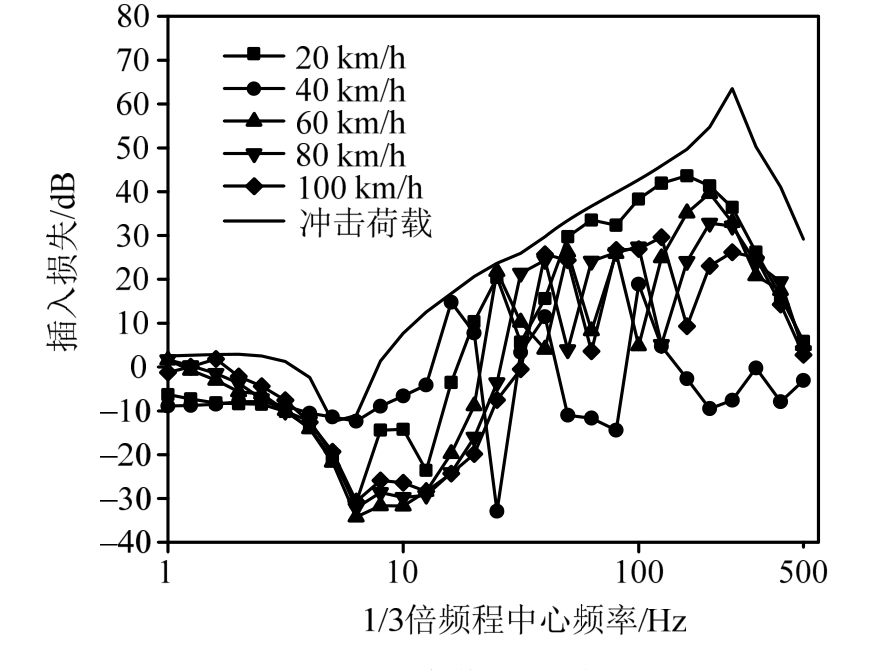
图9 冲击荷载与移动常力作用下拾振点的插入损失
Fig.9 Insert loss curves of receiver point under impact load and moving constant load
与移动常力作用相似，同样考虑 5种车速(20 km/h、40 km/h、60 km/h、80 km/h、100 km/h)情况下拾振点的插入损失，在模型中同时考虑了有轨道不平顺和无轨道不平顺两种情况。
如图 10所示，与移动常力作用相比，移动单节车辆(无不平顺)作用下插入损失曲线更趋近于冲击荷载作用下的插入损失曲线，在fl附近达到最小值，fu附近达到最大值。另外，与冲击荷载作用下的插入损失曲线进行对比可发现，10 Hz(浮置板轨道1阶自振频率)以下的频率范围，插入损失大于冲击荷载的插入损失；在125 Hz～400 Hz频率范围，插入损失小于冲击荷载的插入损失；其它频率范围，插入损失与冲击荷载的插入损失基本相同。综上，移动车辆(无不平顺)作用下，在 f1附近以下的频段(<10 Hz),冲击荷载会低估钢弹簧浮置板的减振效果；在 fu附近的频段(125 Hz～400 Hz)，冲击荷载会高估钢弹簧浮置板轨道的减振效果，其余频段两种作用对减振效果的评估基本相同。
图10 移动单节车辆(无不平顺)拾振点的插入损失
Fig.10 Insert loss curves of receiver point under moving single vehicle (without irregularity)
对于有轨道不平顺的情况，采用美国5级谱作为激励，依然考虑车速为 20 km/h、40 km/h、60 km/h、80 km/h、100 km/h五种情况下拾振点的插入损失(图11)。与移动单节车辆(无不平顺)作用相比，两者插入损失曲线基本呈现相同的规律，但在>10 Hz的频段，插入损失曲线更趋近于冲击荷载作用下的插入损失曲线，<10 Hz的频段，插入损失曲线分布变化明显，以车速60 km/h为例，插入损失相差约10 dB。综上，“有轨道不平顺”和“无轨道不平顺”两种情况下，插入损失曲线基本呈现相同的规律，但“有轨道不平顺”对小于10 Hz频段内的插入损失影响较大。
图11 移动单节车辆(有不平顺)拾振点的插入损失
Fig.11 Insert loss curves of receiver point under moving single vehicle (with irregularity)
本文利用二维车-轨耦合有限元模型，对冲击荷载和列车荷载两种激励作用下得到的钢弹簧浮置板轨道减振效果进行了比较和分析，得到以下结论：
(1) 冲击荷载作用与移动常力作用对比后发现，冲击荷载作用下计算得到的插入损失会在全频段内大于移动常力作用下计算得到的插入损失，即冲击荷载与移动常力相比会高估钢弹簧浮置板轨道的减振效果。
(2) 不考虑不平顺影响时，与移动单节车辆作用相比，在<10 Hz的频段，冲击荷载作用会低估钢弹簧浮置板轨道的减振效果；在125 Hz～400 Hz的频段，冲击荷载作用会高估钢弹簧浮置板轨道的减振效果；在其余频段，两种作用下钢弹簧浮置板轨道减振效果基本相同。
(3) 当考虑不平顺时，与结论(2)基本一致。钢弹簧浮置板轨道减振效果在小于10 Hz的频段内变化明显。
参考文献：
[1]刘维宁, 马蒙, 刘卫丰, 等. 我国城市轨道交通环境振动影响的研究现况 [J]. 中国科学: 技术科学, 2016,46(6): 547―559.Liu Weining, Ma Meng, Liu Weifeng, et al. Overview on current research of enviromental vibration influence induced by urban mass transit in China [J]. Scientia Sinica: Technologica, 2016, 46(6): 547―559. (in Chinese)
[2]Lombaert G, Degrande G, François S, et al.Ground-borne vibration due to railway traffic: a review of excitation mechanisms, prediction methods and mitigation measures [J]. Notes on Numerical Fluid Mechanics & Multidisciplinary Design, 2015, 126:253―287.
[3]Ma M, Liu W, Li Y, et al. An experimental study of vibration reduction of a ballasted ladder track [J].Proceedings of the Institution of Mechanical Engineers,Part F: Journal of Rail and Rapid Transit, 2017, 231(9):1035―1047.
[4]王文斌. 基于脉冲实验的地铁环境振动响应传递函数预测方法研究 [D]. 北京: 北京交通大学, 2011.Wang Wenbin. Study on metro train-induced enviromental vibration and transfer function prediction based on pulse experiment Method [D]. Beijing: Beijing Jiaotong University, 2011. (in Chinese)
[5]金浩, 刘维宁. 枕下减振垫铺设方式对梯式轨道减振性能影响试验研究 [J]. 土木工程学报, 2015, 48(2):73―78.Jin Hao, Liu Weining. Experimental study on vibration reduction characteristics of ladder track with different arrangement of sleeper pads [J]. China Civil Engineering Journal, 2015, 48(2): 73―78. (in Chinese)
[6]李克飞, 刘维宁, 孙晓静, 等. 北京地铁5号线地下线减振措施现场测试与分析[J]. 铁道学报, 2011, 33(4):112―118.Li Kefei, Liu Weining, Sun Xiaojing, et al. In-situ test of vibration attenuation of underground line of Beijing metro line 5 [J]. Journal of the China Railway Society,2011, 33(4): 112―118. (in Chinese)
[7]Ma M, Liu W, Qian C, et al. Study of the train-induced vibration impact on a historic Bell Tower above two spatially overlapping metro lines [J]. Soil Dynamics and Earthquake Engineering, 2016, 81: 58―74.
[8]谷爱军, 张宏亮. 钢弹簧浮置板轨道结构在不同频段的隔振效率 [J]. 噪声与振动控制, 2009, 21(1): 39―42.Gu Aijun, Zhang Hongliang. Analyses of vobration isolation effect in different frequency band for steel-spring floating slab track [J]. Noise and Vibration Control, 2009, 21(1): 39―42. (in Chinese)
[9]Xia H, Cao Y M, Zhang N. Numerical analysis of vibration effects of metro trains on surrounding environment [J]. Proceedings of the International Journal of Structural Stability and Dynamics, 2007, 7(1): 151―166.
[10]马龙祥. 基于无限—周期结构理论的车轨耦合及隧道—地层振动响应分析模型研究[D]. 北京: 北京交通大学, 2015.Ma Longxiang. Study on the model of coupled vehocle& track and the prediction model for tunnel-ground vibration response based on the periodic-infinite structure theory [D]. Beijing: Beijing Jiaotong University, 2015. (in Chinese).
[11]刘维宁, 丁德云, 李克飞, 等. 钢弹簧浮置板轨道低频特征试验研究[J]. 土木工程学报, 2011, 44(8): 118―125.Liu Weining, Ding Deyun, Li Kefei, et al. Experimental study of the low-frequency vibration characteristics of steel spring floating slab track [J]. China Civil Engineering Journal, 2011, 44(8): 118―125. (in Chinese)
ANALYSIS FOR THE VIBRATION REDUCTION CHARACTERISTICS OF STEEL SPRING FLOATING SLAB TRACKS UNDER DIFFERENT TYPES OF EXCITATION
LI Lin-feng , MA Meng , LIU Wei-ning , DU Lin-lin
(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract:To investigate the vibration reduction characteristics of steel spring floating slab tracks (FSTs) under different types of excitation, a two-dimensional train-track coupling dynamic finite element model was established, and two kinds of track types of monolithic track and spring steel floating slab track were considered.The impact load, the moving constant load and the train load were used to study the vibration responses of the track structure in terms of insert loss. The results indicated that: 1) Compared with the moving constant load, the impact load overestimated the vibration reduction characteristics of FSTs; 2) Compared with the moving single vehicle, the vibration reduction characteristics of FSTs was underestimated below FST natural frequency under the impact load and was overestimated between 125 Hz and 400 Hz.
Key words:vibration reduction effect; steel-spring floating slab track; train-track coupled model; impact load;train load; insert loss
中图分类号：U211.3
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.05.S048
文章编号：1000-4750(2018)Suppl-0253-06
收稿日期：2017-05-27；修改日期：2017-11-14
基金项目：国家自然科学基金项目(51508022)
通讯作者：李林峰(1990―)，男，黑龙江大庆人，博士生，主要从事环境振动与隧道结构动力学研究(E-mail: rooneyisthebest@163.com).
作者简介：马 蒙(1983―)，男，四川成都人，副教授，博士，主要从事轨道交通环境振动研究(E-mail: mameng@bjtu.edu.cn);
刘维宁(1960―)，男，江西人，教授，博士，主要从事地下工程与铁道工程研究(E-mail: wnliu@bjtu.edu.cn);
杜林林(1988―)，男，河南周口人，博士生，主要从事车辆轨道耦合模型和环境振动研究(E-mail: linlindu07@163.com).