
图1 映秀-汶川二级路皂角湾桥梁体平转
Fig.1 Zaojiawan Bridge body flat turn
焦驰宇1,3,胡 彪1,刘陆宇1,龙佩恒2
(1. 北京建筑大学未来城市设计高精尖创新中心,北京 100044;2. 北京建筑大学工程结构与新材料北京市高等学校工程研究中心,北京 100044;3. 同济大学土木工程防灾国家重点实验室,上海 200092)
摘 要:目前已有大量针对曲线桥主梁建模方法的研究,但其实用性仍存在一些不足,特别是缺乏针对不同下部结构形式的主梁数值模拟方法适用范围的探讨。该文以京开立交某匝道桥为工程原型,建立不同曲率半径、桥面宽度以及下部支承形式的曲线桥主梁数值分析模型,并以曲线桥边墩支座变形及中墩墩底剪力作为关键结构响应,探讨单梁法、脊梁法、梁格法模型在桥梁地震反应中的误差规律。该文研究结果针对不同类型曲线桥的主梁建模方法提出了合理化的建议,对曲线桥在抗震设计中提高建模的精度和效率具有重要意义。
关键词:曲线桥;主梁;建模方法;曲率半径;跨宽比;下部支承形式
近年来我国交通事业发展迅速,曲线桥由于能够较大程度地满足复杂交通路线的要求,故被广泛应用于城市立交和山区道路,而这些地区必须充分考虑桥梁的抗震性能。然而与直线桥相比,曲线桥动力特性更为复杂,对抗震设计的要求也更高。杜俢力等[1]提出,曲线桥在地震中发生落梁和垮塌主要由支座变位以及墩柱内力超限所致。2008年汶川地震中,映秀-汶川二级路的皂角湾桥曲线梁桥由于支座产生不可恢复位移而使主梁发生横向移位震害[2],如图1所示。基于上述问题的严峻性,国内外专家[3-6]对曲线桥主梁的建模方法开展了相关研究,但目前针对不同结构参数的曲线桥主梁,还缺乏不同建模方法的对比研究。基于此,本文拟通过建立不同跨宽比、不同曲率半径以及不同墩柱形式的多重结构参数耦合的桥梁模型,对比其由不同主梁数值模拟方法导致的结构地震响应分析的差异。旨在针对不同类型曲线桥的主梁建模方法提出合理化的建议,提高曲线桥在抗震设计中建模的精度和效率。

图1 映秀-汶川二级路皂角湾桥梁体平转
Fig.1 Zaojiawan Bridge body flat turn
在本文中,笔者结合实际工程情况及分析的需要,在以往研究[7]的基础上,在保持曲线桥其他参数不变的条件下,通过拟定不同的曲率半径R、跨宽比L/B、下部支承形式的曲线桥结构,并基于OpenSEES进行建模分析。在满足一定精度的前提下,探讨不同结构类型曲线桥主梁建模方法的适用范围。
本文选取京开路立交 A匝道桥两联中的一联作为工程原型,其结构形式详见图2~图4,设计参数见表1。
表1 桥梁抗震设计参数
Table 1 Bridge seismic design parameters

1.2.1 结构参数的确定
国内学者兰燕等[8]等研究表明,独柱墩曲线桥抵抗弯扭能力与双柱墩曲线桥相比存在较大差异。基于此,本文以上述单箱双室曲线梁桥作为基准,在保持上部结构形式不变的条件下,中墩分别采用独柱墩和双柱墩的结构形式,实现两类桥梁结构的对比研究。此外,由《城市桥梁抗震设计规范》[9]可知,由于曲率半径R和跨宽比L/B是影响其地震响应的主要因素,故在保持总跨径不变的条件下,改变曲率变径R和桥宽B,开展变参数研究。

图2 京开立交桥A匝道平面图 /cm
Fig.2 Jing-Kai Ramp A viaduct ichnography
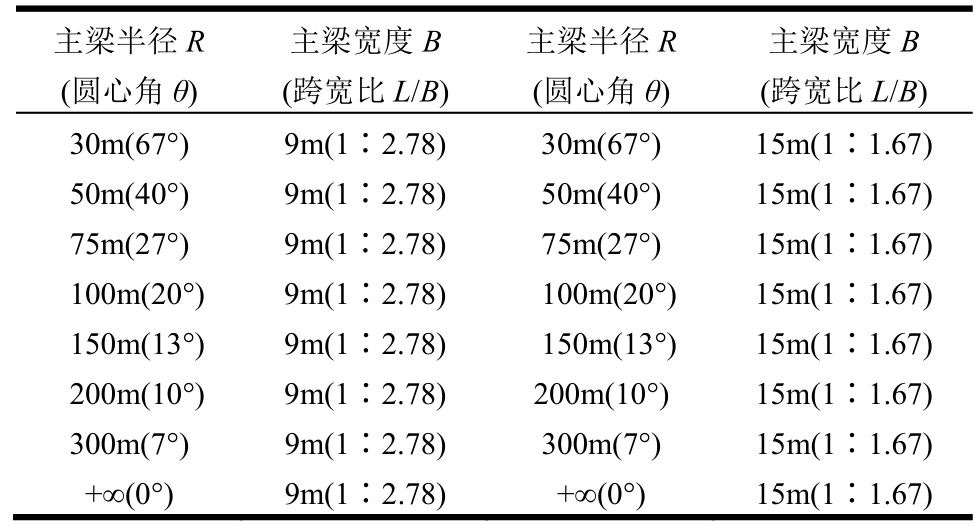
综上,本文建立下部结构为独柱墩、双柱墩的两种支承形式,上部结构以主梁的曲率半径R、宽度B为重要结构变量的曲线桥梁模型,开展变参数研究(曲率半径R分别设置为30 m、50 m、75 m、100 m、150 m、200 m、300 m、+∞;主梁宽度B分别设置为9 m,15 m),共建立32组有限元模型,具体如表2所示。

图3 边墩柱及基础尺寸图 /cm
Fig.3 Side pier and foundation dimensions
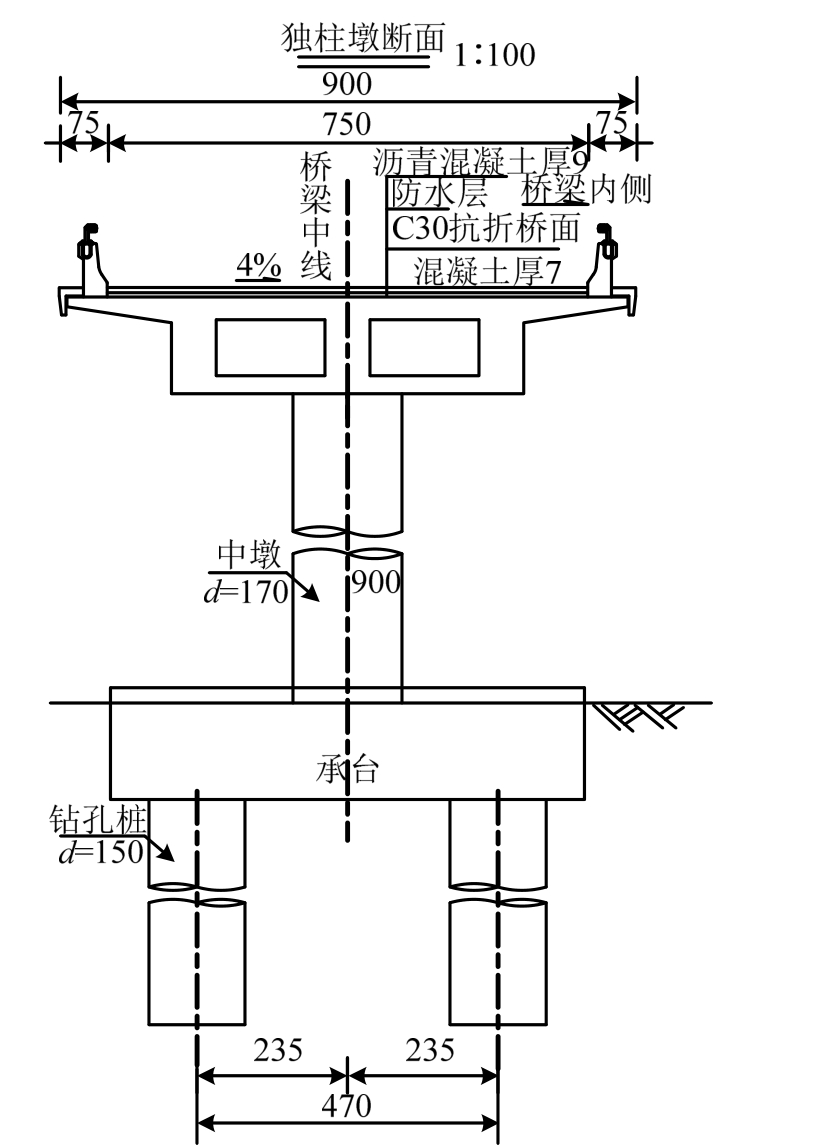
图4 中墩柱及基础尺寸图 /cm
Fig.4 Middle pier and foundation dimensions
表2 曲线桥主梁变参数表(以中墩独柱墩为例)
Table 2 Main girder variable parameter of curved bridge(Taking the middle pier as an example)
1.2.2 关键地震响应的选取
历次震害表明:曲线桥的震害主要表现为桥墩及支座的损坏[10],因此选取边墩支座变形及中墩底剪力作为关键结构响应,对比单梁法、脊梁法、梁格法所建模型在地震反应中的精度差异。
为揭示强震下桥梁的损伤机理,依据《城市桥梁抗震设计规范》[9],选取E2地震下的3组人工地震波输入,按照曲线桥两端连线方向和垂直于两端连线方向进行最不利方向的地震输入。具体地震动参数为:设防烈度8度,Kh=0.20;场地条件II类,Tg=0.35 s,Ci=0.45,Cz=0.33。本文采用E2地震反应谱及拟合的人工地震波,如图5、图6所示。
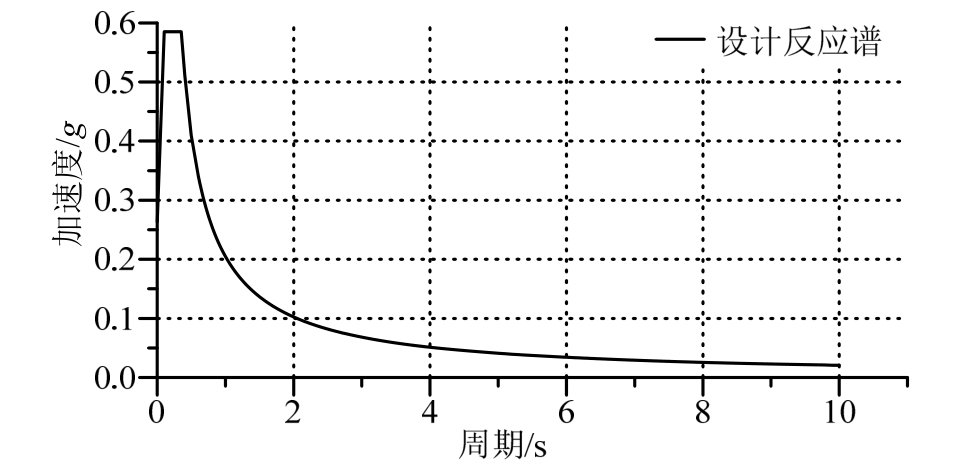
图5 地震设计反应谱
Fig.5 Earthquake response spectrum
1) 单梁法
单梁法[11]是将主梁模拟为集中于其形心处的梁单元,并假定受力后该桥梁横截面不发生翘曲变形,且截面形状保持不变。其理论简单,建模方法简便,易于计算且效率高。但该方法将结构的质量刚度集中于形心,没有考虑主梁横截面的畸变,翘曲。如图7所示。
2) 脊梁法
脊梁法[12]的基本模型及力学特性与单根梁模型类似,但在单梁法的基础上,其又在半截面质心位置设置节点,将上部结构恒载集中在此节点,并把这些分布两侧的节点同主梁主节点刚性连接。脊梁模型在单梁模型的基础上可以考虑主梁质量沿横桥向的不均匀分布。如图8所示。

图6 地震波时程(第一组)
Fig.6 Earthquake wave duration (group 1)

图7 单梁法模型
Fig.7 Single-girder method model
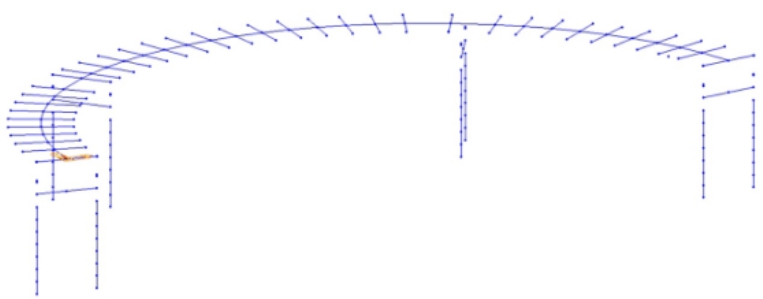
图8 脊梁法模型
Fig.8 Spine method model
3) 梁格法
梁格法的基本原理为[11]:将主梁用等效的平面梁格或空间结构来模拟,主梁的抗弯、抗扭刚度集中在其相应的梁格中。当梁格模型和原型结构所受荷载相同时,两者挠曲变形相等,且对应梁格的内力与实际截面的受力等相同或接近。该法充分考虑了结构质量和刚度的不均匀分布。如图9所示。
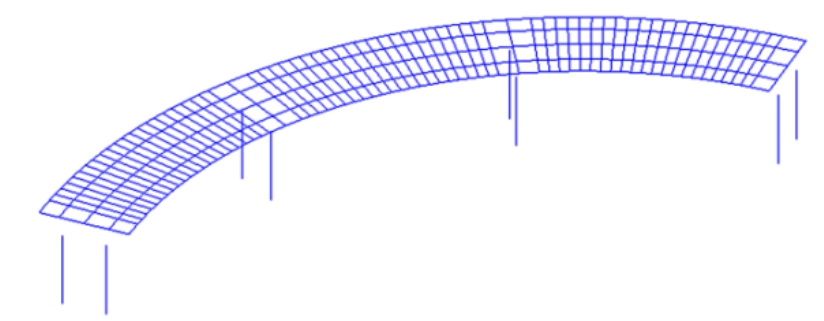
图9 梁格法模型
Fig.9 Grillage method model
从建模难度和计算速度上可以看出:梁格法>脊梁法>单梁法。但 3种建模方法的精度存在多大差异?还需要通过对不同结构形式的曲线桥进行地震响应分析,并在满足精度要求的前提下,给出不同建模方法的适用范围。
曲线桥下部结构支承形式:边墩采用双柱墩且支座选用板式橡胶支座;中墩采用独柱墩,桥墩与上部结构固结,其下部结构布置形式如图10所示。分别用3种数值模拟方法建立曲线桥模型,假定梁格模型最为精确,以此为基础,将单梁、脊梁模型的计算结果与其对比分析。其中模型的边界条件为:支座采用节点弹性连接,墩梁之间采用刚性连接。

图10 下部结构布置
Fig.10 Layout of the lower structure
为更直接地反映不同建模方法的误差与跨宽比L/B关系,将相同跨宽比下各地震响应参数的计算结果取平均,如图11~图12所示。

图11 单梁法边支座变形及中墩剪力模型误差与跨宽比关系图
Fig.11 Single-girder method side support deformation and middle pier shear error and span ratio diagram
注:x为顺桥向结构响应;y为横桥向结构响应。
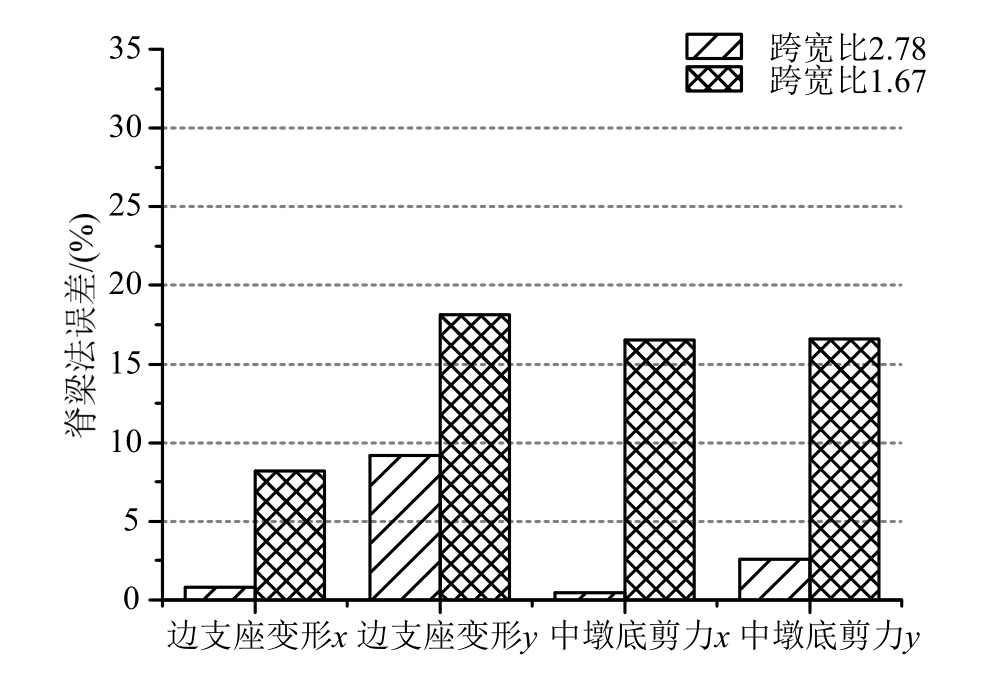
图12 脊梁法边支座变形及中墩剪力模型误差与跨宽比关系图
Fig.12 Spine method side support deformation and middle pier shear error and span ratio diagram
注:x为顺桥向结构响应;y为横桥向结构响应。
表3 边支座变形及中墩剪力与圆心角的关系
Table 3 Side support deformation and the middle of the pier shear force with the relationship between the central angle

对于中墩为独柱墩的曲线桥模型,经对比表 3后发现规律如下:
1) 边支座变形的误差规律不明显。可看出 3种建模方法模拟出的顺桥向边支座变形误差基本上随曲率半径R的增大而减小。且单梁模型误差大于脊梁模型(少数离散点除外),横桥向边支座变形的误差规律与之相反。总体来看,平均误差随跨宽比的降低而增加。
2) 中墩底剪力的误差规律较明显。可看出单梁、脊梁模型与梁格模型的误差基本上随曲率半径R的增大而减小(个别特异点除外),且脊梁模型误差小于单梁模型。另外,平均误差随跨宽比L/B的降低而增加,桥宽9 m时误差均小于10%,桥宽15 m时误差均大于15%。
为与前述模型对比,将曲线桥下部结构改为边墩及中墩均采用双柱墩板式橡胶支座的结构形式,其下部结构布置形式如图 13所示。考虑墩柱弹塑性抗震性能作用,假定梁格模型计算结果最为准确,将单梁、脊梁模型与其计算结果进行对比分析。

图13 下部结构布置图
Fig.13 Layout of the lower structure
为更直观反映不同建模方法的误差与跨宽比L/B关系,将相同跨宽比下各地震响应参数的计算结果取平均,汇总如图14、图15所示。

图14 单梁法边支座变形及中墩剪力模型误差与跨宽比关系图
Fig.14 Single-girder method side support deformation and middle pier shear error and span ratio diagram
注:x为顺桥向结构响应;y为横桥向结构响应。
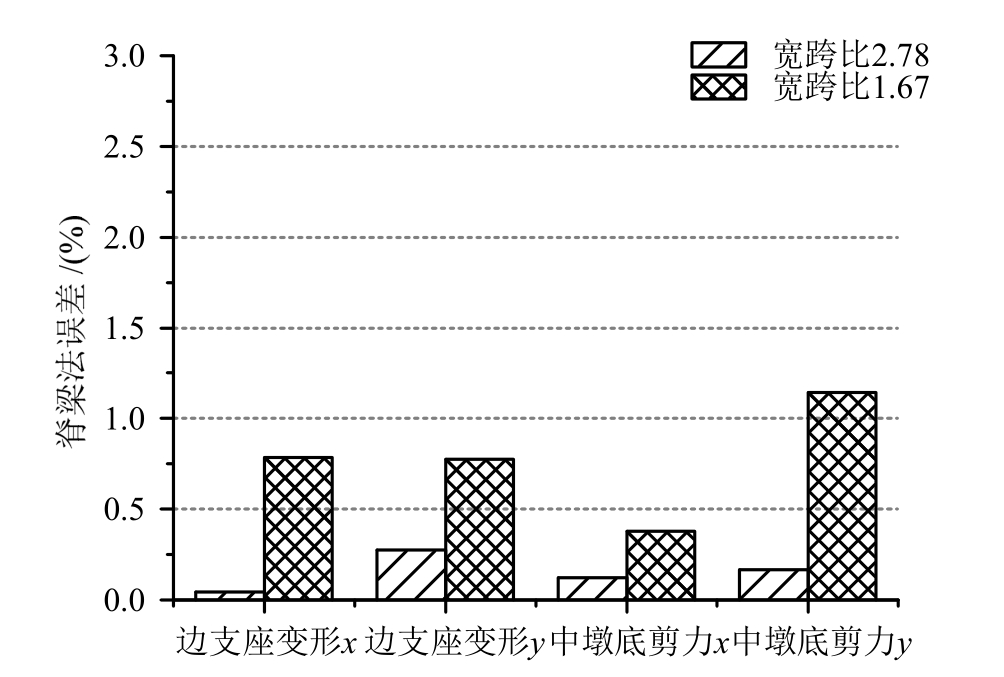
图15 脊梁法边支座变形及中墩剪力模型误差与跨宽比关系图
Fig.15 Spine method side support deformation and middle pier shear error and span ratio diagram
注:x为顺桥向结构响应;y为横桥向结构响应。
表4 边支座变形及中墩剪力误差与圆心角关系图
Table 4 Side support deformation and the middle of the pier shear force with the relationship between the central angle

对于中墩为双柱墩的曲线桥模型,经对比表4后发现规律如下:
3种建模方法模拟出的边支座变形和中墩底剪力间的误差都具有较为明显的规律。可看出单梁、脊梁模型与梁格模型误差基本随曲率半径R的降低而降低,且单梁模型误差大于脊梁模型(少数离散点除外)。除当曲线桥圆心角θ>40°且跨宽比L/B=1.67时,单梁模型中边支座顺桥向变形误差大于10%外,其余情况误差均小于10%;而脊梁模型误差均未超过 3%,因而当全桥均采用双柱墩时,曲线桥抗震的分析可仅采用单梁法。
对比分析不同数值模拟方法的模型计算结果,不难得出以下结论:
(1) 下部支承形式为中墩采用双柱墩的曲线桥,其关键结构参数的地震响应受主梁模拟方法影响很小,采用单梁法基本可满足曲线桥建模的精度要求。其原因主要是:独柱墩曲线桥抗扭主要受主梁刚度影响,而双柱墩曲线桥抗扭主要由墩柱决定,主梁的参与度较小。
(2) 下部支承形式为中墩采用独柱墩的曲线桥,其地震响应有较为明显的规律。即对墩底剪力而言:圆心角θ越大,跨宽比越小,单梁法误差越大;同单梁法相比,脊梁法除整体误差偏小以外,其它误差规律相同;其中最主要的影响因素是跨宽比L/B。边支座变形的误差规律表现为:横桥向的误差规律为圆心角越小,跨宽比越小,单梁法误差越大;顺桥向地震响应的误差规律同墩底剪力的规律。其原因在于曲线桥圆心角越大,横向地震作用对于梁端横向位移的贡献就越小,从而造成单梁及脊梁模型误差整体偏小。
参考相关文献[7]可知,在建模分析中多以90%的概率做为近似保证率,故将单梁法、脊梁法模型与梁格法模型做对比,分析误差不超过10%的曲线桥结构形式,并根据以上研究结果,给出了针对中墩为独柱墩的支承形式下,不同曲线桥型主梁建模方法适用表格,如表5所示(其中1为单梁法,2为脊梁法,3为梁格法)。
(3) 通过对以上3种建模方法的分析,其建模的难易程度及精度总结如表6所示,用户可根据本研究所得结论,结合实际情况选取对应的曲线桥主梁建模方法。
表5 主梁合理建模方法适用表格
Table 5 Applicable table of reasonable modeling method for main girder
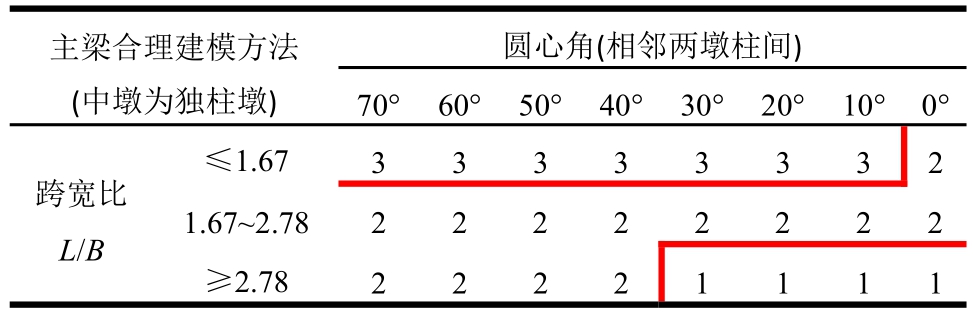
表6 曲线桥主梁建模方法汇总表格
Table 6 Curved bridge main girder modeling method summary table

归纳以上所得结论,汇总不同墩柱形式的曲线桥主梁建模流程如图16所示。
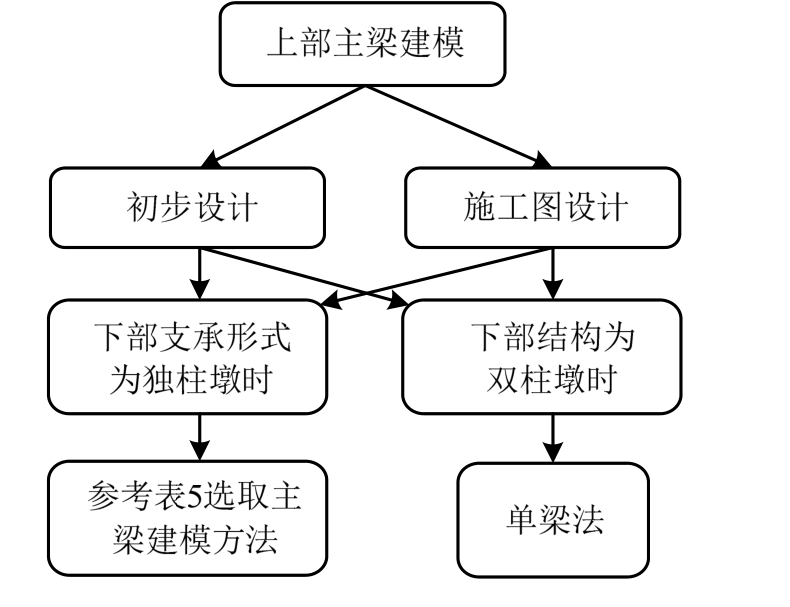
图16 曲线桥主梁建模流程图
Fig.16 Curved bridge girder modeling flow
参考文献:
[1]杜修力, 韩强, 李忠献, 等. 5.12 汶川地震中山区公路桥梁震害及启示 [J].北京工业大学学报, 2008, 34(12):1270―1279.Du Xiuli, Han Qiang, Li Zhongxian, et al. Earthquake damage and ts implications for highway bridges in Wenchuan earthquake [J]. Journal of Beijing University of Technology, 2008, 34 (12): 1270―1279. (in Chinese)
[2]庄卫林, 刘振宇, 蒋劲松. 汶川大地震公路桥梁震害分析及对策 [J]. 岩石力学与工程学报, 2009, 28(7):1377―1387.Zhuang Weilin, Liu Zhenyu, Jiang Jinsong. Earthquake damage analysis and countermeasures of Wenchuan earthquake of highway bridges [J]. Journal of Rock Mechanics and Engineering, 2009, 28 (7):1377―1387.(in Chinese)
[3]李国豪, 石栋, Heins C P. 曲梁桥地震分析的有限单元法[J]. 同济大学学报(自然科学版), 1984 (1): 4―24.Li Guohao, Shi Dong, Heins CP. Finite element method for earthquake analysis of curved girder bridge [J].Journal of Tongji University (Natural Science Edition),1984 (1): 4―24. (in Chinese)
[4]魏双科, 李鸿晶, 罗寒松, 等. 立交桥曲线箱梁动力分析模型[J]. 地震工程与工程振动, 2006, 26(4): 168―174.Wei Shuangke, Li Hongjing, Luo Hansong, et al.Dynamic analysis model of curved box girder of overpass. [J]. Earthquake Engineering and Engineering Vibration, 2006, 26 (4): 168―174. (in Chinese)
[5]曾敏. 小半径曲线梁桥地震响应分析及减隔震研究[D]. 长沙: 中南大学土木建筑学院, 2009.Zeng Min. Earthquake response analysis and seismic isolation research of small radius curved girder bridge[D]. Changsha: School of civil engineering and architecture, Central South University, 2009. (in Chinese)
[6]张培君, 胡世德, 涂雪, 等. 曲线梁桥地震分析中的合理建模 [J]. 中国水运: 下半月, 2012, 12(3): 200―201.Zhang Peijun, Hu Shide, Tu Xue, et al. A rational model for earthquake analysis of curved girder bridges [J]. China Water Transport: Second Half, 2012, 12(3): 200―201. (in Chinese)
[7]郭波. 混凝土曲线梁桥建模分析方法及适用条件研究[D]. 包头 内蒙古科技大学, 2012.Guo Bo. Study on the modeling and analysis method of concrete curved girder bridge and its applicable conditions [D]. Baotou: Inner Mongolia University of Science and Technology, 2012. (in Chinese)
[8]兰燕.桥墩造型及其抗震性能研究[D]. 西安: 长安大学, 2005.Lan Yan. Study on modeling and seismic performance of bridge pier [D]. Xi’an: Chang'an University, 2005. (in Chinese )
[9]CJJ 166―2011, 城市桥梁抗震设计规范[S]. 北京: 中国建筑工业出版社, 2011.CJJ 166―2011, Code for seismic design of urban Bridges [S]. Beijing: China Construction Industry Press,2011. (in Chinese)
[10]侯文杰. 城市曲线桥梁地震反应分析 [D]. 甘肃: 兰州交通大学, 2012.Hou Wenjie. Earthquake response analysis of urban curved bridges [D]. Gansu: LanZhou JiaoTong University,2012. (in Chinese)
[11]焦驰宇, 张羽, 龙鹏恒, 等. 单梁法分析曲线梁桥的适用条件研究 [J]. 工程力学, 2016, 33(增刊 1): 150―155.Jiao Chiyu, Zhang Yu, Long Pengheng, et al. Study on the applicable condition of curved girder bridge by single girder method [J]. Engineering Mechanics, 2016,33(Suppl 1): 150―155. (in Chinese)
[12]刘陆宇. FPS 支座双轴耦合效应及其对曲线桥抗震性能影响研究[D]. 北京: 北京建筑大学, 2016.Liu Luyu. Biaxial coupling effect of FPS bearing and its influence on seismic performance of curved bridge [D].Beijing: BUCEA, 2016. (in Chinese)
STUDY ON REASONABLE NUMERICAL SIMULATION METHOD FOR CURVED BRIDGE GIRDER WITH DIFFERENT PIERS
JIAO Chi-yu1,3, HU Biao1, LIU Lu-yu1, LONG Pei-heng2
(1. Beijing Advanced Innovation Center for Future Urban Design, BUCEA, Beijing 100044, China;2. Engineering Structure and New Materials Engineering Research Center of Beijing High School, BUCEA, Beijing 100044, China;3. State Key Laboratory of Disaster Prevention in Civil Engineering, Tongji University, Shanghai 200092, China
Abstract:At present, a lot of researches on the modeling method of the main girder of the curved bridge have been carried out, but its practicality still has some shortcomings, especially lack of the numerical simulation method of the main girder under different lower parts of the structure. Based on the Jing-Kai overpass, this paper establishes a numerical model of the main girder of the curved bridge with different radius of curvature, bridge width and lower support form. Furthermore, the error law of the single-girder method model, the spine method model and the grillage method model in the bridge earthquake response is discussed by using the deformation of side support and middle pier shear as the key structure. Advices for the main girder modeling method of different types of curved bridges are proposed, which are helpful to improve the modeling accuracy and efficiency in the seismic design of curved bridges.
Key words:curved bridge; main girder; modeling method; radius of curvature; span to width ratio; lower support form
文章编号:1000-4750(2018)Suppl-0246-07
中图分类号:U448.21;U442.55
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.06.S047
收稿日期:2017-06-08;修改日期:2018-01-07
基金项目:北京市自然科学基金面上项目(8162012);北京市优秀人才培养青年拔尖个人项目(2015000026833ZK05);土木工程防灾国家重点实验室开放基金项目(SLDRCE-14-02);建设部研究开发项目(2015-R2-039);北京市教委科技计划面上项目(2013)(KM201310016007);国家青年自然科学基金项目(51508019)
通讯作者:龙佩恒(1964―),男,北京人,教授,博士,主要从事桥梁抗震研究(E-mail: phjz@163.com).
作者简介:焦驰宇(1980―),男,陕西人,副教授,博士,主要从事桥梁抗震研究(E-mail: jcy@bucea.edu.cn);
胡 彪(1991―),男,山东人,硕士生,主要从事桥梁抗震研究(E-mail:tm2281732719@163.com);
刘陆宇(1990―),男,北京人,硕士生,主要从事桥梁抗震研究(E-mail:410197804@qq.com).