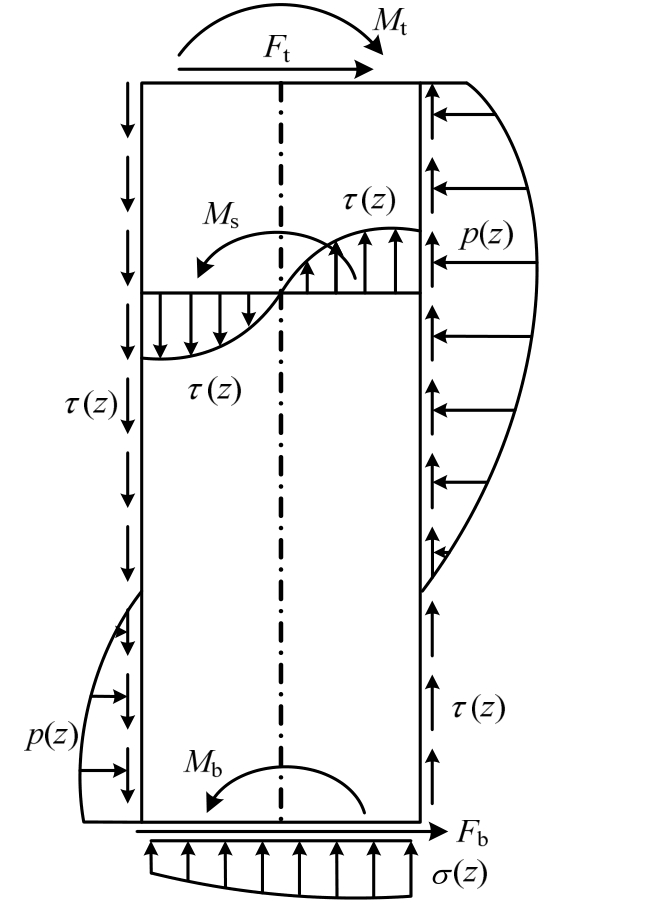
图1 大直径桩基受力示意图
Fig.1 Force diagram for large-diameter pile foundation
竺明星1,龚维明2,卢红前1,王 磊1
(1. 中国能源建设集团江苏省电力设计院有限公司,江苏,南京 211102;2. 东南大学土木工程学院,江苏,南京 210096)
摘 要:为研究桩侧竖向摩阻力、桩端竖向阻力及水平剪应力对基桩水平承载特性的影响,该文首先根据桩侧摩阻力三折线τ-s曲线推导得出了附加弯矩-转角本构模型线性解析表达式。随后在四弹簧模型基础上结合该文所提出的桩侧、桩端附加弯矩以及桩端水平剪力本构关系进而建立桩身受力微分方程,并采用Laplace变换解得桩身弹性、塑性段的传递矩阵系数解析解。最后在给出的迭代求解方法基础上进而求得考虑侧阻与端阻影响的基桩水平承载力响应解。通过两组案例对比分析不但验证了该文推导的正确性,也证明了该文所提出的桩侧、桩端附加弯矩以及桩端水平剪力本构模型的合理性;同时结果也表明当地基土体较好、桩径较大时桩侧附加弯矩Ms、桩端附加弯矩Mb和剪力Fb对水平承载特性影响不可忽略。
关键词:桩基;水平承载特性;附加弯矩;四弹簧模型;传递矩阵法
基于Winkler地基梁模型的p-y曲线法是目前求解水平受荷桩最常用的方法[1]。然而弹性地基梁的一维杆单元假设使得计算模型不能考虑桩径尺寸的影响。事实上,随着桩径尺寸的增加,大直径单桩水平承载特性的尺寸效应将逐渐凸显[2],此时桩侧竖向摩阻力、桩端竖向应力与水平阻力对桩身响应影响越来越显著,如图1所示。

图1 大直径桩基受力示意图
Fig.1 Force diagram for large-diameter pile foundation
Dodds等[2]、Lam 等[3]认为桩侧竖向摩阻力形成的力偶作用随着桩径、桩身截面转角的增加而显著,并将该力偶作用定义为附加弯矩。Mcvay等[4]开展了嵌岩桩中桩侧竖向摩阻力对水平承载力影响的离心实验研究,结果表明嵌岩桩中较高的竖向摩阻力产生的附加弯矩影响不能忽略,并提出了附加弯矩计算方法。王伯惠等[5]认为大直径桩或刚性短桩需要考虑桩端基底土抗力产生的附加弯矩作用,并给出了基底附加弯矩的理论计算公式。Ashour等[6]建立了大直径灌注桩侧竖向摩阻力产生的附加弯矩和桩端底部水平剪力的理论公式,并基于应变楔理论解得桩身响应。然而,上述研究均只考虑图1所示影响因素中的部分因素。Alikhanlou[7]基于能量法开展了图1所示的超大直径基础承载特性研究,计算结果表明考虑这些影响因素的计算结果与实测值更接近。Gerolymos等[8]、Varun等[9]提出考虑如图 1所示考虑所有影响因素的四弹簧模型,并解得地基土体为线弹性时的沉井基础水平变形特性。然而这些研究成果均将地基土体假设为线弹性模型,当荷载水平较大时,这些理论计算所得结果将明显偏小。
本文在四弹簧模型基础上,桩土相互作用采用能够考虑土体非线性、塑性特性的p-y曲线模型;桩侧竖向摩阻力采用能够考虑土体硬化、软化影响的三折线τ-s曲线模型,并据此推导得出桩侧竖向摩阻力作用下的Ms-θ(附加弯矩-转角)计算模型;最后,分别建立大直径桩端底部Fb-yb(桩端水平剪力-位移)和Mb-θb(桩端附加弯矩-转角)计算模型,并结合Laplace正逆变换求得考虑侧阻与端阻影响时的桩基水平承载力传递矩阵解。通过两组案例对比分析验证了本文研究的合理性与正确性。
如图2所示,总桩长为L,桩长范围内共有n层地基土,则每层地基土内桩长、桩径和抗弯刚度分别为Hi、di和EIi。桩顶分别作用水平力Ft和弯矩Mt作用。桩土相互作用、桩端底部水平剪力Fb以及桩侧和桩端附加弯矩Ms、Mb均采用弹簧单元模拟。推导过程中假定桩身变形y以向右为正;转角θ以逆时针旋转为正;水平力以绕研究对象顺时针旋转为正;弯矩作用以研究对象右侧受压为正;土抗力以向左为正。

图2 大直径桩基受力示意图
Fig.2 Force diagram for large-diameter pile foundation
肖宏彬[10]在大直径桩基荷载传递机理研究过程中提出一种三折线τ-s曲线模型,如图3所示。该模型既能考虑桩侧摩阻力硬化、软化的情况,也可以模拟线弹性-塑性和双曲线模型,因而具有较好的通用性,本文采用该三折线τ-s曲线模拟桩侧摩阻力发挥,如下式所示:

式中:τ/kPa为侧摩阻力值;s/m为桩土竖向相对位移值;λ1/(kN/m3)、λ2/(kN/m3)和λ3/(kN/m3)分别为每段折线的斜率;su1为第1段与第2段折线的位移界限值;su2为第2段与第3段折线的临界相对位移值。
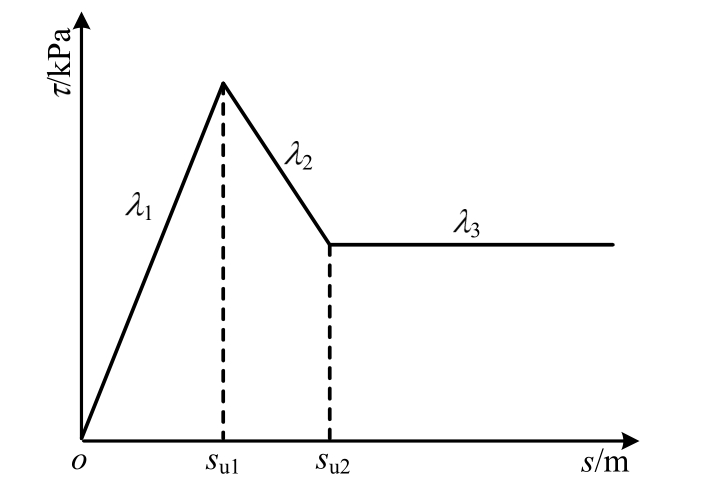
图3 三折线τ-s曲线模型Fig.3 Trilinearτ-scurve model
取图1所示任意位置处的桩身横截面,离散后如图4所示。考虑到水平荷载作用下土压力主动侧土体会与桩身脱离[6,11],从偏于安全的角度出发假定附加弯矩只由土压力被动侧(半圆周)的竖向摩擦力产生[6]。将1/4圆弧AC和BC分别按照等角度分成nβ等份,等分后圆弧段节点编号分别为0 ~nβ,桩身截面等份后每小份的编号为1 ~nβ。
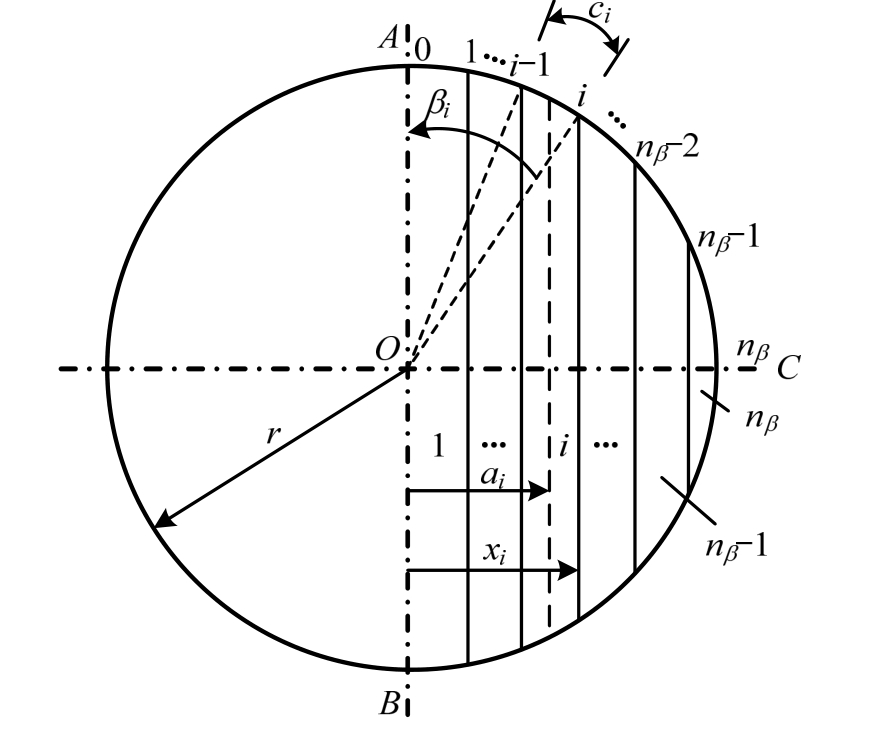
图4 桩身横截面离散示意图
Fig.4 Discretization for pile cross-section
如图4所示,等分后每小段弧长ci=0.5πr/nβ,R为桩身半径;线Oi与OA之间夹角βi=0.5π×i/nβ(i=0,1,…,nβ);图 4 中所示距离第i点相对位移为si=xi×θ,则圆弧AC中第i段桩侧平均竖向位移为save(i)=(si-1+si)/2=ai×θ,ai=R(sinβi-1+sinβi)/2。根据式(1)可得:
式中,τave(i)为圆弧AC中第i段桩侧平均竖向侧摩阻力作用;系数Ai和Bi如下所示:
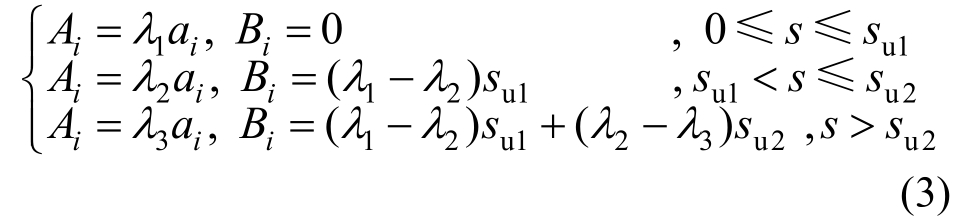
根据图4可知,圆弧AC中第i段桩侧平均竖向摩阻力对O点的弯矩作用为Msi=τave(i)×ci×ai,联合式(2)可得土压力被动侧(半圆弧ACB)竖向摩阻力产生的总附加弯矩Ms为:

式中,Ms/(kN·m/m)为桩身竖向侧摩阻力作用产生的附加弯矩作用,正方向与桩身弯矩正值方向一致,其物理含义是桩身单位长度上作用的弯矩值[4,12];系数Ts和Tc分别采用下式计算:
其中:ci=0.5 πR/nβ;ai=R(sinβi-1+sinβi)/2;Ai和Bi系数采用式(3)计算。
王伯惠等[5]、《公路桥涵地基与基础设计规范》[13]等均认为大直径桩端部附加弯矩Mb与基底转角θb近似满足线性关系,并给出初始刚度kbθ为:
式中:kbθ/(kN·m)为桩端附加弯矩初始刚度;kv/(kN/m3)为基底土体的地基竖向反力系数,《公路桥涵地基与基础设计规范》[13]中规定kv=max{mL,10m},m/(kN/m4)为地基反力系数,可根据规范[18]查表得;Ib/m4为基底截面惯性矩。
Varun等[9]在研究沉井水平承载特性时提出如下所示的kbθ计算公式:
式中,E和ν分别为基底土体弹性模量、泊松比。
Gerolymos 等[14]、Karapiperis 等[15]通过有限元模拟分析发现桩端附加弯矩Mb存在极限值。同时,Gerolymos等[14]发现桩端土体竖向应力近似呈正弦函数分布,在此基础上,本文开展如下所示极限附加弯矩Mbu推导。
如图5所示,设半圆ACB区域为桩端旋转变形时的应力增加区,则桩端附加弯矩Mb由该区域的土体竖向应力产生。Gerolymos等[14]认为附加弯矩Mb达到极限附加弯矩Mbu时,C点处的土体承载力将达到极限值,则根据图5积分可得:
式中:Mbu/(kN·m)为桩端极限附加弯矩;qbu/kPa为土体极限端阻力,根据地勘或经验公式确定。

图5 桩端极限附加弯矩积分示意图
Fig.5 Integral schematic diagram for ultimate additional moment of pile tip
桩端土体为粘性土时,Salgado[16]推荐极限端阻力qbu=9.6Cu~10Cu,Cu/kPa为粘性土不排水抗剪强度 , 代 入 式 (8)得Mbu=(0.4~0.417)πCud3, 这 与Gerolymos 等[12]有限元分析结果(Mbu=0.4πCud3)几乎一致,证明了式(8)推导的正确性。
根据式(6)~式(8),本文建立如下所示的线弹性-塑性Mb-θb计算模型:
式中:Mb/(kN·m)为桩端附加弯矩;Mbu采用式(8)计算;θb/rad为桩端转角;根据实际情况选择式(6)或式(7)进行kbθ计算。如果可同时按照式(6)和式(7)计算kbθ值时,则建议选择两者中的最小值作为Mb-θb模型的初始刚度:
Ashour等[6]认为大直径灌注桩在水平荷载作用下需要考虑桩端水平阻力的影响;Gerolymos等[14]研究沉井水平承载特性时也认为需要考虑沉井底部土体水平剪应力的影响。因此,本文建立如下所示的线弹性-塑性Fb-yb计算模型:
式中:Fb/kN为桩端水平阻力;yb/m为桩端水平变形;kby/(kN/m)为桩端水平阻力初始刚度[14]:
Fbu/kN为桩端水平阻力极限值,如下式所示:
其中:c/kPa为土体粘聚力,特别地,砂土c=0;σv/kPa为桩端位置处上覆土体的自重产生的有效竖向应力;δ/(°)为桩端与土体之间的截面摩擦角,一般取为 0.75φ[17],φ/(°)为桩端土内摩擦角。
如图6所示,假设第i段桩-土相互作用为弹性阶段,该小段桩长为hi,建立如下微分方程组:
式中:Ab/m2为桩端横截面面积;τbu/kPa为桩端与桩端土之间的极限摩阻力,当桩端土粘性土时,τbu等于不排水抗剪强度Cu;当桩端土为砂土或c-φ土时,τbu采用下式计算:


图6 第i段桩身受力示意图
Fig.6 Force diagram for ith pile section
式中,yi、θi、Mi和 Qi分别为第 i段桩底部位移、转角、弯矩和剪力。
Ts,ave(i)、Tc,ave(i)为式(5)中 Ts和 Tc在第 i段的平均值,采用下式计算:
其中:Ts(i-1)、Tc(i-1)为第i段桩顶部的Ts和Tc值;类似地,Ts(i)、Tc(i)为第i段桩底部的Ts和Tc值。
kave(i)为第i段桩的桩侧土抗力模量平均值:
式中,k(i-1)、k(i)分别为第 i段桩顶部和底部位置处的土抗力模量值。
设 αi=Ts,ave(i)/(4EIi)、ηi=kave(i)/(4EIi),根据文献[18―19]的方法对式(15)进行Laplace正、逆变换后可得本文考虑桩侧附加弯矩影响时弹性段桩身传递矩阵系数Ui如下式所示:
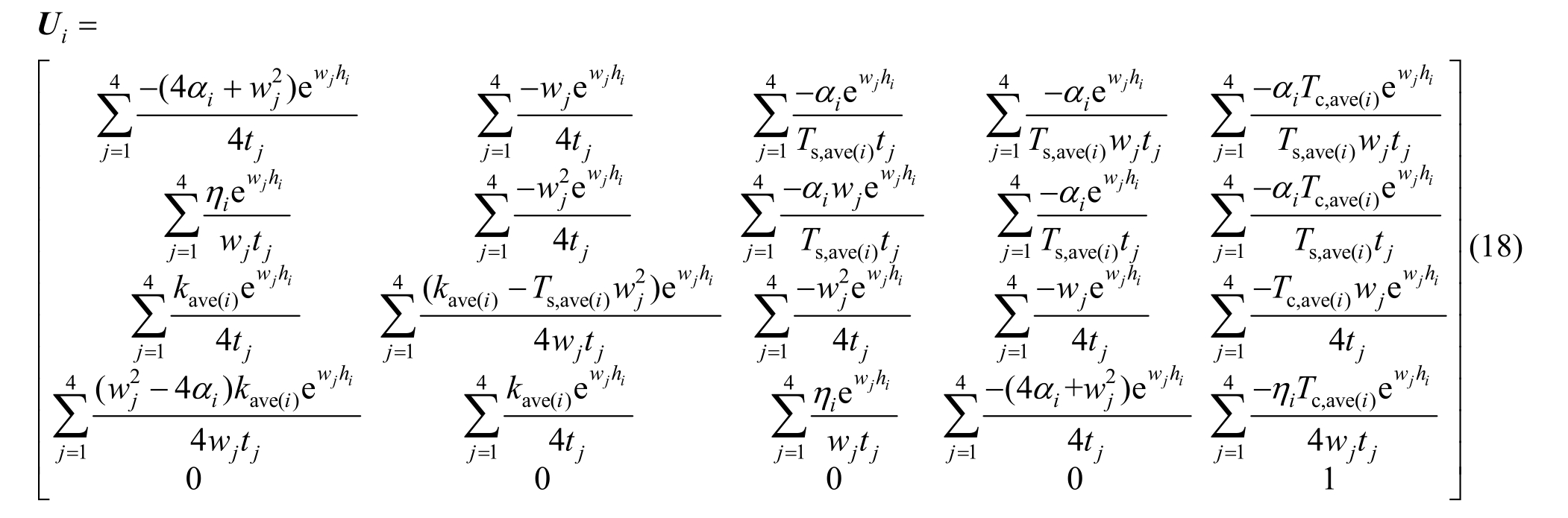
式中:![]() (共 2组共轭复数根),
(共 2组共轭复数根),![]()
特别地,当不考虑附加弯矩Ms作用时Ts,ave(i)、Tc,ave(i)均为0,如果直接代入式(18)时无法计算。此时Ui采用竺明星等[20]给出的公式计算:

式中:ψi=[kave(i)/(4EIi)]0.25;φ1i、φ2i、φ3i和 φ4i为:
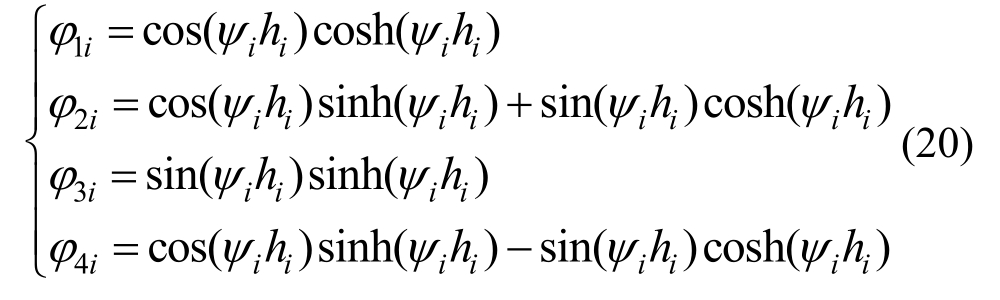
当桩身离散后假设其中第i段桩的桩-土相互作用处于塑性阶段时,将如图 6中所示,将式(15)改成如下形式:
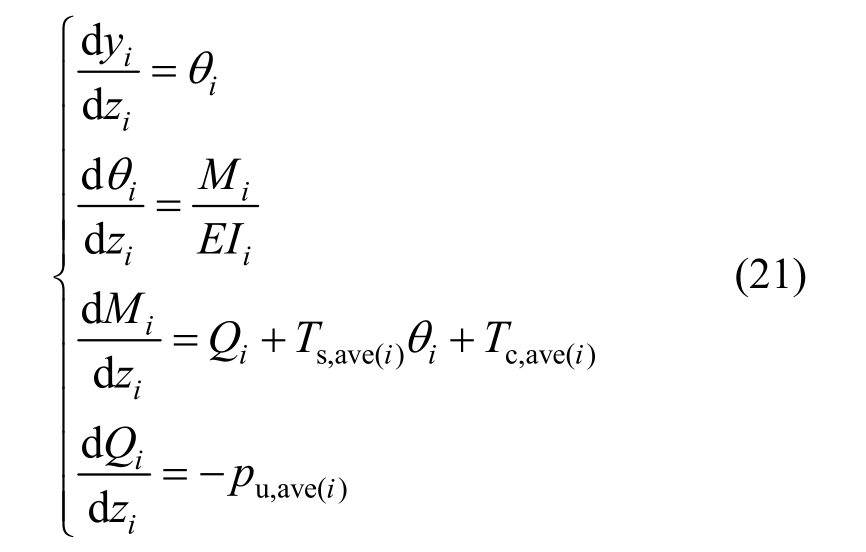
式中,pu,ave(i)为第i段桩桩侧极限土抗力平均值,采用下式计算:
式中,pu(i-1)、pu(i)分别为第i段桩顶部和底部位置处的极限土抗力值。
根据文献[18―19]的方法可推导得本文塑性段桩身传递矩阵系数Ui为:
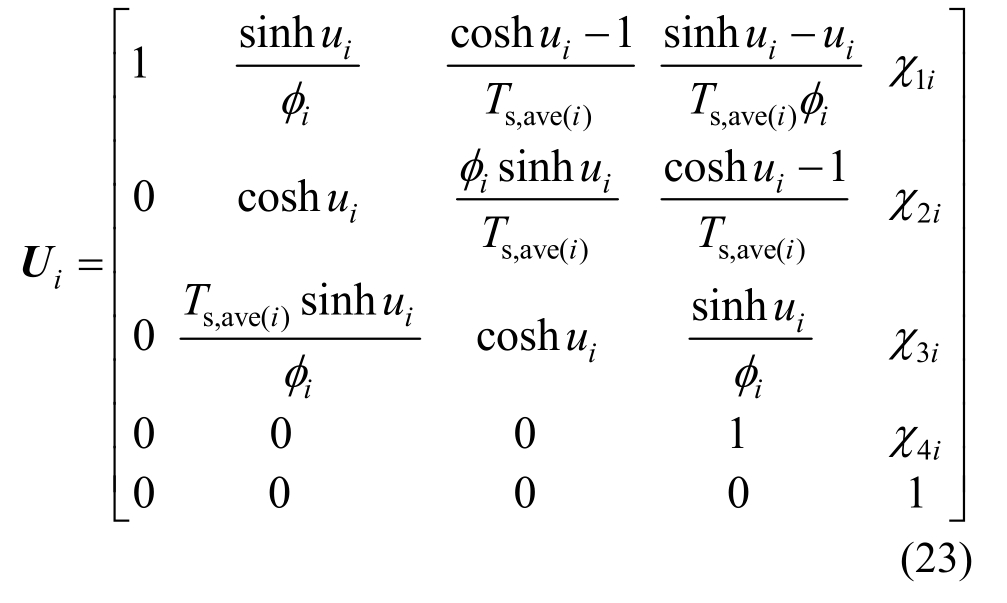
式中,ϕi=(Ts,ave(i)/EIi)0.5;ui=ϕi×hi;χ1i、χ2i、χ3i、χ4i如下所示:
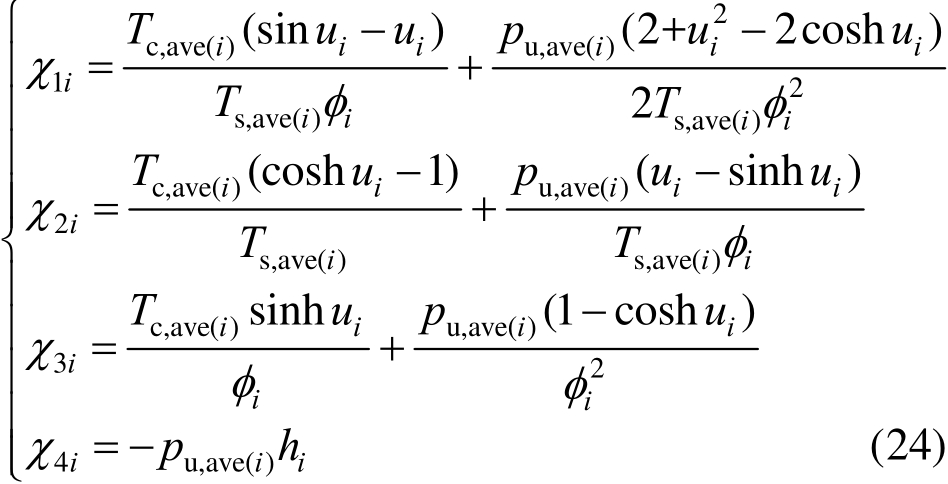
根据传递矩阵原理和Laplace正逆变换[18―21],结合式(18)、式(19)和式(23),可得整个桩身的传递矩阵方程为:
式中:Sn=[yn,θn,Mn,Qn, 1]T、S0=[y0,θ0,M0,Q0, 1]T分别为整个桩的桩端、桩顶处变形、转角、弯矩和剪力的矩阵向量;Ui为第i段桩身传递矩阵系数,当桩土相互作用为弹性时Ui采用式(18)计算;当桩土相互作用为塑性阶段时Ui采用式(23)计算;当不考虑附加弯矩Ms作用时Ui采用式(19)计算。
常见的约束条件主要有自由、铰接和嵌固,因此可得如下桩顶、桩端的约束边界条件:

式中:Ft、Mt分别为桩顶的水平荷载与弯矩作用;Mb和Fb分别采用式(9)和式(11)计算。
将式(26)~式(27)的桩顶、桩端边界代入式(25)即可解得桩顶响应解S0。进而根据下式求解任意截面处桩身响应:
式中,Si=[yi,θi,Mi,Qi, 1]T为任意第i段桩端、桩顶处变形、转角、弯矩和剪力的矩阵向量。
由于桩侧附加弯矩Ms作用依赖于桩身圆周截面处每点的竖向相对位移,这在计算初始阶段是无法知晓,因此需要通过迭代的方式进行求解,如图7所示为迭代计算流程图。

图7 桩身响应计算流程图
Fig.7 Flow chart for calculating pile responses
Mcvay等[4]开展了桩侧竖向摩阻力对水平承载特性影响的大直径嵌岩桩67 g离心模型实验研究,换算后桩径d=1.838 m,嵌岩深度为L=5.1816 m,抗弯刚度EI=1.68×107kN/m2。Mcvay等[4]根据离心实验结果并扣除桩侧摩阻力影响后得出p-y曲线见表1。
表1 归一化p-y曲线
Table 1 Normolizedp-ycurve

表1中:p/(kN/m)为土抗力值;qu/kPa为人造岩石抗压强度,取为 957.61 kPa。Mcvay等[4]根据竖向加载试验后得出桩侧摩阻力τ-s曲线如下所示:

其中:极限侧摩阻力τu=363.89 kPa。由于式(29)是一个多段曲线组合而成,则根据图 8(a)将式(29)近似转换成式(1)所示的三折线型τ-s曲线可得:λ1=45360 kN/m3、λ2=1480 kN/m3、λ3=0、su1=6.43×10-3m、su2=5.51×10-2m。根据式(4)可知相应的Ms-θ曲线如图8(b)所示。
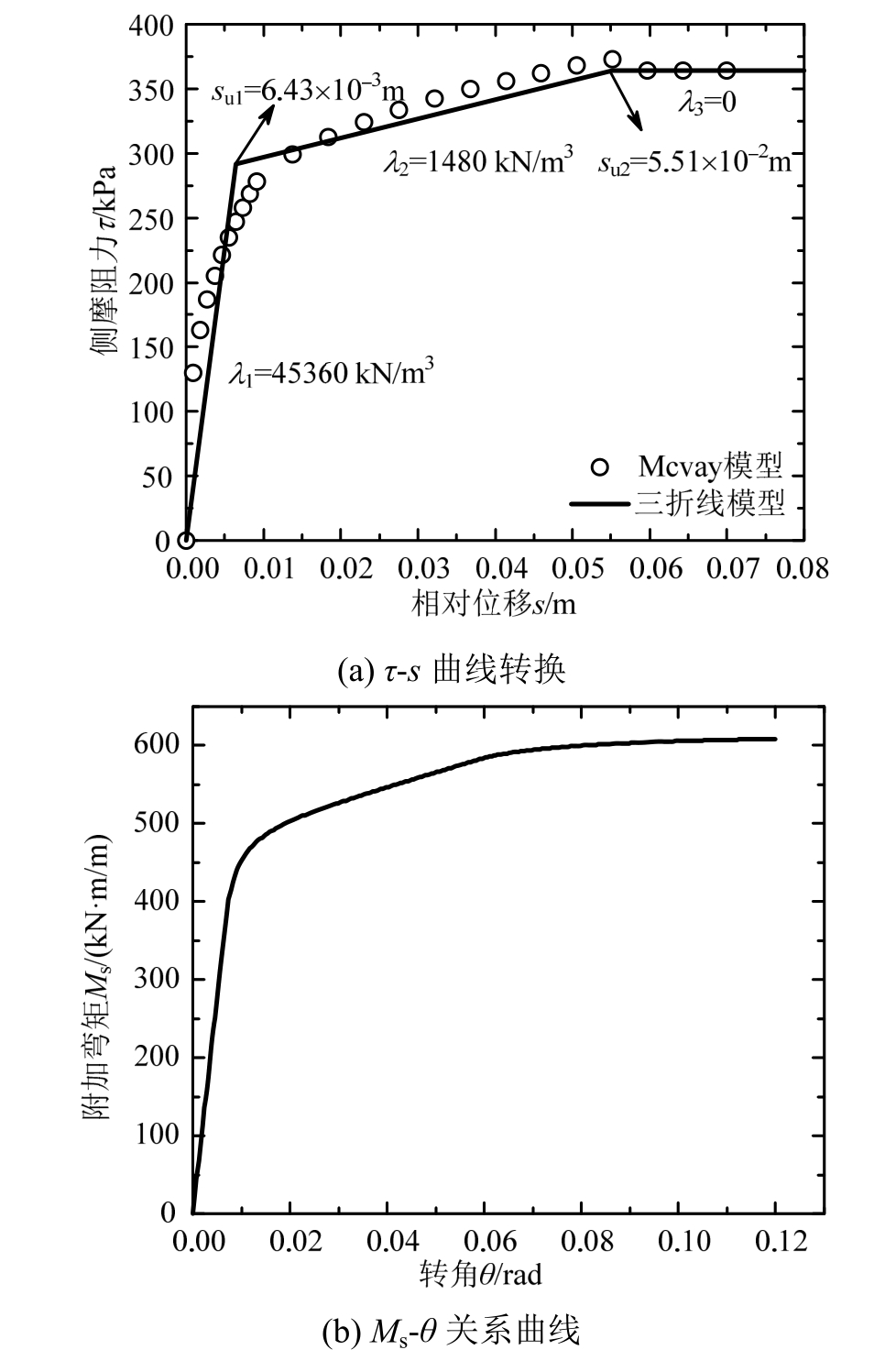
图8 桩侧附加弯矩-转角计算模型建立
Fig.8 Establishment of calculation model of additional
moment vs slope for pile shaft
由于试验过程中在模型桩底部设置了聚乙烯泡沫材料以消除桩端剪力Fb和附加弯矩Mb的影响,因此本文计算过程中只需考虑桩侧竖向摩阻力产生的附加弯矩Ms影响,则计算所得结果与实测值[4]、FB-Pier软件[4](不考虑附加弯矩Ms影响,采用软件自带软岩p-y曲线)计算值对比如图9所示,结果表明本文方法所得结果与实测值几乎完全吻合,由此可知桩侧竖向摩阻力所产生的附加弯矩Ms对水平承载特性的影响是不能忽略的。
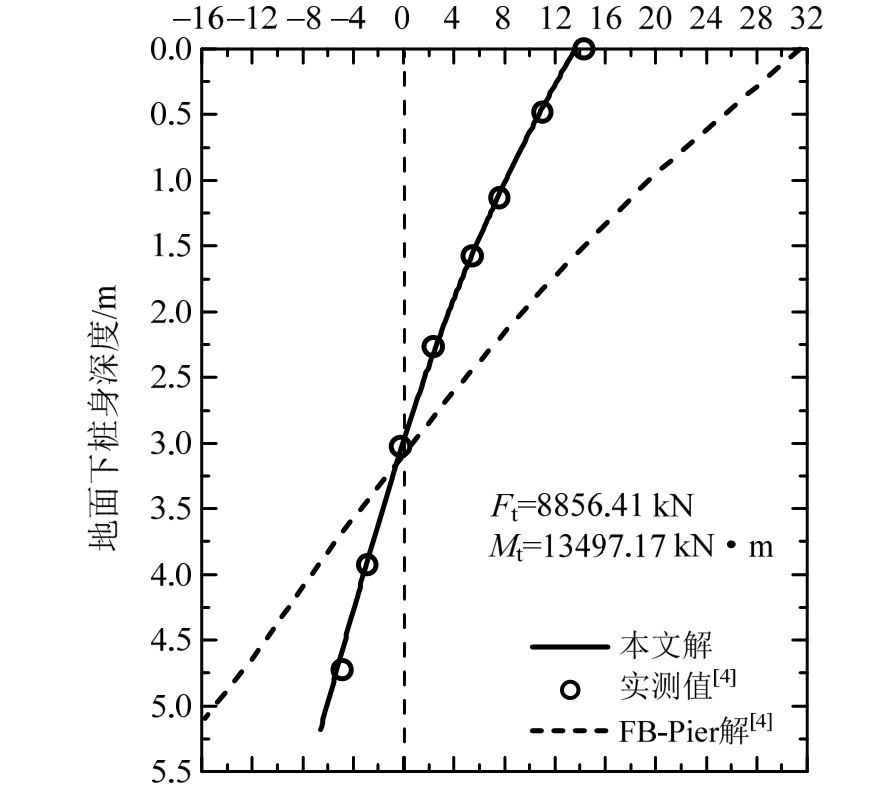
图9 桩身变形对比
Fig.9 Comparison of pile deflection
Bhushan等[22]在超固结硬质粘土中开展了灌注桩水平承载特性原位试验研究。地面下桩长L=4.995 m,桩径d=1.22 m,抗弯刚度EI=2.25×106kN/m2,桩顶水平力为Ft,弯矩Mt=0.23Ft。桩长范围内土体为均质硬粘土,土体弹性模量E=24.44 MPa,泊松比ν=0.3。桩土相互作用p-y曲线采用API规范[23]的粘土模型,见表2。
表2 API规范粘土p-y曲线
Table 2 API codep-ycurve for clay

表 2 中:pu=min{3Cud+γzd+ξCuz, 9Cud},不排水剪切强度Cu=227 kPa;有效重度γ=18.8 kN/m3;ξ为系数,取为 0.5;yu=2.5ε50d,其中ε50=0.0072。
由于该试验过程中未开展相关竖向侧摩阻力研究,因此τ-s曲线采用API[23]推荐模型进行计算,如表3所示。
表3中:相对位移极限值su取为0.01d[23];API规范[23]附录规定“不排水剪切强度Cu>72 kPa时,τu=0.5Cu”,因此极限侧摩阻力τu=113.5 kPa。
表3 API规范τ-s曲线
Table 3τ-scurve of API code

将表3近似转换成式(1)所示的三折线型τ-s曲线可得:λ1=9303 kN/m3、λ2=-2791 kN/m3、λ3=0、su1=1.22×10-2m、su2=2.44×10-2m。根据式(4)可计算得相应的Ms-θ曲线如图10所示。
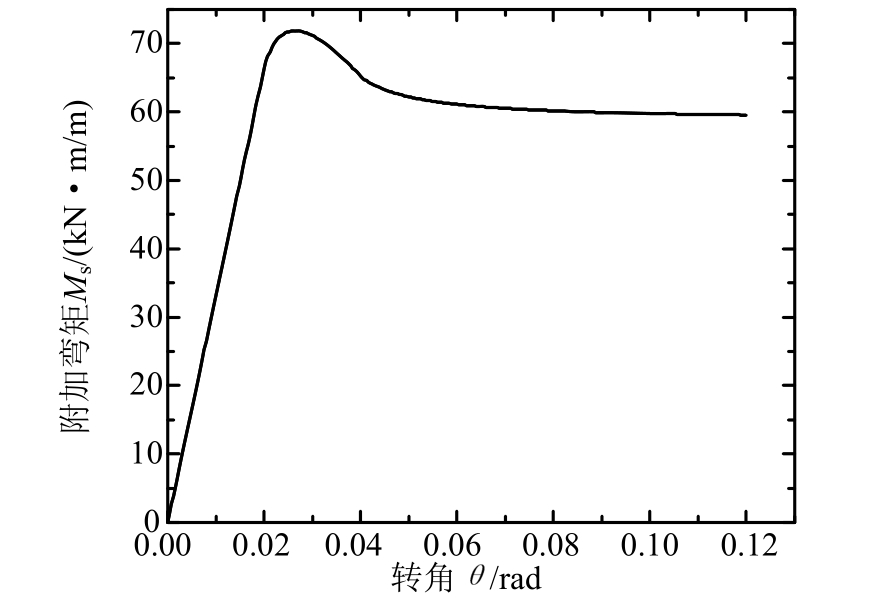
图10 软化Ms-θ模型
Fig.10 Soften model ofMs-θ
根 据 式 (9)计 算 可 得kbθ=8128 kN/m,Mbu=518 kN/m;由式(11)可得kby=26984 kN/m,Fbu=132.68 kN,则对比结果如图11所示。

图11 不同影响因素下桩顶荷载-位移对比
Fig.11 Comparison of load-deflection for pile head under different influence factors
由图11可知:当只考虑p-y曲线模型作用时与实测值相差较大,且这一差异随着荷载的增加而显著增加;由于地基土为超固结硬质粘土,相应的桩侧摩阻力值较大(τu=113.5 kPa),当考虑附加弯矩Ms作用时桩顶水平荷载-变形曲线已明显地接近实测值;同时,随着考虑的影响因素增加,计算值与实测值越来越接近,当完全按照四弹簧模型考虑附加弯矩Ms、桩端剪力Fb和附加弯矩Mb的影响时所得理论计算结果与实测值几乎吻合,证明了本文计算理论的正确性与合理性。
为研究桩侧竖向摩阻力、桩端水平与竖向阻力对大直径桩水平承载特性的影响,本文首先引入基于Winkler弹性地基梁的四弹簧模型;随后采用能够考虑土体硬化、软化作用的三折线τ-s曲线模型,并据此推导得出桩侧竖向摩阻力作用的线弹性-塑性附加弯矩-转角Ms-θ计算模型;最后,分别建立大直径桩端底部Fb-yb和Mb-θb计算模型。结合Laplace正逆变换分别求得考虑桩侧竖向摩阻力与端阻力作用时弹性段、塑性段桩身传递矩阵系数解析解,并给出桩身响应求解的迭代计算流程进而解得桩身响应解。
通过两个案例对比分析,不但验证了本文推导的正确性,也验证了本文所建立的四弹簧模型中Ms-θ、Fb-yb和Mb-θb计算模型的合理性;同时案例分析也说明了当地基土体较好时,桩侧附加弯矩Ms、桩端剪力Fb和附加弯矩Mb对大直径灌注桩水平承载力有着不可忽略的影响,计算时应充分考虑这些影响因素,否则结果将偏于保守。
参考文献:
[1]Basu D. Analysis of laterally loaded pile in layered soil[D]. West Lafayette: Purdue University, 2006: 10―14.
[2]Dodds A M, Martin G R. Modeling pile behavior in large pile groups under lateral loading [R]. Buffalo:Multidisciplinary Center for Earthquake Engineering Research, 2007: 56―58.
[3]Lam I P, Martin G R. Seismic Design of Highway Bridge Foundations [R]. Virginia: Department of Transportation,Federal Highway Administration, 1986: 44―45.
[4]Mcvay M C, Niraula L. Development of P-Y curves for large diameter piles/drilled shafts in limestone for FBPIER [R]. Florida: Civil and Coastal Engineering Dept, University of Florida, 2004.
[5]王伯惠, 上官兴. 中国钻孔灌注桩新发展[M]. 北京:人民交通出版社, 1999: 89―90.Wang Bohui, Shangbuan Xing. New development for bored pile in China [M]. Beijing: China Communication Press, 1999: 89―90. (in Chinese)
[6]Ashour M, Helal A. Contribution of vertical skin friction to the lateral resistance of large-diameter shafts [J].Journal of Bridge Engineering, 2014, 19(2): 289―302.
[7]Alikhanlou F. A discrete model for the analysis of short pier foundations in clays [D]. Lubbock: Texas Technology University, 1981.
[8]Gerolymos N, Gazetas G. Winkler model for lateral response of rigid caisson foundations in linear soil [J].Soil Dynamics and Earthquake Engineering, 2006, 26(5):347―361.
[9]Varun, Assimaki D, Gazetas G. A simplified model for lateral response of large diameter caisson foundations-Linear elastic formulation [J]. Soil Dynamics and Earthquake Engineering, 2009, 29: 268―291.
[10]肖宏彬. 竖向荷载作用下大直径桩的荷载传递理论及应用研究[D]. 长沙: 中南大学, 2005.Xiao Hongbin. Theoretical and application research on load transfer of vertically loading large diameter piles[D]. Changsha: Central South University, 2005. (in Chinese)
[11]李灿. 大直径钢管桩水平承载特性研究[D]. 大连: 大连理工大学, 2012.Li Can. A study on bearing capacity performance of large-diameter monopile foundation under lateral loads[D]. Dalian: Dalian University of Technology, 2012. (in Chinese)
[12]Gerolymos N, Gazetas G. Static and dynamic response of massive caisson foundations with soil and interface nonlinearities-validation and results [J]. Soil Dynamics and Earthquake Engineering, 2006, 26(5): 377-394.
[13]JTG D63―2007, 公路桥涵地基与基础设计规范[S].北京: 人民交通出版社, 2007.JTG D63―2007, Code for design of ground base and foundation of highway bridges and culverts [S]. Beijing:China Communication Press, 2007. (in Chinese)
[14]Gerolymos N, Gazetas G. Development of Winkler model for static and dynamic response of caisson foundations with soil and interface nonlinearities [J]. Soil Dynamics and Earthquake Engineering, 2006, 26: 363―376.
[15]Karapiperis K, Gerolymos N. Combined loading of caisson foundation in cohesive soil: finite element versus Winkler modeling [J]. Computers and Geotechnics, 2014,56: 100―120.
[16]Salgado R. The engineering of foundations [M]. New York: McGraw-Hill, 2008: 582―583.
[17]费康. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2010.Fei Kang. The application of ABAQUS in geotechnical engineering [M]. Beijing: China Water & Power Press,2010. (in Chinese)
[18]Zhu M, Zhang Y, Gong W, et al. Generalized solutions for axially and laterally loaded piles in multilayered soil deposits with transfer matrix method [J]. International Journal of Geomechanics, 2017, 17(4): 04016104.
[19]竺明星. 组合荷载作用下被动桩承载机理研究[D]. 南京: 东南大学, 2016.Zhu Mingxing. Research on bearing mechanism of passive pile under combined loads [D]. Nanjing:Southeast University, 2016. (in Chinese)
[20]竺明星, 龚维明, 何小元. 成层地基土中水平受荷桩桩身响应的矩阵传递解[J]. 岩土工程学报, 2015,37(增刊 2): 46―50.Zhu Mingxing, Gong Weiming, He Xiaoyuan. Transfer matrix solutions for responses of laterally loaded piles in multilayered soil deposits [J]. Chinese Journal of Geotechnical Engineering, 2015, 37(Suppl 2): 46―50.(in Chinese)
[21]王友凯, 龚耀清. 任意荷载作用下层状横观各向同性弹性地基的直角坐标解[J]. 工程力学, 2006, 23(5): 9―13.Wang Youkai, Gong Yaoqing. Analytical solution of transversely isotropic elastic multilayered subgrade under arbitrary loading in rectangular coordinates [J].Engineering Mechanics, 2016, 237(5): 9―13. (in Chinese)
[22]Bhushan K, Fong P T, Haley S C. Lateral load tests on drilled piers in stiff clays [J]. Journal of the Geotechnical Engineering Division, 1979, 105(8): 969―985.
[23]American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design [S]. Washington: API Recommended Practice 2A-WSD (RP 2AWSD), 2000.
TRANSFER MATRIX SOLUTIONS FOR LATERAL BEHAVIOR OF PILE FOUNDATION CONSIDERING THE SKIN AND END RESISTANCE EFFECT
ZHU Ming-xing1, GONG Wei-ming2, LU Hong-qian1, WANG Lei1
(1. China Energy Engineering Group Jiangsu Power Design Institute Co., LTD, Jiangsu, Nanjing 211102, China;2. School of Civil Engineering, Southeast University, Jiangsu, Nanjing 210096, China)
Abstract:To investigate the contributions of vertical skin friction, vertical end resistance and horizontal shear stress of pile tip to the lateral bearing capacity of a pile foundation, this work firstly deduces analytical expression of a linear constitutive model characterizing the relationship between additional moment and slope based on the trilinear τ-s curve model of pile shafts. Furthermore, combining the four-type spring model with the presented constitutive relations for additional moment of pile shafts and pile ends, as well as the shear force of pile tip, the differential equations for a pile section is established and the corresponding transfer matrix coefficients for piles in elastic and plastic stage are derived analytically by means of Laplace transformation. Finally, transfer matrix solutions for the lateral behavior of a pile foundation is obtained on the basis of a proposed iterative methodology.The agreement between test data and the calculated results by the proposed method is quite good, which verifies the correctness of the derivation and confirms the rationality of the produced constitutive relations for additional moment of pile shafts, as well as additional moment and shear force of pile tip. Moreover, the comparison also implies that the values of additional moment Msof pile shafts, additional moment Mband shear force Fbof pile ends have a significant influence on the lateral load-bearing capacity of piles when large-diameter piles are embedded in stiff materials.
Key words:pile foundation; lateral behavior; additional moment; four-type spring model; transfer matrix method
中图分类号:TU473.1+1
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.05.S045
文章编号:1000-4750(2018)Suppl-0230-09
收稿日期:2017-05-24;修改日期:2017-11-13
基金项目:中国博士后科学基金面上项目(2017M611955);江苏省博士后科研资助计划项目(1701028B);中能建江苏院科技项目(32-JK-2016-001);国家重点基础研究发展计划(973计划)项目(2013CB036304)
通讯作者:竺明星(1985―),男,江苏人,博士后,主要从事桩基工程理论研究(E-mail: zhumingxing@jspdi.com.cn).
作者简介:龚维明(1963―),男,江苏人,教授,博士,博导,主要从事桩基工程理论研究(E-mail: wmgong@seu.edu.cn);卢红前(1971―),男,江苏人,教授级高工,博士后合作导师,主要从事风电设计工作研究(E-mail: luhongqian@jspdi.com.cn);王 磊(1975―),男,江苏人,高工,硕士,主要从事风电、光伏等新能源设计工作(E-mail: wanglei@jspdi.com.cn).