
谭 辉,刘晶波,王东洋,宝 鑫,李述涛
(清华大学土木工程系,北京 100084)
摘 要:针对地下结构地震反应分析问题,现有研究中常采用的计算模型存在较大差异。该文选取竖直入射剪切波作用下的二维土体模型,依据波场分解理论对比了不同边界条件和选择不同波场求解等效输入地震荷载的方法所得的土体反应。为了模拟有地下结构时产生散射波场的情况,建立了土体内部有隧洞的计算模型并计算了采用不同方法时的地震反应。通过与解析解或远置边界解的对比表明,地下结构地震反应分析中,所有截断边界均设置人工边界,并且在迎波面边界选择入射波场或者自由波场,非迎波面边界选择自由波场求解等效输入地震荷载时,地震动输入的精度最高,计算结果最可靠。
关键词:地下结构地震反应;地震动输入;波动法;人工边界;自由波场
随着近年来国内外对地下空间的开发利用,地下结构地震反应分析成为研究领域的一个热点问题。相较于地上结构,地下结构由于埋设于土体之中,其试验研究与现场观测难度大、资料少,数值模拟成为主要的研究方式。而受限于计算技术的发展,考虑土-结构相互作用的地下结构地震反应数值模拟通常只能截取有限的计算区域,此时设置合理的人工边界来模拟实际的半无限土体变得十分必要。因此,对于地下结构地震反应分析问题而言,人工边界的设置以及地震动输入方法都直接影响到数值模拟结果的精确度和可靠性。
设置人工边界的目的是模拟连续介质的辐射阻尼,保证计算区域的外行波在到达人工边界处时穿过边界而不发生反射[1]。粘弹性人工边界是一种应力型局部人工边界[2],由于其较高的精度和易于在通用软件中添加的优点,近年来得到广泛使用[3-6]。伴随着人工边界的研究发展,地下结构地震反应分析的波动法被提出[7],波动法采用分离体的概念,在保证边界处应力和位移与自由场一致的前提下,将输入地震动转化为人工边界上的等效输入荷载。相关研究[8, 9]证明,波动法相较于传统的振动法具有较高的计算精度,并且可以考虑波动传播的延时效应。有学者[10]对七种不同边界条件和地震动输入选择方法进行了对比,认为波动法计算精度高但应用麻烦,推荐采用底部粘弹性边界、侧面竖向位移约束、底面应力输入的方法。
波动法需要根据自由波场求解相应的等效输入地震荷载,按照波场分解理论,自由波场可分解为入射波场和反射波场,由于计算模型存在迎波面和非迎波面,在不同边界面上选择不同的波场求解等效输入地震荷载会对计算结果产生影响。本文以竖直入射剪切波作用下的二维土体模型为研究对象,同时为了模拟有地下结构时产生散射波场的情况而增加了土体内部有隧洞的计算模型,通过改变不同边界上波场的选择和边界条件,对不同计算方法结果进行对比,给出最合理的波场选择方式和人工边界条件,为地下结构地震反应分析提供参考。
二维土体自由场计算模型如图1(a)所示,计算模型尺寸为50 m×50 m,土体密度ρ= 2 000 kg/m3,泊松比ν=0.25,剪切波速cs= 2 00 m/s 。相应的隧洞模型如图1(b)所示,在二维土体计算模型内有一横截面为边长10 m、顶部埋深10 m的正方形隧洞,以此模拟地下结构,并且暂不考虑隧洞衬砌,A、B、C、D、E分别为数值模拟时的观测点,单元尺寸为1 m×1 m。人工边界采用目前常用的粘弹性人工边界,相应参数按照文献[11]中二维粘弹性人工边界参数取值。对于粘弹性人工边界,文献[7]给出的等效输入地震荷载形式如式(1)所示。

其中:B代表人工边界上的一个节点;(x B , yB)为B点位置坐标;F B(t)为节点B处的等效输入地震荷载;σ 0(x B , y B ,t)、u 0(x B , y B ,t)、u˙0(x B , y B,t)分别为已知波场在人工边界处产生的应力、位移和速度,C B、K B分别为粘弹性人工边界的阻尼系数和刚度系数;A为人工边界节点代表的面积。

图1 计算模型
Fig.1 Computational model
对于二维土体计算模型(图 1(a)),自由波场uf可分解为竖直向上入射的剪切波ui和经自由表面反射的竖直向下的反射波ur如式(2)所示,相应的动力反应有解析解作为对照。而对于土-地下结构计算模型(图 1(b)),由于地下结构的存在,入射波场会在地下结构四周产生散射波,到达自由表面的入射波和经由自由表面反射的反射波也会发生变化,还会伴随波型转换,产生压缩波,因此波场分析十分复杂,解析解难以获得。对于土-地下结构计算模型,通过将边界远置,保证在计算时间内散射波和反射波无法从边界反射回到观测点,从而获得远置边界解作为参考。对于常用的矩形计算区域,侧面和底面为截断边界,需设置人工边界,根据人工边界处求解等效输入地震荷载的波场的选择,采用表1所示的前三种计算方法分别进行地震动输入,表1中的方法四采用文献[10]推荐的侧面边界采用竖向约束水平自由的边界条件,底面采用人工边界并施加等效输入地震荷载的方法。图2为四种方法的计算模型示意图,其中ui表示上行入射波场,ur表示下行反射波场。
数值算例的输入地震动为底面竖直入射脉冲剪切波,脉冲波采用式(3)所示δ函数的有限差分近似[2],脉冲持时T=0.2 s,时间步长取满足计算稳定性的 0.002 s,计算时长 1 s,底面入射波位移时程如图3所示。分别建立图1中的两种有限元计算模型,采用上节提到的四种计算方法,利用入射波场位移求得自由波场的位移、速度和应力,从而得到等效输入地震荷载,分别进行动力计算,得到观测点A、B、C、D、E的水平位移时程,并分别与解析解或远置边界解对比,所得计算结果见图4~图8。
表1 不同方法的边界条件和地震动输入波场选择
Table 1 Boundary conditions and input wave field selections of different methods

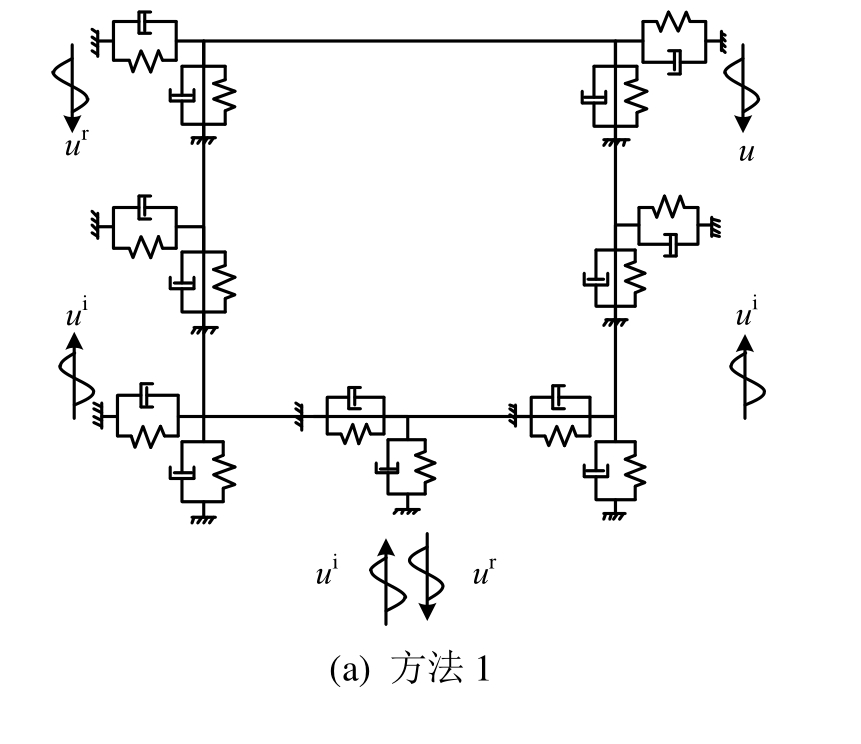
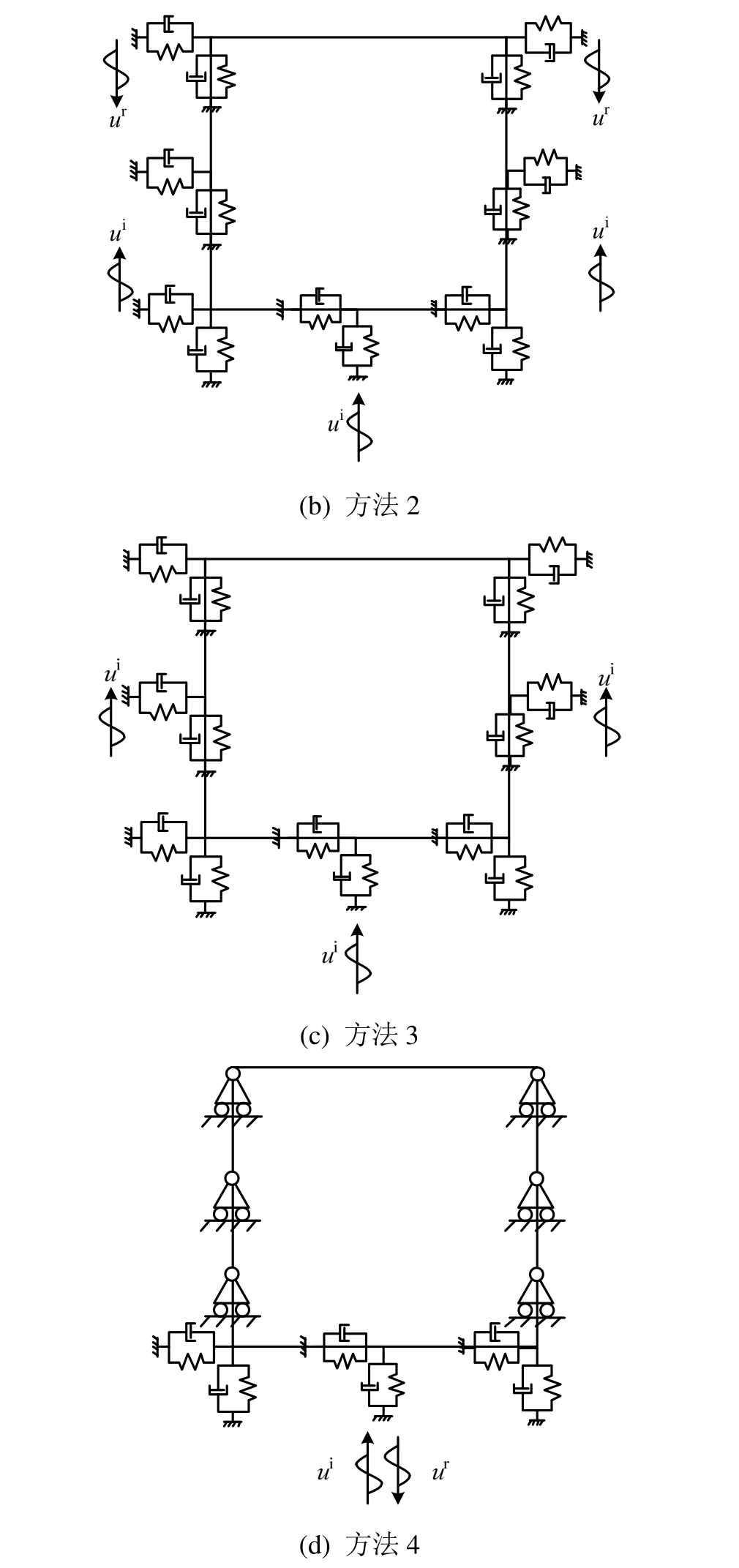
图2 四种方法计算模型示意图
Fig.2 Computational models of 4 methods

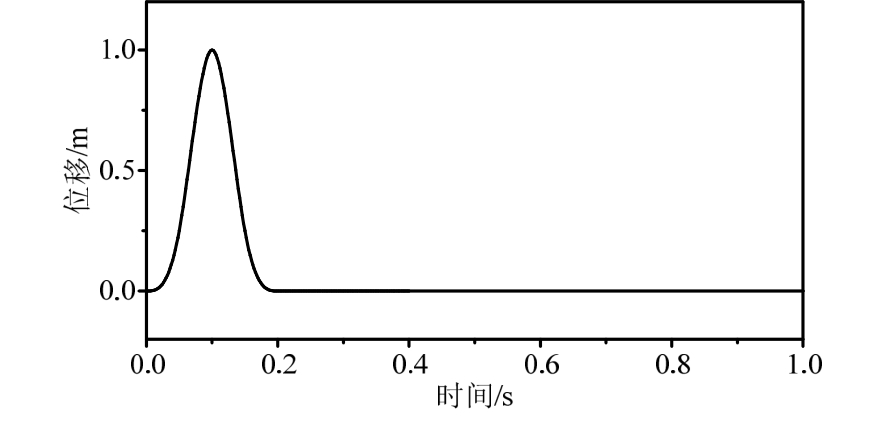
图3 入射脉冲波位移时程
Fig.3 Displacement of input pulse wave
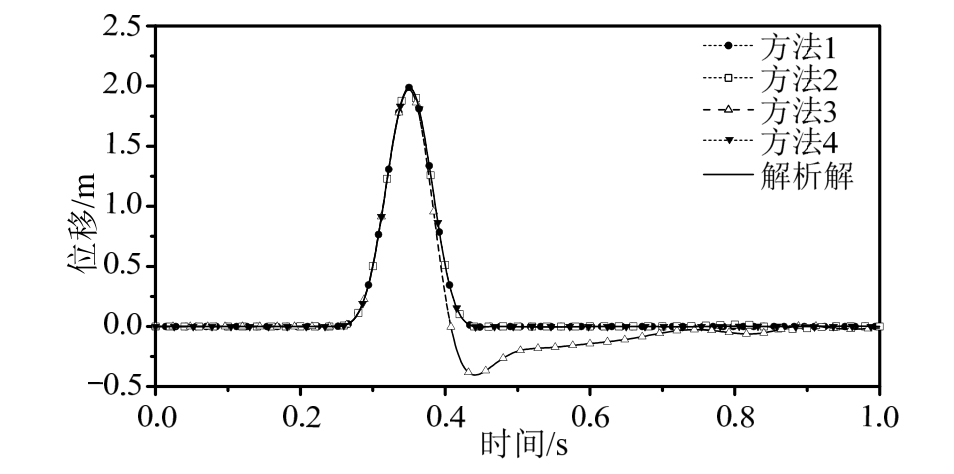
图4 自由场模型A点水平位移时程
Fig.4 Horizontal displacement of point A on free field model
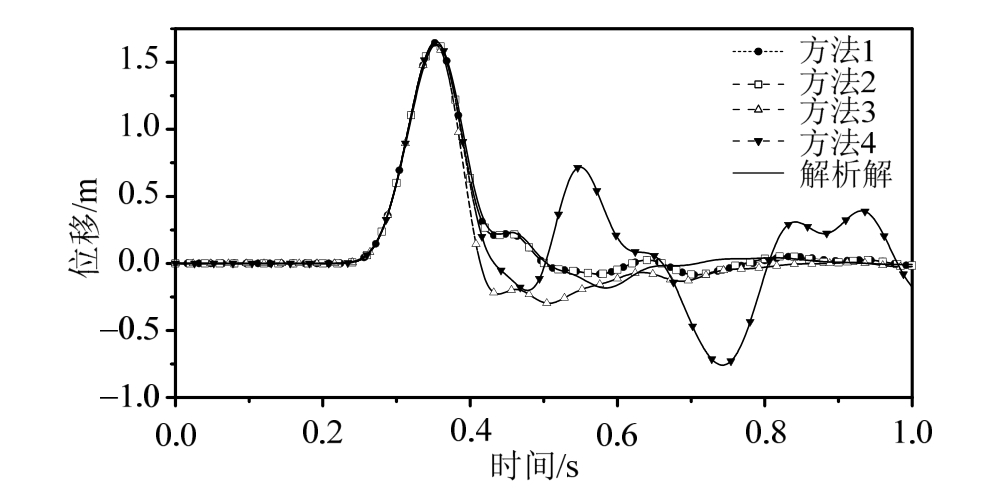
图5 土-地下结构计算模型B点水平位移时程
Fig.5 Horizontal displacement of point B on soil-structure model

图6 土-地下结构计算模型C点水平位移时程
Fig.6 Horizontal displacement of point C on soil-structure model
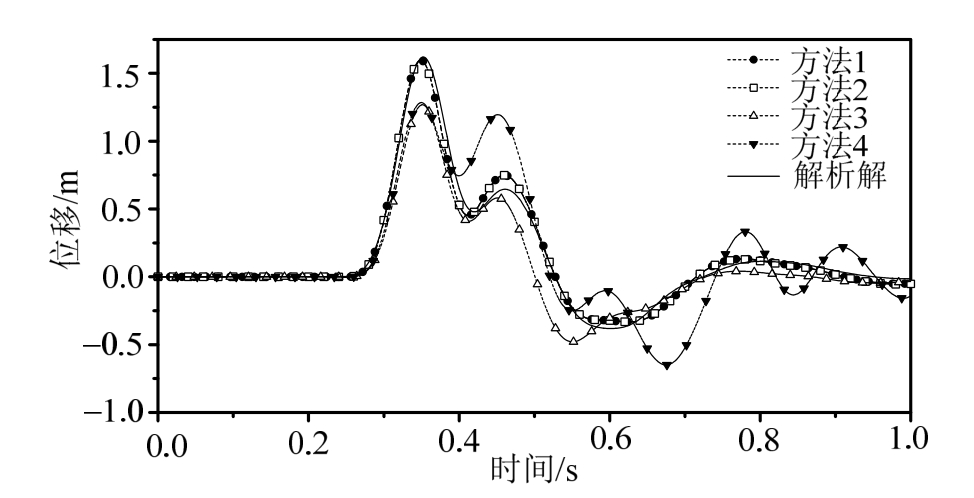
图7 土-地下结构计算模型D点水平位移时程
Fig.7 Horizontal displacement of point D on soil-structure model
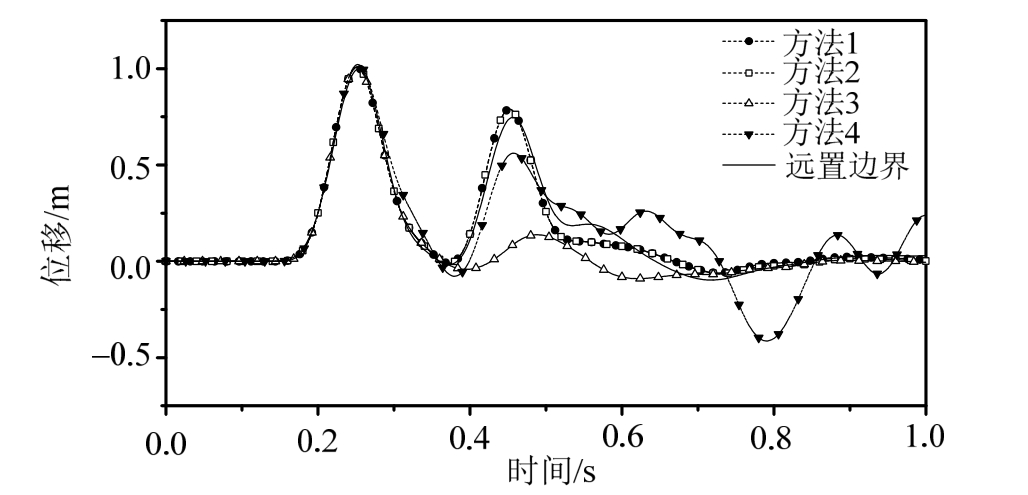
图8 土-地下结构计算模型E点水平位移时程
Fig.8 Horizontal displacement of point E on soil-structure model
由图4所示的A点的水平位移时程数值计算结果与解析解对比可以看出,方法1、方法2、方法4都与解析解吻合,只有方法三出现了一定的误差。方法 1和方法 2的差别在于迎波面的输入荷载不同,对于方法 1,输入荷载包括了地震动的输入,又包括了反射波引起的荷载,因而可以平衡自由表面的反射波,对于方法 2,输入荷载只完成了地震动的输入,反射波则由人工边界吸收,因此二者的计算结果一致,都可以实现地震动的有效输入。相对于方法2,方法3的误差源自侧面边界上波场的选择,对于本算例而言,侧面边界上的波场行进方向是平行于边界面的,没有波动能量进出侧面边界,因而侧面边界上施加的荷载作用是为保持侧面边界与自由波场运动一致而平衡人工边界存在所带来的附加荷载,这个附加荷载在入射波场和反射波场均存在,因此只选择入射波场求解侧面边界上的荷载是不全面的,导致计算结果出现误差。正是基于上述原因,方法4采用的侧边界处理方法恰好与自由波场位移条件一致,相当于施加了位移边界条件,因此同样可以得到正确的结果。
由图5~图8所示的B、C、D、E四个观测点的水平位移时程数值计算结果与远置边界求得的结果对比可以看出,方法1和方法2都与远置边界结果吻合度较高,仅仅在后半段出现了较小的误差,这是因为粘弹性人工边界在推导中存在一定的假设,导致其对于散射波无法完全吸收,仍有小部分散射波被反射回计算区域内,但是其对计算结果的影响较小;另一方面,由于地下结构相对于计算模型较小且与底面人工边界相距较远,其对到达底面人工边界处的反射波场影响有限,因此方法1和方法2计算结果没有出现明显的差别,二者均可以满足工程精度要求。方法3如前文所说,侧面人工边界会引入一部分附加荷载,从而使计算区域内的动力反应出现明显偏差。本算例中方法4相对于其他几种方法则出现了较大误差,原因是侧面的滑动边界不再是该计算模型的位移边界条件,无法吸收内部产生的散射波,导致散射波被反射回计算区域,从而使得观测点的位移出现较大的振荡,与真实结果误差较大。
综合以上计算结果,方法1和方法2模拟精度较高,对于计算区域内有散射波的情况也能给出满足工程精度要求的结果,更加适合地下结构地震反应分析;方法3由于侧面边界缺少了部分荷载的施加,使得计算区域的反应出现一定的偏差;方法 4对于无散射场的计算模型可以得到精度较高的结果,这与文献[11—12]结论一致,但是对于有散射波的模型,由于侧面边界无法吸收内部产生的散射波,导致计算结果出现振荡,误差变大。
本文从地下结构地震反应分析的波动法入手,利用波场分解,针对竖直剪切波作用下的二维计算模型,讨论了不同边界处求解等效输入地震荷载的波场选择方式,列举了四种计算方法,对均匀计算区域和土-地下结构计算模型进行计算得到观测点的位移反应,并通过与解析解或远置边界解的对比研究,得到以下结论:
(1) 无论计算模型内部是否存在散射波场,截断边界面均采用粘弹性人工边界和利用自由波场求解等效输入地震荷载的方法 1,和迎波面利用入射波场求解等效输入地震荷载而其他处理与方法 1一致的方法 2,均可以较好地完成地震动输入,计算误差较小,可以满足工程精度要求,适用于地下结构地震反应分析。
(2) 截断边界均采用粘弹性人工边界和利用入射波场求解等效输入地震荷载的方法 3,由于在侧面人工边界上等效输入地震荷载求解时缺少考虑反射波场,导致计算误差无法避免,因此在地下结构地震反应分析中应避免采用该方法。
(3) 侧面采用水平自由竖向约束的滑动边界,底面采用粘弹性人工边界并且施加等效输入地震荷载的方法 4,由于采用的滑动边界不能吸收由计算区域产生的散射波,导致散射波在侧面边界上被反射回计算区域,从而引起较大误差,不适合用于地下结构地震反应分析。
参考文献:
[1]刘晶波, 王振宇, 张克峰, 等. 考虑土-结构相互作用大型动力机器基础三维有限元分析[J]. 工程力学,2002, 19(3): 34―38.Liu Jingbo, Wang Zhenyu, Zhang Kefeng, et al. 3D finite element analysis of large dynamic machine foundation considering soil-structure interaction [J]. Engineering Mechanics, 2002, 19(3): 34―38. (in Chinese)
[2]刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6): 46-51.Liu Jingbo, Wang Zhenyu, Du Xiuli, et al.Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems [J]. Engineering Mechanics, 2005, 22(6): 46―51. (in Chinese)
[3]尹广斌, 张燎军, 俞佩斯. 基于ADINA软基上地震动输入方法研究及其应用[J]. 水电能源科学, 2012,30(1): 135-138.Yin Guangbin, Zhang Liaojun, Yu Peisi. Study on method of earthquake input on soft foundation based on ADINA and it’s application [J]. Water Resources and Power, 2012, 30(1): 135―138. (in Chinese)
[4]梅魁, 孟凡深. 粘弹性人工边界在ABAQUS中的实现及应用[J]. 水电能源科学, 2010, 28(7): 82-84.Mei Kui, Meng Fanshen. Implementation of viscoelastic artificial boundaries and its application in ABAQUS [J].Water Resources and Power, 2010, 28(7): 82―84.(in Chinese)
[5]李彬, 刘晶波. 粘弹性人工边界在Marc中的实现[C]//全国结构工程学术会议, 烟台市, 2005: 289-293.Li Bin, Liu Jingbo. Realization of visco-elastic artificial boundary in Marc [C]// Proceedings of the 14th National Conference on Structure Engineering, Yantai, 2005:289―293. (in Chinese)
[6]宋贞霞, 丁海平. 粘弹性人工边界在大型程序中的应用[J]. 防灾减灾工程学报, 2007, 27(增刊): 43-46.Song Zhenxia, Ding Haiping. Application of visco-elastic artificial boundaries in large program [J]. Journal of Disaster Prevention and Mitigation Engineering, 2007,27(Suppl): 43―46.(in Chinese)
[7]刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报, 1998, 31(3): 55-64.Liu Jingbo, Lv Yandong. A direct method for analysis of dynamic soil-structure interaction [J]. China Civil Engineering Journal, 1998, 31(3): 55―64. (in Chinese)
[8]黄胜, 陈卫忠, 伍国军, 等. 地下工程抗震分析中地震动输入方法研究[J]. 岩石力学与工程学报, 2010,29(6): 1254-1262.Huang Sheng, Chen Weizhong, Wu Guojun, et al. Study on method of earthquake input in aseismic analysis for underground engineering [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1254―1262. (in Chinese)
[9]赵源, 杜修力, 赵密, 等. 地下结构地震响应中的地震动输入探讨[J]. 土木建筑与环境工程, 2010, 32(增刊2): 192―197.Zhao Yuan, Du Xiuli, Zhao Mi, et al. Study on the seismic motion input of seismic response of underground structures [J]. Journal of Civil, Architectural &Environmental Engineering, 2010, 32(Suppl 2): 192―197. (in Chinese)
[10]孙纬宇, 欧尔峰, 严松宏. 基于黏弹性边界的地震动输入方法和边界条件选择研究[J]. 地震工程学报,2016, 38(6): 929-934.Sun Weiyu, Ou Erfeng, Yan Songhong. Earthquake input method and selection of boundary conditions based on viscoelastic boundaries [J]. China Earthquake Engineering Journal, 2016, 38(6): 929―934. (in Chinese)
[11]刘晶波, 杜义欣, 闫秋实. 粘弹性人工边界及地震动输入在通用有限元软件中的实现[J]. 防灾减灾工程学报, 2007, 27(增刊): 37-42.Liu Jingbo, Du Yixin, Yan Qiushi. Realization of viscoelastic artificial boundaries and seismic motion input in general finite element software [J]. Journal of Disaster Prevention and Mitigation Engineering, 2007,27(Suppl): 37―42.(in Chinese)
COMPARISON ON ARTIFICIAL BOUNDARIES AND SEISMIC WAVE INPUT METHODS IN SEISMIC ANALYSIS OF UNDERGROUND STRUCTURES
TAN Hui , LIU Jing-bo , WANG Dong-yang , BAO Xin , LI Shu-tao
(Department of Civil Engineering, Tsinghua University, Beijing 100084, China)
Abstract:For seismic analysis of underground structures, different computational models are used in existing studies. The two-dimensional soil model under vertical incident shear wave is performed by comparing different boundary conditions and wave fields selected for the calculation of equivalent input seismic loads. In order to simulate the condition of scattered wave produced by underground structures, the tunnel-soil model is established and its seismic response is calculated by different methods. The comparisons with the analytic solution or the remote boundary solution show that: in the seismic analysis of underground structures, the accuracy of seismic wave input is the highest, and the calculation result is the most reliable only when artificial boundary condition is set on all the cutoff boundaries; and the equivalent input seismic loads are calculated by incident wave field or by free wave field on the boundary with wave incidence, or by free wave field on the boundary without wave incidence.
Key words:seismic response of underground structures; wave method; seismic wave input; artificial boundaries; free field
中图分类号:TU311.3
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.05.S042
文章编号:1000-4750(2018)Suppl-0212-05
收稿日期:2017-05-09;修改日期:2017-10-30
基金项目:国家重点研发计划(2016YFC1402800);国家自然科学基金项目(51478247)
通讯作者:刘晶波(1956―),男,辽宁人,教授,博士,博导,从事结构工程及防灾减灾工程等工作(E-mail: liujb@mail.tsinghua.edu.cn).
作者简介:谭 辉(1989―),男,陕西人,博士生,从事地下结构抗震研究(E-mail:huitanhui@163.com);
王东洋(1988―),女,辽宁人,博士生,从事地下结构抗震研究(E-mail:dongyangw@126.com);
宝 鑫(1992―),男,辽宁人,博士生,从事结构抗震与减震研究(E-mail:18810456710@163.com);
李述涛(1984―),男,辽宁人,博士生,从事结构抗震与减震研究(E-mail:list16@mails.tsinghua.edu.cn).