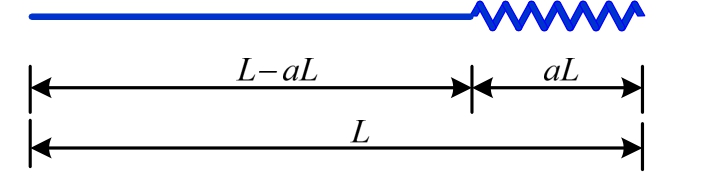
图1 杆件-节点弹簧串联示意图
Fig.1 Illustration of the series member-joint spring
杨风利
(中国电力科学研究院,北京 100192)
摘 要:在ANSYS中建立了考虑节点螺栓连接滑移特性的输电铁塔塔身节段三维有限元模型,分别计算得到了垂直荷载和水平荷载作用下塔身节段杆件轴力和节点位移,分析了螺栓连接节点类型、荷载类型和螺栓滑移距离对塔身节段杆件内力和变形的影响。垂直荷载作用下,斜材与主材节点螺栓连接滑移对塔身节段杆件轴力及节点位移的影响更为明显,塔身主材、塔腿斜材和第2节间倒K斜材轴力变化大都高于水平荷载工况;而水平荷载作用下,横隔面杆件与主材螺栓节点的连接滑移是主要影响因素,其对加载点附近塔身主材和交叉斜材轴力的影响显著,第3节间主材和交叉斜材轴力的变化幅度分别达到34.8%和45.2%。螺栓滑移距离对塔身主材和塔腿斜材轴力最大值影响较小,但对加载点竖向变形影响明显。
关键词:输电铁塔;连接滑移;弹簧单元;节点类型;荷载类型
螺栓孔径一般都要比螺栓直径大约 1.5 mm~2.0 mm,滑移量的大小取决于螺孔中螺栓的相对位置及螺栓间隙。现有输电铁塔计算中大都未考虑螺栓连接滑移,使某些工况下输电铁塔结构分析的精度甚至是准确度受到较大影响,这一影响涉及输电铁塔设计、运行维护和防灾减灾三个方面。一是输电铁塔设计时变形计算值偏小,低估了导线对地距离,造成输电线路存在放电等安全隐患;二是基础发生沉降、倾斜等大变形的情况下,输电铁塔杆件内力计算值偏高,结构设计偏于保守,也给输电铁塔运行维护带来了麻烦;三是螺栓连接滑移影响输电铁塔结构动力特性的计算精度,造成大风、断线等动力荷载和输电铁塔动力响应与实际情况存在一定偏差。
近十几年来,国内外学者提出了如理想连接滑移模型、线性模型、多项式模型以及指数模型等多种模型[1-3]。例如:Kitipornchai等[1]给出了瞬间滑移模型和连续滑移指数模型两种理想的连接模型。Ungkurapinan等[2]通过分析螺栓数量、间隙大小对连接滑移的影响,提出了一种采用分段多项式表达的螺栓连接滑移模型。这些成果可为研究输电铁塔螺栓连接节点的滑移模型提供重要参考和理论依据。
一些学者提出了在桁架结构分析中考虑连接滑移影响的方法和理论,但相关假设与螺栓节点的实际受力状况还存在一定区别,尤其是未能准确体现不同类型螺栓连接滑移形态和力学行为的差异,尚不能完全满足输电铁塔结构精细化分析的需求[4-8]。例如:基于虚功原理的增量位移计算方法中假定增量位移与螺栓连接节点上的外荷载无关。夏军武等[6]假定所有形式螺栓连接的刚度折减系数取值相同,引入有滑移杆件轴向刚度折减系数,编制了考虑滑移的空间弹性节点模型程序。王朋等[7]、舒前进等[8]分别采用 COMBIN39单元和等效应力-应变关系材料模型,在商业有限元软件ANSYS中实现了输电铁塔螺栓连接滑移的模拟。
尽管国内外学者均认为螺栓连接滑移对输电铁塔变形具有显著影响,但具体结论还存在一定差别。例如:江文强等[9]认为螺栓连接滑移影响程度与铁塔所受荷载形式有关,弯曲工况和扭转工况下起控制作用的分别是主材螺栓连接滑移和交叉斜材螺栓连接滑移。Ahmed等[10]则认为塔身主材螺栓连接滑移对竖向位移影响较大,斜材和横隔面杆件螺栓连接滑移对横向位移影响较大。对输电铁塔杆件内力的影响方面,不同学者的结论甚至相反。例如:Kitipornchai等[1]采用以垂直载荷为主的载荷工况,发现连接滑移对输电铁塔的极限承载力影响不大。部分学者的研究则表明,螺栓连接滑移对输电铁塔结构受力尤其是基础变形工况下的极限承载力影响显著。舒前进等[8]认为不考虑节点滑移影响时,计算得到的采动区输电铁塔基础位移限值过于保守。Ahmed等[10]认为对于冻融循环区基础变形铁塔,考虑螺栓连接滑移后塔腿轴力、交叉斜材轴力最大降低70%以上。造成上述差异存在的主要原因在于分析时未对输电铁塔荷载形式和荷载水平进行系统分类,且没有关注螺栓连接滑移与输电铁塔塔型、几何参数的关系,因而很难获得关于螺栓连接滑移对输电铁塔变形及内力影响的普遍规律。
本文以一个典型的塔身节段为研究对象,在通用有限元软件ANSYS中建立了考虑节点螺栓连接滑移特性的三维空间有限元模型,分析了螺栓连接节点类型、荷载类型、螺栓滑移距离对塔身节段杆件内力和变形的影响,获得了塔身节段杆件内力和节点变形在加载过程中的变化规律,可为后续深入研究考虑螺栓连接滑移的输电铁塔结构分析方法提供参考和依据。
1) 基本假定:杆件为线弹性的直杆,不考虑杆件、螺栓连接节点进入塑性的情况;节点在一个方向轴向受力时,对在另外方向产生的节点变形的影响忽略不计。
2) 基本原理:对于螺栓连接的空间桁架结构,螺栓连接节点一般采用弹簧单元模拟。与一般的空间桁架结构相比,原来的杆单元变为一个杆与弹簧串联的单元。如图 1所示,假定杆件的截面刚度为EA,总长度为L,螺栓节点长度为αL,除去节点剩余长度杆件的轴向刚度为K1=EA/(L-αL),螺栓节点刚度为KJ,则考虑螺栓节点影响的杆件刚度K为:K=K1KJ/(K1+KJ)。当KJ=EA/αL时,等效刚度K=EA/L,即考虑螺栓连接节点影响后的杆件刚度与杆件初始刚度一致,不会对杆件的受力或变形产生影响。

图1 杆件-节点弹簧串联示意图
Fig.1 Illustration of the series member-joint spring
本文的螺栓连接滑移模型采用分段多项式模型。图2所示的理想螺栓节点荷载-变形曲线共可以分为4个阶段。I区为线性摩擦传力阶段(微观滑移阶段),II区为外荷载基本不变的滑移阶段(宏观滑移阶段),III区为线性螺栓承压传递荷载阶段,IV区为非线性荷载传递阶段,直至螺栓节点达到其极限荷载。螺栓连接节点理想的荷载-变形曲线可以通过A、θ1、O、Q、B、R、C共7个参数进行描述,图2曲线的表达式如式(1)所示[2]。
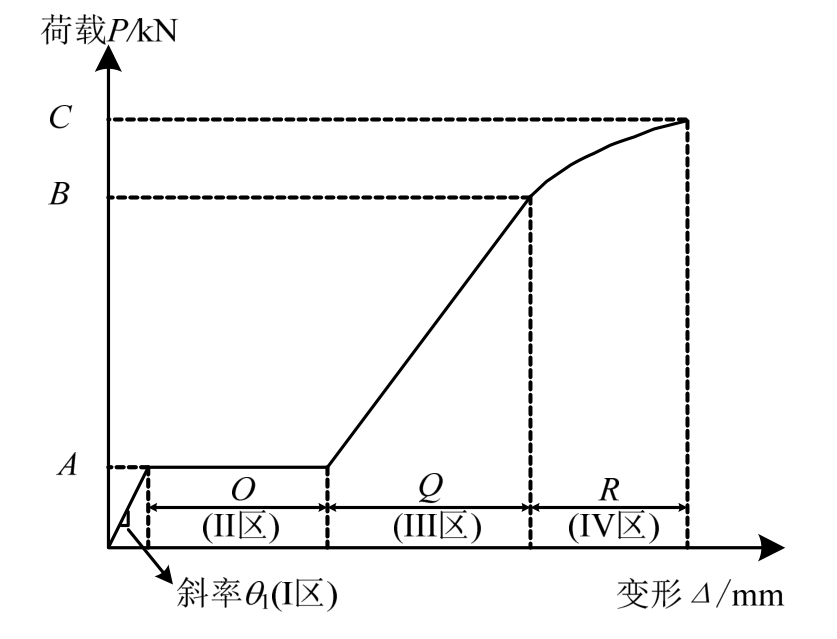
图2 理想的荷载-变形曲线
Fig.2 Idealized load-deformation curve

式中:P/kN为螺栓节点的轴向荷载;Δ/mm为螺栓节点的轴向变形。
IV区为螺栓节点非线性荷载-变形曲线,可采用三次多项式拟合,则式(1)中IV的表达式变为:
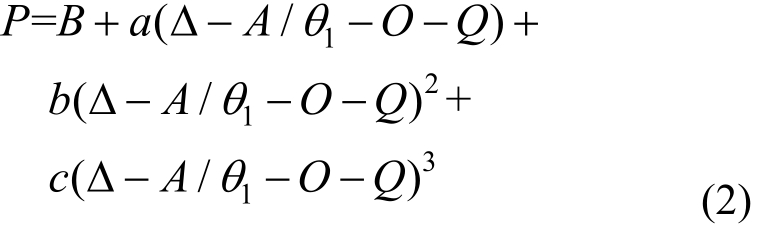
式中,a、b、c为三次多项式拟合参数。
由1.1节中的基本假定可知,本文研究中不考虑螺栓连接节点进入塑性阶段,因此选用分段多项式模型(I段~III段)描述螺栓连接节点的荷载-变形曲线。
以文献[7]中的塔身节段模型为研究对象,该模型中塔身主材采用 L40×3角钢,横隔面杆件和塔身斜材采用L25×3角钢,塔身第2和第3节间的正、侧面斜材非对称布置。在通用有限元软件ANSYS中建立塔身节段的三维有限元模型,其中塔身主材和横隔面杆件采用BEAM4梁单元模拟,塔腿斜材和塔身斜材采用LINK8杆单元模拟。塔身主材为一根连续杆件,中间无螺栓连接节点。分析中考虑横隔面杆件、斜材与塔身主材之间螺栓连接滑移的影响,分别在对应位置建立COMBIN39非线性弹簧单元,通过单元控制选项将其设定为轴向三维弹簧单元,弹簧单元长度可设置为杆件长度的1/1000。COMBIN39单元的荷载-变形曲线采用分段多项式模型,根据文献[7]中的螺栓节点拉伸试验曲线,L40×3角钢与L25×3角钢螺栓连接节点的滑移荷载A=2.2 kN,I区斜率θ1=14.7 kN/mm,滑移距离O=1.85 mm,III区线性段的临界荷载B=12 kN,III区线性段的变形量Q=2.2 mm。该类型角钢-角钢螺栓连接节点的简化荷载-变形曲线如图3所示。
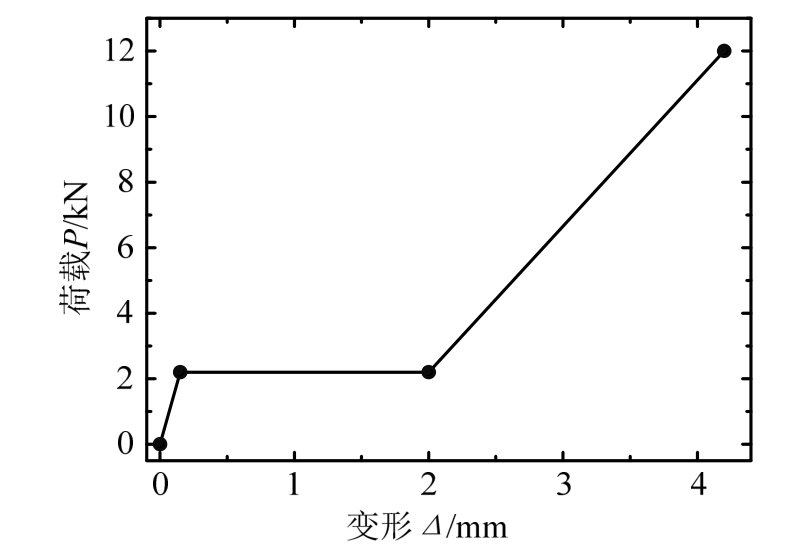
图3 角钢-角钢螺栓连接简化荷载-变形曲线
Fig.3 Load-deformation curve of an angle-angle steel bolt joint
为研究螺栓连接节点滑移及其类型对塔身节段受力和变形的影响,本次分析中建立三种模型。模型I:塔身主材及横隔面杆件采用梁单元、斜材采用杆单元的梁-杆混合单元模型简称;模型II:以模型I为基础,在横隔面杆件与塔身主材之间建立模拟螺栓连接节点弹簧单元的模型;模型III:以模型II为基础,在塔身斜材与塔身主材之间建立模拟螺栓连接节点弹簧单元的模型。“模型III”的ANSYS有限元分析模型及典型节点详图如图4(a)所示,模型具体尺寸可参见文献[7];为便于后面分析,塔身节段模型中的杆件类型及编号如图4(b)所示。
在ANSYS中打开大变形选项,通过非线性静力分析获得加载过程中塔身节段杆件轴力和节点位移的变化曲线,研究螺栓连接节点部位、螺栓间隙大小、荷载类型及大小对塔身节段模型节点螺栓连接滑移效应的影响规律。考虑两种荷载工况,工况1为图4中的塔脚B、C、D固定约束,塔脚A约束处UZ以外的所有自由度,在塔脚A处施加垂直荷载Pz=20 kN;工况2为塔脚A、B、C、D全部固定约束,在模型顶部节点E、F分别施加水平荷载Px=10 kN。工况1的荷载类型与采动区输电铁塔基础发生不均匀沉降的情况类似,工况2的荷载类型与大风作用下的情况类似。
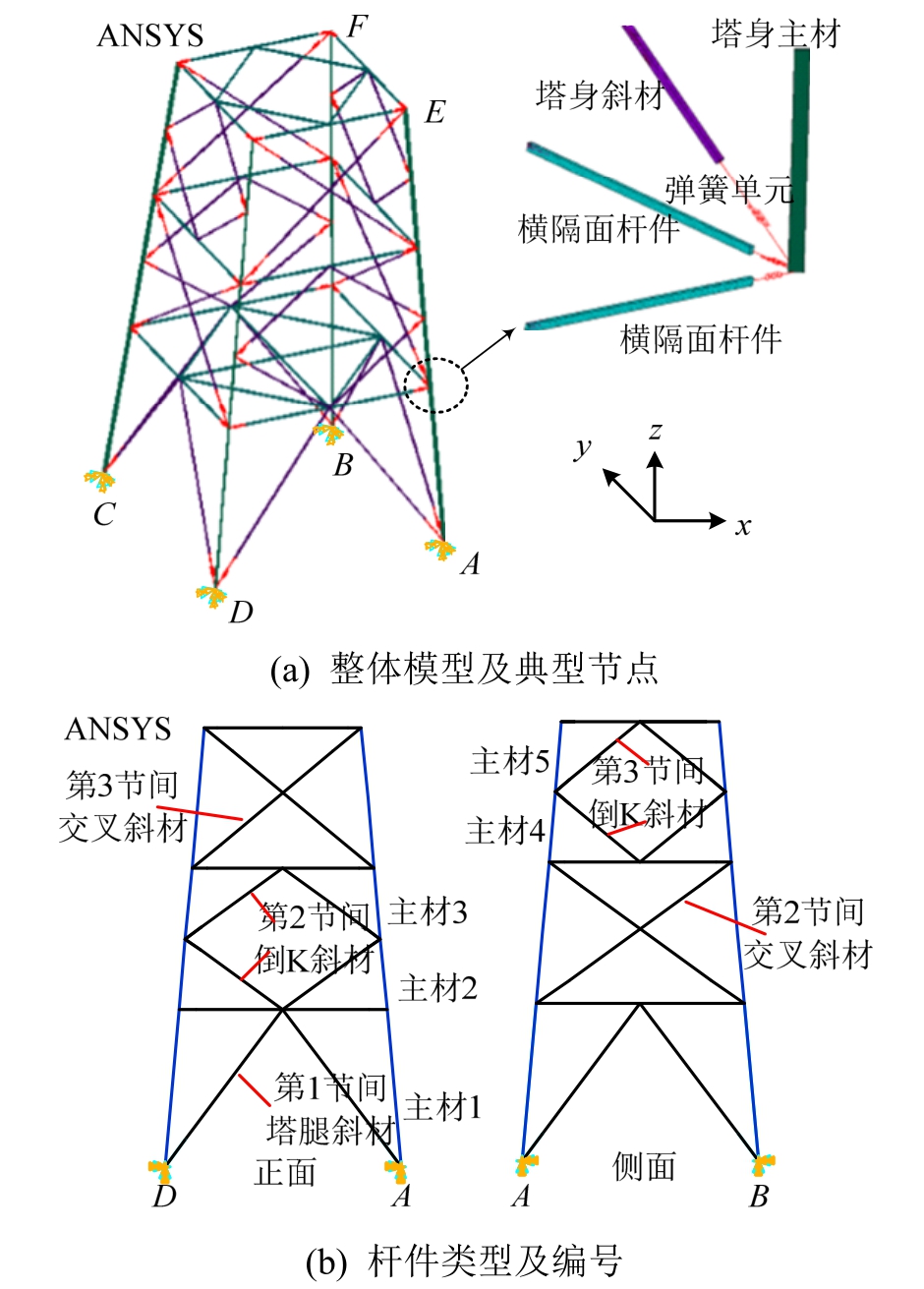
图4 塔身节段有限元模型及杆件说明
Fig.4 FEA model of tower body and illustration on members
由初步试算可知,在工况1和工况2荷载作用下,塔身节段杆件轴力均不会超过其承载力设计值,即塔身节段杆件均处于线弹性状态。假定杆件钢材强度级别为 Q345,同时考虑受压稳定和强度设计,主材和斜材杆件的极限承载力分别不低于20 kN和13 kN。
分别采用模型I、模型II和模型III,计算工况1荷载作用下塔身节段模型的轴力和A点竖向位移zA,图4中所示典型杆件轴力计算结果见表1,表中仅列出受压杆件的轴力。模型I、模型II和模型III计算得到的zA值分别为1.66 mm、1.78 mm和15.82 mm。当不考虑节点螺栓连接滑移影响即采用模型I计算时,杆件轴力计算值与文献[7]计算值基本一致。
表1 工况1的三种模型杆件轴力计算值对比
Table 1 Comparison on calculated member forces by three models for load case 1

由表1可知,模型II与模型I计算结果相比,仅考虑在横隔面杆件与主材之间建立螺栓连接单元,塔腿斜材轴力增大6.2%,塔身主材和斜材轴力减小6.3%~7.1%;A点竖向位移增加7.2%。模型III与模型I计算结果相比,若同时考虑横隔面杆件与主材、斜材与主材之间建立螺栓连接单元,从下到上的塔身主材轴力增加9.1%~49.6%,第2层和第3层倒K斜材轴力分别增大9.8%和5.4%,第2层和第3层交叉斜材轴力分别减小49.1%和18.7%;A点竖向位移增大约8.5倍。模型II和模型III中,考虑节点螺栓连接滑移对杆件刚度的影响后,原有杆件刚度变为杆件与弹簧的串联刚度,塔身节段各杆件的内力进行重新分配。在垂直荷载作用下,相对于横隔面杆件与主材螺栓连接节点,斜材与主材节点螺栓连接滑移对塔身节段杆件轴力及节点位移的影响更为明显。
在加载过程中,三种模型计算得到的主材1和塔腿斜材轴力变化曲线如图5所示。可以看出,模型I和模型II主材及斜材轴力随荷载增加而线性变化。在斜材轴力达到滑移荷载(2.2 kN)之前,斜材-主材螺栓连接节点处于微观滑移阶段,模型 III主材和斜材轴力线性增加,斜材轴力大于模型 I、模型II计算值,主材轴力小于模型I、模型II计算值;斜材轴力超过滑移荷载之后,主材及斜材轴力均呈现非线性变化,在螺栓宏观滑移阶段结束后,模型III斜材轴力小于模型I、模型II计算值,主材轴力大于模型I、模型II计算值。

图5 荷载(Pz)-轴力(N)曲线
Fig.5 Load (Pz)-axial force (N) curve
分别采用模型I、模型II和模型III,计算工况 2荷载作用下塔身节段模型的杆件轴力和加载点水平位移xE,螺栓连接节点的荷载-变形模型采用图3所示曲线。图4中所示典型杆件轴力计算结果见表 2,模型 I、模型 II和模型III计算得到的xE值分别为2.37 mm、5.10 mm和22.47 mm。
表2 工况2的三种模型杆件轴力计算值对比
Table 2 Comparison on calculated member forces by three models for load case 2

由表2可知,模型II、模型III与模型I的计算结果相比,第1和第2节间塔身主材轴力变化较小,考虑节点螺栓连接滑移影响后的杆件轴力变化范围为-0.7%~9.0%;节点螺栓连接滑移对加载点所在第 3节间的主材轴力影响较大,增大幅度为27.5%~34.8%。节点螺栓连接滑移对第1节间塔腿斜材、第2节间倒K斜材的影响较小,斜材轴力变化范围为-2.3%~1.7%;对加载点所在第3节间的交叉斜材轴力影响较大,模型II和模型III的计算轴力分别减小45.2%和35.8%。工况2侧面第2节间交叉斜材和第3节间倒K斜材轴力相对较小,其差异此处不做分析。
图6对比了工况1和工况2荷载作用下,模型II、模型III与模型I杆件轴力的相对差值分布。由图6(a)可以看出,与作用垂直荷载的工况1相比,当塔身节段顶部节点作用工况2的水平荷载时,考虑横隔面杆件与塔身主材节点螺栓连接滑移影响后,部分主材、斜材轴力变化趋势并不一致,例如考虑节点螺栓连接滑移使工况1的主材轴力略有减小,而工况2的第3节间塔身主材轴力则大幅增加;横隔面杆件与塔身主材节点螺栓连接滑移对加载点附近塔身主材和交叉斜材轴力的影响显著,说明这种类型的螺栓连接对水平荷载较为敏感。由图6(b)可以看出,同时考虑横隔面杆件与塔身主材、斜材与主材的节点螺栓连接滑移时,工况1作用下塔身主材、塔腿斜材和第2节间倒K斜材轴力相对差值大都高于工况2,而工况2作用下第3节间交叉斜材轴力的相对差值较大。

图6 轴力相对差值对比
Fig.6 Comparison on relative difference of axial forces
根据目前输电铁塔节点加工情况可知,螺杆与螺栓孔之间的间隙e一般在1.5 mm~2.0 mm。受螺栓初始安装状态的影响,螺栓构造间隙有最大构造间隙2e、理想构造间隙e和最小构造间隙为零三种情况。对照图3中的荷载-变形曲线,滑移距离O取0.5 mm、1.5 mm、2.5 mm和3.5 mm,其他参数不变。采用模型III分析工况1作用下塔身节段模型的杆件内力和节点位移,加载过程中不同滑移距离下塔身节段杆件轴力-节点位移曲线如图7所示。由图7(a)可以看出,滑移距离对主材轴力最大值影响较小,但对A点竖向变形影响明显,四种滑移距离O对应的A点竖向变形 zA最大值依次为 1 1.8 6 m m、15.17 mm、17.53 mm和20.17 mm。由图7(b)可以看出,斜材轴力达到滑移临界荷载前,滑移距离O对斜材轴力和A点竖向变形均没有影响;斜材轴力达到临界滑移荷载后,滑移距离O越大,则A点竖向变形zA的滑移段越长;螺栓连接节点的宏观滑移结束后,塔腿斜材轴力随则A点竖向变形zA线性增大,而滑移距离O对斜材轴力最大值的影响并不明显。

图7 轴力(N)-节点位移(zA)曲线
Fig.7 Axial force (N)-nodal displacement (zA) curve
本文考虑输电铁塔螺栓连接滑移特性,对某典型塔身节段进行了垂直荷载和水平荷载两种工况作用下的非线性静力分析,研究了螺栓连接节点类型、荷载类型和螺栓滑移距离对塔身节段杆件内力和变形的影响,得到了如下结论:
(1) 螺栓连接滑移对杆件轴力和节点变形的影响程度与节点类型和荷载类型有关。垂直荷载作用下,相对于横隔面杆件与主材螺栓连接节点,斜材与主材节点螺栓连接滑移对塔身节段杆件轴力及节点位移的影响更为明显;而水平荷载作用下,横隔面杆件与主材螺栓节点的连接滑移是主要影响因素。与垂直荷载工况相比,当塔身节段顶部节点作用水平荷载时,横隔面杆件与塔身主材螺栓连接滑移对加载点附近塔身主材和交叉斜材轴力的影响显著;同时考虑横隔面杆件与塔身主材、斜材与主材的螺栓连接滑移时,垂直荷载作用下塔身主材、塔腿斜材和第2节间倒K斜材轴力变化大都高于水平荷载工况,而水平荷载作用下第3节间交叉斜材轴力的变化较大。
(2) 螺栓滑移距离对塔身主材轴力最大值影响较小,但对加载点竖向变形影响明显。斜材轴力达到滑移临界荷载前,滑移距离对斜材轴力和加载点竖向变形均没有影响;斜材轴力达到临界滑移荷载后,滑移距离越大,则加载点竖向变形的滑移段越长;螺栓连接节点的宏观滑移结束后,塔腿斜材轴力随则加载点竖向变形线性增大,而滑移距离对斜材轴力最大值的影响不明显。
参考文献:
[1]Kitipornchai S, AI-Bermani F G A, Peyrot A H, et al.Effect of bolt slippage on ultimate behavior of lattice structures [J].Journal of Structural Engineering, 1994,120(8): 2281―2287.
[2]Ungkurapinan N, De S R, Chandrakeerthy S, Rajapakse R K N D, et al. Joint slip in steel electric transmission towers [J]. Engineering Structures, 2003, 25: 779―788.
[3]杨风利, 朱彬荣, 邢海军. 输电铁塔螺栓节点连接滑移特性及模型参数研究[J]. 工程力学, 2017, 34(10):116―127.Yang Fengli, Zhu Binrong, Xing Haijun. The slip characteristics and parametric study of bolted connections for transmission towers [J]. Engineering Mechanics, 2017, 34(10): 116―127. (in Chinese)
[4]Yang Fengli, Zhu Binrong, Li Zheng. Numerical analysis and full-scale experiment on K-joint deformations in the crank arms of lattice transmission towers [J]. Structural Design of Tall and Special Buildings, 2018, 27(5): 1―15.
[5]李文武, 黄才良, 张哲. 非线性间隙杆单元的特性及其迭代算法[J]. 工程力学, 2011, 28(1): 65―69.Li Wenwu, Huang Cailiang, Zhang Zhe. Mechanical behavior of nonlinear gap truss element and its iterative calculation method [J]. Engineering Mechanics, 2011,28(1): 65―69. (in Chinese)
[6]夏军武, 孙冬明, 董正筑. 考虑滑移的空间弹性节点“模糊”精化分析及其在送电线路铁塔中的应用[J].工程力学, 2012, 29(6): 292―299.Xia Junwu, Sun Dongming, Dong Zhengzhu. “Fuzzy”precision analysis of space flexible joint with slippage and its application in transmission line tower [J].Engineering Mechanics, 2012, 29(6): 292―299. (in Chinese)
[7]王朋, 高康, 黄伟东, 等. 螺栓滑移对格构式结构静动态特性的影响研究[J]. 固体力学学报, 2013, 33(增刊1): 211―215.Peng Wang, Kang Gao, Weidong Huang, et al. Effect of bolt slippage on the static and dynamic response of lattice structure[J]. Chinese Journal of Solid Mechanics,2013, 33(Suppl 1): 211―215. (in Chinese)
[8]舒前进, 袁广林, 王永安, 等. 考虑节点滑移时采动区输电铁塔基础的位移限值[J]. 中国矿业大学学报,2014, 43(1): 16―22.Shu Qianjin, Yuan Guanglin, Wang Yongan, et al. Limits to foundation limits on electrical transmission tower with joint slippage considered in mining subsidence areas [J].Journal of China University of Science & Technology,2014, 43(1): 16―22. (in Chinese)
[9]江文强. 构造节点的精细模拟及其在输电铁塔结构分析中的应用[D]. 保定: 华北电力大学, 2011.Jiang Wenqiang. Accurate modeling of structural joint and its application in lattice transmission tower analysis[D]. Baoding: North China Electric Power University, 2011. (in Chinese)
[10]Ahmed K I E, Rajapakse R K N D, Gadala M S.Influence of bolted-joint slippage on the response of transmission towers subjected to frost-heave [J].Advances in Structural Engineering, 2009, 12(1) : 1―17.
STRUCTURAL ANALYSIS ON A TYPICAL TRANSMISSION TOWER BODY SECTION WITH BOLT SLIPPAGE EFFECTS
YANG Feng-li
(China Electric Power Research Institute, Haidian District, Beijing 100192, China)
Abstract:By considering bolt slippage effect, three dimensional FEA model for a typical transmission tower body section was established in general software ANSYS. The member axial forces and the nodal deflections were separately calculated under vertical and horizontal loading. The effects of bolted joint type, load type and bolt slip distance on member axial forces and on nodal deflections were analyzed. For the vertical loading case, the bolt slippages between diagonal members and main members have a more significant effect on member axial forces and on nodal deflections. The axial force variations of the main member, the leg diagonal member and the inverse K diagonal member at the second segment are almost higher than those of the horizontal load case. For the horizontal load case, the variations of axial forces and nodal deflections are mainly induced by the bolt slippages between transverse separator members and main members. These bolt slippages have significant effects on the main member axial forces and on the horizontal nodal deflections near the loading points. The axial force variations of the main members and the diagonal members at the third segment are up to 34.8% and 45.2%,respectively. The bolt slippage distance has little effect on the maximum axial forces of main members and leg diagonal members. However, it has a significant effect on the vertical deflection at the loading point.
Key words:transmission tower; bolt slippage; spring element; joint type; load type
中图分类号:TM753
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.04.S039
文章编号:1000-4750(2018)Suppl-0193-07
收稿日期:2017-04-18;修改日期:2017-10-29
基金项目:国家自然科学基金项目(51408568)
作者简介:杨风利(1980―),男,河北人,教授级高工,博士,从事输电线路结构及防灾减灾研究(E-mail: yangfl1@epri.sgcc.com.cn).