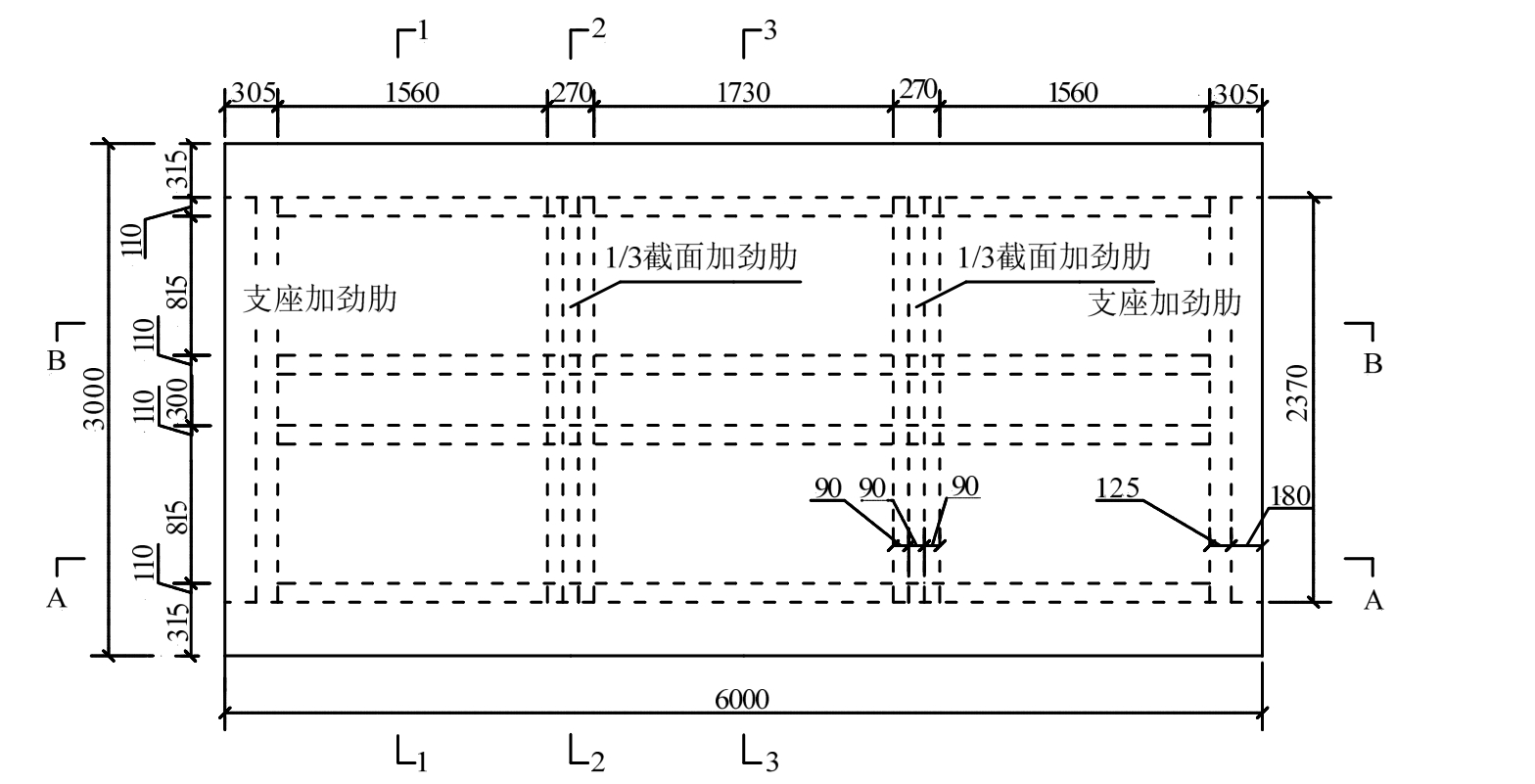
图1 箱梁模型平面布置尺寸图
Fig.1 Box girder model plane layout size figure
祝明桥,张紫薇,蒋 俏,石卫华
(湖南科技大学土木工程学院,湖南,湘潭 411201)
摘 要:该文对双层交通箱梁试验模型的顶板不同位置在弹性范围内进行单点加载(6个工况)的试验研究。基于试验结果建立有限元模型对其进行分析,在分析值与试验值吻合良好的基础上,进一步探究了双层交通混凝土箱梁的传力路径。研究表明:箱梁的桥面板按双向板传递;节间荷载(内横梁、纵梁)的剪力按简支梁形式传到节点,再按节点的荷载分配系数分到到每榀框架梁,最后传到两端支座。
关键词:双层交通;混凝土箱梁;数值模拟;传力路径;荷载分配系数
混凝土箱梁具有良好的受力性能,通过取消其横隔板,使顶、底板均成为桥面系,同时在腹板上开设必要的孔洞以满足通风、采光及消防等要求,可实现双层交通[1]。混凝土双层交通箱桥梁[2]特别适用于中小跨度的城市桥梁,其既可有效缓解城市土地资源紧缺,又能极大地缓解城市交通流量[3]。
双层交通混凝土箱梁取消了传统箱梁结构中的横隔板,并在梁腹板开设孔洞。这种新型结构能否直接采用传统混凝土箱梁理论,箱梁室内能否实现交通,仍需进行研究。因此,对于双层交通混凝土箱梁的相关研究具有重要的意义。
本文以双层交通混凝土箱梁的 1∶8缩尺试验模型为基础,对箱梁模型的顶板在弹性范围内分别进行了单点加载(6个工况)试验研究,并建立了有限元模型对试验进行模拟分析。在分析值与试验值吻合良好的基础上,进一步探究了双层交通混凝土箱梁的传力路径。
双层交通箱试验模型按照与实桥 1∶8左右的比例设计浇筑而成,其混凝土强度等级为C40,采用HPB300和HRB335钢筋。箱梁模型采用宽顶板、窄底板、直腹板的单箱三室截面,并于腹板上开孔以满足箱内通风、采光、消防、逃生等要求,开孔形式采用了圆形和椭圆形等形式,该模型取消了常规设置的横隔板,用横向加劲肋来替代横隔板,使其顶板、底板均成为桥面系。试验模型平面图如图1所示。腹板处具体开孔尺寸如图2所示,图中左边为边腹板A-A剖面尺寸,右边为B-B剖面尺寸。

图1 箱梁模型平面布置尺寸图
Fig.1 Box girder model plane layout size figure
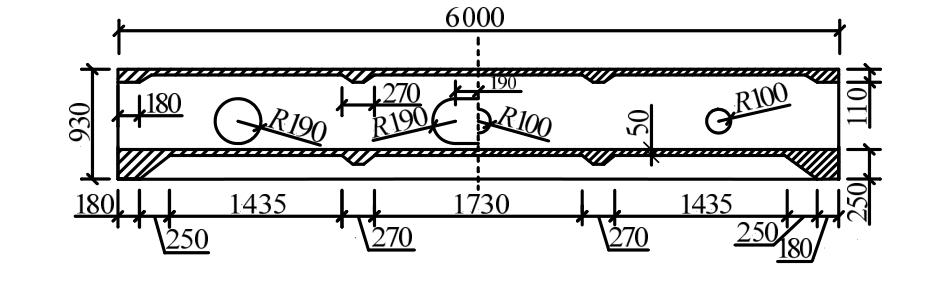
图2 边腹板A-A与中腹板B-B剖面尺寸图
Fig.2 Section diagram of A-A edge web with B-B middle web
考虑到腹板开孔、横向加劲肋对箱梁模型的影响以及箱梁试验模型的对称性,将箱梁的关键截面即箱梁的控制截面选在1/6处开孔的截面1-1、1/3处加劲肋截面2-2、1/2处跨中截面3-3,具体截面尺寸如图3所示。其中1-1截面和3-3截面尺寸一样,图中左边为加劲肋截面2-2,右边为1-1截面和3-3截面。

图3 3个控制截面的截面尺寸图
Fig.3 The sectional dimension of three control sections
由于试验箱型梁模型各个部件的对称分布,因此只需选择箱梁的主要键部件,对其进行局部集中加载试验和组合局部集中加载试验;试验的关键部件有箱梁桥面板B1,顶板加劲肋J1,纵向梁L1、L2,以及箱型梁边节点JD1、中节点JD2。单点加载设计了6种试验工况;分别是在弹性范围内对部件B1、J1、L2、L1、JD2、JD1上施加局部集中荷载,加载点的位置及集中荷载的大小如图4所示。在箱梁的3个控制截面的纵向腹板梁下分别设置4个一维位移计来测量挠度。在顶板中跨中以及板的四条边的中间贴有应变片,具体如图5所示,并在顶板跨中布置了位移计用于测量顶板的中心挠度。采用钢板作为加载砝码,在正式试验前进行相关预加载,检查位移计测得的挠度、应变采集箱采集的应变数据是否异常。
工况1为对顶板桥面板B1单点加载,所施加的总荷载为 10 kN;顶板 B1的尺寸为 815 mm×1560 mm×50 mm,其长短边之比为 1.911,属于双向板。随着荷载逐渐增加,B1板的4条边中部应变及板中心挠度也随之增加,其变化趋势如图6所示。
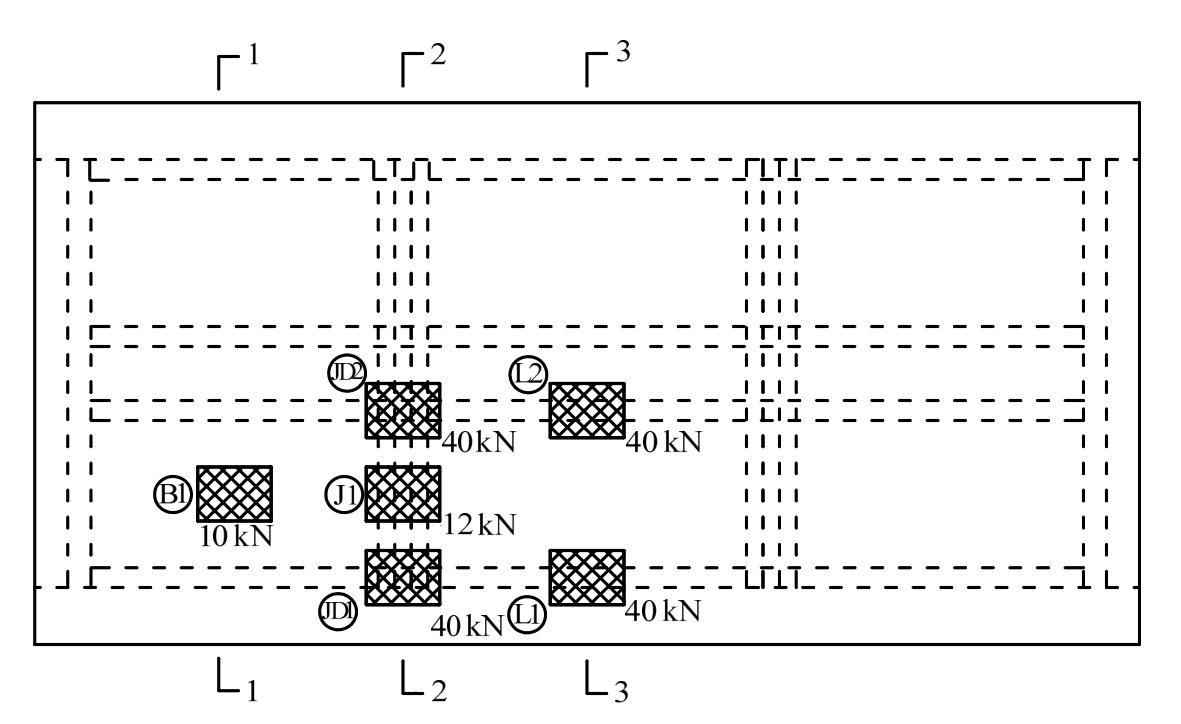
图4 单点加载位置图
Fig.4 Single point load locations
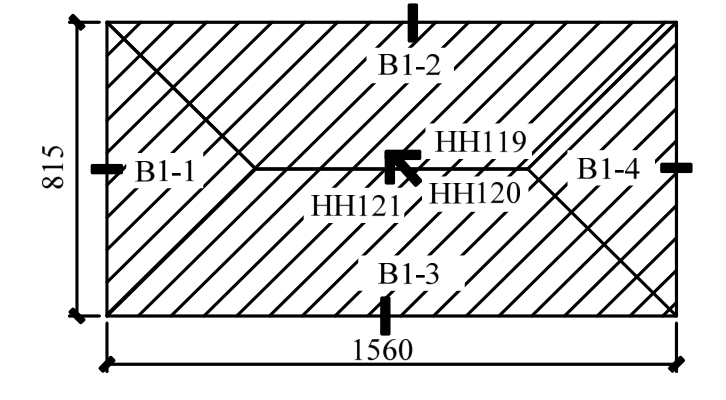
图5 顶板B1
Fig.5 The roof B1

图6 板的应变及挠度变化图
Fig.6 The strain and deflection of plate
从图6可以看出B1中心挠度以及其应变变化情况与试验荷载加载值呈线性关系,整体试验过程处于弹性阶段,与预期试验控制在弹性范围内基本相同,板4条边的应变基本稳定,其长短边的应变之比为2.81左右,其与B1按双向板划分区域图5的等腰梯形与等腰三角形的面积之比 2.82吻合较好,符合双向板的传力特征。表明顶板B1承受荷载时按双向板进行荷载传递。在弹性范围内该顶板每条长边分配的比例为36.9%,每条短边分配的比例为13.1%。
工况2为对顶板加劲肋J1跨中加载,所施加的总荷载为12 kN,加劲肋J1跨度为815 mm,计算净跨为695 mm,截面为T形截面,如图7所示。

图7 J1加劲肋形式
Fig.7 The form of stiffening rib J1

图8 顶板加劲肋J1跨中挠度
Fig.8 The mid-span deflection of roof stiffening rib J1
图 8中的铰接挠度-荷载关系曲线由公式![]() 计算得到,固接挠度-荷载关系曲线由
计算得到,固接挠度-荷载关系曲线由![]() 公式计算得到。实测的挠度曲线基本呈直线变化,符合弹性范围内试验特征。从图8可知,加劲肋跨中挠度曲线位于两端固接与铰接之间。
公式计算得到。实测的挠度曲线基本呈直线变化,符合弹性范围内试验特征。从图8可知,加劲肋跨中挠度曲线位于两端固接与铰接之间。
工况3、工况4分别为对中腹板梁L2及边腹板梁L1的跨中单点集中加载试验,分别加载40 kN,试验测得两种工况下箱型梁3个控制截面挠度值分布规律如图9(a)、图9(b)所示。
工况5、工况6试验位置分别为中节点JD2、边节点JD1,两节点都处于箱型梁整体1/3跨度的2-2截面;两种工况节点处施加的总荷载均为40 kN,试验过程中具体挠度分布如图9(c)、图9(d)所示。
从图9可以看出,工况5、工况6与前面对应工况3、工况4挠度分布情况基本相同;在不同工况作用下,该箱梁模型3个控制截面的挠度分布曲线呈现出一致的变化规律,且2-2截面与3-3截面的挠度分布曲线较为接近,这说明了3-3截面开孔处的环箍对截面横向刚度起到了一定的补强作用。


图9 不同工况下3个控制截面的挠度分布图
Fig.9 Deflection distribution of three control sections under different working conditions
本文采用ABAQUS[4-6]对试验箱梁建模,钢筋和混凝土分别采用T3D2和C3D8R单元模拟,钢筋本构采用双线性模型,混凝土采用混凝土损伤塑性模型,边界条件与试验一致,有限元模型如图 10所示。

图10 箱梁有限元模型
Fig.10 Box girder finite element model
通过适当地调整箱梁模型的网格大小及相关参数,利用 ABAQUS分析软件对已做的箱梁弹性范围内的4个工况进行数值模拟,并且与试验所得的结果进行了对比分析。图11表示工况3、工况4、工况5和工况6的箱梁模型跨中截面的挠度分布对比图。

图11 跨中截面的挠度对比分析
Fig.11 Contrast analysis of deflection of cross section
从图 11可以看出,有限元分析得到的挠度与试验实测值吻合较好,说明采用 ABAQUS软件进行箱梁数值模拟是合理可行的。
为了更好地分析试验箱梁模型的传力路径,结合箱梁的设计理论及截面形式,可将箱梁顶板与腹板交界处的主梁、箱梁底板与腹板交界处的主梁及连接其上层主梁与下层主梁之间的腹板作为一榀框架,因此整个箱梁试验模型可简化成由 ZKJ1、ZKJ2、ZKJ3、ZKJ4 这四榀纵向框架和 HKJ1、HKJ2、HKJ3、HKJ4这四榀横向框架构成的空间刚架体系,如图12所示。

图12 刚架平面示意图
Fig.12 The schematic diagram of rigid plane
本文通过箱梁荷载横向分布系数[7―10]来分析箱梁的传力路径。结合双层交通箱梁模型的特点,选择刚性横梁法[11](偏心压力法)、刚接梁法以及位移挠度法来计算节点加载的荷载横向分布系数;将该荷载分配系数计算的每榀纵向框架所承受的荷载与箱梁有限元模型对应工况分析中提取出四榀纵向框架下各支座反力,并将反力进行求和得到每榀纵向框架所承受的荷载,进行对比。
1) 刚性横梁法
由于假定横梁是刚体,在荷载P的作用下,中间横梁像一片刚度无穷大的刚性梁一样保持直线形状,因此可以按刚体力学关于力的平移原理将荷载P移到扭转中心,用一个作用在扭转中心上的竖向力P和一个作用于刚体上的偏心力矩M代替。偏心荷载的作用应为P和M作用的叠加。
表1给出了刚性横梁法计算得到的四榀纵向框架的荷载横向分配系数。
表1 刚性横梁法计算得到的荷载分配系数
Table 1 Load distribution coefficient of rigid beam method

2) 横向刚接梁法[12]
刚接梁法的基本假定是在铰接板(梁)桥计算理论(只传递竖向剪力)的基础上,在铰接处补充引入赘余弯矩,就可建立计及横向刚性连结特点的赘余力正则方程,其适用于翼缘板刚性连接的肋梁桥。
计算步骤为:1) 求主梁截面竖向惯矩;2) 求主梁截面抗扭惯矩;3) 求内横梁的截面竖向抗弯惯矩并化成等刚度桥面板的抗弯惯矩;4) 求主梁的抗弯刚度与抗扭刚度比例参数γ和主梁抗弯刚度与桥面板抗弯刚度比例参数β;5) 根据计算出来的系数,并参考文献中刚接板、桥梁荷载横向分布影响线表,可以查得边主梁的横向分配系数以及中主梁的横向分配系数。
表2给出了横向刚接梁法计算得到的四榀纵向框架的荷载分配系数。
表2 横向刚接梁法计算得到的荷载分配系数
Table 2 Load distribution coefficient obtained by transverse rigid connection beam method

3) 位移挠度法
试验测得3个控制截面处ZKJ1~ZKJ4的挠度分布比例基本一致,通过计算对比可以发现每个控制截面的四4个挠度值之间的比例关系基本相同;本文取3个控制截面的4个挠度值之间的比例关系的平均比例作为不同梁上加载的荷载横向传递分配系数。即可得到中节点加载和边节点加载时ZKJ1~ZKJ4荷载横向分配系数。
表3 位移挠度法计算得到的荷载分配系数
Table 3 Load distribution coefficient obtained by displacement deflection method
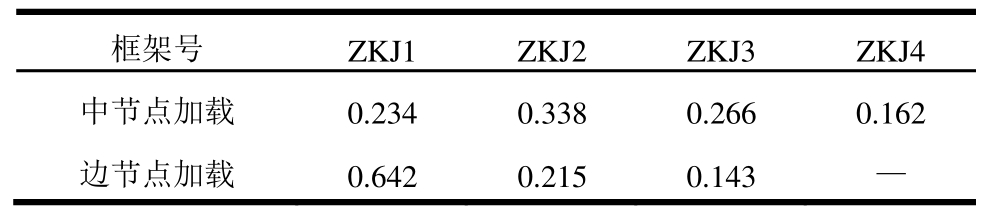
通过上述不同方法得到的荷载横向分配系数,可以计算出四榀纵向框架 ZKJ1~ZKJ4所分配的荷载值,与分析值进行对比,两者之间的误差如表4、表5所示。
表4 中节点加载时荷载分配计算值与分析值的误差 /(%)
Table 4 The error between the calculated value and the analytical value of load distribution under loading at intermediate node

表5 边节点加载时荷载分配计算值与分析值的误差 /(%)
Table 5 The error between the calculated value and the analytical value of load distribution under loading at the edge node

可以看出:3种计算方法中,用位移挠度法计算的结果与分析值最接近。故本文采用位移挠度法进行相关计算与分析。
桥面板按双向板传递;节间荷载(内横梁、纵梁)的剪力按简支梁形式传到节点,再按节点荷载分配到每榀框架,得到与分析值之间的差值如表6所示,相差比例基本上在16%以内,因此可基本认为双层交通箱梁构件的试验荷载主要由板、加劲肋、腹板梁传递给边节点和中节点,再按节点荷载横向分布系数分配到每榀框架梁。
表6 箱梁不同部位加载时荷载分配计算值与分析值的差值 /(%)
Table 6 The difference between the calculated value and the analytical value of load distribution under loading at different parts of box girder

4) 修正后的横向刚接法
考虑到位移挠度法得到的横向分布系数是根据试验挠度得到的,局限性较大。因此进一步针对前文介绍的横向刚接法,对其进行一定的修正,为工程应用提供一定的依据。按横向刚接法计算得到的横向分布系数,针对不同的加载位置,对 ZKJ1和ZKJ2的横向分布系数进行修正,在ZKJ1加载时,ZKJ2的乘以系数0.5;在ZKJ2加载时,ZKJ1的乘以系数 0.5;荷载分配系数如表 7所示,其与分析值之间的差值如表8所示。可以看出,用修正后的横向刚接法计算得到的反力与分析值的误差比例在12%以内。由此可知,该修正方法基本可行。
表7 对横向刚接梁法修正得到的荷载分配系数
Table 7 Load distribution coefficient corrected for transverse rigid beam method
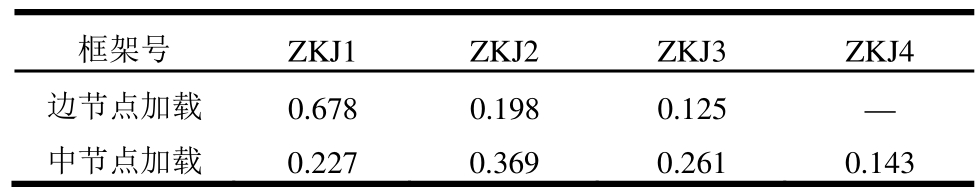
表8 修正后的荷载分配计算值与分析值的差值 /(%)
Table 8 The difference between the corrected calculated value and the analytical value of load distribution

综上所述,可得出以下结论:
顶板单点加载时,荷载按双向板传力规律分配至支承板的 4个梁上,每条长边分配的比例为36.9%,每条短边分配的比例为13.1%。
运用ABAQUS建立双层交通箱梁的数值模型,对6个试验工况进行了分析,分析结果与试验值吻合较好,验证了该数值模型的合理可行性。
比较了刚性横梁法、横向刚接梁法以及位移挠度法计算的节点加载的横向分布系数,发现位移挠度法的计算结果较接近试验值;在此基础上,对横向刚接梁法进行了修正,修正后的横向刚接梁法可有效计算四榀框架梁的横向分配荷载。
参考文献:
[1]祝明桥, 蒋伟中, 霍海强. 混凝土巨型箱形截面梁及其设计理论[J]. 建筑科学与工程学报, 2010, 27(3):85―88.Zhu Mingqiao, Jiang Weizhong, Huo Haiqiang. Design theory of concrete giant box beam [J]. Journal of Architecture and Civil Engineering, 2010, 27(3): 85―88.(in Chinese)
[2]汪建群, 谢子蓉, 祝明桥, 等. 面向双层交通的混凝土箱梁抗弯性能试验研究[J]. 工程力学, 2016, 33(增刊):196―200.Wang Jianqun, Xie Zirong, Zhu Mingqiao, et al.Experimental study on the bending performance of concrete box girder oriented to the double traffic [J].Engineering Mechanics, 2016, 33(Suppl): 196―200. (in Chinese)
[3]杨永贤, 张天明, 于长皓, 等. 重庆高家花园复线桥公轨双层交通方案构思[J]. 交通科技, 2013(5): 100―103.Yang Yongxian, Zhang Tianming, Yu Changhao, et al.The concept of double-track public transportation in Chongqing Gaojia Garden double-track bridge [J].Transportation Science & Technology, 2013(5): 100―103. (in Chinese)
[4]刘展, 祖景平, 钱英莉, 等. ABAQUS6.6 基础教程与实例详解[M]. 北京: 中国水利水电出版社, 2008.Liu Zhan, Zu Jingping, Qian Yingli, et al. Based tutorials and example explanation of ABAQUS6.6 [M].Beijing: China Water & Power Press, 2008. (in Chinese)
[5]王玉琢, 傅传国. ABAQUS 结构工程分析与实例详解[M]. 北京: 中国建筑工业出版社, 2010.Wang Yuzhuo, Fu Chuanguo. ABAQUS structural engineering and example explanation [M]. Beijing:China Architecture Industry Press, 2010. (in Chinese)
[6]ABAQUS Analysis Users Manual ABAQUS Inc [M].2006.
[7]章娜娜, 陈永生, 卢稳健. 公路桥梁荷载横向分布系数综述[J]. 四川建筑, 2009, 29(6): 148―150.Zhang Nana, Chen Yongsheng, Lu Wenjian. Summary of load transverse distribution coefficient of highway and bridge [J]. Sichuan Architecture, 2009, 29(6): 148―150.(in Chinese)
[8]陈勇军, 张会远. 桥梁横向分布系数计算方法对比分析研究[J]. 公路工程, 2015, 40(3): 148―151.Chen Yongjun, Zhang Huiyuan. Comparison and analysis of calculation methods for lateral distribution coefficient of bridges [J]. Highway Engineering, 2015, 40(3): 148―151. (in Chinese)
[9]Li Chong, Niu Yuting, Li Songhui. Study on the transverse load distribution coefficient of different spans of reinforced concrete rigid fame arch bridge [J]. Applied Mechanics and Materials, 2011, 94/95/96: 1070―1073.
[10]陈记豪, 赵顺波, 赵继涛. 既有预应力空心板桥加宽设计的荷载横向分布的计算方法[J]. 工程力学, 2012,29(9): 265―271.Chen Jihao, Zhao Shunbo, Zhao Jitao. Calculation method of lateral distribution of load for widening design of pre-stressed hollow slab bridges [J]. Engineering Mechanics, 2012, 29(9): 265―271. (in Chinese)
[11]Liu Hanbing, Wang Baiying, Wang Xianqian, Jiao Yubo.Calculation of bridge transverse load distribution coefficient based on generalized rigid cross-beam method[J]. Advanced Materials Reserch, 2013, 694/695/696/967: 3164―3167.
[12]李国豪. 公路桥梁荷载横向分布计算[M]. 北京: 人民交通出版社, 1984.Li Guohao. Calculation of lateral distribution of highway and bridge load [M]. Beijing: China Communications Press, 1984. (in Chinese)
EXPERIMENTAL ANALYSIS ON THE FORCE TRANSMISSION PATH OF A DOUBLE-DECK TRAFFIC CONCRETE BOX GIRDER
ZHU Ming-qiao , ZHANG Zi-wei , JIANG Qiao , SHI Wei-hua
(School of Civil Engineering, Hunan University of Science and Technology, Xiangtan, Hunan 411201, China)
Abstract:Experimental studies of single point loading (6 working conditions) in the elastic range of the roof of a double-deck box girder test model was carried out. A finite element model was developed, and the force transmission path of the double-deck traffic concrete box girder was further explored on the basis of good agreement between the analytical and the experimental values. The analysis showed that the bridge deck of the box girder was transmitted by the two-way plate. The shear force of the internode load (inner beam and stringer)was transmitted to the node in the form of a simply supported beam, and then the load distribution coefficient of the joint was divided into each frame beam, and finally reached the ends of the bearing.
Key words:double-deck traffic; concrete box girder; numerical simulation; force transmission path; load distribution coefficient
中图分类号:U448.12
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.05.S035
文章编号:1000-4750(2018)Suppl-0181-07
收稿日期:2017-05-03;修改日期:2017-12-26
基金项目:国家自然科学基金项目(51378202,51578236)
通讯作者:祝明桥(1968―),男,安徽太湖人,教授,博士,主要从事混凝土结构理论及其新材料应用研究(E-mail: 1531290279@qq.com).
作者简介:张紫薇(1993―),女,河南新乡人,硕士生,主要从事混凝土结构理论及其新材料应用研究(E-mail: 953129428@qq.com);
蒋 俏(1992―),女,湖南娄底人,硕士生,主要从事混凝土结构理论及其新材料应用研究(E-mail: 824743550@qq.com);
石卫华(1978―),男,湖南衡阳人,讲师,博士,主要从事钢-混凝土组合结构研究(E-mail: 26493494@qq.com).