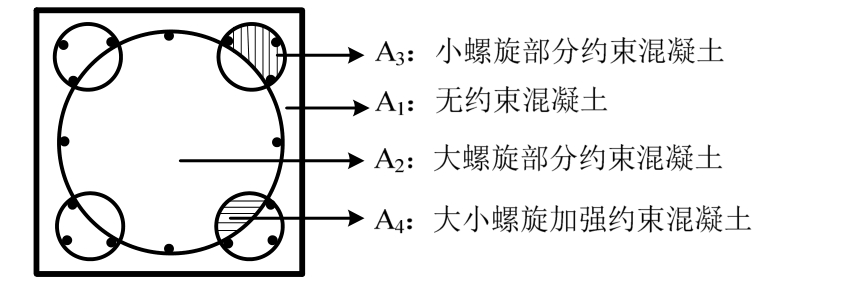
图1 多螺旋箍筋混凝土柱截面
Fig.1 Typical cross-section of multi-spiral hoops reinforced concrete column
唐 琼1,李 易1,陆新征2,闫维明1
(1. 北京工业大学工程抗震与结构诊治北京市重点实验室,北京 100124;2. 清华大学土木工程安全与耐久教育部重点实验室,北京 100084)
摘 要:多螺旋箍筋能够显著提高矩形混凝土柱的轴压承载力。该文采用有限元方法分析了多螺箍筋约束对矩形混凝土截面应力分布和幅值的影响。采用试验数据对多国规范的约束混凝土柱轴压计算方法进行了分析验证,分析了不同计算方法引起承载力计算结果出现差异的因素。基于数值分析结果,推导了适用于多螺旋箍筋柱的轴压承载力计算公式,其中不同部位的混凝土根据约束条件采用不同的约束混凝土本构。试验结果的对比分析表明该方法具有更高的计算精度。
关键词:多螺旋箍筋柱;轴压承载力;数值模拟;约束本构方程;理论计算方法
螺旋箍筋能够显著提高混凝土柱的承载力和延性[1]。但传统的螺旋箍筋技术主要用于圆形截面的钢筋混凝土柱,在应用于矩形截面柱时受限。多螺箍筋(Multi-spiral hoops)是一种新型组合式螺旋箍筋,它可以将螺旋箍筋推广应用于矩形截面的混凝土柱。它由传统单螺箍在4个角部增加小螺箍而形成(如图1),这4个小螺箍具有以下功能:① 约束矩形柱截面 4个角落的混凝土;② 对大螺旋箍筋提供侧向束制、减缓大螺旋箍筋的外扩现象;③ 固定角落的主筋并提供其侧向支撑[2]。在施工方面,多螺旋箍筋钢筋构造相对复杂,适合在工厂预制、工地组装,可有效节省人力与缩短工期[3]。目前这种形式的钢筋混凝土柱已在台湾、上海、江苏等地的桥梁工程中获得应用。
国内外学者对传统单螺旋箍筋对混凝土的约束效应做了深入的试验和理论研究。Kent、Park等[4]提出了螺旋箍筋约束的混凝土全应力应变曲线,其中约束效果与箍筋强度和配箍率成正比。Mander等[5]开展了螺旋、圆形和矩形箍筋约束混凝土柱的轴压试验,结果表明配置螺旋箍筋可以增强试件的强度与延性,并修正了Park的强度预测公式。在螺旋箍筋约束下,混凝土处于三向受压状态,不同区域混凝土的约束效应也有区别,这在多螺旋箍筋中表现得尤为明显。史庆轩等[6]通过 31根高强螺旋箍筋混凝土方形截面柱的轴心受压试验,对该类型柱的破坏形态、应力-应变关系曲线等进行了研究,分析了箍筋强度、箍筋间距、箍筋形式及截面尺寸对延性的影响。黄维等[7]研究了剪跨比、轴压比及配箍率对型钢混凝土柱延性的影响。对于多螺旋箍筋,Yin等[8]对 15个五螺旋箍筋柱进行了轴压试验,研究了不同小螺旋箍筋尺寸对轴压承载力的影响,根据试验结果提出了参数优化设计原则。Chen等[9]分析了多螺箍对截面不同区域混凝土的约束效应,并采用有限元方法分析了螺旋箍筋直径与间距的影响。齐虎等[10]将6种不同的箍筋约束混凝土单轴滞回本构在有限元软件中进行二次开发,验证了 Mander模型的有效性。在设计规范方面,美国ACI规范[11]采用经验系数考虑螺旋箍筋的贡献,中国混凝土规范[12]直接给出了螺旋箍筋约束柱的轴压承载力公式,但两个规范主要针对单螺旋箍筋的情况。
为了分析多螺箍筋柱的轴压承载力,本文首先基于有限元软件分析了多螺箍筋对混凝土柱的约束加强规律。然后,在现有国内外规范的基础上,根据 Mander等优化的约束混凝土本构关系式,推导适用于多螺箍筋混凝土柱的轴压承载力公式,并验证其合理性。
多螺箍筋混凝土柱由大螺旋箍筋、小螺旋箍筋、纵筋和混凝土4部分组成。鉴于不同区域混凝土受螺旋箍筋的约束条件不同,将混凝土截面分成无约束混凝土部分(A1)、大螺旋部分约束混凝土部分(A2)、小螺旋部分约束混凝土部分(A3)、大小螺旋加强约束混凝土部分(A4),如图1所示。

图1 多螺旋箍筋混凝土柱截面
Fig.1 Typical cross-section of multi-spiral hoops reinforced concrete column
本文采用 ABAQUS有限元软件对多螺旋箍筋混凝土柱进行分析,其中:混凝土采用8节点减缩积分的三维实体单元 C3D8R来模拟;钢筋采用线性桁架单元T3D2模拟;考虑轴压柱的钢筋混凝土相对滑移较小,钢筋采用嵌入式单元 Embedded Element的形式插入混凝土单元,不考虑受力过程中的粘结滑移。
有限元分析中由于采用三维精细建模方法,钢筋对混凝土的约束效应能够自动考虑。混凝土基于Rankine准则的塑性损伤模型,其单轴本构采用文献[9]建议的模型。在后续理论分析计算中,为考虑箍筋约束效应,对图1中不同区域的混凝土采用了约束混凝土本构进行分析,其中,未约束区域 A1采用文献[9]的模型,约束区域 A2、A3、A4采用Mander的模型。Mander等[5]提出的圆形箍筋约束的混凝土应力-应变本构关系模型,其应力-应变曲线如图2所示,其计算公式如下:
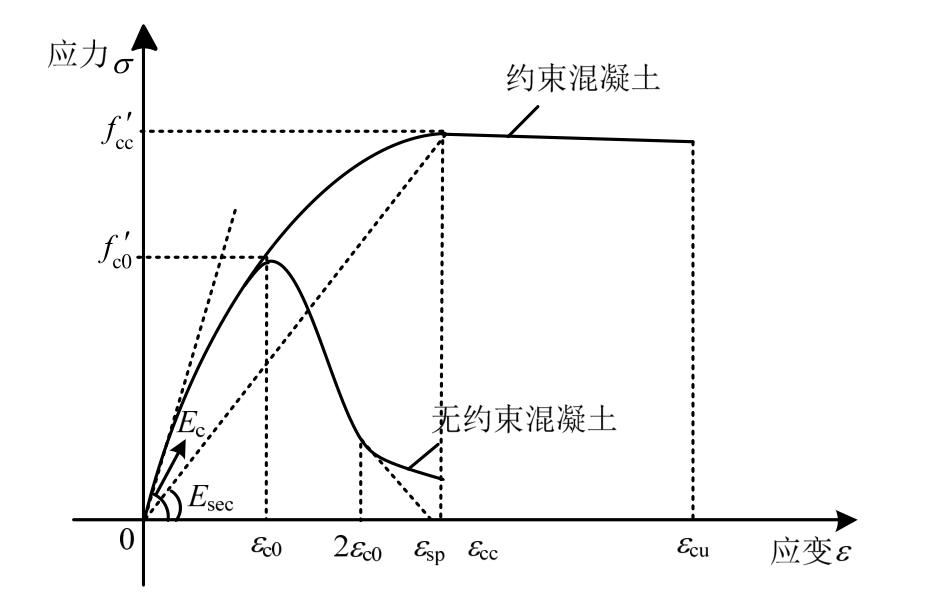
图2 混凝土受压应力-应变曲线
Fig.2 Compression stress-strain curve of concrete

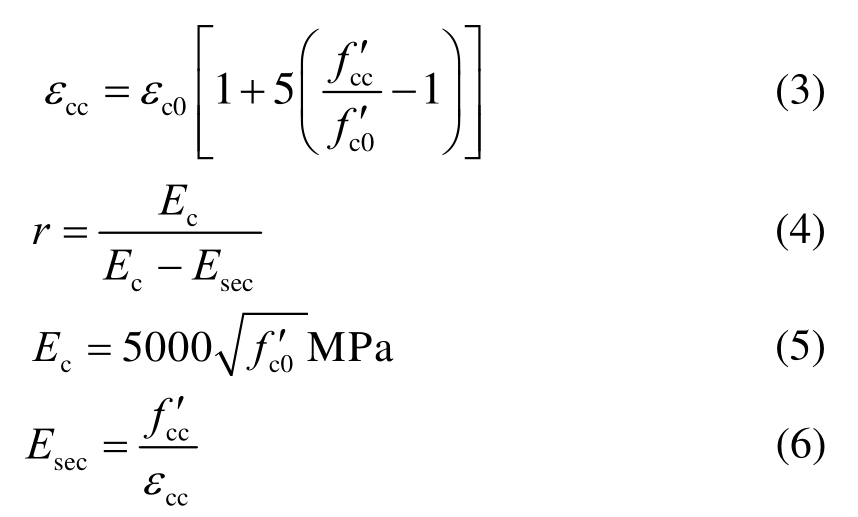
式中:σc为混凝土压应力;fc′c为约束混凝土抗压强度;fc′0为未约束混凝土抗压强度;εc为混凝土压应变;εc0为对应无约束混凝土抗压强度fc′0的峰值压应变,通常取0.002;εsp为混凝土保护层完全开裂时对应的应变;εcc为对应fc′c的约束混凝土峰值压应变;εcu为第1根箍筋断裂时对应的混凝土应变;Ec为混凝土弹性模量;Es e c为约束混凝土对应峰值应力εcc的割线模量。其中,峰值压应力可由下式得到:
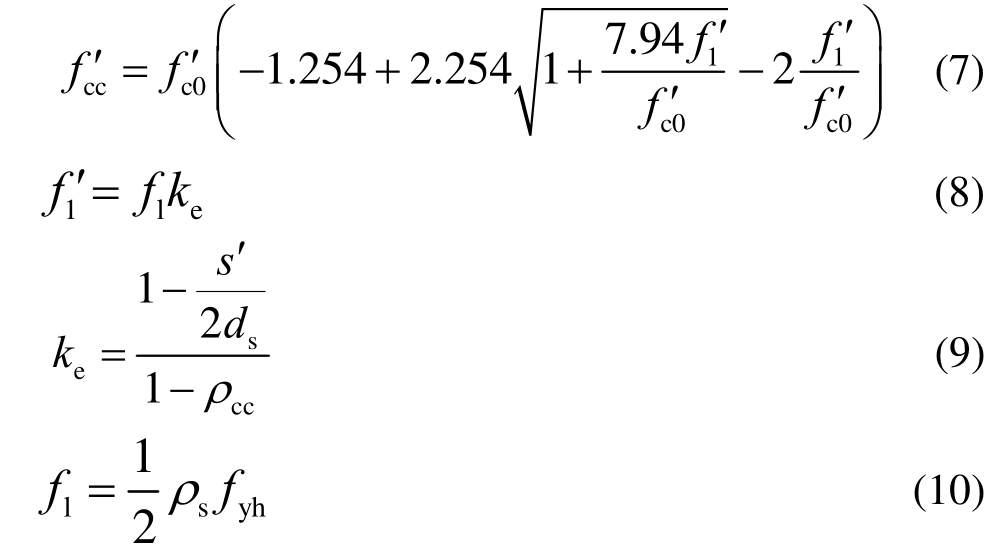
式中:f1′核心混凝土横向约束压力;fc′0为对应无约束混凝土抗压强度;s′为箍筋净间距;ds为截面上箍筋中心线间距;ρcc为核心混凝土截面的纵向钢筋配筋率;f1为横向钢筋对混凝土的侧向约束力;ρs为核心区混凝土区域体积配箍率;fyh为箍筋屈服强度。
钢筋采用理想弹塑性模型,如图3所示。钢筋泊松比取 0.3,弹性模量取 2×105GPa,其表达式如下:
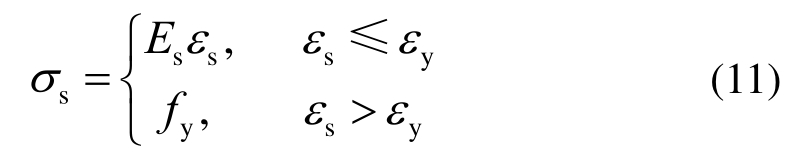
式中,Es、fy分别为柱纵向钢筋的弹性模量、屈服强度实测值。
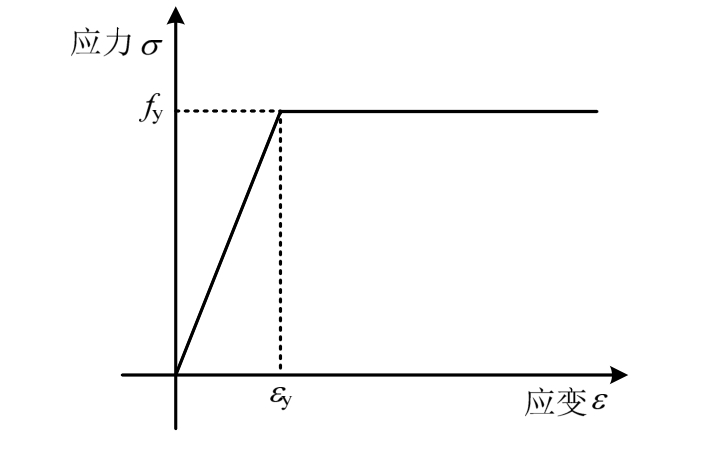
图3 钢筋应力-应变曲线
Fig.3 Stress-strain curve of steel reinforcement
选取文献[6]中的4根五螺旋箍筋柱进行分析,各构件材料参数与有限元模拟结果见表 1。可以看出,模拟值与试验值较为接近,平均误差为3.7%。各试件模拟的位移-荷载曲线如图 4所示,选取Y1-S-95试件作进一步分析,对比相同轴向应变(取素混凝土柱极限应变)时素混凝土柱、单螺旋箍筋柱和五螺旋箍筋柱的截面应力分布。
如图5所示。可见,素混凝土柱的最大应力出现在截面中心区域,4个角部应力最小,应力等值线近似呈方形。单螺旋箍筋柱的应力等值线呈圆形且截面应力水平明显提高。五螺旋箍筋柱的截面高应力区的面积进一步扩大,其中中心核心区和小螺旋箍筋约束区提高显著,这说明四角的小螺旋箍筋约束加强区对中央区域也施加了附加约束作用,间接提高了核心区混凝土的强度。
表1 典型构件试验模拟结果对比
Table 1 Comparison of numerical and test results of typical specimens

注:D表示箍筋直径。
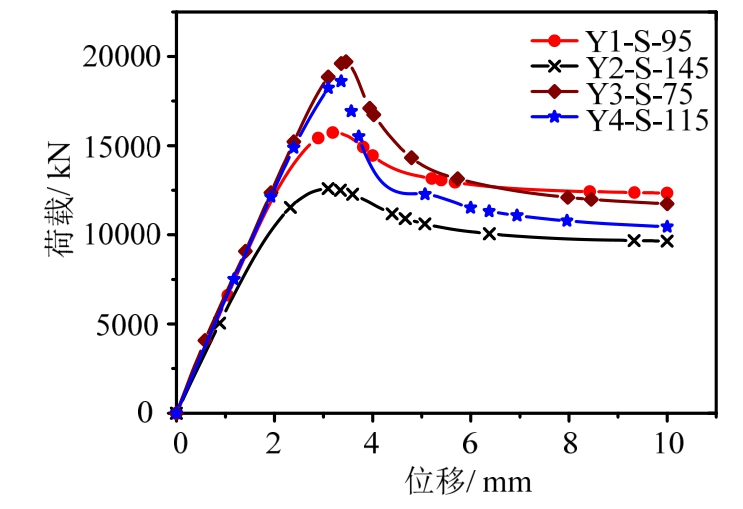
图4 荷载-位移曲线
Fig.4 Load-displacement curves

图5 不同柱截面的应力分布 /MPa
Fig.5 Stress distribution of cross-sections of different columns
对于轴心受压构件,美国规范[8]规定的短柱受压承载力计算公式为:
式中: fc′为圆柱体混凝土轴心抗压强度;Ag为柱构件全断面积;Ast为纵向钢筋总断面积;fy为纵向钢筋屈服强度标准值;式中第1个0.85为结构抗力折减系数;第2个0.85是混凝土强度的尺寸效应影响系数,混凝土圆柱试验的抗压强度会随着试件尺寸的增加而逐渐降低。
文献[5]中,台湾大学尹衍梁等提出了以下计算公式:
式中: fc′为圆柱体混凝土轴心抗压强度标准值;Acc为柱构件箍筋所约束的混凝土断面积。
式(1)、式(2)中的 fc′为正常状态下圆柱体混凝土抗压强度标准值,未考虑螺旋箍筋对混凝土约束后导致混凝土抗压强度的增强效果。
混凝土结构设计规范[12]规定的螺旋箍筋极限受压承载力计算公式为:
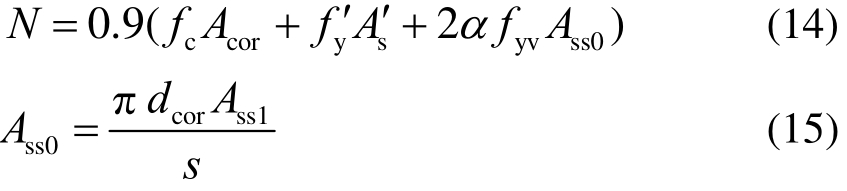
式中:fyv为间接钢筋的抗拉强度设计值;Acor为构件的核心截面面积;Ass0螺旋箍筋的换算截面面积;dcor为构件的核心截面直径;Ass1为螺旋箍筋单根截面面积。s为箍筋沿构件轴线方向的间距;α为螺旋箍筋对混凝土约束的折减系数(当混凝土强度等级不超过C50时,取1.0,当混凝土强度等级为C80时,取0.85,其间按线性内插法确定)。
公路钢筋混凝土及预应力混凝土桥涵设计规范[13]也有类似说明,对于钢筋混凝土轴心受压构件,当配置螺旋式或焊接环式间接钢筋,且间接钢筋的换算截面面积 Aso不小于全部纵向钢筋截面面积的25%;间距不大于80 mm或dcor/5,构件长细比 l0/i≤48时,其正截面抗压承载力计算应符合下列规定:
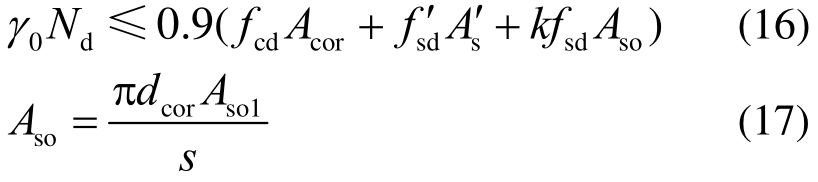
式中:γ0为桥梁结构的安全性系数,按公路桥涵的设计安全等级,一级、二级、三级分别取用1.1、1.0、0.9;Acor为构件核心截面面积;Aso为螺旋式或焊接环式间接钢筋的换算截面面积;dcor为构件截面的核心直径;k为间接钢筋影响系数,混凝土强度等级C50及以下时,取k=2.0,当混凝土强度等级为C50~C80时,取k=2.0~1.7,中间值直线插入取用;Aso1为单根间接钢筋的截面面积;s为沿构件轴线方向间接钢筋的螺距或间距。
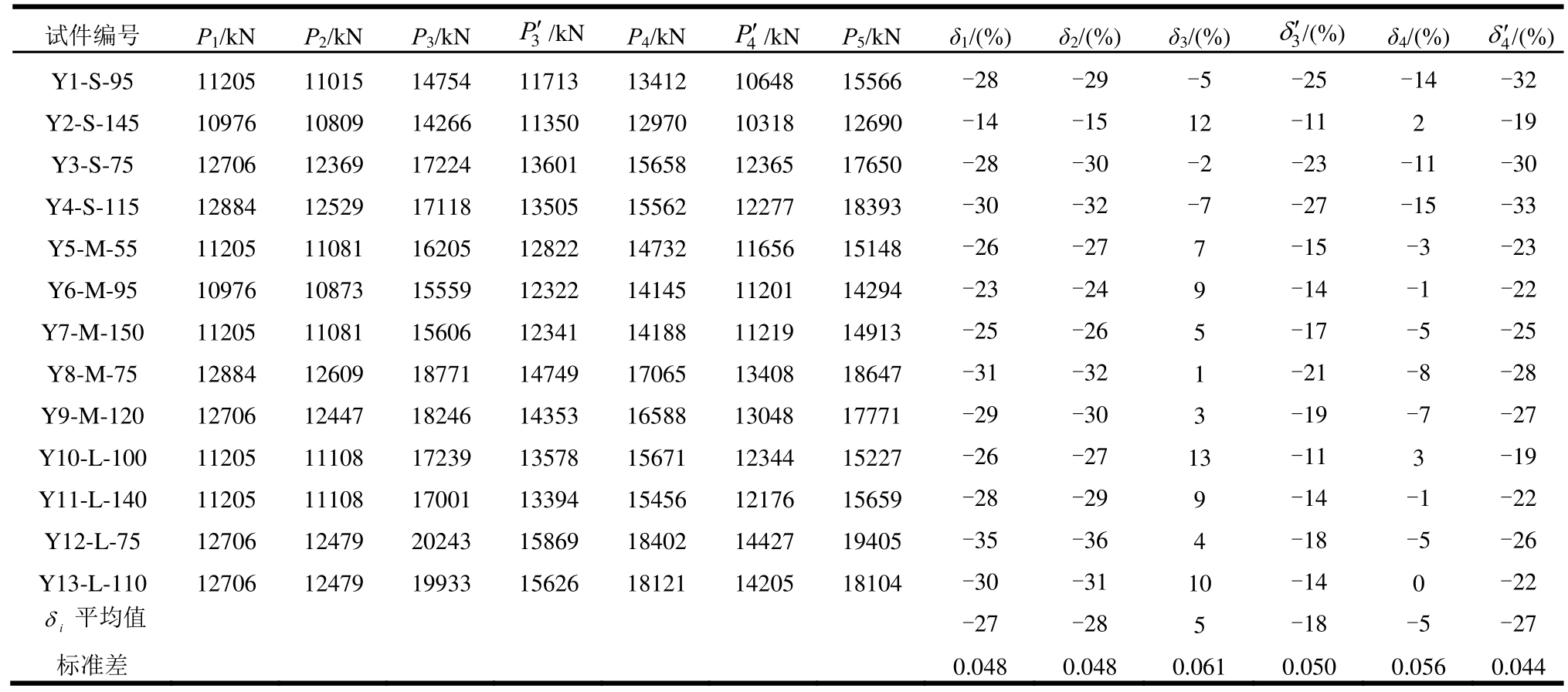
采用上述4种计算方法计算时,美国规范为圆柱体轴心抗压强度,中国规范为立方体轴心抗压强度,为使两国规范概念统一,美国规范取0.85倍圆柱体抗压强度标准值代入相应公式中,最终得到柱子轴心受压承载力的理论值,如表2所示。其中,P1是美国规范的计算值,P2是文献[8]中的计算值、P3、P3′分别对应着混凝土结构设计规范的标准值与设计值,P4、P4′则对应着桥涵规范的标准值与设计值,P5为试验值。在得出计算结果以后,将理论值与试验值进行对比,得出相对误差,用δ表示,![]()
由表1可知,美国规范[11]与台湾大学尹衍梁[8]提出公式的标准值计算结果均大幅小于试验值;中国混凝土结构设计规范[12]与中国公路桥涵设计规范[13]标准值计算结果较大,接近试验值。原因是前者虽然考虑了混凝土材料的尺寸效应以及混凝土和纵向钢筋提供的竖向抗压力,但仅采用经验系数考虑螺旋箍筋的贡献;文献[12]与文献[13]将箍筋对混凝土的约束作用,附加了约束承载力,因而后两者的计算标准值相对于美国和台湾的计算公式更接近试验值。
表2 轴压承载力计算
Table 2 Calculation of bearing capacity under axial load
上述理论计算方法针对单螺旋箍筋柱的情况,虽然个别规范计算误差较小且偏保守,但没有考虑多螺旋箍筋的特殊性,因此计算结果的离散性较大。为了更合理地考虑多螺旋箍筋混凝土截面的受力情况,本文根据A1~A4四个区域的不同约束情况,采用 Mander模型分别考虑箍筋约束效应。由以上有限元模拟可知,小螺旋箍筋对中央核心约束区域(A2与A4)有附加约束作用,因此,通过增加核心区域的体积配箍率,来考虑这部分附加约束,体积配箍率可按式(18)进行计算。被约束的混凝土抗压强度,采用式(7)计算。最后可求得轴压承载力,如式(19)所示,式中D为大圆的直径。试验值与计算值的对比结果,如表3所示。可以看到,本文方法计算的平均误差和标准差均小于现有规范方法,具有更好的计算精度。
表3 计算值与试验值对比
Table 3 Comparison of calculation and test results

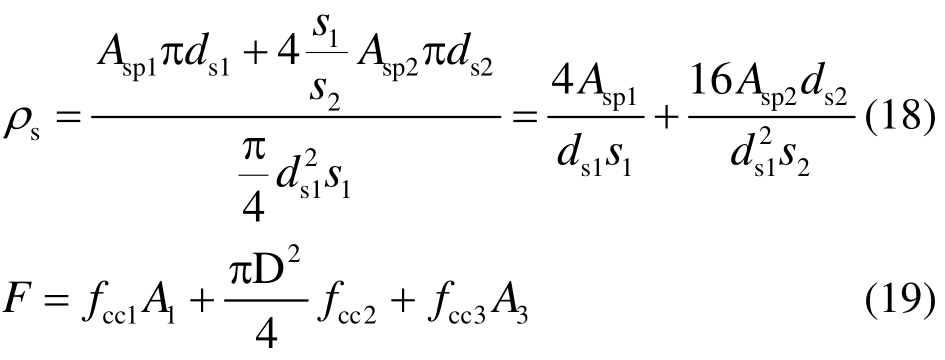
本文采用数值方法分析了多螺箍筋柱的截面应力分布,并推导出了多螺旋箍筋柱的轴心受压承载力计算公式,主要结论有:
(1) 轴压承载力的模拟值与试验值较为稳合,误差在-0.8%~11.67%之间。多螺旋箍筋可以显著提高柱子的轴压承载力,其中小螺旋箍筋不仅增强了4个角落的混凝土抗压强度,还间接提高了中央核心区的混凝土抗压强度。
(2) 现有规范中的单螺旋箍筋柱承载力计算方法中,美国规范与台湾地区规范均采用经验系数来考虑箍筋的约束,计算结果较为保守。中国规范按等体积原则将箍筋换算成纵向钢筋,计算多螺旋箍筋柱承载力时的精度更高
(3) 本文计算方法对不同区域的混凝土分别考虑其约束条件,包括小螺旋箍筋对核心混凝土的间接约束,取得了更高的计算精度。
参考文献:
[1]Murat S, Salim R. Strength and ductility of confined concrete [J]. Structural Engineering, 1992, 118(6):1590―1607.
[2]翁正强, 尹衍樑. 五螺箍矩形RC柱之轴压试验与优化设计研究[J]. 结构工程, 2010, 25(1): 71―105.Weng Zhengqiang, Yin Yanliang. Experimental studies of reinforced concrete confined by multi-spiral hoops [J].Structural Engineering, 2010, 25(1): 71―105. (in Chinese)
[3]Yin Y L, Wu T L, Liu T C, et al. Interlocking spiral confinement for rectangular columns [J]. ACI Concrete International, 2011, 33(12): 38―45.
[4]Kent D C, Park R. Flexural members with confined concrete [J]. Journal of the Structural Division, ASCE,1971, 97(7): 1969―1990.
[5]Mander J B, Priestly M J N, Park R. theoretical stress-strain model for confined concrete [J]. Journal of The Structural Division, ASCE, 1988, 114(8): 1804―1826.
[6]史庆轩, 杨坤, 刘维亚, 等. 高强箍筋约束高强混凝土轴心受压力学性能试验研究[J]. 工程力学, 2012,29(1): 141―149.Shi Qingxuan, Yang Kun, Liu Weiya, et al. Experimental study on mechanical behavior of high strength concrete confined by High-Strength Stirrups under concentric loading [J]. Engineering Mechanics, 2012, 29(1): 141―149. (in Chinese)
[7]黄维, 钱江, 周知. 考虑混凝土不同约束效应的型钢混凝土柱抗震性能模拟研究[J]. 工程力学. 2016,33(5): 157―165.Huang Wei, Qian Jiang, Zhou Zhi. Numerical simulation of the seismic performance of steel reinforced concrete columns with various confinement effect [J]. Engineering Mechanics, 2016, 33(5): 157―165. (in Chinese)
[8]Yin Y L, Wang J C, Wang P H. Development of multi-spiral confinements in rectangular columns for construction automation [J]. Journal of the Chinese Institute of Engineers, 2012, 35(3): 309―320
[9]Chen Y, Feng J, Yin S. Compressive behavior of reinforced concrete columns confined by multi-spiral hoops [J]. Computers and Concrete, 2012, 9(5): 359―373
[10]齐虎, 李云贵, 吕西林. 箍筋约束混凝土单轴滞回本构实用模型[J]. 工程力学, 2011, 28(9): 95―102.Qi Hu, Li Yungui, Lü Xilin. A practical confined concrete constitutive model under uniaxial hysteresis load [J]. Engineering Mechanics, 2011, 28(9): 95―102.(in Chinese)
[11]ACI318―2014, Building code requirements for structural concrete [S]. ACI Concrete Institute, 2014.
[12]GB 50010―2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB50010―2010, Code for design of concrete structures[S]. Beijing: China Architecture Industry Press, 2010. (in Chinese)
[13]JTG D62―2012, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京: 人民交通出版社, 2012.JTG D62―2012, Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S]. Beijing: China Communication Press, 2012. (in Chinese)
STUDY ON AXIAL COMPRESSION CAPACITY OF MULTI-SPIRAL HOOPS CONFINED CONCRETE COLUMNS
TANG Qiong1, LI Yi1, LU Xin-zheng2, YAN Wei-ming1
(1. Beijing Key Laboratory of Earthquake Engineering and Structural Retrofit, Beijing University of Technology, Beijing 100124, China;2. Key Laboratory of Civil Engineering Safety and Durability of Ministry of Education, Tsinghua University, Beijing 100084, China)
Abstract:Axial bearing capacities of rectangular concrete columns can be significantly improved by the confinement of multi-spiral hoops (MSHs). The confining effect of multi-spiral hoops on the stress distribution and amplitude of concrete cross section was analyzed by the finite element method. Subsequently, the calculating methods for the axial bearing capacity of rectangular concrete columns in various codes were validated by test data. The deviation of the calculated results of different methods was also analyzed. Based on the results of numerical simulations, the axial compression calculation formulas for MSH confined columns were proposed, and different stress-strain laws were considered for different parts of the concrete cross section. The comparison of test results showed that the theoretical calculation method had better accuracy.
Keywords:multi-spiral confined concrete column; axial bearing capacity; numerical simulation; confined stress-strain law; theoretical calculation method
中图分类号:TU375.3
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.06.S033
文章编号:1000-4750(2018)Suppl-0166-06
收稿日期:2017-06-16;修改日期:2017-12-18
基金项目:国家重点研发计划项目(2016YFC0701400);国家自然科学基金项目(51578018);北京科技新星计划项目(xx2017093)
通讯作者:李 易(1981―),男,湖北人,副研究员,博士,从事工程结构防灾减灾研究(E-mail: yili@bjut.edu.cn).
作者简介:唐 琼(1991―),女,安徽人,硕士生,从事工程结构抗震研究(E-mail: melanie@emails.bjut.edu.cn);
陆新征(1978―),男,安徽人,教授,博士,所长,主要从事结构非线性计算和仿真研究(E-mail: luxz@tsinghua.edu.cn);
闫维明(1960―),男,黑龙江人,研究员,博士,副院长,主要从事工程结构减震控制研究(E-mail: yanwm@bjut.edu.cn).