表1 各徐变计算模型考虑的主要因素Table 1 The main factors to consider in the calculation model of the creep
汪建群1,2,吕 鹏1,许 巧1,罗许国1,祝明桥1
(1. 湖南科技大学土木工程学院,湖南,湘潭 411201;2. 长沙理工大学桥梁工程安全控制省部共建教育部重点试验室,长沙 410004)
摘 要:混凝土的徐变预测关系到结构长期性能的合理确定。目前已有多种混凝土徐变预测模型,为便于设计和研究,对各计算模型的影响因素进行了分析和综述。基于试验实测和参考文献结果,对各预测模型对高强混凝土徐变、早龄混凝土的压缩/拉伸徐变的实用性进行了评价。结果表明:JTG D62―2012和GL 2000模型较适用于高强混凝土;GL 2000模型较适用于早龄混凝土的压缩和拉伸徐变,但压缩徐变误差超过26.4%,拉伸徐变误差大于46.1%,其他预测模型的误差不可接受。因此,既有的混凝土徐变模型不适用于早龄混凝土的拉伸与压缩徐变预测。如要对早龄结构进行受力分析,需采用反映早龄混凝土结构拉伸/压缩徐变特性的徐变模型。
关键词:压缩徐变;拉伸徐变;计算模型;早龄混凝土;成熟混凝土
徐变是混凝土材料本身固有的材料特性,会导致混凝土结构受力与变形随着时间的变化而变化,直接影响结构的受力性能和长期变形。因此,混凝土徐变效应分析是结构设计的重要内容之一。徐变效应分析的有效性取决于混凝土徐变系数计算模型的选取及分析方法的合理运用[1―2]。在工程实践中往往直接选用规范给出的徐变预测模型,根据少量的试验数据,对已有模型进行修正,以此来推算混凝土徐变的长期时效特性。
目前,国外常见的徐变模型主要有:CEB-FIP系列模型、ACI系列模型、GL2000模型、B3模型、AASHTO、BS―5000模型,国内的主要模型有JTG D62―2012、TB 1002.3―2005、中国建科院-1986模型等[1―7],这些模型均为经验公式或理论半经验公式。不同模型的建立机理不完全相同,参数的选用也各有特点。为了考虑混凝土中诸多材料参数和环境因素对徐变的影响,均在大量的试验数据上进行了统计回归,形成预测模型中的经验参数。
为便于设计和研究,对各计算模型的影响因素进行了分析和综述;并基于试验实测和参考文献结果,对各预测模型对高强混凝土徐变、早龄混凝土的压缩/拉伸徐变的实用性进行了评述。提出了一些有益建议,为相关结构设计提供参考。
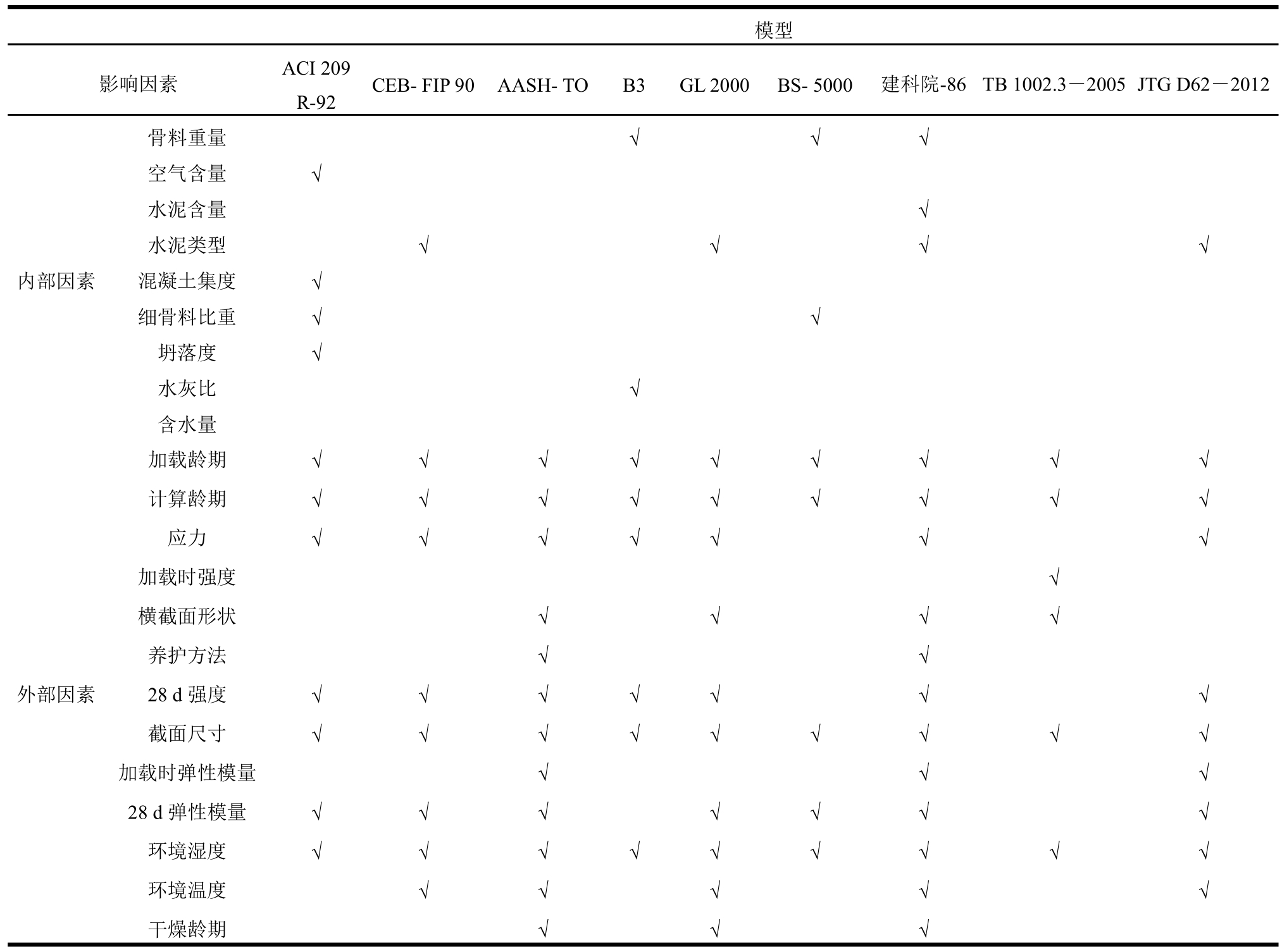
混凝土的徐变已有较多的研究成果,目前主要的徐变理论主要有粘弹性理论、粘性流动理论、塑性流动理论、力学变形理论、渗出理论、微裂缝理论、内力平衡理论等。其中以内力平衡理论和微裂缝理论在学术界较为普遍接受。混凝土为多相人工合成材料,其徐变受到自身的因素和外部因素的影响。表1列出了各徐变计算模型主要考虑的因素。
表1 各徐变计算模型考虑的主要因素Table 1 The main factors to consider in the calculation model of the creep

由表1可知:
1) 目前的徐变计算模型主要考虑了外部因素的影响。内因决定混凝土具有徐变特性,但混凝土的徐变主要由外部因素导致并受外因影响。
2) 既有的混凝土徐变计算模型均为考虑各影响因素的半理论半经验模型。
3) 各模型中,考虑较多的外因有加载龄期、计算龄期、截面尺寸、环境湿度。这说明这些因素是对混凝土徐变影响较大的外因。
目前描述混凝土徐变的表达式按照所表达的徐变本质可分为三类:将徐变分为基本徐变和干燥徐变,代表性的模型有B3模型;将徐变分为可恢复徐变与不可恢复徐变,代表性的模型有 TB 1002.3―2005模型;整体描述徐变规律,除上述两种模型外,其余各模型均为此类型。多数模型整体描述徐变规律,徐变计算公式较为简单,能方便地应用于电算。
在试验室制作了 5组棱柱体试件,用于 7 d、14 d、28 d和90 d的徐变加载和收缩测试。混凝土的设计强度等级为C50。试验室的温、湿度条件维持在20±2℃,湿度为(85±5)%,载荷水平为40%棱柱体抗压强度,持荷 360 d。相关试验和测试过程详见参考文献[8]所述。为评述上述规范的实用性,对目前应用较为广泛的徐变计算规范如JTG D62―2012、GL 2000、ACI 209R及AASHTO规范公式对试件的徐变进行预测,并与徐变试验结果进行比较,对规范相应计算公式的适用性进行验证。比较结果如图1所示。
由图3和图4可知:
1) JTG D62和GL 2000基本能适用于各加载龄期的试件徐变预测。7 d加载时,JTG D62和GL 2000计算得到的 360 d徐变系数与实测值误差分别为-1.7%和 5.7%;14 d加载时误差值分别为 9.5%和6.2%;90 d加载分别为19.6%和-15.4%;
2) ACI 209R所推荐的徐变计算模式只适用于加载龄期较小的情形。7 d加载时,计算的360 d徐变系数与实测值误差为-3.3%,而加载龄期为14 d、28 d和 90 d时,其误差呈增长的趋势,分别达15.5%、21.5%和44.4%。


图1 各规范对高强混凝土徐变的实用性
Fig.1 Practicality of various specifications on high strength concrete creep
3) 对于 AASHTO模型,加载龄期为 14 d和28 d时,计算的360 d徐变系数和实测值的误差分别仅为-2.8%和2.2%;而加载龄期为7 d和90 d时,其计算误差分别达-17.9%和22.1%,这说明当加载龄期较小(≤7 d)或较大(≥28 d)时,AASHTO 因误差较大而不实用。
基于上述试验结果对对各规范的实用性评述,建议采用GL 2000和JTG D62徐变模型对高强混凝土的徐变进行计算。
根据混凝土的成熟度或者徐变应力特征可以将混凝土的徐变分为不同的类型。目前的研究认为7 d以内的混凝土为早龄期混凝土,在此期间加载产生的徐变为早龄徐变,否则为成熟混凝土的徐变。根据混凝土受压应力和拉应力作用,又可将其徐变分为压缩/拉伸徐变。现有的研究在成熟混凝土的压缩徐变方面取得了较多成果,但在早龄期混凝土的拉伸徐变和压缩徐变方面的研究成果极少。而对早龄结构受力进行分析,必须以早龄混凝土的徐变为依据。采用成熟混凝土的徐变模式替代早龄徐变,可能会得到不精确的计算结果。既有的徐变研究主要侧重于成熟混凝土,早龄混凝土徐变相关的科学研究较为缺乏。目前混凝土早龄期压缩徐变并未引起足够重视,其关注度甚至不及早龄拉伸徐变,相关研究成果极少。
本文采用目前应用较为广泛的JTG D62―2012、CEB-FIP(1990)、GL 2000、ACI 209R及AASHTO模型,对参考文献[9]早龄混凝土压缩徐变试验结果的实用性进行了评述。相关计算结果如表2所示。
表2 参考文献[9]压缩徐变系数和各规范预测徐变系数
Table 2 Reference [9]compression coefficient of creep and prediction of creep coefficient of various specifications

注:持荷时间为30 d。
由表2比对结果可知:
1) 2 d加载混凝土持荷30 d,其压缩徐变系数为4.25;5 d加载试件持荷30 d其徐变系数为2.46;前者为后者的1.73倍。这说明早龄混凝土的压缩徐变对加载龄期非常敏感。加载龄期越早,徐变系数越大。
2) 各规范中,仅GL 2000的计算值与实测值较为接近。但2 d和5 d加载的试件计算徐变系数为2.85和1.81,误差分别达32.9%和26.4%。ASSHTO模型预测结果误差最大,2 d和5 d徐变其误差分别达75.5%和62.2%。这说明,既有混凝土徐变预测模型只适用于成熟混凝土,对于早龄混凝土的压缩徐变其误差不可接受。
3) 随着加载龄期的增大,各徐变计算模型的预测误差有减小的趋势。
一些混凝土结构在早龄硬化期间容易出现开裂现象。结构开裂从本质上讲是因为拉应力超限所导致,其徐变以拉徐变为主。因此,对于早龄结构的开裂现象进行准确预测有赖于选取合适的早龄混凝土拉伸徐变预测模型。当前对于早龄混凝土拉伸徐变的研究已趋于成为热点问题,其关注度甚至超过早龄压缩徐变。但早龄期混凝土的拉伸徐变研究起步较晚,主要研究对象针对于室内小尺寸试件,相关成果亦较为缺乏。其主要原因为:目前并没有规范规定的标准试验方法,亦缺乏拉伸徐变仪器,试验操作难度较大。目前仍少有针对早龄混凝土材料特性的拉伸徐变计算模型。
本文采用目前应用较为广泛的JTG D62―2012、CEB-FIP(1990)、GL 2000,ACI 209R 及 AASHTO模型,对参考文献[10]早龄混凝土拉伸徐变试验结果的实用性进行了评述。相关计算结果如表3所示。
表3 参考文献[10]拉伸徐变系数和各规范预测徐变系数
Table 3 Reference [10]tensile creep coefficient and prediction of creep coefficient of various specifications

注:持荷时间为28 d。
由表3比对结果可知:
1) 1 d加载混凝土持荷28 d,其压缩徐变系数为6.9;3 d加载试件持荷28 d其徐变系数为3.45;前者为后者的2.0倍。这说明早龄混凝土的拉伸徐变对加载龄期亦非常敏感。加载龄期越早,徐变系数越大。
2) 各规范中,仅GL 2000的计算值与实测值较为接近。但1 d和3 d加载的试件计算徐变系数为2.87和1.86,误差达58.4%和46.1%。ASSHTO模型预测结果误差最大,1 d和3 d徐变其误差分别达83.2%和70.4%。这说明,既有混凝土徐变预测模型只适用于成熟混凝土,对于早龄混凝土的拉伸徐变其误差不可接受。
3) 与早龄混凝土压缩徐变一致的是,随着加载龄期的增大,各徐变计算模型的预测误差有减小的趋势。
(1) 既有的混凝土徐变计算模型均为考虑各影响因素的半理论半经验模型。目前的徐变计算模型主要考虑了外部因素的影响,内因决定混凝土具有徐变特性,但混凝土的徐变主要由外部因素导致。各模型中,考虑得较多的外因有加载龄期、计算龄期、截面尺寸、环境湿度。这说明这些因素是对混凝土徐变影响较大的外因。
(2) 各徐变模型具有一定的实用性。就本文试验结果而言,建议高强混凝土的徐变预测采用 GL 2000和JTG D62徐变模型进行计算。
(3) 目前既有的混凝土徐变模型不适用于早龄混凝土的拉伸与压缩徐变预测,其误差不可接受。如要对早龄结构进行受力分析,需采用反映早龄混凝土结构拉伸/压缩徐变特性的徐变模型。
参考文献:
[1]CEB-FIP, Model Code for Concrete Structures [S].Comite Euro-international du Beton/Federation International de la Precon-strainte Paris, 1990.
[2]汪建群, 方志. 大跨预应力混凝土箱梁桥早期开裂与远期下挠控制[D]. 长沙: 湖南大学, 2011.Wang Jianqun, Fang Zhi. Early crack and long-term deflection control for long span prestressed concrete box girder bridge [D]. Changsha: Hunan University, 2011.
[3]ACI Committee 209, Prediction of creep, shrinkage and temperature effects in concrete structures (209R-92) [S].America Concrete Institute, Farmington Hills, Mich.,1992.
[4]Gardner N J,Lockman M J. Design provisions for drying shrinkage and creep of normal-strength concrete [J]. ACI Materials Journal, 2001, 98(2): 159―167.
[5]Bazant Z P,Baweja. Creep and shrinkage prediction model for analysis and design of concrete structures(Model B3) [R]. Northwestern University, submitted to ACI Comm. 209, 1994.
[6]龚洛书, 惠满印, 杨蓓. 砼收缩与徐变的实用数学表达式[J]. 建筑结构学报,1988(5): 37―41.Gong Luoshu,Hui Manyin,Yang Bei. Practical mathematical expression of concrete shrinkage and creep[J]. Journal of Building Structures , 1988(5): 37―41.
[7]JTG D62―2012, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京: 人民交通出版社, 2012: 160―164.JTG D62―2012, Code for design of highway reinforced and prestressed concrete bridges and culverts [S].Beijing: China Communications Press, 2012: 160―164.(in Chinese)
[8]汪建群, 方志, 邓波, 等. 粉煤灰对高强混凝土收缩徐变的影响试验研究及其修正模型[J]. 土木建筑与环境工程, 2016, 38(3): 110―117.Wang Jianqun, Fang Zhi, Deng Bo, et al. Experimental analysis of shrinkage and creep of high strength concrete with fly ash and the correction model [J]. Journal of Civil, Architectural and Environmental Engineering,2016, 38(3): 110―117. (in Chinese)
[9]谢楠, 杨成永, 欧阳杰, 等. 喷射混凝土早龄期徐变的试验研究及预测[J]. 工程力学, 2013, 30(3): 365―370.Xie Nan, Yang Chengyong,Ou Yangjie, et al.Experimental Research And Prediction On Shotcrete Creep At Early Age [J]. Engineering Mechanics, 2013,30(3): 365―370. (in Chinese)
[10]杨杨, 吴炎平, 朱张丰, 等. 基于等效龄期与结构单元的HPC早龄期拉伸徐变评价[J]. 东南大学学报自然科学版, 2010, 40(增刊 2): 165―171.Yang Yang, Wu Yanping, Zhu Zhangfeng, et al.Evaluation of tensile creep of HPC at early ages based on equivalent age and internal structure [J]. Journal of Southeast University (Natural Science Edition), 2010,40(Suppl 2): 165―171. (in Chinese)
CALCULATION MODEL FOR CONCRETE CREEP AND ITS PRACTICAL APPLICATION
WANG Jian-qun1,2, LÜ Peng1, XU Qiao1, LUO Xu-guo1, ZHU Ming-qiao1
(1. College of Civil Engineering, Hunan University of Science & Technology, Xiangtan, Hunan 411201, China;2. Key Laboratory of “Bridge Engineering Safety Control” built by Hunan Province and Ministry of Education,Changsha University of Science & Technology, Changsha 410004, China)
Abstract:The concrete creep prediction is related to the reasonable determination of the long-term performance of a structure. At present, a variety of concrete creep prediction models have been developed. In order to facilitate design and research, the influencing factors of various calculation models are analyzed and summarized. Based on the experimental measurements and reference results, the applicability of various prediction models for high strength concrete creep and early age concrete compression/tensile creep is evaluated. The results showed that:JTG D62 2012 and GL 2000 model is more suitable for high strength concrete. GL 2000 model is suitable for early age concrete compressive/tensile creep, but the compression creep error exceeds 26.4%, the tensile creep error is greater than 46.1%, and the error of the other prediction models are not acceptable. Therefore, the existing creep model of concrete is not suitable for early age concrete tension and compression creep prediction. For the analysis of an early age structure, the creep model which reflects the tensile/compression creep characteristics of early age concrete structures is needed.
Key words:compression creep; tensile creep; calculation model; early age concrete; mature concrete
中图分类号:TU528
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.01.S029
文章编号:1000-4750(2018)Suppl-0156-05
投稿日期:2017-06-02;修改日期:2018-01-16;
基金项目:国家自然科学基金项目(51408218,51378202);长沙理工大学桥梁工程安全控制省部共建教育部重点实验室开放基金项目(13KB02)
通讯作者:汪建群(1982―),男,湖北黄冈人,副教授,博士,主要从事混凝土结构理论研究(E-mail:121095359@qq.com).
作者简介:吕 鹏(1994―),男,湖南永州人,硕士生,主要从事混凝土结构理论研究(E-mail: 1182951096@qq.com);
许 巧(1992―),男,湖南娄底人,硕士生,主要从事混凝土结构理论研究(E-mail: 399848259@qq.com);
罗许国(1969―),男,湖南耒阳人,副教授,博士,主要从事混凝土结构理论研究(E-mail: luodakai2003@yahoo.com.cn);
祝明桥(1968―),男,安徽太湖人,教授,博士,主要从事混凝土结构理论研究(E-mail: 1531290279@qq.com).