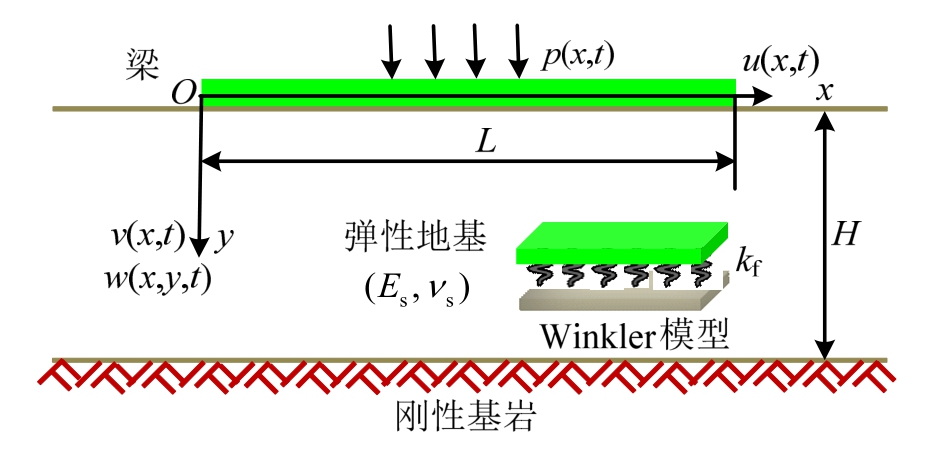
图1 弹性地基上有限长梁模型
Fig.1 Finite length beam on elastic foundation
马建军，聂梦强，高笑娟，秦紫果
(河南科技大学土木工程学院，洛阳 471023)
摘 要：基于Winkler地基模型、Euler梁理论和弹性地基的运动方程，建立了考虑土体质量影响的Winkler地基上有限长梁的非线性动力学模型。利用特征值分析和多尺度方法，分别求得梁的线性和非线性固有频率及模态构型。进而通过数值分析，研究了土体质量对Winkler地基上有限长梁线性和非线性自由振动的影响。研究结果表明：若将土体质量对梁动力响应的影响引入Winkler地基上有限长梁的动力学模型，梁的固有频率降低；土体质量对梁的高阶非线性模态构型影响显著。
关键词：Winkler地基；Euler梁；土体质量；固有频率；非线性自由振动
弹性地基梁理论在工程中土-结构相互作用问题的静力和动力响应分析中应用广泛。为促进理论研究及满足工程需求，国内外学者对弹性地基梁的建模方法和计算理论进行了大量研究，取得了丰硕的成果[1－4]。已有研究表明，在土-结构相互作用系统的理论和数值分析中，土介质的力学特性可用多种地基模型进行模拟。与其它地基模型相比，Winkler地基模型将土场模拟为一系列独立的线性弹簧[5－6]，其概念最简洁，在工程实践中的应用也最广泛[7－9]。
目前，关于Winkler地基上梁的线性和非线性动力响应研究成果已很多[10－12]，但这些研究均基于传统的Winkler模型，而忽略了土体质量对土-结构相互作用系统动力学特性的影响。然而从理论层面讲，由于土-结构相互作用的影响，在动力响应过程中将有一部分土体与其支承结构共同运动。显然，土体质量的影响将改变土-结构相互作用系统的动力学特性[13－15]。同时还应注意，土-结构相互作用效应对弹性地基梁非线性动力响应的影响也常被忽略[16－18]。因此，为精确揭示Winkler地基上梁的非线性动力特性，有必要在同时考虑土体质量的影响和土-结构相互作用效应的条件下开展弹性地基梁的非线性动力学研究。
该文基于Winkler地基梁的非线性动力学模型和弹性地基的运动方程，建立了考虑土体质量影响的Winkler地基上有限长梁的非线性动力学模型。利用特征值分析和多尺度方法分别求解弹性地基梁的线性和非线性自由振动方程，得到其线性和非线性固有频率及模态构型，进而通过数值计算分析了土体质量对Winkler地基上有限长梁非线性自由振动的影响。
本文以弹性地基上有限长梁为研究对象。如图1所示，H为地基深度，L、b、h分别为梁的长、宽、高；以未变形的梁端为坐标原点O，其中轴线为x轴建立平面直角坐标系O- x y；p(x,t)=Pcos Ωt为简谐横向激励，P和Ω分别为外激励幅值和频率；u(x,t)和v(x,t)分别为梁沿x和y方向的位移，
w(x,y,t)为梁下土场沿y方向的位移。
图1 弹性地基上有限长梁模型
Fig.1 Finite length beam on elastic foundation
根据弹性地基梁类结构的变形特征，本文仅考虑梁的横向位移v(x,t)。基于Winkler地基模型和Euler梁理论，可得Winkler地基上有限长梁的非线性运动方程[17]：
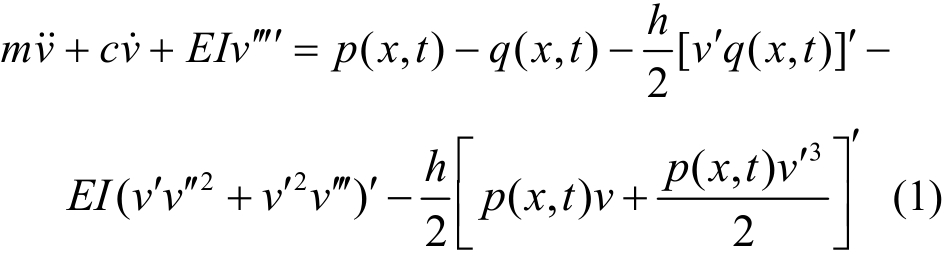
其中：c为梁的粘滞阻尼系数；q(x,t)为地基反力；m=ρA为单位长度梁的质量；ρ和A分别为梁的密度和横截面积；E和I分别为梁的弹性模量和惯性矩；(˙)和()′分别为对变量t和x求偏导。
设有限深度地基为线弹性各向同性体，则其运动方程为[15]：
其中：ρs为土体密度；cs为土体的粘滞阻尼系数；kf为Winkler地基刚度系数；w r为梁与地基的相对位移。由式(2)可得地基反力为：
为便于分析，引入下列归一化参数：
将式(4)代入式(1)，可得弹性地基梁的归一化运动方程：
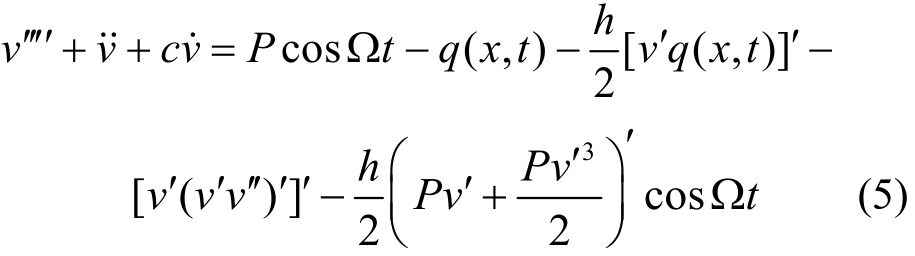
其中，为便于表述，已忽略归一化参数的上标。同样，可得弹性地基的归一化运动方程：
梁与地基的变形应满足连续性条件，即w(x,y,t)满足w(x, 0,t)=v(x,t)；w(x,H,t) = 0。则需引入衰减函数φ(y)，令w(x,y,t)=v(x,t)φ(y)，wr(x,0,t)=v(x,t)[1 -φ(y)]，衰减函数为[19]：
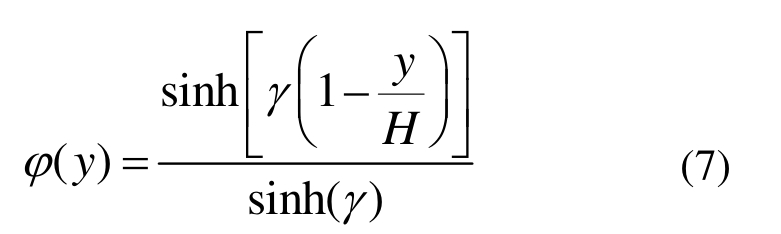
其中，γ为衰减系数，可取γ=0.01。边界条件为：φ(0) = 1；φ(H)=0。将式(7)代入式(6)，并在y∈(0,H)内积分可得：
将式(8)代入式(5)，可得：
此时，式(9)中包含了土体质量、深度和阻尼系数等，利用该式可开展土体质量等参数对 Winkler地基上梁动力学特性的影响研究。
为进行线性自由振动分析，忽略式(9)中的非线性项、阻尼项和外激励项，可得：
其中，
为地基与梁的质量比。梁运动方程的解设为
为模态构型函数，ω为固有频率，
将该形式解代入式(10)，可得梁的振动方程。运用特征值方程[16]，可得模态函数解：
其中，
为常数。以固支-自由梁为例，可得超越方程：
利用式(12)，可求得梁的第i阶固有频率ωi。相应地，可得梁的第i阶模态构型函数φ i(x)：
其中：C为待定系数；
利用多尺度方法[20]，梁的位移可表示为：
其中，ε是小参数，
为研究非线性自由振动，忽略式(9)中的阻尼项和外激励项，可得：
其中：
为线性算子；G 21=
为平方非线性
算子；
为立方非线性算子。将式(14)代入式(15)，可得ε阶、ε 2阶、ε 3阶系数分别为：
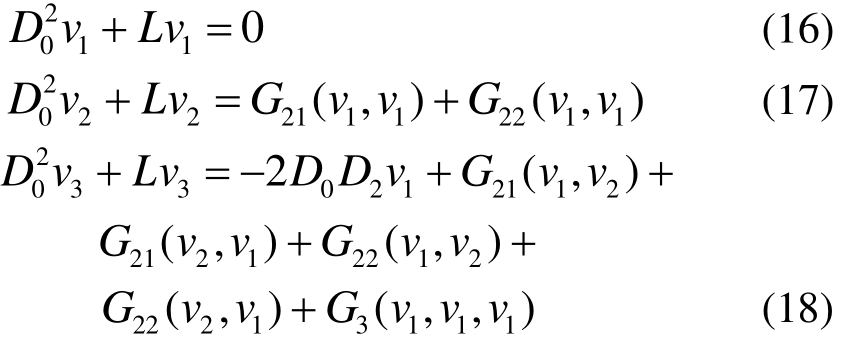
对于非线性自由振动而言，式(16)的解为：
其中：An为幅值；cc表示复共轭项。将式(19)代入式(17)，可得：
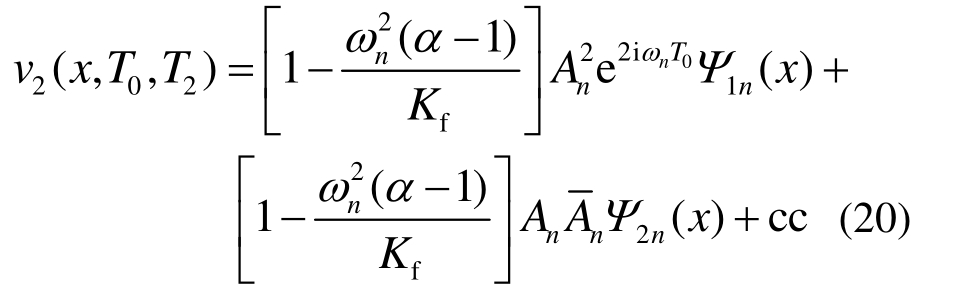
其中：
为A n的共轭；Ψ 1n(x)和Ψ 2 n(x)为二阶构型函数，满足边值方程：
将式(19)和式(20)代入式(18)，可得可解性条件为：
其中：
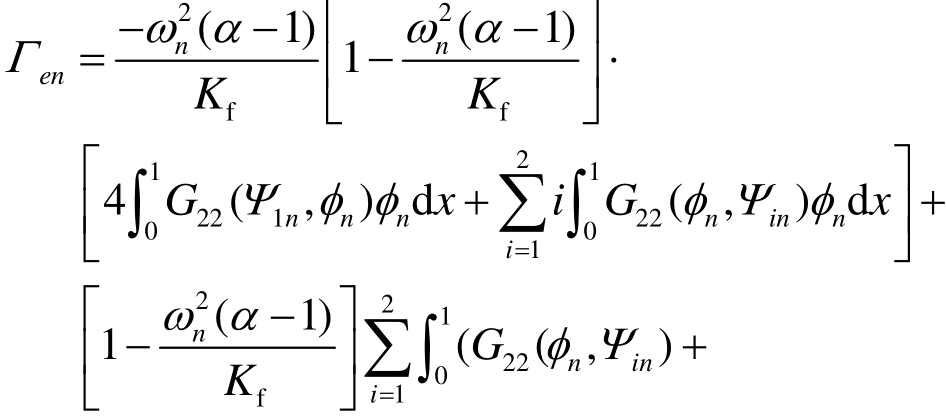
设
其中an和βn均为实函数，将其代入式(22)，分离实部和虚部可得：
求解式(24)，可得：
其中，βn0为常数。进而可得梁位移的二阶近似解：
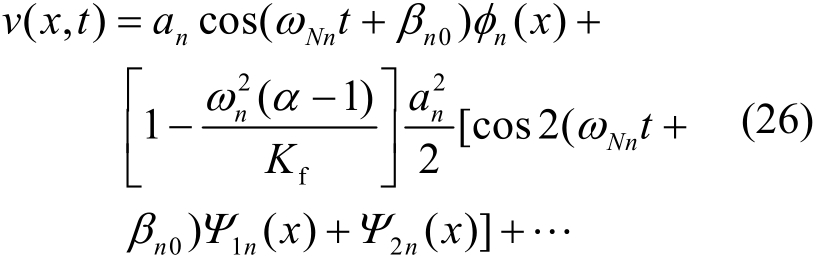
其中，
为非线性频率。相应地，速度的近似表达式为：
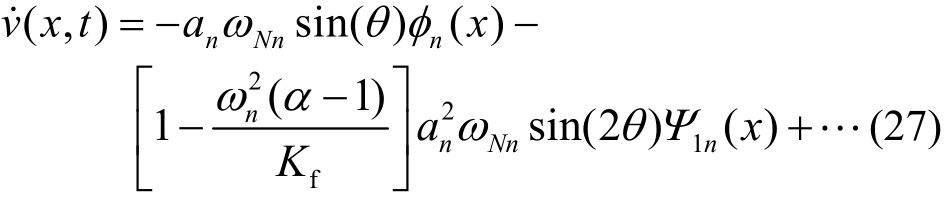
其中，
利用文献[21]的方法，可得梁的非线性模态：
其中
为进行数值分析，弹性地基和梁的物理参数取值如表 1所示。参考文献[16]，地基参数为：
其中
12(1-ν2)。利用表1中物理参数，计算可得β= 3 .802。
图2给出了Winkle地基上有限长梁的前三阶固有频率随参数β的变化情况，其中土体密度取值在合理范围内，即β为[0,6]。若β=0，则不考虑土体质量影响；若β=6，则ρs=2.683× 1 03kg/m3。由图2可知，梁的固有频率随β增大而减小。图2中Δ表示由β增加引起的固有频率减小值，由Δ变化可知，参数β对固有频率的影响效应随其增大而降低。当β=3.802时，梁的固有频率显著小于β=0时的频率值。因此，为精确模拟Winkler地基上有限长梁的动力学特性，必须将土体质量的影响引入到梁的动力学模型中。由固有频率随β的变化情况可知，土体质量对高阶频率的影响更显著。
表1 弹性地基和梁的物理参数值
Table 1 Physical parameters of elastic foundation and beam
图2 参数β对Winkler地基上有限长梁固有频率的影响
Fig.2 Effect ofβon natural frequencies of the finite length beam on Winkler foundation
图3 以ω N1 /ω1为横坐标，响应幅值a1为纵坐标，在β分别为0.0、0.5、1.0、4.0、6.0时，给出了 Winkler地基上有限长梁的第一阶模态骨架曲线。由图3可知，参数β对非线性固有频率影响较小。随土体质量增大，梁一阶模态骨架曲线的刚度软化特性减弱。但当β=4.0和β=6.0时，梁一阶模态骨架曲线间的差异很小，其表明在建模分析时仅需考虑一定深度土体质量的影响即可。
图4给出了β=3.802时Winkler地基上有限长梁的前三阶线性和非线性模态构型，其中实线和虚线分别表示梁的线性和非线性模态。由图4可知，随模态的阶数增加，梁的线性和非线性模态间差异增大。由式(28)可知，参数Λ对梁的非线性模态有直接影响。表2给出了Λ值随参数β的变化情况，当β=0.00，Λ= 1.000。随参数β增大，Λ的值迅速减小。当β= 3 .802，参数Λ的绝对值随模态的阶数增加而迅速增大，此时参数β对梁的非线性模态的影响非常显著。
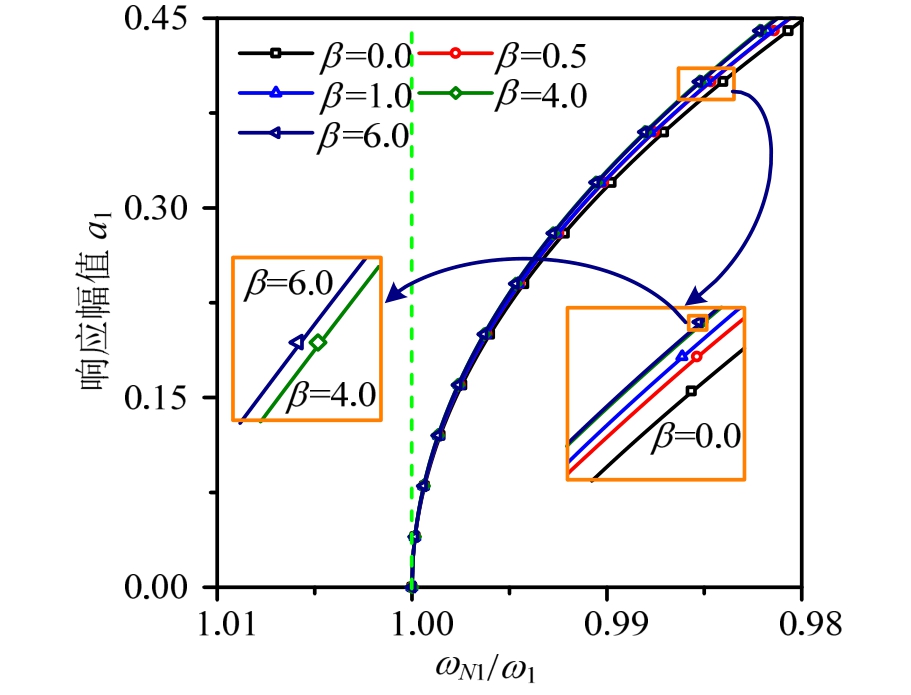
图3 参数β对Winkler地基上有限长梁一阶模态骨架曲线的影响
Fig.3 Effect ofβon backbone curves of the first mode of the finite length beam on Winkler foundation
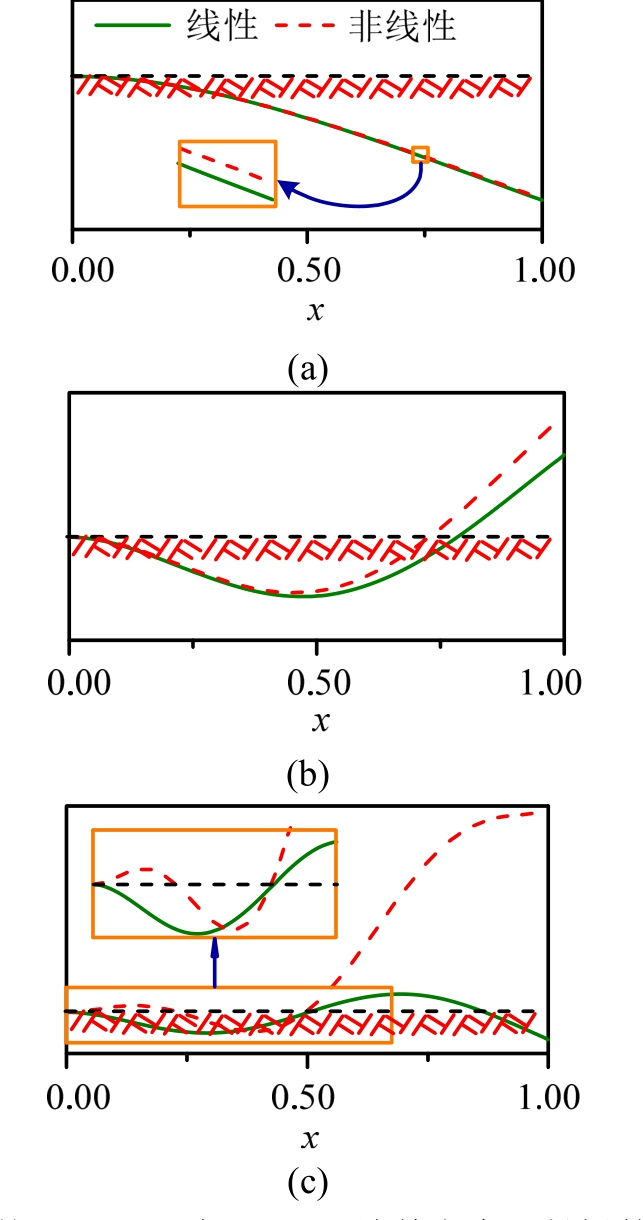
图4 参数β= 3 .802时Winkler地基上有限长梁的线性和非线性模态构型
Fig.4 Linear and nonlinear mode shapes of the finite length beam on Winkler foundation whenβ=3.802
表2 参数β对Λ值的影响
Table 2 Effect ofβon the values ofΛ
本文建立了考虑土体质量影响的Winkler地基上有限长梁的非线性动力学模型，利用特征值分析和多尺度方法分别求得梁的线性和非线性固有频率和模态构型，进而通过数值计算研究了土体质量对梁非线性动力学特性的影响。参数分析结果表明：随着参与振动的土体质量增大，Winkler地基上有限长梁的固有频率减小；在动力响应过程中，仅有限深度土体质量对梁的非线性动力学特性有影响；土体质量对梁的高阶非线性模态影响显著。
参考文献：
[1]Hetényi M. Beams on elastic foundation [M]. Ann Arbor: University of Michigan Press, 1946: 50―63.
[2]龙驭球. 弹性地基梁的计算[M]. 北京: 人民教育出版社, 1981: 2―14.Long Yuqiu. Calculation of elastic foundation beam [M].Beijing: People’s Education Press, 1981: 2―14. (in Chinese)
[3]Wang Y H, Tham L G, Cheung Y K. Beams and plates on elastic foundations: a review [J]. Progress in Structural Engineering and Materials, 2005, 7(4): 174―182.
[4]李潇, 王宏志, 李世萍, 等. 解析型 Winkler弹性地基梁单元构造[J]. 工程力学, 2015, 32(3): 66―72.Li Xiao, Wang Hongzhi, Li Shiping, et al. Element for beam on Winkler elastic foundation based on analytical trial functions [J]. Engineering Mechanics, 2015, 32(3):66―72. (in Chinese)
[5]Clastornik J, Eisenberger M, Yankelevsky D Z, Adin M A. Beams on variable Winkler elastic foundation [J].Journal of Applied Mechanics, 1986, 53(4): 925―928.
[6]Yankelevsky D Z, Eisenberger M, Adin M A. Analysis of beams on nonlinear Winkler foundation [J].Computers and Structures, 1989, 31(2):287―292.
[7]肖世国, 夏才初, 朱合华, 等. 管幕内箱涵顶进中顶部管幕竖向变形预测[J]. 岩石力学与工程学报, 2006,25(9): 1887―1892.Xiao Shiguo, Xiao Caichu, Zhu Hehua, et al. Vertical deformation prediction on upper pipe-roof during a box culvert being pushed within a pipe-roof [J]. Chinese Journal of Rock Mechanics and Engineering, 2006,25(9): 1887―1892. (in Chinese)
[8]任青, 黄茂松. 分层地基中柔性高承台群桩基础的竖向振动特性[J]. 土木工程学报, 2009, 42(4): 107―113.Ren Qing, Huang Maosong. Analysis of axial vibration of floating pile groups with flexible caps in layered soils[J]. China Civil Engineering Journal, 2009, 42(4): 107―113. (in Chinese)
[9]丁敏, 李潇, 马倩, 等. 基于 Winkler弹性地基梁模型的半刚性轻钢柱脚底板受力分析[J]. 工程力学, 2014,31(5): 158―165.Ding Min, Li Xiao, Ma Qian, et al. Mechanical analysis of the sole plate of semi-rigid light steel column footings based on Winkler model of elastic foundation beams [J].Engineering Mechanics, 2014, 31(5): 158―165. (in Chinese)
[10]Thambiratnam D, Zhuge Y. Free vibration analysis of beams on elastic foundation [J]. Computers & Structures,1996, 60(6): 971―980
[11]楼梦麟, 沈霞. 弹性地基梁振动特性的近似分析方法[J]. 应用力学学报, 2004, 21(3): 149―153.Lou Menglin, Shen Xia. An approach for analyzing dynamic characteristic of reinforced concrete beam on elastic foundation [J]. Chinese Journal of Applied Mechanics, 2004, 21(3): 149―153. (in Chinese)
[12]马建军, 刘齐建, 王连华, 等. Winkler地基上有限长梁非线性自由振动[J]. 工程力学, 2012, 29(8): 58―62.Ma Jianjun, Liu Qijian, Wang Lianhua, et al. Non-linear free vibration of finite-length beams on the Winkler foundation [J]. Engineering Mechanics, 2012, 29(8):58―62. (in Chinese)
[13]Saito H, Murakami T. Vibrations of an infinite beam on an elastic foundation with consideration of mass of a foundation [J]. Bulletin of JSME, 1969, 12(50): 200―205.
[14]Iyengar R N, Pranesh M R. Dynamic response of a beam on a foundation of finite depth [J]. Indian Geotechnical Journal, 1985, 15(2): 53―63.
[15]Jaiswal O R, Iyengar R N. Dynamic response of a beam on elastic foundation of finite depth under a moving force [J]. Acta Mechanica, 1993, 96(1/2/3/4): 67―83.
[16]Wang L, Ma J, Zhao Y, et al. Refined modeling and free vibration of inextensional beams on the elastic foundation [J]. Journal Applied Mechanics, 2013, 80(4):041026.
[17]Wang L, Ma J, Peng J, et al. Large amplitude vibration and parametric instability of inextensional beams on the elastic foundation [J]. International Journal of Mechanical Sciences, 2014, 67: 1―9.
[18]Ma J, Peng J, Gao X, et al. Effect of soil-structure interaction on the nonlinear response of an in extensional beam on elastic foundation [J]. Archive of Applied Mechanics, 2015, 85(2): 273―285.
[19]Vallabhan C V G, Das Y C. Modified Vlasov model for beams on elastic foundations [J]. Journal of Geotechnical Engineering, 1991, 117(6): 956―966.
[20]Nayfeh A H, Mook D T. Nonlinear oscillations [M].New York: Wiley, 1995: 56―59.
[21]Nayfeh A H, Nayfeh S A. Nonlinear normal modes of a continuous system with quadratic nonlinearities [J].Journal of Vibration and Acoustics, 1995, 117(2): 199―205.
NONLINEAR FREE VIBRATION OF A BEAM ON WINKLER FOUNDATION WITH A CONSIDERATION OF SOIL MASS EFFECT
MA Jian-jun , NIE Meng-qiang , GAO Xiao-juan , QIN Zi-guo
(School of Civil Engineering, Henan University of Science and Technology, Luoyang 471023, China)
Abstract:Based on the Winkler model, Euler beam theory, and the motion equation of elastic foundation, the nonlinear dynamics model of a finite-length beam on Winkler foundation with a consideration of the effect of soil mass is obtained. Applying the eigenvalue analysis and the method of multiple scales, the linear and nonlinear natural frequencies and mode shapes of the beam are obtained. By means of the numerical calculation, the effect of soil mass on the linear and nonlinear free vibrations of the finite-length beam on Winkler foundation are explored. The numerical results show that: the natural frequencies of beam decrease, when the effect of soil mass on the dynamic response of the beam is included in the nonlinear dynamic model of the finite-length beam on Winkler foundation. Moreover, it is significant for the effect of soil mass on the high-order nonlinear mode shapes of the beam.
Key words:Winkler foundation; Euler beam; soil masses; natural frequency; nonlinear free vibration
中图分类号：TU348
文献标识码：A
doi:10.6052/j.issn.1000-4750.2017.06.S027
文章编号：1000-4750(2018)Suppl-0150-06
收稿日期：2017-06-04；修改日期：2017-11-07
基金项目：国家自然科学基金项目(11502072，51474095)
通讯作者：马建军(1982―)，男，河南孟州人，副教授，博士，主要从事桩基非线性动力响应研究(E-mail: majianjun@haust.edu.cn);
作者简介：聂梦强(1992―)，男，河南洛阳人，硕士生，主要从事弹性地基梁的非线性动力学研究(E-mail: 594143157@qq.com);高笑娟(1973―)，女，河南偃师人，副教授，博士，所长，主要从事岩土工程方面研究(E-mail: gaoxjly@163.com);秦紫果(1993―)，女，河南洛阳人，硕士生，主要从事桩基的非线性动力学研究(E-mail: 448080838@qq.com).