康 雷1，应祖光1，倪一清2
(1. 浙江大学航空航天学院力学系，杭州 310027；2. 香港理工大学土木及环境工程系，香港九龙)
摘 要：铁路轨道的动刚度或频响特性是支承列车安全平稳运行的重要动力学性能指标，轨道由离散周期性轨枕支承提供刚度与阻尼，但实际轨道不可避免存在周期支承缺失，它将对轨道的频响与动力学性能产生影响，故需要研究轨道在周期支承缺失情况下的频响特性及其影响规律。该文研究周期支承缺失对于轨道梁频响特性的影响，建立非周期离散支承轨道梁的频响函数方程，应用Galerkin法得到轨道梁的频响函数表达式，适用于非周期与周期情形。计算分析典型轨道梁在支承刚度阻尼损失、支承位置周期性偏移等周期支承缺失情况下的频响特性，通过非周期与周期支承等情况的频响比较说明各种周期支承缺失的影响特性，得到支承刚度阻尼损失对于邻近跨中频响第一个共振幅值影响较为显著、支承刚度阻尼周期性损失与支承位置周期性偏移将产生新的频响峰、支承位置随机偏移对于较高频段相位差有较大影响等，不同周期支承缺失模式对于频响的影响规律为进一步通过轨道梁频响的周期支承异常识别提供理论基础。
关键词：轨道梁；周期支承；周期性缺失；频响特性；宽频带
铁路轨道的动刚度或频响特性是支承列车安全平稳运行的重要动力学性能指标，研究轨道的频响特性具有重要的实际意义[1―2]。列车运行过程的作用以垂直方向为主，故水平轨道的垂向动力学特性需要首先考虑[3]。铁路轨道由离散周期性轨枕支承，提供刚度与阻尼，但导致轨道刚度空间分布的周期性[4―5]，形成空间参变动力学问题。轨道垂向振动的固有频率及受激振动频率均较高[4―6]，需要考虑较宽频带的响应特性。因此轨道的频响特性不同于普通梁，特别是由于制造误差、环境作用引起退化与损伤等在所难免，导致实际轨道的支承无法确保严格的周期性，从而使周期支承缺失，它将对轨道的频响与动力学性能产生影响，故需要研究轨道在周期支承缺失情况下的频响特性及其影响规律。目前关于周期支承轨道梁受周期激励的响应、车轨耦合动力学、轨道噪声等已有很多研究[1―8]，Thompson等[9]用数值方法计算分析了随机轨枕间距、随机支承刚度对轨道导纳的影响，然而非周期支承轨道梁的动力学尚缺少研究。另一方面，关于失谐周期性结构的动力学特性已有一定研究[10―11]，其方法可应用到轨道梁在周期支承缺失情况下的频响特性分析。本文考虑非周期与周期支承长轨道梁的宽频带垂向动力学特性，建立非周期离散支承轨道梁的偏微分运动方程，转化为常微分的频响函数方程，再用Galerkin法化为代数方程组求解，得到轨道梁的频响函数表达式，可用于非周期与周期情形。对于典型轨道梁，计算分析支承刚度阻尼损失、支承位置周期性偏移等周期支承缺失情况下的频响特性，并与周期支承情况的频响比较说明周期支承缺失的影响特性，为进一步通过轨道梁频响的周期支承异常识别提供理论基础。
考虑水平铁路轨道在垂直力作用下的动力学特性，将无缝铁轨简化为长弹性梁，其基础支承为离散弹性力与阻尼力，如图1所示。对于长梁中低频弯曲振动情况，剪切变形与转动惯性的影响相对于较小，可不计。按照Bernoulli-Euler梁理论，离散支承轨道梁的垂向振动偏微分方程为：
式中：w(x,t)是梁的垂向位移；ρ是质量密度；A是横截面积；E是弹性模量；I是截面惯性矩；cb是梁的阻尼系数；x是梁长度方向的坐标；ksk是第k支承力的刚度；csk是第k支承力的阻尼系数；xsk是第k支承力的坐标；δ(⋅)是 Dirac delta 函数；f(x,t)是垂直外作用力；N1、N2是整数，表示原点左右两边支承个数，按梁动响应的有效长度选取，有效长度根据响应的衰减程度确定。对于周期性支承情形，相邻支承的间距Δxi=xsi-xs,i-1为常数，对于周期支承缺失情形，它具有不同值。
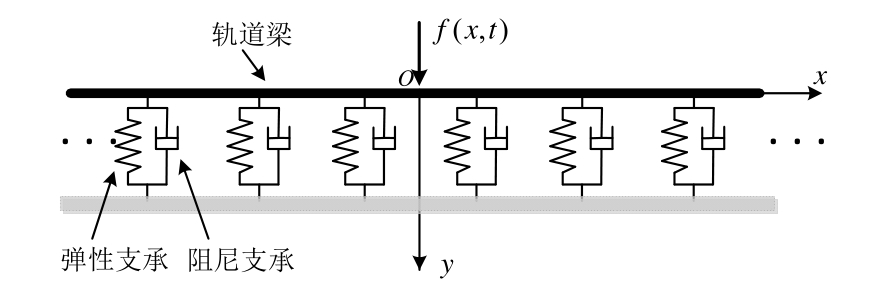
图1 轨道梁模型图
Fig. 1 Track beam with supports
设轨道梁的简谐激励与响应分别为：
式中：F0是激励力幅值；x0是激励力坐标；j是虚数单位；ω是振动频率；W(x)是位移响应，随频率的变化即为频响。将式(2)代入式(1)，简化后得到关于频响的微分方程：
中间作用力对于长梁两端的影响接近零，故可设两边界约束条件为响应W及其1阶、2阶导数等于零，其中一个条件用于确定有效长度。设梁左右段有效长度分别为L1、L2，按照Galerkin法，响应W可展开为：
式中：Ai、Bi是常数；M0是整数，将式(4)代入方程式(3)，利用三角函数的正交性，简化后得到：
式中：δli是 Kronecker delta函数。式(5)和式(6)是关于Ai、Bi的代数方程组，写成矩阵形式为：
式中：Z=[A1,A2, …,AM0,B1,B2, …,BM0]T是待解常向量；D0是2M0维复数方阵；E是2M0维列向量，由式(5)和式(6)确定。求解代数方程式(7)得到向量Z，将其代入式(4)即得频响W。非周期性支承与周期性支承的不同主要在于系数阵D0，对于周期支承，第i个位置坐标xsi=xs,i-1+Δxi，其中Δxi=ΔxT为相邻支承的间距，是常数；对于周期支承缺失情形，它具有不同值，从而导致两种情形下不同的系数阵D0。分别计算两种情况的系数阵并由式(7)解得Z=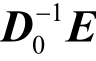
，代入式(4)分别得到频响，可用于比较分析。
根据典型周期支承轨道梁选取基本参数：ρ=7.85×103kg/m3，E=206 GPa，A=7.745×10-3m2，I=3.217×10-5m4，F0=1 N，x0=0，ksi=6.0×107kN/m，csi=3.625×104N/(m/s)，周期支承Δxi=0.6 m，阻尼系数按模态阻尼比0.001确定。考虑下列4种典型周期支承缺失，分别给出数值结果。
设力作用点处左边第1个支承刚度与阻尼同时损失，损失百分比用损失系数α描述。图 2、图 3分别展示了力作用点处位移频响幅值与相位差，可见存在频率170 Hz与1440 Hz两个共振，支承刚度与阻尼损失对第1共振幅值影响较为显著，其幅值随损失系数α非线性增加。第 2共振常称为“pinned-pinned共振”，其振动波长等于周期支承间距的两倍。支承刚度与阻尼损失对较低频相位差影响较大，第二共振时相位差保持π/2不变。
图2 1个支承刚度阻尼损失时位移频响幅值
Fig. 2 Frequency response amplitude under one support
stiffness and damping reduction
设支承刚度与阻尼同时存在周期性损失，3个支承成一周期，损失系数为α。图4、图5分别展示了力作用点处位移频响幅值与相位差，可见频响模式与图2、图3类似，但是当损失系数达到0.75时，频响幅值与相位在 370 Hz附近均出现一个新的小峰。因此，支承刚度与阻尼周期性损失可能形成新的频响峰。
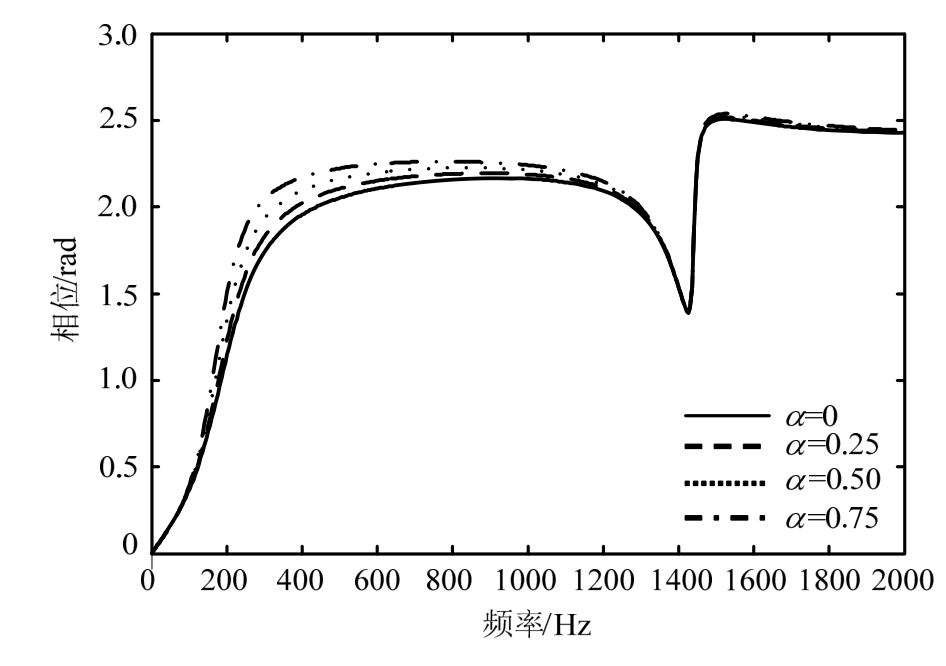
图3 1个支承刚度阻尼损失时位移频响相位
Fig. 3 Frequency response phase under one support stiffness and damping reduction
图4 支承刚度阻尼周期性损失时位移频响幅值
Fig. 4 Frequency response amplitude under periodic support stiffness and damping
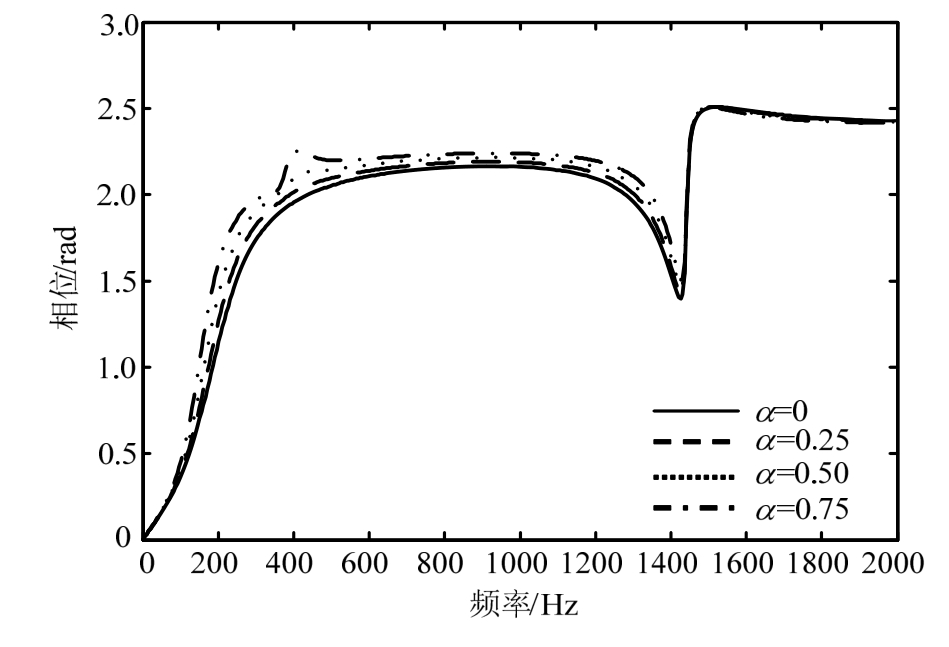
图5 支承刚度阻尼周期性损失时位移频响相位
Fig. 5 Frequency response phase under periodic support stiffness and damping
设支承位置相对于原等间距存在周期性偏移，偏离幅度为0即无偏移。图6、图7分别展示了不同偏离幅度下力作用点处位移频响幅值与相位差，可见周期性偏移对于频响有一定影响，第1共振幅值随偏离幅度而增加，第2共振幅值随偏离幅度而减小，特别是在频率380 Hz附近出现一个新的频响峰。相位差在400 Hz～1400 Hz频段随偏离幅度而明显增加，特别是第2共振相位差随偏离幅度显著增加。这种支承位置的周期性偏移在某种意义上类似于支承刚度与阻尼的周期性波动，从而可能导致频响类似的变化。
图6 支承位置周期性偏移时位移频响幅值
Fig. 6 Frequency response amplitude under periodic change of support positions
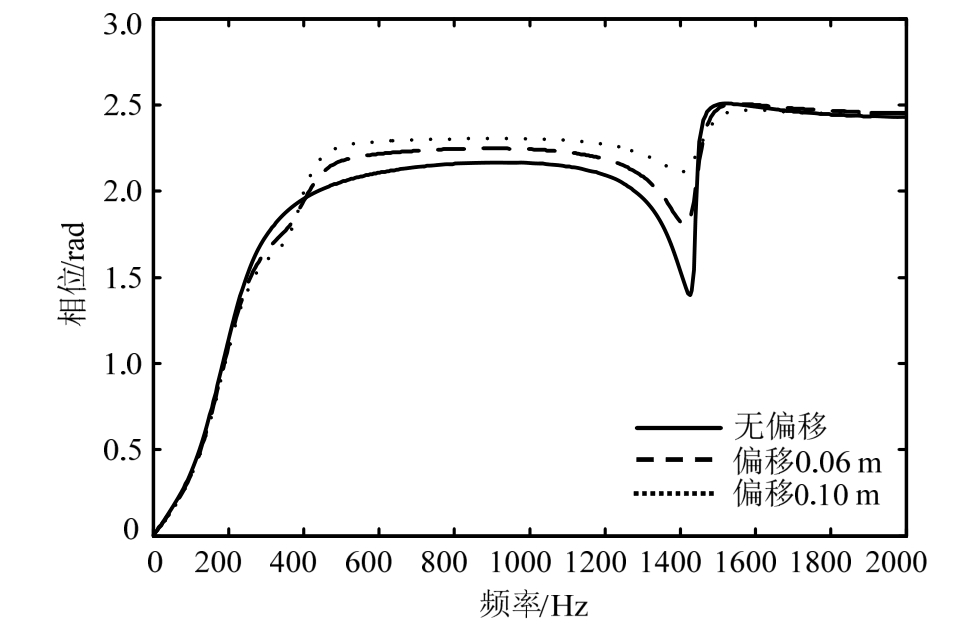
图7 支承位置周期性偏移时位移频响相位
Fig. 7 Frequency response phase under periodic change of support positions
设支承位置相对于原等间距存在随机偏移，偏离幅度服从零均值高斯分布。图8、图9分别展示了力作用点处位移频响幅值与相位差，可见随机偏移对于频响也有一定影响，第1、第2共振幅值随偏离幅度增加而减小，但没有出现新的频响峰，较高频段相位差随偏离幅度变化较明显。当支承位置随机偏移(标准差为 0.08 m)同时力作用点处左边第1个支承刚度与阻尼损失时，图10、图 11分别展示了力作用点处位移频响幅值与相位差，可见支承刚度与阻尼损失对第1共振幅值影响较为显著，类似于图 2，支承刚度与阻尼损失对较低频相位差有一定影响，类似于图 3。因此，支承位置偏移与刚度阻尼损失对于频响有不同的影响模式，支承位置偏移时的刚度阻尼损失仍然能通过频响反映。
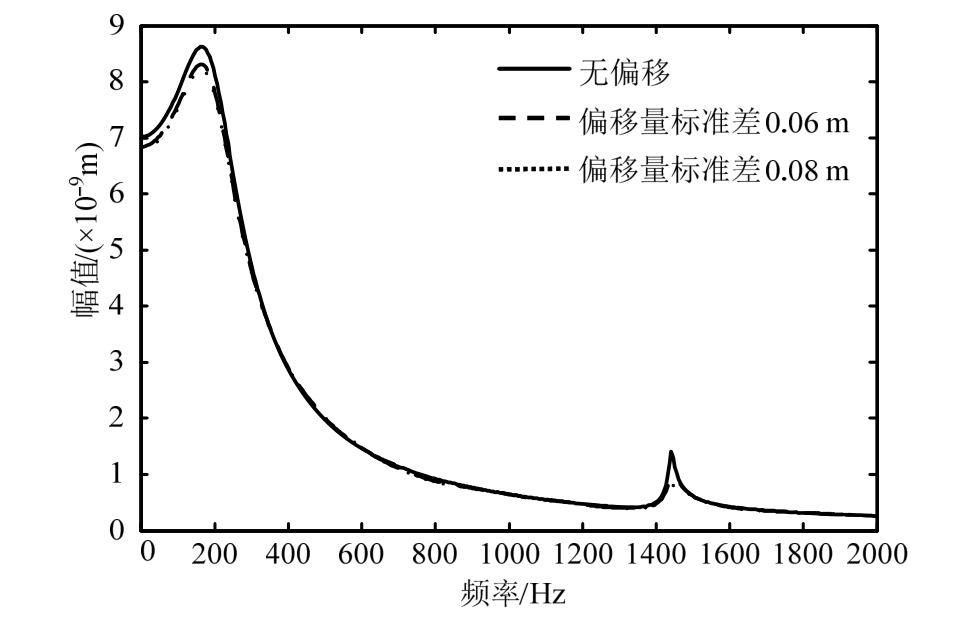
图8 支承位置随机偏移时位移频响幅值
Fig. 8 Frequency response amplitude under random change of support positions
图9 支承位置随机偏移时位移频响相位
Fig. 9 Frequency response phase under random change of support positions
图10 支承位置随机偏移且1个支承损失时位移频响幅值
Fig. 10 Frequency response amplitude under random change of support positions and one support stiffness and damping reduction
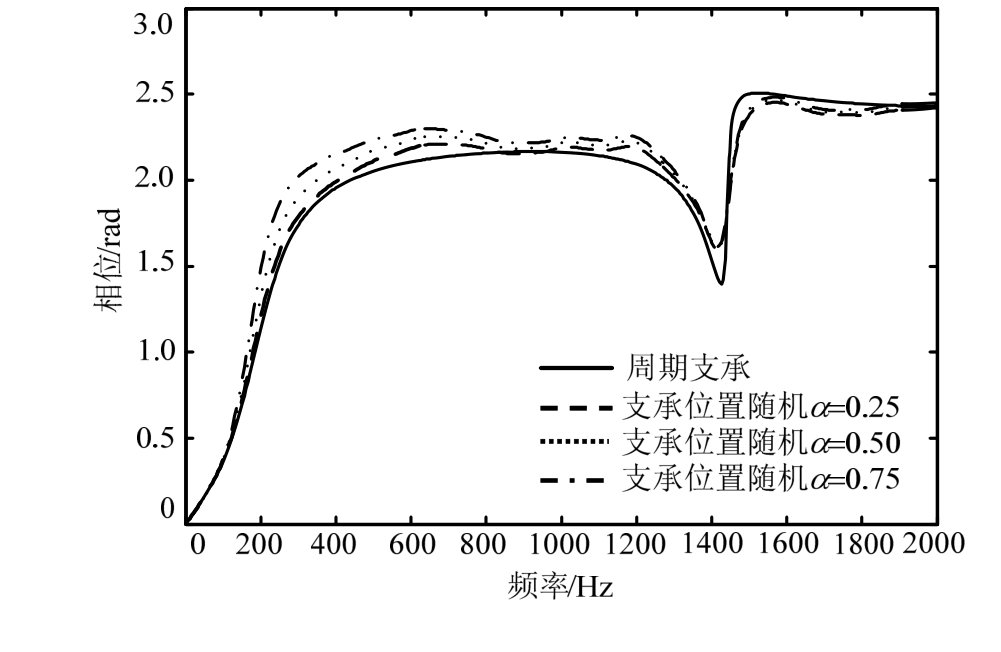
图11 支承位置随机偏移且1个支承损失时位移频响相位
Fig.11 Frequency response phase under random change of support positions and one support stiffness and damping reduction
本文研究了长轨道梁在周期支承缺失情况下的频响特性，首先建立非周期离散支承轨道梁的偏微分运动方程，转化为常微分的频响函数方程，再展开频响函数，运用Galerkin方法得到关于系数的代数方程组，求解之得到频响函数表达式，它适用于非周期与周期情形。对于典型轨道梁，计算分析了1个支承刚度阻尼损失、支承刚度阻尼周期性损失、支承位置周期性偏移、支承位置随机偏移等周期支承缺失情况对于频响的影响特性，数值结果表明：
(1) 支承刚度阻尼损失对于邻近跨中频响第 1个共振幅值影响较为显著，支承刚度阻尼同时周期性损失将产生新的频响峰；
(2) 支承位置周期性偏移对于跨中频响第1、第2共振幅值与相位差都有一定影响，并产生新的频响峰，中间频段及第2共振相位差改变较明显；
(3) 支承位置随机偏移对于跨中频响第1、第2共振幅值及较高频段相位差有一定影响，同时的支承刚度阻尼损失也对邻近跨中频响第1个共振幅值影响较为显著。因此，周期支承缺失以一定模式反映在轨道梁的频响特性中，它将为进一步通过轨道梁频响的周期支承异常识别提供理论基础。
参考文献：
[1]翟婉明. 车辆-轨道耦合动力学[M]. 北京: 科学出版社, 2015.Zhai Wanming. Vehicle-Track coupled dynamics [M].Beijing: Science Press, 2015. (in Chinese)
[2]Thompson D. 铁路噪声与振动-机理、模型和控制方法[M]. 北京: 科学出版社, 2013.Thompson D. railway noise and vibration: mechanisms,modelling and means of control [M]. Beijing: Science Press, 2013. (in Chinese)
[3]刘学毅, 王平. 车辆-轨道-路基系统动力学[M]. 成都:西南交通大学出版社, 2010.Liu Xueyi, Wang Ping. The vehicle track subgrade system dynamics [M]. Chengdu: Southwest Jiao Tong University Press, 2010. (in Chinese)
[4]Cox S J, Kang K D. The dynamic response of railway track with flexible sleepers to high frequency vertical excitation [J]. Proceedings of the Institution of Mechanical Engineers Part D, Journal of Automobile Engineering, 1984, 198(2): 117―124.
[5]Grassie S L, Gregory R W, Harrison D, et al. The dynamic response of railway track to high frequency vertical excitation [J]. Archive Journal of Mechanical Engineering Science, 2006, 24(2): 97―102.
[6]Thompson D J. Wheel-rail noise generation, part I:introduction and interaction model [J]. Journal of Sound and Vibration, 1993, 161(3): 387―400.
[7]Belotserkovskiy P M. On the oscillations of infinite periodic beams subjected to a moving concentrated force[J]. Journal of Sound and Vibration, 1996, 193(3): 705―712.
[8]Sheng X. Generalization of the Fourier transform-based method for calculating the response of a periodic railway track subject to a moving harmonic load [J]. Journal of Modern Transportation, 2015, 23(1): 12―29.
[9]Wu T X, Thompson D J. The influence of random sleeper spacing and ballast stiffness on the vibration behaviour of railway track [J]. Acta Acustica United with Acustica, 2000, 86(2): 313―321.
[10]Pierre C, Tang D M, Dowell E H. Localized vibrations of disordered multi-span beams-Theory and experiment [J].AIAA Journal, 1987, 25(9): 1249―1257.
[11]Bisegna P, Caruso G. Dynamical behavior of disordered rotationally periodic structures: a homogenization approach [J]. Journal of Sound and Vibration, 2011,330(11): 2608―2627.
FREQUENCY RESPONSE CHARACTERISTICS OF TRACK BEAMS WITH DETUNING PERIODIC SUPPORTS
KANG Lei1, YING Zu-guang1, NI Yi-qing2
(1. Department of Mechanics, School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China;2. Department of Civil and Environmental Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong, China)
Abstract:The dynamic stiffness or frequency response characteristics of railway tracks are an important dynamic performance index for safe and stable commissioning of trains. The tracks are supported by discrete periodic sleepers which provide support stiffness and damping for tracks. However, actual periodic support detuning is unavoidable, causing the frequency response characteristics or dynamic performance of railway tracks degenerate. Therefore, the frequency response characteristics of tracks with detuning periodic supports and the relationship between them need to be studied. In this paper, the vertical dynamic characteristics of a long track beam with detuning periodic supports were considered. The partial differential equation of motion of the beam with discrete support stiffness and damping was established, and transformed to ordinary differential equation for the frequency response function. The frequency response function expression was obtained by solving the equation using the Galerkin method, which was suitable for non-periodic and periodic support cases. The frequency response characteristics of the beam with detuning periodic support stiffness and damping and the beam with detuning periodic support positions were calculated. The influence of detuning periodic supports was evaluated by comparing the frequency responses of the quasi-periodic-support and periodic-support beams.Numerical results illustrated that the periodic support detuning had high effects on the first resonance peak around the support and generated new frequency response peaks, and the random support positions had certain effects on the phase of high frequency response. The relationship between the frequency response characteristics and periodic support detuning was instrumental for the periodic support damage identification of tracks through frequency response.
Key words:track beam; periodic support; periodicity detuning; frequency response characteristics; broadband
中图分类号：U213.2+1
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.05.S026
文章编号：1000-4750(2018)Suppl-0145-05
收稿日期：2017-05-14；修改日期：2017-12-08
基金项目：国家自然科学基金项目(11572279)；浙江省自然科学基金项目(LY15A020001)；香港理工大学智能铁路技术与应用项目(BBY1)
通讯作者：应祖光(1963―)，男，浙江人，教授，博士，博导，主要从事结构系统动力学、识别与控制研究(E-mail: yingzg@zju.edu.cn).
作者简介：康 雷(1993―)，男，安徽人，研究生，主要从事结构动力学分析及损伤监测研究(E-mail: 2664200708@qq.com);
倪一清(1964―)，男，浙江人，教授，博士，博导，主要从事工程结构动力学、损伤检测与控制研究(E-mail: ceyqni@polyu.edu.hk).