
图1 两种摇摆结构体系
Fig.1 Two kinds of rocking structure system
贾明明1,2,周 洲1,2,吕大刚1,2,杨 宁1,2
(1. 哈尔滨工业大学结构工程灾变与控制教育部重点实验室,哈尔滨 150090;2. 哈尔滨工业大学土木工程学院智能防灾减灾工业与信息化部重点实验室,哈尔滨 150090)
摘 要:建筑结构抗震设计所希望的结构地震失效模式是完全梁铰式失效,由于各种不确定性的存在,在实际地震中,结构是否能发生完全梁铰式失效是无法预知的。而防屈曲支撑构件(BRB)延性较大,在地震作用下可稳定地耗散地震输入结构的能量。鉴于此该文提出了一种摇摆桁架-BRB-钢框架体系,采用静力推覆分析方法,识别出了结构的主要地震失效模式,对其失效路径以进行了分析;对传统钢框架结构、摇摆桁架-钢框架体系、摇摆桁架-BRB-钢框架体系在小震、中震、大震作用下进行时程分析,并基于峰值层间位移角评价了三种结构的抗震性能。结果表明摇摆桁架-BRB-钢框架体系,在结构耗能减震、失效模式的优化控制,降低结构的残余变形等方面均起到了重要作用,新结构的侧向变形较传统钢框架结构更加均匀,结构整体参与耗能的能力更强。
关键词:抗震结构;摇摆桁架-BRB-钢框架体系;失效模式;变形均匀性;功能可恢复性
摇摆结构的基本思想是:当局部约束得以释放,构件或结构可以发生转动和平动,并将合适的阻尼器设置在结构体系变形较大的部位,以便地震中将结构损伤集中于阻尼器。阻尼器既能消耗地震作用输入结构的能量,也可以作为保险丝通过更换对结构进行震后修复,大大改善结构的可恢复性能和抗震性能。
自从Housner发现摇摆原理以来,许多学者对此进行了研究。Midorikawa等[1―2],采用抬升柱脚,并在柱脚与基础间加设翼型钢板,在地震作用下钢框架结构摇摆振动,柱脚抬起,翼型钢板屈曲耗能;Eatherton等[3]提出了一种具有自复位能力的摇摆框架,其中可更换的软钢阻尼器耗散地震能量,同时降低震后结构残余变形;Eatherton等[3]提出了一种可控的摇摆消能钢支撑框架体系,在框架上施加预应力筋提供恢复力,使框架地震后能恢复到变形前位置,金属阻尼器设置在框架中错动变形较大处并在地震中屈服耗能,地震后维修更换。Rojas[4]将摩擦板引入自复位钢框架来实现能量的耗散,形成自复位-摩擦型梁柱节点,此种节点耗能效果显著,构造经济。但是存在耗能不稳定,摩擦效果受环境影响大,布置上与楼面板容易存在冲突。Grigorian等[5]介绍了一种可以防止倒塌、具有自复位能力和可恢复性强的摇摆墙结构,摇摆墙可以避免结构薄弱层的出现以防止倒塌,后张拉预应力筋可以赋予结构自复位能力,通过附加摇摆墙限值结构损伤集中在梁端和非结构构件上,提高了结构的可恢复能力,减少了修复成本和经济损失。冯玉龙、吴京等[6]提出了一种连续摇摆墙-屈曲约束支撑框架结构体系,分析表明屈曲约束支撑和连续摇摆墙结构降低了结构的地震响应。吴守君、潘鹏等[7]结合山东省某医院加固工程实例的研究表明,框架-摇摆墙结构中增设阻尼器和预应力钢筋能够增加结构体系耗能能力并减少震后残余变形。并将现浇混凝土墙板与周围梁柱组成刚性填充墙,墙体两侧框架柱与基础接触但不连接,允许柱底抬起可以实现刚性摇摆填充墙[8]。摇摆墙与框架之间的连接方式得以简化,结构的剪力分布更加均匀,能够有效控制框架的变形模式,有利于实现材料性能的充分利用。可见,摇摆结构形式正成为一种具有良好工程应用前景的新型结构形式和理念。
本文提出了一种摇摆桁架-BRB-钢框架体系,并对钢框架和摇摆桁架之间的界面上的 BRB构件的布置进行了研究。首先分析摇摆桁架-BRB-钢框架体系的地震失效模式,就其失效路径与损伤程度进行分析与评价,并研究采用摇摆桁架和 BRB控制钢框结构架地震失效模式的机理。最后,基于损伤集中系数、峰值层间位移角、残余层间位移角对摇摆桁架-钢框架体系、摇摆桁架-BRB-钢框架体系进行抗震性能分析与对比。
如图1所示,在钢框架和摇摆桁架之间的界面上布置BRB构件,一方面可以耗散地震能量,降低主体结构的损伤,另一方面可以改善控制钢框架的地震失效模式,使其形成优化的BRB构件—SCED构件—钢框架梁端—钢框架柱端的结构地震失效顺序,从而提高结构抗震性能。

图1 两种摇摆结构体系
Fig.1 Two kinds of rocking structure system
要实现结构失效模式的控制和提高结构的抗震性能,BRB构件刚度过小,则在地震作用下,能够较早地屈服,耗散的地震能量较少;若 BRB构件刚度过大,摇摆桁架-钢框架体系原有的性能有可能发生改变,不能实现预定的失效顺序[9],在地震作用下,也不能较早地屈服,耗散地震能量;若BRB刚度过小,所耗散的能量又较小。依据已有的研究结论[10],本文选取 BRB构件与钢框架结构层刚度比为1.0,并建立OpenSEES有限元模型。
如图1所示,分析模型为8层结构,建筑场地类型为8度II类场地,取结构的一榀框架作为分析对象,共3跨,跨度7.2m。楼面恒荷载3.0 kN/m2,楼面活荷载 2 kN/m2,基本风压 0.45 kN/m2,基本雪压0.25 kN/m2。首层层高3.9 m,其余标准层层高3.3 m,表1给出了其中钢框架结构的楼层信息。根据《钢结构设计规范》,防屈曲支撑Q235钢内芯的屈服强度设计值为215 N/mm2,2层BRB屈服段的截面面积为1466.67 mm2;3~5层BRB屈服段的截面面积为1211.91 mm2;6~8层BRB屈服段的截面面积为746.07 mm2。考虑到BRB转换段和连接段截面增大,采用构件的有效刚度作为建模的依据。OpenSEES模型中钢框架梁柱采用非线性梁柱单元模拟,摇摆桁架采用Truss单元模拟,自复位耗能元件(SCED)采用Two Node Link单元模拟。
表1 钢框架结构楼层信息
Table 1 Information of steel frame structure

FEMA P695基于22个台站信息,给出了44条远场地震动。本文从中选取了 22条(编号 GM1~22)[11],各条地震动的加速度反应谱以及所有地震动的中位值反应谱如图2所示。

图2 22条地震动加速度反应谱及其中位值反应谱
Fig.2 The acceleration spectrum of the 22 earthquake records
采用 Pushover静力推覆分析方法将摇摆桁架-BRB-钢框架体系推至顶点位移角为6%,得到的结构体系能力曲线如图3所示,并将结构体系中构件的失效顺序在能力曲线上予以标注。

图3 摇摆桁架-BRB-钢框架体系地震失效路径分析
Fig.3 Seismic failure path analysis of truss-BRB-steel frame
摇摆桁架-BRB-钢框架体系地震失效顺序为:摇摆界面BRB构件屈服-钢框架柱底屈服-钢框架梁端屈服-钢框架柱顶屈服,是一种理想的结构失效模式。图3中右构件失效顺序用塑性铰的位置予以标注。在将体系推至顶点位移角为 6%的过程中,当顶点位移角为0.25%时,摇摆界面上BRB构件开始屈服,其后 BRB构件进入塑性开始耗散能量,结构体系仍处于弹性阶段;当顶点位移角约为 0.6%时,主体钢框架结构一层柱底屈服形成塑性铰,结构柱底形成塑性铰后不仅不会对结构体系造成大的影响,反而会减少地震动加速度向上部结构的传递,从而使结构具有一定的隔震功能;当顶点位移角约为0.8%时,钢框架结构梁端陆续屈服形成塑性铰,直至顶点位移角为1.75%时,1层~7层梁端全部屈服形成塑性铰(图 3(d));当顶点位移角大于1.75%时,8层2列、3列柱顶屈服形成塑性铰,同时8层梁端也完全屈服。可以看出,此种结构地震失效模式是一种理想的完全梁铰式失效模式,同时摇摆界面上 BRB构件屈服耗能也会降低主体钢框架塑性损伤,使结构体系整体抗震性能得到了更大的提高。
在分析失效路径的基础上,分析采用摇摆桁架和BRB控制钢框架结构的地震失效模式的机理[12]。同时针对抗震规范中的小震和大震作用对控制机理进行讨论。
将所选择的 22条地震动调幅至小震作用,进行时程分析。分析显示,22条地震动中仅有9条地震动使部分BRB构件屈服,且此时屈服的BRB构件绝大部分仅是刚刚屈服,主体钢框架没有构件屈服,结构保持弹性,没有损伤发生。在小震作用下,摇摆桁架-BRB-钢框架体系中BRB构件率先发挥作用,但其耗能作用尚未充分发挥。
如图4所示,将22条地震动调幅至大震作用,摇摆桁架-BRB-钢框架体系在地震作用下仅BRB构件和结构梁端屈服耗能,还没有出现梁柱铰混合失效模式。结构体系具有较大的安全储备来抵御更大的地震作用,如若结构遭遇到极罕遇地震,那么内柱柱铰便会出现,配合前两个过程共同抵御地震作用。同时,塑性铰形成过程之间并没有非常明确的界限,各控制过程之间可能会有搭接重叠,共同构成结构体系抵抗地震作用的全过程。

图4 大震作用下摇摆桁架-BRB-钢框架体系失效模式发展过程
Fig.4 Failure modes development process of truss-BRB-steel frame under rare earthquake
峰值层间位移角也可以用来评价结构构件和结构整体的损伤程度[13],对于每一条地震动,本文通过时程分析得到结构体系在小震、中震以及大震作用下对应的最大层间位移角值。
依据 22条地震动作用下的结构响应,计算了最大层间位移角值的50%和84%分位值,50%分位值可以近似表示结构在不同地震动作用下的地震需求中位值,84%分位值可以体现结构地震响应的离散程度。图5所示为不同结构体系在小震、中震、大震作用下不同分位值的峰值层间位移角响应。
由图5可以看出,钢框架结构附加摇摆桁架后,在小震、中震以及大震作用下,不同分位值水平下的峰值层间位移角都得到降低,结构体系的损伤比钢框架结构更小。同时,层间位移角值也更加均匀。而摇摆桁架-BRB-钢框架体系的侧向变形模式与摇摆桁架-钢框架体系基本一致,只不过层间位移角值更小,说明摇摆界面上的 BRB构件基本不提供侧向刚度,只发挥耗能作用。

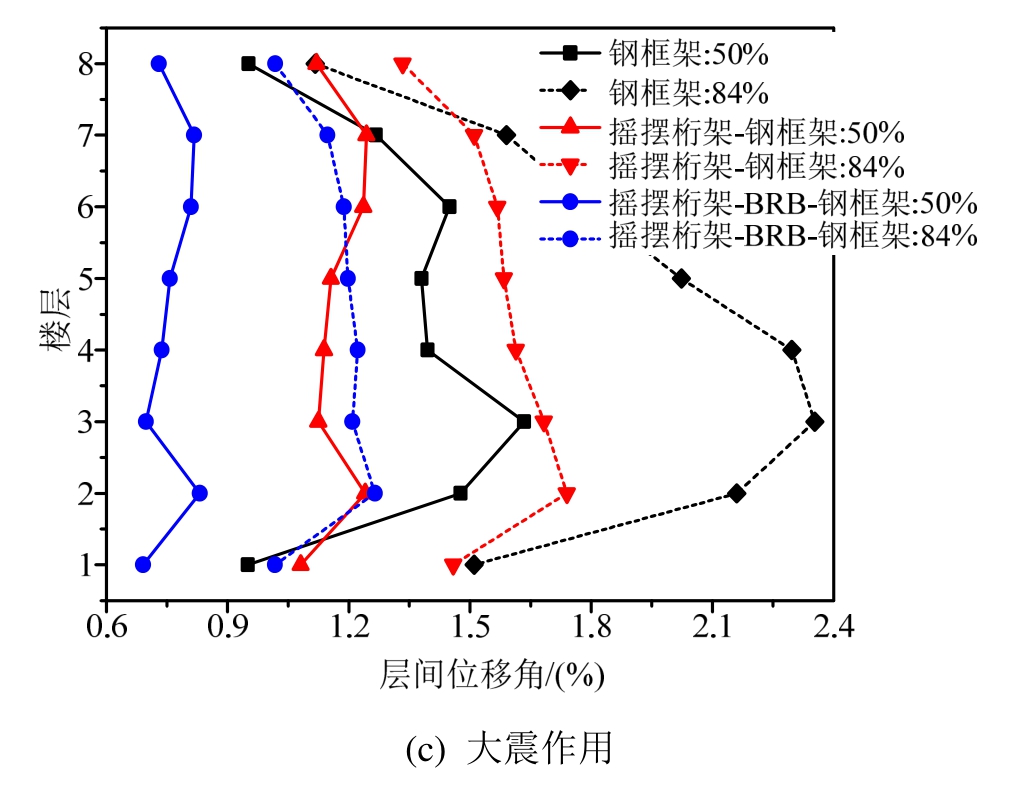
图5 三种结构体系在小震、中震、大震作用下的峰值层间位移角响应
Fig.5 Peak drift responses of three structures systems under frequency earthquakes, moderate earthquakes and rare earthquakes
层间位移集中系数即损伤集中系数[14](damage concentration factor,DCF)可以用来评价结构抵御薄弱层出现的能力以及结构整体参与耗能的能力,其计算公式如下:
式中:Δ、Δr分别为结构层位移和结构顶点位移;hs、hn为结构层高和结构整体总高度。
本文计算了钢框架结构、摇摆桁架-钢框架体系以及摇摆桁架-BRB-钢框架体系在大震作用下的损伤集中系数。由于地震动较强的随机性,在本文选取的 22条地震动作用下计算出的结构损伤集中系数具有较大的离散性,如图6所示,可以选取其平均值进行对比分析。
根据图6可以看出,原钢框架损伤集中系数平均值较大,大震作用下为1.72,这反映了原钢框架在地震动作用下结构侧向变形不均匀,结构损伤集中在薄弱层。然而,摇摆桁架-钢框架体系和摇摆桁架-BRB-钢框架体系在相同的地震动作用下,其损伤集中系数得到了降低,说明了此两种结构体系的侧向变形模式得到了良好的控制,结构损伤更加均匀。因此,从上述分析可以看出:
1) 摇摆桁架-钢框架体系和摇摆桁架-BRB-钢框架体系在地震动作用下的侧向变形较原钢框架结构更加均匀,结构整体参与耗能的能力更强。
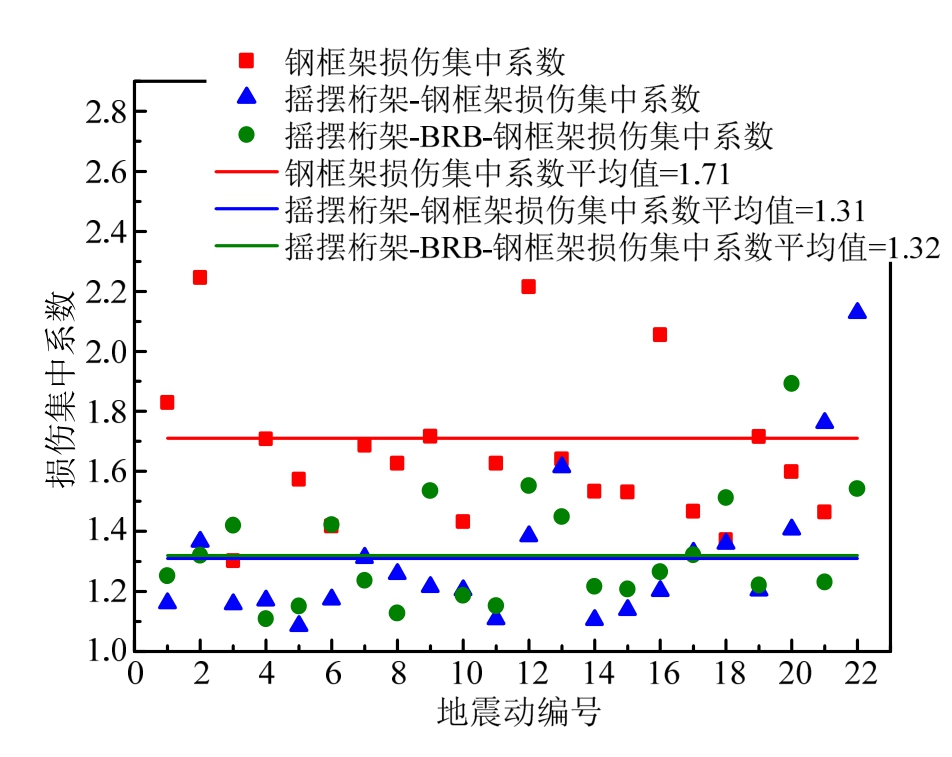
图6 三种结构在大震作用下损伤集中系数及其平均值
Fig.6 Damage concentration factor and its mean value of three structures under rare earthquakes
2) 随着地震动强度的增加,由中震到大震,摇摆桁架和 BRB对结构侧向不均匀变形控制能力更强。
3) 在摇摆界面加入的BRB耗能元件在结构发生侧向变形时耗散地震能量,而摇摆桁架起主要的结构侧向变形控制作用。
残余层间位移角是结构残余层间位移与层高的比值,此指标也可以用来评价结构的损伤程度,也为结构的可恢复性提供了评价依据。若结构残余变形过大,结构可能失去使用功能需要重建,此时的经济代价最高。
本文主要针对大震作用,研究了钢框架结构、摇摆桁架-钢框架体系、摇摆桁架-BRB-钢框架体系的残余层间位移角,并取其50%、84%分位值绘制于图7中。

图7 3种结构体系在大震作用下残余层间位移角曲线
Fig.7 Residual drift curves of 3 kinds of structural systems under rare earthquakes
由图7可以看出,摇摆桁架-钢框架体系的残余层间位移角较纯钢框架的残余层间位移角小,最大值降低了 78.7%左右。然而,摇摆桁架-BRB-钢框架体系的残余层间位移角与摇摆桁架-钢框架体系的残余层间位移角相比有增大的趋势,这主要是因为 BRB构件屈服耗能带来了金属的残余变形,但是较钢框架结构残余层间位移角还是降低了。摇摆界面上的残余变形可以通过更换BRB构件来恢复,BRB也起到了保险丝的作用,BRB屈服耗能,甚至损伤破坏,保护了主体结构,震后修复简便且成本较低。
本文提出了摇摆桁架-BRB-钢框架体系,给出了摇摆界面上 BRB构件的布置方式以及合理刚度选择的建议,并进行了失效模式和体系的抗震性能评价,结论如下:
1) 摇摆桁架-BRB-钢框架体系的失效顺序为:摇摆界面BRB构件屈服-钢框架柱底屈服-钢框架梁端屈服-钢框架柱顶屈服。在小震作用下,结构基本处于弹性;中震作用下,BRB构件开始屈服耗能;大震作用下,钢框架结构梁端陆续屈服。此种失效模式是一种理想的耗能构件-梁铰式失效模式,BRB构件实现了对结构失效模式的控制。
2) 通过结构侧向变形均匀性评价、结构耗能能力分析和结构功能可恢复性评价对摇摆桁架-BRB-钢框架体系的抗震性能进行了研究,分析表明摇摆桁架-钢框架和摇摆桁架-BRB-钢框架体系具有最优的侧向变形模式;而摇摆桁架-BRB-钢框架体系耗能能力最强;摇摆桁架-钢框架体系残余变形最小。
3) 加入BRB构件后,在小震、中震、大震作用下,由于 BRB的耗能减震作用,结构的地震响应得到控制,层间位移角明显减小。大震作用下,BRB构件屈服耗能带来了金属的残余变形,结构残余层间位移角略有增大,但摇摆界面上的残余变形可以通过更换 BRB构件来恢复,这样做既保护了主体结构,又使震后修复成本大大降低。
研究表明摇摆桁架—钢框架体系加入BRB后,在结构耗能减震、失效模式的优化控制,降低结构的残余变形等方面都起到了很好的作用。
参考文献:
[1]Azuhata T, Midorikawa M, Ishihara T. Earthquake response reduction of buildings by rocking structural systems [C]. SPIE’s 9th Annual International Symposium on Smart Structures and Materials, San Diego,California, United States, 2002. Proceedings Volume 4696: 265―272.
[2]Midorikawa M, Azuhata T, Ishihara T. Shaking table tests on seismic response of steel braced frames with column uplift [J]. Earthquake Engineering & Structural Dynamics, 2006, 35(14): 1767―1785.
[3]Eatherton M R, Hajjar J F, Deierlein G G. Controlled rocking of steel-framed buildings with replaceable energy-dissipating fuses [C]. The 14th World Conference on Earthquake Engineering, Beijing, China, 2008: No.05-06-0026.
[4]Rojas C P P. Seismic analysis, design, and evaluation of post-tensioned friction damped connections for steel moment resisting frames [D]. Bethlehem: Lehigh University Department of Civil and Environmental Engineering, 2003.
[5]Grigorian M, Grigorian C. An introduction to the structural design of rocking wall-frames with a view to collapse prevention, self-alignment and repairability [J].The structural design of tall and special buildings, 2016,25(2): 93―111.
[6]冯玉龙, 吴京, 孟少平. 连续摇摆墙-屈曲约束支撑框架抗震性能分析[J]. 工程力学, 2016, 33(Suppl 1): 90―94.Feng Yulong, Wu Jing, Meng Shaoping. Seismic performance analysis of continuously rocking wall-buckling restrained braced frames [J]. Engineering Mechanics, 2016, 33(Suppl 1): 90―94. (in Chinese)
[7]吴守君, 潘鹏, 张鑫. 框架-摇摆墙结构受力特点分析及其在抗震加固中的应用[J]. 工程力学, 2016, 33(6):54―60, 67.Wu Soujun, Pan Peng, Zhang Xin. Characteristics of frame rocking wall structure and its application in aseismic retrofit [J]. Engineering Mechanics, 2016,33(6): 54―60, 67. (in Chinese)
[8]吴守君, 潘鹏. 摇摆填充墙-框架结构抗震性能研究[J]. 建筑结构学报, 2015, 36(10): 81―87.Wu Shoujun, Pan Peng. Seismic performance evaluation of rocking infilled wall-frame structure [J]. Journal of Building Structures, 2015, 36(10): 81―87. (in Chinese)
[9]贾明明, 张素梅, 吕大刚, 等. 抑制屈曲支撑布置原则对钢框架抗震性能的影响[J]. 工程力学, 2009, 26(7):140―146.Jia Mingming, Zhang Sumei, Lü Dagang, et al. Influence of layout principle of buckling-restrained braces on aseismic performance of steel frame [J]. Engineering Mechanics, 2009, 26 (7): 140―146. (in Chinese)
[10]杨宁. 采用摇摆桁架和BRB的钢框架结构地震失效模式优化与控制[D]. 哈尔滨: 哈尔滨工业大学, 2016.Yang Ning. Optimization and control of failure modes of steel frames with rocking truss and BRBs [D]. Harbin:Harbin Institute of Technology, 2016. (in Chinese)
[11]FEMA P695, Quantification of building seismic performance factors [S]. Washington, D.C.: Federal Emergency Management Agency, 2009.
[12]贾明明, 吕大刚, 张素梅, 等. 防屈曲支撑钢框架基于延性的抗震性能设计[J]. 工程力学, 2010, 27(增刊 2):201―206.Jia Mingming, Lü Dagang, Zhang Sumei, et al. Seismic performance-based design based on ductility of buckling-restrained braced steel frame [J]. Engineering Mechanics, 2010, 27(Suppl 2): 201―206. (in Chinese)
[13]吕大刚, 贾明明. 钢框架结构基于变形可靠度的全概率抗震设计[J]. 工程力学, 2011, 28(5): 117―123.Lv Dagang, Jia Mingming. Full probability aseismic design of steel frame structures based on deformation reliability [J]. Engineering Mechanics, 2011, 28(5):117―123. (in Chinese)
[14]曲哲, 和田章, 叶列平. 摇摆墙在框架结构抗震加固中的应用[J]. 建筑结构学报, 2011, 32(9): 11―19.Qu Zhe, Wada Akria, Ye Lieping. Seismic retrofit of frame structures using rocking wall system [J]. Journal of Building Structures, 2011, 32(9): 11―19. (in Chinese)
SEISMIC FAILURE MODES AND SEISMIC BEHAVIOR ANALYSIS OF ROCKING TRUSS-BRB-STEEL FRAME SYSTEMS
JIA Ming-ming1,2, ZHOU Zhou1,2, LÜ Da-gang1,2, YANG Ning1,2
(1. Key Lab of Structure Dynamic Behavior and Control of China Ministry of Education, Harbin Institute of Technology, Harbin 150090, China;2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disaster of the Ministry of Industry and Information Technology,Harbin Institute of Technology, Harbin 150090, China)
Abstract:The seismic failure mode of seismic design of building structures is the failure of full beam hinges. In reality, it is difficult to foresee the full beam hinge failure mode of the structure due to uncertainties. Owing to large ductility, Buckling-Restrained Braces (BRBs) can dissipate the energy impacted on structures subject to earthquakes. In view of this feature, a rocking truss-BRB-steel frame system is proposed in this study. The main failure modes of the structure were identified by the pushover analysis and its failure path was analyzed. Based on the time history analysis for cases of earthquakes with mild, moderate and severe intensities, peak story drifts and seismic performance of a conventional steel frame structure, a rocking truss-steel frame system and a rocking truss-BRB-steel frame system were compared and analyzed. The results showed that the rocking truss-BRB-steel frame system played an important role in the structural energy dissipation, the optimal control of the failure modes, and the reduction of the residual deformation of the structures. The lateral deformation of the rocking truss-BRB-steel frame system was more uniform than that of the traditional steel frame structure and the energy consumption of the whole-parts-structure was stronger.
Key words:earthquake resistant structure; rocking truss-BRB-steel frame system; failure modes; deform uniformity; functional recovery
中图分类号:TU352.1
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.06.S009
文章编号:1000-4750(2018)Suppl-0073-07
收稿日期:2017-06-01;修改日期:2017-12-15
基金项目:国家自然科学基金项目(51378162,51678209);国家科技支撑计划子课题项目(2013BAJ08B01);教育部留学回国人员科研启动基金项目(2014);黑龙江省留学归国人员科学基金项目(40000045-6-15455);哈尔滨市科技创新人才基金项目(2013RFQXJ122)
通讯作者:贾明明(1978―),男,内蒙古人,副教授,博士,主要从事结构抗震、组合结构、结构可靠度等研究(E-mail: jiamingming@hit.edu.cn).
作者简介:周 洲(1991―),男,河北廊坊人,博士生,从事地震易损性、结构抗倒塌设计研究(E-mail: zzhouhit@163.com);吕大刚(1970―),男,黑龙江人,教授,博士,博导,副院长,主要从事结构可靠度、工程风险分析、地震工程等研究(E-mail: ludagang@hit.edu.cn);杨 宁(1990―),男,陕西人,硕士生,主要从事结构抗震和新型结构体系研究(E-mail: 1014646874@qq.com).