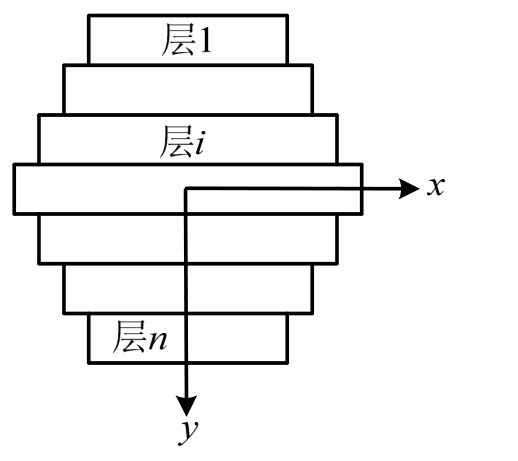
图1 多层组合梁截面示意图
Fig.1 Cross section of the multilayered composite beams
张永平，徐荣桥
(浙江大学土木系，杭州 310058)
摘 要：目前对组合梁的研究大多集中在两层组合梁，对多层组合梁的研究甚少。该文推导了考虑各层层间滑移的多层组合梁控制方程，求解了其在均布荷载与简支边界条件下的挠度计算的解析表达式，给出了挠度放大系数公式，结合规范中的折减刚度法，可以方便地用于工程设计。
关键词：多层组合梁；层间滑移；挠度放大系数；等效抗弯刚度；折减刚度法
组合梁是将不同的材料和截面通过剪力键连接在一起共同工作的组合结构，并且已经得到了广泛的研究和应用。但是目前对组合梁的研究几乎集中在以钢-混组合梁为代表的两层组合梁上，对于多层组合梁的研究则相对匮乏。多层组合梁在工程中同样常见，例如钢-混凝土-钢形式的夹心组合梁，木结构中的层合木梁等，故对其进行研究具有重要意义。
组合梁界面处具有滑移效应的特点导致其计算分析变得困难，为此研究人员提出了一系列的计算模型。例如：Newmark 等[1]基于欧拉-伯努利梁理论推导了考虑层间滑移的组合梁计算理论；Goodman[2]提出了组合木结构的计算理论；Girhammar 和 Gopu[3]推导了考虑层间滑移的组合梁的挠度控制方程，进而求解得到了解析解，并给出了简化的计算公式；Xu和Wu[4]基于铁木辛柯梁理论研究了考虑转动惯量和剪切变形的组合梁的静、动力性能及屈曲特性；余志武等[5]根据Goodman弹性夹层假设分析了均布荷载下的组合梁变形计算；丁敏等[6]提出了整体-局部弯曲模型分析组合梁变形；聂建国等[7]提出了组合梁变形计算的折减刚度法，并被规范采用[8]；徐荣桥和陈德权[9]在总结比较了不同的计算方法之后，针对规范中折减刚度法存在的问题，提出了组合梁挠度计算的改进折减刚度法。
上述方法都是针对两层组合梁的计算，对于多层组合梁的计算，目前还没有简便有效的方法。Xu和Wu[10－11]用二维平面应力模型分析组合梁静动力性能时采用的状态空间法可以实现多层组合梁的计算；Sousa Jr和da Silva[12]推导了以多层组合梁层间滑移为未知量的微分方程，也可以用来计算多层组合梁。但这两种方法计算过程复杂，无法给出统一的计算公式，不适用于工程设计。
本文在二层组合梁分析理论基础上，推导了考虑各层层间滑移的多层组合梁的控制方程，求出了相应的解析解，并给出了挠度计算公式、挠度放大系数等，结合折减刚度法，可以方便地用于工程设计。
假设多层组合梁有n层，其基本假设与两层组合梁基本一致，如下：
1) 各层截面曲率一致；
2) 各层截面挠度一致，竖向紧密接触不发生脱离；
3) 各层截面之间可以发生滑移，且滑移量与层间剪切力正比。
另外，为简化公式，这里考虑各层具有相同的弹性模量和层高，且各层截面关于整体截面的中性轴处对称，各层之间滑移层的抗滑刚度保持一致。对于截面弹性模量不一致、截面不对称和滑移层抗滑刚度不一致的情况，可以作为下一步的研究内容。一个典型的多层组合梁截面如图1所示。
图1 多层组合梁截面示意图
Fig.1 Cross section of the multilayered composite beams
取一微元体如图2所示，由整个截面的平衡关系可得：
式中：M为截面上总弯矩；Q为竖向总剪力；q为外荷载；N i为第i层的轴向力。设M i是第i层的弯矩，那么：
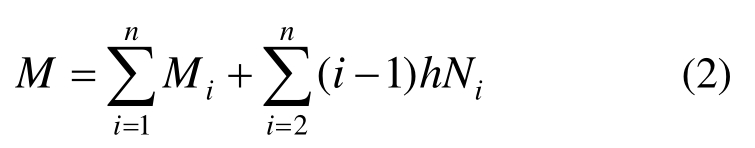
式中，h是每层的高度。
图2 微元体平衡示意图
Fig.2 Infinitesimal element equilibrium
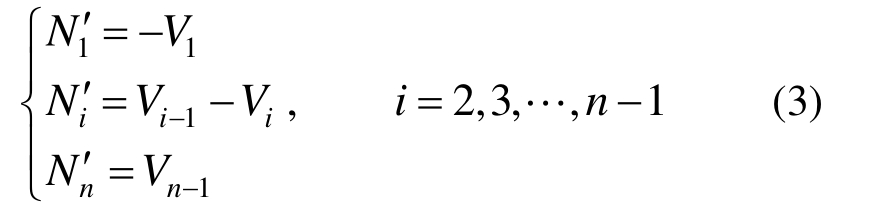
由每层水平方向的平衡可得：
式中，Vi是第i个界面处的剪切力，它与该界面处的相对滑移Δui的关系为：
而相对滑移Δui与轴向位移和挠度之间关系为：
式中：ui为第i层形心处的轴向位移；W为挠度。
根据经典梁理论：
式中，E Ii是第i层的抗弯刚度。把式(6)代入式(2)，并求导一次得：
式中，
将式(3)联合式(4)代入式(7)得：
把式(5)代入式(8)，再求导一次得到：
式中，
并利用
代入式(9)得：
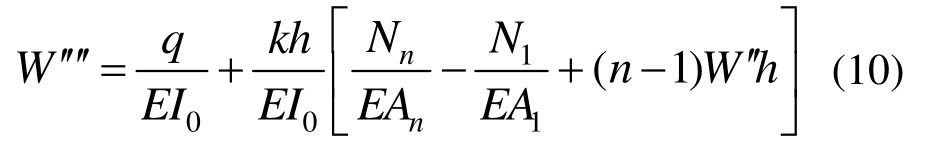
利用截面对称性 E A1= EAn与力的反对称性Nn=-N1，式(10)可化为：
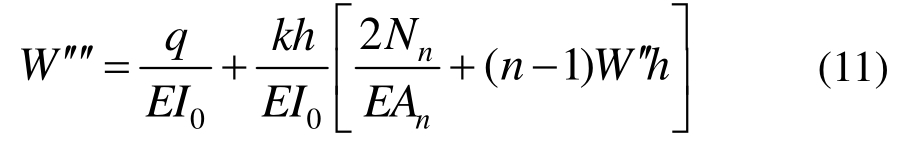
如果假设第i个界面处的滑移与第1个界面处的滑移有如下关系：
式中，ηi是一个与截面几何性质与抗滑刚度有关的常数，其计算公式为：
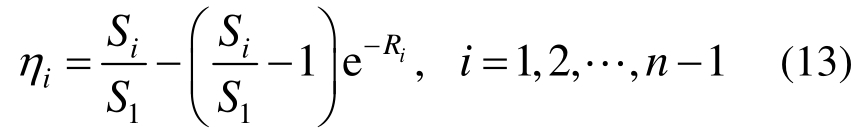
式中： Si为第i滑移面所在位置处的静矩； Ri为一个表征了第i滑移面相对抗滑刚度的无量纲量，这里采用文献[12]中的公式：
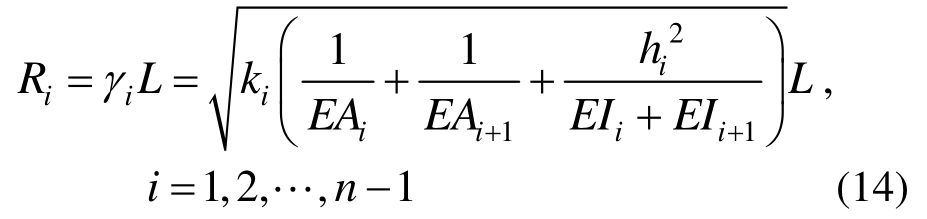
式(13)可以表达出 Δ ui/Δu1随着抗滑刚度k从零到无穷大的过程而发生的变化。当抗滑刚度ki→0时，各层滑移趋于一致， Δ ui/Δ u1→1；当ki→∞时，接近于完全粘结梁的状态，此时同一截面处各层滑移与其所在位置处的剪切力Vi/(N/m)有关，而剪切力 Vi= τibi=QSi/I∞(I∞是完全粘结状态下的整个截面的惯性矩)，故有Δui/Δu1→ Si/S1。
把式(12)代入式(8)得：
式中：
由式(11)和式(15)消去 Nn，得：
式中，EI∞为完全粘结状态下的截面抗弯刚度，且：
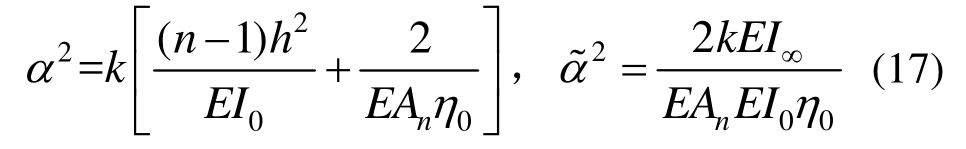
再求导一次，得到关于挠度的6阶控制方程：
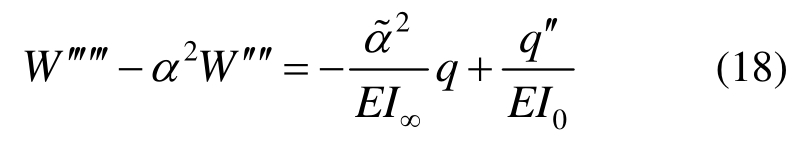
由此可以看到，控制方程和文献[3]中的两层组合梁的控制方程具有相似的形式，区别在于多层组合梁的α2和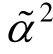
不一样。当层数n=2，此时只有一个滑移层且η0=1，将其代入式(17)则可以得到α2=
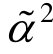，此时式(18)与文献[3]中的挠度控制方程一致，多层组合梁退化到两层组合梁。
均布荷载作用下，挠度控制方程为式(18)，这是一个六阶的非齐次微分方程，其通解为：
其中： ai( i = 1 ,2,… ,6 )为待定系数； Wp s为特解且有如下表达式：
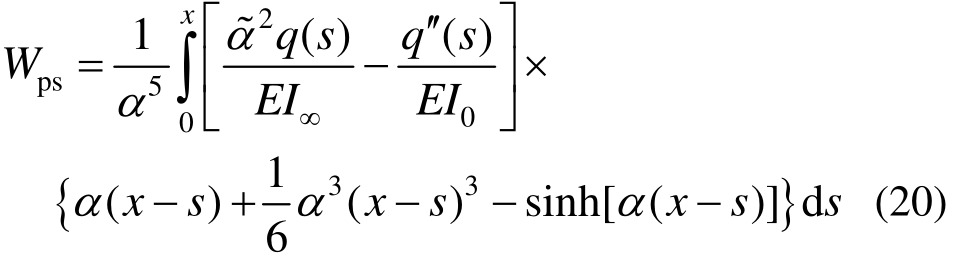
式中，s为积分变量。
边界条件有6个，首先根据两端位移和弯矩为零的条件，有：
式中，L为跨径。
又由式(11)得到：
将边界条件式(21)和式(22)代入式(19)求得待定系数，整理后得到挠度表达式(23)，将 x = 0.5L代入式(23)得到跨中最大挠度式(24)，在均布荷载下完
全粘结梁的跨中挠度为
得到挠度放大系数为式(25)，且等效抗弯刚度为式(26)。
式(24)与文献[3]所给的两层组合梁在简支边界条件下受到均布荷载所得到的跨中最大挠度精确解对比，可见两者有着相似的结构，都可以分成完全粘结作用下的挠度加上滑移作用下的挠度，区别在于多层组合梁情况下的α2和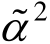
不一样。同样，当层数 n =2时可以得到 α2=
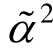，此时式(23)和式(24)与文献[3]所给的挠度表达式和跨中最大挠度公式的结果一致，表明多层组合梁的挠度解析表达式同样可以退化到到两层组合梁的挠度解析表达式。
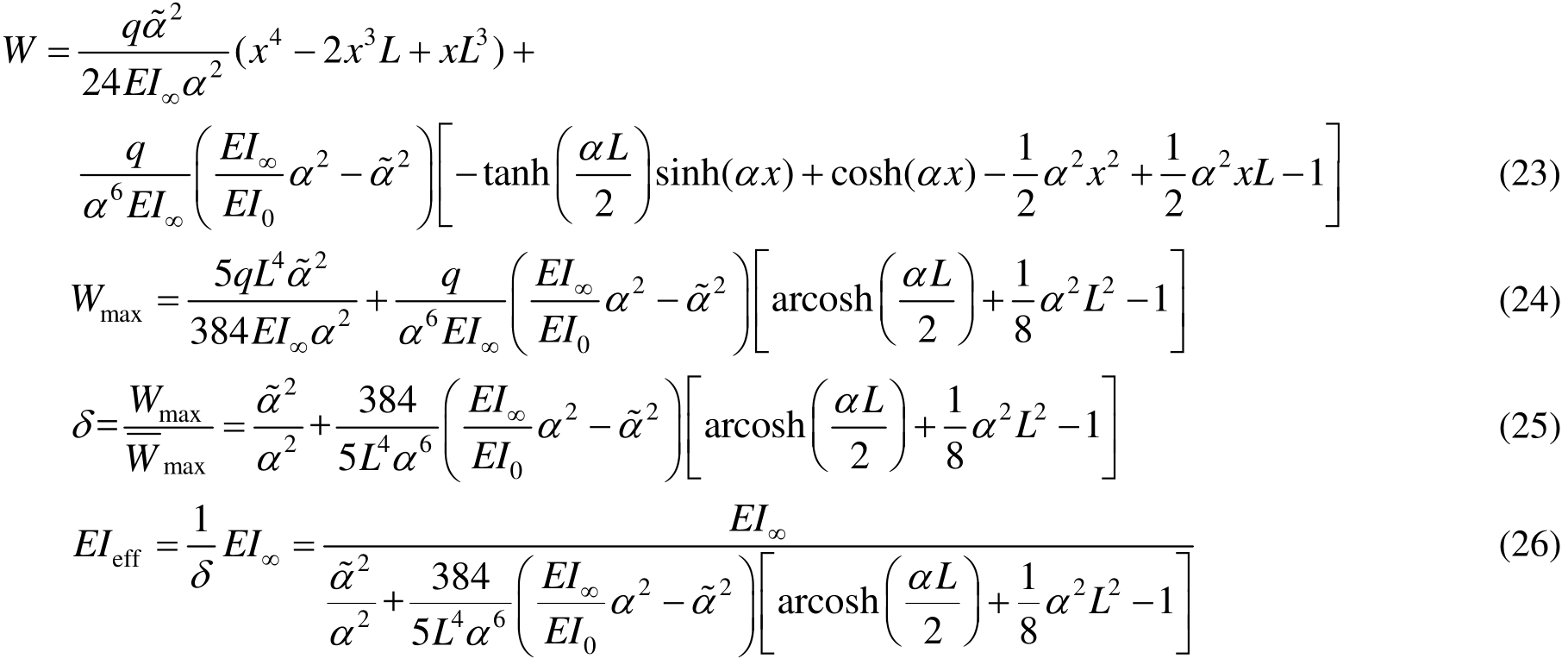
如图3所示，多层组合梁跨径L=4 m，边界为简支，受均布荷载作用，截面总高度为 0.4 m，宽为0.3 m，共有5层，每层高度为0.08 m，弹性模量为8 GPa，泊松比为0.3。
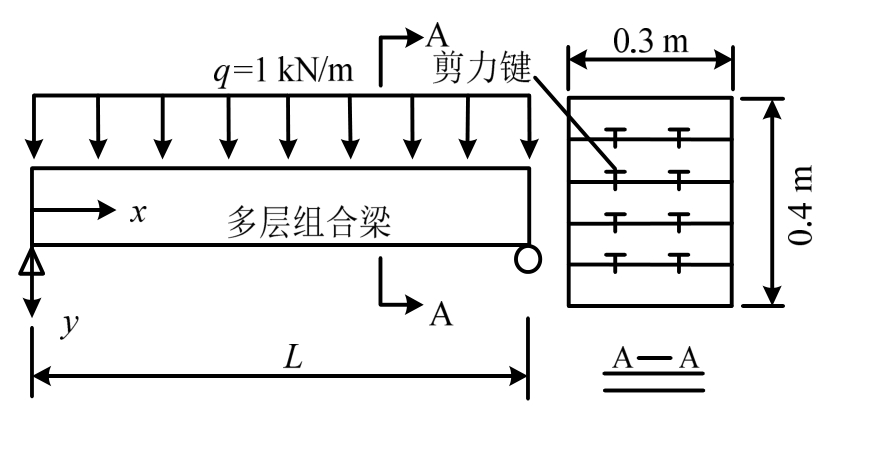
图3 计算模型示意图
Fig.3 Configuration of the numerical model
图中 多层组合截面完全粘结状态的抗弯刚度为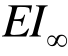
=1.28× 1 07/(N· m2)，完全不粘结状态的抗弯刚度为E I0= 5 .12× 1 05/ (N· m2)。当组合梁趋近于完全不粘结状态时应有δ max=E I∞/E I0=25，等效抗弯刚度接近于E I0，且得到跨中最大挠度理论值
当组合梁趋于完全粘结状态时应有δmin=1，组合梁等效抗弯刚度接近于EI∞，同样可得到跨中最大挠度理论值为Wmax=5q L4/(384E I∞)= 0 .26mm 。
图 4为根据式(25)计算得到的挠度放大系数随剪力连接键抗滑刚度k变化的关系图，从图4可以看到挠度放大系数在趋于完全不粘结状态时收敛到25，而在趋于完全粘结状态时收敛到1，与理论值相符。得到挠度放大系数后，就可以按照折减刚度法求出等效抗弯刚度用于工程设计。
图 5为根据式(24)求出的跨中最大挠度随抗滑刚度k变化的关系图，从图5中可见抗滑刚度趋于零时挠度为6.51 mm，抗滑刚度趋于无穷时挠度为0.26 mm，与理论值相符。图4和图5中两种极限状态的计算结果都与理论值一致，证明了公式计算准确。
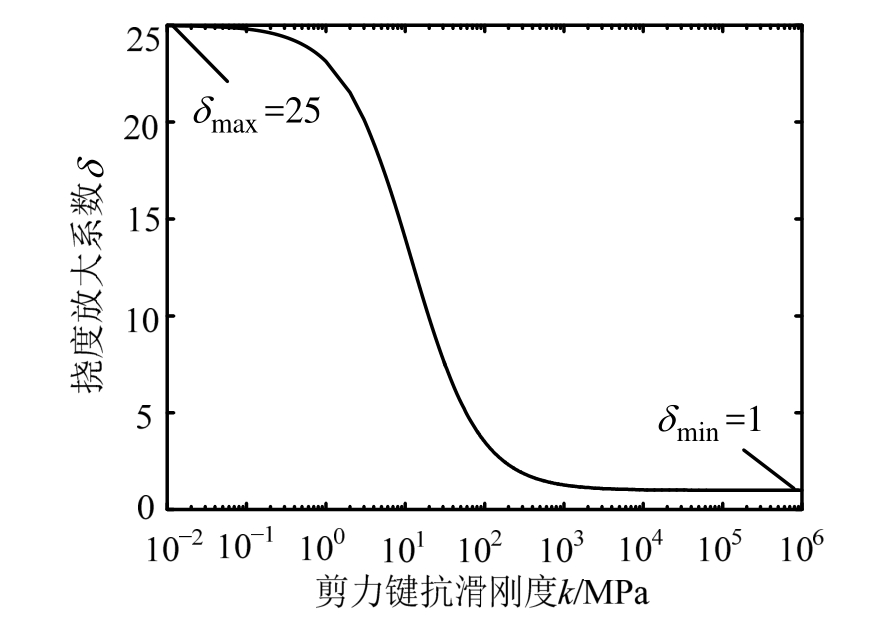
图4 挠度放大系数随抗滑刚度k的变化图
Fig.4 Variation of deflection magnification coefficient versus slip rigidityk/MPa
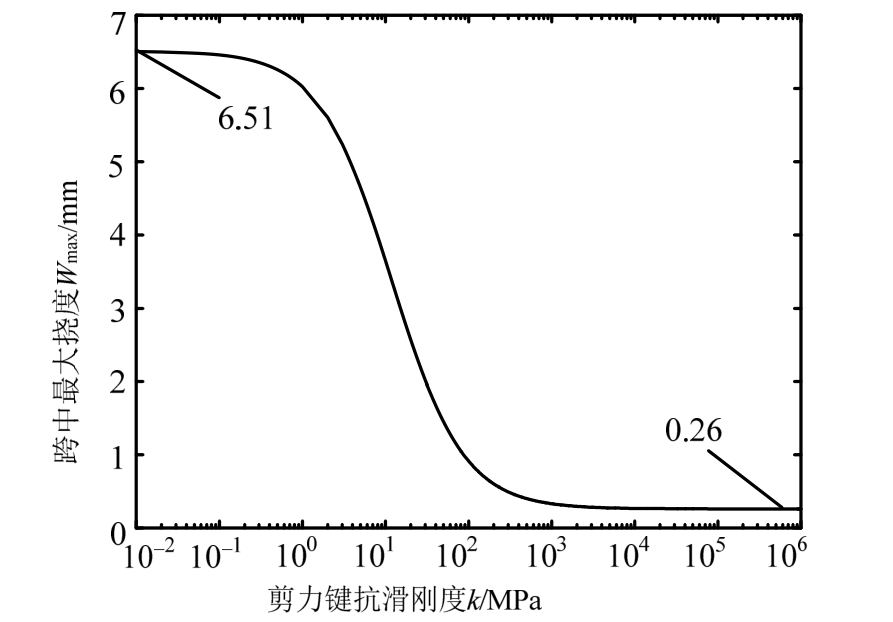
图5 跨中最大挠度随抗滑刚度k的变化图
Fig.5 Variation of mid-span maximum deflection versus slip rigidityk/MPa
图6 和图7分别反映了挠度放大系数和等效抗弯刚度系数随表征剪力键连接强度的无量纲参数αL变化的关系图，从图中可见α L∈[1,100]区间内αL的增大可以显著提高抗弯刚度，当α L＞100时则对抗弯刚度的提高很有限。这表明在工程应用中通过增大αL来提高组合梁抗弯刚度应控制αL在100以内。
图6 挠度放大系数随参数αL的变化图
Fig.6 Variation of deflection magnification coefficient versus nondimensional parameterαL
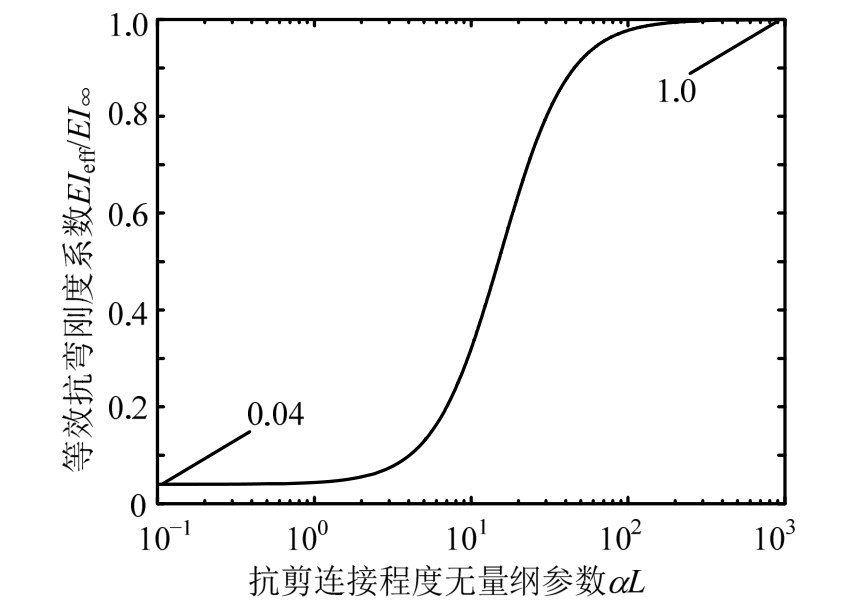
图7 等效抗弯刚度系数随参数αL的变化图
Fig.7 Variation of equivalent bending stiffness coefficient versus nondimensional parameterαL
本文在考虑层间滑移的两层组合梁理论基础上推导了考虑各层层间滑移的多层组合梁的控制方程，求解了挠度解析表达式，得到了挠度放大系数计算公式，经算例计算分析，表明该公式计算准确可靠。得到挠度放大系数后，就可以结合折减刚度法得到等效抗弯刚度，求出跨中最大挠度，用于多层组合梁的工程设计。
参考文献：
[1]Newmark N M, Siess C P, Viest I M. Test and analysis of composite beams with incomplete interaction [J].Proceedings of the Society for Experimental Stress and Analysis, 1951, 9(1): 75―92.
[2]Goodman J R. Layered Wood Systems with Interlayer Slip [D]. CA: University of California, Berkeley, 1967.
[3]Girhammar U A, Gopu V K A. Composite beam-columns with interlayer slip-exact analysis [J]. Journal of Structural Engineering (United States), 1993, 119(4):1265―1282.
[4]Xu R Q, Wu Y F. Static, dynamic, and buckling analysis of partial interaction composite members using Timoshenko's beam theory [J]. International Journal of Mechanical Sciences, 2007, 49(10): 1139―1155.
[5]蒋丽忠, 余志武, 李佳. 均布荷载作用下钢-混凝土组合梁滑移及变形的理论计算[J]. 工程力学, 2003,20(2): 133―137.Jiang Lizhong, Yu Zhiwu, Li Jia. Theoretical analysis of slip and deformation of steel-concrete composite beam under uniformly distributed loads [J]. Engineering Mechanics, 2003, 20(2): 133―137. (in Chinese)
[6]丁敏, 蒋秀根, 孟石平, 等. 整体-局部弯曲模型及其在简支组合梁中的应用[J]. 工程力学, 2012, 29(12):233―240.Ding Min, Jiang Xiugen, Meng Shiping, et al.Global-local bending model and its application in simply supported composite beam [J]. Engineering Mechanics,2012, 29(12): 233―240. (in Chinese)
[7]聂建国, 沈聚敏, 余志武. 考虑滑移效应的钢-混凝土组合梁变形计算的折减刚度法[J]. 土木工程学报.1995, 28(6): 11―17.Nie Jianguo, Shen Jumin, Yu Zhiwu. A reduced rigidity method for calculating deformation of composite steel-concrete beams [J]. China Civil Engineering Journal, 1995, 28(6):11―17. (in Chinese)
[8]GB 50017―2003, 钢结构设计规范[S]. 北京: 中国计划出版社, 2003.GB50017―2003, Code for design of steel structures [S].Beijing: China Planning Press, 2003. (in Chinese)
[9]徐荣桥, 陈德权. 组合梁挠度计算的改进折减刚度法[J]. 工程力学. 2013, 30(2): 285―291.Xu Rongqiao, Chen Dequan. Modified reduced stiffness method for calculating the deflection of composite beams[J]. Engineering Mechanics, 2013, 30(2): 285―297. (in Chinese)
[10]Xu R Q, Wu Y F. Two-dimensional analytical solutions of simply supported composite beams with interlayer slips [J]. International Journal of Solids and Structures,2007, 44(1): 165―175.
[11]Xu R Q, Wu Y F. Free vibration and buckling of composite beams with interlayer slip by two-dimensional theory [J]. Journal of Sound and Vibration, 2008,313(3/4/5): 875―890.
[12]Sousa Jr J B M, da Silva A R. Analytical and numerical analysis of multilayered beams with interlayer slip [J].Engineering Structures, 2010, 32(6): 1671―1680.
ANALYTICAL ANALYSIS FOR CALCULATING DEFLECTIONS OF MULTILAYERED COMPOSITE BEAMS WITH INTERLAYER SLIPS
ZHANG Yong-ping , XU Rong-qiao
(Department of Civil Engineering, Zhejiang University, Hangzhou, Zhejiang 310058, China)
Abstract:Most of the researches on composite beams with interlayer slips are concentrated on two-layered composite beams, while few works have been done on multi-layered composite beams. In this paper, the gonverning equations are derived for multi-layered composite beams taking into account the slips between layers,the analytical solutions for deflection calculations under uniformly distributed load and simply supported boundary conditions are obtained, and the formula for deflection magnification factor is presented. These solutions can be utilized to engineering applications by conveniently combining with reduced stiffness method.
Key words:multi-layered composite beams; interlayer slips; deflection magnification factor; effective bending stiffness; reduced stiffness method
中图分类号：TU398+9
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.06.S031
文章编号：1000-4750(2018)Suppl-0022-05
收稿日期：2017-06-02；修改日期：2017-11-10
基金项目：国家自然科学基金项目(51478422)
通讯作者：徐荣桥(1972―)，男，浙江人，教授，博士，博导，从事组合桥梁结构分析研究(E-mail: xurongqiao@zju.edu.cn).
作者简介：张永平(1989―)，男，福建人，博士生，从事组合桥梁结构分析研究(E-mail: zhangyongping@zju.edu.cn).