钮 鹏1,2,李 旭1,李世荣3,金春福4,柳 杨1
(1. 沈阳大学建筑工程学院,辽宁,沈阳 110044;2. 沈阳大学辽宁省环境岩土工程重点实验室,辽宁,沈阳 110044;
3. 扬州大学建筑科学与工程学院,江苏,扬州 225127;4. 辽宁省交通高等专科学校公路工程质量检测中心,辽宁,沈阳 110122)
摘 要:综合考虑构件轴线伸长和1阶横向剪切变形等条件下,建立横向受热作用且周围有弹性支承约束的夹层梁几何非线性精确数学模型。利用打靶法数值方法获得了两端转角弹簧与横向弹性地基共同约束时夹层梁的静态热过屈曲数值解。改变梁端转角弹簧刚度,获得不同的临界屈曲温度;当改变夹层梁物性参数时,给出平均升温参数与水平轴向压力之间的关系曲线;当两端转角弹簧刚度和弹性地基刚度同时给定时,分析非均匀升温参数与夹层梁热过屈曲和热弯曲组合变形之间的关系。
关键词:夹层梁;热屈曲;热弯曲;弹性约束;打靶法
梁受热后的屈曲和弯曲问题作为结构力学的热点问题,其力学行为一直受到人们的重视和关注[1-4]。弹性梁受热载作用下会因轴线方向热膨胀而导致热屈曲,因此其稳定性研究中不可忽视轴线可伸长的特性。李世荣等[5]建立弹性直梁在横向热-机荷载共同作用下的几何非线性静平衡控制方程。同样考虑构件的轴线伸长和一阶横向剪切因素影响,通过建立夹层梁在热-机械载荷下的控制方程,作者得到夹层梁的静态非线性弯曲和过屈曲变形数值解[6-8]。
当将弹性梁置于可变的弹性约束中时,温度变化对梁屈曲及弯曲影响研究具有现实工程背景和意义[6-7]。文献[9]分析弹性地基上欧拉梁的热屈曲模态跃迁特性。文献[10]在此基础上研究了弹性地基上复合材料夹层梁的热过屈曲等问题。当端部有任意转角约束时,作者[11]给出了连续梁压杆临界载荷求解的等效方法。
文献调查表明,复合材料夹层梁在弹性约束下的热屈曲和热过屈曲的行为研究并不为多见。本文将利用文献[6]、文献[10]、文献[12]在考虑构件中心轴线伸长因素影响及一阶横向剪切变形的基础上,建立既有弹性地基作用,又有弹性转角约束作用的复合材料夹层梁受到横向热载荷作用下的几何非线性控制方程。求解各种参数的变化对夹层梁的静态热过屈曲和热弯曲变形影响。重点讨论转角弹簧刚度及弹性地基刚度变化而获得的临界屈曲温度;分析夹层梁不同的物性参数比所对应的平均升温参数与水平轴向压力之间的关系。
几何方程。考虑一矩形截面复合材料夹层弹性直梁,其长宽高分别为l、b、h0(参见图1)。面板和夹芯层的物性参数已在图1(a)中标出。横截面尺寸如图1(b)所示。上下面板由同一种材料组成,厚度为t。设该梁受到横向线性变化的升温场T(z)影响,温度场为上正下负。梁受底部弹性地基以及两端转角弹簧作用,其弹性刚度分别为K c、K a、K b。引入轴向伸长和横向剪切变形条件来考虑夹层梁的热屈曲静态响应问题。给出变形后的轴线上物质点的运动学关系:
其中:s 0(x)为梁受荷变形之后的截面中心轴线的弧长;u0和w0分别为水平和竖向方向的位移;Λ0为轴线伸长后的伸长率。夹层梁在受荷变形后,其横截面上任意一点的正应变ε和剪应变γ′如下:

图1 受弹性地基和转角弹簧约束的夹层梁Fig.1 Geometry of the sandwich beam under elastic
foundation and rotational springs
其中:φ=θ+γ,θ为变形后轴线切线与x轴正向之间的夹角,γ为剪切角。
物理方程。假设认为夹层梁中各层材料之间是线性,热弹性的,并且各层材料之间的变形也是连续的。因此第j层材料的应力-应变之间关系可表示为![]() 其中E j和G j分别为第j层的拉伸模量和剪切弹性模量,αj为材料热膨胀系数,且j= 1 ,2,3。最终夹层梁受热后,其内部产生的轴力N(x)、热弯矩M(x)和剪力Q分别为:
其中E j和G j分别为第j层的拉伸模量和剪切弹性模量,αj为材料热膨胀系数,且j= 1 ,2,3。最终夹层梁受热后,其内部产生的轴力N(x)、热弯矩M(x)和剪力Q分别为:

其中:k为Timoshenko梁剪切修正系数k= 3 /2;C1、C2、C 3和C 4为刚度系数;N T为热轴力;MT为热弯矩。
假设从自然状态起,结构外部环境升温为横向线性变化,则梁内的温度可表示为:
其中:Tm为横截面内的平均升温;Td为上下表面升温之差。
平衡方程。H和V为x和z向的内力分量,其表达式为:

无量纲控制方程。引入下列无量纲量以方便计算:

相应的无量纲边界条件为:

剪切变形与参数β相关,参考文献[4],其表达式为:

常数c在(0,1)范围内时,其梁截面为三层两种材料组成结构。
由于式(6)和式(7)属于非线性常微分方程两点边值问题,很难用解析方法求解。因此这里利用数值方法--打靶法[6-10]来求解。计算时考虑梁的上下表面层均为金属材料、中间为软芯夹层材料,这里既考虑有弹性地基约束作用又考虑两端弹性转角约束作用的情形。假设材料常数的比值分别为:K1=E 2/E 1= 0 .10,K2=α2/α1=0.70,ν2/ν1=0.27/0.30 = 0 .85。
图2给出了不考虑弹性地基刚度参数,均匀梁与夹层梁两端仅考虑转角弹簧刚度的影响,当给定左侧转角弹簧刚度系数时,绘制出临界温度与右侧转角弹簧刚度系数之间的关系曲线。
Ka= 0 ,K b=0,梁的两端为不可移动支承;当K a=∞,K b=0,梁的左侧为固定,右侧为不可移动支承。随着K b逐渐增大,梁的右侧约束逐渐变化趋于固定约束。
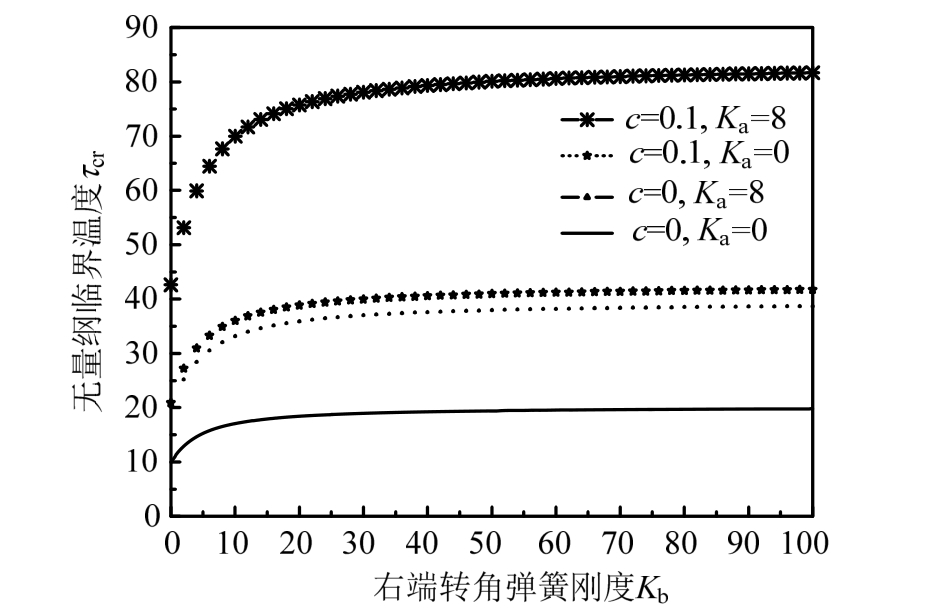
图2 右端转角弹簧刚度与临界温度之间的关系曲线(τd=0,Kc=0)
Fig.2 The relationship curve between the parameters of the right end corner spring stiffness and the critical temperature(τd=0,Kc=0)
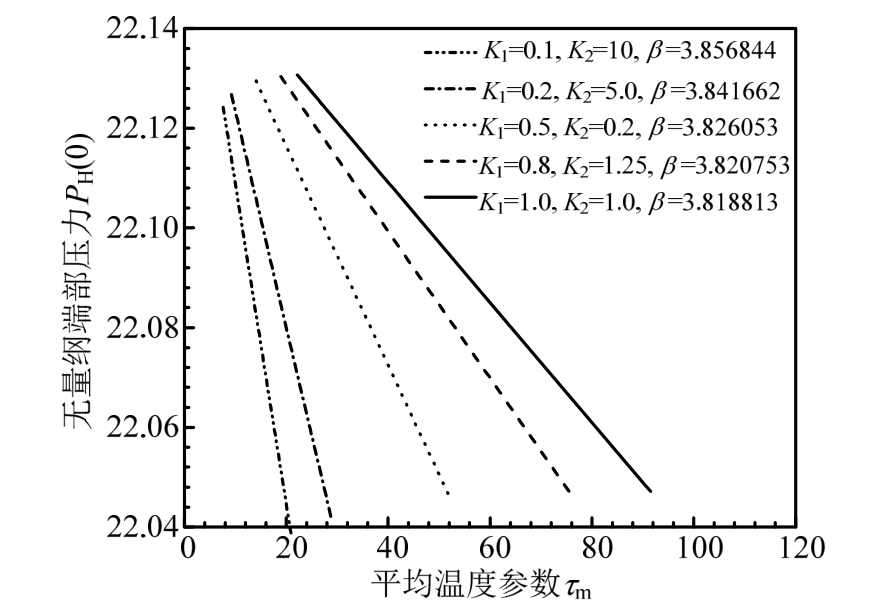
图3 当物性参数变化时,τm-PH(0)关系曲线(τd=0,Ka=1,Kb=50,Kc=0,c=0.1)
Fig.3 The relationship curve betweenτm-P H(0)when the physical parameters change(τd=0,Ka=1,Kb=50,Kc=0,c=0.1)
由图中可知,无论两端转角弹簧刚度如何变化,夹层梁的临界屈曲温度均比均质梁临界屈曲温度要高出大约一倍。这是由于夹层梁截面由三层两种材料组成,造成其整体刚度比均质梁刚度高。图中4条曲线在右侧转角弹簧刚度系数小于20时,无量纲临界屈曲温度变化较大,而右侧转角弹簧刚度系数大于 20时,无量纲临界屈曲温度变化较平缓,趋于稳定。
图3绘出了均匀升温情况下,夹层梁截面物性参数比K 1、K 2变化时温度参数与梁端部水平压力之间的关系曲线。当K 1、K 2值给定时,随着温度参数值的增加,梁的变形增加,此时水平压力却不断减小。在同一个升温参数下,随着β值不断减小,剪切刚度不断增加,水平力也不断减小。

图4 当τd变化时对应的φ( 0 )-τm关系曲线(K a= 1 ,Kb=50,Kc=10,c= 0 .1)
Fig.4 The relationship curve betweenφ(0)-τmwhen theτdchange(Ka=1,Kb=50,Kc=10,c= 0 .1)

图5 弹性地基刚度变化时φ( 0 )-τm关系曲线(Ka=1,Kb= 5 0,c= 0 .1)
Fig5. The relationship curve betweenφ( 0 )-τmwhen the elastic foundation stiffness change(Ka=1,Kb= 5 0,c= 0 .1)
当同时考虑左右转角弹簧和梁底部弹性地基作用时,图4给出了当升温参数的不断变化,夹层梁左侧转角与平均升温参数之间的关系曲线。在τd=0时,夹层梁发生热过屈曲。当τd>0时,夹层梁发生组合变形,即热过屈曲时同时发生热弯曲。当端部转角一定时,随着非均匀升温参数τd的逐渐提高,热弯曲也越明显。
给定转角弹簧刚度系数及地基刚度系数变化时,图5反映了在非均匀升温参数τd=30情况下,左端转动角度与平均升温参数之间的关系。当弹性地基刚度越大,端部转角转动一定角度所需的平均升温参数越高。弹性地基刚度一定的情况下,随着平均升温参数的增加,左侧端部转角所转动的角度也越大。
在温度荷载的作用下,具有两端转角弹簧及弹性地基约束时夹层梁会因轴线方向发生热膨胀而热过屈曲变形和热弯曲。由于夹层梁由多层材料叠合而成,在热荷载的作用下需考虑其剪切变形。利用打靶法数值求解同时考虑轴线伸长和剪切变形的常微分方程两点边值问题,讨论夹层梁在弹性地基和两端转动弹簧约束条件下的热屈曲和热弯曲响应特性。着重论述了地基刚度参数,转动弹簧刚度参数,物性参数等因素变化时升温参数与转动角度及水平压力之间的关系,研究结果表明:
当夹层梁的两端只有转角弹簧单独作用时,转角弹簧刚度系数取不同值时,代表不同形式的支撑情况。夹层梁的临界温度比同种约束情况下的均质梁的无量纲临界温度高很多,充分发挥了夹层梁刚度大的优势。当夹层梁的物性参数给定,随着温度参数值的增加,梁的变形增加,水平压力却不断减小,说明梁在发生弯曲变形时,同时释放了轴向的压力。
考虑弹性地基和两端转角弹簧共同约束夹层梁时,非均匀升温参数为零,夹层梁发生热过屈曲;当非均匀升温参数大于零时,夹层梁发生热过屈曲和热弯曲的组合变形。非均匀升温参数及两端转角弹簧刚度给定时,当弹性地基刚度越大,左侧端部转角转动一定角度所需的平均升温参数越高。弹性地基刚度一定的情况下,随着平均升温参数的增加,左侧端部转角所转动的角度也越大。
参考文献:
[1]Coffin D W, Bloom F. Elastic solution for the hydrothermal buckling of a beam [J]. International Journal of Non-Linear Mechanics, 1999, 34(5): 935―947.
[2]Li S R, Zhou Y H. Geometrically nonlinear analysis of Timoshenko beams under thermo-mechanical loadings[J]. Journal of Thermal Stresses, 2003, 26(9): 867―872.
[3]徐业鹏, 周叮. 机械荷载与热荷载共同作用下变厚度梁的热弹性力学解[J]. 固体力学学报, 2011, 32(增刊1), 426―430.Xu Yepeng, Zhou Ding. Thermoelastic solution of beams with variable thickness subjected to thermo-mechanical loads [J]. Chinese Journal of Solid Mechanics , 2011,32(Suppl 1), 426―430. (in Chinese)
[4]钱海, 周叮, 刘伟庆, 等. 均匀热荷载作用下层合简支梁的弹性力学解[J]. 力学季刊, 2013, 34(2): 331―336.Qian Hai, Zhou Ding, Liu Weiqing, et al. Elasticity solution of simply supported laminated beams subjected to uniform thermo-load [J]. Chinese Quarterly of Mechanics, 2013, 34(2): 331―336. (in Chinese)
[5]李世荣, 夏荣厚. 机械和热载荷共同作用下梁的非线性弯曲和稳定性[J]. 兰州理工大学学报, 2007, 33(3):164―167.Li Shirong, Xia Ronghou. Nonlinear bending and stability of beams subjected to mechanical and thermal loads [J]. Journal of Lanzhou University of Technology,2007, 33(3): 164―167. (in Chinese)
[6]李世荣, 钮鹏. 非均匀升温下Timoshenko夹层梁热过屈曲精确数学模型及其数值解[J]. 兰州理工大学学报,2007, 33(4): 156―160.Li Shirong, Niu Peng. Exact mathematical model and its numerical solution of sandwich Timoshenko beams subjected to non-uniform temperature rise [J]. Journal of Lanzhou University of Technology, 2007, 33(4): 156―160. (in Chinese)
[7]钮鹏, 李世荣. 热和机械载荷共同作用下 Timoshenko夹层梁的非线性分析[J]. 甘肃科学学报, 2007, 19(4):135―140.Niu Peng, Li Shirong. Nonlinear analysis of Timoshenko sandwich beams under thermal and mechanical loads [J].Journal of Gansu Sciences, 2007, 19(4): 135―140. (in Chinese)
[8]钮鹏, 李世荣, 金春福, 等. 热荷载作用下Timoshenko功能梯度夹层梁的静态响应[J]. 固体力学学报, 2011,32(5): 483―489.Niu Peng, Li Shirong, Jin Chunfu, et al. Static response of Timoshenko sandwich beam made of functionally graded materials under thermal loads [J]. Chinese Journal of Solid Mechanics, 2011, 32(5): 483―489. (in Chinese)
[9]李世荣, 刘平. 弹性地基上Euler-Bernoulli梁的热屈曲模态跃迁特性[J]. 应用力学学报, 2011, 28(1): 90―95.Li Shirong, Liu Ping. Characteristics of thermally buckling mode transition of Euler-Bernoulli beams resting on an elastic foundation [J]. Chinese Journal of Applied Mechanics, 2011, 28(1): 90―95. (in Chinese)
[10]钮鹏, 李旭, 李世荣, 等. 弹性地基上复合材料夹层梁的热过屈曲[J], 工程力学, 2017, 34(增刊 1): 26―30.Niu Peng, Li Xu, Li Shirong, et al. The Thermal buckling of composite sandwich beam on elastic foundation [J],Engineering Mechanics, 2017, 34(Suppl 1): 26―30. (in Chinese)
[11]张进国, 史岩, 梁绍波, 等. 端部任意转角约束连续梁压杆临界载荷求解的等效法[J]. 莱阳农学院学报,1998, 15(3): 211―213.Zhang Jinguo, Shi Yan, Liang Shaobo, et al. Equivalent method for solving the critical load of continuous beam[J]. Journal of Laiyang Agricultural College, 1998, 15(3):211―213. (in Chinese)
[12]李世荣, 郁汶山. 弹性地基上加热弹性圆板的热过屈曲及临界屈曲模态跃迁[J]. 工程力学, 2007, 24(5):63―66.Li Shirong, Yu Wenshan. Thermal post-buckling and the critical buckling mode transition of heated elastic circular plates on elsstic foundation [J]. Engineering Mechanics,2007, 24(5): 63―66. (in Chinese)
THE THERMAL BUCKLING BEHAVIOR OF TIMOSHENKO SANDWICH BEAM UNDER ELASTIC CONSTRAINT
NIU Peng1,2, LI Xu1, LI Shi-rong3, JIN Chun-fu4, LIU Yang1
(1. Institute of architectural engineering, Shenyang University, Shenyang, Liaoning 110044, China;2. Key Laboratory of Geoenvironmental Engineering of Liaoning Province, Shenyang University, Shenyang, Liaoning 110044, China;3. School of Civil Science and Engineering, Yangzhou University, Yangzhou, Jiangsu 225127, China;4. Highway Engineering Quality Inspection Center of Liaoning Provincial College of Communications, Shenyang, Liaoning 110122, China)
Abstract:On the basis of considering axial extension and the first-order transverse shearing deformation, the geometric mathematical model of a Timoshenko sandwich beam with elastic supports, subjected to thermal loads,are formulated. By means of shooting method, the static thermal post-buckling numerical solution of the sandwich beam under angle springs and a lateral elastic foundation is obtained. The spring stiffness at the ends of the beam is changed and different critical buckling temperatures are obtained. When the physical parameters of the sandwich beam are changed, the relationship between the mean temperature parameter and the horizontal axial pressure is plotted. When the stiffness of the springs at both ends and the stiffness of the elastic foundation are given at the same time, the non-dimensional temperature produces the combined deformation of the thermal post-buckling and thermal bending of the sandwich beam.
Key words:sandwich beam; thermal buckling; thermal bending; elastic constraint; shooting method
中图分类号:O344.7; TU391
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.01.S028
文章编号:1000-4750(2018)Suppl-0013-04
收稿日期:2017-06-06;修改日期:2018-01-16
基金项目:国家自然科学基金项目(11272278);辽宁省博士启动基金项目(20141092);辽宁省高等学校优秀人才支持计划项目(LJQ2015076)
通讯作者:钮 鹏(1979―),女,辽宁抚顺人,副教授,博士,硕导,主要从事结构稳定性研究(E-mail: np777@126.com)
作者简介:李 旭(1992―),女,辽宁锦州人,硕士生,主要从事结构稳定性研究(E-mail: lx1993z@163.com);
李世荣(1957―),男,甘肃永登人,教授,博士,博导,主要从事结构振动和稳定性研究(E-mail: srli@yzu.edu.cn);
金春福(1977―),男,辽宁沈阳人,副教授,博士,硕导,主要从事地下结构工程及桥梁监控研究(E-mail: kim777@126.com);
柳 杨(1998―),女,辽宁大连人,主要从事结构工程研究(E-mail: 1182254048@qq.com).