姜志琳，赵均海，吕美彤，张 磊
(长安大学建筑工程学院，陕西，西安 710061)
摘 要：基于双剪统一强度理论与双线性强化模型，考虑材料拉压强度的不同及中间主应力效应的影响，推导了均匀内压作用下双层厚壁圆筒的弹、塑性极限内压解，分析了强化模量系数、拉压强度比、统一强度理论参数、内外半径比及分层半径对弹、塑性极限内压统一解的影响。结果表明：随着外径与内径之比的增大，弹、塑性极限内压增加，随着统一强度理论参数的增大，其值增加，随着拉压强度比的增大，其值减小；弹性极限内压与强化模量系数的取值无关，塑性极限内压随着强化模量系数的增大而增加；内外筒的分层半径对弹性极限内压有显著影响，而对塑性极限内压的影响较小。工程应用中，应选择较为合理的壁厚，使其在安全的基础上承受更大的内力；应充分考虑材料中间主应力及拉压强度比的影响，更准确的计算其受力情况，充分发挥材料的潜能。
关键词：结构工程；双层厚壁圆筒；双剪统一强度理论；双线性强化模型；极限内压；拉压强度
组合厚壁圆筒作为一种重要的结构，在工程中有广泛的应用，如传动轴与轴套，组合冷挤压凹模，复合立井井壁等[1－4]。这些结构常采用的材料包括高强钢等线性强化材料[5]，而以往对于组合厚壁圆筒的推导大多是基于理想弹塑性模型，故不能充分利用材料的性能。
现有的针对组合厚壁圆筒的研究主要有：徐秉业等[6]采用Tresca准则，推导了组合厚壁圆筒的弹、塑性极限内压，但Tresca准则仅适用于拉伸屈服极限与压缩屈服极限相同的材料且不能考虑中间主应力效应；袁格侠等[7]基于 Mises准则及理想弹塑性模型，研究了双层缩套厚壁筒加载时的应力解及卸载时的残余应力解，但Mises准则仅适用于某一类材料；赵均海等[8]基于统一强度理论及理想弹塑性模型，分析了组合厚壁圆筒的弹、塑性极限内压，结果表明拉压强度比、统一强度理论参数均对极限内压解有明显影响，但该结果只适用于理想弹塑性材料；张宁等[4]采用统一强度理论，对功能梯度材料的双层厚壁圆筒弹塑性性能进行了分析，且假定材料为理想弹塑性；Zhu Qian等[9]基于三剪屈服准则及弹脆塑性本构模型，分析了双层厚壁圆筒的弹、塑性极限内压，但该结果仅适用于弹脆塑性材料。
本文基于双剪统一强度理论与双线性强化模型，分析了材料拉伸屈服极限与压缩屈服极限的不同、中间主应力效应、内外筒分层半径的大小及壁厚对双层厚壁圆筒的弹、塑性极限内压的影响。
为了推导双层厚壁圆筒的极限荷载，考虑双线性强化条件，将其代入双剪统一强度理论表达式[10]可得屈服极限表达式为[11]：
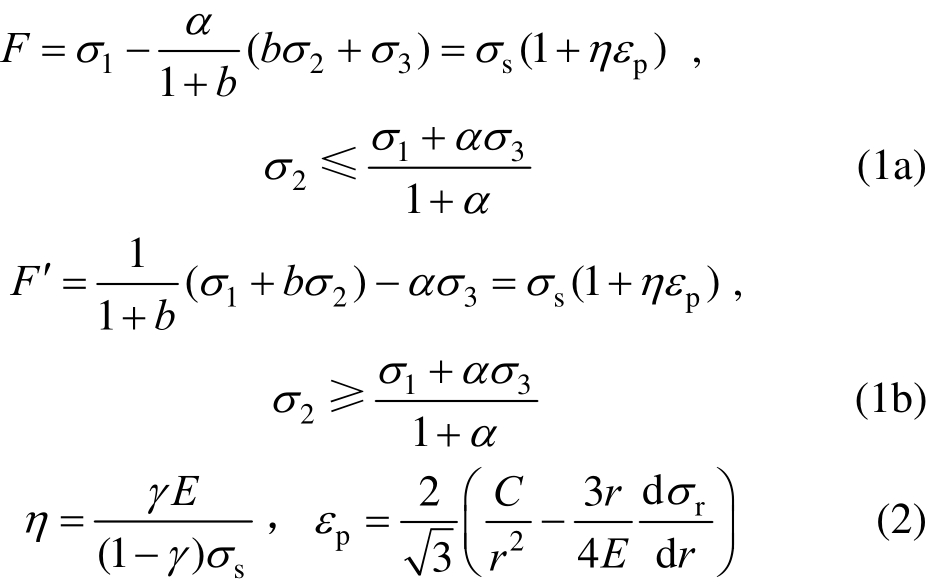
式中：γ为强化模量系数；σs为材料的初始拉伸屈服极限；E为材料的弹性模量；εp为有效塑性应变。
设一受均匀内压p作用的长厚壁套筒，其材料服从双线性强化本构模型，内半径为ra、外半径为rb，分层半径为rc，如图1所示。假定q为内外筒间的套装压力，σr为径向应力，σθ为环向应力，σz为轴向应力。
图1 双层厚壁圆筒力学模型
Fig.1 Mechanical model of double-layered thick-walled cylinder
长厚壁圆筒处于平面应变状态，其平衡方程为[6]：
厚壁圆筒的内外筒均处于弹性状态时，内筒受内压p及套装压力q的作用，外筒仅受套装压力q的作用，则内筒(ra ≤r≤rc)与外筒(rc≤r≤rb)的应力分量分别为[6]：
当内外筒的内壁同时进入屈服状态时，可使弹性极限内压取得最大值[8]。假定外筒的内壁处r=rc刚达到屈服状态时，外筒所受的内压为qe，将r=rc代入式(5)可得此处的应力分量为：
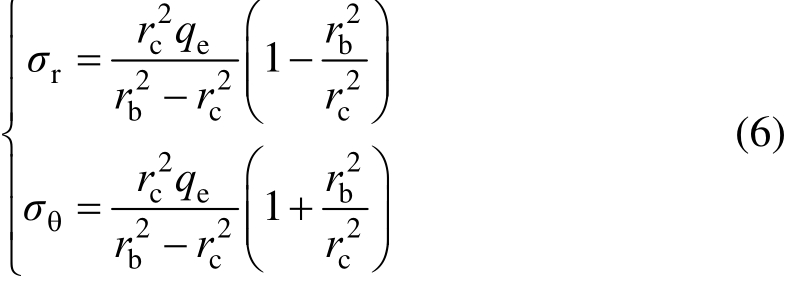
对于双层厚壁圆筒，应力状态满足σ2≤
即屈服条件为式(1a)；由于外筒内壁刚达到屈服状态，有效塑性应变εp为0，故将式(6)代入式(1a)，且令εp=0，可得外筒所受的弹性极限内压qe为：
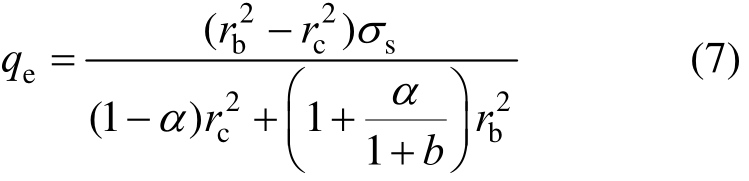
令r=r a，代入式(4)，可得刚进入屈服状态的内筒内壁处的应力分量为：
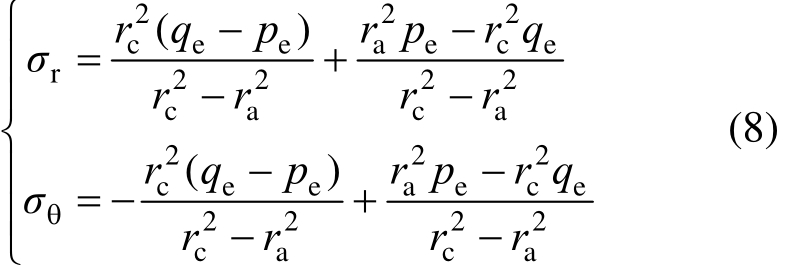
联立式(1a)、式(7)及式(8)，且令εp=0，可求得双层厚壁圆筒的弹性极限内压p e为：
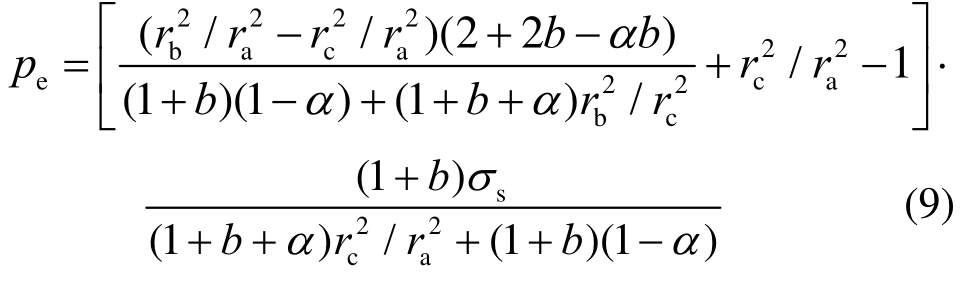
为得到弹性极限内压的最大值，假定内外半径ra
与rb不变，分层半径rc为变量，使将式(9)代入，可得分层半径rc与内外半径ra与rb的关系为：
将式(10)代入式(9)可得双层厚壁圆筒的最大弹性极限内压为：
随着均匀内压p的增大，内外筒均进入弹塑性阶段，设外筒弹塑性交界处的半径为rdo，外筒内壁处内压为qd，内筒弹塑性交界处的半径为rdi，内筒内壁处内压为p s，如图2、图3所示。
假定外筒弹塑性交界处，即r=r do处的内压为pdo，则外筒弹性区(rdo≤r≤rb)的应力分量为：
图2 外筒力学模型
Fig.2 Mechanical model of the outer cylinder
图3 内筒力学模型
Fig.3 Mechanical model of the inner cylinder
令rc=r do代入式(7)，可得r=r do处的内压p do为：
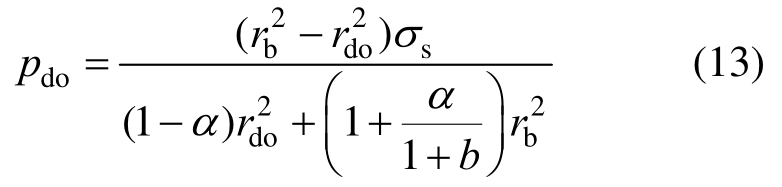
由文献[11]可知，外筒塑性区(rc ≤r≤rdo)的应力分量为：
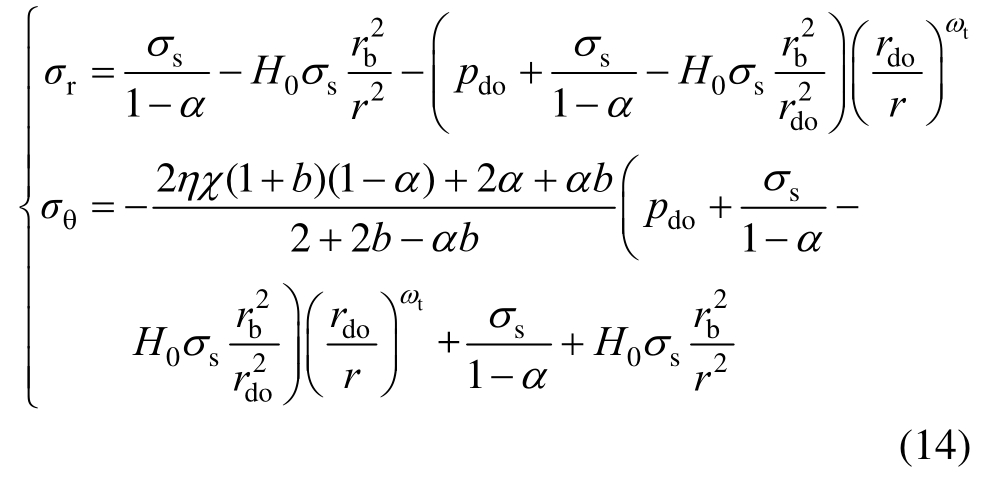
式中：
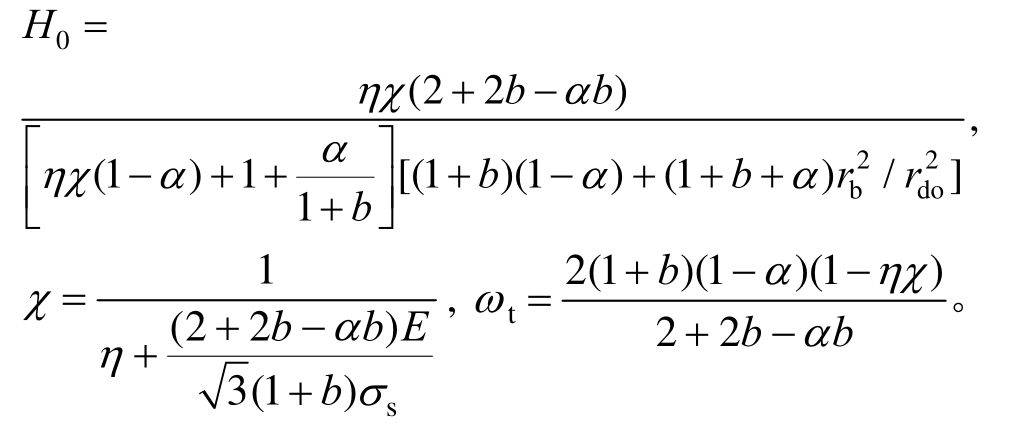
外筒内壁处的径向应力
令r=r c，代入式(14)可得：
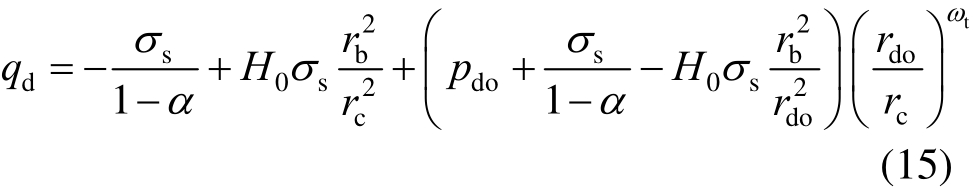
假定内筒弹塑性交界处，即r=r di处的内压为pdi，则内筒弹性区(rdi≤r≤rc)的应力分量为：
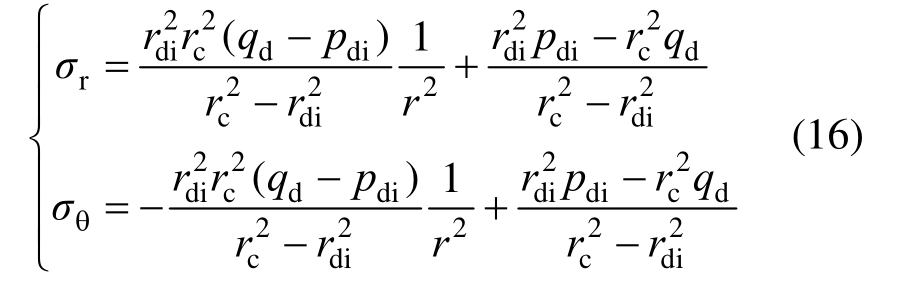
在内筒的弹塑性交界处，即r=r di处刚好进入屈服状态，令r=rdi，εp=0。将式(16)代入屈服条件式(1a)，整理可得：
令r=r di，由平衡方程式(3)及式(16)可得：
在r=rdi处，有效塑性应变εp=0，由式(2)、式(18)可得：
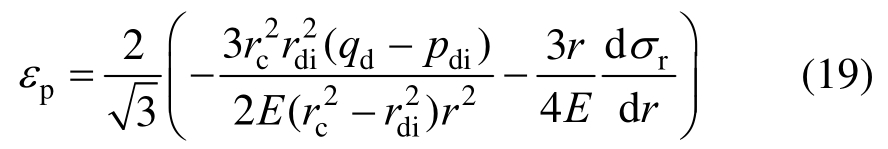
联立平衡方程式(3)及屈服条件式(1a)可得：
由式(19)、式(20)可求得有效塑性应变εp为：
将式(21)代入式(20)可得：
将式(22)积分，结合边界条件
可得内筒塑性区的径向应力σr为：
由式(23)及屈服条件式(1a)可得：
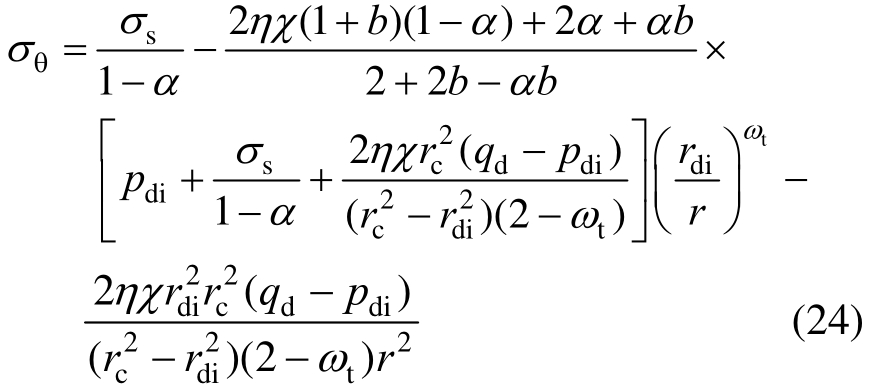
综上，内筒塑性区(ra≤r≤rdi)的应力分量为：
，代入式(25)可得弹塑性状态下，双层厚壁圆筒的内压p s为：
由边界条件
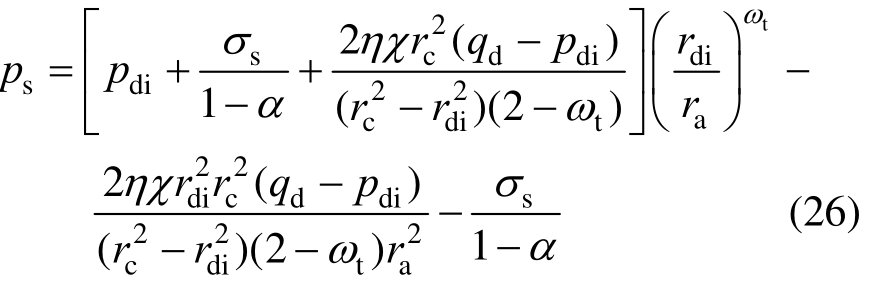
当内压p增大到一定值时，内筒处于完全塑性状态，外筒有两种情况：1) 弹塑性状态；2) 完全塑性状态。
首先分析第一种情况，外筒处于弹塑性状态时，内外筒分层处的内压为qd，则令rd i=r c代入式(26)可得双层厚壁圆筒的塑性极限内压p p 1为：
对于第二种情况，外筒处于完全塑性状态时，内外筒分层处的内压为qp，则令rd o=r b代入式(26)可得双层厚壁圆筒的塑性极限内压p p2为：
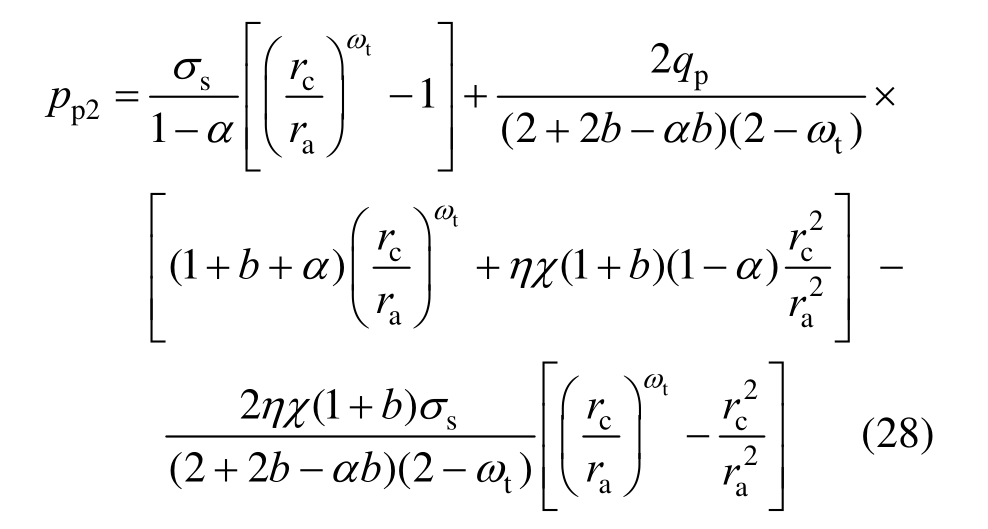
式中：
综上所述，双层厚壁圆筒的塑性极限内压p p为：
本文主要研究了双线性强化材料的双层厚壁圆筒弹塑性极限内压解，为验证本文的正确性，令强化模量系数γ=0，即退化为理想弹塑性材料，将其代入式(28)可得：
本文退化结果式(30)与文献[8]中双层厚壁圆筒的塑性极限内压结果相同。
令拉压强度比α=1，统一强度理论参数b=0，强化模量系数γ=0，代入式(28)可得：
本文退化结果式(31)与文献[6]的结果相同。故本文计算结果可作为双层厚壁圆筒极限内压的统一解。
采用式(9)，分析了内外半径比rb/ra、分层半径与内半径的比rc/ra、统一强度理论参数b与拉压强度比α对弹性极限内压p e/σs的影响，结果如图4所示。
图4pe/σs与rb/ra、rc/ra、α、b的关系
Fig.4 Correlation ofp e/σswithrb/ra、rc/ra、αandb
由图4(a)可知，当壁厚一定，材料拉压强度比不变，分层半径
时，弹性极限内压p e/σs取得最大值；在其他条件保持不变的情况下，pe/σs随b的增大而增加，如令rc/r a= 2 ，b从0增大到1时，p e/σs增大了8.49%，说明考虑中间主应力的影响可提高弹性极限内压，即充分利用材料的潜能。从图 4(b)可看出，随着rb/ra的增大，pe/σs逐渐增大，如令α=0.6，rb/ra从2.5变化到3时，pe/σs增大了14.94%，当壁厚增加到一定值后，p e/σs的增加不再明显，趋于稳定；p e/σs随着α的增大而减小，令rb/r a= 3 ，α从1减小到0.6时，p e/σs增大了18.14%，说明不考虑拉压强度的不同时，p e/σs的计算值偏于保守，不能充分利用材料的性能。
设一双层厚壁圆筒由同一材料制成，该材料的弹性模量E=210 GPa ，初始屈服极限σs=560 MPa。由式(29)可知，塑性极限内压存在两种情况，由于p p1/σs与p p 2/σs的变化规律相同，故在此仅分析塑性极限内压p p2/σs随着内外半径比rb/ra、分层半径与内半径的比rc/ra、统一强度理论参数b、拉压强度比α及强化模量系数γ的变化而变化，其规律如图5所示。
由图5(a)可知，其他条件不变时，塑性极限内压pp2/σs随rb/ra的增大而增加，令γ=0.2，rb/ra从2.5增大到3时，p p 2/σs增大了33.20%；随着γ的增大，p p 2/σs逐渐增加，令rb/r a= 3 ，γ从 0增大到0.2时，p p 2/σs增大了11.04%，强化模量系数越大说明材料强度越高，即塑性极限内压pp2/σs越高。从图 5(b)可看出，p p2/σs随b的增大而增加，令α=0.6，b从0增大到1时，pp2/σs增大了22.67%，根据材料的性能，确定统一强度理论参数的取值，可更准确地计算双层厚壁圆筒的受力；pp2/σs随着α的增大而减小，令b= 0 .5，α从1减小到0.6时，pp2/σs增大了19.37%。由图5(c)可知，在其他条件不变时，rc/ra从1.6增大到2.8时，p p 2/σs增大了5.88%。说明分层半径rc的取值对p p2/σs的影响不大。由文献[8]可知，对于理想弹塑性材料，内外筒的分层半径对塑性极限内压无影响，而对于线性强化材料，分层半径对p p 2/σs有较小影响。
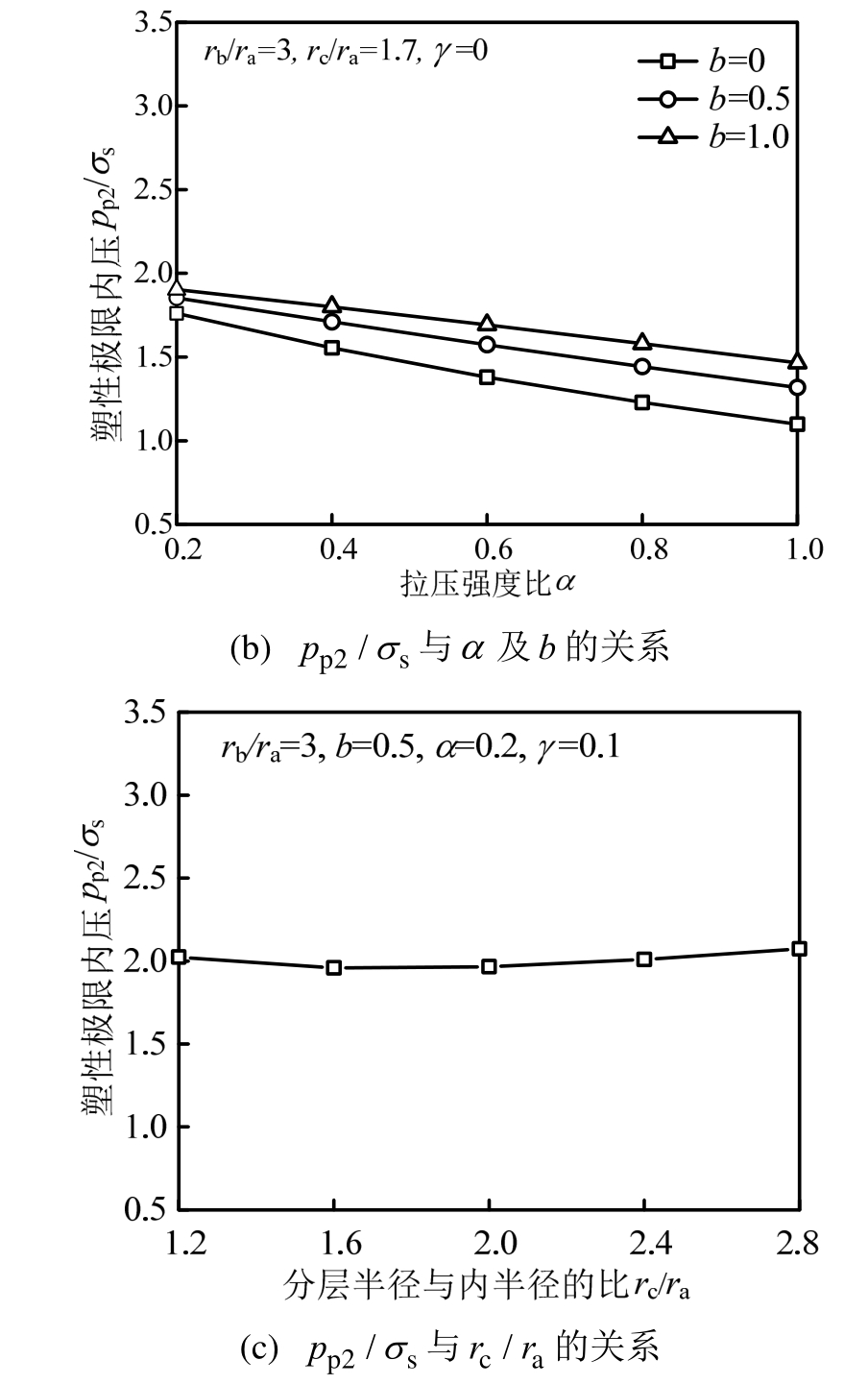
图5p p 2/σs与rb/ra、rc/ra、α、b的关系
Fig.5 Correlation ofpp2/σswithrb/ra、rc/ra、αandb
(1) 本文基于统一强度理论与双线性强化本构模型，考虑中间主应力及材料拉伸屈服极限与压缩屈服极限的不同，得到均匀内压作用下双层厚壁圆筒的弹、塑性极限内压解。通过变化参数的取值，该解可退化为理想弹塑性材料及不同屈服准则的极限内压解。
(2) 随着外径与内径之比的增大，弹、塑性极限内压增加，但随着壁厚的增加，极限内压增加到一定程度后，将不再明显增加，趋于稳定，故应选择合适的壁厚使其受力更加合理，材料性能使用更充分。内外筒的分层半径对弹性极限内压有显著影响，而对塑性极限内压影响较小，故应根据工程要响，而对塑性极限内压影响较小，故应根据工程要求，合理选择分层半径，使其能够更好地承受内压的作用。
(3) 随着拉压强度比的增加，弹、塑性极限内压逐渐减小，说明不考虑材料拉伸屈服极限与压缩屈服极限的不同时，弹、塑性极限内压计算值偏于保守，使得材料的性能不能得到充分的利用；随着强度理论参数的增大，弹、塑性极限内压也逐渐增加，故应根据材料的特性选择不同的屈服准则，更准确的计算其受力情况，充分发挥材料的潜能；弹性极限内压的大小与强化模量系数的取值无关，塑性极限内压随着强化模量系数的增大而增加，说明对于双线性强化材料，应考虑其强化部分，以便材料能够得到更充分地利用，减少工程造价。
参考文献：
[1]崔建波. 液压联轴器 CAD专家系统的研究[D]. 无锡:江南大学, 2008: 1―4.Cui Jianbo. Study on hydraulic coupling CAD expert system [D]. Wuxi: Jiangnan University, 2008: 1―4. (in Chinese)
[2]Yang Q H, Chen X, Meng B, et al. Optimum design of combined cold extrusion die for bevel gear [J].International Journal of Engineering and Technology,2012, 4(4): 348―351.
[3]杨丰钰, 胡成亮, 赵震, 等. 自增强理论在线性强化材料组合凹模设计中的应用[J]. 锻压技术, 2016, 41(6):78―82.Yang Fengyu, Hu Chengliang, Zhao Zhen, et al.Application of autofrettage theory in the design of linear strengthening material combined die [J]. Forging Stamping Technology, 2016, 41(6): 78―82. (in Chinese)
[4]张宁. 功能梯度混凝土立井井壁承载性能研究[D]. 北京: 华北电力大学, 2012: 1―8.Zhang Ning. study on bearing behavior of functionally graded concrete shaft lining [D]. Beijing: North China Electric Power University, 2012: 1―8. (in Chinese)
[5]曹雪叶, 赵均海, 张常光. 基于三剪统一强度准则的厚壁圆筒自增强分析[J]. 中国机械工程, 2017, 28(1):75―81.Cao Xueye, Zhao Junhai, Zhang Changguang. Autofrettage analysis of thick-walled cylinder based on triple-shear unified strength criterion [J]. China Mechanical Engineering, 2017, 28(1): 75―81. (in Chinese)
[6]徐秉业, 刘信声. 应用弹塑性力学[M]. 北京: 清华大学出版社, 1995: 183―229.Xu Bingye, Liu Xinsheng. Application of elastic-plastic mechanics [M]. Beijing: Tsinghua University Press,1995: 183―229. ( in Chinese)
[7]袁格侠, 刘宏昭, 赵迎祥, 等. 双层缩套厚壁筒自增强残余应力分析[J]. 中国机械工程, 2012, 23(11): 1364―1368.Yuan Gexia, Liu Hongzhao, Zhao Yingxiang, et al.Analysis of autofrettaged residual stress of shrink-fit two-layer thick-wall cylinders [J]. China Mechanical Engineering, 2012, 23(11): 1364―1368. ( in Chinese)
[8]赵均海, 朱倩, 张常光, 等. 基于统一强度理论的组合厚壁圆筒弹塑性统一解[J]. 固体力学学报, 2014,35(1): 63―70.Zhao Junhai, Zhu Qian, Zhang Changguang, et al.Elastic-plastic unified solutions for combined thick wall cylinder based on unified strength theory [J]. Chinese Journal of Solid Mechanics, 2014, 35(1): 63―70. (in Chinese)
[9]Zhu Qian, Zhao Junhai, Zhang Changguang, et al.Elastic-brittle-plastic analysis of double-layered combined thick-walled cylinder under internal pressure [J]. Journal of Pressure Vessel Technology, 2016, 138(1): 011201.
[10]Yu Maohong. Unified strength theory and its applications [M]. Berlin: Springer Press, 2004: 129―156.
[11]马景槐. 线性强化材料厚壁圆筒统一自增强分析[J].石油化工设备, 2003, 32(3): 26―30.Ma Jinghuai. Autofrettage analysis of thick wall cylinder of linear strength material based on the unified strength theory [J]. Petro-Chemical Equipment, 2003, 32(3): 26―30. (in Chinese)
UNIFIED SOLUTION OF LIMIT INTERNAL PRESSURE FOR DOUBLE-LAYERED THICK-WALLED CYLINDER BASED ON BILINEAR HARDENING MODEL
JIANG Zhi-lin , ZHAO Jun-hai , LÜ Mei-tong , ZHANG Lei
(School of Civil Engineering, Chang’an University, Xi’an, Shaanxi 710061, China)
Abstract:Considering the different tensile-compressive strength of materials and the effect of intermediate principal stress, the unified solutions of the elastic limit internal pressure and the plastic limit internal pressure of a double-layered thick-walled cylinder under internal pressure are deduced, based on twin shear unified strength theory and a bilinear hardening model. The influence of parameters on the unified solution of elastic and plastic limit internal pressure is analyzed. It is shown that: each unified solution increases with increase of the radius ratio and unified strength theory parameter, but decreases with increase of the tension-compression ratio. The elastic limit internal pressure is irrelevant to the strain-hardening modulus coefficient, but the plastic limit internal pressure increases with the increase of the strain-hardening modulus coefficient. The delamination radius has a significant influence on the elastic limit internal pressure, but has a slight influence on the plastic limit internal pressure. For the engineering applications, reasonable wall thickness should be chosen so as to bear a greater internal force on the basis of safety. The consideration of the intermediate principal stress effect and tension-compression ratio can make materials develop their full potential ability.
Key words:structural engineering; double-layered thick-walled cylinder; twin shear unified strength theory;bilinear hardening model; limit internal pressure; strengths in tension and compression
中图分类号：TU398+.9
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.05.S025
文章编号：1000-4750(2018)Suppl-0006-07
收稿日期：2017-05-27；修改日期：2017-11-10
基金项目：国家自然科学基金项目(51508028，41202191)；中国博士后科学基金项目(2016T90879，2014M562357)；中央高校基本科研业务费专项资金项目(310828173402)
通讯作者：赵均海(1960―)，男，陕西人，教授，博士，博导，主要从事固体力学、强度理论和岩土工程等方面的研究工作(E-mail: zhaojh@chd.edu.cn).
作者简介：姜志琳(1993―)，女，山西人，硕士生，主要从事固体力学和结构工程研究(E-mail: jiangzhilin0322@163.com);
吕美彤(1993―)，女，陕西人，硕士生，主要从事岩土工程研究(E-mail: lvmeitong0722@163.com);
张 磊(1991―)，男，陕西人，硕士生，主要从事强度理论研究(E-mail: zzz_zhang_l@126.com).