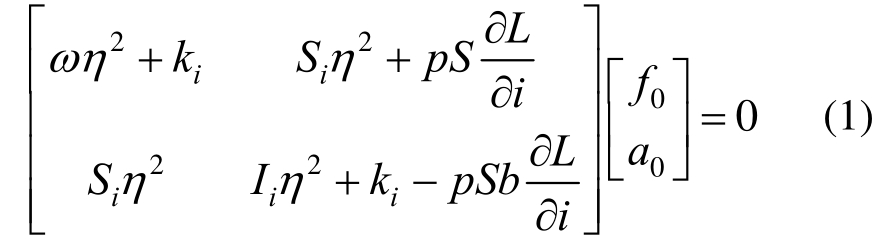
郑 欣1，刘宇斌1，陈 璞2，沈 峰3，张圣君3，傅向荣1
(1. 中国农业大学水利与土木工程学院，北京 100083；2. 北京大学工程学院，北京 100871；3. 中国电投集团中央研究院，北京 102209)
摘 要：首先，该文基于颤振研究的频率重合理论，对两组悬臂壳体结构进行了弯扭耦合模态的颤振规律研究，提出一种简便的颤振频率预估方法，并进行了两组模型校检。第一组模型控制均质梯形薄板掠角作为单一变量，对颤振模态与耦合模态进行了规律性研究，并对颤振频率计算方法进行试算，为带掠角的梯形翼颤振参数初选提供了参考。第二组模型以单向铺层结构的矩形悬臂薄板的铺层角度作为基本变量，给出颤振方向性对颤振参数的影响规律，同时也检验了复合材料薄板的颤振频率预算结果，为复合材料机翼设计提供相应参考依据。
关键词：频率重合理论；振动模态；颤振频率；掠角；铺层角度
颤振是在其本身的运动引起的，与气动力相互作用下所发生的一种自激振动[1]。而在进行机翼的颤振模拟过程中，会因为模型的构建过程、结构和气动网格耦合状态、马赫数和颤振频率的匹配方式等诸多因素带来模拟颤振参数初选的未知性与往复性[2]。本文的研究基础是基于简化的频率重合理论，将模型本身的颤振参数与悬臂壳体的各阶模态振型以及弯扭耦合模态加以对比，得到一种简易有效的颤振频率推测公式，用于颤振频率的初选和预测。
本文主要针对两种角度的变化问题，设计两种形式下的二维悬臂板模型，一组研究均质材料机翼后掠角和前掠角取值大小与颤振参数的相关性；另一组仅采用矩形悬臂版，并设计了单一化的复合材料铺层，研究其方向性对颤振参数与振动模态的影响。两组模型设计除了用于将所得颤振分析结果与颤振频率预测方法比对，验证本文方法的有效性和合理性以外，还需进一步讨论两种角度变化对颤振属性的影响。特别地，考虑到单一化铺层可能引起某些材料性能的极端性[3]，因此补充设计了一组内夹层0º的对照组与该组模型进行对比，验证第二组模型设计的可行性，并进一步探讨铺层的方向性对动力模块和颤振模块的影响规律，为研究二维复合材料薄板问题提供了相应的参考依据。
对颤振问题最早的理解即把机翼的弯扭耦合振动作为主要导因，机翼飞行过程的弯曲变形导致攻角改变，同时引起升力与气动力矩的扰动，并再次引起弯曲，反馈到弯扭振动中。频率重合理论的颤振机理为：来流速度的增大会引起机翼两个振型分支的频率变化，来流速度继续增大，同时两个分支频率相互接近至完全相等，耦合性增强，耦合振动会从气流中吸取能量直至达到颤振临界点[5]。如下给出典型二元机翼的简化运动方程：
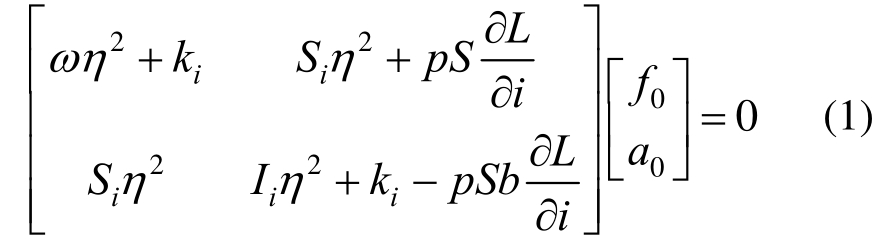
式中：
为翼段升力线斜率；ω为翼段质量；k为为扭转弹簧刚度；S为翼段参考面积；Si为翼段对刚心的静矩，Si=ωσ；Ii为翼段对刚心的惯量，
为气动中心到刚心距离，沿气流正方向为正；p为气流动压，
为空气密度；f0为刚心处挠度，向下为正；a0为刚心处转角，抬头为正。
由式(1)可得到特征方程：
求得特征根：
当μ=0时，表示无气流状态，
求得真空中两个固有频率，即自由振动频率：当有气流时，
依然有两个振动频率，随p变化；当p增大到Y 2-4X Z＜0时，η2会成为复数。η的实部取正值时，振幅会不断扩大，此时运动不稳定，即发生颤振[6]。
针对一端固支的矩形截面悬臂梁，其模型见图1，且有有如下振动方程[7]：
图1 矩形悬臂板
Fig.1 Rectangular cantilever wing
通过积分并代入边界条件，得到扭转固有频率的简单表达式：
式中：ωT为扭转固有频率；n为序号，即1、2、3等；b为径向壳体厚度；G为剪切弹性模量：G=
其中，E为弹性模量；μ为泊松比；ρ为密度；It为扭转阻力：I t=K t⋅b⋅t 3：其中K t为扭转系数，如图2；Ip为极平面惯性矩：I P=I x+I y=
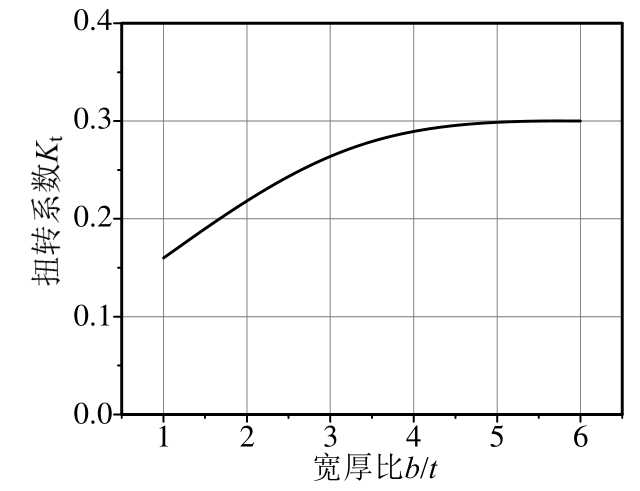
图2 系数Kt
Fig.2 CoefficientKt
在对颤振模态的贡献系数研究的文章[8]中可以得知：各阶模态固有频率在颤振发生时的参与程度相对较为悬殊，在基于弯扭耦合理论的前提下，采用了一阶扭转与一阶弯矩频率作为主要耦合频率的推测公式：
式中：F 0为推算颤振频率；f n1为第一弯曲固有频率；f t1为第一扭转固有频率。
本文验证模型为均质悬臂壳体，几何结构采用二元后掠直角梯形机翼，材料采用铝合金材质矩形悬臂壳体，模型结构和力学性能相关参数见表 1，在保持半展长l=1 m不变的前提下，选择参考弦长b为单一变量。图3所示为梯形壳体模型的结构网格划分和气动网格划分示意图，壳体单边固支，其余三边自由。模型物理参数见表 1。设计了八组模型，分别取后掠角与前掠角各四组，模型编号与几何构造示意见图4。
在掠角相同的情况下，模型几何构造是相同的，因此两组模型在掠角相同情况下的固有频率与振动模态是相等[9]；但由于气流正方向的差异，颤振分析结果并不相同，最终的颤振分析结果、频率预测结果与公式预测误差率汇总于表2。
表1 梯形悬臂机翼物理参数
Table 1 Trapezoidal cantilever wing properties
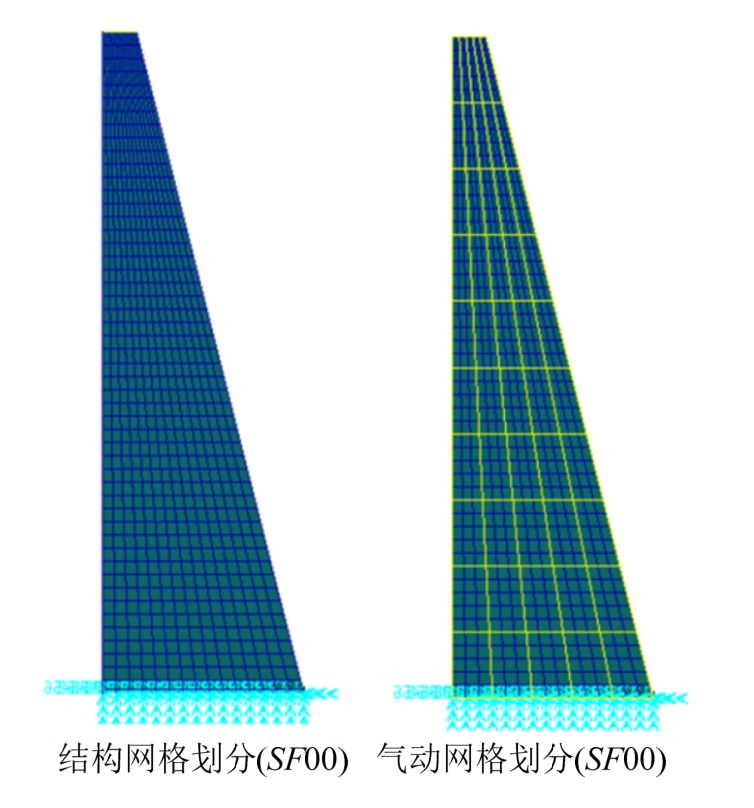
图3 梯形悬臂壳体的结构和气动网格划分
Fig.3 The structural meshing and the aerodynamic meshing
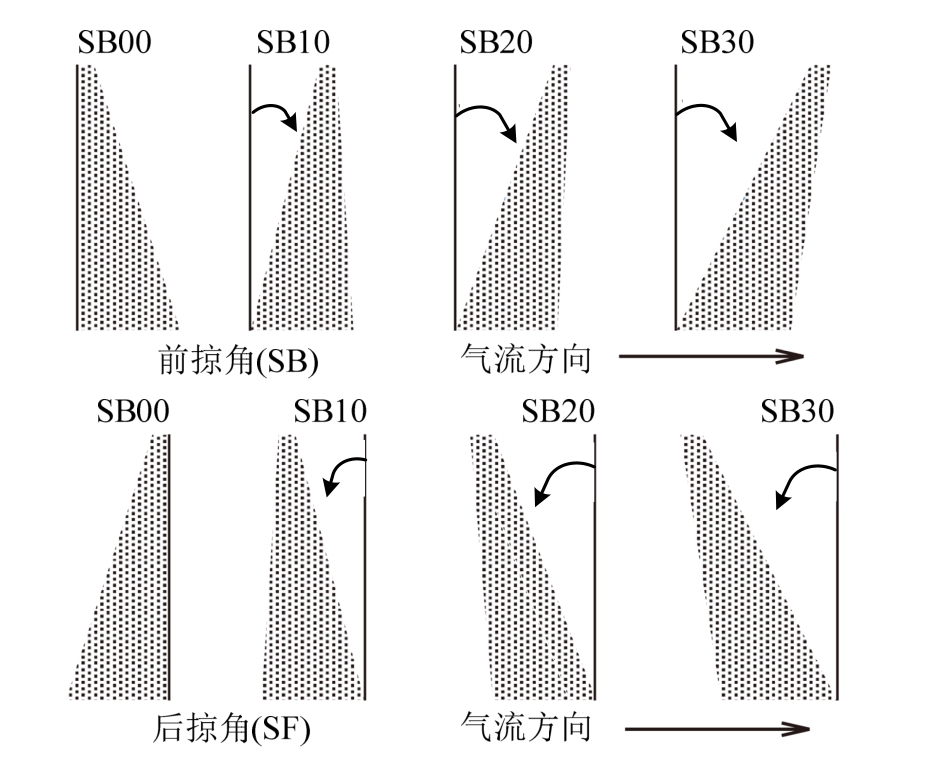
图4 八组模型几何构造与编号示意图
Fig.4 Geometric construction and numbering schematic of eight models
表2 8组模型相应颤振参数
Table 2 Corresponding parameters for 8 models
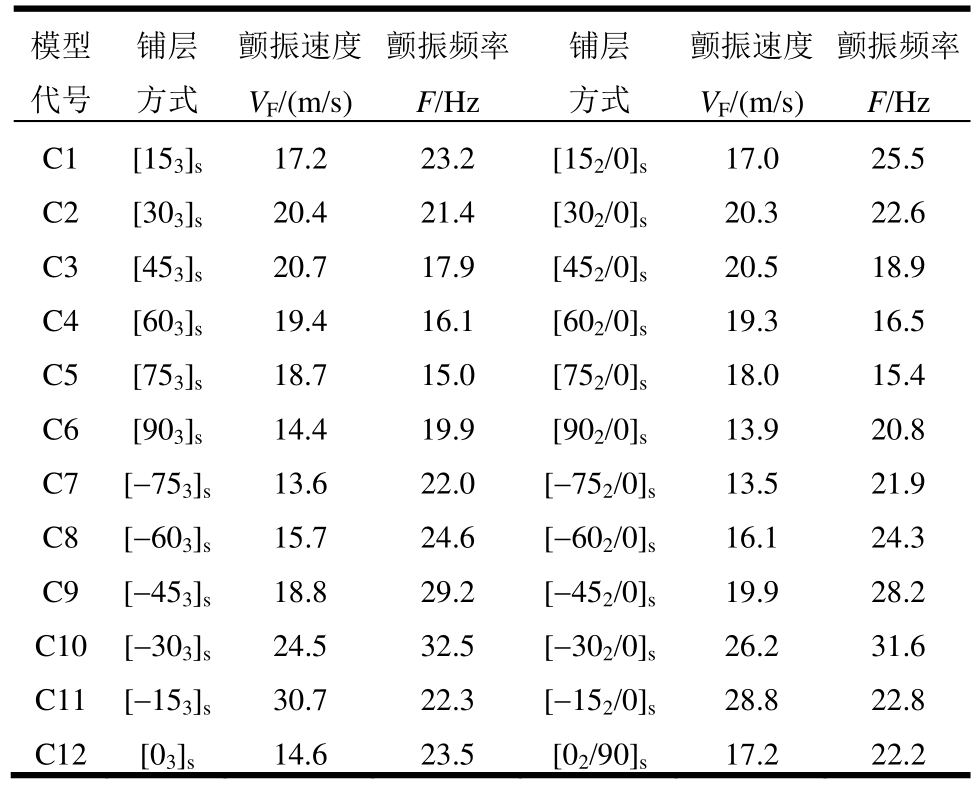
将八个模型统一按照后掠角为变量(即计算SF00、SF10、SF20与 SF30模型的后掠角度)，进一步探讨后掠角与颤振速度的关系，模型后掠角与颤振速度关系见表3，柱状图绘制见图5。
表3 8组模型颤振速度与掠角
Table 3 The flutter speeds and the sweep angles of eight models
在推测式(5)的前提下，分析探讨颤振与弯扭耦合理论的关系，得到如下结论：
1) 对推测公式所得预估频率与颤振频率对比后可得，八组模型的误差率控制在一个较为合理的范围内，证明该公式的合理性，同时对于颤振参数初选具有参考价值。
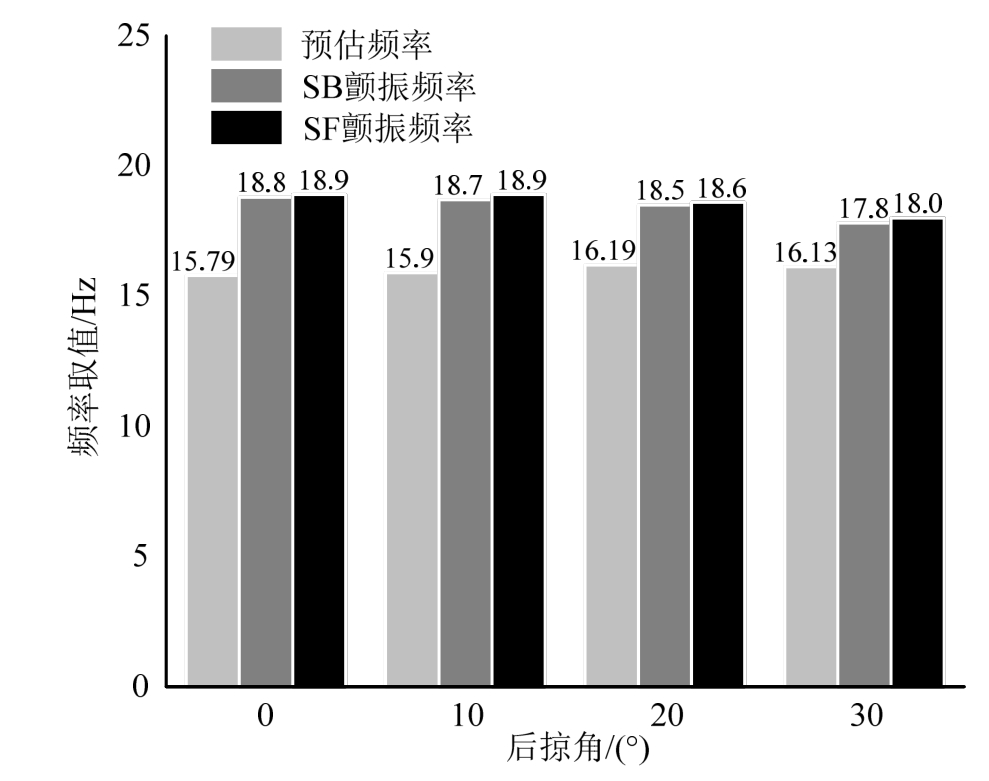
图5 四组模型颤振频率与推算频率柱状图
Fig.5 Flutter frequencies and calculated frequencies column chart of four models
2) 从图6可以看出，对于该均质二维模型，前掠角与后掠角都能有利于提高颤振速度，降低颤振发生的可能性，但相比前掠角，后掠角对于提高颤振速度更为显著。
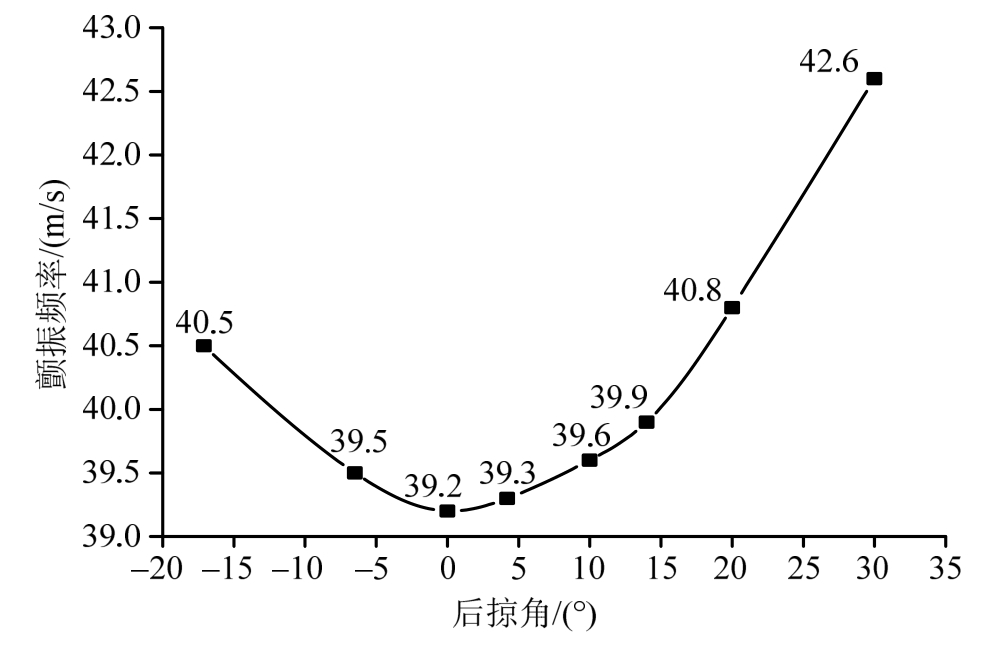
图6 不同掠角下悬臂壳体颤振速度
Fig.6 The flutter speeds of cantilever shells at different grazing angles
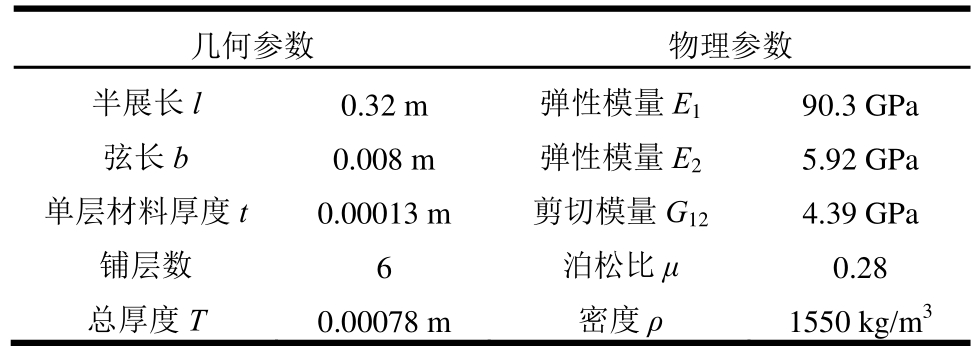
采用复合材料的矩形悬臂结构进行第二组模拟验证，以铺层角度作为单一变量，研究颤振结果与角度变化的规律，同时对式(5)的合理性进行进一步验证。对应的结构参数和物理参数见表4。
表4 模型参数
Table 4 Model parameters
为简化结构的铺层问题分析，采用六层完全相同的铺层方式，便于对铺层角度的规律问题进行探讨，同样地，对 12组模型同样进行动力分析和颤振分析，统计结果与误差率见表 5。在掠角相同的情况下，模型几何构造是相同的[10]，因此两组模型在掠角相同情况下的固有频率与振动模态依旧相等。最终的颤振分析结果与频率预测结果对比见柱状图7，特别地，设计另一组中间两层0°铺层的模型，用于验证单一方向铺层的设计合理性，同时探讨铺层角度与颤振参数的规律变化关系，在铺层角度发生改变时，扭转频率和弯曲频率均会发生相应改变，结构计算和气动计算的相互转换也会发生相应改变，从而导致颤振参数的变化。12组模型的对比结果汇总于表6。
表5 12组模型的颤振频率预估结果
Table 5 Flutter frequency prediction results of 12 models
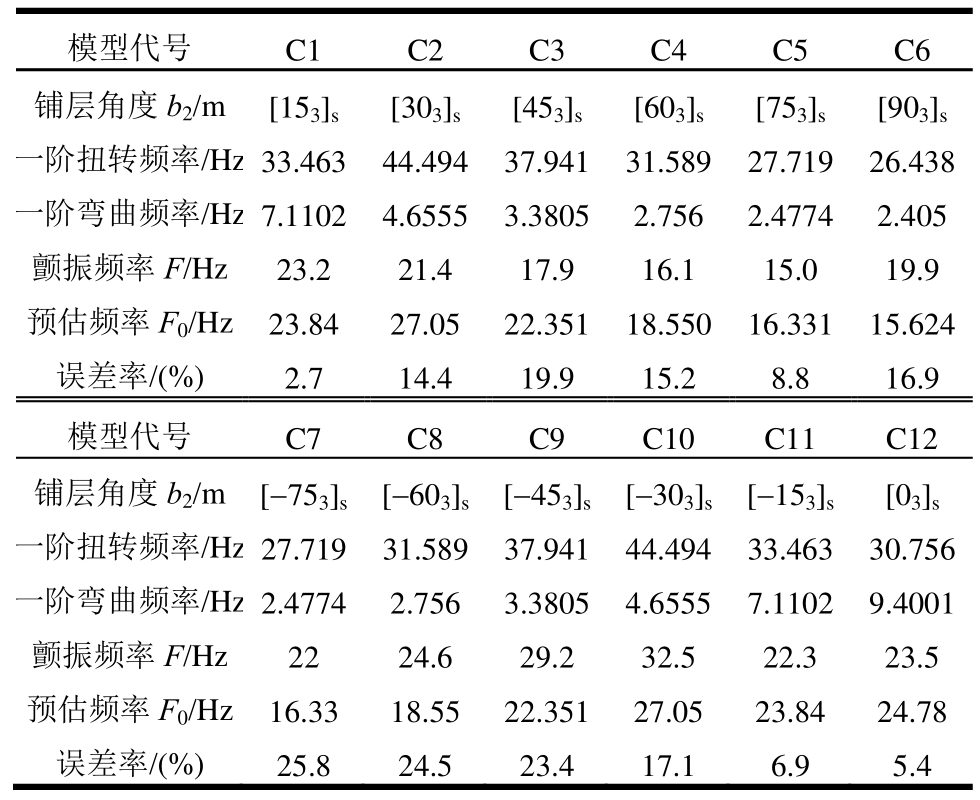
图7 12组模型的颤振频率与预估频率对比图
Fig.7 Flutter frequencies and estimated frequencies of 12 models
表6 相应参数对比
Table 6 Corresponding parameters comparison
1) 由表5和图7的分析可知：在预测公式所得频率与颤振频率的比较中可知，12组模型的错误率在合理范围内控制，进一步证明了公式的合理性。对于正层铺层模型，预测频率一般较高，而对于大多数负向铺层结构，预测频率一般较低。
2) 由表 6可得，具有 0°夹层的复合材料组与六层铺层均相同的模型结果相差不大，且有相同的规律性。
3) 由于表面45°方向铺层是以承受剪切效应为主[11]，因此对于具有正向铺层的模型1～模型5，模型3模型对于颤振速度的影响最为明显；对于具有负向铺层的模型6～模型10，随着模型角度趋于0°，颤振速度和频率逐渐增加；模型11和模型12比较的结果(即主轴方向弯曲刚度和垂直方向的变化)，增加0°铺层对模型减小颤振速度更有利。
由8种掠角不同与12种材料铺角度不同的机翼模型的预估公式验证结果与颤振分析结果的综合分析可得：
(1) 对两组模型进行颤振分析后，其颤振频率取值与预估式(5)计算所得误差率控制在30%以内，且变化趋势与两组模型均保持一致，式(12)的适用性得到了较好的验证。
(2) 对于第一组模型而言，后掠角与颤振速度存在较为明显的规律性，随着后掠角取值由负到正，颤振速度存在一个最小值，由此可知掠角较小时更易于引起颤振，同时SF30模型颤振速度最大，亦最不易发生颤振。掠角有助于提高颤振速度；而单一角度的铺层与内夹层为0°的十二组模型相比，其颤振结果并没有显著变化，因而内夹心层对颤振结果的影响并不显著。
本文预估公式为颤振频率的范围初选提供了一种较为便捷的途径，并进一步证实了弯扭耦合理论在处理某些颤振问题上的合理性和便捷性。本文所研究的模型类别具有局限性，未给出相应的误差修正。可以进一步将掠角问题铺层问题相结合，由此给出一个较为合理的，误差更小的频率预估公式。
参考文献：
[1]王远. 考虑气动热的飞行器颤振数值计算[D]. 江苏:南京空航天大学, 2009.Wang Yuan. Calculation of flutter vibration of aircraft with aerodynamic heating [D]. Jiangsu: Nanjing University of Aeronautics and Astronautics, 2009. (in Chinese)
[2]杨智春, 赵令诚. 飞行器气动弹性力学[M]. 陕西: 西北工业大学航空学院, 2009, 7: 36―95.Yang Zhichun, Zhao Lingcheng. Aeroelastic mechanics of aircraft [M]. Shaanxi: Northwestern Polytechnical University Institute of Aviation, 2009, 07: 36―95. (in Chinese)
[3]杨詠昕. 平板断面扭弯耦合颤振机理研究[J]. 工程力学, 2006, 23(12): 1―8.Yang Yongxin. Study on the mechanism of the coupling flutter of the curved section of the flat section [J].Engineering Mechanics, 2006, 23(12): 1. (in Chinese)
[4]陈桂彬, 杨超, 邹丛青. 气动弹性设计基础[M]. 第 2版. 北京: 北京航空航天大学出版社, 2010: 106―108.Chen Guibin,Yang Chao, Zou Congqing. Foundation of aeroelastic design [M]. 2nd ed. Beijing: Beijing University of Aeronautics and Astronautics press, 2010:106―108. (in Chinese)
[5]王纪瑞, 左曙光, 雷镭. 基于 MSC. Marc的中凸螺旋弹簧刚度特性研究[J]. 佳木斯大学学报(自然科学版),2009, 27(6): 807―810.Wang Jirui, Zuo Shuguang, Lei Lei. Study on the stiffness characteristics of mid-convex helical springs based on MSC. Marc [J]. Journal of Jiamusi University(Natural Science Edition), 2009, 27(6): 807―810. (in Chinese)
[6]Li Z W, Cao P K, Zhou T X. Numerical simulation of wing flutter based on modal coupled method [J].Aeronautical Computing Technique Research Institute,2008, 38(2): 43―46.
[7]Yang Y X, Ge Y J, Xiang H F. Research on the coupled bending-torsional flutter mechanism for thin plate sections [J]. State Key Laboratory for Disaster Reduction in Civil Engineering, 2006, 23(1): 1―8.
[8]Pratik Shrestha, Min-Soo Jeong, In Lee. Flutter characteristics of a morphing flight vehicle with varying inboard and outboard folding angles [J].International Journal of Aeronautical and Space Sciences, 2013, 1/2/3/4(1): 133―139.
[9]Irani S, Sazesh S. A new flutter speed analysis method using stochastic approach [J]. Journal of Fluids and Structures, 2013, 40(1): 105―114.
[10]Shreyas Mandre, Mahadevan L. A generalized theory of viscous and inviscid flutter [C]. Proceedings of the Royal Society A, 2009, 466(1): 141―156.
[11]Robert M J. Mechanics of composite materials [M].Philadelphia, Taylor & Francis, 1999: 23―27.
TWO-DIMENSIONAL WING FLUTTER FREQUENCY CALCULATION METHOD BASED ON BENDING TORSION COUPLING THEORY
ZHENG Xin1, LIU Yu-bin1, CHEN Pu2, SHEN Feng3, ZHANG Sheng-jun3, FU Xiang-rong1
(1. College of Water Conservancy and Civil Engineering, China Agricultural University, Beijing 100083, China;2. College of Engineering, Peking University, Beijing 100871, China; 3. State Power Investment Corporation Central Research Institute, Beijing 102209, China)
Abstract:Based on the frequency superposition theory calculation method, a forecast method of flutter frequency is established and verified by the following two models: 1) The first group of models are a homogeneous trapezoidal plate with a sweep angle as a single variable. A chatter frequency calculation method is proposed, the correlation between flutter modes and bending-torsional coupling modes under different sweep angles is discussed, and the results’ accuracy is identified. 2) The second group models are a rectangular cantilever plate with a single layer orientation as a single variable, the flutter parameters regularity is developed, and the chatter frequency of a composite sheet is examined. This method provides a reference for the composite wing design and internal mechanism of chatter problems.
Key words:frequency coincidence theory; vibration mode; flutter frequency; sweep angle; layer angle
中图分类号：U215.3+4
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.05.S002
文章编号：1000-4750(2018)Suppl-0001-05
收稿日期：2018-01-03；修改日期：2018-03-12
通讯作者：傅向荣(1972―)，男，湖南人，教授，博士，从事计算力学方面研究(E-mail: fuxr@cau.edu.cn).
作者简介：郑 欣(1995―)，女，山西人，助教，硕士，从事结构工程方面研究(E-mail: 476238231@qq.com);
刘宇斌(1992―)，男，浙江人，助教，硕士，从事结构工程方面研究(E-mail: lybcau@qq.com);
陈 璞(1962―)，男，重庆人，教授，博士，从事计算力学与结构动力学方面研究(E-mail: chenpu@pku.edu.cn);
沈 峰(1973―)，男，江苏人，教师级高级工程师，博士，从事反应堆物理、热工方面研究(E-mail: shenfeng@snptc.com.cn);
张圣君(1985―)，男，山东人，工程师，博士，从事反应堆热工方向研究(E-mail: zhangshengjun@snptc.com.cn).