
以钢为主要建造材料的船舶与海洋工程结构,由于长期服役在富含盐分的强电解质腐蚀性环境,易于遭受腐蚀损伤,降低结构的设计寿命。点蚀是一种常见的腐蚀损伤,其成因复杂,难于测量和防护,且会引起应力集中,使得结构构件发生疲劳或强度破坏,导致结构的整体失效。然而,金属材料在海洋环境中的腐蚀行为非常复杂,点蚀的形成及其演化过程尚不十分清楚,迄今为止,点蚀的预测和模拟仍是一个难题[1―2]。
准确地评估损伤后结构的极限强度,有利于确定结构的剩余寿命和合理的结构维护和加强方案。构件试验和数值模拟是实现这一目标的有效途径。构件试验能真实地反映构件损伤后的实际强度,但点蚀损伤与构件位置、服役环境、结构的运营方式等因素密切相关,有限的构件试验仍然很难得出普适性的结论,且构件试验的代价高昂。因而,构建损伤结构的数值分析模型,应用有限元技术研究结构极限强度是更有效的解决方案,但在数值分析模型的构建方面,由于点蚀的分布形态、蚀坑形状和深度存在复杂的随机性,在损伤构件的表面模拟数以千计的随机蚀坑依然十分困难[3]。因此,在DNV、API和IASC等现行规范中[4-6],评估点蚀损伤的影响,普遍采用的方法仍是将点蚀简化为局部化的均匀腐蚀损伤。
点蚀损伤结构的极限强度研究近来年备受关注。Paik等[7]较早开展了点蚀板的试验研究,构建规则分布蚀坑的数值分析模型,开展大量的非线性分析,研究点蚀损伤强度与极限强度退化之间的关系,认为板的极限强度由点蚀损伤位置的最小横截面积决定。Nakai等[8-9]开展了点蚀试件的拉伸试验、点蚀板的轴压试验和腹板受点蚀损伤的散货船强构件弯曲试验,认为点蚀损伤严重削弱构件拉伸强度及其变形能力,且点蚀轴压板的压缩强度略小于或等于均匀腐蚀板。Jiang等[10]研究了单轴、双轴压缩下不同损伤强度无加筋板的极限强度退化规律,给出了回归公式描述腐蚀强度与结构剩余强度的关系。国内学者[11-14]在点蚀损伤结构的评估方面也开展了大量的工作,旨在研究点蚀强度与极限强度退化之间的关系。尽管点蚀损伤程度与结构强度退化的量化关系还难以达成共识,但是大多的研究认为腐蚀体积能较好地描述结构强度的退化程度[10,15-16]。然而,点蚀损伤对结构的影响不仅与腐蚀强度相关,与结构尺寸也有不容忽视的关联。Rahbar-Ranji等[17]通过研究不同厚度板的非线性有限元分析,认为点坑深度与腐蚀强度(degree of pitting intensity,DOP,被腐蚀的构件表面积与原始构件表面积之比)对结构极限强度的影响,与板厚密切相关。Shenoi课题组[18]研究了不规则分布点蚀损伤下,无加筋板和加筋板的极限强度退化规律,认为点蚀影响与板的初始柔度、长细比和长宽比等因素相互关联,且当腐蚀分布在结构支承边界时,对结构极限强度的削弱要比分布在板中央严重得多[19]。Nakai等[8]开展的规则分布点蚀板试验也证实,点坑分布在压缩板的两端边界要比板中央更有危害。然而,Zhang等[20]基于点蚀损伤加筋板试验,却认为点坑分布在板中央要比在支承边界对极限强度的削弱更大,且认为极限强度的退化主要取决于DOP,而腐蚀体积损伤(corroded volume loss)影响甚微。但是,Zhang等[16,21]开展了实船板试验和大量的加筋板数值分析,认为腐蚀体积仍是评估极限强度退化的主要指标,并以腐蚀体积为自变量,给出了加筋板结构的剩余强度回归公式。
虽然点蚀损伤影响结构极限强度的研究已获得大量的进展,但是在随机态点蚀损伤下的结构强度退化规律方面,还鲜有研究。特别是针对点蚀损伤与构件尺度之间的耦合关系,目前已有的研究还有待完善。近年来,人工神经网络(ANN)由于其高度并行、容错性等优点,已广泛应用于结构可靠性、强度预测等研究领域[22-24]。在无加筋板和加筋板的极限强度预测方面,ANN已被验证有比传统回归公式更好的计算精度[25-26]。因此,Ok和 Pu等[27]将沿板边界分布的点蚀简化为局部均匀腐蚀,引入ANN综合板的长细比、腐蚀面积和腐蚀深度的影响,精确地预测了含腐蚀损伤板的极限强度。有鉴于此,本文引入ANN来考虑点蚀损伤的分布形式、点蚀形状和深度的随机性,及其与结构尺寸之间的耦合关系,预测点蚀损伤板的极限强度。通过构建200个随机态点蚀损伤的无加筋板有限元模型,开展非线性分析,研究不同腐蚀状态、长宽比和长细比下,板的极限强度退化规律;建立人工神经网络模型,预测点蚀损伤结构的极限强度,揭示点蚀损伤和结构尺寸与板的极限强度之间的定量关系。
无加筋板计算模型的主要结构参数和材料性能均取自 ISSC 2012会议报告[28]。基准板的板长a=2550 mm,板宽b=850 mm,板厚t=16 mm。Zhang[29]通过研究船体长度在150 m~400 m的油船和散货船的结构板尺寸,发现结构板的长宽比(α)大约为3.5~6.7,而板宽b大约在0.7 m~1.0 m。因此,为提高本文研究的适用性,在确定计算模型的主要结构尺寸时,均参考上述常规结构板的尺寸范围,详细的结构尺寸如表1所示。两个重要的结构参数,长宽比α和长细比β的定义见式(1)和式(2)。材料屈服强度σy=313.6 MPa,弹性模量E=205.8 GPa,泊松比为ν=0.3,其材料本构为理想弹塑性模型。模型的边界条件取为四边简支,荷载为沿板长度方向单轴向压缩,取弹性屈曲一阶失稳模态作为结构的初始缺陷模式,其幅值为0.1β2t。

表1 计算模型的结构尺寸
Table 1 Structural dimension of calculated models

模型组a/mmb/mmαt/mmβNo.1 850 850 1 9.5 11 13 16 22 3.49 3.02 2.55 2.07 1.51 No.2 1700 850 2 9.5 11 13 16 22 3.49 3.02 2.55 2.07 1.51 No.3 2550 850 3 9.5 11 13 16 22 3.49 3.02 2.55 2.07 1.51 No.4 3400 850 4 9.5 11 13 16 22 3.49 3.02 2.55 2.07 1.51
点蚀的形态受结构的服役环境、构件尺度及其位置、结构板的制造工艺等复杂因素的影响[1-2]。实船的腐蚀观测表明,尽管点蚀在构件表面的分布极其离散,但其形状主要是圆柱、圆锥或椭球状,且蚀坑的最大直径在25 mm~80 mm[7-8]。但相比其他形状的蚀坑,圆柱形蚀坑更易于在有限元(FE)模型中实现,且就极限强度计算而言,蚀坑形态的差异不会明显影响最终的计算结果[30-31]。因而圆柱形蚀坑被广泛用于船舶结构[10,21,32]和海洋工程结构[15]的试验及数值模拟研究。
点蚀的分布形式、蚀坑尺寸和深度均有复杂的随机性,蚀坑深度被认为是描述点蚀演化的主要指标[33-36]。事实上,在构建点蚀结构的FE模型时,如何合理地反映蚀坑深度的随机性,是能否正确理解点蚀结构力学行为的关键[3]。本文引入随机模拟方法,利用三个随机参数描述点蚀的分布形式、蚀坑形状和深度,生成随机态的点蚀形貌,及其精细的四边形有限元网格模型[37-38]。在所模拟的随机点蚀中,点坑直径在20 mm~70 mm变化,服从均匀分布,均值为 21.68 mm,标准差为 7.54 mm。IACS[6,39]规范规定:当腐蚀面积比超过15%时要开展腐蚀测量,且强框架构件的剩余壁厚不小于75%的原始厚度;舷侧板的剩余厚度不小于70%的原始厚度。因此,本文模拟的随机点坑深度在0~t(板厚)变化,均值为0.5tmm,标准差为0.24tmm,如图1所示为一个代表性的点蚀板有限元模型。

图1 点蚀损伤板的有限元分析模型
Fig.1 Numerical model of pitted plate
根据每一个随机点坑的蚀坑半径和深度,考虑所有的点坑影响,可依据式(3)和式(4)计算出结构的腐蚀强度和DOP腐蚀体积比DOV。

式中:n为点蚀构件的点坑总数;![]() 为第i个点坑面积,di和hi分别为第i个点坑的直径和深度。
为第i个点坑面积,di和hi分别为第i个点坑的直径和深度。
有限元模型的单元类型选用ANSYS软件的4节点6自由度的shell181单元。在建立蚀坑细节FE模型时,将蚀坑内的壳体单元沿板厚方向往板的一侧偏移,偏移后钢板一侧仍为完善表面,而另一侧出现凹坑,以模拟单侧点蚀损伤。在批量的非线性分析之前,为了验证非线性计算的精度,以 ISSC报告[28]的无加筋板和 Paik等[7]的点蚀板(DOP为33.2%,点坑深度 0.5t)的结果为基准,研究了有限元网格密度的影响。不同的网格控制尺寸下,各板的计算极限强度见表2。
表2 网格密度敏感度分析
Table 2 Sensitivity analysis of mesh density

控制尺寸/mm 7.5 12.5 18.5 28 42.5 ISSC /MPa 214.6 214.7 214.8 215.2 215.8 Paik /MPa 175.4 175. 5 175. 7 176.0 176.4
表2中的网格灵敏度研究结果表明,针对无腐蚀损伤的完善板,由于 ISSC报告和本文所采用的缺陷模式不同,使得报告中计算的极限强度(216.4 MPa)略高于本文的极限强度,但其最大相对误差不及 1%;在点蚀板的极限强度方面,本文计算结果与Paik的计算结果(175.5 MPa)吻合良好。然而,表2结果表明,尽管精细的FE模型具有较好的计算精度,但过于精细的网格并未实质性地提升计算结果,而其需要消耗更多的计算资源。例如,Paik点蚀钢板的控制网格尺寸为7.5/18.5 mm时,FE单元数为22052/4553个,计算时间737/171 s。考虑到描述细观的蚀坑需要精细的网格,最终确定点蚀板结构中,FE网格的控制尺寸取为18.5 mm;在点坑周围,由于存在复杂的应力梯度变化,统一采用16个FE网格来描述蚀坑,详细的蚀坑细节如图1(c)所示。
以板为主要受力构件的船舶与海洋工程结构,其整体结构的性能依赖于板的屈曲和极限强度,而板的长细比被认为是起决定性作用的因素[29]。但在受点蚀损伤的板结构中,研究表明板的长宽比也是影响结构剩余强度的一个因素[18]。因此,本文主要研究长宽比α、长细比β和腐蚀体积比DOV三个因素对极限强度的影响。为便于描述极限强度退化的程度,定义式(5)的折减因子(Rs)来衡量随机态点蚀引起的极强强度退化。

式中,σu和σu0分别为点蚀损伤板和无损伤板的极限强度,由加载边的平均应力表征(加载边全部节点的反力之和与其面积之比)。
在损伤强度DOV为 11.05%的随机点蚀损伤下,计算表1中四组模型的极限强度退化。针对同一壁厚的板,保持板宽不变,板长发生变化,研究四种长宽比(α=1、α=2、α=3 和α=4)的极限强度变化规律。长宽比的变化与相应的折减系数变化如图2所示。图2结果表明,同一厚度的板在相同点蚀损伤下,长宽比越大随机点蚀引起的强度退化越严重。然而,极限强度的退化程度与板厚有复杂的关联。当板厚为t=22 mm时,随长宽比增大,点蚀引起的强度退化要较其他所有板(t=9.5 mm、t=11 mm、t=13 mm 和t=16 mm)严重得多。当板厚减薄(t=13 mm 和t=16 mm),随长宽比增大,强度退化趋于平缓;特别当t=13 mm时,长宽比增大的结构甚至有更高的极限强度,这意味着这一特定壁厚的板对点蚀损伤并不敏感。但是,当壁厚进一步减薄(t=9.5 mm和t=11 mm),随着长宽比增大,点蚀损伤又会引起严重的强度退化。

图2 强度退化与长宽比的关系
Fig.2 Relation between strength reduction and aspect ratio
上节长宽比的影响研究表明,长宽比越大,强度退化越严重。因此,为了更好地体现点蚀损伤的影响,取强度退化最严重的一组模型(No.4),研究长细比变化与强度退化之间的关系。如表1所示,模型组No.4的结构尺寸为a=3400 mm,b=850 mm,α=4,板的长细比分别取为1.51、2.07、2.55、3.02和3.49。针对每一种长细比的结构,均考虑在多种腐蚀状态下的极限强度退化。各种不同腐蚀状态下,随机点蚀引起的材料腐蚀体积比DOV分别为7.6%、8.93%、10.27%、11.05%和17.59%,相应的强度退化如图3所示。

图3 强度退化与长细比的关系
Fig.3 Relation between strength reduction and slenderness ratio
图3的结果表明,当腐蚀体积比DOV大约为10%时(7.6%、8.93%、10.27%和 11.05%),长细比与强度折减因子Rs之间的关系,呈现出极值函数的特征。例如,当长细比为β=2.55时(t=13 mm),在各种腐蚀状态下,该板的强度退化要比其他壁厚的板小得多(剩余强度最大),但随着长细比变化(板厚加大或减薄),板的强度退化均变得越来越严重。此外,当β<2.55时,随机点蚀损伤板的极限强度,随腐蚀程度的加大退化极为明显;但当β>2.55时,在各种腐蚀状态下,板的强度退化趋于一致。这意味着当长细比超过2.55后,大长细比的板对腐蚀强度的变化不敏感,且长细比决定了板的极限强度。
特别值得注意的是,当β<2.55时,随机点蚀会引起明显的极限强度变异,在相同的长细比下(如β=2.55),较轻程度的随机点蚀(DOV为 10.27%)损伤会引起较大的强度退化,甚至可能超过较为严重的点蚀(DOV为11.05%)。
梳理上节中长细比α=4板的计算结果,以腐蚀体积比为自变量,因变量(强度折减因子)的变化规律如图4所示。同时,为进一步阐明极强强度退化与结构尺寸和点蚀损伤之间的耦合关系,将研究范围扩展至不同结构尺寸的点蚀板(a=850 mm,b=850 mm),其长宽比α=1。该板也受不同程度腐蚀损伤(DOV为7.60%、8.93%、10.27%和11.05%),相应的极限强度退化如图5所示。从图4和图5的结果可知,随着腐蚀体积比的增大,虽然损伤板的极限强度退化总体呈下降趋势,但是腐蚀的随机性会引起严重的强度变异,其表现为较低程度的腐蚀损伤,引起了严重的结构强度退化,退化程度甚至高于较高强度的腐蚀。例如,在图5的壁厚t=16 mm(β=2.07)的板中,点蚀强度DOV=8.93%时引起了最严重的强度退化,其导致的强度退化甚至超过了点蚀强度DOV=11.05%。

图4 强度退化与腐蚀体积比的关系(α=4)
Fig.4 Relation between strength reduction and corrosion volume percentage (α=4)

图5 强度退化与腐蚀体积比的关系(α=1)
Fig.5 Relation between strength reduction and corrosion volume percentage (α=1)
上述的结构尺寸及腐蚀特性参数研究表明,随机态点蚀损伤在同一尺寸、同等腐蚀强度的板中,引起了明显离散的计算强度;板的长宽比、长细比和腐蚀强度均是影响强度退化的重要因素,且强度退化与三个因素之间有复杂的非线性关系。因此,本文借助人工神经网络的强非线性拟合能力,选取三个影响因素作为预测模型的输入参数,构建如式(6)所示的BP神经网路模型,预测随机点蚀板的极限强度。
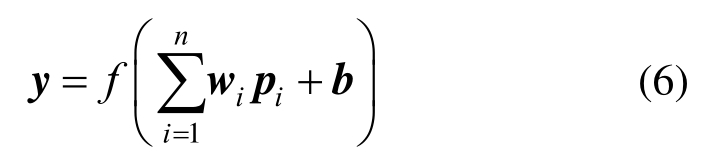
其中:y表示输出向量;pi表示输入向量;wi为权值向量;b为阈值向量;f表示神经元的输入输出关系,即传输函数。
BP网络模型的输入量为长宽比α、长细比β和腐蚀体积比DOV,输出量为极限强度折减因子Rs。由于任何三层的BP网络可以满足任何一般函数的拟合逼近问题,故神经网络的层数取为 3,且只包含一个隐含层。经过多次试算,隐含层中神经元个数取为12,最终确定图6所示的三层BP网络的拓扑结构为3-12-1。其中,网络输入层与隐含层,以及隐含层与输出层之间的传递函数均采用Tansig函数。考虑到网络的规模和学习时间,选用 Trainlm函数对网络进行训练,最大训练步数为1000,目标误差为0.001。

图6 人工神经网络模型
Fig.6 Artificial neural network model
为了提高神经网络预测模型的拟合精度,在上节FE结果的基础上扩大输入样本数据的规模,一共计算200个随机点损伤板的模型。按输入量(三个影响因素)的差异将这些输入数据分为三类,第一类数据为板的长宽比,取值为1、2、3、4,共4组;第二类数据为板的长细比,取值为1.51、2.07、2.55、3.02、3.49,共 5组;第三类数据为腐蚀体积比,取值为7.60%、8.93%、10.27%、11.05%、17.59%,共5组;合计100(4×5×5)组数据。此外,为了增强BP模型的适用性,应考虑到随机点蚀状态下,相同的腐蚀强度存在多种可能的点蚀分布形态。因此,在每种腐蚀强度下(DOV相同),均考虑两种点蚀分布形态。也就是说,针对上述100个随机点蚀损伤板,考虑在相同DOV下点蚀分布的随机性,均建立两种不同点蚀形态的有限元模型,计算强度折减因子。最终,预测模型的输入样本数据一共包含200(100×2)组FE结果。
显而易见,三个影响因素的输入数据的取值范围存在明显差异。为避免这种因数据差异引起的网络预测误差,采用式(7)所示的方法对初始输入样本数据进行归一化,以xi为例,若将xi归一化到[L,U]范围内,则归一化后的![]() 中按下式计算:
中按下式计算:
其中:

式中:ximin、ximax为数据序列中的最小、最大值;U、L为归一化范围的上、下限,分别为1和-1。
从200组样本中,选取覆盖不同长宽比、长细比和腐蚀体积的 10组作为测试样本,剩余的 190组作为训练样本,以检验网络预测效果。将190组训练样本输入神经网络,训练18次达到误差要求,预测结果与FE结果的相关性及其相对误差分别见图7和图8。

图7 神经网络预测值与FE值的相关性
Fig.7 Correlation between predicted results of neural network and FE results
图7中结果显示均方误差(MSE)为0.002 64,相关系数(r)为0.807 85,说明所构建的神经网络模型的结构设计合理,其隐含层的层数和隐含层的神经元个数的确定恰当;图8表明了神经网络的输出值与FE值吻合较好,说明所构建的神经网络模型的训练效果良好。

图8 预测值与FE值的比较
Fig.8 Comparison of predicted results and FE results
运用训练好的BP网络,预测剩余的10组检验数据,检验样本的预测值与FE值的比较结果见表3。从表中结果看来,10组模型中,预测值与 FE值的最大和最小相对误差(预测值与FE值的差值与FE值的比值)分别为 9.88%和-1.38%,均不超过10%,这说明预测值与 FE值吻合良好。因此,所构建的神经网络模型能够很好地预测结构尺寸与点蚀损伤强度之间的耦合关联,用于评估点蚀损伤板的极限强度时有很好的计算精度。
表3 预测值与FE值的比较
Table 3 Comparison of predicted and FE results
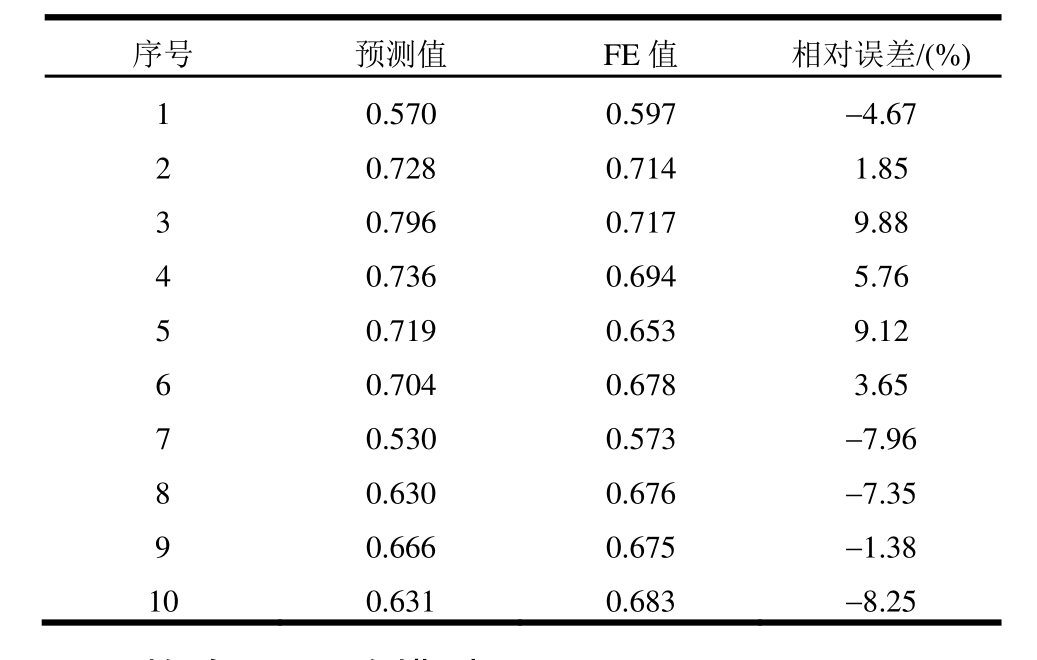
序号 预测值 FE值 相对误差/(%)1 0.570 0.597 -4.67 2 0.728 0.714 1.85 3 0.796 0.717 9.88 4 0.736 0.694 5.76 5 0.719 0.653 9.12 6 0.704 0.678 3.65 7 0.530 0.573 -7.96 8 0.630 0.676 -7.35 9 0.666 0.675 -1.38 10 0.631 0.683 -8.25
为检验所构建的BP网络模型的适用性,将其应用于预测 Paik等[7]的五个点蚀板模型的极限强度。原文中板的长宽比α为1,长细比β为3.31、2.21、1.66,DOP为 4.91%、9.62%、15.90%、23.75%、33.2%,腐蚀深度为0.25t,0.5t,0.75t和t。根据DOP和腐蚀深度,计算出相应板的腐蚀体积比DOV。将上述长宽比、长细比和腐蚀体积比作为输入量,输入训练好的神经网络模型,得到相应结构的极限强度折减因子Rs,如表4所示。
比较表4中BP模型的预测结果与文献[7]中结果可以发现,五个计算模型的最大相对误差均不超过10%,考虑到点蚀的随机性也会引起计算强度的变异性,故可认为两者计算结果吻合良好。因此,本文所构建的BP网络能够用于受点蚀损伤钢板的极限强度预测。
表4 BP预测值与Paik结果Rs对比
Table 4 Comparison of results of BP model and Paik

序号 长宽比 长细比DOV/(%)Rs/PaikRs/BP 相对误差/(%)1 1 2.21 24.90 0.65 0.602 7.44 2 1 3.31 23.75 0.63 0.609 3.33 3 1 2.21 15.9 0.67 0.610 9.36 4 1 2.21 9.62 0.76 0.702 7.65 5 1 3.31 33.2 0.57 0.603 -6.24
本文利用随机模拟方法构建随机态点蚀损伤钢板结构的有限元数值模型,并开展200个点蚀板的极限强度分析;揭示了不同长宽比、长细比和腐蚀强度下,随机态点蚀损伤引起的极限强度退化的规律;并构建合理的BP网络预测点蚀钢板的极限强度。得到如下结论:
(1) 随机态点蚀损伤会引起明显的极限强度变异,这使得较小的腐蚀体积损伤引起严重的强度退化,甚至超过较大的腐蚀体积损伤。
(2) 随机态点蚀损伤下,板的强度退化与其结构参数(长宽比和长细比)密切相关。相同腐蚀损伤下,长宽比越大的板,腐蚀引起的强度退化越严重;相比于薄板和厚板,中等厚度的板不易受点蚀损伤的影响。
(3) 随机态点蚀损伤下,板的强度退化与长细比β之间的关系呈极值函数的特征。随着点蚀强度增大,β<2.55板的强度退化明显;β=2.55板的强度退化最小;而β>2.55板的强度退化不明显。
(4) 人工神经网络能够预测随机点蚀损伤板的极限强度,其预测结果与FE有限元分析结果的最大相对误差不超过10%。
[1]Wang Y, Wharton J A, Shenoi R A. Ultimate strength analysis of aged steel-plated structures exposed to marine corrosion damage: A review [J]. Corrosion Science,2014, 86: 42―60.
[2]Bhandari J, Khan F, Abbassi R, et al. Modelling of pitting corrosion in marine and offshore steel structures-A technical review [J]. Journal of Loss Prevention in The Process Industries, 2015, 37: 39―62.
[3]Yamamoto N, Ikegami K. A study on the degradation of coating and corrosion of ship’s hull based on the probabilistic approach [J]. Journal of Offshore Mechanics and Arctic Engineering, 1998, 120(3): 121―128.
[4]DNV. DNV Class Notes 72.1: Allowable thickness diminution for hull structure [S]. ed, 2014.
[5] API/ASME. API 579-1/ASME FFS-1 Fitness-For-Service [S]. ed, 2016.
[6] IACS. Requirements concerning STRENGTH OF SHIPS[S]. vol. UR S, ed. London: International Association of Classification Societies, 2016.
[7]Paik J K, Lee J M, Ko M J. Ultimate compressive strength of plate elements with pit corrosion wastage [J].Journal of Engineering for the Maritime Environment,2003, 217(M4): 185―200.
[8]Nakai T, Matsushita H, Yamamoto N, et al. Effect of pitting corrosion on local strength of hold frames of bulk carriers (1st report) [J]. Marine Structures, 2004, 17(5):403―432.
[9]Nakai T, Matsushita H, Yamamoto N. Effect of pitting corrosion on local strength of hold frames of bulk carriers (2nd Report)-Lateral-distortional buckling and local face buckling [J]. Marine Structures, 2004, 17(8):612―641.
[10] Jiang X, Guedes Soares C. Ultimate capacity of rectangular plates with partial depth pits under uniaxial loads [J]. Marine Structures, 2012, 26(1): 27―41.
[11] 张岩, 黄一. 点蚀损伤船体板格单轴压缩极限强度[J]. 天津大学学报, 2016, 49(4): 429―436.Zhang Yan, Huang Yi. Ultimate strength of ship structural plate with pitting corrosion damnification under uniaxial compression [J]. Journal of Tianjin University, 2016, 49(4): 429―436. (in Chinese)
[12] 张岩, 黄一. 点蚀损伤船体板屈曲强度评估的工程应用[J]. 上海交通大学学报, 2016, 50(8): 1186―1192.Zhang Yan, Huang Yi. Application of buckling strength assessment of hull structural plate with pitting corrosion damage in engineering [J]. Journal of Shanghai Jiaotong University, 2016, 50(8): 1186―1192. (in Chinese)
[13] 王燕舞, 崔维成. 考虑腐蚀影响的船舶结构可靠性研究现状与展望 [J]. 船舶力学, 2007, 11(2): 307―320.Wang Yanwu, Cui Weicheng. Current status and future directions for reliability analysis of ship structures under corrosion [J]. Journal of Ship Mechanics, 2007, 11(2):307―320. (in Chinese)
[14] 徐强, 万正权. 含坑点腐蚀的深海耐压球壳有限元分析[J]. 船舶力学, 2011, 15(5): 498―505.Xu Qiang, Wan Zhengquan. FE analysis of deep-sea sphere shell with Pitting corrosion under pressure [J].Journal of Ship Mechanics, 2011, 15(5): 498―505. (in Chinese)
[15] 王仁华, 方媛媛, 林振东, 等. 点蚀损伤下海洋平台结构剩余强度的多尺度分析方法 [J]. 工程力学, 2016,33(1): 238―245.Wang Renhua, Fang Yuanyuan, Lin Zhengdong, et al.Multi-scale analysis of residual strength of offshore platforms with pitting corrosion [J]. Engineering Mechanics, 2016, 33(1): 238―245. (in Chinese)
[16] Zhang Y, Huang Y, Wei Y. Ultimate strength experiment of hull structural plate with pitting corrosion damage under unaxial compression [J]. Ocean Engineering, 2017,130: 103―114.
[17] Rahbar Ranji A, Niamir N, Zarookian A. Ultimate strength of stiffened plates with pitting corrosion [J].International Journal of Naval Architecture and Ocean Engineering, 2015, 7(3): 509―525.
[18] Sultana S, Wang Y, Sobey A J, et al. Influence of corrosion on the ultimate compressive strength of steel plates and stiffened panels [J]. Thin-walled Structures,2015, 96: 95―104.
[19] Wang Y, Wharton J A, Shenoi R A. Influence of localized pit distribution and bench-shaped pits on the ultimate compressive strength of steel plating for shipping [J].Corrosion, 2014, 70(9): 915―927.
[20] Zhang J, Shi X H, Guedes Soares C. Experimental analysis of residual ultimate strength of stiffened panels with pitting corrosion under compression [J].Engineering Structures, 2017, 152: 70―86.
[21] Zhang Y, Huang Y, Meng F. Ultimate strength of hull structural stiffened plate with pitting corrosion damage under unaxial compression [J]. Marine Structures, 2017,56: 117―136.
[22] Perera R, Barchín M, Arteaga A, et al. Prediction of the ultimate strength of reinforced concrete beams FRP-strengthened in shear using neural networks [J].Composites Part B: Engineering, 2010, 41 (4): 287―298.
[23] Sharifi Y, Tohidi S. Lateral-torsional buckling capacity assessment of web opening steel girders by artificial neural networks — elastic investigation [J]. Frontiers of Structural and Civil Engineering, 2014, 8(2): 167―177.
[24] Tohidi S, Sharifi Y. A new predictive model for restrained distortional buckling strength of half-through bridge girders using artificial neural network [J]. KSCE Journal of Civil Engineering, 2016, 20(4): 1392―1403.
[25] Pu Y, Mesbahi E. Application of artificial neural networks to evaluation of ultimate strength of steel panels[J]. Engineering Structures, 2006, 28(8): 1190―1196.
[26] Mesbahi E, Pu Y. Application of ANN-based response surface method to prediction of ultimate strength of stiffened panels [J]. Journal of Structural Engineering,2008, 134(10): 1649―1656.
[27] Ok D, Pu Y, Incecik A. Artificial neural networks and their application to assessment of ultimate strength of plates with pitting corrosion [J]. Ocean Engineering,2007, 34(17/18): 2222―2230.
[28] Paik J K, Amlashi H, Boon B, et al. ISSC Committee III.1 Ultimate Strength [C]. Proceedings of the 18th International Ship and Offshore Structures Congress(ISSC 2012). vol. 1, ed ROSTOCK, GERMANY, 2012:285―363.
[29] Zhang S. A review and study on ultimate strength of steel plates and stiffened panels in axial compression [J].Ships and Offshore Structures, 2016, 11(1): 81―91.
[30] Nakai T, Matsushita H, Yamamoto N. Effect of pitting corrosion on the ultimate strength of steel plates subjected to in-plane compression and bending [J].Journal of Marine Science and Technology, 2006, 11(1):52―64.
[31] Huang Y, Zhang Y, Liu G, et al. Ultimate strength assessment of hull structural plate with pitting corrosion damnification under biaxial compression [J]. Ocean Engineering, 2010, 37(17/18): 1503―1512
[32] Paik J K, Lee J M, Ko M J. Ultimate shear strength of plate elements with pit corrosion wastage [J].Thin-walled Structures, 2004, 42(8): 1161―1176.
[33] Melchers R. Pitting corrosion of mild steel in marine immersion environmentpart 1: maximum pit depth [J].Corrosion, 2004, 60(9): 826―834.
[34] Valor A, Caleyo F, Rivas D, et al. Stochastic approach to pitting-corrosion-extreme modelling in low-carbon steel[J]. Corrosion Science, 2010, 52 (3): 910―915.
[35] Paik J K, Kim D K. Advanced method for the development of an empirical model to predict time-dependent corrosion wastage [J]. Corrosion Science, 2012, 63: 51―58
[36] Mai W, Soghrati S, Buchheit R G. A phase field model for simulating the pitting corrosion [J]. Corrosion Science, 2016, 110: 157―166.
[37] 王仁华, 方媛媛. 一种点蚀损伤圆柱壳的四边形有限元网格自动生成方法[P]. ZL201410352564.1, 2014.Wang Renhua, Fang Yuanyuan. An automatic generation method of quadrilateral finite element mesh for pitting corrosion cylindrical shell [P]. ZL201410352564.1,2014. (in Chinese)
[38] 王仁华, 孙洁, 方媛媛. 点蚀随机分布的圆柱壳数值模型的参数化构建方法 [P]. ZL201510238911.2, 2015.Wang Renhua, Sun Jie, Fang Yuanyuan. "Parametric construction of cylindrical model of pitting random distribution [P]. ZL201510238911.2, 2015. (in Chinese)
[39] IACS. Requirements concerning survey and certification[S]. vol. UR Z, ed. London: International Association of Classification Societies, 2016.
ULTIMATE STRENGTH PREDICTION OF STEEL PLATE WITH RANDOM PITTING CORROSION DAMAGE