
图1 试验系统
Fig.1 The experiment system
直升机或运输机等在砂石地面环境低空或者超低空飞行时,砂尘颗粒被气流卷起并被发动机吸入,对发动机叶片产生严重的冲击和磨损,轻则造发动机使用寿命缩短,重则机毁人亡。近年来,航空发动机抗砂尘冲蚀问题逐渐成为研究的热点。为开展相关研究,实验室中通常将粒子加速至一定的速度,并以一定的角度、距离冲蚀发动机叶片,以模拟5级砂尘环境对叶片的冲蚀过程。
冲蚀试验设备是最常见的粒子加速设备之一,它利用喷管中的高速气体带动粒子加速,由于其对粒子的加速效果明显,而获得广泛应用[1]。它可为冲蚀实验提供高速运动的砂粒,用以考量砂尘环境中试件的抗冲蚀和抗磨损性能[2]。作用于试件表面的砂粒速度是涂层抗冲蚀和磨损性能研究中的最关键因素之一。试验中,为了获得喷管喷出的砂粒速度,通常可以采用PIV、双盘测速等方法来测量。其中 PIV方法是依据脉冲激光和高速相机(CCD)结合影像分析技术实现速度测量[3―4],其测量原理及结构较为复杂,造价昂贵,因而难以广泛应用于砂粒速度测量;双盘测速则是依靠测量颗粒在两个间距固定的圆盘间运动的时长来实现测速[5],其结构相对简单,测量方便,工程上应用广泛。然而PIV和双盘测速都只能对颗粒在喷管外部的速度进行测量,无法获得喷管内的粒子速度分布。
数值模拟则可以获得全面的数据,借助这些数据可以分析粒子的具体运动情况,可为优化喷管结构奠定基础。王研艳和翁春生[6]设计了塞式收扩喷管,但只研究了管内的非定常流动而未涉及颗粒流运动;王金东等[7]通过数值模拟获得了不同直径的直喷管对粒子速度的影响;章利特等[8]运用一元流动理论和拉格朗日方法研究了收缩-扩张喷管对颗粒的加速作用同颗粒大小及喷管长度之间的关系;孙建国[9]采用数值模拟方法研究了超声速喷管内颗粒浓度对气流运动的影响;张腾飞等[10]对后混喷嘴内的磨料颗粒运动开展了数值模拟和实验研究。可惜的是,其数值模拟和实验结果之间缺乏定量对比分析。综上,收缩-扩张喷管对稀疏砂尘颗粒加速的具体过程有待通过数值模拟开展深入探究、且数值模拟需定量实验数据的支撑。
本文通过实验和数值模拟的方法,研究了不同入口总压条件下,收缩-扩张式喷管对粒径为0.1 mm的SiO2稀疏砂尘颗粒的加速情况,并通过气粒相对速度、气流密度以及拽力系数,详细分析了气固两相流的运动规律。
本文采用的喷砂试验系统,由储气罐、压力表、供砂系统、混合器以及超音速喷管组成,如图1所示。储气罐为整个试验系统提供高压气体,压力表将高压气体压力调节至实验压力。压力表后气路分成两路,其中一路通过供砂系统,将储砂器内的砂尘颗粒(经过筛选后,直径集中为0.1 mm的二氧化硅颗粒)运送至混合器中;另一路直接将气流输送至混合器与砂粒混合。经混合器流出的气砂混合流通过喷管实现加速。实验中,颗粒的供给量固定为5 g/min。

图1 试验系统
Fig.1 The experiment system
冲蚀试验采用的喷管为二维轴对称收缩-扩张喷管,喷管内壁尺寸如图2所示。其中BD为对称轴,AB为喷管入口段,CG为喉道半径,DE为喷嘴半径,AHGFE为管壁,GF为平直喉道段,长0.003 m。

图2 喷管内壁尺寸 /m
Fig.2 The size of the nozzle inner wall
为准确获得喷管入口总压及沿程压力分布,采用压力传感器对喷管内不同位置的壁面静态压力进行了测量,其测量示意图如图3所示。以喷管的轴线为x轴,坐标原点位于喷管入口截面,则3个传感器0、1、2分别位于x=0.005 m、x=0.065 m、x=0.08 m的位置。其中,0号传感器位置处喷管横截面较大,气流速度可忽略(后续模拟结果也表明该处流速极低),因此将其测得的静压近似为喷管的入口总压。

图3 喷管壁面静压的测量原理图
Fig.3 Schematic of static pressure measuring on the nozzle inner wall
压力测量时,将压力表分别调至 0.3 MPa~0.7 MPa,并关闭供砂气路。测量结果见表1。可见,气流到达喷管入口处的总压仅为压力表读数的80%左右,不能将压力表读数作为喷管的入口总压。后续数值模拟中均采用传感器0所测压力作为喷管的入口总压,分别记为 0.23 MPa、0.32 MPa、0.40 MPa、0.48 MPa、0.56 MPa。
随入口总压的减小,喷管逐渐由不完全膨胀状态向过渡膨胀状态转变(见图 12及其分析)。当入口总压为0.23 MPa时,喷管内出现激波,且位于x=0.08 m之前(见图9和图12),因此x=0.08 m位置的压力快速增大,测量结果同其他情况下的趋势相反。
表1 静压测量结果
Table 1 The results of static pressure measurements

压力表读数/Pax=0.005 m处/Pax=0.065 m处/Pax=0.08 m处/Pa 300000 233956.1 59458.4 81749.1 400000 317035.3 78799.9 61582.8 500000 401067.3 102223.5 83193.4 600000 481126.7 123563.1 105260.6 700000 559839.3 142611.7 118590.5
试验中,高压气体经过收缩-扩张喷管可加速至超音速,超音速气体将稀疏砂尘颗粒加速,同时采用双盘测速测量颗粒速度。双盘测速是利用运动的颗粒通过距离一定的两个圆盘所需的时间来获得颗粒的速度值[11]。而这一时间则可通过转速已知的圆盘转过的角度来求得。
双盘测速示意图如图4所示,图中,l1=0.02 m,l2=0.1 m。喷管固定在基座上。电机高速转动,通过联轴器连接转轴,带动两个直径为0.2 m的圆盘同步旋转,其中靠近电机侧的圆盘在半径0.09 m处开一个直径为4 mm的小孔。如是,当小孔正对喷管出口时,颗粒才能顺利通过第一个圆盘,并在另一个无孔圆盘上产生冲击并留下痕迹。实际上,为了在无孔圆盘上获得清晰的颗粒撞击位置,可在圆盘上粘贴一张刮画纸,颗粒撞击刮画纸时会留下清晰的痕迹。

图4 双盘测速实验原理图
Fig.4 Schematic of Double-Disk speed measuring experiment
测量中电机正转和反转条件下,颗粒在无孔圆盘上分别留下撞痕,测量它们与圆盘圆心形成的夹角θ。如图5所示,根据颗粒在纸上的撞痕画圆以确定其圆心,并将其作为撞痕的中心,分别在两个撞痕的中心与圆盘圆心画一条直线,形成并测量夹角θ。利用颗粒在圆盘间运动的时间与圆盘转动θ角度所需的时间相等,可计算出颗粒速度:
式中:l2为两个圆盘的间距;n1、n2分别为电机正、反转的转数绝对值。

图5 夹角θ的测量方法
Fig.5 Angleθmeasurement method
对于每个入口总压条件,分别开展3次测量,测量结果如图6所示。可见,实验过程中各次测量结果波动不大,表明实验重复性良好;颗粒速度随入口总压的增加而增大,变化范围为 140 m/s~215 m/s。测量结果存在一定的波动,其原因跟双盘测速方法有关。根据测量过程,由于撞痕圆心的确定以及夹角θ的测量均存在一定的误差,因此导致测速结果误差较大。

图6 喷管出口颗粒速度(x=0.11 m)
Fig.6 Particles velocity out of the nozzle (x=0.11 m)
实验中颗粒供给量固定为5 g/min,而气体流量随入口总压的增大而增加,因此当入口总压为0.23 MPa时颗粒浓度最大,此时颗粒的无量纲平均间距最小,为16.33,大于10,属于稀疏颗粒流[12―13];同时颗粒的体积分数为3.93%,小于10%,因此数值模拟采用欧拉-拉格朗日法,其中气体流动用欧拉法模拟,而颗粒运动用拉格朗日法[14―15]。具体模拟中采用FLUENT软件的离散型模型(Discrete Phase Model,简写为 DPM)[16―17]。
气体流动部分,超音速喷管内的气流属于可压缩气流,不可忽略气体密度及温度的变化情况,需采用可压缩 Navier-Stokes方程[18]以及湍流方程联合求解[19],其中湍流模型采用Realizablek-ε模型,这是因为该模型在模拟射流、撞击等复杂流动效果较好,特别是圆孔射流方面[20]。
对于颗粒相,本文将颗粒简化为表面光滑的球形颗粒,固体颗粒在超音速气流作用下受到的力主要为轴向的气动拽力:
式中:F为颗粒所受到的气动拽力;CD为拽力系数;gρ为气流的密度;vg、vp分别为气流速度和颗粒速度;S为颗粒的迎风面积。
对于本文研究的颗粒运动,由于喷管内气流速度可达超音速,而颗粒速度由喉道处的极低速加速到喷管出口处的高速,因此气流和颗粒的相对运动的马赫数Map(后文简称为颗粒马赫数)存在大于 0.4的区域,因此必须考虑马赫数对拽力系数的影响[21]。
数值模拟中采用二维计算以减少计算量,提高计算效率。计算域及计算网格如图7所示。以对称轴为x轴,以径向为y轴,喷管入口截面圆心位置为坐标原点。因此喷管出口位于x=0.09 m位置,实验中带孔圆盘对应的位置为x=0.11 m。
设置BN为对称轴,AB为压力入口,出口QPMN为无反射压力出口,出口压力为大气压,其他边界设置为无滑移绝热壁面;气流相为理想气体,初始温度均为 300 K;所有方程的求解均采用二阶迎风格式。
颗粒相的计算采用DPM模型。待气流相计算收敛后,在喷管入口处加入颗粒群,颗粒直径为0.1 mm,密度为2.65×103kg/m3,并选用high-Machnumber受力模型。设置颗粒与管壁的碰撞为弹性碰撞,BN为对称轴,QPMN边界设置为逃逸。

图7 计算域及网格
Fig.7 Domain and mesh of simulation

图8 不同网格下气流马赫数及颗粒速度曲线
Fig.8 The curves of air mach number and particles velocity with different meshes
为提高计算结果的准确度,排除网格疏密程度对计算结果的影响,首先开展网格无关性验证研究。对网格数进行加密,其中喷管轴向和径向网格数为 450×50、500×60、600×65、700×70,分别记为Coarse 1、Coarse 2、Basic、Fine。选择入口总压为0.56 MPa的工况,采用上述4套网格进行数值模拟。得到图8所示的不同网格数量下喷管轴线位置的气流和颗粒速度变化曲线。由图可见,网格Basic和Fine所得气流马赫数和颗粒速度均几乎重合。认为此时网格数量对计算结果的影响可以忽略不计。因此,后续研究中选取Basic开展数值模拟。
将数值模拟获得的喷管壁面压力及喷管出口颗粒速度同实验数据进行对比,如图9所示。数值模拟获得的喷管壁面静压结果和颗粒速度值均与实验测量值吻合较好。
对于压力结果,随入口总压的减小,1号传感器测量的压力随之减小,而2号传感器测量的压力先减小后增大!这是由于当入口总压为 0.23 MPa时,激波向管内移动至1号传感器之前(见5.1节图12所示),经过激波压力增大。
对于喷管出口颗粒速度,由于出口颗粒速度随轴向位置变化(见 5.2节图 13所示),因此选取x=0.11 m位置处的数值模拟结果同实验进行比较。结果表明,数值模拟结果与实验值吻合较好,最大相对误差为3.46%。

图9 数值模拟结果与实验结果比较
Fig.9 Comparison between numerical simulation and experimental results
气流相的计算是后续跟踪离散相颗粒的基础,为此分析不同入口总压条件下气流相的流场。图10所示的气流在超音速喷管作用下的轴线马赫数分布。对于不同的入口总压,气流马赫数在喷管内部几乎相同,而在喷管出口位置附近发生明显变化。

图10 轴线位置的马赫数分布
Fig.10 Mach number at the nozzle axis
在喷管内部,气流马赫数在喉道初始位置(x=0.037 m)快速增长,在喉道结束位置(x=0.04 m)出现波动,随后在扩张段缓慢增大。
选取入口总压0.56 MPa条件下,喉道位置附近的气流马赫数分布来分析,如图 11所示。可见气流马赫数在喉道初始位置便达到1,然后膨胀加速,并紧接着在壁面处产生激波,激波向轴线发展,并在轴线位置附近形成马赫盘、反射激波。马赫盘的正激波使轴线气流速度降为亚音速。反射激波向下游发展与壁面相交于x=0.04m,再次形成反射激波,但由于该位置为喉道结束位置,亦即扩张段开始位置,因此再次反射的激波强度减弱,后续流动变得较为平滑均匀。

图11 入口总压0.56 MPa下,喷管喉道处马赫数云图
Fig.11 Contours of Mach number in the nozzle throat at the condition of 0.56 MPa total pressure
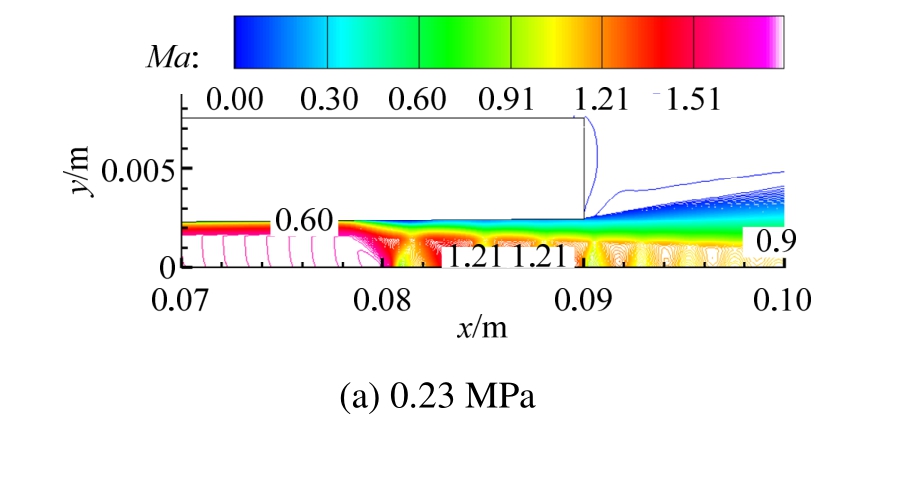
选取入口总压分别为0.236 MPa和0.56 MPa条件下,喷管出口位置附近的马赫数分布来分析,如图12所示。可见,当入口总压较小,如0.23 MPa时,由于总压不足,喷管内出现激波,因此轴线马赫数先减小,此时流动属于过渡膨胀;当入口总压较大,如0.56 MPa时,喷管出口外出现膨胀波,气流马赫数增大,此时流动属于不完全膨胀。

图12 喷管出口附近的气流马赫数分布
Fig.12 Contours of Mach number at nozzle exit
喷管中的颗粒在超音速气流的作用下加速,其速度分布如图 13所示。可见,粒子速度从喉道位置开始快速增大,之后增长速度逐渐放缓,至x=0.15 m位置(距喷管出口0.06 m,即12倍喷管出口直径)附近时粒子速度几乎保持不变。颗粒的加速主要发生在喷管的扩张段。

图13 轴线位置的颗粒速度分布
Fig.13 The curves of particles velocity at the axis
粒子速度随距离的增长速度同受力(加速度)直接相关,粒子所受力主要为气动拽力。由式(2)可知,对于粒径固定的颗粒,气动拽力的大小由颗粒-气流之间的相对速度、气流密度及拽力系数共同决定。图14~图17分别为轴线上颗粒受到的气动拽力、相对速度、气流密度及拽力系数的分布。

图14 轴线位置的气动拽力分布
Fig.14 The curves of particles drag at the axis

图15 轴线位置的相对速度分布
Fig.15 Relative velocity between particle and gas at the axis

图16 轴线位置的气流密度分布
Fig.16 The curves of gas density at the axis
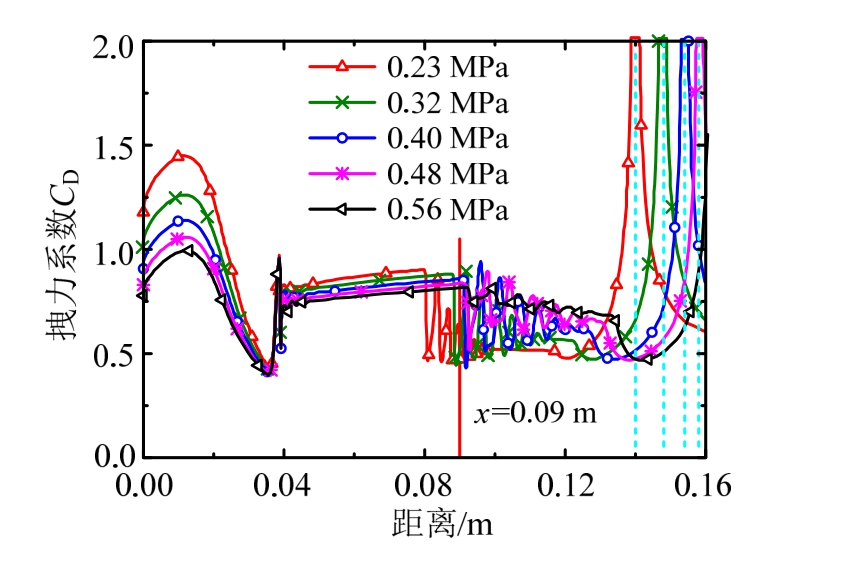
图17 轴线位置的拽力系数分布
Fig.17 The curves of drag coefficient at the axis
可见喉道之前,气流速度及粒子速度均非常小,相对速度也很小,故颗粒受到的气动拽力趋于零,气流对颗粒几乎没有加速作用,此时颗粒速度几乎不变。经过喷管喉道位置时,气流速度的迅速增大,使得气、粒间的相对速度迅速增加,颗粒受力增大,使加速度增大从而颗粒速度也快速上升。
扩张段,气流和粒子均继续加速,而它们的相对速度基本保持不变,气流的继续膨胀(加速)使得气流密度下降,如图 16所示,导致气动拽力或加速度在扩张段逐渐下降。
喷管出口附近,流场出现激波或膨胀波结构,气流速度随之波动,气动拽力(加速度)亦出现波动。但由于颗粒穿越激波的时间短,颗粒速度变化平缓。
喷管外x=0.15 m位置之后,气动拽力或加速度均很小。对于入口总压低于0.32 MPa的情况,其原因是相对速度接近 0;而对于入口总压大于0.40 MPa的情况,虽然仍存在明显相对速度,但相比于喉道位置,气流密度明显减小,因此气动拽力(加速度)仍很小。
对于拽力系数,在喷管外x=0.13 m位置之后出现峰值。这是由于当地相对速度趋近于 0(见图 15的虚线位置),导致雷诺数也趋于 0,由 Clift等[21]的拽力系数公式可知,此时的拽力系数趋于无穷大,即出现图17中所示峰值。
对于不同入口总压的情况,由图 10可知,气流速度在喷管内部基本一致,而气流密度随入口总压的增高而增大,使得气动拽力和加速度也随入口总压的增高而增大,颗粒加速效果也越好。喷管扩张段内颗粒速度的增大使气、粒之间的相对速度以及拽力系数随入口总压的增加反而减小,如图15、图17中所示。
本文通过实验和数值模拟研究了收缩-扩张喷管对砂尘颗粒的具体加速情况。实验中采用压力传感器测量喷管内壁压力,并通过双盘测速的方法获得了喷管出口粒子速度。通过研究得到以下结论:
(1) 双盘测速是利用运动的颗粒通过距离一定的两个圆盘所需的时间来获得颗粒的速度值。实验中,通过正、反转条件下,测量颗粒在无孔圆盘上分别留下的撞痕同圆盘圆心形成的夹角θ,来计算获得粒子速度。
(2) 喷嘴出口处粒子速度随入口总压的增大而增大,总压小于0.4 MPa时的增长速率较大,而总压大于0.4 MPa时的增长速率较小。
(3) 气-固两相流数值模拟结果同实验结果吻合。当入口总压太小时,管内出现激波,不利于颗粒加速。
(4) 数值模拟结果表明,超音速喷管对固体颗粒的加速主要发生在喷管的扩张段,其最主要的原因是该段颗粒-气流之间的相对速度大,且加速距离较长。
(5) 扩张段颗粒加速度随入口总压的增大而增大,其原因是气流密度的变化,而不是相对速度的变化。事实上扩张段里的相对速度随入口总压的增大而减小。
[1]谢安琦, 刘道新, 刘明霞, 等. 表面处理对 17-4PH 不锈钢抗固体粒子冲蚀性能的影响[J]. 航空材料学报,2015, 35(2): 43―53.Xie Anqi, Liu Daoxin, Liu Mingxia, et al. Effects of surface treatment on solid particle erosion resistance of 17-4PH Stainless Steel [J]. Journal of Aeronautical Materials, 2015, 35(2): 43―53. (in Chinese)
[2]何光宇, 李应红, 柴艳, 等. 航空发动机压气机叶片砂尘冲蚀防护涂层关键问题综述[J]. 航空学报, 2015,36(6): 1733―1743.He Guangyu, Li Yinghong, Cai Yan, et al. Review of key issues on coating against sand erosion of aero-engine Compressor Blade [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1733―1743. (in Chinese)
[3]Johnson B, Leishman J G, Sydney A J. Investigation of sediment entrainment using dual-phase, high-speed particle image velocimetry [J]. Journal of the American Helicopter Society, 2010, 55(4): 1―16.
[4]Sydney A J, Leishman J G. Time-resolved measurements of rotor-induced particle flows produced by a hovering rotor [J]. Journal of the American Helicopter Society,2014, 59(2): 1―16.
[5]Stevenson A N J, Hutchings I M. Scaling laws for particle velocity in the gas-blast erosion Test [J]. Wear,1995, 181(95): 56―62.
[6]王研艳, 翁春生. 非定常流动中塞式收敛扩张喷管的研究[J]. 工程力学, 2014, 31(12): 223―227.Wang Yanyan, Weng Chunsheng. Analysis of plug-inconvergent-divergent nozzle in unsteady flow [J].Engineering Mechanics, 2014, 31(12): 223―227. (in Chinese)
[7] 王金东, 吕志利, 刘树林, 等. 基于FLUENT的气动喷砂两相流场分析[J]. 科学技术与工程, 2009, 9(17):5113―5115.Wang Jindong, Lü Zhili, Liu Shulin, et al. FLUENT based on the pneumatic blasting two-phase flow field analysis [J]. Science Technology and Engineering, 2009,9(17): 5113―5115. (in Chinese)
[8]章利特, 徐廷相. 缩放喷管内的气固两相流动和缩放喷管长度的研究[J]. 西安交通大学学报, 2004, 38(7):702―704.Zhang Lite, Xu Tingxiang. Study on gas-solid two-phase flow in laval nozzle and laval nozzle length [J]. Journal of Xi’an Jiaotong University, 2004, 38(7): 702―704. (in Chinese)
[9]孙建国. 基于缩放喷管的超声速气固两相流动特性数值研究[D]. 杭州: 浙江理工大学, 2012: 13―14.Sun Jianguo. A study on gas-solid two-phase flow in convergent-divergent nozzle. [D]. Hangzhou: Zhejiang Sci-Tech University, 2012: 13―14. (in Chinese)
[10] 张腾飞, 邓松圣, 陈晓晨, 等. 后混磨料射流颗粒运动仿真和实验分析[J]. 重庆理工大学学报(自然科学),2015, 29(2): 57―60.Zhang Tengfei, Deng Songsheng, Chen Xiaochen, et al.Simulation and analysis of post-mixed abrasive water jet particle trajectory [J]. Journal of Chongqing University of Technology (Natural Science), 2015, 29(2): 57―60.(in Chinese)
[11] 李平, 肖良华, 何卫锋, 等. 收缩-扩张喷管中稀疏颗粒加速运动及喉道优化[J]. 空军工程大学学报(自然科学版), 2017, 18(5): 7―12.Li Ping, Xiao Lianghua, He Weifeng, et al. Particles motion and throat optimization for accelerating sparse particles in supersonic convergent-divergent nozzle [J].Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(5): 7―12. (in Chinese)
[12] Crowe C, Sommerfeld M, Schwarzkopf J, et al. Multiphase flows with droplets and particles [M]. Boca Raton:CRC Press, 1998: 17―35.
[13] 边飞龙, 朱有利, 杜晓坤, 等. 基于 CFD 方法的气动喷丸两相流场特性研究[J]. 计算机仿真, 2015, 32(1):264―269.Bian Feilong, Zhu Youli, Du Xiaokun, et al. Research on performance of two-phase flow field of the pneumatic shot peening based on CFD method [J]. Computer Simulation, 2015, 32(1): 264―269. (in Chinese)
[14] 周晅毅, 谭敏海, 晏克勤, 等. 风致积雪重分布的拉格朗日方法与现场实测研究[J]. 工程力学, 2017, 34(2):21―27.Zhou Xuanyi, Tan Minhai, Yan Keqin, et al. Lagrangian method modeling and field measurement on snowrift [J].Engineering Mechanics, 2017, 34(2): 21―27. (in Chinese)
[15] 周晅毅, 刘长卿, 顾明, 等. 拉格朗日方法在风雪运动模拟中的应用[J]. 工程力学, 2015, 32(1): 36―42.Zhou Xuanyi, Liu Changqing, Gu Ming, et al.Application of lagrangian method to snowrift model [J].Engineering Mechanics, 2015, 32(1): 36―42. (in Chinese)
[16] Deen N G, Annaland M V S, Hoef M A V D, et al.Review of discrete particle modeling of fluidized beds[J]. Chemical Engineering Science, 2007, 62(1/2): 28―44.
[17] Zhang Z, Cheng X W, Zheng Y G, et al. Numerical simulation of erosion-corrosion in the liquid solid twophase flow [J]. Chinese Journal of Chemical Engineering, 2000, 8(4): 347―355.
[18] 丁英涛, 姚朝辉, 何枫. 微喷管内气体流动特性研究[J]. 工程力学, 2004, 21(3): 190―195.Ding Yingtao, Yao Zhaohui, He Feng. Gas flow characte-ristics in micro-nozzle [J]. Engineering Mechanics, 2004, 21(3): 190―195. (in Chinese)
[19] Salvador F J, Martinez-lopez J, Caballer M, et al. Study of the influence of the needle lift on the internal flow and cavitation phenomenon in diesel injector nozzles by CFD using RANS methods [J]. Energy Conversion & Management, 2013, 66(3): 246―256.
[20] 汪琦. 气固流化床两相流动的CFD模型研究和实验验证[D]. 武汉: 华中科技大学, 2012: 8―15.Wang Qi. Comparative analysis of CFD models of gas-solid fluidized bed and experimental verification [D].Wuhan: Huazhong University of Science & Technology,2012: 8―15. (in Chinese)
[21] Clift R, Grace J R, Weber M E. Bubbles, drops, and particles [M]. Mineola: Dover Publications, 1978: 330―347.
RESEARCH ON MOVEMENT LAW OF GAS-SOLID TWO-PHASE FLOW IN CONVERGENT-DIVERGENT NOZZLE