功能梯度扁球壳在热-机械荷载作用下的屈曲分析

(1．青海大学土木工程学院，西宁 810016；2．东莞理工学院生态环境与建筑工程学院，东莞 523808)

摘要：基于经典壳理论，应用虚功原理和变分法推导了均匀变温场中的功能梯度圆底扁球壳在均布外侧压力作用下的位移型几何非线性控制方程。考虑固定夹紧边界条件，运用打靶法计算获得了球壳轴对称变形的数值结果。考察了材料体积分数指数、组分材料弹性模量和均匀变温场对壳体平衡路径，上、下临界荷载以及平衡构型的影响。数值结果表明，随材料体积分数指数的增加和组分材料弹性模量的减小，壳体上、下临界荷载均会显著减小。均匀升温，会使壳体上临界荷载显著增加，下临界荷载轻微减小。为方便工程设计人员进行几何、材料、荷载和变温参数的选取，给出了一个实用数表和一些实用的数值曲线。

关键词：功能梯度材料；圆底扁球壳；均布压力；均匀变温场；屈曲；打靶法

扁球壳作为一类薄壁弹性结构，是很多工程结构(诸如航空、航天、核反应、化工工程、精密仪器)的一个重要的组成部分。屈曲力学行为是此类壳结构设计工作需要考虑的最核心的问题。自从 von Kármán和 Tsien[1]首先指出薄壳的屈曲现象是一个非线性现象，并首先对球壳的屈曲进行了非线性分析之后，人们应用非线性分析方法对扁球壳的屈曲做了大量的研究工作[2―5]。迄今，有关扁球壳的屈曲力学行为仍然备受研究人员关注。Li等[6]基于一阶壳理论并运用修正迭代法研究了外侧均布压力作用下的各向同性扁球壳的屈曲行为。李斌等[7]用修正迭代法研究了弹性支撑扁球壳在均布外压作用下的非线性稳定性。张平等[8]用有限元法研究了用于自适应进气道的各向同性扁薄球壳的双稳态力学行为。李忱等[9]用Ritz法研究了各向同性薄球壳在均布外压与温度耦合作用的热屈曲问题。

功能梯度扁球壳构件在材料上兼具高热阻和高强度的双重优越性能的同时，在几何构造上还具有特殊的用途。因此，其在诸如太空舱的端盖、核反应堆的密封顶盖等现代高技术设备中得到了越来越多的应用，研究功能梯度扁球壳在热环境中的几何非线性力学行为，具有很现实的工程应用背景。Shahsiah等[10]基于 Donnell壳理论和 Sanders非线性应变-位移关系结合变分法研究了功能梯度扁球壳的热屈曲。Bich等[11]基于经典壳理论，考虑温度效应和几何缺陷，研究了功能梯度扁球壳在均匀分布的外侧压力作用下的非线性轴对称响应。Boroujerdy等[12―13]考察了带压电层的功能梯度扁球壳在热与机械荷载联合作用下的非线性轴对称响应和热屈曲问题。Mao等[14]考察了受低速冲击作用的功能梯度扁球壳的动态响应和损伤演化。

有关扁球壳轴对称变形的研究文献多以壳中曲面横向位移W(即挠度)和径向薄膜内力Nr(或应力函数Φ)为基本未知函数建立控制方程。此类研究方法经常需要预设一个满足边界条件的关于挠度W的形状函数以帮助得到方程的近似解答。由于形状函数只是对真实形状的近似，同时球壳屈曲前、后的构型有显著的差异，但预设的形状函数并不考虑这种差异，因此，难免会引入人为误差，当变形较大时，误差应该不能被忽视(现有文献中，不同研究方法得到的临界屈曲直至后屈曲阶段的解存在较大差异)。

考虑到在轴对称的情况下，如果用壳中曲面横向位移W和径向位移U为未知函数建模，问题的控制方程和边界条件将是用这两个位移函数表示的非线性常微分方程和位移型边界条件，属典型的两点边值问题。已经知道，打靶法可容易且有效的求解两点边值问题。由于该方法不需要对未知函数作任何预设，从而可避免该环节引入人为误差。基于此，2015年，赵伟东等[15]运用打靶法研究了均匀变温场中的各向同性扁球壳在外侧均布压力作用下的屈曲特性，获得的数值解与文献[4](该文不预设挠度的形状函数)用逐步加载法得到的解能很好一致。根据作者调阅的文献，迄今，很少有用打靶法求解功能梯度扁球壳的相关文献。因此，本文在文献[15]工作的基础上，考虑变温效应，运用虚功原理推导了功能梯度圆底扁球壳在均布压力作用下的轴对称变形的位移型几何非线性控制方程，考虑固定夹紧边界条件，用打靶法求解了该边值问题，分析得到了一些壳体的几何非线性力学行为。考虑到工程中更关注壳体的上临界荷载(即承载力)，文末给出了可供设计人员查阅实际参数壳体上临界荷载的一个实用数表和一些实用的数值曲线。

1 功能梯度扁球壳

考虑一中曲面曲率半径为R，厚度为h，圆底半径为a的功能梯度圆底扁球壳(如图1所示)，球坐标系(φ,θ,z)(坐标原点位于壳中曲面上)分别指子午、圆周和厚度方向，z(-h/2≤z≤h/2)坐标与外法线方向一致为正。设球壳材料由陶瓷和金属两种材料沿z坐标方向按照如下体积分数关系融合而成[11]：

式中：Vc和Vm分别指陶瓷和金属材料的体积分数；非负指数k指材料的体积分数指数。

由于构成功能梯度材料的常见组分材料其材料常数对变温依赖性并不显著，再考虑到本文计算数据所考虑的变温幅度较小，因此，下文功能梯度材料常数Peff不考虑变温的影响，并设其沿厚度方向的变化规律[11]为：式中：P指的是不依赖温度的材料常数；下标c和m分别指陶瓷和金属组分。

由式(1)和式(2)不难得到FGM球壳的材料弹性模量E、热膨胀系数α如下：

式中

当z=h/2时，

另外，假设材料泊松比ν为常数[11]。

2 边值问题

2.1 控制方程

对于扁球壳，引入平行于底圆的变量r(r=Rsinφ)和近似关系 dr=Rdφ(cosφ≈1)是方便的。在前述坐标系和轴对称的情况下，壳体上任意点A(φ,θ,z)的径向位移U及横向位移W(即挠度，与z轴正向一致为正)仅是半径r的一元函数。根据经典壳理论，轴对称变形时球壳的应变-位移关系为[12]：

式中，(·),r表示(·)对r的一阶导数。

考虑温度应力的应力-应变关系为：

式中，T为相对初始无应力状态的均匀变温场。

设q为沿壳体中曲面法向均匀分布力集度(与z轴一致为正)，根据虚功原理有：

式中，A为球壳圆底面积域。

将式(4)～式(5)代入式(6)，经变分运算(限于篇幅，文中未给出运算过程)，并考虑如下无量纲量：

式中：w和u分别指中曲面上任一点处的无量纲横向和径向位移；x指无量纲径向坐标；Q指无量纲法向均匀分布力集度；µ指相对初始无应力状态的无量纲变温；

得如下无量纲形式的位移型几何非线性控制方程：

2.2 边界条件

固定夹紧边界条件，x=1时：

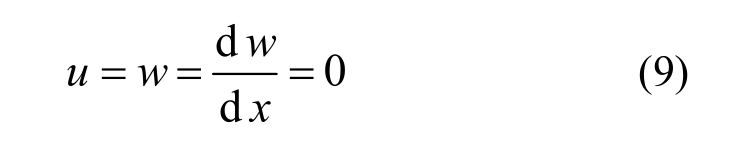
中心对称条件，x=0时：

3 打靶法求解说明

式(7)、式(8)、边界条件式(9)及中心对称条件式(10)为均匀变温场中的、均布压力作用的固定夹紧边功能梯度圆底扁球壳轴对称弯曲变形的常微分方程两点边值问题，易用打靶法计算得到其数值结果。

为了用打靶法求解上述两点边值问题，设：

考虑到式(7)、式(8)及中心对称条件式(10)在x=0处存在奇异性，为保证数值结果收敛，将求解区间取为[Δx1]，其中Δx→0+。则原两点边值问题可化为下述初值问题：

式中：iφ(i=1,2)从非线性方程式(7)、式(8)中得到。由于位移函数在x=0处连续可微，当Δx充分小时，可用Δx处的值代替x=0处的边界条件：

式中：η为x=Δx处的初始挠度(赋值)；Vi(i=1,2,3)为待定参数，由x=1处的边界条件确定。

4 数值结果分析

由于本文研究球壳在外侧压力作用下的屈曲问题，为了直观起见，下文给出的挠度W(r)和压力集度q均以向内凹的一侧为正。

4.1 退化模型结果验证

功能梯度材料的数值分析过程需要沿材料梯度方向划分单元以反映梯度参数分布特性，这将导致更为复杂的应力场，给数值求解带来一定的困难。文献[16]的研究结果表明，二阶一致无网格法是功能梯度材料数值分析的有效方法，该方法有望用来分析功能梯度扁球壳的屈曲力学行为。文献[17]的研究结果对求解功能梯度扁球壳的屈曲过程有很好的借鉴作用。限于现有条件，下面将本文模型退化为各向同性球壳，并用有限元结果来验证打靶法解。由本文模型可知，当k=0或+∞(对后者，与令Ec=Em、αc=αm及任意的k等效)时，功能梯度扁球壳分别退化为弹性模量为Ec或Em的各向同性扁球壳(需要指出的是，当球壳曲率半径R充分大时，扁球壳模型将退化为圆薄板模型，可以用其分析功能梯度圆薄板大挠度问题)。现在考虑文[4]球壳几何参数

限定的各向同性扁球壳，可取底圆半径a=160 mm、壳体厚度h=5 mm、材料泊松比ν=0.3，经换算，球壳曲率半径R≈1057.454 mm，设材料弹性模量E=380 GPa。表1同时给出了该模型的均布外侧压力对应的壳体中心挠度有限元解与打靶法解。从表1(加粗的数据为球壳上临界荷载及对应的壳体中心挠度)可以看出，对于各向同性扁球壳，当壳体接近临界屈曲状态时，打靶法解与有限元解偏离程度有所增大，其余情况二者均能较好一致。需要说明的是，该模型的打靶法解与文献[4]的解高度一致[15]。

4.2 功能梯度扁球壳屈曲平衡路径

为了揭示功能梯度圆底扁球壳屈曲平衡路径，图2在给定材料体积分数指数k=1、球壳圆底半径a=160 mm、厚度h=5 mm和不变温的情况下，分别给出了球壳曲率半径R=700 mm、800 mm、1000 mm、1661 mm、2000 mm、4000 mm和1010mm对应的荷载-挠度曲线。计算表明，当R≥1661 mm时，挠度是荷载的单值函数，结构体现为具有一定初始挠度的圆板。需要特别说明的是，当R大于并接近 1661 mm时，荷载-挠度曲线出现了一个明显的类似“屈服平台”的区段。在该区段，微小的压力变化对应显著的挠度变化，又由于压力与挠度具有一一对应关系，根据这一特点，若开发此类构件作为仪表的弹性元件，可以灵敏且连续(不突变)的显示工程设备的压力工况，对用于自动控制的精密传感元件也应该有一定的开发前景。当R＜1661 mm时，曲线出现了迂回，这是典型的扁壳弹性屈曲的特征，在已有文献中已有介绍，此处不再赘述。需要作出说明的是，在所考虑的范围内，用打靶法求解得到的固定夹紧边圆底扁球壳在均布压力作用下的下临界荷载总是大于零，当边界为不可移铰支撑时，下临界荷载会出现小于零的情况[18]，这些结果与牛顿-样条函数法(见文[3])求解得到的相应结果保持一致。为了揭示材料体积分数指数k对球壳屈曲平衡路径的影响，在给定R/h=200、a/R=0.16和不变温的情况下，图3给出了不同k值的球壳的荷载-挠度曲线。从图可以看出，随指数k的增加，球壳上、下临界荷载均显著减小，但随k的增加，影响程度在减弱。这是因为k较小时，其变化会导致球壳材料中陶瓷和金属含量的显著改变，进而导致球壳弯曲刚度显著变化所致；随着k的增加，其变化对球壳中两种组分材料含量的影响显著减小，从而对球壳弯曲刚度的影响会显著减弱。

为了揭示组分材料模量变化对球壳荷载挠度曲线的影响，也为了便于与图3中的数据作对比，在其他参数不变的情况下，将图 3中的陶瓷(Ec=380 GPa)用氧化锆(Ec=151 GPa)替换，并由图4给出该球壳的荷载挠度曲线。与图3比较可以看出，在金属组分模量不变的情况下，陶瓷组分模量显著减小会导致球壳荷载-挠度曲线的上、下临界荷载都显著减小，除此之外其他变化规律与图3类同。需要说明的是：图3、图4纵坐标给出的是有量纲荷载，进行扁球壳结构设计时，只要壳体几何参数(R、a、h)符合图中比例关系，对不同几何尺寸的壳体，对应的有量纲荷载不会改变。

为了考察均匀变温对壳体荷载-挠度曲线的影响，在给定R/h=200、a/R=0.16和k=1的情况下，图5给出了均匀变温T=120℃、90℃、60℃、30℃、0℃、-30℃、-60℃和-106.7℃这8个变温参数时的壳体荷载-挠度曲线。从图看出，变温对荷载-挠度曲线有显著的影响，温度升高，上临界荷载显著增加，下临界荷载轻微减小(据此不难判断，在球壳稳定性试验中，需要认真分析变温效应)。温度降低，会使壳体上、下临界荷载趋同直至不出现上、下临界荷载。数值计算表明，图中T=-106.7 ℃对应的曲线上、下临界荷载趋于相等。另外易见，温度升高，屈曲点对应的无量纲中心挠度在减小，屈曲过程的跳跃幅度会显著增加，这与文献[11]的结论一致。

4.3 功能梯度扁球壳双稳态构型

为了更加直观一些，在外压力q=3 MPa和不变温时，图6给出了指数k=0.6和k=1对应的壳体屈曲前和屈曲后的稳态构型，为了比较，同时给出了球壳的初始构型。从图6可以看出，当k=0.6时，对应的屈曲前和屈曲后的变形均小于k=1时的相应变形，这里再次清楚地显示了材料体积分数指数k增加时，导致壳体弯曲刚度减小进而导致变形增加的现象。在外压力q=3 MPa和指数k=1时，图7给出了变温T=30℃、0℃和-30℃，对应的壳体屈曲前和屈曲后的稳态构型。为了比较，同时给出了球壳的初始构型。从图7可以看出，壳体屈曲前，随着温度升高，壳体变形明显减小，反之则明显增加。这是因为：1) 温度升高时，由于膨胀的原因，使壳体拱高增加，导致承载力(指上临界荷载)显著增加，和相应的变形(指屈曲前)显著减小(如图5所示)；2)温度升高时，由于膨胀的原因，壳体横向变形沿凸面外法线方向，与荷载引起的向内侧的挠度相抵消。还可以看出，温度升高，屈曲过程对应的跳跃幅度会显著增加，这从另一个角度验证了文献[11]的有关结论。

5 实用数表和曲线

第4节已经说明了壳体几何参数、材料体积分数指数、组分材料弹性模量以及变温对壳体力学特性的影响规律。进一步的计算表明，对给定几何参数a2/(Rh)和材料体积分数指数k的球壳，应用本文模型得到的无量纲荷载-挠度曲线仅取决于组份材料弹性模量比，与弹性模量绝对值无关。为便于工程设计人员在结构设计时选取参数，在Em/Ec=7/38和未变温的情况下，下面通过表2给出一组几何参数a2/(Rh)和一组材料体积分数指数k对应的壳体无量纲上临界荷载Qu(工程中更关注上临界荷载，即承载力)。用表2中的数据可以换算得到实际结构的有量纲上临界荷载。例如：对于a2/(Rh)= 5.12和k=1的壳体，查表得到Qu=213.4882，若取R=1000 mm、a=160 mm和h=5 mm (符合前述几何参数关系)，取Em=70 GPa，Ec=380 GPa(符合前述模量比)，则根据公式Q=12(1-ν2)qa4/(Êh4)(式中Ê见表2的表注，代k=1)，可换算出有量纲的上临界荷载qu=3.53141 MPa；根据设计需要，如需选取其他几何参数和组分材料，如取a=100 mm、h=2 mm，根据a2/(Rh)=5.12(对应R≈976.563 mm)和k=1，仍有Qu=213.4882，若取Em=35 GPa和Ec=190 GPa(符合制表所用模量比7/38，假定这种组分材料存在)，可得qu=0.29624 MPa。如需取其他几何参数和组分材料的球壳，只要符合扁壳条件和模量比Em/Ec=7/38，则仍可根据该表换算得到相应的上临界荷载，方法类同。需要强调的是，对于其他组分材料模量比，表2不再适用。

由于球壳服役环境温度变化是不可避免的，因此，制作类似表2的数表应该会使结构设计工作变得容易。但是，当考虑变温作用时，壳几何参数、材料体积分数指数和无量纲变温的组合种类很多，需要大量的数表来表达。限于篇幅，下面仅在组分材料Em=70 GPa，αm=23×10-6/℃(铝)和Ec= 380 GPa，αc=7.4×10-6/℃(陶瓷)给定的情况下，针对几何参数的四组比例关系(R/h，a/h)=(200，0.13)、(200，0.15)、(200，0.17)和(200，0.19)，并考虑一组体积分数k=0(陶瓷)、0.2、0.4、0.6、1、2、5 和k=+∞(铝，取Ec=70GPa、αc=23×10-6/℃计算)，通过图 8(a)～图8(d)给出了壳体上临界荷载随温度变化的关系曲线。需要说明的是，只要壳体几何参数满足图中所给比例关系，变温与上临界荷载的关系即为图中所示之值。另外，从图8可以看出，变温对壳体上临界荷载影响明显。为了方便设计人员选用图中数据，现以图8(c)为例说明如下：考虑k=2，T=60℃的情况，如取壳体几何参数R=1000 mm、a=170 mm和h=5 mm(符合图 8中的比例关系)，则上临界荷载qu=3.8 MPa；如取R=500 mm、a=85 mm和h=2.5 mm，也符合图中比例关系)，则仍有qu=3.8 MPa。当壳几何参数按照同样的比例增加时，上临界荷载仍然不会改变。因此，工程设计人员根据图8(a)~图8(d)选取所需的壳几何尺寸比例关系和材料体积分数指数之后，再根据所关心的变温参数，就可以找到所关心的壳体上临界荷载。

6 结论

(1) 功能梯度固定夹紧边圆底扁球壳：材料体积分数指数对壳体上、下临界荷载有显著影响，随体积分数指数增加，上、下临界荷载均会显著减小，但影响程度逐渐减弱。

(2) 功能梯度固定夹紧边圆底扁球壳：组分材料弹性模量对壳体上、下临界荷载有显著影响，随组分材料弹性模量减小，上、下临界荷载均会显著减小。

(3) 功能梯度固定夹紧边圆底扁球壳：当壳体几何参数和材料体积分数指数确定时，均匀升温，会使壳体上临界荷载显著增加，使下临界荷载轻微减小。因此，对球壳失稳临界压力(上临界荷载)测试时，需要仔细分析变温影响，但由于球壳的超静定特性，如何消除变温对边界条件的影响存在很大困难。

[1]von Kármán Th. Tsien H S. The buckling of spherical shells by external pressure [J]. Journal of the Aeronautical Sciences, 1939, 7(2): 43―50.

[2]Weinitschke H J. On the stability problem for shallow spherical shells [J]. Journal of Mathematics and Physics,1959, 38(4): 209―231.

[3]叶开沅, 宋卫平. 均布压力作用下圆底扁薄球壳的轴对称屈曲[J]. 兰州大学学报(自然科学版), 1987, 23(2):18―27.Ye Kaiyuan, Song Weiping. Axisymmetrical buckling of thin shallow circular spherical shells under the action of uniform pressure [J]. Journal of Lanzhou University(Natural Science), 1987, 23(2): 18―27. (in Chinese)

[4]严圣平. 扁球壳在均布压力作用下的非线性弯曲问题[J]. 应用力学学报, 1988, 5(3): 21―29.Yan Shengping. Non-linear bending of a shallow spherical shell under uniformly distributed pressure [J].Chinese Journal of Applied Mechanics, 1988, 5(3): 21―29. (in Chinese)

[5]Liu R H, Wang F. Nonlinear dynamic buckling of symmetrically laminated cylindrically orthotropic shallow spherical shells [J]. Archive of Applied Mechanics, 1998, 68 (6): 375―384.

[6]Li Q S, Liu J, Tang J. Buckling of shallow spherical shells including the effects of transverse shear deformation [J]. International Journal of Mechanical Sciences. 2003, 45(9): 1519―1529.

[7]李斌, 董保胜, 刘江华, 等. 均布外压下弹性支撑扁球壳的非线性稳定性分析[J]. 西北工业大学学报, 2006,24(6): 795―799.Li Bin, Dong Baosheng, Liu Jianghua, et al.Approximate critical load in analytic form of uniformly corroded shallow spherical shell under uniform external pressure [J]. Journal of Northwestern Polytechnical University, 2006, 24(6): 795―799. (in Chinese)

[8]张平, 周丽, 邱涛. 用于自适应进气道的扁薄球壳双稳态特性分析[J]. 工程力学, 2013, 30(10): 264―271.Zhang Ping, Zhou Li, Qiu Tao. Analysis of bi-stable behavior of shallow thin spherical shell applied in adaptive inlet [J]. Engineering Mechanics, 2013, 30 (10):264―271. (in Chinese)

[9]李忱, 田雪坤, 王海任, 等. 薄球壳在均布外压与温度耦合作用下的热屈曲研究[J]. 应用数学和力学, 2015,36(9): 924―935.Li Chen, Tian Xuekun, Wang Hairen, et al. Thermal buckling of thin spherical shells under interaction of uniform external pressure and uniform temperature [J].Applied Mathematics and Mechanics, 2015, 36(9):924―935. (in Chinese)

[10] Shahsiah R, Eslami M R, Naj R. Thermal instability of functionally graded shallow spherical shell [J]. Journal of Thermal Stresses, 2006, 29(8): 771―790.

[11] Bich D H, van Tung H. Non-linear axisymmetric response of functionally graded shallow spherical shells under uniform external pressure including temperature effects [J]. International Journal of Nonlinear Mechanics,2011, 46(9): 1195―1204.

[12] Boroujerdy M S, Eslami M R. Nonlinear axisymmetric thermomechanical response of piezo-FGM shallow spherical shells [J]. Archive of Applied Mechanics, 2013,83 (12): 1681―1693.

[13] Boroujerdy M S, Eslami M R. Thermal buckling of piezo-FGM shallow spherical shells [J]. Meccanica,2013, 48(4): 887―899.

[14] Mao Y Q, Ai S G, Chen C P, et al. Nonlinear dynamic response and damage analysis for functionally graded metal shallow spherical shell under low-velocity impact[J]. Archive of Applied Mechanics, 2015, 85 (11):1627―1647.

[15] 赵伟东, 杨亚平. 扁球壳在均布压力与均匀温度场联合作用下的屈曲[J]. 应用数学和力学, 2015, 36(3):262―273.Zhao Weidong, Yang Yaping. Buckling of shallow spherical shells under uniform pressure in uniform temperature field [J]. Applied Mathematics and Mechanics, 2015, 36(3): 262―273. (in Chinese)

[16] 邵玉龙, 段庆林, 李锡夔, 等. 功能梯度材料的二阶一致无网格法[J]. 工程力学, 2017, 34(3): 15―21.Shao Yulong, Duan Qinglin, Li Xikui, et al.Quadratically consistent meshfree method for functionally graded materials [J]. Engineering Mechanics, 2017, 34(3): 15―21. (in Chinese)

[17] 张鹏飞, 罗尧治, 杨超. 薄壳屈曲问题的有限质点法求解[J]. 工程力学, 2017, 34(2): 12―20.Zhang Pengfei, Luo Yaozhi, Yang Chao. Buckling analysis of thin shell using the finite particle method [J].Engineering Mechanics, 2017, 34(2): 12―20. (in Chinese)

[18] 赵伟东, 高士武, 马宏伟. 扁球壳在热-机械荷载作用下的稳定性分析[J]. 应用数学和力学, 2017, 38(10):1146―1154.Zhao Weidong, Gao Shiwu, Ma Hongwei. Thermomechanical stability analysis of shallow spherical shells[J]. Applied Mathematics and Mechanics, 2017, 38 (10):1146―1154. (in Chinese)

THERMOMECHANICAL BUCKLING ANALYSIS OF FUNCTIONALLY GRADED SHALLOW SPHERICAL SHELLS

ZHAO Wei-dong1, GAO Shi-wu1, MA Hong-wei1,2
(1. School of Civil Engineering, Qinghai University, Xining 810016, China;2. School of Environment and Civil Engineering, Dongguan University of Technology, Dongguan 523808, China)

Abstract:Based on the classical shell theory, with the virtual work principle and the variational method, the displacement-type geometric nonlinear governing equations for functionally graded shallow circular spherical shells in uniform temperature field under uniform external pressure were derived. With the shooting method, the numerical results of the axisymmetric deformation of the shells in the clamped boundary condition were obtained.The effects of material volume fraction index, elasticity modulus of constituent materials and uniform temperature field on the equilibrium paths, the upper/lower critical loads and equilibrium configurations of the shells were investigated. The numerical results show that the upper/lower critical load of the shells decreases significantly with the increase of volume fraction index and the decrease of elasticity modulus of constituent materials. The rise of the uniform temperature brings obvious increase of the upper critical load and slight decrease of the lower critical load. A practical numerical table and some practical numerical curves are given for the convenience of designers to select geometry, material, load and temperature parameters.

Key words:functionally graded materials; shallow circular spherical shells; uniform pressure; uniform temperature field; buckling; shooting method

马宏伟(1966―)，男，山西人，长江学者特聘教授，博士，博导，主要从事结构损伤检测和加固，冲击动力学研究(E-mail: tmahw@jnu.edu.cn).

高士武(1985―)，男，陕西人，讲师，硕士，主要从事计算力学与工程仿真研究(E-mail: swgao99e@163.com);

通讯作者：赵伟东(1972―)，男，甘肃人，副教授，硕士，硕导，主要从事结构非线性振动和结构屈曲分析研究(E-mail: zhwd.xbl@163.com).