
图1 管道模型
Fig.1 Model of pipeline
埋地管道工程是基础设施建设中的重要环节,在人民生活和社会生产中扮演着重要角色,被称作生命线工程。地面塌陷对管道的危害主要是引起地面沉降后,导致管道弯曲下沉或悬空,造成管道一些部位应力集中,当应力超过管道强度极限后,管道就会发生破坏。
为全面地分析管道在塌陷作用下的力学响应问题,明确管-土之间的相互作用机理是必要的,已有许多的学者在此方面做了相关研究。Klar等[1]使用弹性连续体来分析管道与土体之间的相互作用,通过迭代计算的等效刚度来分析土体的非线性,解出管道的最大管道弯矩计算表达式。Yuan等[2]建立15个非线性方程组模型,保证了管线的位移、倾角、弯矩和剪力的连续性,研究了静力和动力铺设对土体阻力和管道埋设的影响。Kouretzis等[3]假定管道在均质土壤中的竖向运动机理类似于圆桩的承受侧向荷载的情况,提出了粘性土和颗粒土中最大作用力的设计表达式。
一些学者通过理论分析、数值模拟和模型试验的方法对管道在地面沉降条件下的力学问题进行了分析。Kouretzis等[4]考虑了材料的非线性影响,对地表沉降和隆起情况下的埋地管线的内力和应变进行了分析研究。Kinash和 Najafi[5]利用壳的塑性理论和薄膜理论,将薄壁圆筒管在组合荷载和内压力作用下的响应问题简化为一维模型进行分析,分析了直管段内压、弯矩、纵向力对管道应力-应变分布的影响。Cao等[6]通过构建力学-经验模型,分析了浅埋钢带增强聚乙烯管道在循环荷载作用下导致的路面变形,并与室内试验对比,发现计算结果良好。Luo等[7]采用ABAQUS对在地基沉降的作用下的 PE管道进行数值模拟,分析了管道的应力-沉降变化关系,并讨论了过渡段长度对管道屈服的影响。Peng和Luo[8-9]分析了沉陷作用下薄壁管道的受力状态,得到了在管道变形与地表变形相同条件下的应力应变计算公式。徐龙军等[10]同样采用数值分析方法研究了跨越海底活动断层管道的力学特性。
国内外一些学者采用弹性地基理论对管道在不同条件作用下的内力变形和应力状态进行了相关研究。王峰会等[11]基于Winkler线性理论,考虑了管道自重、内压、上方黄土和黄土的粘聚力等对管道的作用, 建立黄土塌陷作用下管土相互作用的力学模型,并给出了管道失效长度。王小龙等[12]通过利用管道埋地段与悬空段的协调变形特性,解出具有局部悬空段的管道在 Winkler地基模型中的挠度变形和内力计算公式。Wang和Moore[13]根据弹性地基梁的各种闭合解建立了设计方程,提出柔性管弯矩传递和弯矩释放联合简化设计公式的表达式,对控制柔性管道接头结构响应的因素进行了分析。Kim等[14]利用Winkler弹性地基理论,分别对处于3种不同沉陷情况下的最大管道应力进行了解析。Yu等[15]采用Winkler地基梁模型提出了隧道开挖沉降对管道影响的计算公式。Limura[16]根据Winkler理论推导出地基沉降作用下埋地管线部分、裸露部分以及介于二者之间的管线部分的应力计算公式。
Winkler模型比较广泛应用于管线分析,但Winkler模型是假设土介质表面任一点的位移与作用在该点的应力成正比而与作用在其它各点的应力无关,其本身存在周围土体连续性上的缺陷,故本文选用Vlasov弹性地基梁模型,并考虑梁宽度对管道变形产生的三维影响来构建塌陷区管道的力学模型,得到了塌陷作用影响下的管道挠度变形和内力计算公式以及管道的应力的计算公式。
地面塌陷会致使管道下方的土体发生流失或者沉陷,出现部分管道悬空的现象。未悬空部分管道的力学模型可以简化为弹性地基上的连续梁模型。考虑到模型整体具有对称性,因此建立以悬空段管道中点为坐标原点的直角坐标系,假设管道在土体发生塌陷以前沿轴向是水平埋设的,令管道塌陷前的轴向方向为x方向,垂直于x轴的方向为y方向,即y轴与模型的对称轴重合,如图1所示。以y轴为模型的对称轴,把模型分为互相对称的两部分,只取模型的右半部进行具体分析。

图1 管道模型
Fig.1 Model of pipeline
埋地段的管道受力模型如图2所示,并建立埋地管道的x1-y1局部坐标。假设埋地段管道为置于弹性地基上的半无限长弹性地基梁。取B点以右的埋地段管道作为研究对象,B点以左的管道悬空段对B点的作用力用剪力P和弯矩M代替。埋地段管道还承受竖向荷载,包括管道上方的填土产生的土压力,管道自身重量以及管道内介质所产生的作用力,可用均布荷载q1代替。
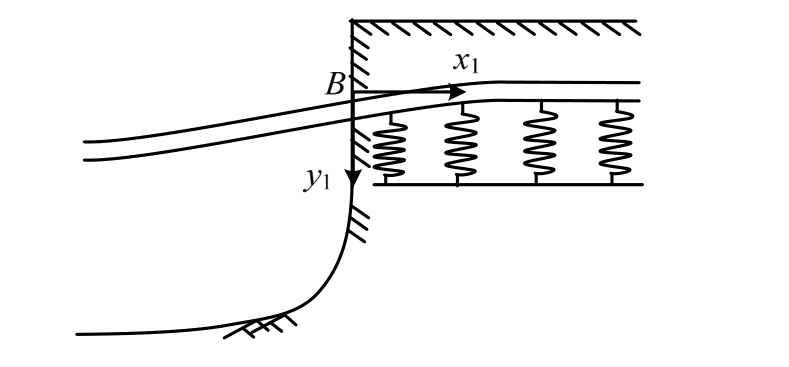
图2 埋地管道模型
Fig.2 Model of buried pipeline
在平衡状态下局部坐标系x1-y1中,可依据Vlasov弹性地基理论构造半无限长弹性地基梁的挠度曲线方程[17-18]:
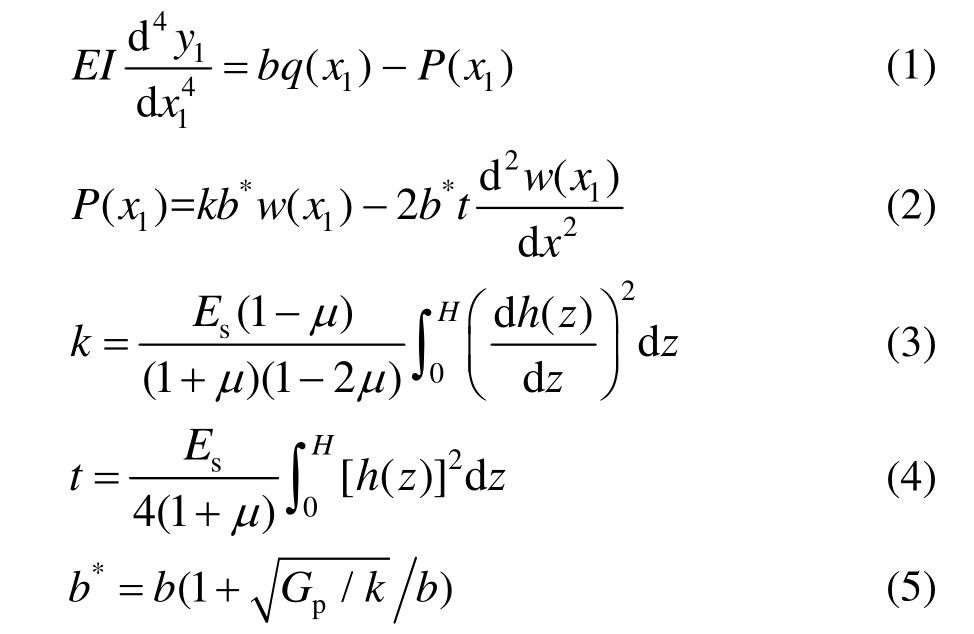
式中:EI为管道的抗弯刚度;P(x1)为管道在Vlasov地基上受到的地基反力;q(x1)为管道在Vlasov地基上受到的竖向荷载;k为地基弹性抗力系数;*b为Vlasov模型中梁的有效作用宽度;Es为土体的弹性模量;H为管道埋置深度。
根据弹性地基梁的相关内容,Vlasov地基模型中的埋地段管道应符合以下关系式:
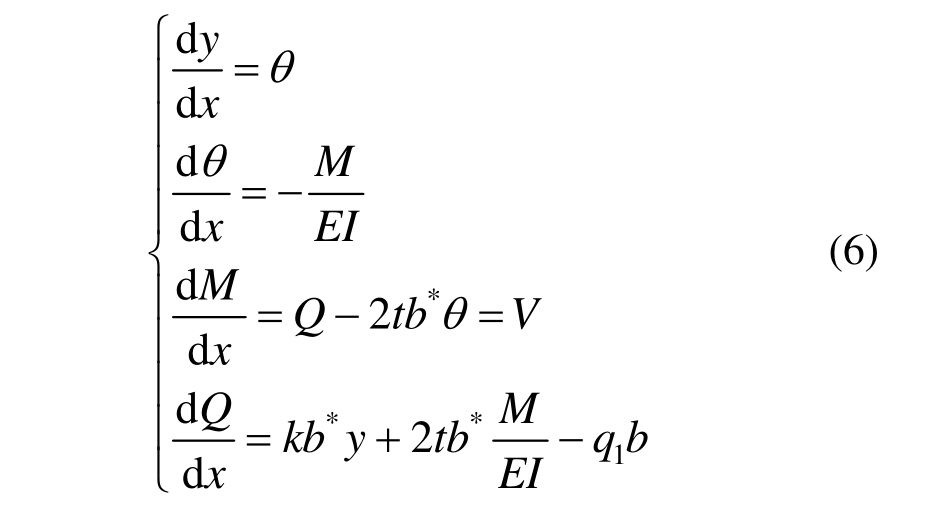
式中:V为传统剪力;Q为广义剪力。
将式(6)写成矩阵形式:
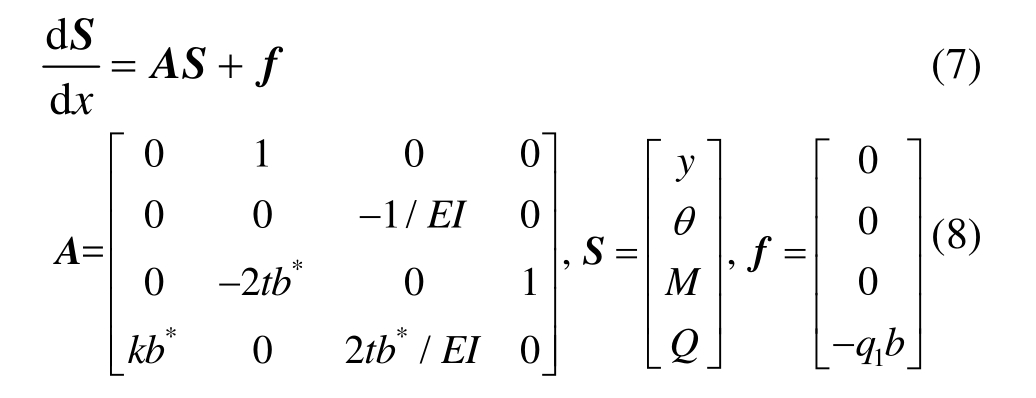
将式(7)的两边都进行拉普拉斯变换(Laplace Transform),经整理可得:
两边左乘![]() 可得:
可得:
其中:



对式(10)进行拉普拉斯逆变换(Inverse Laplace Transform),可得:

式中:


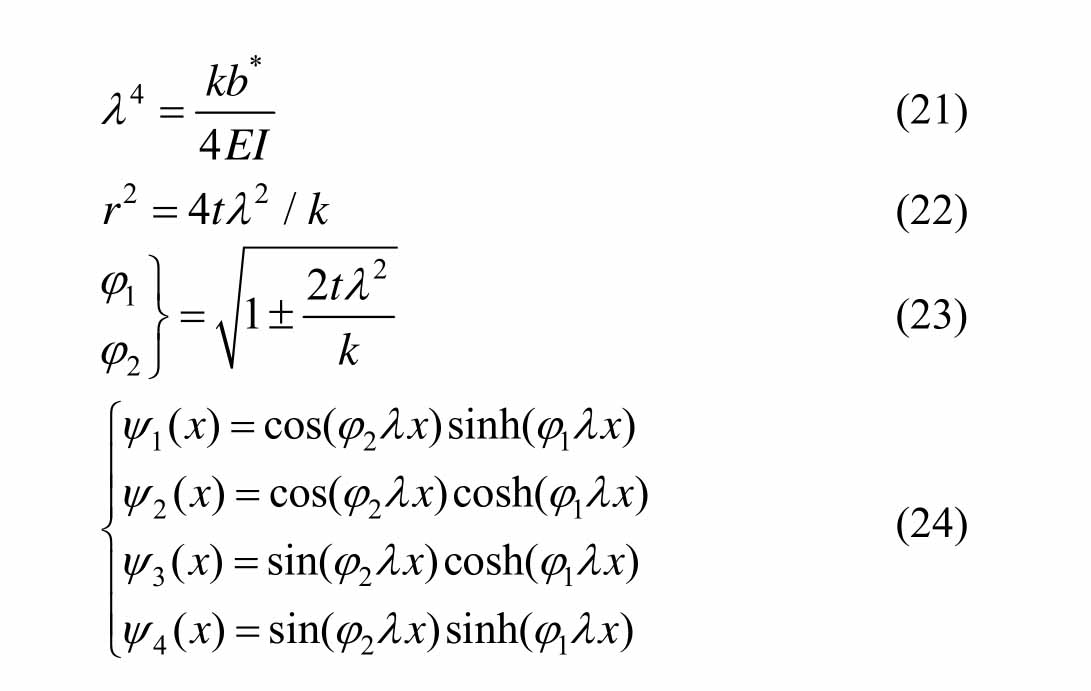
结合模型的整体坐标,将埋地段管道的位移与内力关系写成增广矩阵形式,即为:


式(25)中的5×5阶方阵U1,即为 Vlasov地基模型埋地段管道的场传递矩阵。
依据管道的几何对称性和连续性,悬空段管道可简化为在两端施加弯矩m的简支梁,悬空段管道的受力模型如图3所示。在平衡状态下建立如图3的局部坐标系x2-y2,其中y2轴为图1中A点的竖向垂线,x2轴上的A点、B点均有y2方向的位移,且两点的位移相同。

图3 悬空管道模型
Fig.3 Model of suspended pipeline
与埋地段管道相似,根据材料力学的相关内容,悬空段管道应满足下列关系式:

以简支梁支座位置的状态向量为初始状态向量,可写成增广矩阵的形式。

式(32)中的5×5矩阵U2,即为悬空段管道的场传递矩阵。
根据建立的模型以及坐标,整个管道模型的传递矩阵可表示为:

根据材料力学的相关内容可知,B点(x=l/2处)的状态向量为:

式中:y0和M0是未知的,可根据埋地段管道末端的边界条件,即埋地段管道末端的转角θ和剪力Q为零,求出相应的值,其值可利用相关数学软件计算所得。
土洞塌陷作用下的管线主要承受以下应力:① 内部流体压力引起的环向应力和轴向应力;② 温度变化产生的轴向应力;③ 管道弯曲引起的轴向应力。
内压引起的切向应力σpt(参照图4)可以通过下式计算[19]:


图4 内压引起的切向应力
Fig.4 Tangential stress of pipeline induced by internal pressure
内压引起的轴向应力σpa可以表示为:
式中,μ为管材的泊松比。
通常情况下,塌陷时的管道温度与铺设安装时的管道温度并不相同。这两种环境下的温差会使管道发生膨胀或者收缩,进而产生拉应力或者压应力,可表示为[20]:
由于不均匀沉降作用,管道会被迫发生轴向变形,进而管道会产生轴向应力。根据材料力学的相关内容,管道处于纯弯曲状态时,其横截面上任一点的正应力bσ可表示为:
结合上文推导出的 Vlasov弹性地基梁弯矩计算公式,将其代入式(39)中,即可得到管道弯曲变形引起的轴向应力表达式。
综上所述,管道的轴向应力aσ,环向应力cσ,径向应力rσ可分别表示为:

则管道的von Mises应力可由下式计算求得:

为保证管线的正常运行,根据von Mises屈服准则可知,管道应满足:
式中,sσ为管材的屈服强度。
根据Vlasov建立的管土相互作用模型,管道和地基土都是建立在弹性假设的基础之上的。因此,式(42)也是采用本文所构建模型计算管道变形与内力的适用条件。
依据文献[21]的相关研究,分别对悬空段长度为 35 m、45 m、55 m的情况进行计算。管道外径1.016 m、壁厚 0.0175 m;管道为 X70型钢管,管道的弹性模量取 210 GPa,管道屈服强度为485 MPa;管材密度为 7850 kg·m-3,土体密度为1700 kg·m-3;土体的弹性模量为20 MPa,具体计算参数可由式(3)和式(4)计算求得,其值列于表1。
表1 计算参数
Table 1 Calculation parameters

地基基床系数k/(MN·m-3)地基土荷载传播率t/(MN·m-1)悬空段均布荷载q/(kN·m-2)5.03 5.8 11.5
分别采用Winkler模型和Vlasov模型方法进行计算,并将沉降值计算结果列于表2。
表2 沉降值计算结果
Table 2 Calculated results of subsidence

塌陷尺寸/m结果类型 数值模拟计算结果Y0/m Winkler模型计算结果Y1/m Vlasov模型计算结果Y2/m 35 0.103 0.108 0.103 45 0.203 0.225 0.213 55 0.37 0.423 0.402
试验中的管道应力主要来自于管道的弯曲。按式(39)计算管道的轴向应力,当塌陷尺寸为35 m、45 m、55 m时的管道所受的最大轴向应力分别为141 MPa、240 MPa、367 MPa,管道处于弹性变形范围内,可运用弹性地基梁模型来进行计算。相比于通过 Winkler模型分析管道在塌陷作用下的变形,Vlasov模型的基本假设考虑了土体的连续性,同时也考虑了荷载与地基反力在横断面上作用范围的不同,因而其计算结果也更贴近实际。
依据本文推导所得的计算公式,分析了管道上方存在上覆土情况下的管道尺寸、管道埋深、塌陷区尺寸、以及管材这四方面因素对管道最大沉降以及最大应力的影响。分析过程中的基本参数选取:地基基床系数取 16.8 MN·m-3;管径分别取0.325 m、0.457 m、0.61 m、0.813 m。为更清晰直观地反映管道的变形以及受力的变化规律,定义管道最大沉降率η和最大应力比φ:
式中:Smax为管道发生的最大沉降;D为管道外径。
式中:σmax为管道最大应力;sσ为管道屈服应力。
图5、图6分别绘出了管道最大沉降与管道最大应力随着管道尺寸变化的趋势。为使得结果趋势更加直观,将横坐标取管道尺寸率(D/t,t为管道壁厚),将纵坐标分别取为管道最大沉降率和管道最大应力比。
图7、图8分别绘出了管道最大沉降与管道最大应力随着管道埋深变化的趋势。为使得结果趋势更加直观,将横坐标取管道埋置率(H/D,H为管道埋深),将纵坐标分别取为管道最大沉降率和管道最大应力比。
图7表明管道的最大沉降率与管道埋置率之间存在良好的线性关系。图 8显示管道的最大应力比与埋置率之间也存在良好的线性关系。随着H/D增长,管道所承受的土压力也会随之增长,使得管道所承受的荷载加大,进而使管道的变形和内力增长。
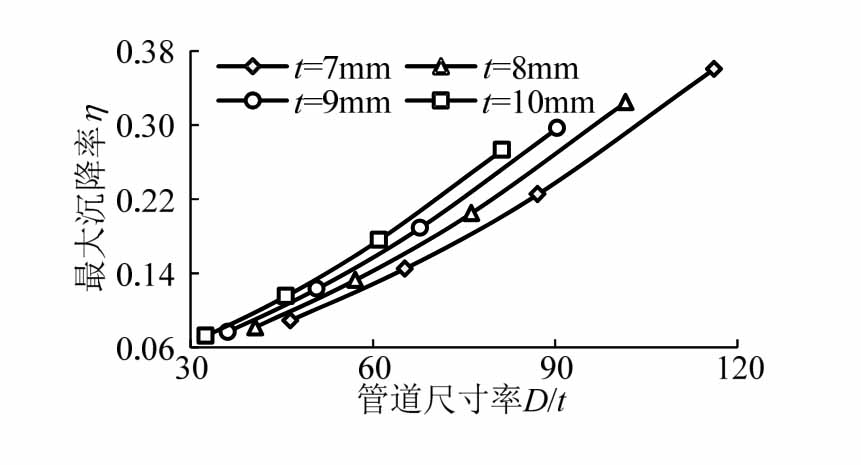
图5 管道尺寸率对最大沉降率的影响
Fig.5 Influence of max sedimentation rate due to ratio between pipe diameter and thickness

图6 管道尺寸率对最大应力比的影响
Fig.6 Influence of m ax stress rate due to ratio between pipe diameter and thickness

图7 管道埋置率对最大沉降率的影响
Fig.7 Influence of max sedimentation rate due to ratio between pipe depth and diameter

图8 管道埋置率对最大应力比的影响
Fig.8 Influence of max stress rate due to ratio between pipe depth and diameter
图9、图10分别绘出了管道最大沉降与管道最大应力随着塌陷尺寸变化的趋势。为使得结果趋势更加直观,将横坐标取塌陷尺寸率(L/D,L为悬空区域的长度),将纵坐标分别取为管道最大沉降率和管道最大应力比。
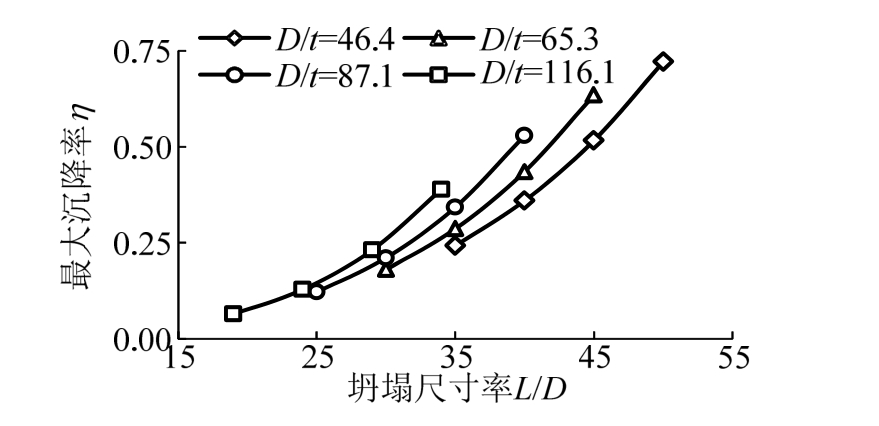
图9 塌陷尺寸率对最大沉降率的影响
Fig.9 Influence of max sedimentation rate due to ratio between collapse size and pipe diameter
图9表明管道的最大沉降率随着塌陷尺寸率的增长呈现出具有一定规律性的非线性增长。图10表明坍塌尺寸率对管道的最大应力比的影响较为显著。随着L/D增长,土体塌陷区域的范围扩大,造成管道的悬空段长度的增长,使得管道的变形和内力急剧增长,L/D是影响管道安全运行的重要因素。

图10 塌陷尺寸率对最大应力比的影响
Fig.10 Influence of max stress rate due to ratio between collapse size and pipe diameter
图11、图12分别绘出了管道最大沉降与管道最大应力随着管道材料的弹性模量变化的趋势。为使得结果趋势更加直观,将横坐标取管道材料的弹性模量,将纵坐标分别取为管道最大沉降率和管道最大应力比。分析表明,管道的最大沉降率随着管材弹性模量的增长呈现出具有一定规律性的减小趋势。图 12表明管道的最大应力比基本不受到管材弹性模量的影响。

图11 管道材料对最大沉降率的影响
Fig.11 Influence of max sedimentation rate due to elastic modulus of pipe

图12 管道材料对最大应力比的影响
Fig.12 Influence of max stress rate due to elastic modulus of pipe
(1) 采用Vlasov弹性地基梁理论,提出了塌陷作用下管道挠曲变形以及内力的计算方法。应用Vlasov地基梁模型,考虑到地基土中的连续性问题,同时还考虑了地基梁宽度对于变形的影响。
(2) 与Winkler模型相比,采用Vlasov模型计算出的结果具有更高的精度,可更好地满足实际工程中对管道运行能力的评估需求。
(3) 对管道在坍塌作用下应力状态进行的分析,为判断管道强度是否失效提供了依据;明确了使用Vlasov模型计算管道变形与内力的适用范围。
(4) 分析了管道尺寸、管道埋深、塌陷区尺寸、以及管材这四方面因素对管道最大沉降以及最大应力的影响,探讨了埋地悬空管道在坍塌作用下受力变形规律。
[1]Klar A, Elkayam I, Marshall A M. Design oriented linear-equivalent approach for evaluating the effect of tunneling on pipelines [J]. Journal of Geotechnical &Geoenvironmental Engineering, 2015, 142(1): 04015062.
[2]Yuan F, Wang L, Guo Z, et al. Analytical analysis of pipeline–soil interaction during J-lay on a plastic seabed with bearing resistance proportional to depth [J]. Applied Ocean Research, 2012, 36(3): 60-68.
[3]Kouretzis G P, Krabbenhoft K, Sheng C, et al. Soilburied pipeline interaction for vertical downwards relative offset [J]. Canadian Geotechnical Journal, 2014,51(10): 1087-1094.
[4]Kouretzis G P, Karamitros D K, Sloan S W. Analysis of buried pipelines subjected to ground surface settlement and heave [J]. Canadian Geotechnical Journal, 2015,52(8): 1058-1071.
[5]Kinash O, Najafi M. Large-diameter pipe subjected to landslide loads [J]. Journal of Pipeline Systems Engineering & Practice, 2012, 3(1): 1-7.
[6]Cao Z, Han J, Xu C. Road surface permanent deformations with a shallowly buried steel-reinforced high-density polyethylene pipe under cyclic loading [J].Geotextiles & Geomembranes, 2016, 44(1): 28-38.
[7]Luo X, Lu S, Shi J, et al. Numerical simulation of strength failure of buried polyethylene pipe under foundation settlement[J]. Engineering Failure Analysis,2015, 48(1): 144-152.
[8]Peng S, Luo Y. Determination of stress field in buried thin pipelines resulting from ground subsidence due to longwall mining [J]. Mining Science and Technology,1988, 6(2): 205-216.
[9]Luo Y, Peng S S, Chen H J, et al. Protection of pipelines affected by surface subsidence [J]. TRANSACTIONS,1998, 302: 98-103.
[10] 徐龙军, 刘庆阳, 谢礼立. 海底跨断层输气管道动力特性数值模拟与分析[J]. 工程力学, 2015, 32(12): 99-107.Xu Longjun, Liu Qingyang, Xie Lili. Numerical simulation and analysis for submarine pipeline systems crossing active strike-slip fault [J]. Eengineering Mechanics, 2015, 32(12): 99-107. (in Chinese)
[11] 王峰会, 赵新伟, 王沪毅. 高压管道黄土塌陷情况下的力学分析与计算[J]. 油气储运, 2004, 23(4): 6-8.Wang Fenghui , Zhao Xinwei, Wang Huyi. Failure of high pressure pipeline under collapse of loess [J]. Oil &Gas Storage and Transportation, 2004, 23(4): 6-8. (in Chinese)
[12] 王小龙, 姚安林. 埋地钢管局部悬空的挠度和内力分析[J]. 工程力学, 2008, 25(8): 218-222.Wang Xiaolong , Yao Anlin. Deflection and internal force analysis of buried steel pipelines in partial hanging [J].Eengineering Mechanics, 2008, 25(8): 218-222. (in Chinese)
[13] Wang Y, Moore I D. Simplified Design Equations for Joints in Buried Flexible Pipes Based on Hetényi Solutions [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 140(3): 04013020.
[14] Kim H S, Kim W S, Bang I W, et al. Analysis of stresses on buried natural gas pipeline subjected to ground subsidence [C]// The 1998 International Pipeline Conference, IPC. Part 2(of 2), Haifa, Israel. American Society of Mechanical Engineers, U.S., 1998: 749-756.
[15] Yu J, Zhang C, Huang M. Soil-pipe interaction due to tunnelling: Assessment of Winkler modulus for underground pipelines [J]. Computers and Geotechnics,2013, 50(1): 17-28.
[16] Limura S. Simplified mechanical model for evaluating stress in pipeline subject to settlement [J]. Construction and Building Materials, 2004, 18(6): 469-479.
[17] Selvadurai A P S, Gladwell G M L. Elastic Analysis of Soil-Foundation Interaction [M]. Amsterdam, Elsevier Scientific Pub. Co, 1979: 71-71.
[18] Vlasov V Z. Beams, Plates and Shells on Elastic foundations [R]. Jerusalem Israel Program for Scientific Translations, Jerusalem, 1966.
[19] GB 50251—2015, 输气管道工程设计规范[S]. 北京:中国计划出版社, 2015.GB 50251—2015, Code for design of gas transmission pipeline engineering [S]. Beijing: China Planning Press,2015. (in Chinese)
[20] Guidelines for the design of buried steel pipe [S].Washington D.C. American Lifelines Alliance, 2001.
[21] 张鹏, 魏韡, 崔立伟, 等. 地表冲沟条件下悬空管道的力学模型与延寿分析[J]. 天然气工业, 2014, 34(4):142-148.Zhang Peng, Wei Wei, Cui Liwei, et al. A mechanical model and life extension analysis of the suspended pipelines under the condition of geological gulch [J].Natural Gas Industry, 2014, 34(4): 142-148. (in Chinese)
MECHANICAL ANALYSIS OF BURIED SUSPENDED PIPELINE UNDER THE ACTION OF COLLAPSE